1 Introduction

Roller bearings are the essential components of rotating transmission systems. A higher failure rate of double row cylindrical roller bearings is caused by rough operation conditions. 30% faults of rotating machinery are caused by the bearings [1]. The defects in the double row cylindrical roller bearings will cause safety problems for the whole system. It is useful to study the dynamics of defective double row cylindrical roller bearings, especially for the defects with the actual shapes rather than the simplified shapes including the rectangles and circles.

Many researchers have conducted different dynamic models and detection methods of local defects in the bearings [2,3,4,5,6,7,8,9]. Liu et al. [10, 11] established dynamic models of bearing with the defect including the time-varying contact stiffness (TVCS), edge shapes of the defect, and rotor deformations on the vibrations. In their works, they modeled the defect with a rectangle shape. Chen and Kurfess [12] established a dynamic model to estimate the effects of rectangle shape defect sizes on bearing vibrations. Gao et al. [13] modeled the defect with a rectangle shape and investigated the bearing dynamics of the bearing including the defect on the rings. Cao et al. [14] established a defect model with a rectangle shape and introduced the defect model to the bearing dynamic model to investigate the effects of deflections and defects on the bearing vibrations. Niu et al. [15] presented a dynamic model of roller bearing including the bearing slipping, size, and defect of roller. They also modeled the roller defect with a rectangle shape. Liu and Wang [16] gave a dynamic model including the defect roughness to analyze the effect of the roughness on the vibrations. The defect was also modeled with the rectangle shape [17]. Arslan and Aktu [18] conducted a dynamic model including the rectangle shape defect of ball to evaluate the effect of the defect on the vibrations. Patil et al. [19] gave a bearing dynamic model including the rectangle shape defect to detect the defect vibrations. Patel and Upadhyay [20] gave a bearing model including the deflection of roller, clearance, and rectangle shape defect of roller. Patra et al. [21] introduced the dynamic model of bearing-rotor system including the rotor unbalance forces to discuss the vibrations. Ali et al. [22] presented a combined model using the mass-lumped and finite element models of roller bearing with the rectangle shape defect. Jiang et al. [23] gave a method to describe the roller movement during the defect area taking into account the ring groove radius. Francesco et al. [24] conducted experiments on bearings with different sloped defect edges. They pointed the defect edge characteristics have a remarkable effect on the bearing vibrations. Wang et al. [25] presented an improved defect modeling model by analyzing the bearing vibration and acoustic signals. It can be found that all the above studies use the rectangle shape to model the bearing defect. Moreover, some scholars used hexagons [26], bias rectangles [27], three-dimensional cubic [23, 28], and circular shapes [26] to establish the bearing defect. However, unfortunately, they still use regular shapes to model the bearing defect.

Through the above analysis, it can be found that most previous works focused on studying the single-row bearing dynamic modeling method. The double row cylindrical roller bearings have a more complex structure, which will cause different dynamic characteristics. Moreover, most previous works simplified the defects to a regular shape to estimate the vibrations of the bearing. In fact, the actual defects are irregularly shaped. The regular shapes cannot accurately describe the shape of the bearing defect. Only by getting rid of the restriction of regular shapes can we accurately describe faults. In this paper, an irregular shape defect modeling method and a dynamic model of a double row cylindrical roller bearing with irregular shape defects are proposed. The dynamic model considers the supporting stiffness of the outer ring and the dynamics of the cage, making it better able to reflect the dynamics of the bearing. Moreover, the proposed dynamic model can be used to study the special dynamics of double row cylindrical roller bearings. In addition, for obtaining accurate calculation results of a defective double row cylindrical roller bearing, the defect shape should be the actual shape rather than the simplified shape, which was not considered in the previous studies. The effects of the bearing load, rotating speed, and different independent defect shapes on the vibrations are studied. The comparisons of vibrations between the independent defect shape and simplified defect shape are discussed.

2 An irregular defect shape model for double row cylindrical roller bearings

The dynamics of double row cylindrical roller bearings have strong nonlinearities. Firstly, the contact between the roller and the ring is Hertzian contact theory, and the relationship between the contact force and contact deformation is not linear. Secondly, the revolution of the bearing roller causes changes in the loaded area, which intensifies the non-linearity of the bearing. In addition, the bearing clearance is also one of the sources of bearing nonlinearity. Finally, when the bearing has a defect, especially in the case of an irregular shape defect, the contact deformation and contact stiffness between the roller and ring in the defect area are both nonlinear, which exacerbates the nonlinearity of the bearing [29, 30]. In this work, the nonlinearity sources mentioned above are all considered, and a dynamic model of a double row cylindrical roller bearing with an irregular shape defect is proposed.

2.1 Modeling irregular defect shape

Figure 1 gives independent and simplified defect profiles. The defect edge will generate elastic deformation when the roller contacts with the defect [31], which will change the contact characteristics between the roller and the defective ring. However, the effect of defect edge elastic deformation on the bearing vibration is not the study focus of this work. Thus, the elastic deformation of the material at the defect edge is not considered in this work. Because of the decrement of material of the defect zone on the ring surface, the roller ECL between the roller and ring will decrease. It can cause the TVCS features. The modeling method of TVCS caused by the defect is as follows. (1) The effective contact length (ECL) between the roller and ring should decrease. (2) The ring cross-section area and the area moment of inertia are changed [32, 33].

Fig. 1
figure 1

A diagram of a defect profile, b circle cross-section profile of rectangular defect, and c radial cross-section profile of defect

Full size image

For simulating the time-varying stiffness features caused by the defect, the main issue is the method for simulating the changes in ECL and cross-section characteristics. The traditional defect modeling simulated the shape of a defect by simplifying the shape of defect to be a rectangle and a circle. The simplified form was used to simulate the ECL and cross-section characteristics and calculate the TVCS features between the roller and ring. In fact, the simplified shape methods are not accurate as discussed in the above descriptions.

In the model of independent defect shape, the ECL and cross-section characteristics are represented by the function rather than the constant values. Therefore, Le = fL(θ), A = fA(θ), and I = fI(θ); where Le is the ECL; A and I are the cross-section area and the moment of inertia; fL(θ), fA(θ), and fI(θ) are the expressions of ECL, cross-section area, and moment of inertia; θ is the angular displacement given in Fig. 1b. The values of fL(θ), fA(θ), and fI(θ) are based on the severity of defect.

Two rectangles BCDE and B'C'DE are given in Fig. 1c, which are used to explain the changes in the defect area. Then, fA(θ) and fI(θ) are

$$ f_{A} (\theta ) = S_{BCDE} = Lh_{a} (\theta ) $$
(1)
$$ f_{I} (\theta ) = I_{B^{\prime}C^{\prime}DE} = \frac{{h_{I} (\theta )^{3} L}}{12} $$
(2)

where SBCDE is the area of rectangle BCDE; ha(θ) is the rectangle BCDE height; IB'C'DE and hI(θ) are the rectangle B'C'DE moment of inertia and height; and L is the width of the roller.

For the simple rectangular defects, the cross-section area at θ is

$$ \begin{array}{*{20}c} {A_{\theta } = 2L_{{\text{s}}} h_{z} - L_{s} h_{s} } & {\theta \in [} \\ \end{array} \theta_{start} ,\theta_{end} ] $$
(3)

where Ls and hs are the defect length and depth. The change (δx) of neutral axis of inertia moment is

$$ \delta_{x} = \frac{{(h_{z} - 1/2h_{S} )L_{S} h_{S} }}{{A_{\theta } }} $$
(4)

Then, the inertia moment of neutral axis A'F' for the defect condition is

$$ \begin{array}{*{20}c} {I_{\theta } = \frac{{2Lh_{z}^{3} }}{3} + 2Lh_{z} \delta_{x} - (\frac{{L_{s} h_{s}^{3} }}{12} + L_{s} h_{s} (h_{z} - 0.5h_{z} + \delta_{x} )^{2} )} & {\theta \in [\theta_{start} ,\theta_{end} ]} \\ \end{array} $$
(5)

Therefore, the corresponding thickness of rectangle ha(θ) and corresponding inertia moment of rectangle hI(θ) are

$$ h_{a} (\theta ) = \frac{{A_{\theta } }}{L} $$
(6)
$$ h_{I} (\theta ) = (\frac{{12I_{\theta } }}{L})^{\frac{1}{3}} $$
(7)

Equations (1) and (2) can be also written as

$$ f_{A} (\theta )\begin{array}{*{20}c} { = 2L_{{\text{s}}} h_{z} - L_{s} h_{s} } & {\theta \in [} \\ \end{array} \theta_{start} ,\theta_{end} ] $$
(8)
$$ f_{I} (\theta )\begin{array}{*{20}c} { = \frac{{2Lh_{z}^{3} }}{3} + 2Lh_{z} \delta_{x} - (\frac{{L_{s} h_{s}^{3} }}{12} + L_{s} h_{s} (h_{z} - 0.5h_{z} + \delta_{x} )^{2} )} & {\theta \in [\theta_{start} ,\theta_{end} ]} \\ \end{array} $$
(9)

The defect coefficients are

$$ \nu_{L} = \frac{{L_{s} }}{L} $$
(10)
$$ \nu_{h} = \frac{{h_{s} }}{{2h_{z} }} $$
(11)

where νL and νh are the ratios of the defect length and depth at θ. Based on Eqs. (3) to (9), the effective section area is

$$ A_{\theta } = 2Lh_{z} (1 - \nu_{L} \nu_{h} ) $$
(12)

Based on Eqs. (6) to (7), the equivalent inner ring thickness ha(θ) is

$$ h_{a} (\theta ) = 2(1 - \nu_{L} \nu_{h} )h_{z} $$
(13)

Based on Eqs. (5) to (9), the inertia moment of the rectangle hI(θ) is

$$ h_{I} (\theta ) = 2h_{z} (K_{I} )^{\frac{1}{3}} $$
(14)
$$ K_{I} { = }\frac{{1{ - }\nu_{h}^{5} \nu_{L}^{3} + (4\nu_{h}^{2} - 6\nu_{h}^{3} - 5\nu_{h}^{4} )\nu_{L}^{2} - (5\nu_{h} + 4\nu_{h}^{3} + - 6\nu_{h}^{2} )\nu_{L} }}{{(1 - \nu_{L} \nu_{L} )^{2} }} $$
(15)

Therefore, the relation between ha(θ) and hI(θ) is

$$ h_{a} (\theta ) = K_{r} h_{c} (\theta ) $$
(16)
$$ K_{r} = \frac{{K_{I}^{\frac{1}{3}} }}{{1 - \nu_{L} \nu_{L} }} $$
(17)

Based on the defect coefficient νL and νh, the ECL, cross-section area, and moment of inertia are

$$ L_{e} (\theta ) = L(1 - \nu_{L} ) $$
(18)
$$ A_{\theta } = Lh_{c} (\theta ) = 2L(1 - \nu_{L} \nu_{L} )h_{x} $$
(19)
$$ I_{\theta } = \frac{{h_{I} (\theta )^{3} L}}{12} = \frac{{(h_{I} (\theta ))^{3} K_{I} L}}{12} $$
(20)

Equations (16) to (18) can be used for the healthy and defective conditions. When the ring is healthy, νL = 0 and KI = 1; When the shape of defect is complex, νL is a function of θ; and νh is the function of defect depth.

2.2 Calculating TVCS of defect with an irregular shape

The contact relationship of the double row cylindrical roller bearing is given in Fig. 2. When the ring has a defect, the roller-ring contact line will be discontinuous. The actual ECL is less than the roller length. The change of ECL will cause the TVCS changes, which affect the vibrations of the double row cylindrical roller bearing.

Fig. 2
figure 2

A diagram of the roller-ring contact relationship

Full size image

In previous studies, most researchers defined the defect shapes as regular, square, or circular ones. In actual situations, the shape of defect is complex and irregular. To solve this question, the TVCS calculation method of the defect with the independent shape of a double row cylindrical roller bearing is proposed.

Compared with different stiffness calculation methods, the Palmgren's stiffness calculation method is simple and accurate [34,35,36], which is

$$ k = 8.06 \times 10^{4} L_{e}^{\frac{8}{9}} $$
(21)

where Le is the roller effective contact length.

During the processing of roller through the defect area, there are two cases: (1) the roller-ring deformation is less than the defect depth. (2) The roller-ring deformation is bigger than or equal to the defect depth. There will be a displacement jump for the roller at this moment.

When the roller-ring deformation is less than the defect depth, as shown in Fig. 3a, there are three cases: (1) when the roller is coming into the defect, the ECL changes to be smaller than the roller length (because of the existence of defect); (2) when the roller is located into the defect, because the defect depth is large and the time-varying contact deformation is small, the surface of roller doesn’t contact with the defect bottom; thus, the part of roller cannot be supported by the ring; (3) when the roller is coming out the defect, the ECL changes to be equal to the one of health condition.

Fig. 3
figure 3

a Roller-ring deformation is less than the defect depth and b roller-ring deformation is bigger than or equal to defect depth

Full size image

In case 1, the ECL changes to be equal to the one of health condition. The TVCS is

$$ k = 8.06 \times 10^{4} L^{\frac{8}{9}} $$
(22)

In case 2, the defect depth is large; and the time-varying contact deformation is small, the surface of roller does not touch the bottom of defect. The TVCS is

$$ k = 8.06 \times 10^{4} (L - L_{s} )^{\frac{8}{9}} $$
(23)

The TVCS of case 3 is the same as that case 2.

In Fig. 3b, the roller-ring deformation is bigger than or equal to the defect depth. For cases 1 and 3, the deformation of roller and defect is less than the defect depth. For case 2, the roller-ring deformation is bigger than the defect depth. The roller will contact with the bottom of defect. Therefore, the ECL is approximately equal to the ECL of health conditions. However, the roller has a displacement at this defect. The deformations of inner/outer ring of jth roller are

$$ \left\{ {\begin{array}{*{20}l} {\delta_{j}^{in} = \left[ {x^{{{\text{in}}}} - x_{j}^{{\text{r}}} } \right]\cos \theta_{j} + \left[ {y^{{{\text{in}}}} - y_{j}^{{\text{r}}} } \right]\sin \theta_{j} - C_{{\text{r}}} \, } \hfill \\ {\delta_{j}^{out} = \left[ {x_{j}^{r} - x^{{{\text{out}}}} - h_{xs} } \right]\cos \theta_{j} + \left[ {y_{j}^{{\text{r}}} - y^{{{\text{out}}}} - h_{xy} } \right]\sin \theta_{j} - C_{{\text{r}}} } \hfill \\ \end{array} } \right. $$
(24)

where, xin and yin are the inner ring displacements in x and y directions; xout and yout are the outer ring displacements in x and y directions; xjr and yjr are the jth roller displacements in x and y directions; θj and Cr are the jth roller position angle and bearing clearance; hxs and hys are the defect depth. Those two situations in this paper can be simulated by the above methods.

The time-varying effective length and depth are used to describe the defect precisely at some moment. The irregular defect is depicted in Fig. 4. Because of the irregular shape of defect, the effective length and the depth are not a constant rather than a function in this paper. The discrete sampling and fitting methods are used to obtain the length and depth of defects. In Fig. 4, l1 to ln is the discrete length of defect at different positions; h1 to hn is the discrete depth of defect at different positions. Therefore, the functions of length and depth are

$$ \begin{array}{*{20}c} {L_{s} (\theta ) = a_{n} \theta^{n} + a_{n - 1} \theta^{n - 1} + \cdots + a_{2} \theta^{2} + a_{1} \theta + a_{0} } & {\theta \in [\theta_{start} ,\theta_{end} ]} \\ \end{array} $$
(25)
$$ \begin{array}{*{20}c} {h_{s} (\theta ) = b_{n} \theta^{n} + b_{n - 1} \theta^{n - 1} + \cdots + b_{2} \theta^{2} + b_{1} \theta + b_{0} } & {\theta \in [\theta_{start} ,\theta_{end} ]} \\ \end{array} $$
(26)

where, a0-an and b0-bn are the constant of fitting function, which can be obtained by using the polyfit function in MATLAB. In this work, the defect is divided into six segments for fitting, with 113 sampling points given for each segment, the fitted defect length function is

$$ L_{s} (\theta ) = \left\{ {\begin{array}{*{20}l} {L - 16 \times \left( { - \sqrt {\frac{{1.6 \times 10^{ - 5} - }}{{\left( {\frac{{1.6695 \times 10^{ - 3} \left( {\theta - \theta_{1} } \right)}}{{\theta_{2} - \theta_{1} }} + 1.1589 \times 10^{ - 3} } \right)^{2} }}} + 3.8284 \times 10^{ - 3} } \right)} \hfill & {\theta_{1} \le \theta < \theta_{2} } \hfill \\ {L - 1.6 \times 10^{ - 2} } \hfill & {\theta_{2} \le \theta < \theta_{3} } \hfill \\ {L - 16 \times \left( {1 \times 10^{ - 3} + \left( {\frac{{\theta - \theta_{3} }}{{\theta_{4} - \theta_{3} }} \times 7.071 \times 10^{ - 4} } \right)^{2} } \right)} \hfill & {\theta_{3} \le \theta < \theta_{4} } \hfill \\ {L - 16 \times \left( {\left( {\sqrt {1 \times 10^{ - 6} - \left( \begin{gathered} \frac{{\theta - \theta_{4} }}{{\theta_{5} - \theta_{4} }} \times 1.4142 \times 10^{ - 3} \hfill \\ - 7.071 \times 10^{ - 4} \hfill \\ \end{gathered} \right)^{2} } } \right) + 1.7071 \times 10^{ - 3} - 7.071 \times 10^{ - 4} } \right)} \hfill & {\theta_{4} \le \theta < \theta_{5} } \hfill \\ {L - 16 \times \left( {1.7071 \times 10^{ - 3} - \left( {\frac{{\theta - \theta_{5} }}{{\theta_{6} - \theta_{5} }} \times 7.071 \times 10^{ - 4} } \right)} \right)} \hfill & {\theta_{5} \le \theta < \theta_{6} } \hfill \\ {L - \sqrt {1 \times 10^{ - 6} - \left( {\frac{{\theta - \theta_{4} }}{{\theta_{5} - \theta_{4} }} \times 10^{ - 3} } \right)^{2} } } \hfill & {\theta_{6} \le \theta < \theta_{7} } \hfill \\ \end{array} } \right. $$
(27)

where θ1 = 4.6148; θ2 = 4.6311; θ3 = 4.6457; θ4 = 4.7795; θ5 = 4.7933; θ6 = 4.8002; θ7 = 4.8099; moreover, the defect depth in this work is assumed to be constant, which is 20 μm.

Fig. 4
figure 4

A diagram for the irregular defect profile

Full size image

3 A dynamic model of the double row cylindrical roller bearing

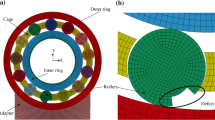
Figure 5 gives the geometrics of the double row cylindrical roller bearing. The double row cylindrical roller bearing has two rows of rollers that share a common inner ring and outer ring, and two cages. Moreover, each row roller has its own motion state, and the motions are independent of each other. The bearing rollers contact with the inner ring, outer ring, and the cage beam. The cage will contact with the outer ring. Due to the significant changes in the roller's rotational speed when entering and exiting the load zone, there can be a difference in between the roller rotational speed about the bearing axis and the cage rotational speed, leading to impacts between them. Additionally, due to the roller rotation about its own axis, there will be tangential friction forces generated during the impact moment. The model of double row cylindrical roller bearing established in this work includes roller translation displacements along x and y axes, rotational displacements about z axis and its’ own axis, inner/outer ring translation displacements along x and y axes, cage translation displacements along x and y axis, and cage rotational displacements along z axis. The dynamic model is comprehensive and can consider the interaction forces between all components.

Fig. 5
figure 5

A diagram of the geometrics of a double row cylindrical roller bearing

Full size image

3.1 Inner ring kinetic equations

The kinetic equations of inner ring are

$$ \left\{ {\begin{array}{*{20}c} {m_{{{\text{in}}}} \ddot{x}_{{{\text{in}}}}^{{}} = - k_{s} x_{{{\text{in}}}}^{{}} - F_{1x}^{{{\text{in}}}} - F_{2x}^{{{\text{in}}}} + f_{1x}^{{{\text{in}}}} + f_{2x}^{{{\text{in}}}} - F_{dx1}^{{{\text{in}}}} - F_{dx2}^{{{\text{in}}}} } & {} \\ {m_{{{\text{in}}}} \ddot{y}_{{{\text{in}}}}^{{}} = - k_{s} y_{{{\text{in}}}}^{{}} - F_{1y}^{{{\text{in}}}} - F_{2y}^{{{\text{in}}}} + f_{1y}^{{{\text{in}}}} + f_{2y}^{{{\text{in}}}} - F_{dy1}^{{{\text{in}}}} - F_{dy2}^{{{\text{in}}}} } & {} \\ \end{array} } \right. $$
(28)

where, min is the inner ring mass; xin and yin and are the inner ring displacement; ks is the contact stiffness of radial; F1x/yin and F2x/yin are the total contact forces between roller and inner ring of first and second rows in the X/Y direction; f1x/yin and f2x/yin are the total frictional forces between roller and inner ring of first and second rows in the X/Y direction; Fdx1in and Fdx2in are the damping forces of first and second rows between the inner ring and roller in the X direction; moreover, Fdy1in and Fdy2in are the damping forces of first and second rows between the inner ring and roller in the Y direction; Moreover, Fixin and Fiyin are [37, 38]

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {F_{ix}^{{{\text{in}}}} } \\ {F_{iy}^{{{\text{in}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {\left[ {K_{{\text{i}}} (\delta_{j}^{{{\text{in}}}} )^{n} P_{j}^{{{\text{in}}}} } \right]} \left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} & {i = 1,2} \\ \end{array} $$
(29)

where θj is the jth roller position angle; Ki is the TVCS between the roller and inner ring; n = 10/9; the inner ring contact coefficients Pjin is

$$ P_{j}^{{{\text{in}}}} { = }\left\{ {\begin{array}{*{20}c} 0 & {\delta_{j}^{{{\text{in}}}} < 0} \\ 1 & {\delta_{j}^{{{\text{in}}}} > 0} \\ \end{array} } \right. $$
(30)

where the deformation of inner rings of jth roller δjin is

$$ \delta_{j}^{{{\text{in}}}} = [x_{{{\text{in}}}} - x_{j}^{r} ]\cos \theta_{j} + [y_{{{\text{in}}}} - y_{j}^{r} ]\sin \theta_{j} - C_{r} $$
(31)

where xjr and yjr are the jth roller displacements; Cr is the bearing radial clearance; and the roller position angle θj is

$$ \theta_{j} = \theta_{c} { + }\begin{array}{*{20}c} {\frac{2\pi (j - 1)}{Z}} & {j = 1,2, \ldots ,Z} \\ \end{array} $$
(32)

where θc is the cage angular displacements; Z is the roller number of one row of double row cylindrical roller bearing; f1x/yin and f2x/yin are the friction forces of first and second rows between the inner ring and roller, which are

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {f_{ix}^{{{\text{in}}}} } \\ {f_{iy}^{{{\text{in}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {[k_{m} K_{{\text{i}}} (\delta_{j}^{{{\text{in}}}} )^{n} P_{j}^{{{\text{in}}}} ]\left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} } & {i = 1,2} \\ \end{array} $$
(33)

where km is the friction coefficient. moreover, Fdx/y1in and Fdx/y2in are

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {F_{{{\text{d}}xi}}^{{{\text{in}}}} } \\ {F_{{{\text{d}}yi}}^{{{\text{in}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {[c_{{\text{c}}} \dot{\delta }_{j}^{{{\text{in}}}} P_{j}^{{{\text{in}}}} ]\left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} } & {i = 1,2} \\ \end{array} $$
(34)

where cc is the contact damping ratio.

3.2 Outer ring kinetic equations

The kinetic equations of outer ring are

$$ \left\{ {\begin{array}{*{20}l} {m_{{{\text{out}}}} \ddot{x}_{{{\text{out}}}}^{{}} = F_{1x}^{{{\text{out}}}} + F_{2x}^{{{\text{out}}}} - C_{{\text{h}}} \dot{x}_{{{\text{out}}}}^{{}} - k_{{\text{h}}} x_{{{\text{out}}}}^{{}} + f_{1x}^{{{\text{out}}}} + f_{2x}^{{{\text{out}}}} + F_{{{\text{d}}x1}}^{{{\text{out}}}} + F_{{{\text{d}}x2}}^{{{\text{out}}}} { - }F_{x}^{{{\text{out}}}} } \hfill \\ {m_{{{\text{out}}}} \ddot{y}_{{{\text{out}}}}^{{}} = F_{1y}^{{{\text{out}}}} + F_{2y}^{{{\text{out}}}} - C_{{\text{h}}} \dot{y}_{{{\text{out}}}}^{{}} - k_{{\text{h}}} y_{{{\text{out}}}}^{{}} + f_{1y}^{{{\text{out}}}} + f_{2y}^{{{\text{out}}}} + F_{{{\text{d}}y1}}^{{{\text{out}}}} + F_{{{\text{d}}y2}}^{{{\text{out}}}} - F_{y}^{{{\text{out}}}} } \hfill \\ \end{array} } \right. $$
(35)

where, mout is the outer ring mass; Fxout and Fyout are the external forces between the roller and bearing outer ring; xout and yout are the outer rings displacements; Ch is the damping ratio of radial; kh is the radial contact stiffness; f1x/yout and f2x/yout are the total frictional forces between the first and second rows of roller and outer ring; F1x/yout and F2x/yout are the total contact forces between the first and second rows of roller and outer ring, which are

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {F_{ix}^{{{\text{out}}}} } \\ {F_{iy}^{{{\text{out}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {\left[ {K_{{\text{e}}} (\delta_{j}^{{{\text{out}}}} )^{n} P_{j}^{{{\text{out}}}} } \right]} \left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} & {i = 1,2} \\ \end{array} $$
(36)

where Ke is the contact stiffness between the roller and the outer ring; the contact coefficient between the roller and outer ring Pjout is

$$ P_{j}^{{{\text{out}}}} { = }\left\{ {\begin{array}{*{20}c} 0 & {\delta_{j}^{{{\text{out}}}} < 0} \\ 1 & {\delta_{j}^{{{\text{out}}}} > 0} \\ \end{array} } \right. $$
(37)

where the deformation between the outer ring and j-th roller δjout is

$$ \delta_{j}^{{{\text{out}}}} = [x_{j}^{r} - x_{j}^{{{\text{out}}}} ]\cos \theta_{j} + [y_{j}^{r} - y_{j}^{{{\text{out}}}} ]\sin \theta_{j} $$
(38)

where xjout and yjout are the outer ring displacements; xjr and yjr are the jth roller displacements; f1x/yout and f2x/yout are the friction forces of the first and second rows between the inner ring and roller, which are

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {f_{ix}^{{{\text{out}}}} } \\ {f_{iy}^{{{\text{out}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {[k_{m} K_{{\text{e}}} (\delta_{j}^{{{\text{out}}}} )^{n} P_{j}^{{{\text{out}}}} ]\left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} } & {i = 1,2} \\ \end{array} $$
(39)

where Fdx/y1out and Fdx/y2out are the damping forces of the first and second rows between the outer ring and roller, which are

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {F_{{{\text{d}}xi}}^{{{\text{out}}}} } \\ {F_{{{\text{d}}yi}}^{{{\text{out}}}} } \\ \end{array} } \right] = \sum\limits_{j = 1}^{Z} {[c_{{\text{c}}} \dot{\delta }_{j}^{{{\text{out}}}} P_{j}^{{{\text{out}}}} ]\left[ {\begin{array}{*{20}c} {\cos \theta_{j} } \\ {\sin \theta_{j} } \\ \end{array} } \right]} } & {i = 1,2} \\ \end{array} $$
(40)

where cc is the contact damping ratio.

3.3 Cage kinetic equations

Figure 6 gives the relative motion between the cage and roller. The kinetic equations of outer ring are

$$ \left\{ {\begin{array}{*{20}l} {m_{{\text{c}}} \ddot{x}_{{i{\text{c}}}} = \sum\limits_{j = 1}^{Z} {( - F_{{i{\text{c}}x}} (j) + f_{{i{\text{c}}x}} (j))} + F_{{i{\text{c}}x}}^{{\text{d}}} } \hfill & {i = 1,2} \hfill \\ {m_{{\text{c}}} \ddot{y}_{{i{\text{c}}}} = \sum\limits_{j = 1}^{Z} {( - F_{{i{\text{c}}y}} (j) - f_{{i{\text{c}}y}} } (j)) + F_{{i{\text{c}}y}}^{{\text{d}}} } \hfill & {i = 1,2} \hfill \\ {I_{{\text{c}}} \ddot{\theta }_{{i{\text{c}}}} = \sum\limits_{j = 1}^{Z} {( - F_{{i{\text{c}}}} \times 0.5D_{{\text{m}}} } ) + M_{{\text{c}}} } \hfill & {i = 1,2} \hfill \\ \end{array} } \right. $$
(41)

where Fcx and Fcy are the components of impact between the cage and roller; fcx and fcy are the friction forces between the cage and roller; mc and Ic are the cage mass and rotational inertia; moreover, Ficxd, Ficyd, and Mc are

$$ \left\{ {\begin{array}{*{20}c} {F_{{i{\text{c}}x}}^{{{\text{d}}^{\prime } }} = \frac{{ - \eta_{0} u_{1} L_{1}^{3} \varepsilon^{2} }}{{C_{{\text{g}}}^{2} (1 - \varepsilon^{2} )^{2} }}} & {i = 1,2} \\ {F_{{i{\text{c}}y}}^{{{\text{d}}^{\prime } }} = \frac{{\pi \eta_{0} u_{1} L_{1}^{3} \varepsilon }}{{4C_{{\text{g}}}^{2} (1 - \varepsilon^{2} )^{3/2} }}} & {i = 1,2} \\ {M_{{\text{c}}}^{\prime } = \frac{{2\pi \eta_{0} V_{1} R_{1}^{2} L_{1} }}{{C_{{\text{g}}} \sqrt {1 - \varepsilon^{2} } }}} & {i = 1,2} \\ \end{array} } \right. $$
(42)

where the lubricating oil traction speed is u1 = R1(ωo + ωc); L1 is the cage guide surface width; Cg is the cage guide surface clearance; ε is the cage eccentricity; the relevant parameters are explained in Refs. [39,40,41,42].

Fig. 6
figure 6

The relative motion between cage and roller

Full size image

The resultant forces and moment Ficxd, Ficyd, and Mc are

$$ \left\{ {\begin{array}{*{20}c} {M_{c} } \\ {F_{icx}^{d} } \\ {F_{icy}^{d} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{c} } & { - \sin \phi_{c} } \\ 0 & {\sin \phi_{c} } & {\cos \phi_{c} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {M_{c}^{\prime } } \\ {F_{icx}^{{d^{\prime}}} } \\ {F_{icy}^{{d^{\prime}}} } \\ \end{array} } \right\} $$
(43)

where, φc = arctan(yc/xc). Fcj and fcj are the roller-cage impact and friction forces. The roller-cage contact is simplified into the spring, and the roller-cage impact force is

$$ \begin{array}{*{20}c} {F_{ic} (j) = k_{ic} (j)\delta_{ic} (j)} & {i = 1,2} \\ \end{array} $$
(44)

where kc is the roller-cage contact stiffness; the roller-cage contact deformation δc is

$$ \delta_{{\text{c}}} (j) = \left\{ {\begin{array}{*{20}c} {z_{{\text{c}}} (j) - C_{{\text{p}}} } & {\left| {z_{{\text{c}}} (j) - C_{{\text{p}}} } \right| > 0} \\ 0 & {\left| {z_{{\text{c}}} (j) - C_{{\text{p}}} } \right| = 0} \\ \end{array} } \right. $$
(45)

where Cp is the cage pocket clearance; the roller-cage angular displacement difference zj is

$$ z_{j} (j) = \left( {\theta_{{{\text{cage}}}} - \theta_{j} } \right)\frac{{D_{{\text{m}}} }}{2} + y_{{\text{c}}} \cos \theta_{j} + z_{{\text{c}}} \sin \theta_{j} $$
(46)

where θcage is the cage angular displacement.

The roller-cage frictional force is

$$ f_{{\text{c}}} (j) = \mu_{{\text{c}}} (j)F_{{\text{c}}} (j) $$
(47)
$$ \mu_{{\text{c}}} (j) = ( - 0.1 + 22.28S(j))e^{ - 181.46S(j)} + 0.1 $$
(48)

where S is the slide-roll ratio of j-th roller. The components of Fc are

$$ \left\{ {\begin{array}{*{20}l} {F_{{i{\text{c}}x}} (j) = F_{{i{\text{c}}}} (j)\sin (\theta_{j} )} \hfill & {i = 1,2} \hfill \\ {F_{{i{\text{c}}y}} (j) = F_{{i{\text{c}}}} (j)\cos (\theta_{j} )} \hfill & {i = 1,2} \hfill \\ \end{array} } \right. $$
(49)

Therefore, the components of fc are

$$ \left\{ {\begin{array}{*{20}l} {f_{{i{\text{c}}x}} (j) = f_{{i{\text{c}}}} (j)\cos (\theta_{j} )} \hfill & {i = 1,2} \hfill \\ {f_{{i{\text{c}}y}} (j) = f_{{i{\text{c}}}} (j)\sin (\theta_{j} )} \hfill & {i = 1,2} \hfill \\ \end{array} } \right. $$
(50)

3.4 Roller kinetic equations

In operation, the roller motion is affected by the bearing cage and rings. The forces applied on the roller are given in Fig. 7. Fjin and Fjout are the double row cylindrical roller bearing contact forces; Fdjin and Fdjout are the oil film resistances between the ring and j-th roller; fjin and fjout are the friction forces between the rings and j-th roller; Fcj and fcj are the roller-cage impact and friction forces.

Fig. 7
figure 7

Forces applied on the roller

Full size image

The kinetic equations of roller are

$$ \left\{ {\begin{array}{*{20}l} {m_{r} \ddot{x}_{j}^{r} = F_{ix}^{{{\text{in}}}} (j) - F_{ix}^{{{\text{out}}}} (j) + F_{dxi}^{{{\text{in}}}} (j) - F_{dxi}^{{{\text{out}}}} (j) - f_{iy}^{{{\text{in}}}} (j) + f_{iy}^{{{\text{out}}}} (j){ - }F_{icx} (j) + f_{icx} (j) \, } \hfill \\ {m_{r} \ddot{y}_{j}^{r} = F_{iy}^{{{\text{in}}}} (j) - F_{iy}^{{{\text{out}}}} (j) + F_{dyi}^{{{\text{in}}}} (j) - F_{dyi}^{{{\text{out}}}} (j) + f_{ix}^{{{\text{in}}}} (j) - f_{ix}^{{{\text{out}}}} (j) + F_{icx} (j) + f_{icx} (j)} \hfill \\ {I_{r} \ddot{\phi }_{ir} = 0.5(f_{i}^{{{\text{out}}}} (j) + f_{i}^{{{\text{in}}}} (j) - f_{ic} (j))d \, } \hfill \\ {I_{or} \ddot{\theta }_{ir} = 0.5(D_{{{\text{out}}}} f_{i}^{{{\text{out}}}} (j) - D_{{{\text{in}}}} f_{i}^{{{\text{in}}}} (j) - D_{{\text{m}}} (F_{ic} (j) + F_{id} (j))) \, } \hfill \\ \end{array} } \right. $$
(51)

where mr and φr are the roller mass and the angular displacement of roller around the roller center; θr is the angular displacement of roller around the bearing center.

4 Results and discussions

4.1 Experimental validation

The dynamic model with the independent defect shape of double row cylindrical roller bearing can be used to calculate the vibrations of inner/outer ring, roller, and cage. A double row cylindrical roller bearing NN3007 of SKF is used to simulate the vibrations. The NN3007 bearing structural parameters are depicted in Table 1.

Table 1 NN3007 bearing structural parameters
Full size table

The stiffness calculation method given by Palmgren can calculate the roller-ring contact stiffness. The contact stiffnesses between the roller and outer/inner ring are 1.898 × 108 N/mn and 1.828 × 108 N/mn. The damping ratio between the roller and ring is 200 Ns/m. The initial velocities of roller and ring are 0 m/s. The initial displacements of roller and ring are 10−6m and 10−6m in the X and Y directions.

Figure 8a gives the test instrument named BVT-5. The double row cylindrical roller bearing is mounted on the shaft. The shaft is driven by the electric motor and the rotational speed of the shaft is 1800 r/min. The external force is applied by two loading arms symmetrically distributed along the axis. The radial load is loaded by the force application arm. The acceleration sensor (PCB-352C04) is installed on the bearing outer ring in the X direction. The LMS system and computer are used to acquire the vibration signals of the double row cylindrical roller bearing. The sampling frequency is set to 25,600 Hz. The bearing is NN3007. The radial load is 300 N. To verify the accuracy of model, the rectangle defect (3 mm × 4 mm) in Fig. 8b, the circular defect (diameter 4.5 mm) in Fig. 8c, and the defect with the independent shape in Fig. 8d are studied. The effective roller lengths when the roller rolls over the rectangle defect, the circular defect, and the defect with the independent shape are given in Fig. 9.

Fig. 8
figure 8

a A bearing vibration test instrument named BVT-5; b a rectangle defect case, c a circular defect case; and d the defect with the independent shape

Full size image
Fig. 9
figure 9

Time-varying effective roller length for a the rectangle defect, b the circular defect, and c the defect with the independent shape

Full size image

4.1.1 Case study: rectangle defect

The comparisons of outer ring accelerations in the X direction between the experimental and simulated are given in Fig. 10. In Fig. 10a and b, the defect frequencies of outer ring from the simulated and experimental are 249.60 Hz and 250.97 Hz. Their difference is 0.55%. In Fig. 10c, the simulated results are familiar to the experimental ones. Figure 10d gives the comparisons of the acceleration impacts when the roller enters and exits the defect area between the simulated and experimental results. The simulated results are familiar with the experimental ones, which can validate the proposed model.

Fig. 10
figure 10

Comparisons of the experimental and simulated results of outer ring for the rectangular defect case. a Simulated spectrum, b experimental spectrum, c simulated and experimental accelerations, and d simulated and experimental accelerations in the defect impact area

Full size image

4.1.2 Case study: circular defect

The comparisons of accelerations of outer ring in the X direction from the experimental and simulated are plotted in Fig. 11. In Fig. 11a and b, the defect frequencies of outer ring of simulated and experimental are 250.39 Hz and 249.23 Hz. Their error is 0.467%. In Fig. 11c, the simulated results are familiar to the experimental ones. Figure 11d gives the comparisons of the acceleration impacts when roller enters and exits the defect area between the simulated and experimental accelerations. The simulated results are familiar with the experimental ones, which can also validate the proposed model.

Fig. 11
figure 11

Comparison of the experimental and simulated results of outer ring for the circular defect case. a Simulated spectrum, b experimental spectrum, c simulated and experimental accelerations, and d simulated and experimental accelerations in the defect impact area

Full size image

4.1.3 Case study: defect with an irregular shape

The comparisons of accelerations of outer ring in the X direction between the experimental and simulated results are given in Fig. 12. In Fig. 12a and b, the defect frequencies of outer ring of simulated and experimental are 249.40 Hz and 250.21 Hz, respectively. Their error is 0.32%. In Fig. 12c, the simulated results of dynamic model are familiar with the experimental ones. Figure 12d gives the comparisons of the acceleration impacts when roller enters and exits the defect area between the simulated and experimental ones. Similarly, the simulated results are familiar with the experimental results, which can validate the proposed model too.

Fig. 12
figure 12

Experimental and simulated results of outer ring. a Frequency-domain simulated signal, b frequency-domain experimental signal, c simulated and experimental accelerations, and d simulated and experimental accelerations in the defect impact area

Full size image

4.2 Comparative analysis of vibrations between irregular and simplified defect shapes

In the following sections, the initial velocities of roller and ring are their theoretical value under pure rolling conditions. The initial displacements of roller and ring are 10−6m and 10−6m in the X and Y directions. The rotating speed is 1800 r/min. The loads in the X and Y directions are 300 N and 0 N.

In the previous studies, most researchers defined the defect shape as the regular shape including the square or circle, as given in Fig. 13a. This method can simplify the calculation, but the accuracy is low. The independent defect is simplified to be a rectangle (7 mm × 4 mm) as given in Fig. 13b. The dynamic models with the simplified and independent defect models are simulated, respectively.

Fig. 13
figure 13

a Traditional defect shape simplification method and b simplification of independent defect shape

Full size image

In Fig. 14a, the acceleration of the simplified defect is larger than that of the actual defect shape. Figure 14b gives the comparison of TVCS between the simplified defect shape and the actual defect shape. The TVCS of actual defects is more accurate than that of simplified defects. The comparison of defect impact between the simplified defect shape and actual defect shape is given in Fig. 14c. Note that the acceleration peak value of impact of simplified defect is greater than that of the actual defect. There are similarities in the acceleration and impact when the roller enters and exits the defect. When the roller enters the defect, the TVCS and ECL of the simplified defect change greatly, but the TVCS and ECL of the actual defect change slowly, which makes different impact characteristics. Thus, the model with the actual defect is more reasonable than that with the simplified defect.

Fig. 14
figure 14

Comparisons of a accelerations of outer ring, b TVCS, and c defect impact between the simplified defect shape and actual defect shape

Full size image

4.3 Effect of irregular defect sizes on double row cylindrical roller bearing vibrations

To study the effects of independent defect sizes on the bearing vibrations, the maximum width sizes of independent defect are 3 mm, 4 mm, and 5 mm, as shown in Fig. 15. Different maximum width cases cause different areas and ECLs of the defect. Figure 16 gives the outer ring accelerations for the irregular defects with different maximum widths. Note that the outer ring accelerations increase with the increment of the maximum width of the defect. Figure 17 gives the effect of the independent defect with different maximum widths on the accelerations of the inner/ring. Note that the inner/outer ring acceleration RMS values increase with the increment of the maximum width of the defect. Moreover, the accelerations in the X direction are larger than those in the Y direction.

Fig. 15
figure 15

Effective roller length when the roller rolls over the different defects

Full size image
Fig. 16
figure 16

Comparisons of accelerations of irregular defects with different maximum widths

Full size image
Fig. 17
figure 17

Effect of the independent defect with different maximum widths on the accelerations of the inner/outer ring

Full size image

4.4 Effects of the load and rotating speed on the double row cylindrical roller bearing vibrations for irregular-shaped defect

To study the effects of the rotating speed on the DRCB vibrations, the rotating speeds are 1000 r/min, 2000 r/min, 3000 r/min, 4000 r/min, and 5000 r/min. The model with the independent defect is used to simulate the accelerations of DRCB. The maximum width of the independent defect is 4mm. Figure 18 gives the effects of the rotating speed on the accelerations of the inner/outer ring and cage. Note that the rotating speed can greatly affect the inner/outer ring and cage vibrations. The inner/outer ring accelerations increase first and then decrease with the increment of the rotating speed. The cage accelerations increase with the increment of the rotating speed.

Fig. 18
figure 18

Effect of the rotating speed on the inner/outer ring and cage accelerations. a RMS values of inner and outer ring accelerations and b RMS values of cage accelerations

Full size image

To illustrate the effect of the load value on the DRCB vibrations, the load is 500 N, 1000 N, 1500 N, 2000 N, and 2500 N. The model with the independent defect is used to simulate the accelerations of DRCB. The maximum width of independent defect is 4 mm. Figure 19 demonstrates the effect of the load on the inner/outer ring and cage accelerations. Note that the load has a remarkable effect on the inner/outer ring and the cage vibrations. The outer ring acceleration in the Y direction increases with the increment of the load value. The outer ring accelerations in the X direction increase first and then decrease with the increment of the load value. The inner ring accelerations increase with the increment of the load value. The cage accelerations increase first and then decrease with the increment of the load value.

Fig. 19
figure 19

Effect of the load value on the inner/outer ring and cage accelerations. a RMS values of inner and outer ring accelerations and b RMS values of cage accelerations

Full size image

4.5 Model comparison

To further demonstrate the advancement of the dynamic model and the defect modeling method proposed in this work, the results obtained by the proposed method and the method in Ref. [43] are compared. The defect width is 4 mm. Figure 20a shows the dynamics obtained by the proposed dynamic model coupled with the proposed defect model and the dynamic model in Ref. [43] coupled with the defect model in Ref. [43]. The RMS value of the results obtained by the proposed dynamic model coupled with the proposed defect model is 30.414 m/s2; while the one of the results obtained by the dynamic model in Ref. [43] coupled with the defect model in Ref. [43] is 29.01 m/s2. Figure 20b compares the result obtained by the proposed dynamic model coupled with the proposed defect model and the proposed dynamic model coupled with the defect model in Ref. [43]. The RMS value of the results obtained by the proposed dynamic model coupled with the defect model in Ref. [43] is 32.06 m/s2. Compare the results obtained by the proposed dynamic model coupled with the proposed defect model and the proposed dynamic model coupled with the defect model in Ref. [43], it can be found that the defect modeling method in Ref. [43] will cause the simulation results that are higher than the actual results. Moreover, compare the results obtained by the proposed dynamic model coupled with the proposed defect model and the dynamic model in Ref. [43] coupled with the defect model in Ref. [43], it can be found that the result obtained by the proposed dynamic model is larger than the one obtained by the dynamic model in Ref. [43], which indicates that the necessity of considering the supporting stiffness of the outer ring and the dynamics of the bearing cage. These can provide some evidence for the advancement of the proposed dynamic model and defect modeling method in this work.

Fig. 20
figure 20

Comparisons of accelerations obtained by a] the proposed dynamic model coupled with the proposed defect model and the proposed dynamic model in Ref. [43] coupled with the defect model in Ref. [43]; and b the proposed dynamic model coupled with the proposed defect model and the proposed dynamic model coupled with the defect model in Ref. [43]

Full size image

5 Conclusions

This paper proposes a novel irregular shape defect modeling method and a dynamic model of double row cylindrical roller bearings, taking into account actual shapes of defects instead of simplified shapes. In this study, the effects of the bearing load, rotating speed, and different irregular defect shapes on vibrations were investigated. To validate the proposed model, a test was carried out, and the simulated vibrations and acceleration spectra of outer rings with rectangle defects, circular defects, and defects with irregular shapes were compared with experimental results. The results showed that the model results were in agreement with the experimental results, thus validating the defect modeling method and the proposed model. The key findings of the study are:

  1. (1)

    The proposed irregular shape defect modeling method and dynamic model accurately simulate vibrations of double row cylindrical roller bearings with rectangular, circular, and irregular-shaped defects.

  2. (2)

    Rotating speed has a significant impact on the acceleration RMS and PTP values of the inner/outer ring, rollers, and cage, with the inner ring having higher values than the outer ring, and the roller values increasing with increasing rotating speed.

  3. (3)

    The TVCS of the actual defect is more accurate than that of the simplified defect, with differences observed in acceleration and impact when the roller enters and exits the defect. The model with the actual defect is more reasonable than that with the simplified defect.

  4. (4)

    Rotating speed has a significant impact on the inner/outer ring and cage vibrations, with acceleration increasing and then decreasing with increasing rotating speed.

  5. (5)

    Load has a significant impact on the inner/outer ring and cage vibrations, with outer ring accelerations in the Y direction and inner ring accelerations increasing with increasing load value, and outer ring accelerations in the X direction and cage accelerations increasing and then decreasing with increasing load value.

  6. (6)

    The simplified defect model will cause the bearing vibrations to be overestimated. The established dynamic model with the actual defect is more reasonable than the simplified defect model.

Overall, the study provides valuable insights into the effects of rotating speed, load, and defect shape on double row cylindrical roller bearing vibrations and demonstrates the importance of considering actual defect shapes in dynamic models for engineering applications. However, there are also some aspects that need to be further studied. First, it is assumed that the defect morphology is ideal. However, the fault morphology is rough and uneven actually. The characteristics of the defect morphology have a significant impact on the contact stiffness between the roller and the ring. Besides, the defect edge elastic deformation is ignored. Moreover, the double row cylindrical roller bearing is typically installed in rotor systems, and the effect of the irregular shape defect on the rotor system dynamics needs to be studied in future work.