Introduction

The rapid progress of the span of cable stayed bridges increases the susceptibility to exhibit large amplitudes vibration under environmental excitations, such as wind [4, 15], rain wind [4, 15, 33, 37] and parametric excitation [8, 46, 52], given that this structures are flexible and have low inherent damping [53]. Vibration can lead to breakdown stay cable connections, damage corrosion protection systems resulting on the fatigue failure of the integrity of bridge. The mitigation of the dynamic response of stay cable using mechanical active, semi active and passive dampers was widely investigated to prevent premature damage in stay cable and improved safety and serviceability of bridges [3, 8, 19,20,21, 35]. Since they provide a significant damping force and present an easy replacement, mechanical dampers are applied in full-scale to medium and long span bridges [7, 54]. The frequency of vibrations induced by the rain wind is mainly between 1 Hz and 3 Hz according to a full scale measurements [31]. This range of frequency covers a number of modes for long stay cables which it is not so far perspicuous how to identify the target mode for damping. Hence, if the damper is designed for optimal performance in a specific mode can lead cable vibration of other modes [23, 29, 47]. Therefore, multi-mode cable vibration control is an important issue for development of cable stayed bridges. Many investigations have been conducted to develop the control of multi-mode cable vibration. Susumpow and Fujino [12] proposed an active control of multi-modal cable vibrations by axial support motion. Wang et al. [50] developed a new active control algorithm for optimal design of viscous dampers to reach multi-modal cable vibration control. The used method provides a high level damping to all concerned modes. Semi-active cable multi-modal vibration control using magnetorheological (MR) damper has been investigated by studies [9, 16, 32]. MR damper showed an effectiveness to provide damping for multi-mode vibration. Nevertheless, this strategy require a power alimentation and real-time detection of vibrations which making it less recommended in practice. In recent studies, the focus is placed on performance of using passive mechanism to enhance the control several modes. The effectiveness of inerter dampers was further evaluated through the comparison with the viscous dampers in [42]. Inerter dampers was better performing than conventional viscous dampers for one mode, providing relatively limited additional damping ratios for other vibration modes. A full scale cable experiments have been carried out in [26, 27] to validate the effect of inertial dampers. Chen et al [6], studied through a parallel arrangement of a Negative stiffness mechanism and a viscous damper the control of a multi-mode cable vibration. The numerical study considering a real cable of Sutong Bridge revealed that the negative stiffness mechanism improves damping effects of all cable modes equally. Following experimental studies, [43, 55] demonstrated the performance of negative stiffness devices. Damping performance dependence of modes frequency was investigated through field tests using viscous and viscoelastic dampers [5]. Observations showed that, for a precisely range of frequency, the two aforementioned dampers provide comparable modal damping for all the tested cable modes. However, in higher modes the damping provided by the viscous damper decreases considerably. In addition, when cables vibrate in modes with frequency higher than 3.0 Hz the performance of the viscous damper has been greatly reduced. The material SMA (shape memory alloys) is smart and functional which provide interesting proprieties not present in traditionally material including large damping capacity, self-centering ability, high fatigue and corrosion strength [2, 17, 40, 45]. The smart material has the capability of undergoing large inelastic deformations and of recovering their shape by releasing applied loads without residual strain [22]. This unique propriety, known as superelasticity, results from the phase transformation separating the two crystallographic structures of the SMA: austenite and martensite. Once the critical stress is reached, a phase transformation of the austenite towards the martensite is caused, the strain of this transformation is added to the elastic strain; once the critical stress of the inverse transformation is reached, the austenitic transformation begins to take place without residual strain [49]. Consequently, the curve stress–strain is a hysteresis through the whole loading–unloading process. It presents the energy dissipation capacity and reflects the conspicuous damping property of the SMA [36, 38].

The number of studies focusing on the feasibility of using SMA as passive energy dissipation system with special emphasis on dynamic control of cable-stayed bridges has grown in the past decade and is still growing. [10] investigated through a campaign of laboratory tests the feasibility of a hybrid control strategy by combining an open loop actuation and wrapped SMA for cable vibration mitigation. Experimental results shown on [11] confirm that the hybrid strategy promising vibration mitigation capabilities when the motion was essentially dominated by the first in-plane mode. Taking 1:60 model of the Runyang cable-stayed bridge (in Jiangsu, China) as a test platform, [13] carried out experimentations on vibration control of a stay cable with SMA damper. Results show that the SMA damper installed in plane of the cable can mitigate 50% of the free vibration. Through two sets of laboratory scale experiments realized on stayed cable, [48] report that SMA damper reduces drastically the oscillation amplitude (between 25% and 50%). The experimental results presented by [24] show that the Nickel–Titanium SMA wires permit an effective reduction of the oscillations time and theirs amplitudes by increasing the damping ratio.

In addition to experimental studies, many analytical approaches have been proposed. The study developed by [25] stated that the superelastic SMA damper can mitigate the cable’s vibration in both cases; at its first mode or at its first few modes. The responses of a stay cable model on a cable-stayed bridge model with/without one SMA damper are numerically investigated by [28]. The study evaluates the additional equivalent modal damping ratio when the combined stay cable/SMA damper system vibrates with a single mode. [39] focused on the effect of temperature under the influence of loading. Showing that the ambient temperature has its marked effect on the superelasticity and shape memory behaviors, SMA damper made of the Ni–Ti wire can effectively quashes the stay cable vibration. A comparison between linear quadratic regulator LQR active control and passive SMA damper for controlling the cable in-plane vibration under excitations has been developed in [56]. The study reveals that the optimal control effect of the SMA damper is approached to the LQR active control effect. Other researchers have paid attention to control seismic response of cable-stayed bridges using SMA devices [14, 41].

This study highlights the performance of superelastic SMA damping device to mitigate multi-modal stay cable vibration, since large amplitude vibrations tend to be dominated by a single mode or the first modes as reported by [4, 30, 33].The damper used is passive and must not need supervision. The paper is divided into four parts. The first part presents vibration equations of a stayed cable-SMA system specifying different hypothesis adopted in problem linearization. The second part contains an outline of the optimization method based on an energy balance used to achieve optimal damping for the first mode of vibration. The potential of SMA damper to mitigate transverse vibration stay cable belongs Rades-La Goulette cable stayed bridge is then evaluated. The case study showed that the optimal size of the SMA damper for the first mode is insufficient for control other modes. Taking into consideration coupled modes, the third part focuses on development of an optimization method based on Irvine criterion. The last part centers on the demonstration of the effectiveness of the optimal multi-mode design of the SMA damper to control all concerned modes.

Governing Equations for a Small Sag Cable

Consider a cable suspended between two supports A and B of different heights subjected to its self-weight (cable with a sag profile). The cable is assumed to have a uniform cross-sectional area \(A_c\) along its length L and constituted by an isotropic linearly elastic material with young’s modulus \(E_c\). The A–B line is inclined of an angle \(\theta\) with respect to the horizontal. The strained static profile of the cable is spanned by the curvilinear co-ordinate s with \(s=0\) at A. The cable configuration is described in Fig. 1.

Fig. 1
figure 1

Inclined cable with an attached damper

Full size image

By setting the Cartesian co-ordinate system (A, x, y), where the y axis is perpendicular to the x axis taken along the cable’s chord, the partial differential equations governing dynamic equilibrium of sagged stay cable can be written as (including the effect of SMA damper):

$$\begin{aligned}\frac{\partial }{\partial s}\Bigg [(T+\tau )\bigg (\frac{dx}{ds}+\frac{\partial u}{\partial s}\bigg )\Bigg ]+F_{e,x}(x,t)=m_c \Bigg [\frac{\partial ^{2} u}{\partial {t^2}}+ g \sin (\theta )\Bigg ] \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial }{\partial s}\Bigg [(T+\tau )\bigg (\frac{dy}{ds}+\frac{\partial v}{\partial s}\bigg )\Bigg ] +F_{e,y}(x,t)-\sum ^{m}_{i=1} F_{d,i}(t)\delta (x-x_d)=m_c \Bigg [\frac{\partial ^{2} v}{\partial {t^2}}- g \cos (\theta )\Bigg ] \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial }{\partial s} \Bigg [(T+\tau )\frac{dw}{\partial s}\Bigg ]+F_{e,w}(x,t)=m_c \frac{\partial ^{2} w}{\partial {t^2}} \end{aligned}$$
(3)

T denotes the static stay cable tension’s, \(\tau\) is the additional dynamic cable tension, \(m_c\) is the mass of the cable per unit length, g is the acceleration of gravity, \(\delta\) is the Dirac’s delta function, while u, v and w are the cable dynamic displacement components in the x, y and z directions, respectively; \(F_{e,x}\), \(F_{e,y}\) and \(F_{e,z}\) are distributed external dynamic loading per unit length in the x, y and z directions, respectively.

The cable is subjected to a transverse concentrated force \(F_d\) generated by the SMA device attached at the location \(x_d\) from the support A in the x direction. Then, using the non-linear relationship between the dynamic cable tension and dynamic deformation:

$$\begin{aligned} \tau ^D =E_c~A_c~\epsilon ^D \end{aligned}$$
(4)

The Green–Lagrange deformation is as follows:

$$\begin{aligned} \epsilon ^D =\frac{\partial (u)}{\partial x}+\frac{dy}{dx}\frac{\partial v}{\partial x}+\frac{1}{2}\Bigg [ \bigg (\frac{\partial u}{\partial x}\bigg )^2+\bigg (\frac{\partial v}{\partial x}\bigg )^2+ \bigg (\frac{\partial w}{\partial x}\bigg )^2\Bigg ] \end{aligned}$$
(5)

The aforementioned non-linear equations are simplified enforcing the following assumptions:(i) the transversal fundamental frequency of the cable is smaller than its longitudinal fundamental frequency; (ii) the cable vibrates only in the xy-plane and its motion in the x-direction is negligibly small; (iii) the static profile of the cable can be approximated to a parabola; (iv) sag length ratio is sufficiently small with respect to unit. These assumptions have been adopted in several studies (See [28, 32, 34, 44, 51] for more details). The free response of the stay cable is considered in this study, because excitations induced by wind lead to initial impulses; then the structure vibrates freely according to its natural vibration modes. The internal damping of the cable is not considered, since stay cables have very extremely low levels of inherent structural damping, typically on the order of a fraction of one per cent as indicated by several bibliographical references and full-scale tests [24].

Cable transverse free vibration, taking into account the control action with the use of a SMA damper, is governed by the following partial differential equation:

$$\begin{aligned} \displaystyle {m_c \frac{\partial ^{2}v}{\partial t^{2}}-T\frac{\partial ^{2} v}{\partial x^{2}}+\frac{E_c A_c}{L}\left( \frac{m_c g \cos \theta }{T}\right) ^{2}\int _{0}^{L}v(x,t)dx=-\sum ^{m}_{i=1} F_{d,i}(t)\delta (x-x_d)} \end{aligned}$$
(6)

The transverse deflection can be approximated using a finite modal superposition of the form:

$$\begin{aligned} v(x,t)=\sum ^n_{i=1} \alpha _i(t) \phi _i(x) \end{aligned}$$
(7)

where \(\alpha _i(t)\) are non-dimensional modal participation factors and \(\phi _i(x)\) are a set of modal shape functions, satisfying the geometric boundary conditions at the cable’s ends A and B:

$$\begin{aligned} \phi _i(0)=\phi _i(L)=0 \end{aligned}$$
(8)

To compute the damping and responses of the cable with the SMA damper, we assume sinusoidal shape functions:

$$\begin{aligned} \phi _{i}(x)=\sin \left( \frac{i \pi x}{L}\right) \end{aligned}$$
(9)

Substituting (7) into the equation of motion (6), and using a standard Galerkin approach under the assumptions of small deflections and of linear elastic constitutive behavior results in (without external load) :

$$\begin{aligned} \begin{aligned}&\sum ^n_{i=1}\Bigg [m_c \ddot{\alpha }_i(t)\int _{0}^{L} \phi _i(x) \phi _j(x) \mathrm {d}x- T \alpha _i(t)\int _{0}^{L} \phi ''_i(x) \phi _j(x) \mathrm {d}x \\&+ \lambda ^{2} \alpha _i(t)\int _{0}^{L}\Bigg ( \phi _j(x) \int _{0}^{L}\phi _i(x) \mathrm {d}x\Bigg )\mathrm {d}x\Bigg ] = -\int _{0}^{L}\sum ^n_{m} F_{d,i}(t)\delta (x-x_d)\mathrm {d}x \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned} \lambda ^2 = \frac{E_c A_c}{L} \left( \frac{m_c~ g~cos \theta }{T}\right) ^2 \end{aligned}$$
(11)

Considering only the first mode of vibration, Eq. 10 reduces to

$$\begin{aligned} \displaystyle {m_{1}\ddot{\alpha _{1}}(t)+\left( k_{1}+\lambda ^2 m_{1} \right) \alpha _{1}(t) = -F_d(t)\phi _{1}(x_d)} \end{aligned}$$
(12)

where

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle { m_{1}=m_c \int _{0}^{L}\varphi _{1}(x)\varphi _{1}(x)dx}=m_c \frac{L}{2}\\ \displaystyle {k_{1}= T\int _{0}^{L}\frac{d \varphi _{1}}{d x}\frac{d \varphi _{1}}{d x}dx}=\displaystyle {\frac{T\pi ^{2}}{2L}} \\ \displaystyle { \phi _{1}(x_d)=\sin \left( \frac{\pi x_d}{L}\right) } \end{array} \right. \end{aligned}$$

Control of the First Vibration Mode with an Attached SMA Damper

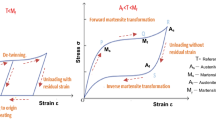
To describe the superelastic behavior of the SMA damper, we consider a one dimensional model proposed by [1]. This model presents a shape memory alloy based damper, which exploits the superelasticity of nickel–titanium alloys (Ni–Ti) wires for energy dissipation. It takes into account one scalar internal variable \(\zeta _s\) designating the martensite fraction and consider the different elastic proprieties between the two crystallographic phases of the SMA (austenite and martensite).

The numerical simulations of the constitutive equations of the model led to the curve stress strain reported in Fig. 2 considering the following properties of the element SMA presented in Table 1.

Table 1 Material parameters of the element SMA
Full size table
Fig. 2
figure 2

Behavior and hysteresis of the one-dimensional model

Full size image
Fig. 3
figure 3

First mode control with the SMA damper

Full size image

The observed curve is formed by two parts. The first consists of loading. It contains an elastic deformation from zero to \(\sigma ^{AS}_s\), where the elastic strain is assumed to be linearly related to the stress: \(\sigma =E\epsilon ^e\) with E is the elastic modulus’s austenite and \(\epsilon ^e\) is the elastic strain. Then, there is conversion of the austenite into martensite oriented from \(\sigma ^{AS}_s\) to \(\sigma ^{AS}_f\). When the transformation is complete, there is again an elastic transformation but the Young modulus used is of the martensite. For the unloading case, the steps are the same but in reverse and the stresses used are those of martensite. As a result one hysteresis loop is formed by a closed stress strain curve in the whole loading unloading process. This hysteresis loop describes the energy dissipation ability of the SMA damper and indicates the conspicuous damper property of the SMA materials.

To investigate the performance of the SMA damper, using the model described above, on the mitigation of a stay cable first mode vibration, we proceed with solving the equation of motion (12) of the combined stay cable/SMA damper system. The device was installed on the cable at location \(x_d=0.1 L\) from the left end. Since the SMA damper force cannot be decoupled due to its hysteretic performance, a nonlinear property occurs in the combined stay cable/SMA damper system. Thus, a Newmark numerical method programmed in MATLAB is developed to compute the dynamic response of the cable. The considered stay cable used to carry out this investigation is the longest cable (S16) in Rades-La Goulette cable-stayed bridge in Tunisia. The geometrical and material properties of the cable (S16) are summarized in Table 2.

Table 2 Geometrical and mechanical design properties of the stay cable (S16) of the Rades-La Goulette cable-stayed bridge
Full size table

It is seen from Fig. 3 that the SMA damper accomplishes a significant reduction of the first mode response, thanks to hysteretic performance, as compared to the case without the damper. Dissipating the energy coming from the motion of the stay cable, the SMA damper can effectively enhance the damping capacity of the cable. It can be also observed that when the SMA is installed the vibration amplitude is reduced very quickly. However, it can be noted from this simulation that the SMA damper is not able to control the small vibration, because the SMA deformation is smaller than \(1\%\). In this zone, the SMA has purely an elastic behavior and the hysteresis is not yet built. Nevertheless, in practice, this is not a real disadvantage, since one focuses on the large vibrations for cable-stayed bridges [34].

Optimal SMA Damper Size for Control the First Vibration Mode

In this study, we address high energy dissipation and complete deformation recovery ability as well provided by the SMA damper model. To determine the parameters leading to a maximum damping capacity, reference is made to a criterion developed in [34], which is based on the energy balance. The optimal parameters of the device in free vibration are selected in a way to maximize the force generated by the SMA damper which is expressed as follows:

$$\begin{aligned} F_d(t) = E \pi R^2_{\text {SMA}} \bigg (\frac{v(x_d,t)}{L_{\text {SMA}}}-\zeta _s \epsilon _L sign(\epsilon )\bigg ) \end{aligned}$$
(13)

In witch \(v(x_d, t)\) denotes the cable transverse displacement at the attached point \(x_d\), \(R_{\text {SMA}}\) is the damper wire radius, \(L_{\text {SMA}}\) represents the length the of the SMA device, \(\zeta _s\) is a scalar internal variable representing the martensite fraction and \(\epsilon _L\) is the maximum residual strain, issue from additive decomposition of the total strain \(\epsilon\):

$$\begin{aligned} \epsilon =\epsilon ^{e}+\epsilon _{L} \zeta _s sgn(\sigma ) \end{aligned}$$
(14)

where \(\epsilon ^{e}\) is the elastic strain.

According to (13), the damper capacity is strongly related to the SMA parameters (length and wire diameter) as well as its attached point. The position leading to a maximum force generated by the actuator is 0.5 L as shown in Fig. 4. However, it is wise to choose for practical reasons a location as close as possible to the deck side anchorage. The considered location is \(x_d =0.1\) L from the support A in the x direction.

Fig. 4
figure 4

Position effect of the attached SMA damper on the cable dynamic response

Full size image

It’s clear that the maximum damper force increases with the increase of the wire diameter and the decrease of the length of the device. To approve this numerically, we proceed first by fixing the length at \(L_{\text {SMA}}=300\) mm and varying the damper radius \(R_{\text {SMA}}\) as 2 mm, 4 mm and 10 mm, then the radius is fixed at 2 mm and the length was ranged. The choice takes into account the objectives cited above, searching for a high energy dissipation and complete deformation recovery ability and avoiding the displacement to be limited by passing solely through the original point. The decay responses of the first mode in the followed 15 s for different sectional areas are plotted for comparison in Fig. 5. It shows that the damping of the stay cable transverse vibration increases when the damper diameter increases; Decreasing the length of the SMA damper, the amplitude of the cable transverse vibration decreases accompanied by an increase in the surface of the hysteresis loop, as shown in Fig. 6. This numerical results confirm the analytical deduction drawn from Eq. (13). Hence, for a damper located at \(10 \%\) of cable length from the left anchorage, the optimum SMA damper parameters set for control the first mode vibration are P1: \(L_{\text {SMA}}= 300\) mm and \(R_{\text {SMA}}= 10\) mm.

Fig. 5
figure 5

Diameter effect of the attached SMA damper on the cable dynamic response—\(L_{\text {SMA}}=300\) mm

Full size image
Fig. 6
figure 6

Length effect of the attached SMA damper on the cable dynamic response—\(R_{\text {SMA}}=2\) mm

Full size image

Then, a numerical investigation which seeks to compare the performance of the optimal SMA damper size with a magnetorheological (MR) damper on the vibration mitigation of the considered cable is carried out. The idea of comparing the two devices amounts to the fact that the MR damper is filled with smart materiel (MR fluid) and also is able to reproduce hysterical behavior. An hysteretic regularized Bingham model (HRB) proposed and developed in [44] is used to describe the force velocity response of the MR device. The damping force defined for every piston velocity \(v_d \in [-v_m,v_m]\) by

$$\begin{aligned} \begin{array}{ll} F_{d}^{\text {HRB}} (t) - F_0 = \\ \left\{ \begin{array}{ll} C_v (v_d-v_h) + F_y \Bigg [1-\exp \bigg (-\text {sgn} (v_d-v_h) \displaystyle \frac{v_d-v_h}{v_0}\bigg )\Bigg ] \text {sgn} (v_d-v_h) \quad \text {for } \dot{v_d}<0 \\ C_v (v_d+v_h) + F_y \Bigg [1-\exp \bigg (-\text {sgn} (v_d+v_h) \displaystyle \frac{v_d+v_h}{v_0}\bigg )\Bigg ] \text {sgn} (v_d+v_h) \quad \text {for } \dot{v_d}>0 \end{array} \right. \end{array} \end{aligned}$$
(15)

where \(v_0\) denotes the regularization parameter, which has a velocity dimension and controls the exponential growth of the damping force, \(v_h\) is a scale factor having the dimension of a velocity which defines the width of the hysteresis loop and \(v_m\) denotes the maximum reached velocity of the damper piston, \(v_d\) is the piston velocity, \(F_0\) is the offset in the damping force due to the presence of the accumulator, \(F_y\) denotes the frictional force related to the yield stress of the MR fluid (generally depending on the applied magnetic field) and \(C_v\) the damping coefficient. The latter is defined as the slope of the damping force versus the piston velocity and is related to the plastic viscosity of the MR fluid.

The obtained hysteresis loop depicted in Fig. 7 is composed of an upper curve relating to the force variation with respect to the decreasing velocities, and a lower curve corresponding to the force variation with increasing velocities. The six parameters \(F_0\), \(F_y\), \(C_v\), \(v_0\), \(v_h\) and \(v_m\) of the HRB model are identified by fitting the model predictions with reported experimental data (see [44]).

Fig. 7
figure 7

Hysteretic regularized Bingham model (HRB)

Full size image
Fig. 8
figure 8

MR damper at various input currents

Full size image

The MR damper used operates with step by step power supply. To switch from one input current to another, the device requires a control law, as shown in Fig. 8. We point out that the value of Fy is sensitive to the change of the electrical current supplied to the damper. However, we use the MR damper for a single step current, that of the maximum input current (2A) which leads to a passive consideration of the damper configuration.

Figure 9 left outlines the vibratory response of cable controlled by MR damper described by HRB model as well as the standard Bingham model. It can be observed from Fig. 9 right the force evolutions computed by considering the HRB model and the Bingham model. It is worth noting that the cable vibration is damped more effectively when using the HRB model.

Fig. 9
figure 9

Control of the first stay cable free vibration: comparison between the HRB model and the Bingham model (current 2A)

Full size image
Fig. 10
figure 10

Control of the first stay cable free vibration: comparison between the optimal SMA damper size P1 and the MR damper described with both models HRB and Bingham (current 2A)

Full size image

Figure 10 compares the modal contributions of the first vibration mode \(\alpha _1(t)\) controlled with MR damper considering Bingham model and HRB model as well as the optimized SMA damper. Modal contributions have been obtained by solving Eq. 12. According to Fig. 10, it can be observed that the largest vibration response using the optimized SMA damper model decay speed than the one obtained using MR damper for both cases. Thus, through these results, we highlight a better performance of a passive designed SMA absorber compared to the MR absorber. These findings are important given that MR damper needs an external power supply which making it less recommended in practice.

Optimal SMA Damper Size for Control Coupled Modes

Governing Equations for Coupled System

Considering the equation of motion (10) and the sinusoidal modal shape given in (9), the elements in the Eq. (10) are calculated as follows:

$$\begin{aligned}&\int _{0}^{L} \phi _i(x) \phi _j(x) \mathrm {d}x = \left\{ \begin{array}{l l} L/2 &{} \quad {\text {if} ~~ i = j}\\ 0 &{} \quad {\text {if} ~~ i \ne j}\\ \end{array} \right. \end{aligned}$$
(16)
$$\begin{aligned} \int _{0}^{L} \phi ''_i(x) \phi _j(x) \mathrm {d}x&= \left\{ \begin{array}{l l} -\frac{(i\pi )^2}{2 L} &{} \quad {\text {if} ~~ i = j}\\ 0 &{} \quad {\text {if} ~~ i \ne j}\\ \end{array} \right. \end{aligned}$$
(17)
$$\begin{aligned}&\int _{0}^{L}\Bigg ( \phi _j(x) \int _{0}^{L}\phi _i(x) \mathrm {d}x\Bigg )\mathrm {d}x =\nonumber \\&\left\{ \begin{array}{l l} \frac{ L^2}{(i\pi )^2}(\cos (i\pi )-1)^2 &{} \quad {\text {if} ~~ i = j}\\ \frac{(L)^2}{ij (\pi )^2} [\cos (j\pi ) \cos (i\pi )-\cos (j\pi )-\cos (i\pi )+1] &{} \quad {\text {if} ~~ i \ne j}\\ \end{array} \right. \end{aligned}$$
(18)

The equations of the system (18) take the form:

$$\begin{aligned}&\frac{(L)^2}{ij (\pi )^2} [\cos (j\pi ) \cos (i\pi )-\cos (j\pi )-\cos (i\pi )+1] =\nonumber \\&\left\{ \begin{array}{l l} \ 0 \quad {\text {if} ~~ i~~ \text {pair}~~ \text {and}~~ j~~ \text {pair}}\\ \ 0 \quad {\text {if} ~~ i~~ \text {pair}~~ \text {and}~~ j~~ \text {impair}}\\ \frac{4(L)^2}{ij (\pi )^2} \quad {\text {if} ~~ i~~\text {impair} ~~ \text {and}~~ j~~ \text {impair}}\\ \end{array} \right. \end{aligned}$$
(19)
$$\begin{aligned}&\frac{ L^2}{(i\pi )^2}(\cos (i\pi )-1)^2 =\nonumber \\&\left\{ \begin{array}{l l} \ 0 \quad {\text {if} ~~ i~~ \text {pair}}\\ \frac{4(L)^2}{i\pi )^2} \quad {\text {if} ~~ i~~ \text {impair}}\\ \end{array} \right. \end{aligned}$$
(20)

Considering the first three mode of vibration and substituting Eqs. (16)–(18) into Eq. (10), the non-dimensional modal participation factors projected, respectively, on the first, second and third mode are found to be

$$\begin{aligned} \left\{ \begin{aligned} m_c\frac{L}{2}~\ddot{\alpha }_1(t)+\bigg (\frac{\pi ^2T}{2L}+\frac{4\lambda ^2L^2}{\pi ^2}\bigg )\alpha _1(t)+\frac{4\lambda ^2 L^2}{3\pi ^2}\alpha _3(t)=-F_d(t)\phi _1(x_d)&\\ m_c\frac{L}{2}~\ddot{\alpha }_2(t)+\frac{4\pi ^2T}{2L}\alpha _2(t)=-F_d(t)\phi _2(x_d)&\\ m_c\frac{L}{2}~\ddot{\alpha }_1(t)+\bigg (\frac{9\pi ^2T}{2L}+\frac{4\lambda ^2L^2}{9\pi ^2}\bigg )\alpha _3 (t)+\frac{4\lambda ^2 L^2}{3\pi ^2}\alpha _1 (t)=-F_d(t)\phi _3(x_d)&\end{aligned} \right. \end{aligned}$$
(21)

Written the previous equations in matrix form:

$$\begin{aligned}{}[\mathbf {\widetilde{M}}][\mathbf {\ddot{\alpha }}]+ [\mathbf {\widetilde{K}}][\mathbf {\alpha }]= -[\mathbf {\widetilde{F}_d}] \end{aligned}$$
(22)

where

\(\mathbf {\widetilde{M}}=\begin{pmatrix} m_c\frac{L}{2} &{} 0 &{} 0 \\ 0 &{} m_c\frac{L}{2} &{} 0 \\ 0 &{} 0 &{} m_c\frac{L}{2} \end{pmatrix}\)

is the mass matrix,

\(\mathbf {\widetilde{K}}=\begin{pmatrix} T\frac{\pi ^2}{2L}+\frac{4\lambda ^2 L^2}{\pi ^2} &{} 0 &{} \frac{4\lambda ^2 L^2}{3\pi ^2} \\ 0 &{}4 T\frac{ \pi ^2}{2L} &{} 0 \\ \frac{4\lambda ^2 L^2}{3\pi ^2} &{} 0&{} 9T\frac{\pi ^2}{2L}+\frac{4\lambda ^2 L^2}{\pi ^2} \end{pmatrix}\) is the stiffness matrix and

$$\begin{aligned} \mathbf {\widetilde{F}_d}= \bigg [F_d \sin \bigg (\frac{\pi x_d}{L}\bigg ) ~~~~ F_d \sin \bigg (\frac{2\pi x_d}{L}\bigg ) ~~~ F_d \sin \bigg (\frac{3\pi x_d}{L}\bigg )\bigg ]^t \end{aligned}$$
(23)

is the force vector. It is useful to observe that the antisymmetric modes of vibration of the transversal dynamical equations (22) are coupled.

Control of the First Three Coupled Modes with the SMA Damper Optimized for a Single Mode

To analyze the effect of optimized SMA damper parameters P1 used to control the first mode of the transverse cable dynamic response, the non-dimensional modal participation factors for the three modes of the stay cable are obtained by solving (22) and considering that the SMA damper is incorporated as previously considered at \(x_d=0.1\) L.

Fig. 11
figure 11

Comparison between non-controlled modes and controlled modes with SMA damper using parameters set P1

Full size image

Figure 11 illustrates the evolution of the first three modes coupled transverse free vibration, where the cable is equipped with the SMA actuator superimposed with the non-controlled modes. It’s observed that the SMA damper is unable to control the three modes as well as the case of decoupling modes, even worse the presence of the SMA damper leads to an enormous increase in the vibration amplitude for the three modes considered. This result imposes the use of other optimization settings for a multi-modal control.

Optimization Criterion to Control Multiple Modes

The optimization criterion considered here is based on the calculation of an aerodynamic instability coefficient known in the literature by the Scruton number \(S_c\) that quantifies the additional damping to the cable. According to Irvine [18], a cable is aerodynamically stable, especially if he is excited by the wind or spouse wind / rain phenomenon, though its Scruton number is above a given threshold value \(S_0\) =10 [18, 50]. This number is expressed as

$$\begin{aligned} S_c=\frac{m_c\xi }{\rho D^2} \end{aligned}$$
(24)

where \(\rho\) is the air density, D is the cable diameter and \(\xi\) is the equivalent damping coefficient that depends on the geometrical parameters of the actuator. Thus, an optimization criterion is formulated as follows:

$$\begin{aligned} \displaystyle \max _{S_c>S_0} \xi (R_{\text {SMA}}, L_{\text {SMA}}) \end{aligned}$$
(25)

The calculation of equivalent damping coefficient requires the determination of the force provided by the SMA damper. It is described by a non-linear hysteresis loop, as shown in Fig. 12. The damping force is expressed on different parts of the hysteresis.

Fig. 12
figure 12

Hysteresis loop produced by a SMA damper

Full size image
$$\begin{aligned} \begin{array}{ll} F_{d}(t) = \\ \left\{ \begin{array}{ll} k_1 v(x_d,t) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \quad \text {on the parts}~~(oab, oa'b')\\ (k_1-k_2) v_{db} ~\text {sgn}(v(x_d,t))+ k_2 v(x_d,t) ~~~~~~~~~~~~\quad \text {on the parts}~~ (bc, b'c') \\ (k_1-k_2) (v_{db}-v_{dc}~ \text {sgn}(v(x_d,t))+ k_1 v(x_d,t) ~~~\quad \text {on the parts}~~ (cd, c'd') \\ (k_1-k_2) v_{da} ~\text {sgn}(v(x_d,t))+ k_2 v(x_d,t) ~~~~~~~~~~\quad \text {on the parts}~~ (da, d'a') \end{array} \right. \end{array} \end{aligned}$$
(26)

where sgn is the sign function; \(k_1\) et \(k_2\) are the respective slopes of the segments ab and bc; \(v_{da}\) and \(F_{da}\) are the displacement and the damper force developed at point a; \(v_{db}\) et \(F_{dy}\) are the displacement and the damper force developed at point b; \(v_{dc}\) et \(F_{dc}\) are the maximal displacement and the damper force developed at pointc. The damping coefficient \(\xi\) is given by [25]

$$\begin{aligned} \xi =\frac{\Delta E_{di}}{4 \pi (E_{\text {ssi}}+E_{\text {sci}})} \end{aligned}$$
(27)

where \(\Delta E_{di}\) is twice the area of the parallelogram abcd shown in Fig. 12, \(E_{\text {ssi}}\) is the deformation energy of the system cable/ SMA damper associated with the appropriate vibration mode and \(E_{\text {sci}}\) means the double surface of the trapezium \(o a b c v_{dc}\) shown in Fig. 12. \(\Delta E_{di}\), \(E_{\text {ssi}}\) et \(E_{\text {sci}}\) are formed as follows:

$$\begin{aligned} E_{ssi}=k_1v_{db}^2+k_1[\alpha v_{dc}+(2-\alpha )v_{db}](v_{dc}-v_{db}) \end{aligned}$$
(28)
$$\begin{aligned} \Delta E_{di}=k_1 v_{db}(1-\beta )(1-\alpha )(v_{dc}-v_{db}) \end{aligned}$$
(29)
$$\begin{aligned} E_{\text {sci}}= \frac{T\pi ^2 i^2 v_{dc}^2}{kL\sin ^2(i\pi x_{d}/L)} \end{aligned}$$
(30)

where \(\beta =F_{da}/F_{dy}\), \(\alpha =k_1/k_2\), \(k=k_1/T\).

The criterion (25) allows to take into account the multi-modal effect given that the force \(F_d\) depends on SMA geometric parameters and also on the displacement \(v(x_d,t)\) of the cable at the point \(x_d\) as indicated in Eq. 13. Since displacement depends on all evoked modes (according to 7), the area of the hysteresis is indirectly dependent on the three modes.

Multi-modal Control Using Optimally Designed SMA Damper

The numerical resolution of the optimization criterion shown in (25) was developed to determine the optimal size for multi-modal control (\(R_{\text {SMA}}\) and \(L_{\text {SMA}}\)). Simulations are based on the mathematical bisection method (Dichotomy). The optimization constraints satisfy: The considered \(R_{\text {SMA}}\) and \(L_{\text {SMA}}\) should be positive values and the length of the damper must be greater than the practical length (20 cm). The non-construction of hysteresis was the stop test. The optimized parameters obtained are : \(R_{\text {SMA}}= 20\) mm and \(L_{\text {SMA}}=850\) mm, which will be noted in the following by P2.

Fig. 13
figure 13

Damping force for both parameter sets P1 and P2

Full size image

The hysteresis curve of the total force provided by the SMA damper for both parameter sets P1 and P2 is shown in Fig. 13. Figure 14 presents the dynamic responses of the first three modes and the damping force produced for each mode considering parameter sets P2. The corresponding damping ratios are \(\xi _1= 0.458 \%\), \(\xi _2= 1.7 \%\), \(\xi _3= 2.4 \%\). Those associated with parameter sets P1 are: \(\xi _1= 0.0042 \%\), \(\xi _2= 0.015\%\), \(\xi _3= 0.034\%\).

Fig. 14
figure 14

Dynamic response of coupled three modes using the parameter sets P2

Full size image
Fig. 15
figure 15

Comparison between the performances of the SMA damper using the two parameter sets P1 and P2

Full size image
Fig. 16
figure 16

Comparison between non-controlled and controlled three modes with SMA damper using parameter sets P2

Full size image

Figure 15 shows the evolution of the first three modal participation of the stay cable (S16) using specific parameter P2 to control coupled modes. These curves are compared with those corresponding to parameter P1 optimized for the first mode. It follows from the comparison that the implementation of parameter sets P2 results in a much better damping than parameter sets P1 optimized for a single mode.

In addition, it mounted in Fig. 16 that optimized settings for multi-modal control P2 lead to a simultaneous control of the first three modes. These results are explained by the fact that the formulated optimization criterion (25) is not satisfied by considering the parameter sets P1, since the Scruton numbers obtained for each mode are: \(S_{c1}=0.21\), \(S_{c2}=0.76\), \(S_{c3}=1.74\). It turns out that when the damper size is optimized only for the first mode, the Scruton numbers are not enough for suppressing multi-mode vibration which much be greater than 10 . However, the corresponding Scruton numbers using parameter sets P2 are: \(S_{c1}=23.31\), \(S_{c2}=86.53\), \(S_{c3}=122.17\). Thus leading to a spectacular reduction in the amplitudes of all concerned modes .

Conclusions

The purpose of this work is to demonstrate the effectiveness of a passive SMA damper with superelastic properties to control coupled multi-mode vibrations. The following conclusions are reported:

  • Numerical simulations carried on the longest cable in the Rades-La Goulette cable-stayed bridge show the capability of SMA devise to reduce strongly the first vibration mode thanks to its excellent propriety of energy dissipation.

  • The capacity of SMA damper is closely linked to its geometric parameters. To achieve high energy dissipation, the damper size is optimized for the concerned mode through a parametric study.

  • The damping performance of the optimally designed SMA damper is numerically investigated in comparison with a magnetorheological damper. The passive designed SMA absorber is able to provide supplemental modal damping compared to MR absorber. These findings are important given that MR damper operates with a step by step power supply which making it less recommended in practice.

  • Optimized parameters for a single mode are insufficient to mitigate simultaneously three coupled modes of vibration.

  • An optimization criterion is analytically formulated aiming at a multi-modal control. The parameters optimized result in a high level damping to the concerned modes. The numerical simulations demonstrate that the passive SMA damper shows an efficiency to control coupled multi-modal vibrations of the stay cable by its superelastic property. This result is important, since the fundamental operation of the passive dampers is generally designed to reduce only one mode of vibration.