Introduction

Sandwich structures are exhaustively employed in spacecraft, civil structures, high-speed transportations, and automotive industries [1, 2] due to their tailored multi-functional features. In general, the sandwich structure construction comprises three parts: upper facesheet, lower facesheet, and middle core. The facesheets consist of a laminated composite structure having excessive stiffness and strength, and the core is made of foam [3] structure with low density to impart low weight. These structures have high energy absorption and impact resistance [4,5,6]. The functionally graded materials (FGM) are composed of two main constitutes, namely ceramic and metal. In FGM, one free surface is metal-rich, providing high strength and stiffness to the structure. In contrast, the other free surface is ceramic-rich, providing sustainability to its strength at elevated temperature and resistance to corrosion. Due to limitations in sandwich structures such as low temperature-resistant and corrosion-resistant properties, its facesheet can be replaced by functionally graded materials (FGM) instead of laminated composites. Therefore, combining both sandwich and functionally graded structures, the hybrid multi-functionally graded sandwich (HMGS) shell is idealised in the present study, exhibiting the novelty of superiority and tailoring in properties.

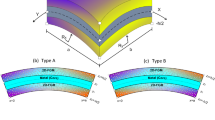
In the past, studies related to such structures were conducted by Tung [7] for the post-buckling, bending, and buckling behaviour of these FG-sandwich plates. The finite element method (FEM) is incorporated to design FG-sandwich plates by employing shear deformation theories [8]. Later on, some researchers [9,10,11,12,13,14] developed various computational models for dynamic characteristics of hybrid functionally graded (FG)-sandwich structure. On referring to these works of literature, generalised observations are obtained. First, advanced computational methods are primarily required for analysing these hybrid FG-sandwich structures. Second, these hybrid structures are employed in advanced applications, and third, it performs better than the conventional sandwich structures. Therefore, the present study focuses on a computational framework for mapping triggering parameter sensitivity (both geometric and material properties). Hence, a novel functional class of HMGS shells is considered for random free vibration. In the present study, six cases are categorised to analyse these hybrid structures as described in Table 1 and furnished in Fig. 1.

Table 1 Shell geometries created on considering a = 2 in the present study (a = numerical value of Rx and Ry, and Rx and Ry is the radius of curvature in x and y direction, respectively)
Full size table
Fig. 1
figure 1

Geometric configurations of HMGS shells: a cylindrical (Scyl.), b spherical (Ssph.), c elliptical paraboloid (Sell.), and d hyperbolic paraboloid (Shyp.) and e, f shell model

Full size image

In aerospace, civil construction, naval, and automobile sectors, hybrid FG shell-type structures play a vital role. But while using shell-type forms, it is challenging to maintain the standard, as they often lead to non-conformity from their deterministic design specification. In addition, the manufacturing processes of these HMGS structures are pretty complicated due to multiple sources of uncertainties. The overall responses have notable stochastic variations because of these uncontrollable fluctuations (material properties and geometric variation). Therefore, adopting such methods is essential to design safe and reliable hybrid structures. Therefore, it is critically needed to consider these uncertainties by promoting an exclusive method for analysing such structures. Hence, the present study is aimed to investigate the sensitivity of elliptical paraboloid, cylindrical, hyperbolic paraboloid, and spherical-shaped HMGS shells (Fig. 2) towards their stochastic dynamic responses.

Fig. 2
figure 2

Six cases of hybrid multi-functionally graded sandwich (HMGS) structures

Full size image

Many researchers worked on a deterministic approach for dynamic analyses of plate and shell structures [15,16,17,18]. An analytical study is performed for the dynamic response of sandwich structures under blast loading [19]. Cui et al. [20] and Zhu et al. [21] worked on sandwich plates having square geometry to find the analytical solution for the dynamic response using the energy balance method. Under blast loading, dynamic responses are studied on rectangular sandwich plates [22, 23]. Dharmasena et al. [24] worked on metal honeycomb sandwich structures under the influence of explosive loading. They observed that the small impulse causes the bending of the plate near the load, and the core gradually buckle. Cui et al. [25] and Zhu et al. [26] worked on a honeycomb sandwich structure with a tetrahedral lattice structured core. The obtained results illustrate that tetrahedral design portrays better impact resistance than the hexagonal sandwich core. Jamil et al. [27] worked on Al-thermoplastic polyurethane sandwich structures and found that the structure executed better blast resistance by adding thermoplastic polyurethane. Reyes [28] applied the energy balance approach to study the impact behaviour of the sandwich structure having thermoplastic fiber–metal laminated facesheet and Al-based core. The result indicates that the residual flexural strength is increased significantly. Low-velocity impact behaviour of sandwich structure having Al-core and glass fiber reinforced polypropylene-fiber–metal laminated facesheet is investigated [29]. Liu et al. [30, 31] worked on an Al-based core and fibre-metal laminated facesheet, wherein low-velocity impact response is studied and then switched to high-velocity impact response. Basturk et al. [32] studied the dynamic response of fiber–metal laminated Al-based core sandwich plate. Six porous models were considered to analyse the wave propagation of a ceramic–metal functionally graded sandwich plate. It was found that fluctuation in hygro-thermal stresses and moisture content plays an important role [33]. Similarly, three different orientations of sandwich beams were considered to analyse the natural frequencies of an FG material. The layup schemes and thickness ratio of skin–core-skin have vital importance in evaluating the non-dimensional natural frequencies [34]. An optimised shear deformation theory was developed for sandwich structures with FG facesheet and FG hardcore [35]. A square sandwich plate was considered to analyse the free vibration of a porous FG material. A varied boundary condition was presented to investigate the effects of porosity in volume fraction, lay-up configuration, and thickness ratio [36]. On the same note, a variation in moisture and temperature was conducted to analyse the free vibration of the FG-sandwich plate. The results show that the damping coefficient is directly proportional to the free vibration of the material [37]. A reliable design was proposed to analyse the thermo-mechanical properties of FG steel incorporating Fourier series expansion and the Galerkin method [38]. Similarly, free vibrational analyses of FG conical shell panels suggested that thickness and boundary conditions have significant effects. A mesh-free Ritz method was employed to perform the analysis [39]. An analytical approach based on Fourier series and Laplace transformation is incorporated to analyse FG piezoelectric cylindrical panels [40]. The hygro-thermal and mechanical behaviour was analysed for FG ceramic plate to investigate the effects of moisture, temperature, and damping coefficients [41]. A bending analysis was performed utilising higher-order shear deformation theory, and a Navier-type solution was obtained under transverse loading conditions [42]. Buckling and free vibration analyses were carried out for functionally graded carbon nanotube-reinforced quadrilateral and skew laminates [45]. Detailed numerical results were obtained by the discrete singular convolution method. An alteration in the weight fraction of carbon nanotubes was considered to analyse the static stability analysis of carbon nanotube reinforced polymeric composite [48]. An imperfect porous FG plate was considered to analyse the free vibrational response, considering the cut-out effect, geometric variation, and volume fraction [49]. More work on functionally graded structures is presented in various literature [37, 43,44,45,46,47, 50,51,52,53]. The literature mentioned above summarised that extensive work on sandwich and FGM structure is carried out. But, the studies on the dynamic response of hybrid structures are limited. In a real-life situation, the sources of uncertainty should be considered for the reliability and safety of these structures. Monte Carlo simulation (MCS) is one of the most preferred approaches for probabilistic modelling. This technique's effectiveness lies in how the random numbers are generated from the pseudo-random number generator. The limitation of this technique is high computational cost and time. MCS is quite an expensive process; the quality of uncertainty prediction directly depends on the number of simulations. Therefore, surrogate models are integrated with the MCS technique to overcome this problem and the computationally efficient overall process. Some literature [54,55,56,57,58,59,60,61] showcased utilising MCS and MARS in the stochastic domain to analyse the natural frequency of FGM cantilever plates at different temperatures. For the present study, MARS is integrated with the finite element framework.

In the past, the sensitivity analysis is linked with the material properties and geometric shape and size [62,63,64,65,66,67,68,69,70,71,72,73]. Many researchers focussed on sensitivity analysis while considering buckling, statics, and transient response problems. In the deterministic regime, sensitivity analysis involved two methods, namely, variational and implicit differentiation [74, 75]. The variational method requires differentiation of the structural response continuum governing equations. Still, this method cannot be applied under challenging problems, while the implicit differentiation method involves the derivation of the discrete formulations of the FE method. Therefore, the latter method became more popular. Later on, the sensitivity analysis is further classified into two parts, namely, local sensitivity and global sensitivity, respectively. The local sensitivity is computed based on the derivate of the response function, while the global sensitivity considers the overall response behaviour. Therefore, it is evident that local sensitivity is more accessible to compute than global sensitivity. The only disadvantage is that it considers sensitivity concerning the base point, which is less critical. The global sensitivity analysis is preferred for determining the overall response behaviour; it deals with system stochasticity. But there are some limitations to these global sensitivity analyses as they require extensive function evaluations; therefore, it becomes computationally expensive and requires enormous time and cost. Surrogate-based global sensitivity is adapted to overcome these limitations. This method aims to make the process computationally efficient by reducing expensive simulations. Hamdia et al. [76].

Hamdia et al. [76] worked on flexo-electric material for sensitivity analysis. Three surrogate models are employed: extended Fourier amplitude, PCE-Sobol, and Morris One-At-a-Time model. Antonio and Hoffbauer [77] performed reliability and sensitivity analysis of composite structures, determining random input parameter’s effect by utilising ANN integrated with MCS. Zhang et al. [78] worked on composite beam damage detection and performed a sensitivity analysis to analyse noise's effect. Sensitivity analysis is adapted on laminated composites utilising the topological derivative mapping method to obtain optimal design [79]. Bishay and Sofi [80] performed sensitivity analysis on composites to construct robotic fingers. A comparative study of variance moment independent based method is conducted by Zadeh et al. [81], whereas Zhao and Bu [82] worked on global sensitivity analysis considering hierarchical sparse meta-modelling approach. Vu-Bac et al. [83] developed software to analyse the probabilistic sensitivity for computationally expensive models.

The earlier discussion concludes that most studies related to the dynamic analysis of hybrid structures are carried out in a deterministic framework. In real-life situations, various uncertainties are involved in every system, which is unavoidable. These uncertainties can be material properties and geometric uncertainties, environmental uncertainties. Therefore, for the safety and reliability of the system, these uncertainties should not be neglected. The stochastic dynamic analysis in the case of hybrid FG-sandwich structure is scarce in past literature. The manufacturing of these hybrid structures is quite complex; in addition to it, the shell-type construction adds to its complexity. Therefore, there is a great chance that the designed structure will contain deviation from the initial design specification. The stochastic study plays great importance as it considers these uncertainties while carrying out the analysis, making the study more reliable. The present study includes the sensitivity analysis in conjunction with random frequency responses of HMGS shells considering various shell geometries and various cases (based on the construction of a hybrid structure). The sensitivity analysis of such structures for dynamic analysis considering traditional MCS is computationally expensive. The MARS model is constructed and integrated with the finite element framework to avoid it. With this analysis, the relative effects of individual material and geometric properties are portrayed in the light of the structure's uncertain global frequency response. There lie two novelties in the present work. This is the first attempt to incorporate MARS with the efficient MCS for stochastic dynamic analysis of HMGS shells. As discussed earlier that MCS is quite an exhaustive process, requiring excessive time and cost. Therefore, implementing the surrogate (here, MARS) with the FE model makes the process computationally efficient. This surrogate-based approach enhances efficiency when dealing with a complex and realistic system. To the best of the authors' knowledge, this is the first attempt to perform the sensitivity analysis of HMGS shells with different geometries and structural forms. From the earlier discussion, it is known that manufacturing these HMGS structures is pretty complicated, involving multiple sources of uncertainty. Because of these uncontrollable fluctuations (material properties and geometric variation), there is a notable amount of stochastic variation in the system's overall response. Therefore, adopting such methods is essential to design a safe and reliable structure. Therefore, it is critical to consider these uncertainties and have an exclusive method for analysing such structures. Such detailed, exhaustive studies are needed while designing such structures.

Theoretical Formulation

The present study deals with hybrid multi-functionally graded sandwich (HMGS) shells with cantilever boundary conditions. The different shell geometries are considered, such as spherical, hyperbolic paraboloid, cylindrical, and elliptical paraboloid geometries (Fig. 1 and Table 1). Six different cases of HMGS (Fig. 2 and Table 2) are considered for the sensitivity analysis in conjunction with random frequency responses.

Table 2 Six cases of hybrid multi-functionally graded sandwich (HMGS) structures
Full size table

Governing Equation

To obtain the material properties FGM sheet, power-law [84, 85] is employed, and the same is expressed as,

$${\mathbf{A}}(h) = {\mathbf{A}}_{\mathrm{m}} + [{\mathbf{A}}_{\mathrm{c}} - {\mathbf{A}}_{\mathrm{m}} ]\left[ {\frac{(2z + h)}{{2h}}} \right]^{n} ,$$
(1)

where n represents the power-law index, A represents the various material properties. Here, \(A_{{\text{m}}}\) indicate the properties of metal while \(A_{{\text{c}}}\) shows the properties of ceramics. In the above equation, h represents the thickness/depth of the FGM plate, whereas \(z = {\raise0.7ex\hbox{${ - t}$} \!\mathord{\left/ {\vphantom {{ - t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\) and \(z = {\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\) indicates the upper and lower layer of the plate, and x represents the power-law exponent. Here, the temperature-dependent material properties are expressed as [86],

$$A = A_{0} + A_{{ - {1}}} T^{ - 1} + 1 + A_{1} T + A_{2} T^{2} + A_{3} T^{3} ,$$
(2)

where T represents the temperature value in Kelvin and \(A_{0}\),\(A_{ - 1}\),\(A_{1}\),\(A_{2}\) and \(A_{3}\) are the values of temperature coefficients. According to the first-order shear deformation theory, the following Eqs. (3), (4), and (5) are employed to represent the displacement field as,

$$a\left( {x,y,z} \right)(\varpi ) = a_{0} \left( {x,y} \right)(\varpi ) - za\left( {x,y} \right)(\varpi ){\mathcal{R}}_{x} \left( {x,y} \right)(\varpi ),$$
(3)
$$b\left( {x,y,z} \right)(\varpi ) = b_{0} \left( {x,y} \right)(\varpi ) - zb\left( {x,y} \right)(\varpi ){\mathcal{R}}_{y} \left( {x,y} \right)\left( \varpi \right),$$
(4)
$$c\left( {x,y,z} \right)(\varpi ) = c\left( {x,y} \right)(\varpi ) = c_{0} \left( {x,y} \right)(\varpi ),$$
(5)

where the stochastic displacement in x, y, and z-direction is represented by \(a(\varpi )\), \(b(\varpi )\) and \(c(\varpi )\), respectively, and the stochastic displacement at mid-plane in x, y, and z-direction is represented by \(a_{0} (\varpi )\), \(b_{0} (\varpi )\) and \(c_{0} (\varpi )\) respectively, whereas rotation in the direction of x and y direction is represented by \({\mathcal{R}}_{x} (\varpi )\) and \({\mathcal{R}}_{y} (\varpi )\) respectively. The symbol ‘\((\varpi )\)’ represents the degree of stochasticity in the respective input parameters. The generalized stochastic dynamic equilibrium equation [9] can be expressed as,

$$\left\{ {{\mathbf{\ddot{u}}}(\varpi )} \right\} + \left[ {{\mathbf{c}}(\varpi )} \right]\left\{ {{\dot{\mathbf{u}}}(\varpi )} \right\} + \left[ {{\mathbf{k}}(\varpi )} \right]\left\{ {{\mathbf{u}}(\varpi )} \right\} = \left\{ {f(\varpi )} \right\},$$
(6)

where \(\left\{ {{\mathbf{u}}(\varpi )} \right\}\) is the global displacement vector, \([m(\varpi )]\) is the global mass matrix, \([{\mathbf{c}}(\varpi )]\) is the global damping matrix, \([{\mathbf{k}}(\varpi )]\) represent the global stiffness matrices, while \(\left\{ {{\mathbf{f}}(\varpi )} \right\}\) is an external force vector. Considering free vibration, the above equation can be reduced as,

$$\left[ {{\mathbf{m}}(\varpi )} \right]\left\{ {{\mathbf{\ddot{u}}}(\varpi )} \right\} + \left[ {{\mathbf{k}}(\varpi )} \right]\left\{ {{\mathbf{u}}(\varpi )} \right\} = 0.$$
(7)

The static components, as well as time-dependent components, are considered for dynamic analysis. Here, the displacement vector \(\left\{ {{\mathbf{u}}({\varpi })} \right\}\) contains both static and a dynamic term \(\left[ {\left\{ {{\mathbf{u}}(\varpi )} \right\} = \left\{ {{\mathbf{u}}_{s} (\varpi )} \right\} + \left\{ {{\mathbf{u}}_{p} (\varpi )} \right\}} \right]\), where \(\left\{ {{\mathbf{u}}_{p} ({\varpi })} \right\}\) is a minor linear time reliant perturbation about \(\left\{ {{\mathbf{u}}_{s} ({\varpi })} \right\}\), while \(\left\{ {{\mathbf{u}}_{s} ({\varpi })} \right\}\) is expressed as the static displaced position. The equation of motion can be stated as,

$$\left[ {{\mathbf{m}}(\varpi )} \right]\left\{ {{\mathbf{\ddot{u}}}_{{\text{p}}} (\varpi )} \right\} + \left[ {{\mathbf{k}}({\varpi })} \right]\left( {\left\{ {{\mathbf{u}}_{{\text{p}}} ({\varpi })} \right\} + \left\{ {{\mathbf{u}}_{{\text{s}}} ({\varpi })} \right\}} \right) = 0.$$
(8)

Neglecting \(\left\{ {u_{{\text{s}}} (\varpi )} \right\}\), the equation of motion for free vibration can be expressed as,

$$\left[ {{\mathbf{m}}({\varpi })} \right]\left\{ {{\mathbf{\ddot{u}}}_{{\mathbf{p}}} ({\varpi })} \right\} + \left[ {{\mathbf{k}}({\varpi })} \right]\left\{ {{\mathbf{u}}_{{\mathbf{p}}} ({\varpi })} \right\} = 0$$
(9)

In Eq. (9), the displacement \(\left\{ {u_{{\text{p}}} (\varpi )} \right\}\) is a function of time and space. In free vibration analysis, the time and space coordinates of displacement function can be expressed as,

$$\left\{ {{\mathbf{u}}_{{\text{p}}} ({\varpi })} \right\} = {\mathbf{A^{\prime}}}{\text{e}}^{i\omega t} \{ {{\varvec{\uptheta}}}\} ,$$
(10)
$$\left\{ {{\mathbf{\ddot{u}}}_{{\text{p}}} ({\varpi })} \right\} = - {\mathbf{A^{\prime}}}\omega^{2} {\text{e}}^{i\omega t} \{ {{\varvec{\uptheta}}}\} .$$
(11)

On substituting the values of \(\left\{ {{\mathbf{u}}_{{\text{p}}} ({\varpi })} \right\}\) and \(\left\{ {{\mathbf{\ddot{u}}}_{{\text{p}}} ({\varpi })} \right\}\) in Eq. (9), the modified equation is

$${\mathbf{A^{\prime}}}e^{i\omega t} ( - {{\varvec{\upomega}}}^{{\mathbf{2}}} [{\mathbf{m}}({\varpi })]\{ {{\varvec{\uptheta}}}\} + [{\mathbf{k}}({\varpi })]\left\{ {{\varvec{\uptheta}}} \right\}) = 0$$
(12)

As \({\mathbf{{\rm A}^{\prime}}}e^{i\omega t} \ne 0\)

$${{\varvec{\upomega}}}^{{\mathbf{2}}} {\mathbf{[m}}(\varpi )]\{ {{\varvec{\uptheta}}}\} = [{\mathbf{k}}(\varpi )]\left\{ {{\varvec{\uptheta}}} \right\}.$$
(13)

Here, \(\omega\) imply natural frequencies. Now, utilising the standard eigenvalue problem [62], ω can be evaluated. QR iteration algorithm is employed to solve the equations. Now, Eq. (13) is further transformed as,

$$[{\mathbf{A}}]{\mathbf{\{ \theta }}\} = {{\varvec{\uplambda}}}(\varpi )\{ {{\varvec{\uptheta}}}\}$$
(14)
$$[{\mathbf{A}}] = [{\mathbf{k}}(\varpi )^{ - 1} ]({\mathbf{m}})\;{\text{and}}\;{{\varvec{\uplambda}}}(\varpi ) = \frac{1}{{({{\varvec{\upomega}}}(\varpi ))^{2} }}.$$
(15)

Finite Element Formulation

The finite element formulation of the hybrid shell is designed considering a bending element (eight noded) of an isoperimetric quadratic structure. Each node has (three translational and two rotational) five degrees of freedom. Polynomial shape functions with coordinates \(\xi ,\,\,\eta {\text{ and }}\,\zeta\) depict the displacement relation between the nodal values and the generalised equation. The interpolation polynomial function is stated as

$$a(\xi ,\eta ) = F_{0} + F_{1} \xi + F_{2} \eta + F_{3} \xi^{2} + F_{4} \xi \eta + F_{5} \eta^{2} + F_{6} \xi^{2} \eta + F_{7} \xi \eta^{2} ,$$
(16)

where \(F_{0} ,F_{1} ,.........F_{7}\) are the degrees of freedom.

The shape functions \(S_{i}\) can be shown as:

$${\mathbf{S}}_{{\mathbf{i}}} = 0.25\left( {1 + {\mathbf{\xi \xi }}_{{\mathbf{i}}} } \right)\left( {{\mathbf{1 + \eta \eta }}_{{\mathbf{i}}} } \right)\left( {{\mathbf{\xi \xi }}_{{\mathbf{i}}} {\mathbf{ + \eta \eta }}_{{\mathbf{i}}} - {\mathbf{1}}} \right)\quad i = 1,\,2,\,3,\,4,$$
(17)
$${\mathbf{S}}_{i} = 0.5\left( {1 + {\mathbf{\eta \eta }}_{i} } \right)\left( {1 - {{\varvec{\upxi}}}^{{\mathbf{2}}} } \right)\quad i = 5,7$$
$${\mathbf{S}}_{i} = 0.5\left( {1 + {\mathbf{\xi \xi }}_{{\mathbf{i}}} } \right)\left( {1 - {{\varvec{\upeta}}}^{{\mathbf{2}}} } \right)\quad i = 6,8.$$

The shape functions accuracy is given by

$$\sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1} ,\;\sum\limits_{i = 1}^{8} {\frac{{\partial {\mathbf{S}}_{i} }}{{\partial {{\varvec{\upxi}}}}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} 0\;{\text{and}}\;\sum\limits_{i = 1}^{8} {\frac{{\partial {\mathbf{S}}_{i} }}{{\partial {{\varvec{\upeta}}}}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.$$
(18)

The bending formulation by utilising the same shape functions for the coordinates (x,y) is stated as

$${\mathbf{x}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{x}}_{{\mathbf{i}}} } \;{\text{and}}\;{\mathbf{y = }}\sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{y}}_{{\mathbf{i}}} } .$$
(19)

The displacement at any point can be shown as (Fig. 3)

$${\mathbf{a}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{a}}_{{\mathbf{i}}} } ,\;{\mathbf{b}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{b}}_{{\mathbf{i}}} } ,\;{\mathbf{c}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{c}}_{{\mathbf{i}}} } ,\;{\mathbf{\varphi }}_{{\mathbf{x}}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{\varphi }}_{xi} } ,\;{\mathbf{\varphi }}_{{\mathbf{y}}} = \sum\limits_{i = 1}^{8} {{\mathbf{S}}_{{\mathbf{i}}} {\kern 1pt} {\kern 1pt} {\mathbf{\varphi }}_{yi} } ,$$
(20)
$${\text{where}},\;\left[ \begin{gathered} {\mathbf{N}}_{{{\mathbf{i,x}}}} \hfill \\ {\mathbf{N}}_{{{\mathbf{i,y}}}} \hfill \\ \end{gathered} \right]{\mathbf{ = }}[{\mathbf{J}}]^{{{\mathbf{ - 1}}}} {\kern 1pt} {\kern 1pt} \left[ \begin{gathered} {\mathbf{N}}_{{{\mathbf{i,\xi }}}} \hfill \\ {\mathbf{N}}_{{{\mathbf{i,\eta }}}} \hfill \\ \end{gathered} \right]{\kern 1pt} \;{\text{and}}\;\left[ {\mathbf{J}} \right]{\mathbf{ = }}\left[ {\begin{array}{*{20}c} {{\mathbf{X}}_{{{\varvec{\upzeta}}}} } & {{\mathbf{Y}}_{{{\varvec{\upzeta}}}} } \\ {{\mathbf{X}}_{{{\varvec{\upeta}}}} } & {{\mathbf{Y}}_{{{\varvec{\upeta}}}} } \\ \end{array} } \right].$$
(21)
Fig. 3
figure 3

Discretization model for hybrid sandwich plate (mesh size 8 × 8)

Full size image

Sensitivity Analysis

Sensitivity analysis (SA) describes the effect of each input parameter and their combined effects on the output responses. The relationship between input and output parameters for a constructed model can be defined as [88]

$${\mathbf{Z}} = f({\mathbf{Y}}_{{\mathbf{1}}} , \ldots ,{\mathbf{Y}}_{{\mathbf{n}}} ),$$
(22)

where Yi are the random input variables, by fixing Yi to be \(y_{i}^{*}\) one at a time, the conditional variance of the output \({\text{Var}}({\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{ = y}}_{i}^{*} )\) is generally less than the total variance \({\text{Var}}({\mathbf{Z}})\), indicating some contribution of variance from the input variable Yi. It states the sensitivity of uncertain output concerning Yi (input). For all possible values of \({\mathbf{y}}_{i}^{*}\), the variable \({\text{Var}}({\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{ = y}}_{i}^{*} )\) is a random variable. Thus, we can calculate its expected value \({\mathbf{\rm E}}[{\text{Var}}({\mathbf{Z|Y}}_{i} )]\). To quantify the importance of Yi (input), one can determine it from a deterministic value \({\text{Var}}({\mathbf{Z}}) - {\mathbf{\rm E}}[{\text{Var}}({\mathbf{Z|Y}}_{i} )]\). Likewise, for all expected values of Yi(input), the conditional expectation is \({\mathbf{\rm E}}[{\text{Var}}({\mathbf{Z|Y}}_{{\mathbf{i}}} )]\) which is also a random variable. Therefore, the contribution of Yi (input) can be depicted by \({\text{Var}}({\mathbf{Z}}) - {\text{Var}}({\mathbf{{\rm E}[Z|Y}}_{i} ])\) as

$${\text{Var}}({\mathbf{Z}}) = {\mathbf{\rm E}}[{\text{Var}}({\mathbf{Z|Y}}_{i} )] + {\text{Var}}({\mathbf{{\rm E}[Z|Y}}_{i} ]).$$
(23)

To quantify the sensitivity of output related to the uncertainty of the ith input, using Sobol' sensitivity index [67, 68, 89, 90]

$${\mathbf{SI}} = {\text{Var}}({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{i} ])/{\text{Var}}({\mathbf{Z}}).$$
(24)

The higher order sensitivity indices predict the interconnection between input variables. Let Yi and Yj are two variables that are taken constantly simultaneously at a time. The combined effect of these two can be measured by \({\text{Var}}({\rm E}[{\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{,Y}}_{j} ])\). The second-order indices are expressed as,

$${\mathbf{SI}}_{ij} = {\text{Var}}({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{,Y}}_{j} ])/{\text{Var}}({\mathbf{Z}}) - {\mathbf{SI}}_{i} - {\mathbf{SI}}_{j} .$$
(25)

Similarly, the equations are derived for higher order indices. Therefore, in general, the total variance can be depicted as

$${\text{Var}}({\mathbf{Z}}) = \sum {_{i} {\mathbf{V}}_{i} + } \sum {_{i,j > i} {\mathbf{V}}_{ij} + } \sum {_{i,j > i,k > j} {\mathbf{V}}_{ijk} + \cdots } + {\mathbf{V}}_{1,2, \ldots ,n}$$
(26)

where \({\mathbf{V}}_{i} = {\text{Var}}({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{i} ])\),

\({\mathbf{V}}_{ij} = Var({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{,Y}}_{j} ]) - {\mathbf{V}}_{i} - {\mathbf{V}}_{j}\),

\({\mathbf{V}}_{ijk} = {\text{Var}}({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{{\mathbf{i}}} {\mathbf{,Y}}_{{\mathbf{j}}} {\mathbf{,Y}}_{k} ]) - {\mathbf{V}}_{ij} - {\mathbf{V}}_{jk} - {\mathbf{V}}_{ik} - {\mathbf{V}}_{i} - {\mathbf{V}}_{{\mathbf{j}}} - {\mathbf{V}}_{k}\), etc.

Therefore,

$$\sum {_{i} {\mathbf{SI}}_{i} + } \sum {_{i,j > i} {\mathbf{SI}}_{ij} + } \sum {_{i,j > i,k > j} {\mathbf{SI}}_{ijk} + } \cdots + {\mathbf{SI}}_{1,2, \ldots ,n} = 1.$$
(27)

For measuring the total effect of all input variables, the total effect index is utilised [91], as shown in Eq. (28)

$${\mathbf{SI}}_{Ti} = 1 - {\text{Var}}({\mathbf{\rm E}}[{\mathbf{Z|Y}}_{1} , \ldots ,{\mathbf{Y}}_{i - 1} ,{\mathbf{Y}}_{i + 1} , \ldots ,{\mathbf{Y}}_{n} ])/{\text{Var}}({\mathbf{Z}}).$$
(28)

The advantage of SA includes that it provides fine-grained information on individual and compound effects of input variables. The limitation of SA is linked with Monte Carlo, wherein it is a computationally exhaustive process requiring time and cost. MARS is utilised as a surrogate model in the present study to overcome this limitation.

Multivariate Adaptive Regression Splines (MARS)

The finite element modelling (in the case of computationally intensive simulation of repetitive nature) [55, 95,96,97,98,99,100,101] can be an alternate way where inefficient analytical solutions [92,93,94] are not possible. The surrogate modelling technique is employed in such intensive simulations to achieve computational efficiency. In the case of MARS relationship between input/output responses of the system is achieved by selecting samples based on some algorithms [102,103,104]. Instead of assuming the functional relationship between dependent and independent variables, here, essential function and set of coefficients are used to develop the times extracted from regression data. By employing MARS, significant dimensional input parameters problems can be obtained, otherwise difficult to solve. The forward and backward approach selects a set of basic functions for approximating the output response. Following steps are employed in MARS-based surrogate approach: step 1: initialisation with a simple model with constant basic function, step 2: addition of the basic functions thereby increasing complexity, step 3: checking with the pre-defined complexity, step 4: using backward approach, remove insignificant basic functions. The basic function of MARS [105] can be expressed as,

$${\mathbf{f(x)}} = \sum\limits_{i = 1}^{J} {{{\varvec{\upalpha}}}_{i} {\mathbf{\rm Z}}_{i}^{x} } ({\mathbf{y}}_{n} ).$$
(29)

The approximation function is represented by \(f(x)\). \(\alpha_{i}\) represents the coefficients of expansion, whereas the multivariate spline basic functions are denoted by \(Z_{i}^{x} (y_{n} )\). For dividing input space into J number of regions, the Eq. (29) becomes

$${\mathbf{f(x) = \alpha }}_{1} ,$$
(30)

where \({\mathbf{Z}}_{i}^{x} ({\mathbf{y}}_{{\mathbf{1}}} {\mathbf{,y}}_{{\mathbf{2}}} {\mathbf{,y}}_{{\mathbf{3}}} {\mathbf{,}} \ldots ,{\mathbf{y}}_{J} ) = 1\) for i = 1. In Eq. (30), the term \(\alpha_{{_{1} }}^{{}}\) is the intercept parameter. The basic function can be expressed as,

$${\mathbf{Z}}_{i}^{x} ({\mathbf{y}}_{n} ) = \prod\limits_{n = 1}^{{n_{i} }} {[{\mathbf{K}}_{{n_{i} }} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )]_{\Pr }^{h} } ,$$
(31)

where \(n_{i}\) represents the interaction order,\(K_{{n_{i} }} = \pm 1\),\(y_{m(n,i)}\) denotes the mth variable,\(1 \le m(n,i) \le j\), and \(Q_{n,i}\) represents the knot location of corresponding variables. The dimension of input variables is defined by j, superscript x denotes the function, and l denotes the spline's order. The function \(f(x)\) contains all the basic functions of ith sub-regions, while the multivariate spline basic function \({\mathbf{Z}}_{i}^{x} ({\mathbf{y}}_{n} )\) contains univariate spline basic function and \(K_{n,i}\). 'Pr' represents the function as a truncated power function. The basic function may be in the following shapes

$$\begin{gathered} [{\mathbf{K}}_{n,i} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )]_{\Pr }^{h} = [{\mathbf{K}}_{n,i} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )]_{{}}^{h} \;for\;[{\mathbf{K}}_{n,i} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )] < 0 \hfill \\ {\text{Otherwise}} \hfill \\ \end{gathered}$$
(32)
$$[{\mathbf{K}}_{n,i} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )] = 0.$$
(33)

Thus, all basic functions are expressed as

$${\mathbf{E}} = \{ [{\mathbf{K}}_{n,i} ({\mathbf{y}}_{m(n,i)} - {\mathbf{Q}}_{n,i} )]_{\Pr }^{h} \} ,{\mathbf{Q}} \in \left\{ {{\mathbf{y}}_{1m} ,{\mathbf{y}}_{2m} ,{\mathbf{y}}_{3m} ......{\mathbf{y}}_{Jm} } \right\}$$
(34)

Stepwise linear regression is employed for forward propagation, but instead of using original input, it uses the function E and their product. For estimating \({{\varvec{\upalpha}}}_{i}\), the residual sum-of-square is minimised. Both forward and backward approaches are employed in MARS to determine the number of basic spline functions and their location. First, the basic spline function is over-fitted at each knot, then for removing insignificant knot, the modified cross-validation criteria are employed [106, 107].

The model uses a modified kind of criterion known as generalised cross-validation (GCV) to automatically screen the variables. For the appropriate spline basis functions, MARS picks the exact value and location of the given element in an onward or backward way. It over-fits the spline function to the defined knot's position. After that, using the generalised cross-validation criterion, the model removes the unneeded knots that contribute the least to the model. The knots that are not needed can be assessed using the lack-of-fit (Z) criterion, which is represented as

$$\mathbf{Z}={G}_{c}\left(k\right)=\frac{\frac{1}{h}{\sum }_{i=1}^{h}[{{\varvec{Y}}}_{i}-{{\varvec{Y}}}_{k}({x}_{i}){]}^{2}}{[1-\frac{\widetilde{c}\left(\widetilde{k}\right)}{n}{]}^{2}},$$
(35)

where \(\widetilde{c}\left(\widetilde{k}\right)=c\left(\widetilde{k}\right)+C.\left(\widetilde{k}\right)\)

'h' represents the total number of samples, \(c\left(\widetilde{k}\right)\)' represents the number of linearly independent basis functions, '\(\widetilde{k}\)' represents the number of knots in the forward process, 'Y' represents the approximated function, and 'C' represents the basis function cost. The smoothness of the function is estimated by the cost function's value. Because 'C' is inversely proportional to the number of knots, when '\(\widetilde{k}\)' is small, C is big, which results in a smooth estimation of the function.

The constructed metamodel is further validated by analysing the relative accuracy and the coefficient of determination (R2) of the individual model. The formulation of the coefficient of determination is stated as

$${\mathbf{R}}^{2} = 1 - \frac{{\sum\nolimits_{i = 1}^{n} {({\mathbf{y}}_{i} - \mathop {{\mathbf{y}}_{i} }\limits^{{\vartriangle }} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {({\mathbf{y}}_{i} - \mathop {{\mathbf{y}}_{i} }\limits^{ - } )^{2} } }}.$$
(36)

Here, \({y}_{i},\)\(\mathop {y_{i} }\limits^{{\vartriangle }}\) and \({\overline{y} }_{i}\) signifies the actual model, predicted model and mean of actual data. In Eq. (57), it is assumed that all the parameters are influential in evaluating the model's efficiency. The relative accuracy of the model is evaluated as

$${\varvec{R}}{\varvec{A}}\left(\%\right)=1-\left|\left.\frac{{{\varvec{J}}\left({\varvec{x}}\right)}_{\mathrm{predicted}}-{{\varvec{J}}\left({\varvec{x}}\right)}_{\mathrm{actual}}}{{{\varvec{J}}\left({\varvec{x}}\right)}_{\mathrm{predicted}}}\right|\right..$$
(37)

\({\mathbf{J(x)}}_{{\mathrm{actual}}}\) and \({\mathbf{J(x)}}_{{\mathrm{predicted}}}\) are the FE response and corresponding predicted response of the MARS model, respectively. The current model is designed with input variables as mentioned in Table 3. The parameters are chosen based on the number of layers and six different types of shell geometries.

$${\mathbf{RMSE}} = \frac{{\sqrt {\sum\nolimits_{i = 1}^{n} {||{\mathbf{y}}_{i} - \mathop {{\mathbf{y}}_{i} }\limits^{{\vartriangle }} ||^{2} } } }}{n}.$$
(38)
Table 3 HMGS shells material properties
Full size table

For numerical predictions, the root mean square error (RMSE) is regarded as an excellent general-purpose error metric. Because RMSE is scale dependent, it should only be used to evaluate prediction errors of different models or model configurations for a single variable, not between variables. It is a metric for determining how well a regression line fits the data points. The following is the formula for computing RMSE.

Results and Discussion

The present study investigates the effect of various random input parameters (like material properties and geometric variations) for the first three natural frequencies response of HMGS shell structures. The sensitivity analysis is performed to identify the effect of each random input parameter on the global response of the structure. The probabilistic results are obtained from the efficient MARS integrated finite element (FE) framework. Figure 4 illustrates the flow diagram for sensitivity analysis for stochastic natural frequency of hybrid multi-functionally graded sandwich (HMGS) shells. The validation of the present model is accomplished in two ways. First, the deterministic model is validated by comparing the FE code with past literature. Second, the stochastic surrogate-based MARS model is validated with traditional MCS-based results. In the present study, elliptical paraboloid, cylindrical, hyperbolic paraboloid, and spherical shell (Fig. 1) of HMGS structures are studied for their dynamic response. The basic materials of HMGS shells are FG-based material of metal and ceramic mixture (aluminium is considered as metal and zirconia as ceramic) [108], the low-density soft core of foam material, and laminated composite (material properties presented in Table 3) [109]. Table 4 shows the first natural frequency for various mesh sizes (6 × 6, 8 × 8, 10 × 10) and for different values of power-law exponent (x) compared with the results presented by Zhao and Liew [39]. The results obtained demonstrate an acceptable approximation of the present study and with the results of Zhao and Liew [39]. Furthermore, mesh convergence of hybrid FG-sandwich cylindrical shells is conducted (refer to Fig. 5). From this mesh convergence study, the optimal mesh size is selected. To reduce computational time 6 × 6 mesh size is considered. Also, it is found that (from Table 3) the percentage of error for other mesh sizes is comparatively higher than that of 6 × 6. The FG cantilever plate of 6 \(\times\) 6 mesh size is considered for deterministic FE analysis, which provides satisfactory results, leading to 36 elements and 133 nodes. The deterministic result obtained is thus validated with that of results available in previous literature [110,111,112], as presented in Tables 5 and 6. There seems to be a good agreement for several cases of t/L ratio and power-law exponent (p) and for various shell geometries. The thickness of the plate is represented by "t", and "l" represents the length of the plate. Once the FE code is verified, the natural frequencies of an elliptical paraboloid, cylindrical, hyperbolic paraboloid, and spherical-shaped HMGS shells with different cases (total six cases) are investigated.

Fig. 4
figure 4

Flow diagram for sensitivity analysis for stochastic natural frequency of hybrid multi-functionally graded sandwich (HMGS) shells

Full size image
Table 4 Validation of mesh convergence for FNF of functionally graded shells subjected to free vibration
Full size table
Fig. 5
figure 5

Mesh convergence study of FE analysis of first three natural frequencies for different mesh size

Full size image
Table 5 Validation for FNF of functionally graded square plate subjected to free vibration
Full size table
Table 6 Validation for various shell geometries and various power-law exponent on FNF of FG shells having (Ec = 380 GPa, ρc = 3800 kg/m3, Em = 70GPa, ρm = 2702 kg/m3, \(\nu\) = 0.3)
Full size table

As per industry standards, for the present analysis, the probabilistic variation of random input parameters is considered as C = 10% concerning the respective deterministic nominal values for obtaining the numerical results [113]. Depth-wise uncertainty is contemplated for variations of material properties (in the z-direction) as it is critical in hybrid multi-functionally graded sandwich structures. The computational efficiency is achieved by employing the MARS as the surrogate model in conjunction with FE code. The predictability of the result obtained through MARS is validated with the results of direct FE simulation through scatter plot. To reduce the computational cost, the surrogate model is formed by considering sample sizes of 256, 512, and 1024. For convergence study, some of the parametric analyses are performed; they are R-squared value, root mean square error (RMSE), mean absolute error (MAE), and mean square error (MSE), as illustrated in Table 7a–d. It is perceived that for sample size 1024, the percentage error is comparatively less than others (refer to Table 7a–d). The probability density function (PDF) plots (Fig. 6a–f) show the predicted outputs obtained while implementing the MARS surrogate model for different sample sizes (256, 512, and 1024) and the output obtained from the original MCS for the sample size of 10,000.

Table 7 Error analysis for the first three random NF (rad/s) of HMGS (a) cylindrical shell, (b) spherical shell, (c) elliptical paraboloid shell, (d) hyperbolic paraboloid shell for 256, 512, and 1024 sample-sized FE-MARS approaches of compound variation arbitrarily selected input parameters (C = 10%)
Full size table
Fig. 6
figure 6figure 6figure 6

a PDF plots of the first three random NF(rad/s) for a case 1, b case 2 c case 3 d case 4 e case 5 and f case 6 using the MARS approach depict the outcome of compound source-uncertainties of random input parameters considering stochasticity "C" = 10%. The details are furnished at the start of Sect. 3. Here represents N = 256MARS, represents N = 512MARS, represents N = 1024MARS and represents N = 10000MCS

Full size image

MCS is a computing technique for the (typically approximate) solution of mathematical problems that employ random samples as its foundation. It is one of the most intriguing computational device for performing statistical inference in the field of stochastic analysis. Many fascinating models have incredibly complicated structures that are difficult to solve using typical methods. The posterior probability distribution encodes all information on which inference can be made within the bounds of the output quantity of interest. We can characterise these distributions and calculate expectations under them using MCS. Thus, it can be inferred that although MCS provides a robust output in probabilistic regime its one disadvantage is the consumption of time and computational efficiency. It is mitigated by the utilization of MARS as the surrogate model.

It is reviewed that the predictions for the 1024 sample size are satisfactory compared to sample sizes 256 and 512. After that, the result obtained by MARS is compared with the conventional MCS for a converged sample size of 1024, as depicted in Fig. 7a–f. The scatter plot for the same sample size, 1024 (refer to Fig. 6-a–f), portrays the minor deviation. Therefore, a sample size of 1024 is considered for further stochastic analysis. Both Figs. 6 and 7 show the excellent forecasting capability of the MARS model irrespective of the shell geometries and generate enough assurance on the MARS-based stochastic analysis for all cases.

Fig. 7
figure 7figure 7figure 7

Scatter plots of the first three random NF (rad/s) for a case 1,  b case 2, c case 3, d case 4, e case 5 and f case 6 using MARS-MCS approach (1024 samples) and full-scale FE-MCS approach depicting the outcome of compound source-uncertainties of random input parameters considering stochasticity "C" = 10%. Here TR true response and PR predicted response

Full size image

The present analysis considers the depth-wise varying framework (in 'z-direction') for four shell geometries of six structural forms. It is noted that the variation in material properties occurs throughout the thickness. The uncertainty in material properties is considered for stochastic analysis. Sensitivity analysis is performed for assessing the relative significance of the stochastic material properties (like Young’s modulus (E), shear modulus (G), Poisson's ratio (µ), mass density (ρ) and stochastic geometric configuration (ply-orientation angle (\(\theta\))) on the free vibration response of different shell geometries for several structural forms. The structures are subjected to free vibration to determine the most significant parameters in the global response of the structure. In the case of HMGS, sensitivity analysis is essential for the optimal design of the structures. It is significant to attribute for controlling of various random input variables, arising during the manufacturing process and different stages of operations. Figure 8a–f presents the sensitivity analysis of elliptical paraboloid, cylindrical, hyperbolic paraboloid, and spherical-shaped HMGS shells. Figure 8a represents the sensitivity analysis of HMGS shells for various geometries for case 1. In this case (case 1), hybrid structures are designed such that the upper facesheet is composed of the laminated composite while the lower facesheet is constructed of FGM, and in between, there is a soft core. From Fig.  8a, shows that for the cylindrical shell, ρ is obtained as the most sensitive parameter followed by E1, E2 and \(\theta\) while other parameters are found to be the least significant. For spherical and elliptical paraboloid shells, ρ is the most sensitive parameter, while E1, E2, \(\theta\), G12 show the moderate effect, and other parameters have negligible effect. In hyperbolic paraboloid shells, \(\theta\) is the most sensitive parameter followed by ρ. At the same time E1, E2 and G12 show moderate effects. Figure 8b represents the sensitivity analysis of HMGS shells for various geometries for case 2. In this case (case 2), hybrid structures are designed such that both the facesheets are of FGM, and in the middle, there is a soft core. From Fig.  8b, it is noted that for all shell geometries, ρ is the most sensitive parameter followed by E1 and G12. In contrast, E2 and \(\upsilon\) have moderate effects, whereas other parameters are obtained as the least significant parameters. Figure 8c represents the sensitivity analysis of HMGS shells for various geometries for case 3. In this case (case 3), hybrid structures are designed to make both the facesheets composed of laminated composite, keeping a soft core in the middle. On careful observation of Fig.  8c, it is found that for cylindrical shell ρ and \(\theta\) are obtained as the most sensitive parameter, followed E1 and E2, while other parameters are obtained as the least significant. In contrast, ρ and E1 (for spherical and elliptical paraboloid shells) show the maximum sensitivity followed by \(\theta\), G12, and E2, keeping other parameters having minor effects. In hyperbolic paraboloid shells,\(\theta\) is obtained as the most sensitive parameter, followed by ρ. At the same time, E1, E2, and G12 show moderate effects. Figure 8d represents the sensitivity analysis of HMGS shells for various geometries for case 4. In this case (case 4), hybrid structures are designed to construct both the facesheet of FGM and laminated composite keeping the soft core in the middle. It is observed in Fig.  8d that for all the shell geometries, ρ predicts the highest sensitivity pursued by E1, E2, and G12. In contrast, other parameters are observed to be the least significant parameters. Figure 8e represents the sensitivity analysis of HMGS shells for various geometries of case 5. In this case (case 5), hybrid structures are designed so that both the facesheets are FGM, and the middle core is laminated composite. Figure 8e shows that for all the shell geometries, ρ predicts the highest sensitivity corresponding to the fundamental natural frequencies. It is followed by E1, E2 and G12, while others are found to be the least significant parameters. Figure 8f represents the sensitivity analysis of HMGS shells for various geometries of case 6. In this case (case 6), hybrid structures are designed so that both the facesheets are laminated composite and FGM's middle core. Figure 8f illustrates that for all the shell geometries, ρ predicts the highest sensitivity. It is followed by E1, E2, and G12, whereas other parameters are comparatively less significant.

Fig. 8
figure 8figure 8figure 8

Sensitivity analysis for the first three random natural frequencies (rad/s) for a case 1, b case 2, c case 3, d case 4, e case 5, and f case 6 considering various shell geometries (i) Scyl., (ii) Ssph., (iii) Sell. and (iv) Shyp.

Full size image

Conclusions

With the increasing attention to have multi-functionality in advanced structures, the necessity of sensitivity analysis corresponding to multiple response quantities simultaneously and to propose a unified sensitivity analysis framework has become apparent from the viewpoint of effective computational modelling and manufacturing quality control. The present study focuses on the sensitivity of frequency responses of hybrid FG-sandwich structures with multi-functional applications. This study is helpful for establishing a unified measure in the case of multi-objective performances. In these hybrid structures, the advantages of each constituting component could potentially be exploited in a single structure. Such a construction could be helpful where the surface is exposed to extreme temperature or environmental conditions. However, an optimum lightweight design can still be achieved based on composite construction and depth‐wise gradation towards the center of the shell. A novel MARS-based sensitivity analysis of these hybrid multi-functionally graded sandwich shells is developed to achieve computational efficiency without compromising with the outcome. Such surrogate-assisted FE approaches are crucial for computationally intensive multi-objective systems. It enumerates the degree of influence of various random input variables in the case of dynamic frequency responses. The MARS surrogate model is coupled with a finite element model to achieve computational efficacy (time and cost reduction). The numerical results indicate the proportional dominance of several random input parameters. Such analysis can provide the most significant parameters and their relative degree of importance in the multi-dimensional structural systems to design safe and reliable materials. It will lead to more optimized designs and better quality control while manufacturing the complex advanced structural systems. The results obtained showcase the sensitivity of the various input parameters like material properties and ply-orientation angle for first three natural frequencies. In most cases it is noted that mass density is the most sensitive parameter. Implementing different structural forms with different geometries in the present study will a vital role in the aerospace, civil construction, marine, naval, and automobile sectors. The detailed sensitivity analysis offers in-depth structure performance and characteristic understanding. The design paradigms can be enhanced, and a compelling performance can be obtained. Thus, the contribution of this article lies in both the development of a computationally efficient sensitivity analysis approach and the insightful numerical results for hybrid structures presented thereafter. The comprehensive and collective sensitivity quantification considering multi-functional objectives, as presented in this article, would lead to efficient computational modelling of complex structural systems for more optimized designs and better quality control during manufacturing. For further study, the computationally efficient uncertainty approach developed in this article can be utilised to investigate the effect of uncertainties in various other structures.