1 Introduction

Functionally graded materials (FGMs) are advanced composite materials characterized by microscopically varying material properties throughout their structure, resulting in a continuous transition from one surface to another. These materials exhibit a spatial gradient in macroscopic mechanical strength and thermal conductivity. Nowadays, the use of functionally graded structures has become increasingly prevalent in various engineering sectors such as aerospace, aircraft, automotive, and others. One of the significant advantages of functionally graded materials over traditional composites is their ability to overcome interface challenges commonly encountered in conventional materials.

In recent years, nanostructures such as nanorods, nanobeams, and nanoplates have attracted considerable attention for their exceptional mechanical, thermal, chemical, and electronic properties [1, 2]. These structures are increasingly used in micro/nano electromechanical systems (MEMS/NEMS) and nano actuators, leading to a growing interest in modeling micro and nanoscale structures. Size effects at the nanoscale are widely acknowledged to be significant, prompting further development of design and analysis methods to accurately simulate their impact on mechanical responses. As a result, improved non-classical continuum-based elasticity theories with scale parameters have been developed to provide a practical framework for considering size effects without excessive computational costs.

One of the most common enhanced continuum-based theories of elasticity is Eringen’s strain-driven nonlocal model [3, 4]. This model assumes that stress at any point is represented by the convolution integral of elastic strain at each point of the medium and a decaying kernel function, introducing a nonlocal constant to evaluate the intensity of long-range interactions in the medium. To circumvent the difficulties inherent in solving the corresponding integro-differential equations found in many structural problems [5, 6], the subsequent differential law is commonly used to replace the original nonlocal integral deformation. Interested readers are encouraged to consult the review literature [7–9] and the articles cited therein.

Numerous studies have been conducted to investigate the mechanical responses of nanostructures using these theories. Researchers have analyzed Euler–Bernoulli nanobeams using nonlocal elasticity theory [10], studied the vibration behavior of functionally graded nanobeams in thermal environments [11], explored the surface effects on deformations of magneto–electro-elastic beams [12], and investigated the vibration and thermal buckling of nonlocal functionally graded nanobeams [13], among other studies. Nonlocal beam theories have been employed to examine the mechanical behavior of micro and nanostructures [14, 15], and comprehensive reviews have been conducted on the benefits and drawbacks of nonlocal theory [8]. Furthermore, exact solutions for bending, buckling, and free vibration of functionally graded carbon nanotube-reinforced composite nanobeams have been proposed based on nonlocal theory [16], and static bending and buckling of functionally graded nanoscale beams have been studied using nonlocal Timoshenko beam models [17]. A study conducted by Ebrahimi and Barati [18] focused on the thermal vibration behavior of functionally graded (FG) nanobeams subjected to different types of thermomechanical loading, including uniform, linear, and nonlinear temperature rise. They utilized a two-parameter elastic foundation based on the third-order shear deformation beam theory and incorporated the nonlocal size-dependent effect to analyze the static and dynamic behavior of isotropic and functionally graded beams at a small scale.

A series of papers by Barretta and co-workers [19, 20] indicated that when adopting the classical Helmholtz-type kernel, Eringen’s model becomes ill-posed in formulating mechanical problems of bounded structures. This occurs due to the constitutive boundary conditions inherent in the differentiation process of the strain-driven integral model being satisfied only by default in problems involving unbounded domains, for example, in problems concerning dislocation and wave propagation studied by Eringen. However, the inherent constitutive boundary conditions for bounded structures may be incompatible with the equilibrium requirements of the corresponding problems, leading to inconsistent results. For instance, perhaps the most well-known inconsistency is the conclusion that raising the nonlocal length scale parameter shows a softening effect for all beam boundary edges except for cantilever nanobeams under point loading conditions [21, 22]. This ill-posedness of Eringen’s strain-driven model is also demonstrated in many recent papers [23–26].

Yang et al. [27] proposed the modified couple stress theory, which considers a symmetric couple stress tensor and includes only one additional parameter. However, the modified couple stress theory can be regarded as a special case of the modified strain gradient theory. Recent theoretical works have focused on the mechanical and dynamic behaviors of small-scaled structures using strain gradient theory and modified couple stress theory [28–32]. These gradient elasticity models have shown a stiffness enhancement effect. It is important to note that nonlocal elasticity models and strain gradient models describe distinct size-dependent mechanical and physical characteristics of small-scaled materials and structures. To investigate the effects of these two size-dependent phenomena on structural responses, researchers have developed nonlocal strain gradient models. Papargyri-Beskou et al. [33] derived the governing equation and boundary conditions for the buckling analysis of an Euler–Bernoulli beam using the variational principle based on the simple theory of gradient elasticity with surface energy. Lim et al. [34] proposed a nonlocal strain gradient theory that combines both strain gradient and nonlocal elasticity models, aiming to evaluate the impacts of nonlocal and length scale parameters on the mechanical and physical responses of size-dependent structures. This model has attracted significant attention from researchers studying small-scale structures.

Li et al. [35] investigated the free vibration analysis of nonlocal strain gradient beams made of functionally graded material. They derived a size-dependent Timoshenko beam model considering through-thickness power-law variation and found significant effects of such grading on natural frequencies and stiffness. Another study by Li et al. [36] delved into the nonlinear bending and free vibration analyses of similar beams, showing smaller nonlinear bending deflections and higher vibration frequencies compared to linear counterparts due to intrinsic stiffening effects. Özmen et al. [37] explored the thermomechanical vibration and buckling response of nonlocal strain gradient porous FG nanobeams in magnetic and thermal fields. They demonstrated the effects of nonlocal differential and strain gradient elasticities on softening and stiffness enhancements. These studies contribute to understanding the complex behavior of nanobeams under various conditions, aiding in the design of micro/nano electromechanical systems. Other recent studies have focused on specific applications, such as Daikh et al. [38] conducting a comprehensive study on the static deflection and buckling stability of axially loaded FG carbon-nanotube-reinforced composite (FGCNTRC) plates with temperature-dependent material properties.

The objective of this paper is to investigate the free vibration response of a novel advanced functionally graded nanobeam. Based on the nonlocal theory, a size-dependent hyperbolic shear deformation beam model is developed for the vibration behavior of FG nanobeam using nonlocal theory. The most interesting feature of this theory is that it accounts for a parabolic variation of the transverse shear strains across the thickness and satisfies the zero traction boundary conditions on the top and bottom surfaces of the beam without using shear correction factors. Governing equations of FGM beam with simply supported boundary conditions are derived using new higher-order shear deformation beam theory. The nonlocal theory is employed to capture the microstructure-dependent effect. Analytical solutions for vibration are provided for simply supported beams, and the obtained results are verified by comparing them with those reported in the literature to ensure the accuracy of the present theory. The influence of structure geometry, gradient index, and nonlocal scale parameters on vibration frequency is investigated.

2 Geometrical modeling and material distribution functions

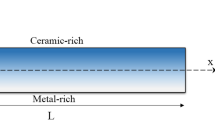
A uniform beam in the Cartesian coordinate system (x, z) with length “L” and thickness “h” is shown in Fig. 1. The beam is made of ceramic and metal. Material properties are graded continuously from surfaces to the core. The effective mechanical properties, such as Young’s modulus \(\left(E\right)\), density (\(\rho \)), and Poisson’s ratio \(\left(\upsilon \right)\), can be portrayed by the law of mixture as

$$P\left(x,z\right)={P}_{\text{m}}+\left({P}_{\text{c}}-{P}_{\text{m}}\right)V\left(x,z\right),$$
(1)

where \({P}_{\text{m}}\) and \({P}_{\text{c}}\) are the corresponding mechanical properties of the metal and the ceramic constituents. \(V\left(x,z\right)\) is the volume fraction of the ceramic phase in the x and z directions.

Fig. 1
figure 1

FG beam geometry

Full size image

Functionally graded materials with coatings find applications in various industrial components like turbine blades, cutting tools, and aircraft engines. Due to the complexity of these structures, there is a demand for both analytical and numerical analysis. This paper introduces a mathematical model for multidirectional functionally graded structures, a novel contribution to the field. This analysis considers two prevalent types of FG structures: FG hardcore (HC) and FG softcore (SC), examined through three schemes: FG-A, FG-B, and FG-C (Fig. 2). The material properties of the FG nanobeam are assumed to undergo continuous variation in both longitudinal and transverse directions, following a combined simple power-law distribution as illustrated in Fig. 3.

Fig. 2
figure 2

Types of FG structures

Full size image
Fig. 3
figure 3

Material distribution schemes

Full size image

2.1 Hardcore FG beam (HC)

(a) HC FG-A beam

$${V}_{\text{FG}-\text{A}}\left(x,z\right)=\left[{\left(\frac{\left|2z\right|}{h}\right)}^{p}-1\right]\left[{\left(\frac{\left|2x-L\right|}{L}\right)}^{k}-1\right].$$
(2)

(b) HC FG-B beam

$${V}_{\text{FG}-\text{B}}\left(z\right)=\left[{\left(\frac{\left|2z\right|}{h}\right)}^{p}-1\right].$$
(3)

(c) HC FG-C beam

$${V}_{\text{FG}-\text{C}}\left(x\right)=\left[{\left(\frac{\left|2x-L\right|}{L}\right)}^{k}-1\right].$$
(4)

2.2 Soft-core FG beam (SC)

(a) SC FG-A beam

$${V}_{\text{FG}-\text{A}}\left(x,z\right)=1-\left[{\left(\frac{\left|2z\right|}{h}\right)}^{p}-1\right]\left[{\left(\frac{\left|2x-L\right|}{L}\right)}^{k}-1\right].$$
(5)

(b) SC FG-B beam

$${V}_{\text{FG}-\text{B}}\left(z\right)=1-\left[{\left(\frac{\left|2z\right|}{h}\right)}^{p}-1\right].$$
(6)

(c) SC FG-C beam

$${V}_{\text{FG}-\text{C}}\left(x\right)=1-\left[{\left(\frac{\left|2x-L\right|}{L}\right)}^{k}-1\right].$$
(7)

3 Kinematic equations

3.1 Displacement field

The formulation is constrained to linear elastic material behavior. The displacement field is selected under the following assumptions:

  • The axial and transverse displacements are divided into bending and shear components.

  • The bending component of axial displacement resembles that described by the CBT.

  • The shear component of axial displacement leads to higher-order variations of shear strain, resulting in shear stress vanishing on the top and bottom surfaces of the beam.

With these assumptions, the displacement fields of various higher-order shear deformation beam theories are provided in a general form [39]:

$$u\left(x,z,t\right)={u}_{0}-z\frac{\partial {w}_{0}}{\partial x}+f\left(z\right){\varphi }_{x},$$
(8a)
$$w\left(x,z,t\right)={w}_{0},$$
(8b)

with,

$$f\left(z\right)=h\text{sinh}\left(\frac{z}{h}\right)-\frac{3{z}^{3}}{2{h}^{2}}.$$
(9)

And

$$g\left(z\right)={f}^{\prime}\left(z\right).$$
(10)

The values \({u}_{0}\) and \({w}_{0}\) are the displacement components in the x and z directions, respectively, and \({\varphi }_{x}\) is the rotation of the cross-section of the beam. The deformations associated with the displacements are

$${\varepsilon }_{xx}={\varepsilon }_{xx}^{0}-z{\varepsilon }_{xx}^{1}+f\left(z\right){\varepsilon }_{xx}^{2},$$
(11a)
$${\gamma }_{xz}=\frac{\text{d}f\left(z\right)}{\text{d}z}{\varphi }_{x}.$$
(11b)

Therefore, we obtain the deformations in the form:

$${\varepsilon }_{xx}^{0}=\frac{\text{d}u}{\text{d}x},$$
(12a)
$${\varepsilon }_{xx}^{2}=\frac{\text{d}{\varphi }_{x}}{\text{d}x},$$
(12b)
$${\varepsilon }_{xx}^{1}=\frac{{\text{d}}^{2}w}{\text{d}{x}^{2}}.$$
(12c)

The constitutive relations can be written as follows:

$$\left\{\begin{array}{c}{\sigma }_{xx}\\ {\tau }_{xz}\end{array}\right\}=\left[\begin{array}{cc}{Q}_{11}& 0\\ 0& {Q}_{66}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{xx}\\ {\gamma }_{xz}\end{array}\right\}.$$
(13)

The stiffness coefficients are expressed as follows:

$${Q}_{11}=\frac{E\left(z\right)}{1-{\upsilon }^{2}},\quad{Q}_{66}=\frac{E\left(z\right)}{2\left(1+\upsilon \right)}.$$
(14)

3.2 Resulting efforts

The resultants of forces and moments can be expressed in terms of stresses in the following form:

$$\left\{\begin{array}{c}{N}_{xx}\\ {M}_{xx}\\ {P}_{xx}\end{array}\right\}=\int\limits_{-h/2}^{h/2}\left\{\begin{array}{c}1\\ z\\ f\left(z\right)\end{array}\right\}{\sigma }_{xx}\text{d}z,$$
(15a)
$${Q}_{xz}=\int\limits_{-h/2}^{h/2}\frac{\text{d}f\left(z\right)}{\text{d}z}{\tau }_{xz}\text{d}z.$$
(15b)

We simplify the Eq. (14) to obtain

$$\left\{\begin{array}{c}{N}_{xx}\\ {M}_{xx}\\ {P}_{xx}\end{array}\right\}=\left[\begin{array}{ccc}{A}_{11}& {B}_{11}& {C}_{11}\\ {B}_{11}& {D}_{11}& {F}_{11}\\ {C}_{11}& {F}_{11}& {H}_{11}\end{array}\right]\left\{\begin{array}{c}{\varepsilon }_{xx}^{0}\\ {\varepsilon }_{xx}^{1}\\ {\varepsilon }_{xx}^{2}\end{array}\right\},$$
(16a)
$${Q}_{xz}={J}_{66}{\gamma }_{xz},$$
(16b)

with

$$\left\{{A}_{11}, {B}_{11}, {D}_{11},{C}_{11},{F}_{11},{H}_{11}\right\}=\int\limits_{-h/2}^{h/2}{Q}_{11}\left\{1, z,{z}^{2},f\left(z\right),zf\left(z\right),{f\left(z\right)}^{2}\right\}\text{d}z,$$
(17a)
$${J}_{66}=\int\limits_{-h/2}^{h/2}{Q}_{66}{\left[\frac{\text{d}f\left(z\right)}{\text{d}z}\right]}^{2}\text{d}z.$$
(17b)

3.3 Strain energy

The strain energy functional of the FG beam is given by the following formula:

$$\delta U=\frac{1}{2}{\int }_{V}\left[{\sigma }_{xx}{\varepsilon }_{xx}+{\tau }_{xz}{\gamma }_{xz}\right]\text{d}V.$$
(18)

Hence, we can rewrite the strain energy of the beam in the following form:

$$\delta U=\frac{1}{2}{\int }_{\text{A}}\left[{N}_{xx}\frac{\text{d}\delta u}{\text{d}x}+{M}_{xx}\frac{{\text{d}}^{2}\delta w}{\text{d}{x}^{2}}+{P}_{xx}\frac{\text{d}{\delta \varphi }_{x}}{\text{d}x}+{Q}_{xz}\delta {\varphi }_{x}\right]\text{d}x\text{d}z.$$
(19)

3.4 Kinetic energy

The kinetic energy of the beam at any instant can be expressed as follows:

$$T=\frac{1}{2}{\int }_{A}\rho \left(x,z\right)\left(\frac{{\partial }^{2}u}{\partial {t}^{2}}+\frac{{\partial }^{2}w}{\partial {t}^{2}}\right)\text{d}x\text{d}z.$$
(20)

3.5 Hamilton’s principle

The kinematic hypotheses (displacement field) being defined for the geometry and the type of excitation studied, the vibrational approach systematically includes the following points:

  1. (1)

    Calculation of deformations.

  2. (2)

    Construction of the Hamilton functional.

  3. (3)

    Externalization of the Hamilton functional.

In order to obtain the kinetic and strain energy, Hamilton’s principle is written as

$${\int }_{{t}_{1}}^{{t}_{2}}(\delta U-\delta T)\text{d}t=0.$$
(21)

3.6 Equations of motion

The appropriate equations of motion for displacement can be derived by using Hamilton’s principle. By substituting Eqs. (19) and (20) into Eq. (21), we obtain

$$\frac{\partial {N}_{xx}}{\partial x}={I}_{0}\frac{{\partial }^{2}{u}_{0}}{{\partial t}^{2}}-{I}_{1}\frac{{\partial }^{3}{w}_{0}}{{\partial x\partial t}^{2}}+{I}_{3}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}},$$
(22a)
$$\frac{{\partial }^{2}{M}_{xx}}{\partial {x}^{2}}={I}_{0}\frac{{\partial }^{2}{w}_{0}}{{\partial t}^{2}}+{I}_{1}\frac{{\partial }^{3}{u}_{0}}{\partial x{\partial t}^{2}}-{I}_{2}\frac{{\partial }^{4}{w}_{0}}{{\partial x}^{2}{\partial t}^{2}}+{I}_{4}\frac{{\partial }^{3}{\varphi }_{x}}{\partial x{\partial t}^{2}},$$
(22b)
$$\frac{\partial {P}_{xx}}{\partial x}-{Q}_{xz}={I}_{3}\frac{{\partial }^{2}{u}_{0}}{{\partial t}^{2}}-{I}_{4}\frac{{\partial }^{3}{w}_{0}}{{\partial x\partial t}^{2}}+{I}_{5}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}},$$
(22c)

where the inertias are defined by

$$\left\{{I}_{0}, {I}_{1}, {I}_{2}, {I}_{3}, {I}_{4}, {I}_{5}\right\}=\int\limits_{-h/2}^{h/2}\rho \left(z\right)\left\{1, z,{z}^{2},f\left(z\right),zf\left(z\right),{f\left(z\right)}^{2}\right\}\text{d}z.$$
(23)

3.7 Nonlocal strain gradient theory

Lim et al. [34] introduced a stress function that incorporates both strain gradient stress and nonlocal elastic stress fields, which can be expressed as

$${\sigma }_{ij}={\sigma }_{ij}^{\left(0\right)}-\frac{{\text{d}\sigma }_{ij}^{\left(1\right)}}{\text{d}x},$$
(24)

where \({\sigma }_{ij}^{\left(0\right)}\) represents the classical stress corresponding to strain \({\varepsilon }_{kl}\), and \({\sigma }_{ij}^{\left(1\right)}\) denotes the higher-order stress corresponding to strain gradient \({\varepsilon }_{kl,x}\). Additionally, their expressions can be described as follows:

$${\sigma }_{ij}^{\left(0\right)}={\int }_{0}^{L}{C}_{ijkl}{\alpha }_{0}\left(x,{x}^{\prime},{e}_{0}a\right){\varepsilon }_{kl,x}\left({x}^{\prime}\right)\text{d}{x}^{\prime},$$
(25a)
$${\sigma }_{ij}^{\left(1\right)}={l}^{2}{\int }_{0}^{L}{C}_{ijkl}{\alpha }_{1}\left(x,{x}^{\prime},{e}_{1}a\right){\varepsilon }_{kl,x}\left({x}^{\prime}\right)\text{d}{x}^{\prime}.$$
(25b)

In this context, \({C}_{ijkl}\) represents an elastic constant, and l is the material length scale parameter introduced to account for the influence of the strain gradient stress field. \({e}_{0}a\) and \({e}_{1}a\) are the nonlocal parameters introduced to consider the significance of the nonlocal elastic stress field. According to the nonlocal kernel functions \({\alpha }_{0}\left(x,{x}^{\prime},{e}_{0}a\right)\) and \({\alpha }_{1}\left(x,{x}^{\prime},{e}_{1}a\right)\), the general constitutive relation for nonlocal strain can be expressed as per Eringen [4]:

$$\left[1-{\left({e}_{1}a\right)}^{2}{\nabla }^{2}\right]\left[1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right]{\sigma }_{ij}={C}_{ijkl}\left[1-{\left({e}_{1}a\right)}^{2}{\nabla }^{2}\right]{\varepsilon }_{kl}-{C}_{ijkl}{l}^{2}\left[1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right]{{\nabla }^{2}\varepsilon }_{kl}.$$
(26)

The symbol \({\nabla }^{2}\) represents the Laplacian operator. In this study, we assume that \(e={e}_{0}={e}_{1}\). The complete nonlocal strain gradient constitutive relation can be formulated as follows:

$$\left[1-\mu {\nabla }^{2}\right]{\sigma }_{ij}={C}_{ijkl}\left[1-\lambda {\nabla }^{2}\right]{\varepsilon }_{kl},$$
(27)

where \(\mu ={\left(ea\right)}^{2}\) and \(\lambda ={l}^{2}\).

Hence, the constitutive relations for a nonlocal shear deformable functionally graded nanobeam can be represented as

$${\sigma }_{xx}-\mu \frac{{\partial }^{2}{\sigma }_{xx}}{\partial {x}^{2}}={Q}_{11}\left({\varepsilon }_{xx}-\lambda \frac{{\partial }^{2}{\varepsilon }_{xx}}{\partial {x}^{2}}\right),$$
(28a)
$${\tau }_{xz}-\mu \frac{{\partial }^{2}{\sigma }_{xx}}{\partial {x}^{2}}={Q}_{66}\left({\gamma }_{xz}-\lambda \frac{{\partial }^{2}{\gamma }_{xz}}{\partial {x}^{2}}\right).$$
(28b)

Thus, the equation governing stress resultants is

$${N}_{xx}-\mu \frac{{\partial }^{2}{N}_{xx}}{\partial {x}^{2}}=\left(1-{\lambda }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{A}_{11}\frac{\partial {u}_{0}}{\partial x}-{B}_{11}\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}}+{C}_{11}\frac{\partial {\varphi }_{x}}{\partial x}\right],$$
(29a)
$${M}_{xx}-\mu \frac{{\partial }^{2}{M}_{xx}}{\partial {x}^{2}}=\left(1-{\lambda }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{B}_{11}\frac{\partial {u}_{0}}{\partial x}-{D}_{11}\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}}+{F}_{11}\frac{\partial {\varphi }_{x}}{\partial x}\right],$$
(29b)
$${P}_{xx}-\mu \frac{{\partial }^{2}{P}_{xx}}{\partial {x}^{2}}=\left(1-{\lambda }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{C}_{11}\frac{\partial {u}_{0}}{\partial x}-{F}_{11}\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}}+{H}_{11}\frac{\partial {\varphi }_{x}}{\partial x}\right],$$
(29c)
$${Q}_{xz}-\mu \frac{{\partial }^{2}{Q}_{xz}}{\partial {x}^{2}}=\left(1-\lambda \frac{{\partial }^{2}}{\partial {x}^{2}}\right)\left[{J}_{66}{\varphi }_{x}\right].$$
(29d)

Substituting Eqs. (29) into Eqs. (22) to obtain

$$\left(1-\lambda {\nabla }^{2}\right)\left({A}_{11}\frac{{\partial }^{2}{u}_{0}}{\partial {x}^{2}}-{B}_{11}\frac{{\partial }^{3}{w}_{0}}{\partial {x}^{3}}+{C}_{11}\frac{{\partial }^{2}{\varphi }_{x}^{1}}{\partial {x}^{2}}\right)-\left(1-\mu {\nabla }^{2}\right)\left({I}_{0}\frac{{\partial }^{2}{u}_{0}}{{\partial t}^{2}}+{I}_{1}\frac{{\partial }^{3}{w}_{0}}{{\partial x\partial t}^{2}}-{I}_{3}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}}\right)=0,$$
(30a)
$$\left(1-\lambda {\nabla }^{2}\right)\left({B}_{11}\frac{{\partial }^{3}{u}_{0}}{\partial {x}^{3}}-{D}_{11}\frac{{\partial }^{4}{w}_{0}}{\partial {x}^{4}}+{F}_{11}\frac{{\partial }^{3}{\varphi }_{x}^{1}}{\partial {x}^{3}}\right)-\left(1-\mu {\nabla }^{2}\right)\left({I}_{0}\frac{{\partial }^{2}{w}_{0}}{{\partial t}^{2}}-{I}_{1}\frac{{\partial }^{3}{u}_{0}}{\partial x{\partial t}^{2}}+{I}_{2}\frac{{\partial }^{4}{w}_{0}}{{\partial x}^{2}{\partial t}^{2}}-{I}_{4}\frac{{\partial }^{3}{\varphi }_{x}}{\partial x{\partial t}^{2}}\right)=0,$$
(30b)
$$\left(1-\lambda {\nabla }^{2}\right)\left({C}_{11}\frac{{\partial }^{2}{u}_{0}}{\partial {x}^{2}}-{F}_{11}\frac{{\partial }^{3}{w}_{0}}{\partial {x}^{3}}+{H}_{11}\frac{{\partial }^{2}{\varphi }_{x}}{\partial {x}^{2}}-{J}_{66}{\varphi }_{x}\right)-\left(1-\mu {\nabla }^{2}\right)\left(-{I}_{3}\frac{{\partial }^{2}{u}_{0}}{{\partial t}^{2}}+{I}_{4}\frac{{\partial }^{3}{w}_{0}}{{\partial x\partial t}^{2}}-{I}_{5}\frac{{\partial }^{2}{\varphi }_{x}}{{\partial t}^{2}}\right)=0.$$
(30c)

4 Analytical solution

The equations of motion are analytically solved for free vibration problems. Navier’s solution method is used to determine the analytical solutions for a simply supported beam. We assume that the solution is of the following form:

$${u}_{0}=\sum_{m=1}^{\infty }{U}_{m}\text{cos}\left(\beta x\right){\text{e}}^{\text{i}\omega t},$$
(31a)
$${w}_{0}=\sum_{m=1}^{\infty }{W}_{m}\text{sin}\left(\beta x\right){\text{e}}^{\text{i}\omega t},$$
(31b)
$${\varphi }_{x}=\sum_{m=1}^{\infty }{X}_{m}\text{cos}\left(\beta x\right){\text{e}}^{\text{i}\omega t},$$
(31c)

where \(\beta =m\pi /L\), and ω denotes the natural frequency, and \({U}_{m}, {W}_{m}, {X}_{m}\) are arbitrary parameters. By replacing the Eqs. (31) in (30), the equations of motion become as follows:

$$\left(\left[L\right]-{\omega }^{2}\left[M\right]\right)\left\{\begin{array}{c}{U}_{m}\\ {W}_{m}\\ {X}_{m}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\end{array}\right\},$$
(32)

where the matrix [L] and [M] are the stiffness and mass matrix, respectively

$$\left[L\right]=\left(1+\lambda {\beta }^{2}\right)\left[\begin{array}{ccc}{L}_{11}& {L}_{12}& {L}_{13}\\ {L}_{12}& {L}_{22}& {L}_{23}\\ {L}_{13}& {L}_{23}& {L}_{33}\end{array}\right],$$
(33a)
$$\left[M\right]=\left(1+\mu {\beta }^{2}\right)\left[\begin{array}{ccc}{M}_{11}& {M}_{12}& {M}_{13}\\ {M}_{12}& {M}_{22}& {M}_{23}\\ {M}_{13}& {M}_{23}& {M}_{33}\end{array}\right],$$
(33b)

with

$$\begin{aligned}&{L}_{11}={-A}_{11}{\beta }^{2}, \quad{L}_{12}={B}_{11}{\beta }^{3},\quad {L}_{13}=-{C}_{11}{\beta }^{2},\nonumber\\&{L}_{22}=-{D}_{11}{\beta }^{4},\quad {L}_{23}={F}_{11}{\beta }^{3},\quad {L}_{33}=-\left({H}_{11}{\beta }^{2}+{J}_{66}\right),\end{aligned}$$
(34)

and

$$\begin{aligned}&{M}_{11}=-{I}_{0}, \quad{M}_{12}={I}_{1}\beta ,\\&\quad {M}_{13}={-I}_{3},\nonumber\\& {M}_{22}=-{I}_{0}-{I}_{2}{\beta }^{2}, \quad{M}_{23}={I}_{4}\beta , \quad{M}_{33}=-{I}_{5}.\end{aligned}$$
(35)

For the classical theory (CPT),

$${L}_{13}={L}_{23}={L}_{33}=0 \quad\text{and}\quad{ M}_{13}={M}_{23}={M}_{33}=0.$$
(36)

5 Numerical results

In this section, several numerical examples are presented and discussed in detail to demonstrate the influences of various parameters, such as nonlocal parameters, length scale parameters, length‐to-thickness ratio, and power‐law index, on the free vibration response of FG nanobeams. The analyzed FG beam is made of a mixture of metal (Aluminum, Al) and ceramic (Alumina-Al2O3). The material properties of both Aluminum and Alumina are given as follows:

$${\text{Aluminum}\, {\text{Al}}{\text{:}}\, E}_{\text{m}}=70\, \text{GPa}, \quad{\rho }_{\text{m}}=2702 \,\text{kg}/{\text{m}}^{3},\quad {\upsilon }_{\text{m}}=0.3,$$
$${\text{Alumina}\, {\text{Al}}_{2}{\text{O}}_{3}{\text{:}}\, E}_{\text{c}}=3960\, \text{GPa}, \quad{\rho }_{\text{c}}=3800 \,\text{kg}/{\text{m}}^{3},\quad {\upsilon }_{\text{m}}=0.3.$$

The non-dimensional functions of deflection, axial stress, shear stress, and transverse stress are defined by

$$\overline{\omega }=\omega \frac{{L}^{2}}{h}\sqrt{\frac{{\rho }_{\text{m}}}{{E}_{\text{m}}}}.$$
(37)

5.1 Comparison study

To validate the accuracy and effectiveness of the suggested model for predicting the free vibration characteristics of FG beams, the numerical outcomes are cross-referenced with previously published findings. Table 1 illustrates the comparison between the current results and those from studies by Thai and Vo [40], Şimşek [41], Vo et al. [42], and Nguyen et al. [39]. The theories utilized encompass the third-order shear deformation theory (TBT), the sinusoidal shear deformation theory (SBT), and the hyperbolic shear deformation theory (HBT). In this comparison, the volume fraction varies across the transverse direction according to the function \({(1/2+z/h)}^{p}\). It is evident that the disparities between the current findings and the cited literature are negligible. Hence, the proposed model demonstrates precision, resilience, and efficiency in analyzing the current model.

Table 1 Comparison of the non-dimensional fundamental natural frequency of FG beams with various boundary conditions (L/h = 5)
Full size table

5.2 Parametric study

5.2.1 Effect of power-law indexes

Table 2 presents the effect of power-law indexes \(p\) and \(k\) on the dimensionless frequencies of various schemes of FG beams. Additionally, Fig. 4 describes the effect of power-law index \(p\) on the dimensionless frequencies of various schemes of bi-coated beams (\(k=2,L/h=10, \mu = \lambda =0\)). Firstly, both types of FG-C beams, hardcore beams and softcore beams, are ignored in the plot because they are independent of “p.” The increase in index \(p\) leads to an augmentation of the proportion of ceramic in FG-A hardcore beams and a reduction of the proportion of ceramic in FG-A softcore (SC) beams; therefore, the dimensionless frequency increases for FG-A hardcore beams and decreases for FG-A softcore (SC) beams.

Table 2 Effect of power-law indexes \(p\) and \(k\) on the dimensionless frequencies of various schemes of FG beams (\(L/h=10, \mu = \lambda =0\))
Full size table
Fig. 4
figure 4

Effect of power-law indexes \(p\) on the dimensionless frequencies of various schemes of FG beams (k = 2, \(L/h=10, \mu = \lambda =0\))

Full size image

The effect of power-law index \(k\) on the dimensionless frequencies of various schemes of FG beams (p = 2, \(L/h=10, \mu = \lambda =0\)) is plotted in Fig. 5. As the previous analysis, the FG-B beams are ignored in the plot because they are independent of “k.” From this figure, the increase in index k leads to an increase in the proportion of ceramic in FG-A hardcore beams and a decrease in the proportion of ceramic in FG-A softcore beams. As a result, the dimensionless frequency increases for FG-A hardcore beams and decreases for FG-A softcore (SC) beams.

Fig. 5
figure 5

Effect of power-law index \(k\) on the dimensionless frequencies of various schemes of FG beams (p = 2, \(L/h=10, \mu = \lambda =0\))

Full size image

5.2.2 Effect of the thickness ratio

Table 3 illustrates the effect of the thickness ratio \(L/h\) on the dimensionless frequencies of various schemes of FG beams. The graphs in Fig. 6 show the effect of the thickness ratio \(L/h\) on the dimensionless frequencies of various schemes of FG beams (\(p=k=5, \mu = \lambda =0\)). From this figure, it is apparent that as the thickness ratio L/h increases, the dimensionless frequencies increase across all types of beams. Furthermore, beyond \(L/h>15\), the dimensionless frequencies remain nearly constant irrespective of the beam type. Thus, it can be inferred that the maximum dimensionless frequencies are achieved for FG-C softcore beams.

Table 3 Effect of the thickness ratio \(L/h\) on the dimensionless frequencies of various schemes of FG beams (\(\mu = \lambda =0\))
Full size table
Fig. 6
figure 6

Effect of the thickness ratio \(L/h\) on the dimensionless frequencies of various schemes of FG beams (\(p=k=5, \mu = \lambda =0\))

Full size image

5.2.3 Effect of the nonlocal and the length scale parameters

The size-dependent effects represented by the nonlocal and length scale parameters are tabulated in Table 4. Figure 7 describes the effect of the nonlocal parameter \(\mu \) on the dimensionless frequencies of various schemes of FG beams (\(p=k=1, L/h=10\)). As observed, an increase in the nonlocal parameter μ leads to a permanent decrease in the beam stiffness and consequently the dimensionless frequencies across all beam types. Conversely, it can be inferred that the minimum frequencies are attained for hardcore FG beams.

Table 4 Effect of the nonlocal parameter \(\mu \) and the length scale parameter \(\lambda \) on the dimensionless frequencies of various schemes of bi-coated beams (\(p=k=1, L/h=10\))
Full size table
Fig. 7
figure 7

Effect of the nonlocal parameter \(\mu \) on the dimensionless frequencies of various schemes of bi-coated beams (\(p=k=1, L/h=10\))

Full size image

Figure 8 illustrates the effect of the length scale parameter \(\lambda \) on the dimensionless frequencies of various schemes of FG beams (\(p=k=1, L/h=10\)). It is crucial to note that as the length scale parameter λ increases, the dimensionless frequencies of different schemes of FG beams increase significantly. This can be attributed to the enhancement in beam stiffness. Additionally, it is noteworthy that the frequencies of hardcore FG beams are lower than those of softcore FG beams.

Fig. 8
figure 8

Effect of the length scale parameter \(\lambda \) on the dimensionless frequencies of various schemes of bi-coated beams (\(p=k=1, L/h=10\))

Full size image

6 Conclusion

This study investigates the inherent vibrational characteristics of an innovative functionally graded nanobeam. Specifically, we explore two prevalent types of functionally graded material (FGM) structures: hardcore FGM and softcore FGM, each comprising three distinct configurations. The FGM nanobeam under consideration has material properties that continuously change in both longitudinal and transverse directions, following a composite power-law distribution based on constituent volume fractions. We employ a novel higher-order shear deformation plate theory to establish the governing equations for the FGM beam, with the beam subjected to simply supported boundary conditions. Additionally, we incorporate the nonlocal strain gradient theory to account for microstructure-dependent effects. Based on the numerical results, several conclusions can be drawn. Firstly, the choice of beam schemes, whether hardcore or softcore, and the specific distribution patterns of materials (FG-A, FG-B, and FG-C) significantly influence the stiffness of the beam, thereby affecting the fundamental frequencies of the system. Furthermore, the data clearly illustrate that an increase in the nonlocal parameter reduces beam stiffness, and decreasing the length scale parameter also results in decreased stiffness [43–50].