1 Introduction

Researchers take inspiration from animals in nature to study bionic robots. In nature, quadrupeds move with a variety of patterns, from pacing at slow speed to galloping at fast speed. Many research results have demonstrated that quadruped robot can run in various gaits, such as walking [1],  trotting[2], pacing [3], bounding [4] and galloping [5]. Some of them can be only achieved in slow-speed cases, and others can also be achieved in fast-speed cases. Hoyt and Taylor [6] studied the gait and energy consumption of horses, concluding that there is the lowest speed range of oxygen consumption under different gaits and horses can reduce energy consumption by changing their gait during acceleration.

Although a variety of gaits have been demonstrated on robots in many studies, robot always performs dynamic motion with a certain gait and step frequency in a specific value. Gait transition is realized only by switching manually, and commands of the remote control correspond to gait mode one-to-one. In these studies, they designed model-based controllers [7] using Model Predictive Control (MPC) to optimize motor commands at high frequency. With such controllers, robustness is a great advantage of the robot, but these controllers usually just assume a predefined contact sequence to make the optimization problem tractable, rather than actively finding a more efficient gait for locomotion. Therefore, it is challenging to design a controller that can adaptively change the gait and step frequency for a quadruped robot. When to switch gait, what gait to switch to, and how to ensure a smooth transition between two gaits without affecting the stability of robot are the key issues to be solved in this paper.

There are two directions for designing a controller of adaptively switching gait according to speed. One is to follow dynamic model-based motion control method, and the other is to use reinforcement learning method. Some researchers have gotten some results by dynamic model-based motion control methods. Zhang et al. [8] presented a holosymmetric Central Pattern Generator (CPG) topological network and parameter-setting principles for a gait matrix for gait transitions. Owaki and Ishiguro [9] constructed a CPG model that is a distributed neural network, by which they realized spontaneous gait transitions between the most energy-efficient patterns exhibited only by changing the intrinsic angular velocity of oscillators without any preprogrammed gait patterns. Shaw and Sartoretti [10] designed a CPG model that relies to keyframes—discrete key leg configurations that can be sequenced into a gait—to define arbitrary legged gaits, realizing following and transitioning among hexapedal and quadrupedal gaits for a hexapod robot. Although the use of CPG has several advantages in trajectory generation and gait transition, it is not easy to design a reasonable rhythm function with the coupling of various parameters. There have been already some more advanced methods, such as VMC, MPC, and WBC. Liu et al. [11] realized the gait transition from walking to trotting by changing walking parameters continuously. However, the transition between gaits is limited to low-speed conditions, not suitable for running gaits at high-speed conditions. Cao et al. [12] examined the problem of transitioning between gaits using a sagittal-plane reduced-order model of quadrupedal running and realize two-way transitions between pronking and bounding with double stance. But they only investigated the conversion between two forms of running gaits at higher speeds, and there is a lack of research on trotting at lower speeds. Xin et al. [13] studied the gait cycle of trotting and walking to find potential switching points and access points, achieving a smooth transition from trotting suitable for flat terrain to walking suitable for rough terrain for the quadruped robot. Boussema et al. [14] proposed a new framework for generating adaptive gaits by considering the set of impulses named Feasible Impulse Set by the contact legs. In addition, they used it to enable variable-speed locomotion with gait transitions and aperiodic behaviors in response to disturbances or complex terrains. In our proposed method, the robot can realize gait transition from slow-trotting in the low-speed conditions to flying-trot in the high-speed conditions during a wide range of speed changes, and it can obtain stability through VMC and WBC. Compared to the locomotion with the fixed gaits, the energy efficiency is significantly improved with adaptive gaits at different speeds. Based on the mechanical power distribution trend, Zhou et al. [15] established an efficient humanoid power redistribution approach to realize energy-efficient gait control of quadruped robots. In order to improve energy efficiency, they focused on the study of foot trajectories, while this paper pays attention to gait transitions. In addition, anti-interference capability is also studied, the robot can quickly restore stability in response to external disturbances by step frequency conversion according to the roll angle of robot’s torso.

Recently, there has been a lot of interest in studying motion policies for legged robots by reinforcement learning. Researchers have proposed a variety of strategies including accurate kinetic modeling [16], imitation of animals[17], and meta-learning [18, 19]. Some of them [20, 21] introduced sinusoidal priors in the policy design to approximate the gait cycle. But no obvious gait transition was observed during the rollout. Li et al. [22] used a learning strategy to tune the objective of a low-order MPC controller with a fixed contact sequence. Yang et al. [23] devised a hierarchical learning framework, where an upper layer gait policy is trained by reinforcement learning to specify the stance time of each leg, while the under-layer MPC controller is used to compute the optimal joint torque for robot to maintain stability at the desired speed. Nevertheless, it is difficult to deploy these learned strategies safely and smoothly on the real robot without extensive trial and error.

In this paper, a unique gait planner is designed, in which stance phase and swing phase are arranged and the gait cycle is adjusted according to robot’s speed. In a gait cycle, different proportions of swing phase can form different gaits. For example, when proportion of stance phase is larger than those of swing phase, the gait is called slow-trotting; trotting is formed when proportion of stance phase is as much as those of swing phase; and when proportion of stance phase is smaller than those of swing phase, robot moves in flying-trot. On the basis of previous research results [6], in order to improve energy efficiency, the robot is expected to move in slow-trotting with low frequency at low speed; at medium speed, it moves in trotting and step frequency is also improved; when the speed is fast enough, robot moves in flying-trot and step frequency is correspondingly faster. At each speed, according to corresponding gait and step frequency, the Virtual Model Controller is used to solve the optimal ground reaction force, and then the Whole-Body Controller is used to compute the desired joint torque for motor to achieve stable and efficient motion of the robot. By using the time state machine to plan stance phase and swing phase of each leg in a gait cycle, the automatic switching of gait at different speeds can be realized, which can improve energy efficiency concluding through extensive experiments. What is more, the anti-interference ability can be improved by increasing the step frequency automatically according to the roll when subjected to the lateral impact.

The main contributions of this paper include:

  • In order to solve the impracticality and flexibility of switching gait artificially for quadruped robot, the gait cycle and step frequency of the robot are studied to realize gait transitions automatically according to the moving speed in real time and achieve the optimal gait adaptation on different terrain.

  • A controller combining Virtual Model and Whole-Body Control is designed. The optimal foot force is calculated by the torso-based VM, and then the desired joint torque is obtained through WBC with prioritized tasks.

  • The proposed method is verified by experiment on quadruped robot SDUQuad_48. The robot can run stably at 4 m/s and energy efficiency is improved significantly through the adaptive gait planner.

This paper is organized as follows. Section 2 presents an adaptive gait planning method. Section 3 introduces a motion controller combining VMC and WBC. Section 4 describes the related experiments and analyzes the experimental results. In addition, in Sect. 5, the conclusion is made.

2 Gait Planner

The control framework is mainly divided into gait planning and motion control, as shown in Fig. 1. Adaptive gait planning is introduced in this section, and motion control will be introduced in the next section.

2.1 Key Parameters in Gait Cycle

The state of four legs during robot’s locomotion is called gait, which is the planning of stance phase and swing phase of each leg. Most gaits of animals are periodic in nature, so the robot’s gait in our planner is also periodic. A phase parameter \(\phi \) (Fig. 2) is defined, and the phase \(\phi \) of each leg represents the progress of the leg in the current gait cycle. The phase starts with 0, and when it increases to 2\(\pi \), it returns to 0 to start a new cycle. To describe a gait, three key parameters are chosen in a gait cycle (Fig. 3): step frequency \(f_{\textrm{step}}\), swing phase ratio \(R_{\textrm{swing}}\), and phase offset \(\varphi _{\textrm{offset}}\).

  1. 1.

    Step frequency: One of the significant features of robot’s movement is step frequency which is the reciprocal of a gait cycle and affect robustness and efficiency. The higher n is, the faster robot can move stably with more robustness and less efficiency. Especially when robot runs at low speed with high frequency, much more energy would be lost. In our strategy, the step frequency ranges from 2 to 3.57 Hz.

  2. 2.

    Swing phase ratio: Another important feature of gait is the ratio of swing phase time in a gait cycle. Swing phase time in slow-trotting accounts for less than 50\(\%\) of a gait cycle, while swing phase time is more than stance phase time in flying-trot, that is, \(R_{\textrm{swing}}\) is higher than 50\(\%\). When robot runs at a fixed step frequency, the larger \(R_{\textrm{swing}}\) is, the longer the leg swings in the air, and generally the faster speed can be achieved.

  3. 3.

    Phase offset: Phase offset \(\varphi _{\textrm{offset}}\) is used to represent the motion order of the four legs in a gait cycle. The phase offsets of the diagonal legs are the same when the robot moves in trotting. The order of the legs is specified as right front (RF) leg, left front (LF) leg, right hind (RH) leg and left hind (LH) leg. Taking RF as the reference, phase offset \(\varphi _{\textrm{RF}}\) of RF is 0, and \(\varphi _{\textrm{LF}}\), \(\varphi _{\textrm{RH}}\) and \(\varphi _{\textrm{LH}}\) represent phase offsets of LF, RH and LH, respectively. Therefore, the phase of LF can be expressed as \(\phi _{\textrm{LF}}=\phi _{\textrm{RF}}+\varphi _{\textrm{LF}}\). For example, \(\varphi _{\textrm{LH}}=0\) means that LH and RF move synchronously.

Fig. 1
figure 1

The control strategy consists of a gait planner and leg controllers. A gait set is obtained by the gait planner, including slow-trotting, trotting and flying-trot. The VMC and WBC are used for stance leg control, and foot step planner and leg VMC are used for swing legs. The state estimator feeds back the real-time state of robot for gait planner and controllers

Full size image
Fig. 2
figure 2

In trotting, the phase \(\phi \) and phase offset \(\varphi _{\textrm{offset}}\) of four legs and swing phase ratio \(R_{\textrm{swing}}\) are presented

Full size image
Fig. 3
figure 3

In the (a) or (b) or (c), the gait is transformed from the expression of one cycle in the left part to the expression of multiple cycles in the right part. In addition, in the right part, high level is stance phase, low level is swing phase, and a pair of stance phase and swing phase forms a gait cycle. RF and LH move synchronously, and LF and RH move synchronously

Full size image
Fig. 4
figure 4

When the speed of robot is from 0 to 4 m/s, the gait changes from slow-trotting to trotting and from trotting to flying-trot, and the step frequency changes from slow to fast. In addition, in the figure, high level is stance phase, low level is swing phase, and a pair of stance phase and swing phase forms a gait cycle

Full size image

2.2 Transition Process of Gait and Step Frequency

The robot’s gait and step frequency vary with speed. The desired speed of robot in the x direction is \(v_{\textrm{x}}^{\textrm{des}}\). According to the principle of “low frequency for low speed, high frequency for high speed” [6], the planned step frequency ranges from 2 to 3.75 Hz in the process of speed varying from 0 to 2.75 m/s. When the speed exceeds 2.75 m/s, the step frequency is maintained at 3.75 Hz. When the roll \(\varphi \) exceeds \(15^{\circ }\), the step frequency is changed from 2 Hz to 3 Hz. So that the robot can restore stability quickly by increasing the step frequency. Step frequency \(f_{\textrm{step}}\) changes with speed and roll as follows:

$$\begin{aligned} Iter= & {} {\left\{ \begin{array}{ll} 250,&{}\left( v_{\textrm{x}}^{\textrm{des}} = 0,\varphi< 15^{\circ }\right) \\ 167,&{}\left( v_{\textrm{x}}^{\textrm{des}} = 0,\varphi \ge 15^{\circ }\right) \\ -40v_{\textrm{x}}^{\textrm{des}} + 250,&{}\left( 0< v_{\textrm{x}}^{\textrm{des}} < 2.75\right) \end{array}\right. } \end{aligned}$$
(1)
$$\begin{aligned} {T}= \, & {} [Iter] / {\textrm{f}}_{\textrm{ctr}} \end{aligned}$$
(2)
$$\begin{aligned} f_{\textrm{step}}= \, & {} 1 / {T} \end{aligned}$$
(3)

where Iter is the number of iterations in a gait cycle T. The control frequency \({\textrm{f}}_{\textrm{ctr}}\) is determined according to the controller bandwidth and the actual performance of the robot, and its value is 500 Hz in this work. The step frequency \(f_{\textrm{step}}\), which equals to the reciprocal of the gait cycle T, is planned with the control cycle as the minimum time unit. A gait cycle is an integer multiple of the control cycle, which can ensure the coordination of gait, thereby ensuring the stability of the robot.

When the speed is in the range from 0 to 0.75 m/s, robot runs in slow-trotting; it runs in trotting at the stage of 0.75 m/s to 1.5 m/s; after speed exceeds 1.5 m/s, it runs in flying-trot, but \(R_{\textrm{swing}}\) does not change after speed exceeds 2.75 m/s. \(R_{\textrm{swing}}\) varies with speed as follows:

$$\begin{aligned} p_{\textrm{sta}}= & {} {\left\{ \begin{array}{ll} -1.6v_{\textrm{x}}^{\textrm{des}} + 6,&{}\left( 0 \le v_{\textrm{x}}^{\textrm{des}} \le 0.75\right) \\ 5,&{}\left( 0.75 \le v_{\textrm{x}}^{\textrm{des}} \le 1.5\right) \\ -1.6v_{\textrm{x}}^{\textrm{des}} + 7,&{}\left( 1.5 \le v_{\textrm{x}}^{\textrm{des}} \le 2.75\right) \end{array}\right. } \end{aligned}$$
(4)
$$\begin{aligned} p_{\textrm{swg}}= \, & {} p_{\textrm{tol}} - p_{\textrm{sta}} \end{aligned}$$
(5)
$$\begin{aligned} R_{\textrm{swing}}= \, & {} p_{\textrm{swg}} / p_{\textrm{tol}} \end{aligned}$$
(6)

A gait cycle is evenly divided into ten “time slices”. In a gait cycle, \(p_{\textrm{tol}}\) is the total numbers of time slices, and \(p_{\textrm{swg}}\) and \(p_{\textrm{sta}}\) are the number of those belong to swing phase and stance phase, respectively. In addition, swing phase ratio is the value of \(p_{\textrm{swg}}\) divided by \(p_{\textrm{tol}}\).

Based on the planning of step frequency \(f_{\textrm{ctr}}\) and swing phase ratio \(R_{\textrm{swing}}\) as described above, the adaptive gait planning is formed, as shown in Fig. 4. In the figure, high level represents stance phase and low level represents swing phase. It can be seen that gait can change from slow-trotting to trotting and then to flying-trot with the increase of speed.

3 Leg Controller

From the gait planner, a gait set is obtained. In addition, Inertial Measurement Unit (IMU) is used for the estimation of the robot’s attitude angle. In addition, based on the IMU datas, the linearized Kalman filter algorithm [24] is used to calculate the actual position of Center of Mass (CoM) and velocity. The estimation of the state of the four legs in the stance phase or the swing phase is based on the time state machine planned ahead. In addition, controllers are developed, respectively, for stance leg and swing leg with planned gaits and state estimation in the next part.

3.1 Stance Leg Control

3.1.1 Virtual Model Controller

When the leg is in stance phase, a Virtual Model at the torso is constructed based on the full-scale model of robot [25]. In addition, the optimal foot force is computed using Quadratic Programming (QP).

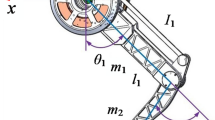
The front and hind legs on the diagonal line are in stance phase at every moment in Trotting. In addition, the force analysis is made on the system consisting of two stance legs and the torso in {b} (Fig.5). Assume that the virtual force at the CoM of torso is \({{\varvec{F}}}_{\textrm{v}}=\left[ f_{\textrm{x}}, f_{\textrm{y}}, f_{\textrm{z}}\right] ^{\textrm{T}}\), and the virtual torque is \({{\varvec{T}}}_{\textrm{v}}=\left[ t_{\textrm{x}}, t_{\textrm{y}}, t_{\textrm{z}}\right] ^{\textrm{T}}\). The virtual force and torque are distributed to the stance legs in the following form:

$$\begin{aligned} \left[ \begin{array}{c} {{\varvec{F}}}_{\textrm{v}} \\ {{\varvec{T}}}_{\textrm{v}} \end{array}\right] =\left[ \begin{array}{cc} {{\varvec{E}}} &{} {{\varvec{E}}} \\ {{\varvec{r}}}_{\textrm{F}} \times &{} {{\varvec{r}}}_{\textrm{H}} \times \end{array}\right] \left[ \begin{array}{l} {{\varvec{f}}}_{\textrm{F}} \\ {{\varvec{f}}}_{\textrm{H}} \end{array}\right] +\left[ \begin{array}{l} {{\varvec{G}}} \\ {{\varvec{0}}} \end{array}\right] \end{aligned}$$
(7)

where \({{\varvec{f}}}_{\textrm{F}}=\left[ f_{\textrm{x}}^{\textrm{F}}, f_{\textrm{y}}^{\textrm{F}}, f_{\textrm{z}}^{\textrm{F}}\right] ^{\textrm{T}}\) and \({{\varvec{f}}}_{\textrm{H}}=\left[ f_{\textrm{x}}^{\textrm{H}}, f_{\textrm{y}}^{\textrm{H}}, f_{\textrm{z}}^{\textrm{H}}\right] ^{\textrm{T}}\) are the ground reaction force on the front and hind feet, respectively. \({{\varvec{r}}}_{\textrm{F}}\) and \({{\varvec{r}}}_{\textrm{H}}\) are the position vectors of ground support point of front and hind feet relative to CoM of torso in {b}, respectively. \({{\varvec{E}}}\in \textrm{R}^{3\times 3}\) is a unit vector. \({{\varvec{r}}}_{\textrm{F}} \times \) and \({{\varvec{r}}}_{\textrm{H}} \times \) are the cross-product form of the position vector. \({{\varvec{G}}} \) is the gravity vector.

The virtual force and torque are designed based on the virtual model of torso that is a three-dimensional spring-damping model. There are force and torque around the axis in each dimension. The designed virtual force and torque are as follows:

$$\begin{aligned} f_{\textrm{x}}&=k_{\textrm{p}}^{\textrm{x}}\left( p_{\textrm{xd}}-p_{\textrm{x}}\right) +k_{\textrm{d}}^{\textrm{x}}\left( v_{\textrm{xd}}-v_{\textrm{x}}\right) \end{aligned}$$
(8a)
$$\begin{aligned} f_{\textrm{y}}&=k_{\textrm{p}}^{\textrm{y}}\left( p_{\textrm{yd}}-p_{\textrm{y}}\right) +k_{\textrm{d}}^{\textrm{y}}\left( v_{\textrm{yd}}-v_{\textrm{y}}\right) \end{aligned}$$
(8b)
$$\begin{aligned} f_{\textrm{z}}&=k_{\textrm{p}}^{\textrm{z}}\left( p_{\textrm{zd}}-p_{\textrm{z}}\right) +k_{\textrm{d}}^{\textrm{z}}\left( v_{\textrm{zd}}-v_{\textrm{z}}\right) \end{aligned}$$
(8c)
$$\begin{aligned} t_{\textrm{x}}&=k_{\textrm{p}}^{\textrm{roll}}\left( \phi _{\textrm{d}}-\phi \right) +k_{\textrm{d}}^{\textrm{roll}}\left( \dot{\phi }_{\textrm{d}}-\dot{\phi }\right) \end{aligned}$$
(8d)
$$\begin{aligned} t_{\textrm{y}}&=k_{\textrm{p}}^{\textrm{pitch}}\left( \theta _{\textrm{d}}-\theta \right) +k_{\textrm{d}}^{\textrm{pitch}}\left( \dot{\theta }_{\textrm{d}}-\dot{\theta }\right) \end{aligned}$$
(8e)
$$\begin{aligned} t_{\textrm{z}}&=k_{\textrm{p}}^{\textrm{yaw}}\left( \psi _{\textrm{d}}-\psi \right) +k_{\textrm{d}}^{\textrm{yaw}}\left( \dot{\psi }_{\textrm{d}}-\dot{\psi }\right) \end{aligned}$$
(8f)

where \({{\varvec{k}}}_{\textrm{p}}\) and \({{\varvec{k}}}_{\textrm{d}}\) are the stiffness and damping coefficient in each dimension. \(\left[ {p}_{\textrm{x}}, {p}_{\textrm{y}}, {p}_{\textrm{z}}\right] ^{\textrm{T}}\) and \(\left[ {v}_{\textrm{x}}, {v}_{\textrm{y}}, {v}_{\textrm{z}}\right] ^{\textrm{T}}\) represent, respectively, the position of CoM of torso and corresponding speed. \(\left[ \phi , \theta , \psi \right] ^{\textrm{T}}\) and \(\left[ \dot{\phi }, \dot{\theta }, \dot{\psi }\right] ^{\textrm{T}}\) are the Euler angles of torso and corresponding angular velocity, respectively. The symbols with subscript \(\textrm{d}\) represent desired variables of robot.

Fig. 5
figure 5

The “SDUQuad_48” robot is running. The robot coordinate system is built for modeling, marked by {b}

Full size image

Equation 7 is transformed into the following form:

$$\begin{aligned} \left[ \begin{array}{c} {{\varvec{F}}}_{\textrm{v}}-{{\varvec{G}}} \\ {{\varvec{T}}}_{\textrm{v}} \end{array}\right] =\left[ \begin{array}{cc} {{\varvec{E}}} &{} {{\varvec{E}}} \\ {{\varvec{r}}}_{\textrm{F}} \times &{} {{\varvec{r}}}_{\textrm{H}} \times \end{array}\right] \left[ \begin{array}{c} {{\varvec{f}}}_{\textrm{F}} \\ {{\varvec{f}}}_{\textrm{H}} \end{array}\right] \end{aligned}$$
(9)

The above formula can be written in the form \({{\varvec{A}}}{{\varvec{x}}}={{\varvec{b}}}\), so the linear matrix equation problem needs to solve to acquire the value of \({{\varvec{x}}}=\left[ {{\varvec{f}}}_{\textrm{F}}, {{\varvec{f}}}_{\textrm{H}}\right] ^{\textrm{T}}\). \({{\varvec{A}}}\) is not a full-rank matrix because of the floating base model, so there is no sole answer. Based on the QP used by the starlETH robot [26], the number of optimization variables is reduced to 6 that are the three-dimensional foot force of the front and hind legs in stance phase to get a real-time solution.

The above problem is solved in the form of a QP problem. The optimization goal is the foot force which is expected to be as small as possible to meet the limit of the motor’s output and achieve high efficiency:

$$\begin{aligned} \min \Vert {{\varvec{A}}}{{\varvec{x}}}-{{\varvec{b}}}\Vert _{{\varvec{Q}}}+\Vert {{\varvec{x}}}\Vert _{{\varvec{R}}} \end{aligned}$$
(10)

s.t.

$$\begin{aligned}&|f_{\textrm{x}}^{\textrm{F}} |<\mu f_{\textrm{z}}^{\textrm{F}} \end{aligned}$$
(11a)
$$\begin{aligned}&|f_{\textrm{y}}^{\textrm{F}} |<\mu f_{\textrm{z}}^{\textrm{F}} \end{aligned}$$
(11b)
$$\begin{aligned}&|f_{\textrm{x}}^{\textrm{H}} |<\mu f_{\textrm{z}}^{\textrm{H}} \end{aligned}$$
(11c)
$$\begin{aligned}&|f_{\textrm{y}}^{\textrm{H}} |<\mu f_{\textrm{z}}^{\textrm{H}}\end{aligned}$$
(11d)
$$\begin{aligned}&0<f_{\textrm{z}}^{\textrm{F}}<f_{\text {max}}^{\textrm{F}}\end{aligned}$$
(11e)
$$\begin{aligned}&0<f_{\textrm{z}}^{\textrm{H}}<f_{\text {max}}^{\textrm{H}} \end{aligned}$$
(11f)

where \({{\varvec{Q}}}\) and \({{\varvec{R}}}\) are diagonal matrices representing following and penalty weight, respectively. The notation \(\Vert {{\varvec{y}}}\Vert _{{\varvec{W}}}\) is used to indicate the weighted norm \({{\varvec{y}}}^{\textrm{T}}{{\varvec{W}}}{{\varvec{y}}}\). The constraint of the optimization objective is the friction cone constraint of foot force, and \(\mu \) is the friction coefficient.

VMC has been already a relatively mature technology in robotics research. More technical details about the VMC can be found in our previous result [25].

3.1.2 Whole-Body Controller

A whole-body motion controller is implemented by constructing a floating base dynamics model. Robot’s motion is decomposed into torso motion and leg motion, and torso motion is further divided into linear and rotational motion. Then, the motion task of the robot is decomposed into torso position task, torso pose task and leg task for priority task hierarchical control. The computed desired joint angle \({{\varvec{q}}}_{\textrm{des}}\) and joint angular velocity \(\dot{{\varvec{q}}}_{\textrm{des}}\) are both used for PD control in joint space. The computed desired joint angular acceleration \(\ddot{{\varvec{q}}}_{\textrm{des}}\) and the optimal foot force \({{\varvec{f}}}_{\textrm{r}}^{\textrm{VM}}\) obtained by VM Controller are used for further optimization using QP:

$$\begin{aligned} \min _{{{\varvec{\delta }}}_{\textrm{f}_{\textrm{r}}},{{\varvec{\delta }}}_{\textrm{f}}} {{\varvec{\delta }}}_{\textrm{f}_{\textrm{r}}}^{\textrm{T}}{{\varvec{R}}}_{1} {{\varvec{\delta }}}_{\textrm{f}_{\textrm{r}}}+{{\varvec{\delta }}}_{\textrm{f}}^{\textrm{T}} {{\varvec{R}}}_{2} {{\varvec{\delta }}}_{\textrm{f}} \end{aligned}$$
(12)

s.t.

$$\begin{aligned}&{{\varvec{S}}}_{\textrm{float}}({{\varvec{M}}}\ddot{{\varvec{q}}}+{{\varvec{b}}}+{{\varvec{g}}})={{\varvec{S}}}_{\textrm{float}} {{\varvec{J}}}_{\textrm{c}}^{\textrm{T}} {{\varvec{f}}}_{\textrm{r}}\end{aligned}$$
(13a)
$$\begin{aligned}&\ddot{{\varvec{q}}}= \, \ddot{{\varvec{q}}}_{\textrm{des}}+\left[ \begin{array}{c} {{\varvec{\delta }}}_{\textrm{f}} \\ {{\varvec{0}}}_{\textrm{n}_{\textrm{j}}} \end{array}\right] \end{aligned}$$
(13b)
$$\begin{aligned}&{{\varvec{f}}}_{\textrm{r}}={{\varvec{f}}}_{\textrm{r}}^{\textrm{VM}}+{\varvec{\delta }}_{\textrm{f}_{\textrm{r}}} \end{aligned}$$
(13c)
$$\begin{aligned}&{\varvec{C}}{{\varvec{f}}}_{\textrm{r}}>{\varvec{0}} \end{aligned}$$
(13d)

The dynamic model of the floating base is showed in Eq. 13a. \(\ddot{{\varvec{q}}}\) and \({{\varvec{f}}}_{\textrm{r}}\) are the desired joint angular acceleration and foot force, and \({{\varvec{\delta }}}_{\textrm{f}}\) and \({\varvec{\delta }}_{\textrm{f}_{\textrm{r}}}\) are relaxation variables for the floating base acceleration and reaction force in Eq. 13b and 13c, respectively. In addition, Eq. 13d represents contact force constraints, where \({\varvec{R}}_{1}\) and \({\varvec{R}}_{2}\) are both diagonal weight matrix. \({\varvec{\delta }}_{\textrm{f}}\) and \({\varvec{\delta }}_{\textrm{f}_{\textrm{r}}}\) are the slack variable of acceleration of the floating base and the foot force, respectively. \({{\varvec{S}}}_{\textrm{float}}\) is the selection matrix of the floating base. \({\varvec{M}}\), \({\varvec{b}}\), \({\varvec{g}}\) and \({{\varvec{J}}}{\textrm{c}}\) are the generalized mass matrix, Coriolis force, gravity and contact Jacobian matrix. \({\varvec{C}}\) is contact constraint matrix.

Bringing \(\ddot{{\varvec{q}}}\) and \({{\varvec{f}}}_{\textrm{r}}\) obtained through QP into the whole-body dynamic equation, the desired joint torque \({\varvec{\tau }}_{\textrm{j}}\) can be calculated and transmitted to the motor to control:

$$\begin{aligned} \left[ \begin{array}{c} {\varvec{\tau }}_{\textrm{f}} \\ {\varvec{\tau }}_{\textrm{j}} \end{array}\right] ={\varvec{M}} \ddot{{\varvec{q}}}+{\varvec{b}}+{\varvec{g}}-{\varvec{J}}_{\textrm{c}}^{\textrm{T}}{{\varvec{f}}}_{\textrm{r}} \end{aligned}$$
(14)

3.2 Swing Leg Control

The swing leg controller consists of swing foot planning and servo control of swing leg. Based on the planning method of foot landing point proposed by Raibert, the swing foot trajectory in the \(\textrm{x}\) and \(\textrm{y}\) directions are designed as follows:

$$\begin{aligned} \bar{x}(t)= \, & {} x(t)+\left[ v_{\textrm{x}} t_{\textrm{sta}} / 2+k_{\textrm{vx}}\left( v_{\textrm{x}}-{v_{\textrm{x}}}^{\textrm{des}}\right) -x(t)\right] \nonumber \\{} & {} /\left[ \left( t_{\textrm{sta}}-t\right) / \delta _{\textrm{t}}\right] \end{aligned}$$
(15)
$$\begin{aligned} \bar{y}(t)= \, & {} y(t)+\left[ v_{\textrm{y}} t_{\textrm{sta}} / 2+k_{\textrm{vy}}\left( v_{\textrm{y}}-{v_{\textrm{y}}}^{\textrm{des}}\right) -y(t)\right] \nonumber \\{} & {} /\left[ \left( t_{\textrm{sta}}-t\right) / \delta _{\textrm{t}}\right] \end{aligned}$$
(16)

where \(\bar{x}(t)\) and \(\bar{y}(t)\) are the desired foot position at time t, x(t) and y(t) are the current foot position, \(v_{\textrm{x}}\) and \(v_{\textrm{y}}\) are the current speed of robot, \(t_{\textrm{sta}}\) is stance phase time, \(k_{\textrm{vx}}\) and \(k_{\textrm{vy}}\) are speed error compensation coefficient, and \(\delta _{\textrm{t}}=\) 2 ms is the interval of gait control.

The trajectory in the \(\textrm{z}\) direction is designed as a quartic curve to ensure the continuity of speed and acceleration, as follows:

$$\begin{aligned} \bar{z}(t)=H_{\textrm{d}}\left( 16 t^{4} / t_{\textrm{sta}}^{4}-32 t^{3} / t_{\textrm{sta}}^{3}+16 t^{2} / t_{\textrm{sta}}^{2}\right) -h_{\textrm{s}} \end{aligned}$$
(17)

where \(H_d\) is the desired maximum height that swing foot can reach, and \(h_{\textrm{s}}\) is the height of the robot while standing.

The servo control of swing leg is realized taking advantage of the leg’s virtual model. The swing leg is equivalent to a spring-damping model, so the virtual foot force \({{\varvec{F}}}^{\textrm{leg}}_{\textrm{v}} =\left[ f_{\textrm{lx}}, f_{\textrm{ly}}, f_{\textrm{lz}}\right] ^{\textrm{T}}\) is designed as follows:

$$\begin{aligned} f_{\textrm{lx}}&=k_{\textrm{px}}(\bar{x}-x)+k_{\textrm{dx}}\left( \bar{v}_{\textrm{x}}^{\textrm{p}}-v_{\textrm{x}}^{\textrm{p}}\right) \end{aligned}$$
(18a)
$$\begin{aligned} f_{\textrm{ly}}&=k_{\textrm{py}}(\bar{y}-y)+k_{\textrm{dy}}\left( \bar{v}_{\textrm{y}}^{\textrm{p}}-v_{\textrm{y}}^{\textrm{p}}\right) \end{aligned}$$
(18b)
$$\begin{aligned} f_{\textrm{lz}}&=k_{\textrm{pz}}(\bar{z}-z)+k_{\textrm{dz}}\left( \bar{v}_{\textrm{z}}^{\textrm{p}}-v_{\textrm{z}}^{\textrm{p}}\right) \end{aligned}$$
(18c)

where \(k_{\textrm{px}}\) and \(k_{\textrm{dx}}\) are the stiffness and damping coefficient in the \(\textrm{x}\) dimension, and the parameters in \(\textrm{y}\) and \(\textrm{z}\) dimension are defined as same.

Using the leg Jacobian matrix \({\varvec{J}}\), the foot force is converted into joint torque \({\varvec{\tau }}\) to control:

$$\begin{aligned} {\varvec{\tau }}={\varvec{J}}^{\textrm{T}} {{\varvec{F}}}^{\textrm{leg}}_{\textrm{v}} \end{aligned}$$
(19)
Fig. 6
figure 6

The robot moves with three gaits in the process of gait transition. The stance legs are marked with red circle, and the swing legs are marked with yellow triangle in above figure

Full size image

4 Results

To verify the effectiveness of the algorithm, the quadruped robot “SDUQuad_48” developed by the Robot Research Center of Shandong University is used for experiments. The robot (Fig. 5) weighs 13.5 kg and its dimension is 0.41\(\times \)0.24\(\times \)0.35 m (0.35 m is the standing height) with 12 degrees of freedom. The robot can move stably in a variety of gaits including slow-trotting, trotting, flying-trot, pronking and bounding. In addition, it has good passability on various complex terrains, such as grass ground, gravel ground, snow ground and so on. In addition, it can climb up the 30-degree slope and the stairs with the step height of 12 cm, and the fastest speed can reach 4 m/s. The robot parameters are shown as in Table 1. The controller in robot system is up-board with the real-time kernel of Ubuntu16.04 and “4+32 G” memory. The joint driver is the brushless DC motor with a reduction ratio of 6:1 and the peak torque is 48 Nm. The motor parameters are shown as in Table 2.

Table 1 Robot parameters
Full size table
Table 2 Motor parameters
Full size table

4.1 Step Frequency and Gait Transition with Speed Varying

The forward speed command is sent to the robot by the remote controller, and its motion process is shown in the Fig. 6.

With the speed increasing, gait cycle is getting shorter and shorter seen from Fig. 7. What is more, in each gait cycle, the proportion of stance phase becomes smaller and smaller and those of swing phase becomes larger and larger oppositely. If measured by swing phase ratio \(R_{\textrm{swing}}\), it can be clearly seen that \(R_{\textrm{swing}}\) is 40 \(\%\) at the beginning and then rises gradually, reaching a maximum of 74 \(\%\).

While the speed increases gradually from 0, the step frequency increases gradually, as shown in Fig. 8. The desired speed reaches up to 4 m/s. The robot has experienced a process of gradually accelerating from 0 to 4 m/s and then gradually decelerating to zero. During this process, velocity tracking performance is good. The step frequency is 2 Hz when speed is 0. As the speed increases, step frequency increases gradually up to a maximum of 3.57 Hz. It shows that robot’s step frequency has a good adaptability with the change of speed.

4.2 Step Frequency Transition While Being Disturbed

When the robot is subjected to a lateral impact as shown in Fig. 9. the posture will be affected, especially roll angle changes most obviously. When the roll angle exceeds the predefined stability range and it is difficult to restore stability in the current frequency, the robot will automatically adjust step frequency to improve the anti-interference ability. In this experiment, the robot was disturbed by man-made for several times. After the robot becomes unstable, it adjusts quickly by increasing the step frequency from 2 Hz to 3 Hz and recovers stable in a short time. At the same time, roll angle also returns to normal state and step frequency recovers to 2 Hz in Fig. 10.

Fig. 7
figure 7

When the speed of robot is from 0 to 4 m/s, the ratio of stance phase time is getting less and less, and the ratio of swing phase time is getting larger and larger in a gait cycle. The step frequency is getting faster. In addition, in the figure, high level is stance phase, low level is swing phase, and a pair of stance phase and swing phase forms a gait cycle

Full size image
Fig. 8
figure 8

The step frequency is changing when the speed of robot changes

Full size image
Fig. 9
figure 9

The robot loses balance after being subjected to a lateral impact, and quickly recovers stable by changing step frequency

Full size image
Fig. 10
figure 10

The step frequency increases when the robot is disturbed

Full size image

4.3 Energy Consumption in Various Gaits

Compared with locomotion of the fixed gait and step frequency, the robot can consume less energy and improve energy efficiency by changing gait and frequency in terms of speed. In this experiment, three gaits slow-trotting, trotting and flying-trot are selected for comparison. The step frequency \(f_{\textrm{step}}\), swing phase ratio \(R_{\textrm{swing}}\) and phase offset \(\varphi _{\textrm{offset}}\) of the gaits are shown in Table 3. The energy consumption is expressed as the accumulation of the product of joint torque and joint angular velocity \(\sum |\tau \omega |\) during the same time. Figure 11 shows the energy consumption in various gaits in the process of robot’s speed from 0 to 4 m/s.

The whole process is divided into three areas: low-speed, medium-speed and high-speed zone. The fastest speed that robot can reach is 1 m/s in slow-trotting. In trotting, the fastest speed is 2 m/s. In addition, the robot can run stably at 4 m/s in flying-trot and the proposed gait. In addition, the robot always consumes the least amount of energy through gait transition during the whole process.

Table 3 Gait parameters of three gaits
Full size table
Fig. 11
figure 11

There are energy consumption of robot with four gaits at a wide range of speed

Full size image

5 Conclusion

An adaptive diagonal gait planner is designed. By changing the gait cycle time and the swing phase ratio of each leg, the quadruped robot can spontaneously switch gait and change the step frequency at different speeds. In addition, a controller combining VMC and WBC is designed to solve the desired joint torque for robot. The effectiveness of the gait planning method and the locomotion controller is verified on a real robot. By adaptively changing the gait, the robot runs from slow-trotting at slow-speed to trotting at medium-speed to flying-trot at high-speed, and the maximum speed of stable motion reaches 4 m/s. Comparing to the three gaits with fixed step frequency, the robot always consumes less energy during the motion in the proposed gait. Moreover, the lateral impact experiment shows that the robot obtains good anti-interference performance by automatically increasing the step frequency. Such experimental results are in line with previous research on biomimetic mechanisms, showing that quadrupeds reduce energy consumption by switching gaits at different speeds. However, it is limited to plan adaptive gait based only on robot’s speed to reduce energy consumption. Our next research direction is to establish an energy consumption model, considering both speed and energy consumption for gait planning, so as to design a more efficient motion controller for the quadruped robot.