Humans Adopt Different Exploration Strategies Depending on the Environment

Abstract

Humans explore to learn the structure of our environment. However, it remains unclear how consistent humans are in the exploration strategies we use and how often we explore across different environments which vary in their volatility. Using a within-subjects design, participants (n = 30) completed (1) a non-stationary bandit task where the reward values changed throughout, and (2) a stationary bandit task where one option always gave better reward. We used a series of reinforcement learning models to understand the exploration strategies humans adopted in the two tasks. We found that most participants adopted a behavioural heuristic strategy (Win-Stay, Lose-Shift) in the non-stationary bandit task. In contrast, most participants adopted a probabilistic, random exploration strategy (Softmax) in the stationary bandit task. We compared our results when fitting models individually within each task to when fitting models across both tasks—that is focusing on long-term predictions. When fitting across both tasks we found that most participants solely adopted a probabilistic, random exploration strategy. In addition, we found a moderate, positive relationship between exploration rate in each of the two bandit tasks. Our findings show that humans can flexibly adopt different exploration strategies depending on task demands, which we suggest is because the two bandit tasks assessed different aspects of learning and required different levels of cognitive flexibility. In addition, we speculate that the relationship between exploration rate could reflect a personality trait such as risk-taking. In sum, we found evidence for the flexible use of exploration strategies, while also observing evidence of the generalization of exploration across tasks.

An Examination of the Explore-Exploit Dilemma in Different Learning Environments

We learn through the act of exploration. To gain knowledge, humans search their environments to learn the causal relationships between stimuli, responses, and outcomes (Berridge, 2000). When we choose to explore, we balance the trade-off between what we know and our expectations of our other options—we attempt to solve the explore-exploit dilemma. Importantly, how we gain knowledge and solve the explore-exploit dilemma is related to the strategies we use to explore. For example, consider what strategies you could use when choosing a film to watch. If you are only considering two or three options, you might adopt a strategy to spend time reading reviews, deciding if you enjoyed prior work by the director, and considering the cast. If instead there were many options, such as when using a streaming service, then you might instead rely on a heuristic like “I enjoy neo-noir movies” rather than considering all options individually. We posit that the strategies we use to explore depend on the context in which we are making the decision.

Here we rely on two pieces of evidence to suggest that humans can flexibly use different exploration strategies across tasks. First, computational modeling work has highlighted a variety of exploration strategies that humans can adopt (e.g., Daw et al., 2006; Payzan-LeNestour & Bossaerts, 2012; Schulz et al., 2018a, b) and people use different exploration strategies concurrently within a task (Wilson et al., 2014). Second, evidence suggests that the same group of people can adopt different exploration strategies depending on task demands (Schulz et al., 2018b; Wu et al., 2020). Thus, in the present work, we sought to expand our understanding of how and why different exploration strategies are used by comparing exploration within learning environments which differed in their volatility. Being able to modulate learning under conditions of environment volatility is a key aspect of learning, and unsurprisingly, humans adapt their learning by modulating action-outcome relationships depending on environmental volatility (e.g., Behrens et al., 2007; Browning et al., 2015). Here we hoped to extend these findings by examining exploration in an environment where reward values changed throughout (a volatile environment, i.e., non-stationary) and an environment where reward values were unchanging (a consistent environment, i.e., stationary).

Further, we investigated whether aspects of exploratory behaviour—in the present work, exploration frequency—are consistent across tasks. While no prior work has investigated whether people are consistent in the frequency with which they explore, there is evidence that switching rates across tasks and sessions is moderately correlated (Yechiam, 2020). We do note that while switching and exploration are likely correlated, switching to another choice can reflect choosing the highest value option while exploration does not. That is, while someone may switch to another option due to a decrease in value of their previous choice, exploration involves investigating an option that currently has a lower value compared to the previously selected option. Although the specific reasons why there is a consistency in switching rates are unclear, it could be related to personality trait differences across people (as suggested by Yechiam, 2020). For example, someone who is more willing to tolerate risk might be more likely to explore across different contexts when compared to someone who is less tolerant of risk. Moreover, there is evidence in a consistency in risk taking across multiple sessions within paradigms that assess learning (Yechiam & Telpaz, 2013).

Methods adapted from reinforcement learning provide a means to investigate exploration strategies, and the drive for knowledge more generally. As noted by Niv (2009), reinforcement learning models are one of the few modeling approaches which provide a solution to Marr’s three levels of analysis for cognitive systems (Marr, 1982). Ideas gleaned from reinforcement learning models demonstrated the role of the dopaminergic system in guiding feedback learning (Schultz et al., 1997) and helped reveal the electrophysiological signals involved in feedback processing (Holroyd & Coles, 2002). More relevant for the present work, tasks adapted from reinforcement learning provide a means of investigating the explore-exploit dilemma (Sutton & Barto, 2018). For example, the application of reinforcement learning models to “multi-arm bandit paradigms” have provided a framework for understanding exploration in both artificial and human agents. In a multi-arm bandit task (Robbins, 1952; Thompson, 1933), an agent makes selections from a series of options (known as arms), receives feedback from their selections, and attempts to learn which arm allows the agent to maximize reward long-term. Within the multi-arm bandit task, the agent must effectively trade-off between exploring to gain knowledge about the arms and exploiting when the arm which provides the best long-term feedback is found. As has been highlighted elsewhere (e.g., Cohen et al., 2007), finding a computationally tractable solution to a multi-arm bandit task can be difficult due to the complexity of correctly modeling future decisions (Gittins & Jones, 1974). Luckily, reinforcement learning models provide a means of approximating a solution to the multi-arm bandit problem (Lattimore & Szepesvári, 2020; Sutton & Barto, 2018), and these models have been effective at modeling human choices in multi-arm bandit tasks (Daw et al., 2006; Gershman, 2019; Li & Daw, 2011).

As to the strategies which humans use to explore, an initial question in the literature was whether humans explore by biasing their selection to options that are more uncertain or whether humans simply explore randomly using value. In fact, the initial evidence on whether humans explored using uncertainty was mixed (e.g., Daw et al., 2006 observed no evidence of uncertainty-guided exploration while Knox et al., 2012 did). However, an important methodological insight led to the observation that humans in fact use multiple forms of exploration concurrently when learning (Wilson et al., 2014). Specifically, Wilson and colleagues (2014) argued that uncertainty-based exploration has not been consistently observed due to conflation of value and information within bandit paradigms. That is, the options which have high value estimates also tend to have been options that have been sampled more often in the past. In fact, careful experimental design separating information and value during learning led to the observation that humans use both “random” and “directed” exploration strategies (Wilson et al., 2014). Random exploration is the stochastic selection of options that is not tied to considerations of stimuli information and uses random sampling to learn about options. That is, under random exploration competing exploratory decisions typically have the same likelihood of being chosen. In contrast, directed exploration is the exploration of a specific choice due to that choice having higher values of information, and the highest uncertainty.

Importantly, work has extended the finding that humans use both directed and random exploration. Specifically, humans use both directed and random exploration in a two-armed bandit task which differed in the levels of risk associated with each arm, and both strategies were shown to coexist to determine how exploration occurs (Gershman, 2019). In addition, work has shown that humans also use both directed and random exploration in a more ecologically valid bandit paradigm which included a larger decision space and spatial relationships between reward values—as might be seen in real-world learning (Wu et al., 2018). That humans can use both directed and random exploration speaks to the importance not only of the application of flexible behavioural strategies but the importance of being able to detect when to apply these strategies. Given the evidence provided by Wilson and colleagues (and others) that humans can use both random and directed exploration strategies within a single task, it seems likely then that task and environmental demands can determine when specific exploration strategies are used.

Random and directed exploration strategies have been operationalized using a variety of choice selection models. In some cases, random exploration has been investigated using a model known as ε-Greedy (e.g., Barron & Erev, 2003). In the case of the ε-Greedy model (Sutton & Barto, 2018), an agent (whether human or artificial) typically chooses the highest value option but will explore the remaining options randomly per an exploration parameter from the model. In addition, a probabilistic exploration model that usually chooses the highest value option but explores the remaining options proportionally to their value (Softmax model; typically considered as a form of random exploration) has been applied to human choice data. In fact, within a non-stationary bandit task humans were found to use probabilistic, random exploration (that is, their behaviour was best fit by the Softmax model) and there was no evidence of humans exploring using uncertainty (Daw et al., 2006).

However, further work has indeed shown evidence that humans use uncertainty-guided exploration strategies within a non-stationary bandit paradigm (e.g., Speekenbrink & Konstantinidis, 2015). Speekenbrink and Konstantinidis found that a strategy akin to Thompson Sampling (Neimark & Shuford, 1959; Thompson, 1933) combined with a Bayesian update rule (the Kalman Filter; Kalman, 1960) provided the best fit of participants’ behaviour—a model that was not considered in the original investigation by Daw and colleagues (2006). We do note that within the bandit paradigm of Speekenbrink and Konstantinidis, a subset of participants continued to adopt different variants of probabilistic, random exploration (Softmax). Relatedly, models which incorporate Thompson sampling have been used as a means of operationalizing random exploration in stationary bandit paradigms as well (Gershman, 2019). Within the same paradigm, Gershman (2019) operationalized directed exploration using a model known as the Upper Confidence Bound model (Auer, 2002), which adds an information bonus tied to uncertainty to exploration. Finally, hybrid models combining both random and directed exploration are used across the literature (Softmax with an exploration bonus model; Meder et al., 2021; Schulz et al., 2018a, 2018b; Speekenbrink & Konstantinidis, 2015; Wu et al., 2020).

While random and directed explorations have been key constructs in our understanding of exploration strategies, there is a wide variety of approaches used to study exploration within bandit tasks. For example, humans adopt different exploration strategies depending on the environment (Schulz et al., 2018a). That is, in a simple bandit task—where binary cues predicted outcomes—humans used an exploration heuristic tied to utility while in a more complex bandit task—where continuous cues predicted outcomes—people used both random and directed exploration strategies. Gradient approaches (R. J. Williams, 1992)—computational models which calculate action preferences rather than directly estimating action values—are also effective at modeling human behaviour in tasks that require exploration (Li & Daw, 2011; Zhang & Yu, 2013), Moreover, Gradient models may be more plausible when compared to models that specifically estimate action values, given the lack of evidence for direct economic computations of value within the brain (Bennett et al., 2021; Hayden & Niv, 2021). Lastly, behavioural heuristics such as Win-Stay, Lose-Shift—which do not assume any learning about the long-term reward values of options—have proven to be effective at modeling both human Iowa Gambling Task performance (Worthy et al., 2013) and bandit task performance (Bonawitz et al., 2014), and have been used to examine exploration (Wu et al., 2018).

Although the above evidence suggests that humans can adopt different exploration strategies, the problem of whether exploration strategies are used consistently across environments remains under investigated. In fact, how we explore appears to not always be consistent across tasks. Two prior investigations have shown that humans can flexibly change their exploration strategy across environments (Schulz et al., 2018b; Wu et al., 2020). For example, when learning in a risky environment (where points could be lost) participants adopted an exploration strategy where they avoided risky choices (a “probability of being safe” strategy). However, when the same group of participants were learning in a safe environment (where no points could be lost) they instead adopted both directed and random exploration (Schulz et al., 2018b). That the introduction of risk would change how humans explore and sample their environment makes sense—the introduction of adversity should change behaviour by encouraging participants to avoid exploring certain options when they carry risky outcomes. Further work has compared learning within spatial and non-spatial environments and found that the same group of participants can adopt different strategies across multiple experimental sessions (Wu et al., 2020). Wu and colleagues found that humans used more directed exploration in the spatial environment while showing a decrease in directed exploration and a concomitant increase in random exploration in the non-spatial environment. These two results highlight that even the same group of participants can indeed adopt different exploration strategies depending on the task demands and structure. There has been a lack of work in humans examining whether exploration strategies change depending on environmental volatility. Thus, we hope to extend these two findings of flexible exploration strategy use to learning under different conditions of volatility.

In the present work, we investigated how humans explored two distinct multi-arm bandit tasks which differed in their level of environmental volatility. Our main goal was to investigate whether humans are consistent in the exploration strategy they adopt across two bandit environments. We tested participants in a non-stationary bandit task where the reward values changed throughout the task, and in a stationary bandit task where one arm always had a higher reward probability. We included a series of models which approximate exploration in different ways to better understand how humans explore in non-stationary and stationary bandit environments—including several state-of-the-art methods widely used in reinforcement learning (though ours are simplified and specialized to our bandit setting). Specifically, we compared a series of seven computational models (and an additional baseline) in their ability to correctly fit human behaviour in the two bandit paradigms.

Briefly we discuss the rationale for the inclusion of each non-baseline model. Given the importance of both directed and random exploration in our understanding of human exploration, we included models which used these approaches for exploration and action selection. We included a random exploration model (ε-Greedy; Sutton & Barto, 2018), a directed exploration model (Upper-confidence bound; Auer, 2002), and a hybrid model which included both directed and random, probabilistic exploration (Softmax with Exploration Bonus; Daw et al., 2006; Speekenbrink & Konstantinidis, 2015). We also examined a random, probabilistic exploration model which explored using value (Softmax), which has proven to be effective at modeling human exploration in a non-stationary bandit paradigm (Daw et al., 2006). Moreover, we included a Bayesian learner (Kalman Filter with Thompson sampling) because it has also been shown to be effective at modeling human learning within non-stationary bandit paradigms (Speekenbrink & Konstantinidis, 2015). We also examined two types of models that have been under-investigated in human exploration. We examined a probabilistic exploration model that explored using action preferences (Gradient bandit algorithm; R. J. Williams, 1992) given that Gradient models can provide parsimonious explanations for human learning (Hayden & Niv, 2021). We also examined a behavioural heuristic (Win-Stay, Lose-Shift), a model which has received comparatively little examination in human exploration studies (although see Wu et al., 2018 for an example) but can provide effective accounts of human learning in bandit-style task (Bonawitz et al., 2014; Worthy et al., 2013).

For our main goal of determining whether exploration strategy use is consistent across tasks, we expected that humans would flexibly use different exploration strategies depending on the task. This finding would extend prior work showing humans adopt different exploration strategies across experimental conditions (Schulz et al., 2018b; Wu et al., 2020). In addition, we investigated whether there were any differences when fitting models within each bandit task individually as compared to fitting the models using the combined data across each task. This sort of method is important because it allows for the investigation of how an approach might lead to more generalizable models (the combined fitting approach across both bandit tasks) and can provide complementary results when compared to fitting the models individually within each bandit task. Lastly, we investigated whether there was any relationship in the frequency of exploration rate across tasks. Given recent concerns raised over the generalizability of reinforcement learning model parameters and the underlying relationship between these parameters and cognition in humans (Eckstein et al., 2022), we hoped to determine if there are generalizable aspects of human exploratory behaviour. Given prior work showing a moderate correlation between switching rates in a bandit-style task (Yechiam, 2020), we expected that there would be a relationship between exploration frequency in the two bandit paradigms.

Method

Participants

In the present experiment, a total of 30 participants (15 males, 15 females; age range 18 to 40, mean age = 21.37, 95% CI [19.69, 23.05]) were recruited from the University of Victoria. The participants we analyzed were in fact recruited for a separate study that examined the effect of acute stress on learning (Ferguson & Krigolson, in-prep) and the analyses here should be considered post hoc. All participants reported in the present work were in the control condition and did not undergo an acute stressor. However, as the sample was selected from an experiment examining the effect of acute stress, we used exclusion criteria adapted from research on acute stress (Shields, 2020). Specifically, participants were excluded if they had any reported neuropsychological or health issues, regularly smoked cigarettes, were on hormonal birth control, or if they had eaten a large meal, exercised, or had smoked for at least two hours prior to the experiment. Participants provided written informed consent prior to the completion of the experimental session, and participants either received course credit for a Psychology course for their participation or were compensated at a rate of 15.00$ Canadian per hour. The Human Research Ethics Board at the University of Victoria approved all experimental procedures (Date: 25-Sep-2019; #19–0230), and all research was performed in line with the principles of the Declaration of Helsinki.

Apparatus and Materials

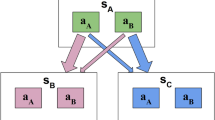
Participants completed two tasks (Fig. 1): (1) a non-stationary bandit task (Berry & Fristedt, 1985; Daw et al., 2006) and (2) a stationary bandit task (Krigolson, 2018; C. C. Williams et al., 2021). Testing occurred in a soundproof room, where participants were seated 12 inches in front of a 23-inch monitor (1680 by 1050 pixels). Stimuli were presented in MATLAB (Version 9.6, Mathworks, Natick, U.S.A.) using the Psychophysics Toolbox extension (Brainard, 1997; Pelli, 1997). For both bandit tasks, all instructions were presented on the computer itself. An experimenter was present to clarify any questions from the participants.

Fig. 1

Methods. A Task structure for the non-stationary bandit task. B Example reward distributions for three sample runs of the task. C Task structure for the stationary bandit task. Trials progressed from left to right for both A and C

Non-Stationary Bandit

In the non-stationary bandit task, four options (i.e., “arms”) were presented to participants. Prior to starting the task, participants were given instructions of the task demands and an example of the arms’ continuous reward (points) probabilities. Participants were told that their goal for the task was to maximize reward and that the number of points the arms gave would be slowly changing across trials. The four arms were visualized as different colour squares—the four colours were randomized for each participant—presented against a black background. Participants used the mouse to select an arm. In the non-stationary bandit task, the four arms remained in the same location on the display throughout the task. Participants completed 400 trials of the task and were given a rest-break after the completion of each block of 100 trials. If the participant did not select an arm within 2000 ms, then the participants were shown a message stating “TOO SLOW” for 1000 ms and were not given any feedback. These too-slow trials were considered invalid.

For the non-stationary bandit task, we used the random-walk parameters from (Daw et al., 2006). Thus, the starting point values for the four arms were randomly selected between 1 and 100 points. Point values were then drawn from a Gaussian distribution with a mean (${\mu }_{k,t}$) and a standard deviation which was equal to four. To calculate the mean of the Gaussian distribution for each arm (k) and each trial (t), the point values of the arms were updated using a Gaussian random walk:

$${\mu }_{t+1,k}={\mu }_{t,k}+\left(1- \lambda \right)\theta +v$$

(1.1)

where $\lambda$ was a decay parameter equal to 0.9836, $\theta$ was the decay center (equal to 50), and $v$ was a diffusion noise parameter. On each trial, the diffusion noise parameter was sampled from a Gaussian distribution with a mean of zero and a standard deviation of 2.8. The point values of the four arms were always rounded to the nearest integer and were never allowed to fall below one or exceed 100. For each participant, these reward values were randomly generated prior to completing the task. The underlying reward values of the arms did not reset at the beginning of each block, instead, the reward values continued drifting per the random walk parameters.

Stationary Bandit

The participants also completed a stationary, two-armed bandit. Participants were given instructions that their goal was to maximize reward by identifying and selecting the bandit arm that won the most often. Following a selection, participants received “WIN” feedback or “LOSS” feedback. Participants were informed that they had to select between two arms and that the two arms differed in their win percentage. If participants did not select in time, then the trial was considered invalid, while if they selected prior to the go cue then they received feedback that said “TOO FAST”. Prior to beginning the task, participants completed two practice rounds of ten trials each to ensure they understood the instructions. In the first practice round, one arm would provide win feedback 100% of the time it was selected while the other arm would provide win feedback 0% of the time. In the second practice round, one arm would provide win feedback 75% of the time it was selected while the other arm provided win feedback 10% of the time. For the task itself, one arm provided win feedback on 60% of the trials it was selected while the other arm provided win feedback 10% of the time. Participants were told the underlying win probabilities for the two arms but were informed that they would have to learn which arm corresponded to which win probability. For each trial, the arms were randomly assigned to either the left or the right side of the screen. Each side of the screen required a different response – to select the left arm participants had to press the “f” key and to select the right arm participants had to press the “j” key. At the conclusion of each block of trials, the colours of the two arms changed, and the participants had to re-learn which arm won more than the other. Participants completed 5 blocks of 20 trials each.

Protocol

We had all participants complete the non-stationary bandit task before beginning the stationary bandit task. On average, the non-stationary bandit task took between 15 and 20 min to complete. In contrast, the stationary bandit task took between 8 and 10 min to complete.

Computational Modeling Approach

To determine what action-selection strategy participants used in the two tasks, we modeled participants’ behaviour using eight different models. The eight models we used were: (1) a bias model to provide a baseline (Love & Gureckis, 2007; Wilson & Collins, 2019), (2) an ε-Greedy model, (3) an Upper-Confidence Bound model, (4) a Softmax model, (5) a Gradient model, (6) a Win-Stay Lose-Shift model, (7) a Kalman filter with Thompson Sampling Model, and (8) a Softmax with exploration bonus model.

Non-Stationary Models

Bias Model

To ensure we had a proper baseline (Love & Gureckis, 2007; Wilson & Collins, 2019), we created the bias model. In the bias model action selection was based on a bias parameter. That is, on each trial (t) the probability of making an action ($a)$ was fit to a parameter biased to select one arm (k) over the others. Thus, the model attempted to account for whether participants were biased to select one arm over the others (for example if they preferred the color) regardless of feedback. To select an action, the model selected the “bias arm” when the bias parameter ($\varphi )$ was greater than a randomly sampled value from a uniform distribution between 0 and 1:

$${P}_{t}\left({a}_{k}\right)=\left\{\begin{array}{c} \varphi\;if\;{a}_{k}\;is\;the\;bias\;arm\\ \left(\frac{1-\varphi }{3}\right)otherwise\end{array}\right.$$

(1.2)

If the model did not select the “bias” arm, then one of the other three arms was selected randomly. As well, the bias arm was pre-determined by the model as the arm selected the most often by the participants. Thus, the bias model does not involve any trial-by-trial updating of parameters from the feedback obtained or estimates of the arm’s reward value (Ahn et al., 2008). For the bias model, we only fit a single bias parameter $(\varphi )$ for each participant (see the parameter optimization section below).

ε-Greedy Model

The ε-Greedy model utilized a near-greedy approach to select an action. To select an action, the ε-Greedy model usually chose the arm with the highest value per the model. However, on a sub-set of trials proportional to the exploration parameter $(\varepsilon ),$ the model chose an arm randomly. On each trial (t) the probability of selecting an arm (k) was determined by:

$${P}_{t}\left({a}_{k}\right)=\left\{\begin{array}{c}(1-\varepsilon ) \ if \ k=argmax \left({q}_{t}\right) \\ \frac{\varepsilon }{3} \ otherwise\end{array}\right.$$

(1.3)

Thus, a larger value for the exploration parameter meant that the model explored more, while a smaller value meant that the model explored less and chose the highest-valued arm more often. We initialized all arm values (${q}_{t}$) to 0 and the values for the selected arm were updated using the following formula:

$${q}_{t+1, k}={q}_{t,k}+ \alpha *{\delta }_{t}$$

(1.4)

With $\alpha$ being the learning rate and ${\delta }_{t}$ being a prediction error with the following formula:

$${\delta }_{t}={r}_{t}- {q}_{t, k}$$

(1.5)

In this case, ${r}_{t}$ is the reward value obtained from the selected arm divided by 100 (60 points would thus be 0.60).¹ We divided the points by 100 to avoid excessively large values when calculating the choice probabilities, as large values can introduce arithmetic problems caused by rounding errors or memory errors in the scripting language we used (Python). For the ε-Greedy model, we fit two parameters: the exploration rate parameter and the learning rate parameter.

Sliding Window Upper Confidence Bound

The sliding window upper confidence bound model computed a confidence bound (uncertainty estimate) around the reward estimate which was then modulated through a sliding window parameter (Garivier & Moulines, 2008). The sliding window parameter added a fixed time horizon to ensure that the model was more heavily weighted towards recent rewards by only including rewards obtained within the window chosen. Thus, the model can account for the non-stationary nature of the task. The model computed two values: a reward (${q}_{t}$) and an uncertainty value (${c}_{t}$) as per the sliding window parameter ($\gamma$). Using the estimated reward and uncertainty values, the model then chose the arm with the maximal value:

$${P}_{t}\left({a}_{k}\right)=\mathrm{argmax}\left(\frac{{q}_{t} \left(\gamma ,k\right)+{c}_{t}\left(\gamma ,k\right)}{\sum {q}_{t} +{c}_{t}}\right)$$

(1.6)

In turn, the reward values were estimated using the following formula:

$${q}_{t} \left(\gamma ,k\right)= \frac{1}{{N}_{t}\left(\gamma ,k\right)}\sum_{s=\mathrm{t}-\gamma +1 }^{t}{\mathrm{X}}_{s}\left(k\right){\mathbb{I}}_{\{{K}_{s}=k\}}, {N}_{t}\left(\gamma ,k\right)= \sum_{s=\mathrm{t}-\gamma +1}^{t}{\mathbb{I}}_{\{{K}_{s}=k\}}$$

(1.7)

where ${\mathrm{X}}_{s}\left(k\right)$ is the history of the reward when arm k was selected within the sliding window. The uncertainty value was estimated as:

$${c}_{t}\left(\gamma ,k\right)=B \sqrt{\frac{\mathrm{\xi log}(\mathrm{t }\bigwedge \gamma )}{{N}_{t}\left(\gamma ,k\right)}}$$

(1.8)

where $\upxi$ is a constant value that we set to 0.95. Thus, on each trial for each arm, the model computed a reward estimate using the history of the actual rewards obtained (${r}_{s})$ across the total number of times the arms were selected within the sliding window. Note that B in Eq. 1.8 is an exploration parameter that we held constant across all participants using a value of 0.1. The inclusion of the uncertainty term in the sliding window upper confidence bound model meant that the model explored arms that have the highest level of uncertainty—that is, the arms which had been selected less. For the sliding window upper confidence bound model, we only fit the sliding window parameter for each individual participant.

Softmax Model

For the Softmax model, action selection was determined using a Softmax equation. Like the ε-Greedy model, the Softmax model typically chose the highest value arm although it explored the other stimuli per the temperature parameter ($\tau$). Thus, on each trial, the probability of selecting an arm was divided by the sum of all possible actions given by the Softmax formula:

$${P}_{t}\left({a}_{k}\right)=\frac{exp(\tau \cdot {q}_{t,k})}{\sum_j exp(\tau \cdot{q}_{t,j})}$$

(1.9)

where the temperature $\tau$ controls the amount of exploration. A higher temperature meant that the model explored less while a lower temperature meant that the model explored more. The value of the arm chosen was then updated as per the update rule specified in the ε-Greedy model. Thus, for the Softmax model, we fit two parameters: the temperature parameter and the learning rate parameter.

Gradient Model

In comparison to the previous models, the Gradient model (R. J. Williams, 1992) computed action preferences for all the arms, which were updated on a trial-by-trial basis for both chosen and unchosen arms. To do this, the model computed the action preference using a Softmax distribution with the following formula:

$${P}_{t}\left({a}_{k}\right)=\frac{{e}^{{H}_{t}(\mathrm{a})}}{\sum_{b=1}^{k}{e}^{{H}_{t}(\mathrm{b})}}={\uppi }_{t}(\mathrm{a})$$

(1.10)

Following this, we used the gradient policy $({\pi }_{t}\left(\mathrm{a}\right))$ to update the action preferences of the model:

$$\begin{array}{c}{H}_{t+1}= {H}_{t}\left({A}_{t}\right)+{\mathrm{\alpha }}_{1}({r}_{t}-{\overline{R} }_{t})(1- {\pi }_{t}\left({A}_{t}\right))\mathrm{ \ and}\\ {H}_{t+1}= {H}_{t}\left(\mathrm{a}\right)+{\mathrm{\alpha }}_{1}\left({r}_{t}-{\overline{R} }_{t}\right){\uppi }_{t}\left(\mathrm{a}\right)\mathrm{ for \ all \ a}\ne {A}_{t}\end{array}$$

(1.11)

where ${H}_{t}\left({A}_{t}\right)$ was the action preference of the chosen arm, ${H}_{t}\left(\mathrm{a}\right)$ were the action preferences of the unchosen arms, ${\mathrm{\alpha }}_{1}$ was the first step size parameter and ${\overline{R} }_{t}$ was the exponentially weighted reward average which was calculated using:

$${\overline{R} }_{t+1} = {\overline{R} }_{t}+{\upbeta (r}_{t}-{\overline{R} }_{t})$$

(1.12)

To account for the non-stationary nature of this bandit task, we computed a second step-size parameter using a reward trace:

$${\upbeta }= \frac{{\mathrm{\alpha }}_{2}}{{\overline{o} }_{t}} {\overline{o} }_{t}={\overline{o} }_{t-1}+\upbeta \left(1- {\overline{o} }_{t-1}\right), \mathrm{for} \ t \ge 0 \mathrm{ \ with \ \ }{\overline{o} }_{t0}=0$$

(1.13)

where ${\mathrm{\alpha }}_{2}$ was a second, fit step-size parameter, and ${\overline{o} }_{t}$ was the reward trace tied to the reward obtained on trial t. The reward trace works by starting with a value of 0, which is then updated to weigh the reward trace with a bias towards more recent rewards. Thus, on each trial, the reward trace is updated by taking the previous trial’s reward trace and modifying it using the second step-size parameter. That is, rather than solely relying on a constant step-size parameter across the task, the reward trace allows the second step-size parameter to change across the task, which is then used to update how reward estimates are treated using more recent outcomes in the reward history. The reward trace allows for the Gradient model to account for the non-stationary aspect of an environment. For the Gradient model, we fit two step-size parameters (${\mathrm{\alpha }}_{1}$ and ${\mathrm{\alpha }}_{2}$).

Win-Stay, Lose-Shift Model

The Win-Stay, Lose-Shift model only depended on the previous trial’s feedback. Thus, in comparison to the ε-Greedy and Softmax models, the long-run values of each of the stimuli were not considered. The selection of an arm used the following simple rules: (1) if the reward (${r}_{t}$) given by the arm on the trial was greater than or equal to the 50 (the long-run average reward of the arms; Hassall, 2019) then the same action is selected with the probability $P(\mathrm{stay }|\mathrm{ win})$ and (2) if the reward given by the arm on the trial was less than the long-run average reward of the arms then the action was avoided with the probability $P(\mathrm{shift}|\mathrm{ loss})$. Thus, two parameters were computed—the probability of staying following a win ($P(\mathrm{stay }|\mathrm{ win}))$ and the probability of shifting following a loss ($P(\mathrm{shift }|\mathrm{ loss}))$. The probabilities of the other two possible actions (shifting following a win, staying following a loss) were simply the opposite probabilities of win-stay and lose-shift respectively.

Kalman Filter with Thompson Sampling

The Kalman Filter with Thompson sampling model has been shown to be an effective model in non-stationary bandit tasks (Speekenbrink & Konstantinidis, 2015). Specifically, the model can account for the changing nature of the environment and reward distributions through the calculation of the Kalman Gain (Kalman, 1960). To select amongst options, the Kalman Filter with Thompson sampling model samples from a normal distribution and selects the arm with the greatest value:

$${P}_{t}\left({a}_{k}\right)= \mathrm{argmax}(\mathcal{N}\left({\mathrm{m}}_{t,k}, {\mathrm{v}}_{t,k}\right))$$

(1.14)

where there are means (m) and variances (v) for each of the four arms (k). We assume both the prior and posterior are drawn from a normal distribution and on each trial, the mean and the variance of the normal distribution are updated by using a Kalman filter:

$$\begin{array}{c}{m}_{t+1, k}={m}_{t,k}+{k}_{t,i}({r}_{t}-{m}_{t,k}) \\ {v}_{t+1, k}=\left(1-{k}_{t,i}\right){v}_{t, k}+{\sigma }_{\xi }^{2}\end{array}$$

(1.15)

while the Kalman Gain was updated by:

$${k}_{t,i}= \left\{\begin{array}{c}\frac{{v}_{t, k}+{\sigma }_{\xi }^{2}}{{v}_{t, k}+{\sigma }_{\xi }^{2}+{\sigma }_{\epsilon }^{2}} \ if \ k=i \\ 0 \quad otherwise\end{array}\right.$$

(1.16)

where ${\sigma }_{\xi }^{2}$ and ${\sigma }_{\epsilon }^{2}$ are the innovation variance and error variance respectively. To fit the model in the non-stationary task, we assumed a prior mean of 0.50 (the long-run average of the arms divided by 100) and a prior variance of 10. On each successive trial, the mean and variances of the chosen arms were updated using the update rule specified above per the participant’s arm choice and reward obtained. For the Kalman filter with Thompson sampling model, the only parameters fit were the innovation variance (${\sigma }_{\xi }^{2}$) and the error variance (${\sigma }_{\epsilon }^{2}$).

Softmax with Exploration Bonus Model

For the Softmax with Exploration Bonus model (Daw et al., 2006; Speekenbrink & Konstantinidis, 2015), action selection was determined using a Softmax equation with the addition of an exploration bonus term. That is, the exploration bonus term added uncertainty to the standard Softmax equation. The Softmax with exploration bonus model chose the highest value arm (both value and uncertainty) but on a subset of trials explored the other arms using the temperature parameter ($\tau$) and the exploration bonus term ($B$). Thus, on each trial, the probability of selecting an arm was divided by the sum of all possible actions given by:

$${P}_{t}\left({a}_{k}\right)=\frac{exp(\tau \cdot {q}_{t,k}+ {B}_{t,k})}{\sum_j exp(\tau \cdot {q}_{t,j}+ {B}_{t,j})}$$

(1.17)

As per Speekenbrink and Konstantinidis (2015), we adopted a simple heuristic whereby the uncertainty of each arm increased in a linear manner following the last trial the arm was selected:

$${B}_{k}={B}_{o}[t-{T}_{k}]$$

(1.18)

where ${T}_{k}$ is the last trial where arm k was selected, t is the current trial, and ${\beta }_{^\circ }$ is the initial exploration bonus parameter. The value of the arm chosen was then updated as per the update rule specified in the ε-Greedy model. We were unable to get the step-size parameter to recover during model validation, and the step-size parameter was set to a constant value of 0.50. Thus, for the Softmax with exploration bonus model, we fit two parameters: the temperature parameter and the initial exploration bonus parameter.

Stationary Models

For the stationary bandit task, we used a nearly identical set of models as in the non-stationary bandit task. The first major difference between the models was that rather than deciding between four arms, only two arms were presented. The second major difference is that in the stationary bandit task, participants received wins and losses as feedback, rather than point values. The obtained reward (${r}_{t})$ was instead 1 for a win and 0 for a loss. Below, we outline the other changes we made to the models.

ε-Greedy Model

In the stationary bandit task, the ε-Greedy model functioned virtually identically to how it functioned in the non-stationary bandit task. During parameter recovery, we were unable to recover a constant learning rate parameter using simulated participants; thus, each participant was given a constant step size value of 0.20 (similar to prior investigations using stationary bandit paradigms—e.g., Guo & Yu, 2018). The only parameter fit for the ε-Greedy model in the stationary bandit task was the epsilon parameter ($\varepsilon )$.

Upper Confidence Bound

For the Upper Confidence Bound model, we used the UCB1 algorithm (Agrawal, 1995; Auer, 2002). Thus, the model selected an action per the following rule:

$${P}_{t}\left({a}_{t}\right)=\mathrm{arg max}({q}_{t}+B\sqrt{\frac{ln \left(t\right) }{{N}_{t}\left(k\right)}})$$

(1.19)

where B is the exploration parameter, t is the trial number, and ${N}_{t}(k)$ is the number of times that the specified arm had been selected. Thus, the only parameter we fit for each participant was the exploration parameter.

Softmax Model

As with the ε-Greedy model, we were unable to recover a constant learning rate parameter using simulated participants, thus, a constant step size value of 0.20 was used. The only parameter fit for the Softmax model was the temperature parameter ($\tau$).

Gradient

For the gradient model, the only major difference was how the reward values were calculated. That is, the model continued to update action preferences for both the chosen and unchosen arms on each trial following selection and receiving reward. Specifically, rather than having to calculate exponentially weighted reward for the baseline of the model, we instead relied on the formula more appropriate for stationary cases:

$${\overline{R} }_{t+1} = \frac{{(r}_{t}+{\overline{R} }_{t})}{t}$$

(1.20)

where ${r}_{t}$ is the reward obtained on the current trial and ${\overline{R} }_{t}$ is the average reward. Thus, for this form of the gradient model the only parameter fit was the first step-size parameter (${\mathrm{\alpha }}_{1}$).

Win-Stay, Lose-Shift

In contrast to the Win-Stay, Lose-Shift model in the non-stationary bandit task, the Win-Stay, Lose-Shift model in the stationary bandit task only included one parameter to fit—a win-stay parameter. Thus, the selection of an arm used the rules that (1) if the reward (${r}_{t}$) given by the arm on the trial was a win then the same action is selected with the probability $P(\mathrm{stay }|\mathrm{ win})$ or else the opposite arm was chosen. If instead the reward obtained on the previous trial was a loss, then the model switched to another arm with the probability of (1 – $P(\mathrm{stay }|\mathrm{ win}$). We only included the win-stay parameter because during parameter recovery we were only able to recover the win-stay parameter effectively (see Supplemental Materials).

Kalman Filter with Thompson Sampling

The only major difference between the two forms of Kalman Filter with Thompson Sampling models was that in the stationary bandit task, we were unable to recover the error variance (${\sigma }_{\epsilon }^{2}$), and we instead included the error variance as a constant value (10). The only parameter fit on an individual basis was the innovation variance (${\sigma }_{\xi }^{2}$).

Softmax with Exploration Bonus Model

To adapt the Softmax with exploration bonus model to the stationary bandit task, we modified how we calculated the uncertainty estimate to account for the stationary nature of the task, which was identical to the Upper Confidence Bound model in the stationary bandit task:

$${\mathrm{B}}_{\mathrm{t}}= {\mathrm{B}}_{0}\sqrt{\frac{\mathrm{ln }\left(\mathrm{t}\right) }{{\mathrm{N}}_{\mathrm{t}}\left(\mathrm{k}\right)}}$$

(1.21)

Thus, identical to the non-stationary bandit task, we fit two parameters in the stationary bandit task for the Softmax with exploration bonus model: the temperature parameter ($\uptau$) and the exploration parameter (${\mathrm{B}}_{0}$).

Model Validation

To validate the models, we both examined each of the models in a testbed environment identical to the bandit tasks the human participants completed and conducted parameter recovery. To determine if the chosen models could learn the tasks, we simulated the models across a series of parameter values to determine the parameter values which led to the best performance. Following this step, we simulated (n = 30) participants to complete both the non-stationary and stationary bandit tasks. All models showed evidence of learning in both bandit tasks (see Supplemental Materials Figure S1). In addition, we ensured that model parameters could be recovered effectively in both the non-stationary bandit task (all r > 0.74) and stationary bandit task (all r > 0.83; see Supplemental Material Figure S3 and S4). We also note that the model parameters did not show evidence of trading off against each other (Daw, 2011; Wilson & Collins, 2019) as there were no meaningful correlations between model parameters during recovery (all | r < 0.23 |).

Parameter Optimization

Parameters were optimized using an optimization algorithm from the SciPy package (Version 1.91) in Python (Version 3.9), using the “trust region constrained” algorithm. To avoid local minima, optimization was conducted multiple times using a randomized starting parameter space (n = 10; see Table S1 and Table S2 in the Supplementary Materials for the distributions and values used). Model parameters were optimized individually for each of the thirty participants. We optimized individual participant parameters for each of the eight models and across both bandit tasks. Using the computed choice probabilities from each of the models in combination with the choices human participants made and the rewards the human participants obtained, we applied a posteriori estimation and optimized the values based on the minimization of the negative log-likelihood (Daw, 2011):

$$L=-\sum log({P}_{t}\left({a}_{k}\right))$$

(1.22)

During action selection the Kalman Filter with Thompson Sampling model sampled from a normal distribution once (see Eq. 1.14). To calculate the log-likelihood, we instead used a Monte-Carlo strategy and sampled from the normal distribution 10,000 times for each arm on each trial, and calculated the trial-by-trial log-likelihood as being the number of times each arm was maximal across the 10,000 samples.

While most of the models had a choice probability that could be extracted on a trial-by-trial basis, the Win-Stay, Lose-Shift model did not as it was a simple behavioural heuristic. The calculation of the negative log-likelihood differed in the case of the Win-Stay Lose-Shift model. Specifically, to calculate choice probabilities for each trial and for each arm (which summed to one), we relied on using the win-stay and lose-shift parameters fit on an individual basis. Thus, when participants stayed following a win, we simply input the likelihood as being the win-stay parameter.

$${L}_{\mathrm{win}-\mathrm{stay}}=log (P (\mathrm{stay} | \mathrm{win}))$$

(1.23)

In contrast, if participants switched following a win, we instead took 1 minus the win-stay parameter divided by the number of arms minus one:

$${L}_{\mathrm{win}-\mathrm{shift}}=log(\frac{1-\left(P (\mathrm{stay} |\mathrm{win}\right)}{3})$$

(1.24)

Identical logic was applied to the lose-shift parameter on cases where participants lost and either shifted or stayed:

$$\begin{array}{c}{L}_{\mathrm{lose}-\mathrm{shift}}=log (P (\mathrm{shift} | \mathrm{loss}))\\ {L}_{\mathrm{lose}-\mathrm{stay}}=log(\frac{1-\left(P (\mathrm{shift }|\mathrm{ loss}\right)}{3})\end{array}$$

(1.25)

In the stationary bandit task where we only used a win-stay parameter and the task only has two arms, the calculation of log-likelihood was:

$$\begin{array}{c}{L}_{\mathrm{win}-\mathrm{stay}}=log (P (\mathrm{stay }|\mathrm{ win}))\\ {L}_{\mathrm{lose}-\mathrm{shift}}=log ( 1- P (\mathrm{stay }|\mathrm{ win}))\end{array}$$

(1.26)

Model Comparison

To determine model effectiveness, we compared whether each model could successfully replicate the behaviour of the participants. To do this, we simulated 30 participants using each model across both bandit tasks. To simulate a participant, we used the optimized parameters of the models for each “human participant” and ran the model on the point values of the four arms (in the non-stationary bandit task) or the win probabilities of the two arms (in the stationary bandit task) that the participants experienced. Thus, each model selected an arm and received feedback by using the optimized parameters of that participant to determine action selection. The above approach was repeated individually for each model and for each task.

As a second method of determining model effectiveness, we compared the models using Bayesian Information Criterion (BIC). We used BIC as it provides a method of penalizing greater levels of model complexity (Lewandowsky & Farrell, 2011). We calculated BIC per the following formula:

$$BIC=-2L+KlnN$$

(1.27)

where L was the negative log-likelihood of the model, K was the number of parameters of the model, and N was the number of datapoints that the likelihood was calculated from. BIC values were computed across all participants and models. Then we calculated a pseudo-R² value (e.g., Ludwig et al., 2022) using the following formula:

$${R}^{2}=1- \frac{BIC \left(\mathrm{non}-\mathrm{bias\ models}\right)}{BIC \left(\mathrm{bias \ model}\right)}$$

(1.28)

As per Ludwig and colleagues (2022), the R² value indicates whether each model provides a better fit than the bias model (the baseline model). Larger R² values thus indicate that the model is a better fit.

Trial Classification

As our principal goal was to investigate how humans explored different bandit environments, we used the models to classify each individual trial of the human data as an exploitation or exploration. To do this, we ran the human choice data through the models, which was repeated across both tasks individually. For four of the models (ε-Greedy, Softmax, Upper Confidence Bound, and Softmax with exploration bonus), we defined an exploit trial as any trial on which the participant selected the highest value choice per the model while an explore trial was one on which they did not select the highest value choice. For the Gradient model, we defined an exploit trial as any trial where the participant selected the highest action preference per the model while an exploration was any trial where the participant did not select the highest action preference choice per the model. For the Kalman Filter with Thompson Sampling model, we defined an exploit trial as any trial where participants selected the arm which produced the maximal value from the normal distribution across the 10,000 samples, while an explore trial was when they selected an arm that was not the maximal value arm. For the Win-Stay Lose-Shift model, trials were classified as exploitation if the participant completed a Win-Stay (selecting the same arm after gaining more points than the previous trial) or a Lose-Shift (selecting a different arm after gaining less points than the previous trial). Trials were classified as explorations if either of the opposing strategies are observed (Win-Shift and Lose-Stay). We did not use the bias model to classify trials as exploitation trials or exploration trials as we considered it our baseline.

Fitting Approach Comparison

We also investigated to what extent our results depend on whether we fit within each bandit task individually (individual model fitting) or using the data from both bandit tasks simultaneously (combined model fitting). Thus, we conducted a model fitting procedure where we input the participant’s data from each bandit task and fit the models across the two tasks (see Table 1 for a summary of the comparison between the modeling fitting approaches).

Table 1 Model parameters when using individual or combined model fitting approach

Because the number of trials differs between the two bandit tasks (400 in the non-stationary bandit, 100 in the stationary bandit task), during combined model fitting the non-stationary task was overrepresented in the negative loglikelihood calculation for each model. To counter this problem, we used a simple approach whereby we increased the number of times we fit the stationary bandit task to four times. This approach is known to help model fitting in machine learning during cases of class imbalance where one task has more data than another task (Japkowicz & Stephen, 2002). That is, when fitting the model to determine the participant’s parameters and negative log-likelihood, we repeated the stationary bandit task fitting four times using the participant’s choices and rewards in the stationary task. We then repeated the model comparison and trial classification in an identical manner to what we did when fitting the models individually within each task.

Data Analysis

Behavioural

To examine participants’ behaviour in the two bandit tasks, we analyzed two measures of performance. In the non-stationary bandit task, we measured participants’ total points averaged across all 400 trials and the number of trials they selected the arm with the highest point values divided by the total number of valid trials (optimal arm selection). To determine whether participants performed better than chance, we then compared the participants’ average points obtained to the long-run average of the arms (50 points). Relatedly, to determine whether participants were able to identify the optimal arm at a level greater than chance, we compared the participants’ optimal arm selection to 25% as there were four arms.

In the stationary bandit task, we examined how often the participants won divided by the total number of trials (win percentage), and how often they selected the optimal arm (the arm that won 60% of the time). To determine whether participants performed better than chance, we compared their win percentage to what would be expected if participants selected arms randomly (35%) which was calculated by taking the expected win percentage if participants selected the 60%-win arm on half of the trials and the 10%-win arm on half of the trials. As well, we compared participants’ average optimal arm selection to 50% as there were only two arms. For all behavioural comparisons, we used one-sample t-tests, measured effect size with Cohen’s d, and measured variability with 95% between-subject confidence intervals.

Computational Modeling

To compare each of the models’ ability to fit behaviour, we examined how well the simulated participants from each model were able to perform the task when compared to the human participants’ data. In the non-stationary bandit task, we examined the ability of the models to correctly replicate the points obtained by the human participants. In the stationary bandit task, we instead examined the win percentage. In the non-stationary bandit task to determine whether the models were able to simulate task performance, we compared performance using between-subjects ANOVAs with nine levels—the “simulated participants” from the eight models, and the human participants’ actual performance. To determine whether there were any differences between the model performance and the human performance, we then followed up each ANOVA by comparing the average performance of the human participants to the simulated participants using between-subject pairwise comparison t-tests with a Benjamini–Hochberg correction (Benjamini & Hochberg, 1995). As a final check, we then compared the best-fitting models for each participant and whether they differed in performance from the human data. Specifically, we compared performance using between-subjects t-tests for both the non-stationary and stationary bandit tasks to compare the performance of the “simulated participant” per the best-fit model to the human participants, measured effect size with Cohen’s d, and measured variability with 95% between-subject confidence intervals.

In addition, we also examined trial-by-trial performance by examining optimal arm choice across the task. To calculate the optimal arm chosen across trials, we computed a running average of the percent of trials the participant selected the optimal arm and divided that by the total number of trials. We repeated this calculation across each participant and then took the average for the simulated participants and the human participants. We examined qualitative fit by visually comparing each model’s curve to the human participants’ curves to determine whether they overlapped. In the non-stationary bandit task, we examined optimal arm choice across all 400 trials, while in the stationary bandit task we averaged across the five blocks and instead examined trials 1 to 20. The reason we choose to average across blocks in the stationary bandit task was that at the beginning of each block, the colors of the two squares were randomly changed and the participants had to re-learn which arm was best. In contrast, in the non-stationary case, the feedback values changed slowly across the entire task but did not reset at any point.

To determine which model provided the best fit of the human data, we first computed each of the model’s R² values on a participant-by-participant basis. Following this calculation, we classified a participant as having used the model’s action selection strategy by selecting the model which had the largest R² value. We calculated the R² individually for each participant in each of the two bandit tasks. A participant could be classified as using one exploration strategy in the non-stationary bandit task while being classified as using a different exploration strategy in the stationary bandit task.

In addition, we investigated whether there was any relationship between how often participants explored the two bandit tasks. To investigate this relationship, we calculated the exploration rate across all models except the Bias model. The exploration rate was defined as the percentage of explore trials divided by the total number of valid trials, in the two tasks. We then ran between-subjects ANOVAs for exploration rate across the seven, non-baseline models in each task and followed-up each ANOVA using between-subject pairwise comparison t-tests with a Benjamini–Hochberg correction (Benjamini & Hochberg, 1995). To ensure model agreement in terms of which trials were classified as explorations and which trials were classified as exploitations, we compared whether the models—except the baseline model—overlapped in their classification of each trial across all participants on a trial-by-trial basis. We conducted this overlap analysis for both the non-stationary and stationary bandit tasks individually.

To choose which model to use to extract the participants’ exploration rate, we used the best-fit model per the R² calculation above on a participant-by-participant and task-by-task basis. Following this, to determine whether explore trials per the best fitting model were associated with less value than exploit trials per the best fitting model (e.g., Hassall & Krigolson, 2020), we then compared participants’ performance on explore trials to their performance on exploit trials. For the non-stationary bandit task, we compared their average points obtained, and for the stationary bandit task, we compared their average win percentage. We compared explore and exploit trial performance using within-subjects t-tests for both the non-stationary and stationary bandit tasks, measured effect size with Cohen’s d, and measured variability with 95% between-subject confidence intervals. Following this, we computed a Pearson correlation between the two exploration rate values of each participant per the best-fitting model and then tested this correlation for significance. We then computed Pearson correlations between the exploration rate of the best-fitting model and performance (optimal arm choice) within each of the two bandit tasks and tested the correlations for significance.

Combined Model Fitting

We repeated the above analyses in the Computational Modeling section for the combined model fitting approach. That is, we repeated each analysis when fitting each model using the combined data from both tasks (rather than individually within each task as we initially did). Thus, following parameter tuning on each individual participant using each combined model we examined average performance on each bandit task using between-subject ANOVAs and follow-up between-subject pairwise comparison t-tests (Hochberg corrected; Benjamini & Hochberg, 1995). Following this, we examined trial-by-trial optimal arm choice curves within each bandit task. We examined model fit across the two tasks by examining the R² values and finding the model which had the highest R² value on a participant-by-participant basis. Next, we examined the exploration rate across the models within each of the two bandit tasks using both between-subject ANOVAs and follow-up between-subject pairwise comparison t-tests (Hochberg corrected; Benjamini & Hochberg, 1995). We then computed a Pearson correlation using the two exploration rate values across each task. Lastly, we then computed Pearson correlations between the exploration rate of the best-fitting model and optimal arm choice within each of the two bandit tasks.

For all significance testing, we used an $\alpha$ value of 0.05. For each between-subjects ANOVA and for each between-subjects t-tests, we applied Levene’s Test (Levene, 1960) to determine whether the data violated the assumption of homogeneity of variance. None of the ANOVAs were found to violate the assumption of homogeneity of variance. For any t-tests where the assumption was violated, we instead computed Welch’s t-test with adjusted degrees of freedom calculation. All statistics were completed in R (version 4.2.0; R Core Team, 2022).

Results

Behavioural Analysis

Prior to modeling the participants’ data, we investigated the performance of the human participants in the two bandit tasks. In the non-stationary bandit task, human participants performed better ($\overline{X }=$ 60.43 points, 95% CI [58.24, 62.62]) than the long-run average of the arms across the task (50 points; t(29) = 9.31, p < 0.001, d = 1.72). In addition, in the non-stationary bandit task, human participants were able to identify the optimal arm ($\overline{X }=$ 58.21%, 95% CI [53.59, 62.84]) at a level greater than chance (25%; t(29) = 14.06, p < 0.001, d = 2.57). In the stationary bandit task, human participants obtained a higher winning percentage ($\overline{X }=$ 48.13%, 95% CI [45.39, 50.87]) than chance (35%; t(29) = 9.40, p < 0.001, d = 1.71). In addition, human participants in the stationary bandit task were able to identify the optimal arm ($\overline{X }=$ 81.03%, 95% CI [77.79, 84.28]) at a level greater than chance (50%; t(29) = 18.74, p < 0.001, d = 3.42).

Computational Modeling

We first examined the ability of the models to accurately replicate the human performance in the non-stationary bandit task (Fig. 2A and 2C). Specifically, the between-subjects ANOVA revealed a difference in non-stationary bandit task performance when comparing the human and simulated participants (F(8, 261) = 12.06, p < 0.001, ${\eta }^{2}$= 0.27). Follow-up pairwise comparisons confirmed what was evident visually—that the simulated participants from both the Bias model (t(58) = 7.59, p < 0.001, d = 1.96) performed worse than the human participants. None of the other models differed in terms of performance when compared to the human participants’ performance (all other models’ adjusted p > 0.91). Comparing non-stationary task performance using the best-fitting model individually for each participant revealed no difference between human and model performance (t(56) =  − 0.15, p = 0.87, d =  − 0.04). The trial-by-trial findings revealed that both the Bias model and the ε-Greedy were unable to replicate the optimal arm choice curves across the non-stationary bandit task and were not considered as possible best-fitting models due to their inability to replicate behaviour (Palminteri et al., 2017).

Fig. 2

Model fit in the non-stationary bandit task. A Average task performance in terms of points acquired. B R² values are in arbitrary units and indicate the difference between each of the five models and the bias model. C Trial-by-trial performance where dashed lines indicate the human participants (identical across all the eight subplots) and the colors indicate simulated participants. For A and B, the coloured dots indicate real participants (human data) or simulated participants (the eight models), while the black dot indicates the mean. All error Bars are 95% confidence intervals. Note: WSLS = Win-Stay, Lose-Shift; UCB-SW = Sliding Window Upper Confidence Bound; KFTS = Kalman filter with Thompson sampling; SM-UCB = Softmax with exploration bonus

When considering which model best accounted for the behaviour in the non-stationary bandit task (Fig. 2B), we found that the Win-Stay, Lose-Shift model provided the best fit for most of the human participants. Given the inability of the ε-Greedy model to correctly simulate the human participants’ behaviour for both average and trial-by-trial performance, we only considered the Win-Stay, Lose-Shift, Softmax, Sliding Window Upper Confidence Bound, Gradient, Kalman Filter with Thompson Sampling, and the Softmax with exploration bonus models for classifying participants’ exploration strategy. Specifically, the Win-Stay, Lose-Shift model provided the best fit for 20 human participants (66.67%). In addition, the Kalman-Filter with Thompson Sampling model provided the best fit for the remaining 5 participants (16.67%), the Softmax model provided the best fit for 4 human participants (13.33%), and the Sliding Window Upper Confidence Bound model provided the best fit for the remaining participant (3.33%).

For the model’s ability to fit behaviour in the stationary bandit task (Fig. 3A and 3C), the between-subjects ANOVA revealed a difference when comparing the human and simulated participants’ average task performance (F(8, 261) = 21.62, p < 0.001, ${\eta }^{2}$ = 0.40). Follow-up pairwise comparisons showed that only the simulated participants from the bias model (t(50.17) = 6.30, p < 0.001, d = 1.62) and the Win-Stay, Lose-Shift model (t(58) = 7.75, p < 0.001, d = 2.00) performed worse than the human participants’ performance (all other model’s adjusted p > 0.82). Interestingly, the simulated participants per the upper confidence bound model performed better than the human participants (t(58) =  − 3.13, p < 0.05, d =  − 0.80). When comparing the performance using the best-fitting model individually for each participant, we found no difference between human performance and model performance (t(58) =  − 1.29, p = 0.20, d =  − 0.34). The trial-by-trial echoed the findings we observed when examining the average win percentage, as both the Bias model and the Win-Stay, Lose-Shift models were unable to replicate the optimal arm choice curves across the stationary bandit task.

Fig. 3

Model fit in the stationary bandit task. A Average task performance in terms of win percentage. B R² values are in arbitrary units and indicate the difference between each of the seven models and the bias model. C Trial-by-trial performance where dashed lines indicate the human participants (identical across all the eight subplots) and the colors indicate simulated participant. For A and B, the coloured dots indicate real participants (human data) or simulated participants (the eight models), while the black dot indicates the mean. All error Bars are 95% confidence intervals. Note: WSLS = Win-Stay, Lose-Shift; UCB1 = Upper Confidence Bound; KFTS = Kalman filter with Thompson sampling; SM-UCB = Softmax with exploration bonus

In the stationary bandit task, when examining which model best accounted for exploratory behaviour (Fig. 3B), we found that the Softmax model provided the best fit for most participants. Specifically, the Softmax model provided the best fit for 20 human participants (66.67%). In addition, the Softmax with exploration bonus provided the best fit for 9 participants (30.00%) while the Kalman Filter with Thompson Sampling model provided the best fit for the remaining participant (3.33%). That the Softmax model provided the best fit for most human participants in the stationary bandit task stands in contrast to the finding that the Win-Stay, Lose-Shift model provided the best fit for most participants in the non-stationary bandit task.

We then examined the proportion at which each model explored in both bandit tasks (Fig. 4A and Fig. 4B). In the non-stationary bandit task, the between-subjects ANOVA revealed a difference when comparing the simulated participants’ exploration rate (F(6, 203) = 10.69, p < 0.001, ${\eta }^{2}$ = 0.24). Follow-up pairwise comparisons showed that the simulated participants from the Gradient model explore more often than the other four models (all p < 0.001). In addition, simulated participants per the Sliding Window Upper Confidence Bound model explored more often than the Win-Stay, Lose-Shift model (p < 0.05). There was no difference in the Softmax, ε-Greedy, Win-Stay, Lose-Shift, Kalman Filter with Thompson Sampling, and Softmax with exploration bonus models (all p > 0.23). In addition, we found high agreement between the models in their classification of which trials were explorations except for the Gradient model, which was only in agreement for trial classification ~ 60% of the time with the other models (Fig. 4B).

Fig. 4

Exploration of the two tasks. A, B Exploration percentage across the seven models in the bandit tasks. The coloured dots indicate real participants (human data) or simulated participants (the seven models), while the black dot indicates the mean. Error Bars are 95% confidence intervals. C, D Trial classification overlap percentages in the two bandit tasks. The left panels are from the non-stationary task while the right panels are from the stationary bandit task. Note: WSLS = Win-Stay, Lose-Shift; UCB-SW = Sliding Window Upper Confidence Bound, UCB1 = Upper Confidence Bound; KFTS = Kalman filter with Thompson sampling; SM-UCB = Softmax with exploration bonus

In the stationary bandit task, the between-subjects ANOVA revealed a difference when comparing across the simulated participants’ exploration rate (F(6, 203) = 50.50, p < 0.001, ${\eta }^{2}$ = 0.60). Follow-up pairwise comparisons showed that the simulated participants from the Win-Stay, Lose-Shift model explored more often than the other six models (all p < 0.001). In addition, simulated participants from the Kalman Filter with Thompson Sampling model also explored more often than the simulated participants from the other models (all p < 0.001). There was no difference in exploration rate between the Softmax, ε-Greedy, Upper Confidence Bound models, Gradient, or Softmax with exploration bonus models (all p > 0.10). We also found high agreement between the models in their classification of which trials were explorations, except for the Win-Stay, Lose-Shift model (Fig. 4D).

As a behavioural check of our classification of explore trials, we found that exploit trials were associated with better performance than explore trials per the best-fitting models. Participants obtained more points on exploit trials ($\overline{X }=66.11$, 95% CI [64.34, 67.88) when compared to explore trials ($\overline{X }=$ 48.79 95% CI [46.43, 51.15]) in the non-stationary bandit task (t(28) = 16.23, p < 0.001, d = 3.02). Moreover, participants had a higher win percentage on exploit trials ($\overline{X }=$ 46.77%, 95% CI [45.71, 47.84]) than explore trials ($\overline{X }=$ 37.02%, 95% CI [31.81, 42.23]) in the stationary bandit task (t(29) = 3.16, p < 0.005, d = 0.94). Lastly, we investigated whether there was a relationship between how often human participants explored in the non-stationary bandit task and how often they explored in the stationary bandit task (Fig. 5). Interestingly, we found evidence of a medium, positive relationship between the exploration rate in the two tasks. That is, participants who explored more often in the non-stationary bandit task also explored more often in the stationary bandit task (r(28) = 0.44, p < 0.05). In addition, we found that participants who explored more often in the non-stationary task had worse performance in terms of optimal arm choice within the non-stationary bandit task (r(28) =  − 0.55, p < 0.005). A similar finding was found in the stationary bandit task—participants who explored more often selected the optimal arm less often (r(28) =  − 0.87, p < 0.001).

Fig. 5

Exploration rate relationships. A Correlation between the exploration rates (percentage of total trials) across each of the two bandit tasks (non-stationary and stationary) per the best-fitting model. B Correlation between non-stationary exploration rate and non-stationary task performance. C Correlation between stationary exploration rate and stationary task performance

Combined Model Fitting

To determine whether the combined model fitting approach was valid, we examined the ability of the models to accurately replicate the human performance in the two bandit tasks. The between-subjects ANOVA revealed a difference in non-stationary bandit task performance when comparing the human and simulated participants (F(8, 261) = 10.24, p < 0.001, ${\eta }^{2}$= 0.24). Follow-up pairwise revealed that only the simulated participants from the Bias model (t(58) = 7.46, p < 0.001, d = 1.96) performed worse than the human participants. None of the other models differed in terms of performance when compared to the human participants’ performance (all other models’ adjusted p > 0.18). When comparing the performance using the best fitting model individually for each participant, we found no difference between human performance and model performance (t(58) = 0.95, p = 0.34, d = 0.24; Fig. 6A). The trial-by-trial findings revealed that both the Bias model and the ε-Greedy were unable to replicate the optimal arm choice curves across the non-stationary bandit task (Fig. 6B) and were not considered as possible best-fitting models.

Fig. 6

Model Performance for the combined model fitting. A Overall best fitting model performance in terms of points (non-stationary bandit top) or win percentage (stationary bandit; bottom). B Trial by Trial performance where dashed lines indicate the human participants (identical across all the eight subplots) and the colors indicate simulated participants. The top panels are data from the non-stationary bandit task while bottom panels are data from the stationary bandit task. All error bars are 95% confidence intervals. Note: WSLS = Win-Stay, Lose-Shift; UCB1 = Upper Confidence Bound; KFTS = Kalman filter with Thompson sampling; SM-UCB = Softmax with exploration bonus

For the model’s ability to fit behaviour in the stationary bandit task, the between-subjects ANOVA revealed a difference when comparing the human and simulated participants’ average task performance (F(8, 261) = 29.84, p < 0.001, ${\eta }^{2}$= 0.48). Follow-up pairwise comparisons showed that the simulated participants from the bias model (t(48.79) = 7.03, p < 0.001, d = 1.81), and the Win-Stay, Lose-Shift model (t(58) = 6.23, p < 0.001, d = 1.60), both performed worse than the human participants’ performance (all other model’s adjusted p > 0.05). When comparing the performance using the best fitting model individually for each participant, we found no difference between human and model performance (t(48.82) =  − 1.96, p = 0.06, d =  − 0.51). The trial-by-trial results demonstrated that the Bias model, and the Win-Stay, Lose-Shift models were both unable to replicate the optimal arm choice curves on the stationary bandit task and were not considered as possible best-fitting models.

When instead considering which combined model best accounted for the behaviour across the two bandit tasks (Fig. 7), we found the Softmax model provided the best fit for 22 human participants (73.33%) while the Softmax with Exploration Bonus model provided the best fit for 8 human participants (26.67%).

Fig. 7

Model R² values for the combined model fitting. R² values are in arbitrary units and indicate the difference between each of the seven models and the bias model. The coloured dots indicate simulated participants, while the black dot indicates the mean. All error Bars are 95% confidence intervals. Note: WSLS = Win-Stay, Lose-Shift; UCB1 = Upper Confidence Bound; KFTS = Kalman filter with Thompson sampling, & SM-UCB = Softmax with exploration bonus

We then examined the proportion at which each model explored in both bandit tasks. In the non-stationary bandit task, the between-subjects ANOVA revealed a difference when comparing across the simulated participants’ exploration rate (F(6, 203) = 18.99, p < 0.001, ${\eta }^{2}$= 0.36). Follow-up pairwise comparisons showed that the simulated participants from the Gradient model explore more often than the other six models (all p < 0.001). In addition, simulated participants from the Sliding Window Upper Confidence Bound model explored more often than the other models (all p < 0.05). There was no difference in the Softmax, ε-Greedy, Win-Stay, Lose-Shift, Kalman Filter with Thompson sampling and the Softmax with exploration bonus models (all p > 0.07).

In the stationary bandit task, the between-subjects ANOVA also revealed a difference when comparing the simulated participants’ exploration rate (F(6, 203) = 105.99, p < 0.001, ${\eta }^{2}$= 0.76). Follow-up pairwise comparisons showed that the simulated participants from the Win-Stay, Lose-Shift model explore more often than the other six models (all p < 0.001), as did the Kalman filter with Thompson sampling model (all p < . 001). There was no difference in exploration rate between the Softmax, ε-Greedy, Gradient, Upper Confidence Bound, and Softmax with exploration bonus models (all p > 0.10).

Lastly, we investigated whether there was a relationship between how often human participants explored in the non-stationary bandit task and how often they explored in the stationary bandit task (Fig. 8A). Much like our individual model fitting analysis, we found evidence of a medium, positive relationship between the exploration rate in the two tasks (r(28) = 0.48, p < 0.01; Fig. 8B). In addition, we found that participants who explored more often in the non-stationary task had worse performance in terms of optimal arm choice within the non-stationary bandit task (r(28) =  − 0.88, p < 0.001). A similar finding was found in the stationary bandit task—participants who explored more often selected the optimal arm less often (r(28) = -0.83, p < 0.001; Fig. 8C).

Fig. 8

Exploration rate relationships for the combined model fitting. A Exploration rates (percentage of total trials) across each of the two bandit tasks (non-stationary and stationary) per the best-fitting model across both tasks. B Non-stationary exploration rate and non-stationary task performance. C Stationary exploration rate and stationary task performance. Task performance was measured as the optimal arm choice percentage across all trials

Discussion

In the present work, we investigated the consistency of both exploration strategies and the frequency of exploration rate across two multi-arm bandit tasks. For our behavioural results, we found that participants were able to successfully perform each task at a level above chance. In terms of the computational analysis, we found that the best fitting models for each participant were able to effectively model both average and trial-by-trial behaviour, a finding which was observed in both bandit tasks (Figs. 2 and 3). Moreover, within each task, the models that provided a good fit of behaviour had a high level of agreement on which trials the models classified as explorations (Fig. 4). These two findings suggest that our best-fitting models were effective at capturing behaviour and determining when participants explored. More importantly, we found that most participants were best fit by the Win-Stay Lose-Shift model (a behavioural heuristic) in the non-stationary bandit task while most participants were best fit by the Softmax model (probabilistic, random exploration) in the stationary bandit task. The difference in exploration strategies used between the two tasks suggests that humans adopt different exploration strategies depending on task demands. When instead conducting a combined model fitting approach across the two tasks, we found that the Softmax model (probabilistic, random exploration) and the Softmax with exploration bonus (hybrid directed and probabilistic, random exploration) provided the best fit of human behaviour (Figs. 6 and 7). Lastly, we found that exploration frequency was correlated across the two bandit tasks—participants who explored more in the non-stationary task explored more in the stationary task (Figs. 5 and 8). We propose that the relationship in exploration rate across tasks could reflect an underlying personality trait such as risk taking or could be tied to the hierarchical control of behaviour by the mid-cingulate cortex, although further work is needed.

We found support for the claim that humans adopt different exploration strategies depending on whether they were in a non-stationary bandit or a stationary bandit. This finding supports a wealth of research that has shown that humans use different exploration strategies (Dubois & Hauser, 2022; Gershman, 2019; Wilson et al., 2014). Our finding extends prior work showing that the same groups of humans can adopt different strategies when learning in different environments (Schulz et al., 2018b; Wu et al., 2020) to changing (non-stationary) versus consistent (stationary) learning environments. Thus, the use of within-subject comparisons is an important, and sometimes overlooked, aspect of human exploratory behaviour. Importantly, we believe that our results can be interpreted within a framework that different neural and behavioural systems can control exploratory behaviour depending on the context.

Three lines of evidence dovetail together for us to make this claim that different control systems guide exploratory behaviour in a flexible manner. First, multiple controllers of exploratory behaviour can be dissociated both by the neural substrates involved in that behaviour and by the information which these different controllers process and use (Dayan, 2013). Second, Costa and colleagues (2016) have shown differences in the neural substrates needed to guide learning in stationary and non-stationary bandit tasks in rhesus macaques. Specifically, ventral striatum lesions impaired non-stationary task performance but not the stationary bandit task. Thus, if performance in non-stationary bandit paradigms can be impaired by ventral striatum lesions while performance in the stationary task is maintained, this could suggest different cognitive processes are at play in the two types of bandit tasks. In the present work then, it seems possible that we assessed different aspects of learning when comparing the non-stationary and stationary bandit tasks (a point suggested by Costa et al., 2016 for their own work). Third, per the model of Yu and Dayan (2003), decisions made in the non-stationary bandit task may be modulated by a different form of uncertainty compared to decisions made in the stationary bandit task. Specifically, unexpected uncertainty may be present in the non-stationary bandit task as the reward values of the arms are always changing, while expected uncertainty may be present in the stationary bandit task as the participants are aware of the stable win percentage differences between the arms. These two distinct forms of uncertainty involve different neuromodulator systems – unexpected uncertainty involves phasic norepinephrine bursts to update behaviour while expected uncertainty involves tonic acetylcholine to ensure the relationship between stimulus and outcome is maintained (Dayan & Yu, 2006; Yu & Dayan, 2003, 2005). These three lines of evidence suggest that different control systems can be elicited by different task demands, and in turn, help guide behaviour in a flexible manner.

Both task complexity and differences in the required cognitive flexibility between the two tasks could contribute to explaining the exploration strategy differences. That is, participants might adopt the Win-Stay, Lose-Shift strategy in the non-stationary bandit rather than computing value estimates on a trial-to-trial basis due to the more complex task structure. In the simpler stationary bandit participants can instead compute estimates of the two arms leading to probabilistic exploration due to the fact that the task structure is simpler and fewer arms need to be explored. Thus, given that humans tend to avoid the effort to remain efficient and preserve cognitive resources (e.g., Kool & Botvinick, 2018), perhaps participants adopted a simpler exploration strategy in the non-stationary bandit to preserve resources. Although cognitive constraints decrease how often humans explore to maintain resources (Brown et al., 2022), no prior work has specifically investigated whether cognitive constraints also shift what exploration strategies humans use. However, humans perform better when they adopt simpler decision-making strategies during harder tasks but can adopt more complex decision-making strategies during easier tasks while maintaining performance (Mone & Shalley, 1995). The difficult nature of the non-stationary bandit task caused greater cognitive constraints on the participants, in turn, possibly causing them to adopt a simpler, behavioural heuristic strategy not tied to direct estimates of arm value. In fact, prior work using the Iowa Gambling Task (which also has four selection options) has shown a Win-Stay, Lose-Shift model provides a better fit of behaviour when compared to reinforcement learning models (Worthy et al., 2013).

A separate explanation for this different strategy adoption between the two tasks is that the instructions given in the stationary bandit task led to slower learning and discouraged the use of a Win-Stay, Lose-Shift strategy. In the set-up of the stationary bandit task, participants were told that the two arms had a win percentage of 60% and 10% respectively. We chose to include these instructions because during piloting a group of participants reported that they thought the stationary bandit task was unlearnable and, consequently, they did not show a preference for one arm over the other. However, by including the specific reward values of the two arms, we likely reduced the need for learning within the stationary bandit task. Two pieces of evidence suggest that this inclusion could have changed participants’ behaviour. First, changes to task instructions differences can impact the type of learning strategies adopted by participants (e.g., Feher da Silva et al., 2023) and hints about task structure can change how participants perform when learning from reinforcement (Fernie & Tunney, 2006). Second, humans have a propensity to infer volatility when learning in stationary bandit tasks (Guo & Yu, 2018). Thus, our decision to include instructions showing the specific reward values of the two arms may have highlighted possible learning and exploration approaches needed for the task. In turn, these instructions might have impacted the adoption of a Win-Stay, Lose-Shift strategy (or, indeed, other exploration strategies) as participants would have understood that receiving multiple wins or losses may not reflect the pattern of the arm entirely, in turn, slowing learning. Thus, the inclusion of the specific reward values in the instructions of the stationary bandit task could explain why participants generally adopted a probabilistic, random exploration strategy (Softmax) within the stationary bandit task rather than another strategy.

Another alternative explanation for why participants adopted different exploration strategies is related to differences in how the bandit arms were displayed across the two tasks. The differences in how the bandit arms were displayed may have led to the influence of spatial-motor codes on learning behaviour (Fitts & Seeger, 1953). Specifically, in the non-stationary task, the arms did not change position, while in the stationary bandit task, the arms could change position on a trial-by-trial basis. In the non-stationary task, because the arms were always in the same place on the screen it could be that spatial-motor codes influenced learning by reducing performance caused by the desire to repeat an action in the same spatial location (e.g., Shahar et al., 2019). That is, outcome-irrelevant features such as the spatial position of an option and the motor response required can change learning behaviour by causing participants to assign value to these outcome-irrelevant features. In the non-stationary bandit task, because participants did not have to worry about the spatial position of the arms, this may have led to participants repeating the same action more easily. Conversely, participants in the stationary bandit task had to consider the spatial location of each arm (and respond with a different key press), meaning participants would have to spend time considering the location prior to responding. Differences in task-induced spatial and motor codes have been shown to be related to how much cognitive control is implemented (e.g., Ferguson et al., 2021). Thus, the strategies adopted by participants in the two tasks could be explained by spatial and motor code differences between the non-stationary and stationary bandit tasks. That is, the possibility that the arms switched position in the stationary bandit task may have encouraged participants to use more “thoughtful” strategies (e.g., Softmax) and could explain why they did not adopt a simpler Win-Stay, Lose-Shift strategy as occurred in the non-stationary bandit task.

When instead using the combined fitting approach across the two bandit tasks, we found that participants were best fit by a Softmax model (probabilistic, random exploration) and a Softmax with Exploration bonus model (a hybrid directed and probabilistic, random exploration model). When considering an approach that more strongly weights generalizability—the ability to fit both tasks rather than each task individually—we found that models which can perform well in both bandit tasks led to the best fit of behaviour. The result from our combined model fitting across both tasks stands in contrast to our findings that participants adopted different exploration strategies, in turn perhaps suggesting participants did not flexibly use different exploration strategies (although of course, the combined model fitting inherently meant that no strategy switching could occur). Thus, the present findings depend on the nature of the predictions the models are used to understand (Ahn et al., 2008). That is, which model is chosen as providing the best fit can depend on whether a researcher is interested in “short-term” or “long-term” predictions.

Our primary analysis in the present work was attempting to model short-term predictions—that is, the model which best captured trial-by-trial behaviour within each of the two bandit tasks. However, once we adopted an analysis better suited for long-term predictions (the combined model fitting approach), we found that the best fitting models could account for behaviour in both tasks and that under this approach participants would not have shown evidence of adopting different strategies. Given concerns over how reinforcement learning models generalize in human learning (e.g., Eckstein et al., 2022), researchers who are more interested in long-term predictions might adopt an approach where models are fit to the data from multiple tasks simultaneously. However, had we adopted such an approach solely, then we might have not observed evidence suggesting different strategies may have been used across tasks. In essence, we would have missed an important finding from our work. Ultimately it is up to the researcher to decide what approach to use, and which approach is more beneficial for their interests—that is, whether they are interested in long-term as compared to short-term model predictions.

In addition, we note that there are other possible approaches to investigating the issue of model generalizability which do not rely on the comparison between combined and individual model fitting. For example, prior work has adopted approaches where the data from one task is used to fit the models in a separate task using techniques such as the “generalization criterion method” (e.g., Ahn et al., 2008; Busemeyer & Wang, 2000). The generalized criterion method is useful because it provides a specific metric for measuring how generalizable models are from one task to the other. Another possible solution to the problem of determining how to quantify the best fit across tasks when considering short and long-term predictions is the application of hierarchical reinforcement learning models (Barto & Mahadevan, 2003; Botvinick, 2012) where specific sub-routines can be used depending on task demands. Hierarchical reinforcement learning might provide a means of accounting for both short-term and long-term predictions and provide an answer for why and when different exploration strategies are instituted. We do note that a key feature of hierarchical reinforcement learning is that it tends to involve the abstraction across much longer timescales and more complex environments than were used in the present work. The future investigation of exploration using a task structure where participants learn across multiple hierarchically organized bandit tasks might be revealing (e.g., like the design in Diuk et al., 2013).

Furthermore, we note another aspect related to the modeling approach that we used in the present work related to how we classified participants as using a specific exploration strategy. In the present work, participants were classified as using one strategy across a task (or across both tasks in the case of the combined model fitting) without consideration given to strategy switching within a task. We should not imply that participants are only using one strategy (for example that they are only using directed or random exploration). In fact, a wealth of evidence shows that humans use directed exploration and random exploration within a task as needed (Gershman, 2019; Wilson et al., 2014; Wu et al., 2020). It is a consequence of the model-fitting approach that we used in the present work which led to us classifying participants as one strategy or the other. In addition, that some participants did not engage in directed exploration in the stationary bandit task could be due to the conflation between information and value within the stationary bandit task (Wilson et al., 2014).

Another major finding from the present work was that the exploration rate was correlated between the two learning environments. The relationship between exploration rates across tasks is an indication that exploratory behaviour can generalize across environments—even if the exploration strategies differ. The positive correlation between exploration rates was maintained regardless of whether we used the individual or combined model fitting approaches—although given the high overlap in trial classification between models perhaps this is unsurprising. Our work extends prior investigations showing moderate correlations in switching rates across tasks and sessions (Yechiam, 2020) to exploratory behaviour specifically.

One explanation for the exploration correlation in the present work is that exploration rate could reflect personality traits such as risk taking, propensity for mind-wandering, or impulsivity, all of which have been suggested to be tied to exploratory behaviour (risk taking: Saragosa-Harris et al., 2022; mind-wandering: Sripada, 2018; impulsivity: Dubois & Hauser, 2022). For example, participants with a higher preference for risk-taking might be more inclined to explore as they have a greater willingness to forgo rewards to gain knowledge about their environment. To this point, the exploration rate in both tasks was negatively correlated with performance. While there have been no direct examinations of exploration rate consistency across tasks and its relationship to personality traits, ethological findings indicate that a link between personality traits and exploration rate could be a realistic suggestion. Specifically, consistent foraging behaviour across contexts in lemurs has been shown to be related to boldness (Dammhahn & Almeling, 2012). We necessarily remain agnostic on which underlying traits specifically could explain our correlation in exploration rate due to a lack of questionnaire data to support our claims. However, we believe that any of the traits specified would be ideal candidates for further investigation into why exploration rate can be correlated across tasks.

A separate, though not necessarily competing, explanation for this relationship in exploration rate across tasks is that exploratory behaviour is controlled in a hierarchical manner. Specifically, the mid-cingulate cortex has been argued to act as a hierarchical controller of motivated, goal-directed behaviour and the mid-cingulate cortex will select specific behavioural plans and the neural circuits to carry out those plans (Holroyd & Yeung, 2012). In addition, the mid-cingulate cortex uses prediction errors signaled by dopaminergic activity to determine which controller of behaviour should be implemented (Holroyd & Coles, 2002). The mid-cingulate cortex may act as a hierarchical controller of behaviour, determining when to apply specific exploration strategies depending on the task. There is evidence that exogenous administration of dopamine increases activity in the medial pre-frontal cortex (of which the mid-cingulate cortex is a part) and changes the meta-cognitive strategies adopted by participants (Joensson et al., 2015). Thus, perhaps the exploration rate reflects a meta-cognitive search strategy related to the activity of dopamine and control signals in the brain (e.g., Cavanagh & Frank, 2014).

Three different approaches would be useful for better understanding the results obtained here. Neuroimaging could help elucidate whether distinct neural circuits underlie these different exploration strategies. There is good reason to believe that this is the case given work showing a different neural basis for random and directed exploration (Zajkowski et al., 2017) and work highlighting dissociable neural circuits in stationary and non-stationary tasks (Costa et al., 2016). In addition, the collection of personality trait measures such as risk taking could reveal the roles of these traits in exploration consistency. Perhaps most importantly, the present findings speak to a need for further investigation into the reliability and consistency of exploratory behaviour. Interesting questions which should be answered include the following: (1) do participants use the same exploration strategy in the same environment when tested repeatedly, (2) are participants consistent in how often they explore in the same environment when tested repeatedly, and (3) does the order of tasks matter and is there evidence of positive and negative transfer effects with task ordering?

While promising, the present work has several limitations. Perhaps the most concerning is the lack of counter balancing, as all participants completed the non-stationary bandit task prior to completion of the stationary bandit task. Thus, motivational and task engagement changes during the experiment could explain the difference in strategy use between tasks. For example, work has shown that time on task is associated with a reduction in neural signals reflecting task engagement (Umemoto et al., 2018). While the authors examined performance across two hours and within a single time-estimation paradigm, similar changes to task engagement could be occurring in the present work and driving the exploration strategy differences. A related limitation is that both the number of arms (four vs two) and the feedback type provided (points vs wins/losses) differed between the two bandit tasks. The difference in both the number of arms and feedback type meant that the two bandit tasks differed across three factors total when considering the stationary and non-stationary task set-up. As such, it remains impossible to distinguish which of these three factors impacted the type of strategies adopted. As an example, point feedback provides a greater amount of information when compared to win-loss feedback, possibly driving the strategy participants adopted to attempt to solve the task. Thus, future work would do well to consider only varying one of these factors (e.g., stationary vs non-stationary) and keeping the other two factors (feedback information, number of choices) consistent.

Conclusions

In sum, we present three key findings. First, using our individual model fitting analysis people’s exploration strategy varies between tasks—replicating prior work showing that people will adopt different strategies due to task demands (Schulz et al., 2018b; Wu et al., 2020). We speculate that the differences in exploration strategies reflect differences in the type of learning assessed or cognitive flexibility needed to successfully complete the two bandit paradigms. Our findings provide evidence of the flexible use of exploration strategies depending on task demands. Second, we found that when instead attempting a combined model fitting approach using data from both tasks concurrently—rather than individually—we could effectively model behaviour across both tasks without showing evidence of exploration strategy switching (inherent to the combined model fitting approach). We thus note that researchers using such an approach must determine whether long-term (across both tasks) or short-term (within a task) predictions are their focus. Third, we found that exploration rate across tasks was correlated which we argued could depend on a personality trait such as risk-taking. Alternatively, these findings could be explained by the hierarchical control of behaviour by the mid-cingulate cortex. Although promising, it is evident that future work replicating and extending these findings is needed. Extending these findings beyond bandit tasks to more ecologically valid tasks such as spatial navigation tasks or multi-stage decision tasks will provide an exciting avenue for future investigation (e.g., Brändle et al., 2022). We believe that the present work reveals the importance of flexibility in human exploratory behaviour while highlighting evidence for generalization in how we explore across contexts.