The computational models of cognition that are most influential on neuroscience were developed in mathematical psychology to account for behavior without regard to neural constraints. For instance, the Atkinson and Shiffrin (1968) model of working memory maintenance was developed to account for behavioral findings from continuous paired associate learning and other behavioral memory tasks. The central idea of the Atkinson and Shiffrin (1968) model—that working memory holds a small number of recently-experienced stimuli in an activated state—went on to be extremely influential on neurophysiological studies of working memory maintenance (e.g., Goldman-Rakic 1996; Fuster and Jervey 1982) as well as computational neuroscience models of working memory (e.g., Goldman 2009; Lisman and Idiart 1995; Compte et al. 2000). Similarly, models for reinforcement learning originally developed to account for behavior (Sutton and Barto 1981) have been extremely influential in understanding the neural basis of reward systems in the brain (Schultz et al. 1997; Waelti et al. 2001). Mathematical models of evidence accumulation (Laming 1968; Link 1975; Ratcliff 1978) have organized and informed a large body of neurobiological work (Gold and Shadlen 2007). There are many neurophysiological phenomena in each domain that do not follow naturally from the neural predictions of these models—this is not surprising insofar as they were developed in most cases long before any relevant neurophysiological data was available. Moreover, the models from each domain seem very different from one another despite the fact that any real-world behavior undoubtedly depends on interactions among essentially the entire brain.

Part of the mismatch perhaps follows from taking models developed at an algorithmic level literally at an implementational or biological level. In this paper, we extend a formalism that has already been applied to behavioral and neural data from working memory experiments (Howard et al. 2015; Tiganj et al. 2018) and neural representations of space and time (Howard et al. 2014) and show that it applies also to models of evidence accumulation. This formalism estimates functions of variables out in the world by constructing the Laplace transform of those functions and then inverting the transform (Shankar and Howard 2012, 2013, Howard et al. 2014). We show that this approach leads to a neural implementation of the diffusion model (Ratcliff 1978). This neural implementation of the diffusion model provides an account of neural data that makes a number of novel quantitative predictions.

The Diffusion Model and Sequential Sampling

Models of response times have been a major focus of work in cognitive and mathematical psychology for many decades (Luce 1986). Evidence accumulation models have received special attention (Laming 1968; Link 1975; Ratcliff 1978). These models hypothesize that during the time between the arrival of a probe and the execution of a behavioral decision, the brain contains an internal variable the dynamics of which describe progress towards the decision. For our purposes, it will be sufficient to describe the dynamics of accumulated evidence with the following random walk:

$$ X_{t+{\Delta}} = X_{t} + {\Delta} \mathcal{E}_{t} $$
(1)

where \(\mathcal {E}_{t}\) is the instantaneous evidence available at time t. Equation (1) describes a perfect integrator. In simple evidence accumulation tasks, \(\mathcal {E}_{t}\) is not known in detail. Under these circumstances, one typically takes \(\mathcal {E}_{t}\) to be a stochastic term.

The diffusion model (Ratcliff 1978) is the most widely used of the evidence accumulation models. In the diffusion model, one assumes \(\mathcal {E}_{t}\) is a normally distributed random variable with a non-zero mean referred to as the drift rate. The units of Xt are usually chosen to be the standard deviation of the normal distribution. The response is emitted when Xt reaches either of two boundaries; the value at the lower and upper boundaries are referred to as 0 and a respectively. In the diffusion model, the starting point of the dynamics is referred to with a parameter z.

The diffusion model can be understood as an implementation of a sequential ratio test, a normative solution to the problem of forming a decision between two alternatives (Wald 1945, 1947, 1948). Suppose we have two alternatives, l and r that could have generated a sequence of independent observations of data, di. Starting with a prior belief about the likelihood ratio of the two alternatives \(\frac {P_{0}(L)}{P_{0}(R)}\), we find that the likelihood ratio of the two hypotheses after observing t data points is

$$ \frac{P(L | d_{1} {\ldots} d_{t})} { P(R| d_{1} {\ldots} d_{t})} = \prod\limits_{i = 1}^{t} \left[ \frac{P(d_{i} | L)} {P(d_{i} | R)} \right] \frac{P_{0}(L)}{P_{0}(R)} $$
(2)

The likelihood ratio on the lhs tells us the degree of certainty we have that the sequence of data was generated by alternative l; the inverse of the likelihood ratio tells us the degree of certainty we have that the data was generated by alternative r. We can determine the level of certainty we require to terminate sampling and execute a decision.

The logarithm of the likelihood ratio is closely related to the diffusion model. Taking the log of both sides of Eq. 2, we find

$$ \log \frac{P(L|d_1 {\ldots} d_t)}{P(R|d_1 {\ldots} d_t)} = \log \frac{P_0(L)}{P_0(R)} + \sum\limits_{i = 1}^t \log \frac{P(d_i|L)}{P(d_i|R)} $$
(3)

Here, the prior log likelihood ratio appears as the starting point of a sum; each additional observation contributes an additive change in the evidence for one alternative over the other. Reaching a criterion can be understood as the log likelihood ratio reaching a particular threshold (recall that log x = −log(1/x)).Footnote 1 In this way, the diffusion model can be understood as an implementation of a sequential ratio test; the parameters of the diffusion model can be mapped onto interpretable quantities. The boundary separation a can be understood as proportional to the log likelihood ratio necessary to make a decision; the starting point z can be understood as a prior probabilityFootnote 2 and the drift rate can be understood as the expectation of the log likelihood ratio contributed by each additional sample.Footnote 3

There are many variants on this basic strategy for evidence accumulation in simple perception tasks that have been explored in the mathematical psychology literature (e.g., Usher and McClelland 2001; Bogacz et al. 2006; Brown and Heathcote 2008). They have various advantages and disadvantages but all retain the feature of dynamics of a decision variable gradually growing towards a boundary of some type. The diffusion model and other models of this class have been used to measure behavioral performance in an extremely wide range of behavioral tasks in humans (e.g., Ratcliff and McKoon 2008).

Neural Evidence for Evidence Accumulation Models

There are two broad classes of evidence from the neurobiology of evidence accumulation that we will review here. First, there is evidence dating from the late 1990s for neurons whose firing rate appears to integrate information to a bound. These studies are typically done in monkeys in the random dot motion paradigm. Second, a more recent body of work shows evidence for neurons that activate heterogeneously and sequentially during information integration. These studies typically use rodents in experimental paradigms where the evidence to be accumulated is under more precise temporal control. These literatures differ not only in species, recording techniques, and behavioral task but also in the brain regions that are investigated. The theoretical framework we will present provides a possible link between these domains, with neurons that integrate to a bound corresponding to the Laplace transform of the function describing distance to the decision bound and neurons that activate sequentially corresponding to the inverse transform of this function.

Neurons that Integrate to a Bound

Models of evidence accumulation have been used to understand the neurobiology of simple perceptual judgments. In a pioneering study, Hanes and Schall (1996) found that the firing rate of neurons in the frontal eye fields (FEF) predicted the time of a movement in a voluntary movement initiation experiment. During the preparatory period, the firing rate grew. When the firing rate reached a particular value, the movement was initiated and could not be terminated via an instruction to terminate the movement. In subsequent studies, neurons in the lateral interparietal area (LIP) appeared to comport with the characteristic predictions of evidence accumulation models in a simple decision-making task.

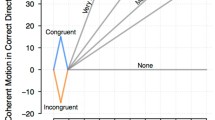
In the random dot motion (RDM) paradigm, a display consisting of moving dots appears in the visual field. Some proportion of dots move in the same direction; a movement (typically a saccade) in the direction of the coherent movement is rewarded. The decision made by monkeys is predicted above chance by the particular sequence of random dots even though there is on average no coherent movement (Kiani et al. 2008). Neurons in the middle temporal area (MT) fire in response to these moving stimuli and predict perceptual discriminability in the task (Newsome et al. 1989; Britten et al. 1992). During performance of the random dot motion task, the firing rate of LIP neurons with fields in the movement direction grows during the decision-making period (Shadlen and Newsome 2001). Conversely, neurons with receptive fields in the other direction show a decrease in firing rate. Similar results have been found in a number of brain regions (see Brody and Hanks 2016, for a review) and LIP is not required for decisions (Katz et al. 2016). For neurons with receptive fields corresponding to the correct direction, firing rate grows faster when the motion coherence is greater and their firing rate is approximately constant around the time at which a response is made (Roitman and Shadlen 2002, see also Cook and Maunsell 2002, for similar results in ventral intraparietal cortex, VIP). Figure 1a summarizes many of these findings (Gold and Shadlen 2007).

Fig. 1
figure 1

Neural evidence for evidence accumulation. a In some brain regions, neurons accumulate evidence towards a bound. These studies typically use random dot motion. The plot shows average firing rate across a number of LIP neurons. When the decision was made in the cells’ preferred direction (solid lines), the firing rate grew as evidence accumulated, with more rapid accumulation for greater degrees of coherence. When the response was in the other direction, firing rate decreased. When aligned on the response (right), the neurons’ firing rate was tightly coupled at the time of response, as if the response was triggered when the firing of the population reached a threshold. After Gold and Shadlen (2007). b In other brain regions (e.g., PPC), the firing rate depends on position along a decision path. In this experiment, the animal ran down a corridor in virtual reality. Visual stimuli were presented on the left or the right; at the end of the corridor, the animal was rewarded for turning in the direction that had more stimuli. Each row represents the firing rate of a neuron as a function of position along the track. The left panels show trials on which all of the stimuli were on the left; the right panels show trials on which all of the stimuli were on the right. The top panels show cells that were selective for left turn trials; the bottom panels show cells that were selective for right turn trials. After Morcos and Harvey (2016)

Full size image

A number of computational neuroscientists and cognitive modelers have understood the firing rate of these integrator neurons as indexing a decision variable that changes as additional evidence is accumulated (e.g., Smith and Ratcliff 2004; Wang 2008; Beck et al. 2008). The standard assumption in these approaches has been that a large population of neurons each provides a noisy estimate of the instantaneous evidence. Each neuron signals the decision variable via its firing rate; by averaging over many neurons, one can compute a better estimate of the magnitude of the decision variable (e.g., Zandbelt et al. 2014).

Sequential Neural Responses During Evidence Accumulation

However, recent evidence suggests that rather than many neurons being noisy exemplars of a single scalar strength, there is in many brain regions heterogeneity in the response of units in simple decision-making tasks (Scott et al. 2017; Morcos and Harvey 2016; Hanks et al. 2015; Meister et al. 2013). In these studies, rather than the RDM paradigm, the task allows more precise control over the time at which evidence becomes available, enabling a detailed investigation of the effect of information at different times on behavior (Brunton et al. 2013) and also neural responses. For instance, one might present a series of clicks on one side of an animal’s head or the other and reward a response to the side that had more clicks (Brunton et al. 2013; Hanks et al. 2015). Other variants of this approach can utilize flashes of light (Scott et al. 2017) or visual stimuli presented along the left or right side of a corridor in virtual reality (Morcos and Harvey 2016).

The critical result from these studies is that rather than changing firing rate monotonically with the decision variable as evidence is accumulated, in several experiments neurons instead respond in a sequence as the decision variable changes. The experiment of Morcos and Harvey (2016) provides a very clear result. In this experiment, mice ran along a virtual corridor. During the run, a series of distinctive visual stimuli were presented along the left or the right side of the virtual corridor. At the end of the corridor, the mice were rewarded for turning in the direction that had more visual stimuli. Morcos and Harvey (2016) observed that neurons in the posterior parietal cortex (PPC) were activated as if they had receptive fields along a decision axis. Figure 1b illustrates the key findings of Morcos and Harvey (2016). On trials where all of the evidence was in one direction or the other, the population fired sequentially, with distinct sequences for progress towards the different decisions. Notably, the neurons in Fig. 1b seem to show an overrepresentation of points near the decision bound. This can be seen from the “hook” in Fig. 1b.

The Laplace Transform in Cognitive Science and Computational Neuroscience

In this paper, we pursue the hypothesis that the two classes of neural data from evidence accumulation experiments can be understood as the Laplace transform and inverse transform of a function describing the net evidence since the decision-making period began. This places models of evidence accumulation in the same theoretical framework as recent models of memory that utilize the Laplace transform and its inverse (Shankar and Howard 2012, 2013) to construct cognitive models of a range of memory tasks (Howard et al. 2015). The Laplace transform can also be used to construct neural models of time cells and place cells (Howard et al. 2014).

The cooperative behavior of many neurons can be understood as representing functions over variables in the world. For instance, individual photoreceptors respond to light in a small region of the retina. The activity of a set of many photoreceptors can be understood as representing the pattern of light as a function of location on the retina. For some variables, such as the location of light on the retina or the frequency of a sound, the problem of how to represent functions amounts to the problem of placing receptors in the correct location along a spatial gradient (e.g., hair cells at different positions along the cochlea are stimulated by different frequencies). For other variables, such as time and allocentric position, we cannot simply place receptors to directly detect the function of interest. For instance, “time cells” observed in a range of brain regions appear to code for the time since a relevant stimulus was experienced (MacDonald et al. 2011; Mello et al. 2015; Bolkan et al. 2017; Tiganj et al. 2018). The stimulus that is being represented is in the past (in some experiments, as much as 1 min in the past). Similarly (at least in some circumstances), place cells in the hippocampus represent distance from an environmental landmark (Gothard et al. 1996). These cells show the same form of activity in the dark (Gothard et al. 2001) and cannot reflect locally available cues. How can the brain construct functions of time and space? One solution is that the brain does not directly estimate the function of interest. Rather, the brain maintains the Laplace transform of the function of interest and then inverts the transform to estimate the function directly.

The Laplace Transform Contains all the Information About the Transformed Function

The mathematics of the Laplace transform are well understood. Given a function f(t), the Laplace transform of f(t) is written as F(s):

$$ F(s) = {\int}_{0}^{\infty} e^{-st^{\prime}} f(t^{\prime})~dt^{\prime} $$
(4)

That is, one starts with a function f(t) that specifies a numerical value at many different values of t. By computing F(s) via (4) with many different values of s, we construct the Laplace transform of f.Footnote 4 Each value of s simply gives the sum of the product of f(t) with an exponentially decaying kernel that peaks at zero. The Laplace transform has been studied for hundreds of years and is widely used in engineering applications.

The most important property of the Laplace transform for present purposes is that the transfrom can be inverted. Put simply, that means that if we know the values of F(s) for each value of s, we can in principle recover the value of f(t) at every value of t. The most widely used algorithms for inverting the transform involve taking the limit of an integral computed in the complex plane. These methods are complicated and difficult to implement neurally. Fortuitously, there is an algorithm for inverting the Laplace transform that only requires real coefficients and nothing more demanding than computing derivatives (Post 1930). This technique, referred to as the Post approximation, yields a scale-invariant approximation of the inverse transform, and thus recovers the original function (Shankar and Howard 2012) and is neurally realistic (Shankar and Howard 2012; Liu et al. in press).

Formally, we can keep track of the Laplace transform with a differential equation:

$$ \frac{dF{\kern-.5pt}(s)}{dt} = -s F\!\left( s\right) + f\!\left( t\right) $$
(5)

The solution to this equation at time t:

$$ F_{t}\left( s\right) = {\int}_{-\infty}^{t} e^{-s\left( t-t^{\prime}\right)} f(t^{\prime}) dt^{\prime} $$
(6)

is just the Laplace transform of f(t′<t). Note that updating (5) as time unfolds requires only information about the input available at time t and the value of F(s) at the immediately preceding moment. Because (5) implements the Laplace transform of f(t′<t), we know that a set of units Ft(s) contains all of the information present in the function f(t′<t). Because the function is the input presented over the past, we can conclude that at time t, F(s) maintains the Laplace transform of the past. If we could invert the transform, we could recover the function of the past itself.

The Post approximation provides a way to approximately invert the transform. This method can be written as follows:

$$\begin{array}{@{}rcl@{}} \tilde{f}\left( \overset{*}{\tau}\right) &\equiv & \mathbf{L}^{-1}_{\mathrm{k}} F(s) \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} &=& C_{k} s^{k + 1} \frac{d^{k}}{ds^{k}} F(s) \end{array} $$
(8)

where \(\overset {*}{\tau } \equiv -k/s\), k is an integer constant that controls the precision of the inverse, Ck is a constant that depends on k and \(\frac {d^{k}}{ds^{k}}\) means to take the k th derivative with respect to s. Post (1930) proved that in the limit as k →∞, the inverse is precise and \(\tilde {f}_{t}(\overset {*}{\tau }) = f(t+\overset {*}{\tau })\). The variable \(\overset {*}{\tau }\) is negative; for each unit in \(\tilde {f}\), its value of \(\overset {*}{\tau }\) characterizes the time in the past that unit represents. When k is small, this method yields only an approximate estimate of the function. The errors in the reconstruction appear as receptive fields in time with a width that increases for time points further in the past. Figure 2a illustrates the time dynamics of F(s) and \(\tilde {f}(\overset {*}{\tau })\) for a simple input. It is worth noting that the time dynamics of F(s) and \(\tilde {f}(\overset {*}{\tau })\) resemble neurophysiological findings of so-called temporal context cells in the lateral entorhinal cortex (Tsao et al. 2018) and “time cells” observed in the hippocampus and other regions (Pastalkova et al. 2008; MacDonald et al. 2011; Mau et al. 2018) respectively.

Fig. 2
figure 2

The Laplace transform for time and space. a The Laplace transform of functions of time. Consider an input f(t) that is non-zero for a brief period. After the input, the different neurons corresponding to the Laplace transform, F(s), activate and then decay exponentially. Different neurons have different values of s and thus decay at different rates. Neurons with these properties have recently been observed in the lateral entorhinal cortex (Tsao et al. 2018). Neurons representing the inverse transform \(\tilde {f}(\protect \overset {*}{\tau })\) respond a characteristic time after the input. They fire when the past stimulus enters their receptive fields, defined by their value of \(\protect \overset {*}{\tau }\). b Neural functions of time. If the brain contained sets of neurons that represented functions of time, we would see sequentially activated neurons. This figure shows simultaneously recorded sequentially activated neurons in the hippocampus recorded using calcium imaging. Each row gives the activation of one neuron as a function of time during the delay. The neurons are sorted according to their peak time. Note the curvature. This means that there are progressively fewer neurons coding for later in the delay. The dashed red line gives an analytic curve under the assumption of logarithmic compression. Although this recording technique does not allow one to measure the width of individual cells’ tuning, many papers using extracellular electrophysiology have shown that time fields also grow wider as the sequence unfolds. After Mau et al. (2018). c Laplace transform for variables other than time. Left: schematic for the method for constructing the Laplace transform of variables x in the world. With access to the time derivative of x, the method modifies the differential equation for maintaining the Laplace tranform of time by \(\alpha (t) = \frac {dx}{dt}\). If the input f is a function of x(t), then F(s) maintains the Laplace transform of f(x). Right: consider a case in which the animal encounters a spatial landmark at x = 0 causing an input via f and then moves in the neighborhood of the landmark (with x > 0). As the animal moves away, dx/dt > 0 and the cells in F(s) decay exponentially. But if the animal turns around and heads back towards the startng point, dx/dt < 0 and the cells grow exponentially. However, firing is always just a function of x. Under these circumstances, the Laplace transform behaves like border cells with different space constants and neurons participating in the inverse Laplace transform behave like place cells. After Howard et al. (2014)

Full size image

Generalization to Hidden Variables Other than Time

Equations 5 and 7 provide a concise account for representing functions of time (Shankar and Howard 2012) that mimics the firing of time cells in a range of brain regions (Fig. 2b, see also Mau et al. 2018; Tiganj et al. 2018) and can be readily implemented in realistic neural models (Tiganj et al. 2015; Liu et al. in press). In this paper, we exploit the fact that this coding scheme can also be used to construct functions over variables other than time. Consider the simple generalization of Eq. 5:

$$ \frac{dF{\kern-.5pt}(s)}{dt} = \alpha(t)\left[ -s F\!\left( s\right) + f\!\left( t\right) \right] $$
(9)

Note that this reduces to Eq. 5 if α(t) = 1. If one can arrange for α(t) to be equal to the time derivative of some variable x, \(\alpha (t) = \frac {dx}{dt}\), then one can use Eq. 9 to construct the Laplace transform of functions over x instead of over time (Howard et al. 2014).Footnote 5 For instance, if f(t) is non-zero only when an animal encounters the start box of a linear track, and if α(t) is the animal’s velocity along the track, then as the animal runs back and forth along the track, α(t) changes sign. During these periods of time, the firing rate of each unit in F(s) decays as an exponentially decreasing function of distance. At the same time, units in \(\tilde {f}\) behave like one-dimensional place cells (Fig. 2c). When the inverse is understandable as a function over some variable other than time, we will write \(\tilde {f}(\overset {*}{x})\).

Optimal Weber-Fechner Distribution of s

Thus far, we have discussed at a formal level how to use many neurons with different values of s to represent the Laplace transform of functions and how to use the operator \(\mathbf {L}^{-1}_{\mathrm {k}}\) to construct an approximation of the original function \(\tilde {f}(\overset {*}{x})\) with many neurons corresponding to many values of \(\overset {*}{x}\). It remains to determine how to allocate neurons to values of s and \(\overset {*}{x}\). Because \(\overset {*}{x}\) is in one-to-one relationship with s, it is sufficient to specify the allocation of neurons to s.

It has been argued that it is optimal to allocate neurons to represent a continuous variable in such a way that receptive fields are evenly spaced as a function of the logarithm of that variable (Howard and Shankar 2018). In addition to enabling a natural explanation of the Weber-Fechner law, positioning receptors evenly along a logarithmic scale also enables the neural system to extract the same amount of information from functions with a wide range of intrinsic scales. This logarithmic scaling requires that receptive field center of the n th receptor goes up like \(\overset {*}{x}_{n} = c^{n}\).Footnote 6 This compression results in a characteristic “hook” in the heatmaps constructed by sorting neurons on their peak time (as in Fig. 2b). Coupled with a linear increase in receptive field width with an increase in x,Footnote 7 this arrangement means that the acuity between adjacent receptors is a constant.

The Laplace Transform of the Diffusion Model

We propose a model of evidence accumulation in which the Laplace transform of accumulated evidence is represented at each moment and inverted via a linear operator. The result is evidence on a supported dimension with logarithmic compression. The diffusion model describes the position of a particle relative to two decision boundaries. Inspired by the curvature present in the Morcos and Harvey (2016) data, we maintain the Laplace transform of the distance to each of the two boundaries, treating the appropriate decision bound as zero for each of the two functions (Fig. 3). This formalism provides a mapping between the diffusion model at an algorithmic level and neurons at an implementational level.

Fig. 3
figure 3

Implementing the diffusion model with many neurons via the Laplace transform. At an algorithmic level, the diffusion model describes an abstract particle representing the quantity of net accumulated evidence moving towards two boundaries. At the implementational level, the position of this particle is represented in the Laplace domain by two sets of units that code for the Laplace transform of position relative to the two boundaries, F(s). These units have exponentially decaying “receptive fields” with respect to net evidence. Each unit is parameterized by a value s that controls its rate of decay—different colors correspond to different values of s. Another set of units \(\tilde {f}(\overset {*}{x})\) approximates the inverse Laplace transform. Units in this representation have receptive fields that tile the evidence axis. Each unit is parameterized by a value \(\overset {*}{x}\) that controls the center of its receptive field. These units are compressed and scale-invariant in the same way that time cells generated by the same equations are (Fig. 2)

Full size image

Let us refer to the two alternative responses as l and r and the net evidence for the left alternative accumulated up to time t as L(t) − R(t). The decision-maker’s goal is to estimate the net evidence that has been experienced since the trial began. The instantaneous evidence gives the time derivative of that variable. In the random dot motion paradigm, we would expect the instantaneous derivative to fluctuate more or less continuously; the mean of this derivative would differ across conditions with different levels of motion coherence. In paradigms with discrete clicks or flashes of light, the presence of a click signals a non-zero value of the derivative, with the side of the click controlling the sign of the derivative.

We start constructing this model by assuming that we have two sets of leaky accumulators FL(s) and FR(s). These correspond to opponent pairs of evidence accumulators. FL(s) codes for the Laplace transform of L − R over the range 0 to a and FR(s) codes for the Laplace transform of R − L over the domain a to 0. We adopt the strategy of assigning each α(t) to the derivative of this decision variable; αL(t) = −αR(t). When evidence accumulation begins, we want to have

$$\begin{array}{@{}rcl@{}} F_{L}(s,0) & = & e^{-sz} \\ F_{R}(s,0) & = & e^{-s(a-z)} \end{array} $$
(10)

where z corresponds to the bias term and a corresponds to the boundary separation. Note that these correspond to the same location on the decision axis, but reference to different starting points. This initialization can be accomplished by “pulsing” each accumulator with a large α value. The sum of the area under these two pulses controls the boundary separation. The difference controls the bias.

After initialization, as evidence is accumulated, we set \(\alpha _{L}(t) = \frac {d(L-R)}{dt}\) and \(\alpha _{R}(t) = \frac {d(R-L)}{dt}\) and evolve both FL(s) and FR(s) according to Eq. 9. In this way, each set of integrators codes for the Laplace transform of the distance to each of the two decision boundaries.

At each moment, a second set of units holds the approximate inversion of the Laplace transform, \(\tilde {f}_{L}(\overset {*}{x})\) and \(\tilde {f}_{R}(\overset {*}{x})\) using

$$\begin{array}{@{}rcl@{}} \tilde{f}_{L}(\overset{*}{x}) &=& \mathbf{L}^{-1}_{\mathrm{k}} F_{L}(s) \\ \tilde{f}_{R}(\overset{*}{x}) &=& \mathbf{L}^{-1}_{\mathrm{k}} F_{R}(s) \end{array} $$
(11)

By analogy to time cells and place cells, these units tile the decision space with compressed receptive fields that grow sharper in precision as each unit’s preferred decision outcome is approached.

Compression of \(\protect \overset {*}{x}\) Gives Equal Discriminability in Probability Space

Noting the characteristic curvature in the Morcos and Harvey (2016) data (Fig. 1), we configure each set of integrators to represent distance to the appropriate decision bound. Following previous work on time and space (Howard and Shankar 2018), we choose a Weber-Fechner scaling of the \(\overset {*}{x}\) axis. Denoting the value of \(\overset {*}{x}\) for each unit like, \(\overset {*}{x}_{1}, \overset {*}{x}_{2} {\ldots } \overset {*}{x}_{n}\) gives \(\overset {*}{x}_{i} \propto C^{i}\), where C is some constant that depends on the number of units and their relative precision (Howard and Shankar 2018). Because of the properties of the inverse Laplace transform, the width of each receptive field goes up proportional to the unit’s value of \(\overset {*}{x}\). From this expression, we can see that units are evenly spaced on a logarithmic scale.

These properties imply that the set of units has greater discriminability for smaller values of \(\overset {*}{x}\); as \(\overset {*}{x}\) increases the spacing between adjacent units increases. In the context of sequential ratio testing, the distance to the bound in the diffusion model can be understood as the distance to the bound for the log likelihood ratio. The logarithmic spacing of \(\overset {*}{x}\) means that discriminability is equivalent in units of likelihood ratio. This is a unique prediction of this approach that may have important theoretical and empirical implications.

Implementing Response Bias and Imposing a Response Deadline

This neural circuit is externally controllable via α(t). Note that α(t) affects each unit in a way that is appropriate to its value of s. It can be shown that affecting α(t) for a single cell is equivalent to changing the slope of the f-i curve relating firing rate to the magnitude of an internal current (Liu et al. in press). Changing α(t) for all the units in F(s) simply means to change the slope of all of their f-i curves appropriately. There are many biologically plausible mechanisms to rapidly change the slope of the f-i curve of individual neurons (e.g., Chance et al. 2002; Silver 2010). Because we can understand the implications of manipulating α(t) in terms of the entire function F(s), this lets us readily determine conditions to implement response bias and change the boundary separation to comply with a response deadline or even a continuously changing estimate of the cost of further deliberation (Gershman et al. 2015).

In order to initialize a response bias as in Eq. 10, starting from zero activation for all the units in both sets of F(s), a pulse in α will push each set of units away from their respective bound. The sum of the pulses across the two accumulators is interpretable as the boundary separation. Response bias can be simply implemented by providing a different magnitude pulse to the two sets of accumulators. If each set of units is given the same magnitude of a pulse in α, there is no response bias. The accumulator that receives the smaller pulse starts evidence accumulation closer to the bound.

Similar mechanisms can be used to change the effective distance to the response boundary rapidly. In the simulations below, we assume that the appropriate response is executed when the activation of the first entry in \(\tilde {f}\), \(\tilde {f}(\overset {*}{x}_{1})\) reaches a threshold. If \(\tilde {f}_{L}(\overset {*}{x}_{1})\) is activated before \(\tilde {f}_{R}(\overset {*}{x}_{1})\), option l is selected. In the same way that αL/R(t) can be used to initialize evidence accumulation by pushing FL/R(s) away from the bound, so too can αL/R(t) be used to evolve the two accumulators towards their respective bounds. By setting both αL(t) and αR(t) to positive values, each set of accumulators evolves towards their respective bounds. The alternative that is closer to the decision bound when this process begins will reach its bound sooner, executing the corresponding response.

Neural Simulations

In order to demonstrate that this approach leads to neural predictions that are in line with known neurophysiological data, we provide simulations of two paradigms that have received a great deal of attention in the neurophysiological literature. We first show that during the random dot motion paradigm units in F(s) show activity that resemble classic integrator neurons such as those observed in monkey LIP. We then show that during performance of a discrete evidence accumulation paradigm, units in \(\tilde {f}(\overset {*}{x})\) show receptive fields along the decision axis not unlike those in mouse PPC.

Constant Input in the Random Dot Motion Paradigm

We simulated the random dot motion paradigm by letting α(t) vary from moment to moment by drawing from a normal distribution at each time step and setting αL(t) = −αR(t). As in most applications of the diffusion model, different levels of coherence were simulated by drawing from normal distributions with different mean values for each of the levels of coherence.Footnote 8 Figure 4a shows the result of a representative unit with s = 2.5 in F(s).

Fig. 4
figure 4

The Laplace transform and the inverse transform capture key findings from the neurobiology of evidence accumulation. a The Laplace transform is shown for one value of s in a simulated random dot motion experiment. In this simulation, αL(t) was set at each moment to a normally distributed random variable with a mean that differed across condition. In the solid curves, the mean was greater than zero; in the dashed curves, the mean was less than zero for αL(t), and thus greater than zero for αR(t). On the left, we see that the firing rate grew with time after information began to accumulate; the rate and direction of accumulation depended on the mean of the random variable. When aligned to the time of response (right), firing rate showed a tight coupling. If we changed the value of s, we would have observed the same qualitative behavior, but with different rates of accumulation and more or less curvature on average. Compare to Fig. 1a. b Heatmaps for neurons participating in the inverse Laplace transform. Each line is the firing rate of a neuron. Neurons participating in \(\tilde {f}_{L}\) are shown on the top; neurons participating in \(\tilde {f}_{R}\) are shown on the bottom. On the left, the firing rate is shown as a function of evidence (confounded with time) when there is consistent evidence for the left option. On the right, the activation is shown when there is consistent evidence for the right option. Compare to Fig. 1b

Full size image

Figure 4a summarizes the results of these simulations. Neurons in F(s) grow towards a bound in a noisy way. When motion coherence is away from the neuron’s preferred direction, the firing rate instead decreases towards zero. The rate of increase is greater when there is more motion coherence (left), resulting in faster responses for higher motion coherence. When aligned to the time of response, the unit’s firing appears tightly aligned. Although the response is actually triggered by the activation of a particular unit in \(\tilde {f}\), the activation in \(\tilde {f}\) is in one-to-one relationship with F(s) (see Eq. 11) and all of the units in F(s) corresponding to the selected response monotonically increase as the decision bound becomes more near.

Note that there is a slight curvature apparent in the model neuron shown in Fig. 4a. This curvature is a consequence of the exponential function in the Laplace transform. Choosing different values of the s would have resulted in more or less curvature. Note the model predicts that neurons encoding the inverse transform would show supported receptive fields as a function of distance from the decision point.

Information Accumulators and Position Along a Decision Axis

Figure 4b shows analytic results from deterministic evidence accumulation. Analogous to the trials in the Morcos and Harvey (2016) paper in which evidence was only presented in favor of one option or the other, after initialization on left trials, we set αL(t) to a fixed positive constant X for the duration of the trial; αR(t) was set to − X. On right trials, the situation was reversed. We show the activation of units in \(\tilde {f}_{L}(\overset {*}{x})\) and \(\tilde {f}_{R}(\overset {*}{x})\) on each type of trial. The model captures the prominent features of the data. Units have receptive fields along a subset of the decision axis. There are more units with receptive fields near the time when the decision is reached. The width of receptive fields near the bound is less than the width of receptive fields further from the bound. Note that this is an analytic solution. Had we simulated detailed trials with sequences that included different amounts of net evidence, the units would still have receptive fields along the net evidence axis.

Note that neurons encoding the transform would grow or decay exponentially in this task as a function of distance to the bound. These neurons would have the same relationship to the neurons in Fig. 4b as border cells (Solstad et al. 2008; Campbell et al. 2018) do to one-dimensional place cells (Howard et al. 2014). That is, in spatial navigation tasks, border cells fire as if they encode an exponential function of distance to an environmental border. If border cells manifest a spectrum of decay rates, then they encode the Laplace transform of distance to that border. Taking the inverse transform would result in cells with receptive fields that are activated in a circumscribed region of space (Lever et al. 2009).

The results in Fig. 4b are closely analogous to predictions for time cells and place cells from the same formalism (Howard et al. 2014; Tiganj et al. 2018). Different sources of evidence trigger different sequences leading to different decisions; this is closely analogous to experimental results from time and place. For instance, a recent study showed that distinct stimuli in a working memory task trigger distinct sequences of time cells in monkey lPFC (Tiganj et al. 2018). Similarly, distinct sequences of place cells fire as an animal moves from a starting point along distinct trajectories (McNaughton and O’Keefe 1983).

Novel Neural Predictions

The present approach is conceptually very different from previous neural implementations of evidence accumulation models. In most prior models, the assumption is that many neurons provide noisy exemplars of the decision variable; an estimate of the decision variable can be extracted by averaging over many neurons (e.g., Zandbelt et al. 2014). In contrast, although the activity of units in F(s) is correlated with the amount of instantaneous evidence, they are not noisy exemplars of that scalar value. Rather, the Laplace transform is written across many units with different values of s. At any moment, the activity of different units in F(s) is a known function of the decision variable, leading to quantitative relationships both as a function of time for a particular unit but also relationships between units. Moreover, the model predicts specific relationships between units in F(s) and \(\tilde {f}(\overset {*}{x})\), which should appear in pairs in decision-making tasks. These properties lead to several distinct neural predictions. These predictions are summarized in Table 1 and detailed below.

Table 1 Summary of novel neural predictions
Full size table

Prediction 1: Exponential Functions

The hypothesis that the brain maintains an estimate of the Laplace transform of the decision variable, rather than a linear function of the decision variable leads to distinct predictions. Even in circumstances where evidence is accumulating at a constant rate, the activity of integrator neurons should not in general be linear. Note that for values of x small relative to 1/s, it is difficult to distinguish e−sx from 1 − x. Moreover, the firing rate as a function of time should be a function of the actual evidence as well as changing decision bounds. However, systematic deviation from linearity is a clear prediction of the present approach.

Note that a recent literature has questioned whether information accumulates continuously in information accumulation neurons or whether it changes abruptly in discrete steps (e.g., Latimer et al. 2015). One could imagine that the exponential function is expressed as a statistical average over a number of units each of which obey step-like evolution following the same constant hazard function. It is also possible that work arguing for discrete steps in activation has not considered the appropriate family of continuously evolving activation. Indeed, recent work has begun to explore non-linear models for activation as a function of time (Zoltowski et al. 2018) and has found relatively nuanced results.

Prediction 2: Spectrum of s Values

The most fundamential prediction of the approach proposed here is that different units coding for the decision variable integrate information with different rate constants s. We can think of each neuron’s value of 1/s as its “evidence constant.” The fundamental prediction of this approach is that s and 1/s) do not take on the same value across neurons. Although it has not to our knowledge been systematically studied, there is evidence suggesting that neurons respond heterogeneously during simple decision-making tasks. For instance, Figure 7 in Peixoto et al. (2018) appears to show that different units discriminate the identity of a future response at different points during a decision. The computational approach proposed here requires heterogeneity in s values; a spectrum of s values is essential to construct an estimate of x via the Laplace domain.

In most RDM experiments, the decision variable fluctuates in an unpredictable way from moment-to-moment. Moreover, changing decision bounds would also change the firing rate for many neurons simultaneusly. However, the hypothesis that different units obey the same equations, but with different values of s suggests a strategy for estimating the spectrum. Although α(t) may fluctuate from moment to moment based on the instantaneous evidence and perhaps also with changing decision bounds, the same value of α(t) is distributed to all of the neurons estimating F(s) coding the distance to a particular bound. Thus, the momentary variability is shared across units. Suppose we had two simultaneously recorded LIP neurons with the same receptive field and rate constants s1 and s2. On individual trials, each unit would appear to fluctuate randomly over the trial as the net evidence fluctuates. One unit would move like a bead on a wire along the curve \(e^{s_{1} x(t)}\); the other would move like a bead on a wire along the curve \(e^{s_{2} x(t)}\). Although the fluctuations along each curve may appear random, plotting the firing rate of one neuron as a function of the other would result in a smooth exponential curve. In practice, one would need to consider an appropriate time bin over which to average spikes and undoubtedly face other technical issues in performing these analyses.

Prediction 3: Laplace/Inverse Pairs Across Tasks

In this paper, we have noted that integrator neurons observed in RDM tasks have properties analogous to the Laplace transform of distance to the bound, F(s), and that sequentially activated cells in a virtual navigation decision task have properties analogous to the inverse Laplace transform estimating distance to the bound, \(\tilde {f}(\overset {*}{x})\). The hypothesis presented here requires that the inverse transform \(\tilde {f}(\overset {*}{x})\) is constructed from the transform F(s). Moreover, the trigger for the actual response in the RDM task is the activation of units with the smallest value of \(\overset {*}{x}\). This approach thus requires that both forms of representation should be present in the brain in both tasks.

In tasks where instantaneous evidence is under experimental control and becomes available at discrete times (such as the Morcos and Harvey 2016 task), the Laplace transform F(s) should remain fixed during periods of time when no evidence is available. When evidence is provided, neurons coding for the transform should gradually step up (or step down) their firing as the decision bound they code for becomes closer (or further away). Note also that one can implement a leaky accumulator by including a non-zero value to α(t) during periods of time when no evidence is presented. Conversely, in tasks where the instantaneous evidence is not well controlled, such as the RDM task, neurons coding for \(\tilde {f}(\overset {*}{x})\) should still have “receptive fields” along the decision axis, although in practice it may be much more difficult to observe these receptive fields.

Geometrically, F(s) and \(\tilde {f}(\overset {*}{x})\) have different properties that might be possible to distinguish experimentally even in an RDM task where it is difficult to measure single-cell receptive fields. Consider a hypothetical covariance matrix observed over many neurons representing either F(s) or \(\tilde {f}(\overset {*}{x})\) during an RDM task in which the animal chooses among two alternative responses l and r. For units representing F(s), at the time of the response, the population consists of two populations. That is, at the time of an l response, neurons participating in FL(s) are maximally activated and neurons participating in FR(s) are deactivated. This distinction will be reflected in the covariance matrix; one would expect the first principal component of the covariance matrix to correspond to this source of variance. Now, for F(s), because neurons change their firing monotonically along the decision axis, this principal component will also load on other parts of the decision axis, changing smoothly.Footnote 9 In contrast, consider the set of neurons active at the time of the response for a population representing \(\tilde {f}(\overset {*}{x})\). Like F(s), that the population of neurons in \(\tilde {f}(\overset {*}{x})\) active at the time of an l response is different than the population active at the time of an r response. However, unlike F(s), because neurons in \(\tilde {f}(\overset {*}{x})\) have circumscribed receptive fields along the decision axis, the neurons active at the time of the response for l are not the same as the neurons active, say, three quarters of the way along the decision axis towards an l response. It may be possible to distinguish these geometrical properties by examining the spectrum of the covariance matrices.

We will avoid committing to predictions about what brain regions (or populations) are responsible for coding F(s) and which are responsible for coding \(\tilde {f}(\overset {*}{x})\) in any particular task. It is clear that many brain regions participate in even simple decisions (e.g., Peixoto et al. 2018). Moreover, the task in Morcos and Harvey (2016) is relatively complicated and may rely on very different cognitive mechanisms than the RDM task. The prediction is that there should be some regions that encode the transform and the inverse in any particular evidence accumulation task; it is possible that these regions vary across tasks.

Prediction 4: Linked Non-uniform Spectra of Rate Constants s and \(\overset {*}{x}\)

Experience with time cells and computational considerations (Shankar and Howard 2013; Howard and Shankar 2018) leads to the prediction that the spectra of s and \(\overset {*}{x}\) values should be non-uniform. Although it may be challenging to evaluate experimentally, Weber-Fechner scaling also leads to a quantitatively precise prediction about the form of the distribution.

It is now clear that time cells are not uniformly distributed. As a sequence of time cells unfolds, there are more neurons that fire early in the sequence and fewer that fire later in the sequence. This phenomenon can be seen clearly from the curvature of the central ridge in Fig. 2b and has been evaluated statistically in a number of studies in many brain regions (e.g., Kraus et al. 2013; Salz et al. 2016; Mello et al. 2015; Jin et al. 2009; Tiganj et al. 2018). If similar rules govern the distribution of neurons coding for distance to a decision bound, we would expect to find more neurons with receptive fields near the bound, with small values of \(\overset {*}{x}\), and fewer neurons with receptive fields further from the bound with larger values of \(\overset {*}{x}\). Weber-Fechner scaling predicts further that the number of cells with a value of \(\overset {*}{x} < \overset {*}{x}_{o}\) should go up with \(\log \overset {*}{x}_{o}\), meaning that the probability of finding a neuron with a value of \(\overset {*}{x}_{o}\) should go down like \(1/\overset {*}{x}_{o}\).

The computational approach proposed in this paper links F(s) and \(\tilde {f}(\overset {*}{x})\). This naturally leads to the prediction that the distributions of values for \(\overset {*}{x}\) and s are linked. Recalling that \(\overset {*}{x} \equiv k/s\) enables us to extend the predictions about the distribution of \(\overset {*}{x}\) values in populations representing \(\tilde {f}(\overset {*}{x})\) to the distribution of s values in populations representing F(s). There should be a larger number of neurons with large values of s and fewer neurons with small values of s. Weber-Fechner scaling predicts that the number of neurons in F(s) with values of s > so should change linearly with log so. Similarly, the probability of finding a neuron with a value of so should go down like 1/so.

Discussion

The present paper describes a neural implementation of the diffusion model (Ratcliff 1978). Rather than individual neurons each providing a noisy estimate of the decision variable, many neurons participate in a distributed code representing distance to the decision bound. Neurons coding for the Laplace transform of this distance have properties that resemble those of “integrator neurons” in regions such as LIP. Neurons estimating the distance itself, constructed from approximating the inverse transform, have receptive fields along the decision axis.

Alternative Algorithmic Evidence Accumulation Models in the Laplace Domain

In this paper, we have focused on implementation of the diffusion model. However, it is straightforward to formulate other algorithmic models in the Laplace domain. For instance, in order to implement a race model, all that needs to be done is to make αL and αR independent of one another rather than anticorrelated as in the present implementation of the diffusion model. Similarly, one can implement a leak term (Busemeyer and Townsend 1993; Usher and McClelland 2001; Bogacz et al. 2006) by including a constant negative term to each of the α(t) values. The magnitude of the constant term is proportional to the leak parameter.

Insofar as these approaches are equivalent to the corresponding algorithmic model, adopting this form for neural implementation entails at most subtle behavioral distinctions to classic implementations of the diffusion model. However, there is one unique property that follows from this approach of formulating decision-making as movement along a Weber-Fechner compressed decision axis. As discussed above, the logarithmic compression along the \(\overset {*}{x}\) axis means that the neural representation is not equidiscriminable in the decision variable X, but in eX. If X is understandable as the log likelihood ratio (3), then this means that the magnitude of the change in the likelihood ratio itself controls the change in the neural representation. This would predict that the just-noticeable-differences in the decision variable are controlled by the likelihood ratio itself rather than the log likelihood ratio. In practice, this prediction would be difficult to assess in any particular experiment because in sequential decision-making tasks, the likelihood ratio as a function of time is not a physical observable but is inferred based on assumptions about the processing capabilities of the observer.

Unification of Working Memory, Timing, and Evidence Accumulation in the Laplace Domain

As mentioned in the introduction, many of the most influential ideas in computational neuroscience are derived from cognitive models developed without consideration of neural data. Often in cognitive psychology, these models are treated as independent of one another. One of the contributions of the present paper is that it enables the formulation of cognitive models of evidence accumulation in the same Laplace transform formalism as cognitive models of other tasks, including a range of memory and timing studies (Shankar and Howard 2012; Howard et al. 2015; Singh et al. in press). This paper also enables consideration of neural models of evidence accumulation in the same formalism as neural models of representations of time and space (Howard et al. 2014; Tiganj et al. 2018).

Although in cognitive psychology models of working memory and evidence accumulation have been treated as largely separate topics (but see Usher and McClelland 2001; Davelaar et al. 2005), in computational neuroscience they have been treated in much closer proximity. Indeed, the state of a perfect integrator reflects its previous inputs (1). In computational neuroscience, decision-making models use similar recurrent dynamics (Wong et al. 2007; Wang 2002) that are used for working memory maintenance (e.g., Chaudhuri and Fiete 2016; Machens et al. 2005; Romo et al.1999). At the neural level, a perfect integrator predicts stable states in the absence of external activation (Funahashi et al. 1989), analogous to the binary presence of an item in a fixed-capacity working memory buffer.

In cognitive psychology models of evidence accumulation and timing have been more closely linked. Noting that in the case of a constant drift rate, Xt is proportional to the time since evidence accumulation began, models have used integrators to model timing (Rivest and Bengio 2011; Simen et al. 2011; Simen et al. 2013; Luzardo et al. 2017b; Balcı and Simen 2016). “Diffusion models for timing” are also closely related to models of learning (Gallistel and Gibbon 2000; Killeen and Fetterman 1988; Luzardo et al. 2017a) and the scalar expectancy theory of timing (Gibbon and Church 1984; Gibbon et al. 1984). At the neural level, these models predict that during timing tasks, firing rate should grow monotonically, a phenomenon that has been reported (e.g., Kim et al. 2013; Xu et al.2014).

In both of these cases, the neural implementations of the cognitive models have found some neurophysiological support. In each of the foregoing cases, neural models implement a scalar value from an algorithmic cognitive model as an average over many representative neurons. In the case of timing models as in evidence accumulation models, this predicts monotonically increasing or decreasing firing rates. As we have seen here, monotonically increasing or decreasing functions can be generated by neurons participating in the Laplace transform of a function representing a scalar value over a set of neurons. However, the present framework also predicts that populations with monotonically changing firing rates should be coupled to populations with sequentially activated neurons like those found in \(\tilde {f}(\overset {*}{x})\) and that these two forms of representation are closely connected to one another. Thus, findings that working memory maintenance is accompanied by sequentially activated cells during the delay period of a working memory task (Tiganj et al. 2018) or that timing tasks give rise to sequentially activated neurons (Tiganj et al. 2017) can be readily reconciled with the present approach but are difficult to reconcile with models that require representation of a scalar value as an average over many representative neurons. The present approach and much previous work in computational neuroscience differ in their account of how information is distributed over neurons.

Function representation via the Laplace domain also has potentially great explanatory power in developing neural models of relatively complex computations. It has been long appreciated that computations can be efficiently performed in the Laplace domain. In much the same way that understanding of the mathematics lets us readily specify how to set α to accomplish various goals such as initializing with a specific response bias in the evidence accumulation framework described here, access to the Laplace domain lets us readily write down mechanisms for translation of functions (Shankar et al. 2016) or perform arithmetic operations on different functions (Howard et al. 2015). Computations in the Laplace domain require a large-scale organization for macroscopic numbers of neurons; this large-scale organization enables basic computations. Insofar as many different forms of information in the brain use the same form of compact compressed coding, one can in principle recycle the same computational mechanisms for very different forms of information, including sensory representations, representations of time and space, or numerosity.