Simulation–optimization model for the structural design of cantilever retaining walls

Abstract

As the trend of retaining wall construction in Egypt continues to grow, it becomes necessary to find ways to reduce their construction costs. There are various types of retaining walls such as cantilever, counterfort, buttressed, and tied back walls. All these types have two elements in common; namely, the stem and the base. The cost of a retaining wall depends primarily on its material, and secondarily on excavation and backfill works. In this study, a new model is implemented in MATLAB to create the optimal design of the cantilever retaining wall elements. The design model is coupled with the shuffled complex evolution algorithm, developed at the University of Arizona (SCE-UA). This developed framework is applied to an existing model previously used by other researchers to demonstrate its efficiency and obtain the best economical solution. The results proved that using the SCE-UA method provides superior outcomes compared to those of other algorithms.

Introduction

In irrigation canals, there are several constructions such as barrages, culverts, syphons, and aqueducts. It is highly required to build upstream and downstream wing walls for all of these constructions to reduce water head loss. Moreover, an abutment is needed to carry the bridge constructed on a water stream. Abutments are kind of retaining walls designed and constructed to resist the lateral pressure of soil and transfer the bridge reaction to the base (Shenouda et al., 2018). Besides, similar to retaining walls, the wing walls are usually designed structurally (Bowles, 1988). Therefore, the most important problem to solve is the minimization of the cost of the retaining wall structures.

There are four types of retaining walls: (i) gravity walls, which rely on the mass of the structure to resist overturning (Younan, 1986). These walls are characterized by their great practicality of production (Günday, 2021). (ii) cantilever walls, rely on the bending strength of the cantilevered slab above the base (Younan, 1986). Such walls are commonly used to support soil, coal, ore piles, and water (Ghazavi & Bonab, 2011). Generally, cantilever walls are constructed of reinforced concrete for heights up to about 7–10 m. Above these heights, counterfort walls are typically more economical (Hazra & Patra, 2008). Additionally, buttressed walls economize their design (García et al., 2020). (iii) counterfort walls, are restrained from overturning by the force exerted by the mass of earth behind the wall (Younan, 1986). (iv) buttressed walls, transmit their thrust to the soil throw buttresses projection from the front of the wall (Younan, 1986). This type can not be used as a wing wall because it will impede the flow of water and cause an increase in water head loss. Therefore, retaining walls may be designed by using gravity, cantilevered, buttressed, and cellular types (Wei & Zhou, 2004).

In general, for the design of any type of retaining wall, an engineer must know the basic parameter of the unit weight, angle of friction, and cohesion of the soil retained behind the wall and the soil below the base slab (Das & Sivakugan, 2018). Knowing the properties of the soil behind the wall enables the engineer to determine the lateral pressure distribution that has to be designed for (Das & Sivakugan, 2018). Consequently, an engineer must assume some of their dimensions. Such assumptions, proportioning, allow the engineer to check trial sections of the walls for stability. If the stability checks yield undesirable results, the sections can be changed and rechecked (Das & Sivakugan, 2018). There are two phases in the design of a conventional retaining wall. In the first phase, with the known lateral earth pressure, the structure as a whole is checked for stability. Then, it is examined for possible overturning, sliding, and bearing capacity failures. In the second phase, each component of the structure is checked for strength, and the steel reinforcement of each component is determined (Das & Sivakugan, 2018). Naturally, this takes much time and effort. Therefore, the algorithms are used to address this issue and come to the optimal solution in terms of cost and design.

Due to the importance of wing walls and their impact on their surroundings, Sarıbaş and Erbatur (1996) presented a detailed study, a prepared computer program (RETOPT), on the optimum design of reinforced concrete cantilever retaining walls using the cost and weight of walls as objective functions. However, the increment value was too small and as a result the variables contain decimals up to thousandths which is not applicable in any site. Later, an application of a simulated annealing (SA) algorithm was proposed for the minimum cost design of reinforced concrete retaining structures where the optimum walls showed a good parabolic correlation (Ceranic et al., 2001) and (Yepes et al., 2008). Another methodology was presented to find the optimal design of concrete retaining wall using Ant Colony Optimization (ACO) algorithm (Ghazavi & Bonab, 2011) where they neglected the cost of secondary steel. Thus, an attempt was undertaken using three heuristic optimization algorithms for automatic design and cost minimization of reinforced cantilever retaining walls (Pei & Xia, 2012). However, the inclined backfill surface should be considered. The seismic response of the retaining walls was investigated using the well-known Mononobe-Okabe analysis method to define the dynamic lateral earth pressure (Kaveh et al., 2013).

It is observed that the charged system search (CSS) method is quite robust and efficient for optimal design of cantilever retaining wall (Kaveh & Behnam, 2013). Contrary to expectation, the increase of the vertical component of the earthquake had a reverse effect on the design of the retaining walls (Kaveh & Khayatazad, 2014). Sheikholeslami et al. (2014) developed a novel optimization method; namely, a hybrid firefly algorithm with a harmony search technique (IFA–HS), to obtain the optimal cost of the reinforced concrete retaining walls satisfying the stability criteria. Besides, the optimal design of retaining walls was achieved by utilizing improved harmony search (HIS), colliding bodies optimization (CBO), and democratic PSO (DPSO) under static and dynamic loading conditions (Kaveh & Soleimani, 2015). Temür et al. (2018) compared between teaching learning based optimization (TLBO), biogeography-based optimization algorithm (BBO), and grey wolf optimizer (GWO) to optimize the cantilever retaining walls. According to the results, the best method for minimizing the objective function is TLBO. Moreover, the particle swarm optimization PSO algorithm was successful in finding the optimum solutions rapidly and consistently in all design cases (Moayyeri et al., 2019). Kalemci et al. (2020) showed that the gray walf optimization (GWO) algorithm is a competitive optimization method for an RC cantilever retaining wall with the shear key design. Another algorithm called Plasma Generation Optimization (PGO), indicated the superiority of the PGO algorithm for the optimal design of reinforced concrete cantilever retaining wall structures (Kaveh et al., 2021). According to the numerical investigations, recent algorithms such as TLBO, FPA, and JA are generally the best at finding the optimum values with the least deviation (Yücel et al., 2021).

Cantilever type retaining walls, which retain earth by a wall cantilevering up from a footing, are the most common type of retaining walls in use today. They are classified as “yielding” due to their ability to rotate freely (about the foundation) as a result of the lack of any lateral restraint. Cantilevered retaining walls are generally made of masonry or concrete, or both (Brooks & Nielsen, 2010).

The previous studies have shown the importance of an accurate design of cantilever retaining walls (CRW). The present study describes a methodology for the optimal design of CRW, where the design model is coupled with a shuffled complex evolution algorithm, which has never been used in the field of structural design of CRW.

Materials and methods

Optimization simulation technique

The simulation–optimization technique is developed to obtain the nearest optimum design of CRW. The cost of CRW is estimated based on 8 variables using the simulation model. The SCE-UA is used to optimize the 8 parameters for the minimum cost. Both the simulation and SCE-UA are integrated into one framework as illustrated in Fig. 1.

Fig. 1

Flowchart of the proposed optimization model to minimize the cost of cantilever retaining walls

Cantilever retaining walls design model

The main elements of a cantilever retaining wall are the base, i.e., toe and heel, and the stem. The stem of the retaining wall must be capable of withstanding the earth pressure applied to it. The active earth pressure coefficient is calculated using Rankine’s earth-pressure theory for a vertical back face of wall and can be calculated using Eq. (1). The base of the retaining wall, i.e. the toe and the heel, must be capable of supporting both weight of the stem and the force resulting from the earth pressure acting upon it without (i) overturning or soil failure, (ii) sliding of the whole construction, (iii) undue settlement (Younan, 1986).

$${K}_{a}={\text{cos}}\beta \frac{{\text{cos}}\beta -\sqrt{{{\text{cos}}}^{2}\beta -{{\text{cos}}}^{2}\phi }}{{\text{cos}}\beta +\sqrt{{{\text{cos}}}^{2}\beta -{{\text{cos}}}^{2}\phi }}$$

(1)

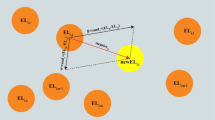
Consider the retaining shown in Fig. 2 with the height of ${h}_{wall}$, top width of the stem,${b}_{T}$, bottom width of the stem, ${b}_{stem}$, the thickness of base, ${h}_{base}$, main reinforcement of stem,${A}_{swall}$, secondary reinforcement of stem, ${{A}^{\mathrm{^{\prime}}}}_{swall}$, top reinforcement of the base,${A}_{sT}$, bottom reinforcement of the base,${A}_{sB}$, shrinkage steel area,${{A}^{\mathrm{^{\prime}}}}_{s}$, the height of soil in front of the wall,$D$, the inclined angle of the soil,$\beta$, the angle of repose of the soil,$\phi$, the specific weight of soil,$\gamma$, the cohesion, the angle of repose and the specific weight of soil underneath the base,${c}^{\mathrm{^{\prime}}}$, ${\phi }^{\mathrm{^{\prime}}}$ and${\gamma }^{\mathrm{^{\prime}}}$, respectively.

Fig. 2

Retaining wall cross section

Description of the structural design for cantilever retaining walls elements

Description of the stem design technique

For designing the stem, its top width, bottom width, and main area steel should be determined. The stem is subjected to lateral loads only. The lateral load comes from earth pressure and can be calculated using Eq. (2).

$${P}_{astem}=\sum_{f=1}^{2}{P}_{f}{\text{cos}}\beta$$

(2)

where ${P}_{f}$ is the horizontal earth Force (kN), $f$ is the lateral load number, and ${P}_{astem}$ is the horizontal component of the active earth pressure acting on the stem (kN), ${P}_{astem}$ should be less than both of the allowable shear force, ${V}_{a}$, Eq. (3) and the allowable shear friction ${V}_{n}$, (Eq. 4); Shear friction is governed by ACI 318- Art. 11–7-5 with a 55 percent reduction for using the alternative design method use $\phi =0.85$ in Eq. 4 (ACI Committee 318, 1992) and (Bowles, 1988).

$${V}_{a}=({b}_{stem}-0.07)\times \frac{\sqrt{{{f}_{c}}^{\mathrm{^{\prime}}}}}{11}\times 1000$$

(3)

$${V}_{n}=0.55\times (0.2\phi {{f}_{c}}^{\mathrm{^{\prime}}}\times {b}_{stem})/1000$$

(4)

where ${{f}_{c}}^{\mathrm{^{\prime}}}$ is the compressive strength of concrete (MPa), the unit is kN for ${V}_{a}$ and ${V}_{n}$, and meter for ${b}_{stem}$.

To determine the main steel quantity, the moment about critical section shown in Fig. 3 (${M}_{stem}$), (kNm) should be determined using Eq. (5). Stem main steel is on the backfill side of wall (Bowles, 1988). The main area of steel, ${A}_{swall}$, can be calculated using Eq. (6) and it should be more than ${A}_{s{\text{min}}w}$ Eq. (7). Since the stem face is exposed, it is required to place temperature and shrinkage (T and S) of steel bars perpendicularly on the main steel (Bowles, 1988), which is neglected in the comparative model and thus not considered.

$${M}_{stem}=\sum_{f=1}^{2}{P}_{f}\times {y}_{f}\times {\text{cos}}\beta$$

(5)

$${A}_{swall}=\frac{{M}_{stem}}{j\times {f}_{s}\times ({b}_{stem}-0.07)}$$

(6)

$${A}_{s{\text{min}}w}=\frac{1.4}{{f}_{y}}\times {b}_{stem}$$

(7)

where ${M}_{stem}$ unit is kNm, $j=0.880$, ${f}_{s}=\mathrm{170,000 }kPa$ and ${f}_{y}=400MPa$ (Bowles, 1988).

Fig. 3

Details of the stem

Description of the base design technique

A retaining wall may fail in any of the following ways: (i) it may overturn about its toe, (ii) it may slide along its-base, (iii) it may fail due to the loss of bearing capacity of the soil supporting the base, (iv) it may undergo deep-seated shear failure, (v) it may go through excessive settlement (Das & Sivakugan, 2018). This paper illustrates the method of analyzing a retaining wall for overturning, sliding stability, and bearing capacity failure only. The paper focuses on water retaining structures such as abutments and wing walls, which shall be designed to be safe against overturning about the toe of the footing, against sliding on the base, and for bearing capacity (Chikute & Sonar, 2019). All of these are required to determine the base height,${h}_{base}$, width, ${b}_{fl}$, top reinforcement,${A}_{sT}$, and bottom reinforcement,$A{}_{sB}{}^{ }$.

Check against overturning

Figure 4 shows the forces acting on a cantilever retaining wall based on the assumption that the Rankine active pressure is acting along a vertical plane AB drawn through the heel of the structure. ${P}_{p}$ is the Rankine passive pressure which can be calculated using Eq. (8).

$${P}_{p}=\frac{1}{2}\times {K}_{p}\times {\gamma }^{\mathrm{^{\prime}}}\times {D}^{2}+2{c}^{\mathrm{^{\prime}}}\sqrt{{K}_{p}}\times D$$

(8)

where ${K}_{p}$ is Rankine passive earth pressure coefficient which can be calculated using Eq. (9) as shown in Fig. 2.

Fig. 4

Check for overturning, assuming that the Rankine pressure is valid

$${K}_{p}=\frac{1+{\text{sin}}{\phi }^{\mathrm{^{\prime}}}}{1-{\text{sin}}{\phi }^{\mathrm{^{\prime}}}}$$

(9)

Firstly, The factor of safety against overturning, $F{S}_{ov}$, about point O, in Fig. 4 may be calculated using Eq. (10) and should be more than 1.5.

$$F{S}_{ov}=\frac{{M}_{R}}{{M}_{o}}$$

(10)

where ${M}_{o}$ is the moment results from forces tending to overturn about point O, which can be calculated using Eq. (11), and ${M}_{R}$ is the moment results from forces tending to resist overturning about point O, which can be calculated using Eq. (12)

$${M}_{o}=\sum_{j=1}^{2}{P}_{aj}\times {\text{cos}}\beta \times {Y}_{j}$$

(11)

$${M}_{R}=\sum_{i=1}^{5}{W}_{i}\times {X}_{i}+\sum_{j=1}^{2}{P}_{aj}\times {\text{sin}}\beta \times \left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)+{P}_{p}\times {Y}_{p}$$

(12)

where ${P}_{aj}$ is the active earth pressure acting on the wall, ${Y}_{j}$ is the vertical length between the active earth pressure and the lower level of the base, ${W}_{i}$ is the soil and wall weights,${X}_{i}$, ${b}_{heel}$, ${b}_{Toe}$ and ${Y}_{p}$ are all illustrated in Fig. 4.

Secondly, the location of the resultant summation of vertical load on the base, $\sum_{i=1}^{5}{W}_{i}$, must be inside the middle third of the base width. This is achieved when the eccentricity, $e$, is less than one sixth of the base width and the value of $\overline{X}$ is more than one third of the base width. The value of $\overline{X}$ and the eccentricity can be calculated using Eqs. (13) and (14), respectively.

$$\overline{X}=\frac{{M}_{R}-{M}_{o}}{\sum_{i=1}^{7}{W}_{i}}$$

(13)

$$e=\frac{\left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)}{2}- \overline{X}$$

(14)

Check for sliding along the base

For a wall to be safe against sliding, the factor of safety ($F{S}_{SL}$) must be greater than 1.5 which can be expressed by Eq. (15).

$$F{S}_{SL}=\frac{{F}_{R}}{\sum_{j=1}^{2}{P}_{aj}\times {\text{cos}}\beta }$$

(15)

where ${F}_{R}$ is the resistance force and can be calculated using Eq. (16)

$${F}_{R}=\sum_{i=1}^{5}{W}_{i}\times {\text{tan}}\left(\frac{2}{3}\times {\phi }^{\mathrm{^{\prime}}}\right)+{B}^{\mathrm{^{\prime}}}\times {c}^{\mathrm{^{\prime}}}+{P}_{p}$$

(16)

where ${B}^{\mathrm{^{\prime}}}$, the effective width of floor, $=\left({b}_{heel}+{b}_{stem}+{b}_{Toe}-2e\right)$

Check for bearing capacity failure

The vertical pressure transmitted to the soil by the base slab of the retaining wall should be checked against the ultimate bearing capacity of the soil (Das & Sivakugan, 2018). The shape of the vertical pressure transmitted by the base slab into the soil is shown in Fig. 4. The values of ${q}_{Toe}$ and ${q}_{heel}$ can be calculated using Eqs. (17) and (18).

$${q}_{Toe}={q}_{{\text{max}}}=\frac{\sum_{i=1}^{5}{W}_{i}}{\left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)}\times \left(1+\frac{6e}{\left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)}\right)$$

(17)

$${q}_{heel}={q}_{{\text{min}}}=\frac{\sum_{i=1}^{5}{W}_{i}}{\left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)}\times \left(1-\frac{6e}{\left({b}_{heel}+{b}_{stem}+{b}_{Toe}\right)}\right)$$

(18)

The value of ${q}_{Toe}$ should not exceed one-third of the ultimate capacity of the soil, ${q}_{u}$, which can be calculated using Eq. (19) (Meyerhof, 1963).

$${q}_{u}={c}^{\mathrm{^{\prime}}}{N}_{c}{F}_{cd}{F}_{ci}+q{N}_{q}{F}_{qd}{F}_{qi}+\frac{1}{2}{\gamma }^{\mathrm{^{\prime}}}{B}^{\mathrm{^{\prime}}}{N}_{\gamma }{F}_{\gamma d}{F}_{\gamma i}$$

(19)

where:

$q$ = effective stress at the level of the bottom of the foundation $={\gamma }^{\mathrm{^{\prime}}}D$

${F}_{cd}$, ${F}_{qd}$, ${F}_{\gamma d}$= depth factors and can be calculated using the following equations (Hansen, 1970):

$${F}_{cd}=1+0.4\frac{D}{{B}^{\mathrm{^{\prime}}}} {F}_{qd}=1+2{\text{tan}}{\phi }^{\mathrm{^{\prime}}}(1-{\text{sin}}{\phi }^{\mathrm{^{\prime}}})\frac{D}{{B}^{\mathrm{^{\prime}}}} { F}_{\gamma d}=1$$

${F}_{ci}$, ${F}_{qi}$, ${F}_{\gamma i}$= Load inclination factors and can be calculated using the following equations (Hanna & Meyerhof, 1980):

${N}_{c}$, ${N}_{q}$, ${N}_{\gamma }$= soil bearing capacity factors. ${N}_{c}$ was originally derived by (Prandtl (1921), ${N}_{q}$ was presented by Reissner (1924), Caquot and Kerisel (1953), and Vesić (1973) gave the relation for ${N}_{\gamma }$ as the following equations:

$${N}_{q}={{\text{tan}}}^{2}\left(45+\frac{{\phi }^{\mathrm{^{\prime}}}}{2}\right){e}^{\pi {\text{tan}}{\phi }^{\mathrm{^{\prime}}}} {N}_{c}=\left({N}_{q}-1\right){\text{cot}}{\phi }^{\mathrm{^{\prime}}} {N}_{\gamma }=2({N}_{q}+1){\text{tan}}{\phi }^{\mathrm{^{\prime}}}$$

The most important check, after the previous three checks, is the check of shear force at the two faces of the stem as illustrated in Fig. 5, i.e. the toe face,${f}_{1}=\left|{f}_{Toe}-{W}_{4}\right|$, (Eq. 20) and the heel one, ${f}_{2}=\left|\sum_{i=1}^{3}{W}_{i}-{f}_{heel}\right|$ (Eq. 21). They should be less than the allowable concrete force of the floor, ${V}_{c}$(Eq. 22).

$${f}_{Toe}=\left[\left(\left(\frac{{b}_{heel}+{b}_{stem}}{{b}_{heel}+{b}_{stem}+{b}_{Toe}}\right)\times \left({q}_{Toe}-{q}_{heel}\right)\right)+{q}_{heel}+{q}_{Toe}\right]\times {b}_{Toe}/2$$

(20)

$${f}_{heel}=\left[\left(\left(\frac{{b}_{heel}}{{b}_{heel}+{b}_{stem}+{b}_{Toe}}\right)\times \left({q}_{Toe}-{q}_{heel}\right)\right)+2{q}_{heel}\right]\times {b}_{heel}/2$$

(21)

$${V}_{c}=({h}_{base}-0.07)\times \frac{\sqrt{{{f}_{c}}^{\mathrm{^{\prime}}}}}{11}\times 1000$$

(22)

where ${{f}_{c}}^{\mathrm{^{\prime}}}$ is the compressive strength of concrete (MPa), the unit of ${V}_{c}$, ${f}_{Toe}$, ${f}_{heel}$ is kN and the rest of dimension parameters are in meters.

Fig. 5

Check for the shear strength of concrete

To determine the top and bottom reinforcement, the moments at critical section shown in Fig. 5 (${M}_{TOP}$,${M}_{BOT}$), (kNm) should be determined using Eqs. (23) and (24). The bottom steel is on the toe side and the top steel is on the heel one. The top reinforcement, ${A}_{sT}$ and bottom one, ${A}_{sB}$ can be calculated using Eqs. (25) and (26), respectively. Moreover, each of them should be more than ${A}_{s{\text{min}}B}$ Eq. (27).

$${M}_{TOP}=\sum_{i=1}^{2}{W}_{i}\times {x}_{i}+{b}_{heel}^{2}\times {h}_{base}\times {\gamma }_{RC}\times \frac{1}{2}-{f}_{heel}\times {x}_{heel}$$

(23)

$${M}_{BOT}={f}_{Toe}\times {x}_{Toe}-{b}_{Toe}^{2}\times {h}_{base}\times {\gamma }_{RC}\times \frac{1}{2}$$

(24)

$${A}_{sT}=\frac{{M}_{TOP}}{j\times {f}_{s}\times ({h}_{base}-0.07)}$$

(25)

$${A}_{sB}=\frac{{M}_{BOT}}{j\times {f}_{s}\times ({h}_{base}-0.07)}$$

(26)

$${A}_{s{\text{min}}B}=\frac{1.4}{{f}_{y}}\times {h}_{base}$$

(27)

where ${M}_{stem}$ unit is kNm, $j=0.880$, ${f}_{s}=\mathrm{170,000}kPa$ and ${f}_{y}=400MPa$ (Bowles, 1988).

SCE-UA algorithm

The shuffled complex evolution – University of Arizona (SCE-UA) method is a general purpose universal optimization evolutionary programming technique that connects the strengths of the simplex procedure with the concepts of controlled random search, competitive evolution, and complex shuffling (Qingyun Duan et al., 1992).

Synthesizing these concepts creates not only an effectual and robust but also a further responsive and adept SCE-UA algorithm. The use of deterministic plots of the SCE-UA algorithm allows direct utilization of response surface information to guide the search. The durability and flexibility are constituted apiece use of random elements. The inherent clustering approach guides to ultimate promising zone of the search space. In addition, the use of the systematic complex purpose helps to guarantee a relatively strong search that is guided by the structure of the objective function (Qingyun Duan et al., 1992).

The SCE-UA technique has been successfully put in an application of conceptual rainfall-runoff models and proved to be a cost-efficient and effective technique, which performed consistently in all test functions and can be construed as a guideline for most applications (QY Duan et al., 1993). Additionally, the technique was found to surpass other optimization algorithms due to its use of multiple complexes rather than a single simplex, especially when the level of parameterization is increased (Thyer et al., 1999). In addition, the SCE algorithm is well suited to address water supply network and infrastructures problems (AWAD et al., 2003; Nunoo & Mrawira, 2004), (Nunoo & Mrawira, 2004). It is used in optimizing management models in the hydrogeology field such as the configuration of groundwater resources as well as the prevention and management of groundwater contamination (Wu & Zhu, 2006). Moreover, the SCE algorithm is adopted for optimizing reservoir operations, where the results show that the SCE algorithm is an efficient tool for optimizing complex systems (Le Ngo et al., 2007). Through computational studies employing well-known examples from literature, the effectiveness of the SCE applied to the reduced multidimensional knapsack issue is confirmed. The method worked well in locating solutions that required little processing time and were close to ideality (M. Daniel Valadão Baroni & F. M. Varejão, 2016). Using SCE technique in the topic of biomass waste pyrolysis, which shows that the optimized kinetic parameters estimated by the SCE algorithm, is potentially promising in evaluating the biomass waste pyrolysis (Liu et al., 2020). Coupled SCE method with a multi-layer perceptron (MLP) to estimate the dissolved oxygen (DO) using the data of the Klamath River Station, Oregon, US, accomplished this task by simpler configurations and can be satisfactorily used for future applications (Moayedi & Mosavi, 2021). Finally, to verify the effectiveness of the proposed SCE based controller, several well-known algorithms have been tested under various operating conditions. The results confirm the superiority of the proposed SCE algorithm among the competing algorithms (Hachana et al., 2022).

However, this algorithm has never been implemented in the field of structural design of CRW. Hence, the current study is considered to be the first attempt in this direction.

Objective function, constraints, variables and SCE-UA formulation

In this study, a Cantilever Retaining Wall (CRW) model implemented is utilized in MATLAB to design all CRW elements. The model follows the previously mentioned descriptions.

The objective function minimizes the total cost of the CRW elements where

$$minimize\to Cos{t}_{CRW}=\sum_{j=1}^{4}V{E}_{j}\times C{E}_{j}$$

(28)

where $Cos{t}_{CRW}$ is the total cost of the CRW elements ($) with $j$ elements, which are the stem, its main steel area, the base, its top and bottom steel area, $V{E}_{j}$ is the volume of the element (m³), and $C{E}_{j}$ is the cost of unit volume of the element ($/m³).

The constraints, tabulated with their limits in Table 1, are listed as follows: (1) the horizontal component of the active earth pressure acting on the stem, ${P}_{astem}$ Eq. (2), should be less than both of the allowable shear force,${V}_{a}$, Eq. (3) and the allowable shear friction,${V}_{n}$, Eq. (4). (2) The main area steel of stem,${A}_{swall}$, Eq. (6) should be more than ${A}_{s{\text{min}}w}$ Eq. (7). (3) The factor of safety against overturning,$F{S}_{ov}$, Eq. (10) should be more than 2. (4) The location of the resultant summation of vertical load on the base, $\sum_{i=1}^{5}{W}_{i}$, must be inside the middle third of the base width. (5) The factor of safety against sliding,$F{S}_{SL}$, Eq. (15) must be greater than 1.5. (6) The value of ${q}_{Toe}$ Eq. (17) should be less than one-third of the ultimate capacity of the soil,${q}_{u}$, Eq. (19). (7) The shear forces,${f}_{Toe}-{W}_{4}$, (Eq. 20) and $\sum_{i=1}^{3}{W}_{i}-{f}_{heel}$ Eq. (21) as shown in Fig. 5 should be less than the allowable concrete force of the floor, ${V}_{c}$ Eq. (22). (8) The top and bottom reinforcement of the base,${A}_{sT}$, ${A}_{sB}$ should be more than ${A}_{s{\text{min}}B}$ Eq. ( 27).

Table 1 Details of constraints

The penalty function is used based on the magnitude of error in meeting the constraints. The eight variables are limited by their lower and upper limits as tabulated in Table 2. The overall procedure is outlined above, containing the SCE-UA algorithm and the model of the CRW. This procedure is coded into MATLAB.

Table 2 Details of variables

Case study

The case study is a retaining wall studied by Ghazavi and Bonab (2011). The height of stem, ${h}_{wall}$ is 4.50m, the top width of the stem, ${b}_{T}$ is 0.25m, the bottom width of the stem, ${b}_{stem}$ is 0.251m, the main reinforcement of stem, ${A}_{swall}$ is 59 cm²/m, the thickness of base, ${h}_{base}$ is 0.40m, the width of the floor at the toe part,${b}_{Toe}$ is 1.143m, the width of the floor at the heel part, ${b}_{heel}$ is 1.385m, the top reinforcement of the base, ${A}_{sT}$ and the bottom reinforcement of the base, ${A}_{sB}$ are all equal to 14 cm²/m, the height of soil in front of the wall, ${h}_{p}$ is 0.75m, the inclined angle of the soil, $\beta$ is 15°, the angle of repose of the soil,$\phi$ is 36°, the specific weight of soil, $\gamma$ is 17.50 kN/m³, and for the soil underneath the base, the cohesion, ${c}^{\mathrm{^{\prime}}}$, is 100kPa, the angle of repose, ${\phi }^{\mathrm{^{\prime}}}$, is 34° and the specific weight, ${\gamma }^{\mathrm{^{\prime}}}$, is 17.50 kN/m³. In order to clarify all the information about the case study, all the data have been placed in Table 3.

Table 3 Input parameters

Results and discussion

In the model, i.e., the newly developed CRW model, there are 8 variables to be optimized (${n}_{opt}=8$). In the SCE-UA, after several initial runs, the number of complexes is selected to be 2. The remaining values are selected based on their equations as follows:

The number of complex populations is ($m=2{n}_{opt}+1=17$) and the number of sub-complex populations is ($q={n}_{opt}+1=9$).

SCE-UA is applied to minimize the objective function of Eq. (28). The number of function evaluation is not fixed for all generations. The number of function evaluations also corresponds to the best solution obtained from any generation in CRW model. The optimal value of the objective function through the relation between generation number,$ng$, and the total cost of the CRW for every number of complexes, $nc$, is shown in Fig. 6. In general, it is obviously seen that for the smaller the $nc$, the more difficult it is to reach the objective function, i.e., the minimum total cost. For more clarification, where $nc=1$, the model reaches the minimum total cost at generation number, $ng$, equals to 14,118. Where $nc=2$, the model reaches it at $ng=5791$, where $nc=10$, the generation number is 1880. However, where $nc=90$, the model reaches the minimum total cost at generation number equal to 1385. Figure 7 shows that where $nc=$ 30, 40 and 50, the model reaches the minimum cost at $ng=$ 6624, 3044 and 2425, respectively. Nonetheless, $ng$ fluctuated from 1880 to 6624 where $nc=$ 2, 10 and 20. Talking about saving time, $nc=60$ showed the minimum time for reaching the minimum cost, i.e. in 26 s. It is noteworthy that the maximum time for the model to reach the optimal solution is 360 s where $nc=100$ (Figure 8).

Fig. 6

The relation between Objective function and generation number for every number of complexes

Fig. 7

The relation between number of complexes and generation number

Fig. 8

The relation between number of complexes and time

The number of complexes is set to 60 and the number of generations is set to 235, bearing in mind that any increase in the number of generations will not improve the optimum solution. The number of function evaluation in these generations is 870,413 (Fig. 9).

Fig. 9

The relation between number of complexes and total population

The newly developed CRW model using the SCE-UA technique is applied to the case study. Tables 4, 5, and 6 illustrate that the model nearing optimal solution are itemized as follows:

• i. The optimal top width of the stem (${b}_{T}$) is equal to 0.30 m and the bottom width of the stem (${b}_{stem}$) is equal to 0.60 m (Table 5). These values are attributed to the limited values of the horizontal component of the active earth pressure acting on the stem,${P}_{astem}$, Eq. (2), the allowable shear force,${V}_{a}$, Eq. (3) (Table 4), and the allowable shear friction${V}_{n}$, Eq. (4) (Table 4). In comparison to (Ghazavi and Bonab (2011) study, the value of the top width of the stem (${b}_{T}$) in the present study is slightly bigger than this value for (Ghazavi and Bonab (2011); In contrast, the value of bottom width of the stem (${b}_{stem}$) is equal to about two and a half times the this value for (Ghazavi and Bonab (2011).

• ii. The main wall reinforcement, ${A}_{swall}$, is equal to 21.75 cm² Eq. (6) (Table 5). This value is more than ${A}_{s{\text{min}}w}$ Eq. (7) (Table 4). This value is much less than (Ghazavi and Bonab (2011) value, the main wall reinforcement in the present study is much less, as it is equal to 36% of (Ghazavi and Bonab (2011) value. This is the main reason for the cost difference between them (Table 6).

• iii. The optimal values of ${b}_{Toe}$ and ${b}_{heel}$ are 0.70m for each. They are less than those in (Ghazavi and Bonab (2011) model (Table 5). The selection of dimension affecting the value and location of the resultant summation of vertical load on the base which, in turn, affects each of the following: (1) the factor of safety against overturning Eqs. (10), (2) the factor of safety against sliding Eq. (15). They are equal to 1.7278 and 6.8792, respectively. They achieved values above 1.5 each as required, (Table 4), (3) the relative between ${q}_{Toe}$ Eq. (17) and ${q}_{u}$ Eq. (19) equals to 0.0316, achieving values less than one-third as required (Table 4), (4) shear force at the two faces of the stem Fig. 5 (Table 4), i.e. the toe face, ${f}_{1}=\left|{f}_{Toe}-{W}_{4}\right|$, Eq. (20) and the heel one, ${f}_{2}=\left|\sum_{i=1}^{3}{W}_{i}-{f}_{heel}\right|$ Eq. (21) are equal to 3.5749kN and 2.0846kN, respectively, achieving the values less than the allowable concrete force of the floor, ${V}_{c}$ Eq. (22) (Table 4). The large conflict in designing the CRW is the total weight coming from the super structure ($\sum_{i=1}^{5}{W}_{i}$), that leads to (1) increasing the resistance force, ${F}_{R}$, Eq. (16), which raises the factor of safety against overturning, $F{S}_{ov}$ and sliding, $F{S}_{SL}$, Eqs. (10, 12, and 15), and (2) increases the pressure transmitted by the base slab into the soil, ${q}_{Toe}$ and ${q}_{heel}$ (Eqs. (17) and (18), which must be less than one third of the ultimate bearing capacity of the soil,${q}_{u}$ Eq. (19).

• iv. The values of top reinforcement, ${A}_{sT}$ and bottom one, ${A}_{sB}$ are equal to 17.90 cm² and 19.00 cm², respectively, Eqs. (25 and 26) Tables 4 and 5). They are greater than the minimum reinforcement ${A}_{s{\text{min}}B}$ Eq. (27) (Table 4). Although the values of top bottom reinforcement in the current study are higher than the values in the study of Ghazavi and Bonab (2011), the cost of reinforcement in the current study is lower than that in the study of Ghazavi and Bonab (2011), because the length of reinforcement in the present study is less than the length of reinforcement in (Ghazavi and Bonab (2011) study. This length of top and bottom reinforcement is the floor length (${b}_{fl}$) and can be calculated from the summation of ${b}_{stem}$, ${b}_{Toe}$ and ${b}_{heel}$. The length of floor equals to 2.00m and 2.771m in the present study and (Ghazavi and Bonab (2011) study, respectively (Table 7).

Table 4 Output set of constraints

Table 5 Output of variables

Table 6 A comparative study for the cross-sectional area of the retaining wall

Table 7 A comparative study for the reinforcement volume of the retaining wall

Considering the chosen design elements, the optimal cost (objective function) decreases from 201.185 $ in the Ghazavi and Bonab (2011) model to 165.293 $ in the present model. In other words, the cost for the optimal solution using the Ant Colony (AC) Optimization method was 21.70% more than that in SCE-UA method (Table 8).

Table 8 A comparative study for the Output of objective function

Figure 10a and b show the impact of the CRW's elements on the total cost of the AC and SCE-UA methods. It could be easily identified that for both of the techniques, the stem had the greatest proportion of cost (≈67%), followed by the floor (≈33%). Further analyzing these figures, one could notice that the cost of the stem without reinforcement for SCE-UA method (81$) approaches the cost of floor reinforcement for AC method (85$). Furthermore, the cost of top and bottom reinforcement of the floor for the two models is very close (23.8$ for AC and 21.55$ for SCE-UA), while the rest of costs of AC are much higher from the costs of SCE-UA.

Fig. 10

Impact of the cost of each CRW element (Absolute and Percentage)

The above analysis shows that the cost of the optimal solution using SCE-UA methodology is less than that with an AC methodology, mainly because of the reduction in stem reinforcement cost.

Conclusions

This research presents the applicability of designing cantilever retaining walls (CRW) using shuffled complex evolution algorithm, developed at the University of Arizona (SCE-UA). A comparison is drawn between SCE-UA and Ant Colony (AC) Optimization algorithms to determine the optimum cantilever retaining wall design criteria. Moreover, this comparison illustrates in full detail how the model works and its relation to the SCE-UA algorithm.

For the CRW used in the present study, a significant change of stem reinforcement could be achieved. Comparing both algorithms, the SCE-UA showed better results over the AC method in the form of lower optimal cost (objective function). The cost for the optimal solution using SCE-UA method was 21.70% less than that in the Ant Colony (AC) Optimization method. The SCE-UA provided good solutions for the studied case.

In conclusion, the developed framework can assist decision-makers in selecting the optimal methodology for designing cantilever retaining walls.