Introduction

In construction project management, optimization is of paramount importance as it facilitates the identification of the most efficient plan and schedule to ensure project completion. Efficiently solving time and cost optimization problems can provide construction companies with a competitive advantage (Chen & Weng, 2009). One type of time–cost optimization is the Pareto front problem, which aims to obtain an optimal solution by minimizing both cost and time simultaneously. Alternatively, a simpler approach to solving time–cost trade-offs may involve finding the minimum project duration or project cost separately. Time optimization aims to identify feasible methods to reduce the project duration without exceeding the revenue generated by early project completion, while cost optimization aims to minimize the overall project cost.

Evolutionary algorithms have become increasingly popular for solving optimization problems across various research fields (Boussaïd et al., 2013). Kaveh and Laknejadi (2011) developed a novel Pareto optimization model based on particle swarm optimization (PSO), while their work in Kaveh and Laknejadi (2013) proposed a new version of the memetic Pareto archive evolution strategy for truss structure layout optimization. Kaveh and Mahdavi (2019) developed a multi-criteria approach based on colliding bodies optimization for truss design, and Kaveh and Ilchi Ghazaan (2020) presented a vibrating particle system-based technique for multi-criteria optimization analysis. Son and Khoi (2020) introduced a novel metaheuristic technique inspired by the hunting behavior of wild dogs in Africa, while Pham and Nguyen (2023) introduced a hybrid sine cosine model for addressing cement transport vehicle routing. Kaveh (2014) reviewed many recent metaheuristic algorithms in his research work.

MVO was introduced by Mirjalili et al. (2016), which has demonstrated performance that is comparable to or superior to other well-known evolutionary algorithms, including the grey wolf optimizer, gravitational search algorithm, and PSO. By employing MVO, it is possible to balance exploring new solutions and exploiting existing ones, while also avoiding local optimization. Therefore, MVO can serve as a valuable tool for solving optimization problems that involve both single-objective and multi-objective cases. Considering the advantages listed above, it can be concluded that MVO is a suitable meta-heuristic method for resolving TCOP.

The next section provides a summary of the existing literature on balancing time and cost. "Optimization model development" section describes the development process of our proposed approach. The outcomes of the validation and implementation of our model are presented in "Computational experiments" section. The study concludes with a summary of the findings and identifies potential areas for future research in "Conclusion" section.

Literature review

PSO introduced by Elbeltagi et al. (2005) has been found to be more efficient in addressing cost optimization challenges when compared to five other evolutionary-based algorithms. Yang (2007) presented a new version of PSO capable of determining the full set of time–cost Pareto solutions. Zhang and Xing (2010) introduced a fuzzy-based PSO that addresses the multi-objective nature of construction project management. The discrete model of PSO (DPSO) was developed by Aminbakhsh and Sonmez (2016) to manage time–cost constraints for complex projects with numerous activities and constraints. PSO was also used by Aminbakhsh and Sonmez (2017) to find a set of Pareto solutions for large-scale construction projects. Albayrak (2020) proposed a GA-PSO algorithm to address the challenge of balancing project completion time and cost in resource-constrained building projects.

In addition to PSO, the genetic algorithm (GA) is frequently employed as an algorithm for addressing the time–cost efficiency considerations. Hegazy (1999) employs genetic algorithms (GAs) as the basis for solving time–cost balancing problems. Zheng et al. (2005) proposed a multi-objective model based on GA to determine a set of Pareto time–cost solutions. Eshtehardian et al. (2008) presented a hybrid GA for solving the fuzzy version of time–cost optimization. Sonmez and Bettemir (2012) proposed an integrated method based on GA to address time–cost balancing problems. The GA was also utilized by Naseri and Ghasbeh (2018) to analyze time and cost for mitigating the negative effects of project delays.

Ng and Zhang (2008) proposed an algorithm based on ant colony behavior (ACO) as an optimization approach for managing time and cost constraints in construction projects. Afshar et al. (2009) developed a novel algorithm based on ant colony optimization (ACO) to tackle the problem of project time–cost management. Kalhor et al. (2011) introduced a hybrid optimization algorithm based on ACO to deal with uncertain factors in time–cost optimization. The shuffled frog-leaping (SFL) technique was employed by Elbeltagi et al. (2007) to optimize project cost. Ashuri and Tavakolan (2015) proposed an SFL model to overcome the complex issue of achieving optimal time, cost, and resource allocation in project planning. Abdel-Raheem and Khalafallah (2011) proposed an optimization algorithm inspired by the behavior of electrons to address the challenge of cost management. An optimization technique that merges two metaheuristic algorithms was proposed by Kaveh et al. (2015) to allocate resources and tackle the time–cost trade-off problem. Bettemir and Talat Birgönül (2017) employed a network analysis algorithm (NAA) that utilizes the principle of minimum cost-slope to derive optimal or near-optimal solutions for the TCOP. Toğan and Eirgash (2019) proposed a multi-objective optimization algorithm (NDS-TLBO) using the nondominated sorting concept in combination with teaching–learning-based optimization to effectively solve the TCOP. Son and Nguyen Dang (2023) presented a hybrid technique based on the sine cosine algorithm to address the large-scale TCOP.

The TCOP has been extensively investigated using various stochastic optimization approaches, such as PSO, GA, SFL, etc. However, the MVO algorithm has not been frequently utilized in previous studies addressing this problem. This knowledge gap motivated the research team to propose an MVO-based model for tackling the TCOP.

Optimization model development

Multi-verse optimizer

The MVO algorithm was inspired by three fundamental concepts of the multi-verse theory: white holes, black holes, and wormholes. It uses white/black hole tunnels for exploration and wormhole tunnels for exploitation within the search space. The algorithm represents solutions based on universes, in which each variable corresponds to an asteroid within that cosmos. The quality of a universe can be evaluated through its inflation rate, which is calculated using a specific objective function.

The algorithm employs the white/black hole concept to represent the exploration processes. MVO suggests that universes with a higher inflation rate are more likely to generate white holes, while those with a lower inflation rate are more likely to produce black holes. Universes with higher-quality solutions are more likely to emit entities through white holes, while those with lower quality tend to receive more entities via black holes. Additionally, regardless of their inflation rates, all entities within universes may experience stochastic displacements toward the most successful universe through the utilization of wormholes.

The transfer of entities between universes through white/black hole tunnels is represented using a roulette wheel mechanism (RWM), as described by Eq. (2). The occurrence of white holes is determined using this mechanism, which is based on a standardized inflation rate.

Consider that:

$$U=\left[\begin{array}{ccc}\begin{array}{cc}{o}_{1}^{1}& {o}_{1}^{2}\end{array}& \dots & {o}_{1}^{d}\\ \begin{array}{cc}{o}_{2}^{1}& {o}_{2}^{2}\end{array}& \dots & {o}_{2}^{d}\\ \begin{array}{cc}\begin{array}{c}\dots \\ {o}_{n}^{1}\end{array}& \begin{array}{c}\dots \\ {o}_{n}^{2}\end{array}\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}\dots \\ {o}_{n}^{d}\end{array}\end{array}\right]$$
(1)

where d and n are the number of parameters solutions (universes), respectively:

$${o}_{i}^{j}=\left\{\begin{array}{c}{o}_{k}^{j} {\alpha }_{1}<NI\left({U}_{i}\right)\\ {o}_{i}^{j} {\alpha }_{1}\ge NI\left({U}_{i}\right)\end{array}\right.$$
(2)

where \({o}_{i}^{j}\) indicates the jth parameter of ith solution; Ui shows the ith solution, NI(Ui) is the standardized inflation rate of the ith solution; α1 is a random number in the range from 0 to 1; and \({o}_{k}^{j}\) indicates the jth parameter of kth solution chosen by RWM.

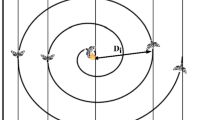
In Fig. 1, objects traveling through wormholes are represented by white points. In the MVO algorithm, the formation of wormhole tunnels between a universe and the best-performing universe established so far is a regular occurrence. The equation that characterizes this mechanism is shown below:

$$o_{i}^{j} = \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {O_{J} + {\text{TDR}} \times \left( {\left( {{\text{ub}}_{j} - {\text{lb}}_{j} } \right) \times \alpha_{4} + {\text{lb}}_{j} } \right) \alpha_{3} < 0.5} \\ {O_{J} - {\text{TDR}} \times \left( {\left( {{\text{ub}}_{j} - {\text{lb}}_{j} } \right) \times \alpha_{4} + {\text{lb}}_{j} } \right) \alpha_{3} \ge 0.5} \\ \end{array} { }\alpha_{2} < {\text{WEP}}} \right.} \\ {o_{i}^{j} \alpha_{2} \ge {\text{WEP}}} \\ \end{array} } \right.$$
(3)

where Oj represents the jth parameter of the best solution formed so far; TDR is traveling distance rate; WEP is wormhole existence probability; lbj and ubj denote the lower and upper bounds of the jth parameter, respectively; \({o}_{i}^{j}\) indicates the jth parameter of ith solution; and α2, α3, α4 present random values that range from 0 to 1.

Fig. 1
figure 1

Conceptual model of the proposed MVO algorithm

Full size image

Figure 2 provides a visualization of the TDR and WEP. TDR determines the rate of displacement of an entity toward the best-performing universe using a wormhole. As shown in Eq. (4), the value of this parameter decreases with each iteration to improve the accuracy of local search and exploration in the vicinity of the current best universe in the MVO algorithm. On the other hand, the WEP parameter regulates the probability of wormhole existence in the universe. It increases linearly with each iteration, as shown in Eq. (5).

$$\mathrm{TDR}=1-\frac{{l}^{1/p}}{{L}^{1/p}}$$
(4)
$$\mathrm{WEP}=\mathrm{min}+l\times \left( \frac{\mathrm{max}-\mathrm{min}}{L}\right)$$
(5)

where p = 6 intensity of exploitation over the iterations; l and L represent the current and maximum iteration numbers; the values of min and max, which are 0.2 and 1, respectively.

Fig. 2
figure 2

Relationship between WEP and TDR

Full size image

Proposed model for TCOP

Each construction activity can be performed in several manners, taking into consideration the resources, technology, and equipment employed. Each operational choice is characterized by a distinct time and cost attributed to it. The primary aim of balancing time and cost, which is typically referred to as minimizing the overall project cost, can be expressed as follows:

$$\mathrm{PC}={\mathrm{SC}}_{\mathrm{dc}}+{\mathrm{SC}}_{\mathrm{ic}}=\sum_{i=1}^{m}{c}_{\mathrm{adc},i}+\mathrm{PD}\times {c}_{\mathrm{ic}}$$
(6)

where PC is the overall project cost; SCdc and SCic are the overall direct and indirect costs respectively, cadc,i is the direct cost of the ith activity; cic is the daily indirect cost of the project.subject to:

$$\mathrm{PD}=\underset{i=1,\dots , m}{\mathrm{max}}({T}_{\mathrm{as},i}+{d}_{a,i})=\underset{i=1,\dots ,m}{\mathrm{max}}({T}_{\mathrm{af},i})$$
(7)

where PD is the project duration; Tas,i and Taf,i are the start and finish time of the ith activity, respectively; di is the duration of the ith activity.

During the optimization process, the preferred alternative is determined based on its lower total project cost, and if both options have equal overall project costs, the option with a shorter completion time is chosen. In the rare case where both options have equivalent time and cost, the optimal choice is randomly selected.

The MVO algorithm is represented through both a pseudo-code (Table 1) and a flowchart (Fig. 3). Table 2 summarizes the set of parameters used, which proved to be an effective combination for the MVO optimization process. The MVO algorithm for the TCOP was coded in Python. The device used for testing all instances of the TCOP was equipped with an i7-8750H 2.20 GHz CPU and 8.0 GB of RAM.

Table 1 Pseudo-code of the MVO for TCOP
Full size table
Fig. 3
figure 3

Flowchart of the MVO for TCOP

Full size image
Table 2 Parameter settings of the MVO model
Full size table

Computational experiments

The case studies reported by Feng et al. (1997), consist of 18 activities and incorporate alternative approaches as recommended by Hegazy (1999), as shown in Table 3. The network diagram of the 18 activities can be found in Fig. 4. It is estimated that there are 5.90 × 109 potential schedules for this project. In Case study 1, the daily indirect costs amount to $200, and the project deadline is set at 110 days. The contractual penalties incurred for delays are $20,000 per day, while incentives of $1000 per day are available for early completion. Case study 2 features daily indirect expenses of $1500, whereas case study 3 showcases indirect expenses totalling $500 per day. Table 4 presents the optimal solutions for case studies 1, 2, and 3. The evaluation of MVO's performance was carried out ten times for each of the three case studies, and the resulting mean deviation (MD) from the optimal schedule is presented in Tables 5, 6 and 7. The MVO algorithm successfully attained the globally optimal solutions in all ten trials for the three problems within 50,000 schedules.

Table 3 18-activity data for Case studies 1, 2 and 3
Full size table
Fig. 4
figure 4

Network diagram of the 18-activity for Case studies 1, 2 and 3

Full size image
Table 4 Optimal solution of Case studies 1, 2 and 3
Full size table
Table 5 Mean deviation from the optimal solution for Case study 1
Full size table
Table 6 Mean deviation from the optimal solution for Case study 2
Full size table
Table 7 Mean deviation from the optimal solution for Case study 3
Full size table

Case study 1

In comparison to more advanced methods, MVO has been demonstrated to be one of the superior algorithms for small-scale TCOPs. As evidenced by the results in Table 5, MVO outperformed GA (Hegazy, 1999; Sonmez & Bettemir, 2012) for case study 1. The optimal value can be obtained by employing a hybrid genetic algorithm with simulated annealing (HA) (Sonmez & Bettemir, 2012), the discrete version of PSO (DPSO) (Aminbakhsh & Sonmez, 2016), the network analysis algorithm (NAA) (Bettemir & Talat Birgönül, 2017), or MVO.

Case study 2

The MVO algorithm has demonstrated superior performance (Table 6) compared to GA (Zheng et al., 2005), the hybrid algorithm based on the ant colony system (ACS-TCO) developed by Ng and Zhang (2008), the ant colony system (ACS), and ACS-SGPU that combine ant colony system and a global updating strategy proposed by Zhang and Thomas Ng (2012) for achieving optimal outcomes. In terms of providing high-quality solutions, MVO can be competed with by other methods, such as Pareto-based PSO (PFPSO) (Aminbakhsh & Sonmez, 2017) and hybrid teaching learning-based optimization (NDS-TLBO) (Eirgash et al., 2019).

Case study 3

The suggested MVO algorithm exhibited superior performance (Table 7) compared to the ACO, SFL, PSO, memetic, and genetic algorithms (Elbeltagi et al., 2005) for solving case study 3. Other modern techniques that can rival the proposed MVO in terms of providing high-quality solutions are the Electimize algorithm (Abdel-Raheem & Khalafallah, 2011), ACS, and ACS-SGPU (Zhang & Thomas Ng, 2012).

Conclusion

The present study has introduced the Multi-Verse Optimizer (MVO) as a novel approach to tackling time–cost optimization problems (TCOP) in small-scale projects. The computational experiments conducted have demonstrated the ability of MVO to produce high-quality solutions for TCOP, outperforming other optimization algorithms in terms of solution quality and computational efficiency. Specifically, MVO was able to obtain high-quality solutions with only 8000 schedules, compared to the 50,000 schedules required by other optimization methods. While the results of this study are promising, it is important to note that the application of MVO was limited to small-scale TCOPs. In practice, construction projects often involve complex and large-scale TCOPs, which may require the development of more advanced MVO-based methodologies to address multi-dimensional decision-making in selecting the optimal time and cost allocations. Therefore, future research should focus on employing MVO to tackle complex large-scale TCOPs and propose methodologies for multi-dimensional decision-making in construction project management.