Introduction

Most of the strong earthquakes in high seismicity regions do not occur as a singular event and are accompanied by a series of shocks. The effect of seismic sequences on a variety of structural systems has been investigated by several researchers (Bayraktar et al., 2019; Durucan & Durucan, 2016; Goda & Salami, 2014; Hatzigeorgiou & Beskos, 2009; Meigooni & Tehranizadeh, 2021; Moustafa & Takewaki, 2011; Ruiz-García et al., 2014; Tauheed & Alam, 2021; Zhai et al., 2015). They showed that the level of response and damage of structures significantly increases by aftershocks. For instance, according to the Taiwan earthquake event on 21st September 1999, a gas station in Taiwan was severely damaged by the main shock and collapsed by the aftershock (Lew et al., 2000).

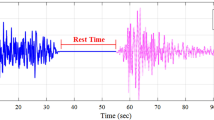
In the time history analysis of structures under seismic sequences, a zero acceleration time (known as a time gap) should be considered between earthquake records to cease the fluctuations of the system before another event, as shown in Fig. 1. The mentioned gap must be sufficiently determined between earthquake records to bring the structure to the steady-state condition under damping (Amirchoupani et al., 2021; Schoettler et al., 2015). In various studies, different values of time gap have been taken between consecutive events. Raghunandan et al., (2014) considered a time gap of 4 s between mainshock and aftershock events to investigate the level of structural damage for special reinforced concrete moment frames under seismic sequences. They also mentioned that this value is not sufficient for tall buildings to achieve stability. Abdollahzadeh et al., (2019) considered a 12-s zero acceleration time gap between mainshock–aftershock events to allow the structure to accomplish its free vibration and be brought to rest before it experiences the next event. Abdelnaby and Elnashai (2014) considered a time gap of 10–20 s between the main and aftershocks to make sure that the structure comes to rest between two events during the performance assessment of a 3-story reinforced concrete frame with deteriorating properties under Tohoku and Christchurch sequences.

Fig. 1
figure 1

Acceleration time history of a sequence

Full size image

Furthermore, Moustafa and Takewaki (2011) considered a time interval of 30 s for evaluating maximum damage created by ground motion sequences. Ruiz-García et al., (2014) considered the 40 s time gap between mainshock and aftershock to execute nonlinear dynamic analyses of 4-, 8-, 12- and 16-story reinforced concrete frames under consecutive earthquakes. Similarly, some other researchers have considered a time gap of the 40 s between successive events in their studies (Amadio et al., 2003; Fragiacomo et al., 2004; Silwal & Ozbulut, 2018). Yang et al., (2019) applied the 50-s zero acceleration time gap between mainshock and aftershock to ensure the structure reaches steadiness for assessing the damage demand of 8-story concrete frames under near-fault seismic sequences. Goda (2012) assumed a time gap of the 60 s between mainshock and aftershocks to calculate peak ductility demand under the seismic sequences. Furthermore, numerous researchers considered the time gap equal to 100 s to analyze the effect of aftershock on the structural response (Faisal et al., 2013; Hatzigeorgiou & Liolios, 2010; Zhai et al., 2012, 2013, 2014, 2015; Zheng et al., 2017). Han et al., (2014) proposed a 3-min time gap to evaluate the seismic performance of 3- and 6-story reinforced concrete frames under seismic sequences. Hatzigeorgiou and Beskos (2009) proposed a time gap of three times the duration of the mainshock between mainshock and aftershock for examining the inelastic displacement ratios under seismic sequences. Recently, Amiri and Bojórquez (2019) set a time gap of the 60 s between main and aftershocks for evaluating the residual displacement ratios of single-degree-of-freedom (SDOF) systems. They also added the 20-s zero acceleration at the end of the aftershock to estimate the exact residual displacement under seismic sequences, regardless of the structural parameters. Furthermore, other researchers considered zero acceleration at the end of the earthquake event to estimate the residual displacement more accurately. Li et al., (2019) applied a 10-s zero acceleration after the seismic event to evaluate the residual displacements of the self‐centering concrete frame system. Han et al., (2017) added the 20-s zero ground acceleration at the end of the earthquake event to assess the residual displacement of the infilled reinforced concrete frame structure. Dong et al., (2022) added the 40 s zero acceleration end of each earthquake record to evaluate the residual displacements of SDOF systems with the Bouc–Wen hysteresis model. Durucan and Durucan (2016) recommended time gap of 25 s by using sensitivity analysis on the \(C_{1}\) coefficient (Inelastic displacement ratio) to evaluate this coefficient under seismic sequences. They used only two SDOF systems and two successive earthquakes in their assessment. However, the influence of other effective structural parameters was ignored. Recently, Pirooz et al., (2021) proposed an equation for estimating the required time gap between mainshock and aftershock. They only considered the effect of the natural period of vibration and duration of the ground motions in bi-linear elastic-perfectly-plastic single-degree-of-freedom systems with constant ductility capacity on the time gap. The mentioned hysteresis model is only applicable for non-degrading structures and ignores the main structural properties such as cyclic deterioration and pinching, with a significant impact on the residual displacement of steel, concrete, and wooden structures (Ibarra et al., 2005).

According to previous studies, many researchers considered a similar time gap for successive events across all periods, regardless of the fundamental features of the structural system. Some researchers have suggested a lower time gap for ceasing the structure vibration, which may not have reached stability (Abdelnaby & Elnashai, 2014; Raghunandan et al., 2014). Others also overestimate a long time gap between mainshock and aftershock, which may lead to a significant inessential increase in analysis duration (Faisal et al., 2013; Han et al., 2014; Hatzigeorgiou & Liolios, 2010; Zhai et al., 2013, 2014, 2015). According to the time-consuming feature of nonlinear time-history analyses, estimating the optimal time gap for applying between consecutive events can significantly speed up the analysis procedure. Moreover, proper decision-making for the retrofit or reconstruction of a building and ensuring its safety in post-earthquakes requires the accurate estimation of residual displacements of the structure in prior events. Therefore, in the dynamics and vibration issues, especially in high-rise buildings, determining the accurate residual displacements requires knowledge of the time at which the free vibration of the system ends. Consequently, this paper aims to estimate the appropriate time gap for structures by considering the effects of structural properties and ground motion characteristics.

In this investigation, the optimal time gap of structures with deteriorating properties was evaluated by different ductility capacity, degradation and pinching. Thus, a total of 160 records according to twenty-one events recorded on far-field and near-field stations in the California region were selected. Furthermore, the effects of forward-directivity, local site conditions, and source-to-site distance were investigated. Finally, a statistical equation was proposed in terms of the fundamental period of vibration and lateral strength ratio (R), which generates a conservative time gap to confirm the stability of the structure after each event. Moreover, the effects of other parameters on the time gap, including ductility capacity, degradation, and pinching, were presented as modification factors. In the end, the proposed equation was verified with two 4- and 12-story MDOF systems.

Methodology

In this study, the required time gap between successive events was evaluated. For this purpose, SDOF systems with the fundamental periods of vibration ranging from 0.1 to 4.1 s with 0.1 s time-step, the 5% damping ratio, and six lateral strength ratios (R = 1.5, 2, 3, 4, 5, and 6) were considered. The lateral strength ratio (yield strength to lateral strength that keeps the system elastic) is defined as follows (FEMA-440, 2005):

$$R = \frac{{m {\text{Sa}}}}{{{\text{Fy}}}}$$
(1)

where \(m\) is the mass of the system, \({\text{Sa}}\) is the spectral acceleration, and \({\text{Fy}}\) is the lateral yield strength.

In this issue, the hysteresis model from the OpenSEES library was selected to consider the influence of various structural properties, including stiffness deterioration, strength degradation, and pinching. This model gives a more realistic behavior of the structural system. Nonlinear time-history analyses on SDOF systems were executed via OpenSEES software (Mazzoni et al., 2006). Figure 2 illustrates the backbone curve of the hysteretic model. As shown in Fig. 2, the nonlinear behavior of the backbone system in the hysteretic model was defined through the following parameters: (1) damage1: The accumulated damage due to ductility; (2) Damage2: The accumulated damage based on energy, which leads to strength and stiffness deterioration, proportional to dissipated energy by strain (it increases as the number of cycles at fixed strain increases); (3) β: The unloading stiffness degradation parameter based on ductility; (4) Ductility Capacity: It is defined as Uc/Uy ratio, where Uc is the displacement at which the system reaches to its maximum strength, and Uy is the yield displacement of structure; (5) Post-Capping Stiffness Ratio (αc): It is the ratio of the softening branch stiffness to the initial elastic stiffness of the system; (6) Post-yield Stiffness Ratio (αs): It is the ratio of the hardening branch stiffness to initial elastic stiffness; (7) Residual Strength: It is the fraction of yield strength; (8) PinchingX: Pinching factor for strain or displacement; (9) PinchingY: Pinching factor for stress or force. When the value of the pinching factors is equal to 1, this effect is not taken into account. However, as it diminishes (tends to zero), the pinching effect becomes intensified. Figure 3 illustrates the influence of PinchX and PinchY parameters on the hysteretic curve under standard loading protocol (Krawinkler, 1992). In this research, the residual strength, post-yield stiffness ratio and post-capping stiffness ratio values were considered as 0.2Fy, 0.03 and − 0.1, respectively.

Fig. 2
figure 2

Backbone curve of hysteretic model (Ibarra et al., 2005)

Full size image
Fig. 3
figure 3

Effect of pinching on hysteretic responses a PinchX, b PinchY

Full size image

Three values of low, medium, and high structural parameters in the hysteresis model were adopted to investigate the effect of different structural parameters on the time gap. The selected properties were ductility, damage, and pinching. The corresponding values of the hysteretic model properties are reported in Table 1. For instance, the effect of low-, medium-, and high-degradation parameters on the hysteretic curve under standard loading protocol is presented in Fig. 4a–d, respectively. It is worth mentioning that the loading protocol, bar slippage, and reinforcement detailing are significant parameters that can influence the stiffness deterioration and strength degradation rate of the reinforced concrete structures. The degradation rate would be increased in concrete, steel, and wooden structural systems due to the increase of the damage level.

Table 1 Hysteretic model parameters
Full size table
Fig. 4
figure 4

Effect of degradation on hysteretic curve, a without degradation, b low-, c moderate-, and d severe-degradation

Full size image

The free vibration in the system occurs when the structure deviates from its equilibrium with an initial force or displacement. The vibration amplitude of such a system decreases over time due to its inherent damping. The time at which the free vibration of a structure terminates after an earthquake occurrence can be determined according to the concept of system energy balance. The energy balance equation based on the relative motion is expressed as follows (Uang & Bertero, 1990):

$$\int\limits_{0}^{t} {m\ddot{u}\dot{u}{\text{d}}t + \int\limits_{0}^{t} c } \dot{u}^{2} {\text{d}}t + \int\limits_{0}^{t} {f_{{\text{s}}} } \dot{u}{\text{d}}t = - \int\limits_{0}^{t} m \ddot{u}_{{\text{g}}} \dot{u}{\text{d}}t$$
(2)
$$E_{{{\text{kr}}}} + E_{{\text{d}}} + E_{{\text{a}}} = {\text{IE}}$$
(3)

where \(\dot{u}_{{\text{g}}} ,\ddot{u},\dot{u},c,f_{{\text{s}}}\) are ground motion acceleration, relative acceleration, relative velocity, damping coefficient, and restoring force of the structure, respectively. Equation (3) is a summary of Eq. (2), where \(E_{{{\text{kr}}}}\) is the relative kinematic energy, \(E_{{\text{d}}}\) is the dissipated energy due to inherent viscous damping and any additional damping devices provided to the system, \(E_{{\text{a}}}\) is the absorbed energy, and IE is the total input energy due to earthquake excitation. Accordingly, the absorbed energy in the system comes from the summation of elastic strain energy and hysteretic energy. The elastic strain energy is related to the elastic deformations of the system. However, the hysteretic one corresponds to the nonlinear behavior of structural components, is dissipated through heat, and plays a significant role in the amount of absorbed energy (damage) in the structure. The values of relative kinematic and elastic strain energy in the system are approximately zero upon completion of the earthquake. According to the energy balance equation, once the earthquake input energy ends, the structure continues to vibrate to reach the equilibrium state. The amount of cumulative damping energy with an ever-ascending trend experiences decreasing in slope over time, and as it reaches zero, the structure achieves stability. Due to the direct correlation between the damping energy and the relative velocity, the criterion of near to zero relative velocity value was adopted to estimate the free vibration duration of the structure and its stabilization aftermath of an earthquake. The selected tolerance was obtained by performing repetitive trial and error processes. At the same time, as the relative velocity of the system reached zero, the amount of permanent displacement and cumulative damping energy would be a constant value at an acceptable level. The mentioned tolerance was chosen as conservatively as possible to consider uncertainties related to the MDOF systems.

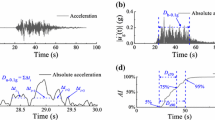
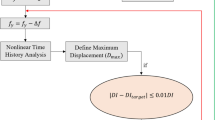
Besides, the residual displacement and cumulative damping energy of an SDOF structural system were monitored to become constant in evaluating accurate time gap duration. For example, the velocity time history, displacement time history, and the cumulative damping energy of the system with a fundamental period of 2.3 s under the Northridge earthquake record with a duration of 29.99 s are demonstrated in Fig. 5. As shown in Fig. 5, the time gap for the mentioned period was estimated to be the 70 s. The cumulative damping energy in the structural system would reach a constant value by the required time gap. According to Fig. 5a–c, as the relative velocity value of the structure reaches zero (with a tolerance of 0.009 mm/s), the relative displacement and slope of cumulative damping energy become constant simultaneously. Figure 6 shows the whole procedure for determining the optimal time gap as a flowchart. Tm, TG, and dt parameters mentioned in the flowchart are mainshock duration, time gap, and the time-step of the records, respectively. As it is clear from the flowchart, the optimal time gap is achieved after the velocity reaches zero when the amount of permanent displacement and cumulative damping ratio becomes constant simultaneously.

Fig. 5
figure 5

Time Gap determination based on a velocity time history, b displacement time history, c cumulative damping energy

Full size image
Fig. 6
figure 6

Optimal time gap full procedure

Full size image

Ground motion records

A total of 160 records, including 62 far-field, 50 no-pulse near-field, and 48 pulse-like near-field records, were considered from the Pacific Earthquake Engineering Research Center Ground Motion Database in this study. Additionally, the 15 km Joyner–Boore (Boore et al., 1997) criterion was adapted as a distance boundary between near-field and far-field records. The forward-directivity effects on the time gap were evaluated by considering two sets of near-field ground motions. Therefore, the first and second groups were selected from pulse-like (48 ground motion records) and non-pulse-like (50 ground motion records) earthquakes, respectively. The far-field, pulse-like near-field and non-pulse-like near-field record characteristics are summarized in Tables 2, 3 and 4, respectively. The earthquake ground motions were classified into three groups based on average shear wave velocity from stations with a shear wave velocity between 183 and 366 m/s (soil class D), 366–762 m/s (soil class C), and greater than 762 m/s (soil class A and B), respectively (ASCE/SEI 7-10, 2010; ASCE/SEI 7-16, 2016). One earthquake component with higher peak ground acceleration (PGA) was selected among ground motion pairs at soil classes C and D. However, both components in soil classes A and B were used due to the limited number of recorded ground motions in this site condition. All non-pulse-like (far-field and no-pulse near-field) and pulse-like records were scaled to hazard level-1 (475-year return period) and hazard level-2 (2475-year return period) for proper spectral matching among ground motions, respectively (ASCE/SEI 7-16, 2016).

Table 2 List of far-field records
Full size table
Table 3 List of near-field pulse-like records
Full size table
Table 4 List of near-field non-pulse-like records
Full size table

The effect of structural parameters and ground motion characteristics on time gap

In this study, 49,140 nonlinear time history analyses (NTHA) were executed on 1638 SDOF systems subjected to 30 ground motions (including ten records in each group, including far-field, pulse-like near-field, and non-pulse-like near-field for site class D). Consequently, specified hysteretic parameters yielding the longest time gap were selected for the reference model. Thereby, the parameters of the reference model were defined as follows: αs = 0.03, αc =  − 0.1, Dc/Dy = 6, Damage1 = 0, Damage2 = 0.05, PinchX = 0.2, PinchY = 0.8, Beta = 0. Moreover, the effects of ground motion characteristics, including distance-to-source, forward-directivity, and soil condition, were investigated in the time gap of the reference model. The influence of different structural properties on the time gap of the reference model was evaluated, including the ductility capacity, the pinching factor for stress, the pinching factor for strain, and the accumulated damage rate. It is worth mentioning that the parameters that lead to an increase or decrease of more than 15 s of the time gap in different periods and lateral strength ratios were considered as the influential parameters since they would lead to a significant effect in analysis speed and permanent displacement accuracy.

The dynamic analyses confirmed that the influence of hysteretic parameters on the time gap is different in various periods of vibration and lateral strength ratios. Hence, the effect of the mentioned structural properties on the time gap was investigated at the period range of 0.1–4.1 s and the lateral strength ratio of 1.5–6, respectively. It should be noted that the arithmetic means of time gap values under entire ground motions were computed at each period of vibration.

The effect of ground motion characteristics

The influence of source-to-site distance on the time gap was evaluated by dividing earthquakes into two categories, including 20 far-field and near-field ground motions in soil class D. The 15 km source-to-site distance boundary was adapted as a difference of far-field and non-pulse-like near-field records. Figure 7a shows that the effect of the far-field and near-field ground motions on the time gap is not prominent in different lateral strength ratios.

Fig. 7
figure 7

The effect of a source-to-site distance, b forward directivity, c soil classification on time gap

Full size image

Moreover, the influence of forward-directivity (pulse) on the time gap was investigated using 20 non-pulse-like and pulse-like near-field ground motion records from soil site D. Figure 7b shows that the influence of forward-directivity on the time gap is not significant. The effect of soil site condition on time gap was investigated by dividing far-field ground motion records into three subsets, including 20 ground motions on soil class B, C, and D, at different periods and lateral strength ratios, as shown in Fig. 7c. In reference to Fig. 7, the effect of source-to-site distance, forward-directivity (pulse), and soil site condition on the time gap (in different lateral strength factors) are not significant and influential.

The effect of structural parameters

Initially, 49,140 nonlinear time-history analyses were executed to identify the ineffective structural parameters of the time gap. Subsequently, for further precise investigation of efficient parameters, the number of dynamic runs was increased to 81,900 (under the entire far-field records listed in Table 2). According to the preliminary analysis results, statistical results showed that the time gaps of the SDOF systems with medium values in the hysteretic properties (mentioned in Table 1) were linearly related to the ones corresponding to the low and high values. Therefore, to investigate the impact of effective hysteretic parameters on the time gap, only the low and high values of these parameters were considered. Furthermore, linear interpolation can be implemented to obtain time gaps for the parameters among these values. The presented curves of this section are associated with time gaps obtained from far-field records (from soil site D).

The effect of ductility capacity

The effect of ductility capacity on the time gap was investigated by considering two low and high values for this parameter (Uc/Uy = 2, 6). The influence of ductility was scrutinized in different periods and lateral strength ratios. As shown in Fig. 8, the effect of ductility on the time gap is noticeable, particularly in medium lateral strength ratios. Regarding Fig. 8, the time gap in the period range of 0.5–4.1 s is reduced by 18–70% for low to high ductility ratios. The limiting period (at which the effect of ductility is significant) is intensified by increasing the lateral strength ratios. For example, the limiting period is 0.5, 0.7, 1, and 1.5 for R = 3, 4, 5, and 6, respectively. Besides, the time gap values are approximately identical for low to medium period ranges (0.1–1.5 s), as shown in Fig. 8, whereas, at higher periods (1.5–4.1 s), the time gap is reduced by 30–60% from low to high ductility. By decreasing the ductility capacity, the structure reaches its maximum strength capacity more rapidly so that the input energy of the system decreases. Hence, the required time for damping the input energy decreases, and less time is required to stop the system.

Fig. 8
figure 8

The effect of ductility capacity ratio on time gap

Full size image

The effect of cumulative damage (effect of degradation)

Two low- and high-degradation levels were taken into account to investigate the effect of cumulative damage (energy based) on the time gap. The mentioned approaches were evaluated in different periods of vibration and lateral strength ratios. As shown in Fig. 9, the effect of increasing strength degradation on the time gap value was not too significant in high lateral strength ratios. The time gap values in low and medium lateral strength ratios increase as the strength degradation decreases. Figure 9 shows that the time gap was reduced by nearly 25–50% in low strength degradation compared to the high one. Hence, the effect of degradation on the time gap is high as the lateral strength ratio and period of vibration increase. The limiting period at which the degradation begins to affect the time gap increases by raising lateral strength ratios. According to the definition of the damage factor, as the deterioration rate increases, the level of strength and stiffness of the structure decreases more rapidly. Consequently, energy dissipation occurs faster, and less time gap is required for achieving stability.

Fig. 9
figure 9

The effect of degradation on time gap

Full size image

Pinching effects

Two 0.2 and 0.8 pinching values were used to examine the effect of PinchX (the pinching factor for strain) on the time gap at different periods and lateral strength ratios. Figure 10 shows that, by decreasing the effect of PinchX (i.e., increasing the PinchX value), the time gap is reduced, especially from R = 2 to R = 4. The time gap reduces from 30 to 60% when the effect of PinchX is decreased from 0.2 to 0.8 in the period range of 1–4.1 s. Moreover, two values of 0.2 and 0.8 were applied to investigate the influence of PinchY (the pinching factor for the strength) on the time gap. Statistical results show that the effect of PinchY on the time gap is generally similar to the PinchX trend at various lateral strength ratios and periods of vibration. As illustrated in Fig. 10, the time gap decreases by increasing the effect of PinchY (i.e., Reducing the PinchY value). Moreover, the time gap is reduced by 40–60%, in the period range of 1–4.1 s and R = 4, when the effect of PinchY increased. The limiting period at which both pinching parameters begin to affect the time gap is increased by lateral strength ratio increments. It is worth mentioning that the stiffness reduction in the system occurs at a slower rate, and the amount of energy entering the structure increases, by growing the pinching effect (decreasing the PinchX value) and decreasing this effect around the force axis (PinchY value). On the other hand, the structure depreciates more energy due to the increase in area under the hysteresis curve. Since the rating of input energy entering the system is higher than the rate of depreciated energy, the structure needs more time to achieve stability.

Fig. 10
figure 10

a The effect of PinchX b PinchY on time gap

Full size image

A relationship to the reference model

Given the importance of time gap on the duration of nonlinear time-history analyses under seismic sequences, or the evaluation of time at which the structure reaches its residual displacement, especially in high-rise buildings, a simple equation was proposed for assessing the attributed time in structural systems. For this purpose, by performing 39,060 time-history analyses with various periods of vibration and lateral strength ratios, a reference model with specific hysteretic parameter values was adopted to present a conservative equation. As cited before, the reference model was selected to estimate the longest time gap in different periods and lateral strength ratios. Additionally, maximum ductility capacity ratio (Dc/Dy = 6), low strength degrading, maximum pinching factor for strain (PinchX = 0.2), and minimum pinching factor for stress (PinchY = 0.8) yield the highest values of time gap in different periods of vibration and lateral strength ratios. Thereby, the parameters of the reference hysteretic model for statistical equation recommendation were defined as follows: Dc/Dy = 6, Damage1 = 0, Damage2 = 0.05, PinchX = 0.2, PinchY = 0.8, Beta = 0. In addition, since no significant effect of soil-to-site distance and forward-directivity of the ground motion records was observed on the time gap, only obtained time gap from far-field records were utilized in determining the time gap equation for the reference model. Moreover, since the soil type of the recording station does not affect the time gap values, all soil type conditions (B, C, and D) were combined, which led to 62 far-field records.

A comprehensive equation for determining the optimal time gap (TG) was developed utilizing the Levenberg–Marquardt nonlinear regression analysis. The corresponding time gap values were obtained from 7812 nonlinear time history analyses (NTHA) on the reference model with T = 0.1–4.1 s and R = 1.5 to R = 6 under 62 far-fault ground motion records (soil types B, C, and D). For this purpose, the mean time gap values in each period of vibration and lateral strength ratio under all records were used to determine the equation with the minimum error. The proposed equation based on the period and lateral strength ratio (R-factor) is expressed as:

$${\text{TG}} = a{\text{RT}}^{b} + c$$
(4)

where R is the lateral strength ratio, T is the period of the vibration, and a, b, and c are constant values. Table 5 reports the constant values of Eq. (4) derived from nonlinear regression analysis for different lateral strength ratios.

Table 5 Coefficient values for determination of time gap (TG)
Full size table

The estimated time gap values in different periods of vibration and lateral strength ratios are illustrated in Fig. 11b, which are very similar to the mean actual values obtained from nonlinear time history analysis (Fig. 11a). Accordingly, the time gap amplifies as the period of vibration increases and the lateral strength ratio decreases. Moreover, the well-known bias and dispersion indices were calculated to evaluate errors in the estimated equation. The bias and dispersion equations were defined as follows:

$${\text{Bias}} = {\text{e}}^{{\frac{{\mathop \sum \nolimits_{i = 1}^{n} ln\left( {\hat{\theta }{ / }\theta } \right)}}{n}}}$$
(5)
$${\text{Dispersion}} = {\text{SD}}\left( {\ln \left( {{\raise0.7ex\hbox{${\hat{\theta }}$} \!\mathord{\left/ {\vphantom {{\hat{\theta }} \theta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\theta $}}} \right)} \right)$$
(6)

where n is the number of records, \(\hat{\theta }\) is the estimated time gap value, and \(\theta\) is the actual time gap value.

Fig. 11
figure 11

a Actual values of time gap, b estimated values of time gap

Full size image

Hence, the bias values were computed as a median of \(\left( {{\raise0.7ex\hbox{${{\hat{\theta }}}$} \!\mathord{\left/ {\vphantom {{{\hat{\theta }}} {\uptheta }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\uptheta }$}}} \right)\) (the median defines as an exponential of the mean of the natural logarithm \(\left( {{\raise0.7ex\hbox{${{\hat{\theta }}}$} \!\mathord{\left/ {\vphantom {{{\hat{\theta }}} {\uptheta }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\uptheta }$}}} \right)\)). It is worth mentioning that the bias predictor lower and higher than unity leads to the underestimation and overestimation of the actual values, respectively. Figure 12a illustrates the bias of the estimated time gap for the entire range of periods and lateral strength ratios. The bias values are close to unity in most period ranges or more than one in some periods for six strength factors. Hence, the optimal time gap equation would lead to conservative results. Furthermore, the dispersion predictor was conducted to evaluate the accuracy of the presented time gap equation. The dispersion was determined by the difference of estimated and median values, expressed as the standard deviation of the natural logarithm of \(\left( {{\raise0.7ex\hbox{${{\hat{\theta }}}$} \!\mathord{\left/ {\vphantom {{{\hat{\theta }}} {\uptheta }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\uptheta }$}}} \right)\). Remarkably, lower dispersion leads to more accurate results (closer to zero). Figure 12b depicts the dispersion values of the time gap obtained from Eq. (4) in different periods and lateral strength ratios.

Fig. 12
figure 12

a Bias, b dispersion

Full size image

Time gap modification factors

Statistical results showed that the time gap values could be influenced by some structural parameters, including ductility capacity (Dc/Dy), strength degradation, the pinching factor for strain (PinchX), and the pinching factor for stress (PinchY). Thus, modification factors were proposed for applying to the time gap values obtained from Eq. (4) to consider the effect of using different parameters from the reference model. The mentioned modification factors can be used for various hysteresis model properties than the reference model to determine the optimal time gap. Modification factors for backbone hysteresis parameters, including ductility, strength degradation, pinching for strain, and pinching for stress, would lead to lower time gap values, given in Table 6. Accordingly, the modification factor reported in Table 6 corresponds to Dc/Dy = 2, Damage1 = 0, Damage2 = 0.15, PinchX = 0.8, and PinchY = 0.2, respectively. The average plus the standard deviation of data were computed to obtain these coefficients for gaining more conservative results. The proposed coefficients are presented mainly in the four structural period ranges and six different lateral strength ratios. By applying the modification factors reported in Table 6 to the time gap from Eq. (4), the speed of time history analysis under seismic sequences could increase prominently. Statistical results from nonlinear time history analysis (NTHA) illustrated that the time gap obtained from the mean values of the parameters reported in Table 1 is linearly proportional to the time gap values from the maximum and minimum of these variables. Therefore, linear interpolation between the upper and lower bound limits can be employed to estimate the appropriate time gap for different periods and lateral strength ratios.

Table 6 Modification factors for determination of time gap (TG)
Full size table

For example, for a structure with a period of vibration of 3 s and a lateral strength ratio of 5, and structural parameters as Dc/Dy = 4, Damage2 = 0.1, PinchX = 0.6, PinchY = 0.6, the time gap would be calculated as follows:

For R = 5 and T = 3 s, the coefficient values for Eq. (4) are a = 0.74, b = 1.78, and c = 1.01, according to Table 5. Hence, by substituting the coefficient values of Eq. (4), the time gap achieves 27 s \(\left( {{\text{TG}} = 0.74 \times 5 \times 3^{1.78} + 1.01 = 27.16{\text{ s}}} \right)\). It is worth mentioning that the calculated time gap is without considering the effect of other structural parameters. Furthermore, according to Table 6, for R = 5 and T = 3 s, MFDuctility for Dc/Dy = 2 is equal to 0.35, while MFDuctility for Dc/Dy = 6 (reference model) is 1. Therefore, by linear interpolating, MFDuctility equals 0.675 for Dc/Dy = 4. Moreover, the value of MFDamage for D2 = 0.15 equals 0.45, while MFDamage for D2 = 0.05 (reference model) equals 1. Accordingly, by linear interpolating, MFDamage equals 0.725 for D2 = 0.1. In addition, MFPinchX for PinchX = 0.8 equals 0.4, while MFPinchX for PinchX = 0.2 (reference model) equals 1. Hence, by linear interpolating, MFPinchX equals 0.6 for PinchX = 0.6. Similarly, MFPinchY for PinchY = 0.2 equals 0.45, while MFPinchY for PinchY = 0.8 (reference model) equals 1. Therefore, by linear interpolating, MFPinchY equals 0.82 for PinchY = 0.6. Ultimately, by multiplying the calculated modification factors, the time gap value for the mentioned model will obtain 6.54 s (TG = TG(RM) × MFDuctility × MFDamage × MFPinchX × MFPinchY = 27.16 × 0.675 × 0.725 × 0.6 × 0.82 = 6.54 s).

Verifying of the proposed equation for MDOF systems

Two models of 4- and 12-story steel frames were considered to verify the proposed equation. These MDOF structures with Special Concentric-Brace Frame dual systems (SCBF) were designed according to AISC 360-6 (American Institute of Steel Construction, 2016) and ASCE 7-16 (ASCE/SEI 7-16, 2016) codes by Amirchoupani et al., (2020). The selected steel frames have columns, beams, and braces with BOX, W-Shape, and UPN sections. Detailed information and configuration of two-dimensional models exist are shown in Fig. 13 and Table 7, respectively. The SeismoStruct V2020 software was utilized to perform the nonlinear time history analysis (NTHA) of MDOF systems by adapting three-dimensional force-based beam-column elements with five integration points along the element length. The pushover analysis of 4- and 12-story buildings were executed to obtain the lateral yield strength and R-factors (Eq. 1). Furthermore, the time gap values of these systems were calculated according to Eq. 4 based on their fundamental period of vibration. The time gaps were 10.45 and 36 s for 4—(T = 0.593 s, R = 1.75) and 12-story (T = 1.541 s, R = 1.5) structures, respectively. The mentioned structures were subjected to ten ground motion records to verify the proposed time gap for MDOF systems. These ground motions were selected according to Baker and Lee’s algorithm (2018) by Amirchoupani et al., (2020). Figure 14a, b illustrates the displacement time history of 4- and 12-story buildings under the Loma Prieta event recorded at Gilroy Array #4 station with an estimated time gap based on Eq. 4. The fluctuation of permanent displacement values almost stopped in the computed time gap duration. Therefore, the estimated time gap for SDOF systems is also compatible with MDOF systems and guarantees their stability after the first event. Similar results were obtained under the Cape Mendocino event presented in Fig. 14c, d. The displacement time history of 4- and 12-story structures under other selected earthquakes was not highlighted due to the limited space and prevention iteration.

Fig. 13
figure 13

The configuration of two-dimensional 4-story and 12-story buildings (Amirchoupani et al., 2020)

Full size image
Table 7 Column, beam and brace element sections (Amirchoupani et al., 2020)
Full size table
Fig. 14
figure 14

Displacement time history of MDOF systems under Loma Perieta event on the a 4-story, b 12-story and Cape Mendocino event on c 4-story, d 12-story structures

Full size image

As another review, a dynamic analysis of the 12-story model was executed under the Northridge event sequence recorded at Hollywood–Willoughby Ave Station to demonstrate the difference in run time using the proposed equation and typical 100 s time gap (used by many researchers like (Faisal et al., 2013; Hatzigeorgiou & Liolios, 2010; Zhai et al., 2015). The duration of the nonlinear dynamic analysis was about 38 and 58 min using the proposed equation and 100 s time gap, respectively. This result shows that the suggested equation reduces the analysis time and evaluates the residual displacement more accurately, especially for high-rise buildings or other complicated structural systems.

Conclusions

In previous studies, the researchers have considered the time gap between seismic sequences regardless of the fundamental features of the structural system across all periods. Regarding the importance of the duration of nonlinear time-history analyses and the calculation of the exact value of residual displacement, the required time gap for the stabilization of structures between seismic sequences was investigated carefully in this study. Therefore, the single-degree-of-freedom systems (SDOF) with three stiffness-strength deterioration approaches at different periods and lateral strength ratios were subjected to 160 ground motions to calculate the optimal time gap. The earthquake ground motions were selected from far-field, pulse-like near-field, and non-pulse-like near-field records. The following conclusions were obtained from this study:

  • The time gap amplifies as the period of vibration increases and the lateral strength ratio decreases. High-rise structures with smaller lateral strength ratios (weaker systems) need more time to reach stability after the earthquake. Furthermore, by increasing the R-factor, the lateral strength of the system decreases, which leads to the less required time for energy dissipation and achieving stability.

  • The effects of source-to-site distance and forward-directivity on the time gap during different periods and lateral strength ratios do not follow a constant trend. Furthermore, local site condition does not have any influence on the time gap.

  • Structural ductility capacity has a direct relation to the time gap. The required time gap increases by increasing the ductility capacity. For example, the time gap for low ductility capacity was about 70% lower compared to high ductility in the medium to high period regions and medium lateral strength ratios.

  • Statistical results indicate that the strength degradation and the time gap values are correlated inversely with each other. Therefore, the time gap decreases with increasing the amount of strength and stiffness degradation in the cyclic behavior of the structure. For example, when the deterioration rate increases, the required time gap for structural stability decreases by about 30–50 s for systems with high period and medium lateral strength ratios.

  • The PinchX (pinching factor for strain) and PinchY (pinching factor for stress) parameters have distinct effects on the time gap. The amount of time gap for structural stability is reduced by increasing PinchX (reducing pinching for strain) and decreasing PinchY (intensifying pinching for stress). The effects of these parameters are considerable. For example, in medium lateral strength ratios, increasing PinchX from 0.2 to 0.8 reduces the time gaps by 40–70%, and decreasing PinchY from 0.8 to 0.2 reduces them by 40–60%.

  • Time history analyses of two-dimensional 4- and 12-story buildings show that the proposed equation is also validated for MDOF systems.

An exponential equation based on the fundamental period of vibration and lateral strength ratio was recommended to determine the required time gap for structural systems. Hence, a reference model was utilized to present this relationship. Furthermore, effective structural parameters in the reference model were chosen to obtain the maximum time gap values conservatively. Therefore, modification factors were proposed suitably to incorporate the effects of influential parameters, including strength degradation, ductility capacity, and pinching.