Required time gap between mainshock and aftershock for dynamic analysis of structures

Abstract

Despite the various studies carried out to evaluate the effects of seismic sequences on structures, the matter of the time gap required to be considered between the mainshock and its corresponding aftershocks in dynamic analyses has never been focused on directly. This subtle but in the meantime effective subject, influences the amount of accumulated damage caused by earthquake sequences. In the present study, 244 near fault ground motion components from 122 earthquakes were applied to a wide variety of single degree of freedom systems having vibrating period of 0.05–7 seconds with linear and nonlinear behavior. Furthermore, 2 planar steel moment-resisting frames, having 3 and 12 stories, were subjected to a set of 30 ground motion components. The purpose of this investigation was to estimate the required time for the structures to cease the free vibration at the end of the mainshock. The main purpose is to generate an estimation that is function of structural system’s parameters and the strong motion duration. Excellent correlations were obtained between the rest time and the following parameters: the combination of natural period of single degree of freedom systems, as well as the strong motion duration of earthquake sequences. In consequence, a formula is proposed which estimates the optimized required rest-time of a structure based on natural vibration period, as well as the duration of strong motion. Additionally, results obtained from the dynamic analysis of the steel frames validate the rest-time values achieved by the proposed formula.

1 Introduction

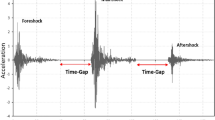
The importance of aftershock effects on response of structures has been highlighted in several recent studies. The effect of successive earthquakes is of high importance not only for more accurate evaluation of framed structures and bridges (Xie et al. 2012a, b) but also in maintaining the monuments and ancient structures (Papaloizou et al. 2016). Examples of seismic events followed by aftershocks of comparable intensity have been observed in various parts of the world, including in Italy (Friuli 1976; Umbria-Marche1997), Greece (1986, 1988), Turkey (1999) and Mexico (1993, 1994, 1995) (Li and Ellingwood 2007). A key feature in the application of seismic sequences within the dynamic analysis of structures, is the time gap of a certain length inserted between the mainshock and the corresponding aftershocks. This silent time interval with zero acceleration is actually applied in dynamic analysis to ensure that the structure ceases the free vibration followed by the elimination of the seismic excitation at the end of the ground motion’s time history (Goda 2012a, b).

In the real situation, usually aftershocks do not occur right after the mainshock time history terminates; There is a time interval from a few minutes to several days between the mainshock and the subsequent aftershocks (Gallagher et al. 1996). The aforementioned time gap is an opportunity for the structure to stop vibration due to damping (Zhai et al. 2014). Amadio et al. (2003) considered a gap of about 40 s between successive events for the structure to stop moving (Amadio et al. 2003). Hatzigeorgiou and Beskos (2009, 2010) applied a time gap between the mainshock event and its following aftershocks which was equal to three times the single event duration (Hatzigeorgiou and Beskos 2009; Hatzigeorgiou and Liolios 2010). In other studies by Hatzigeorgiou (2010a, b), a time gap of 100 s was applied between two consecutive seismic events (Hatzigeorgiou 2010a, b). Moustafa and Takewaki (2011) applied the 40 s separating time interval between events (Moustafa and Takewaki 2011).

Also, a silent time interval of 20 s was defined between the seismic sequences in an study by Ruiz-Garcia et al. (Ruiz-García and Negrete-Manriquez 2011; Huang et al. 2012). Goda (2012a, b) inserted 60 s of zeros, while in another study by Goda (2015), 30 s of zeros was added between the repeated earthquake time histories to ensure that the structural system returns to at-rest condition before the aftershock is applied (Goda 2012a, 2012b, 2015). Zhai et al. (2014) considered a time gap of 100 s and claimed that this time gap is sufficient for any civil structure to stop vibrating due to damping (Zhai et al. 2013, 2014). Han et al. (2015) used different time gaps for different mainshock-aftershock sequences (Han et al. 2015). Mirtaherf et al. (2017) applied the aftershock sequences immediately after the mainshock and claimed that the scenario could result in the most critical evaluation of the structural models (Mirtaherf et al. 2017). Pu and Wu (2018) considered a time interval of 15 times the fundamental period of structures employed for analysis (Pu and Wu 2018). Hosseini et al. (2019) considered 200 s of zero acceleration time gap between selected sequences to ensure that the structure reaches the steady-state position (Hosseini et al. 2019). In a more recent study, damage-based yield point spectra were developed for repeated earthquake ground motions by analyzing single degree of freedom systems in which a time gap of 100 s was considered between mainshock-aftershock sequences (Zhang et al. 2020). In another recent study, considering 20 s time gap, seismic performance of buckling-restrained braced frames were evaluated under successive earthquakes (Hoveidae and Radpour 2020).

This study is presented to investigate the time required to be applied between earthquake sequences in dynamic analyses in a way that it can be representative of the time applied between the mainshock and its aftershocks in real cases. A formulation is proposed for estimation of this time gap with respect to structural system’s properties and the ground motion’s features as the input parameters. Estimation of the minimum required time gap for the dynamic analyses based on the above-mentioned parameters is worthy since wide variety of investigations that are conducted in earthquake engineering field for examining the effects of earthquake sequences on structures, do confront it. As of the writing of this paper, no study has been conducted to investigate the optimized required time gap between seismic sequence in dynamic analyses. On the other hand, the cost of analyses is of a great importance especially in the repeated earthquake researches whereas the duration of seismic sequences is often long. Therefore, an optimized estimation of the required time gap is highly demanded.

To this end, a formula is extracted using the curve fitting mathematical technique performed on the outputs of linear and nonlinear analyses of single degree of freedom systems. The influence of strain hardening, damping and ground motion scaling is taken into account in the proposed formulation. It is worth mentioning that results of two planar steel moment-resisting frames having 3 and 12 number of stories were examined to authenticate the validity and accuracy of the proposed formulation.

2 Theoretical background

As mentioned earlier, the rest time between the mainshock and the aftershock is defined as the time in which the vibrating structure is no more subjected to lateral loads and it begins to enter the free vibration phase. The free vibration lasts till the amplitude of vibration is gradually diminished or gets close to the zero value at the end. An example of time gap is illustrated in Fig. 1 for better conceiving the rest time definition.

Fig. 1

An illustration of the rest time definition for a sample mainshock-aftershock earthquake sequence

The velocity response of the structure obtained from the equation of motion when solved for the free vibration status of the structure after mainshock excitation, clarifies the rest time’s influential parameters.

The dynamic equilibrium equation of motion for a single degree of freedom system is given in Eq. (1) (Chopra 2006):

$$m\ddot{u} + c\dot{u} + ku = - m\ddot{u}_{g}$$

(1)

where m is the mass of the system, c the viscous damping, k the stiffness, u the relative displacement, $\dot{u}$ the relative velocity, $\ddot{u}$ the relative acceleration and $\ddot{u}_{g}$ the ground motion acceleration.

If Eq. (1) is solved for a free vibrating system where the right term is set to zero, the general form of the velocity response would be depicted as Fig. 2.

Fig. 2

General form of the velocity response of a SDOF system

From Fig. 2, it is evident that the amplitude of vibrational response reduces with time and finally drops to the value very close to zero. The time required for the velocity of the system to get close to zero, is function of the system’s damping ratio. The influence of damping on response of the system is also depicted in Fig. 3, in which the velocity responses of a SDOF system considering two different damping ratios are compared.

Fig. 3

Effect of damping ratio on the amplitude of velocity response and the required time for the response to be fully damped

It is inferred that not only the amplitude of vibrational response is lessened as damping ratio is increased, but also the required time for the system response to be fully damped and get close to zero value is shortened drastically compared to the system with lower damping ratio ($\xi ={2.5}\%$). A similar trend for the MDOF systems applies except that mass (m), stiffness (k) and the damping coefficient (c) parameters are replaced by the mass matrix, stiffness matrix and damping matrix. The acceleration, velocity and the displacement responses ($\ddot{u}$,$\dot{u}$,$u$) are also replaced by their corresponding vectors in Eq. (1) (Far 2017).

3 Description of structural models

3.1 Single degree of freedom models

22 elastoplastic single degree of freedom (SDOF) systems with the vibration period of T, ranging from 0.05 to 7 s are used in this study (Table 1). The nonlinear behavior of SDOF systems is represented by a bilinear elastoplastic force–displacement curve as shown in Fig. 4 (Samimifar et al. 2019). The equivalent bilinear force–displacement curves were obtained through pushover analyses which were carried out on framed structures as was recommended by Massumi and Monavari (2013) (Massumi and Monavari 2013). Strain-hardening ratio (h) or the ratio of post-yielding stiffness to the initial stiffness of the model, is assumed to be 0%, 1%, 2% and 3%. The ratio of ultimate displacement to yield displacement (ductility) was set to 8 for all systems. Three damping values of 2.5%, 5% and 7.5% were also considered for viscous damping ratio ($\xi$) of SDOF systems. Response of the models under ground motion acceleration time histories were computed using the Newmark $\beta =1/4$ numerical method for solving dynamic equation of motion (Clough and Penzien 1995). It is worth mentioning that the soil-structure interaction is not required to be modeled for the assumed soil type (type II with shear velocity in range of 375–750 m/s) and conventional fixed base modeling is reliable (Tabatabaiefar et al. 2012).

Table 1 Fundamental period of vibration of single degree of freedom systems in seconds (T)

Fig. 4

Model of nonlinear behavior for an SDOF system

3.2 Multi degree of freedom models

Two planar steel moment-resisting frames having 3 and 12 stories were modeled. The considered frames were designed according to AISC 360-16 (2016) and ASCE 7-16 (2017) provisions.

A more detailed description of the frame models is provided in Tables 2 and 3. The geometry and the elevation view of the frame models are also illustrated in Fig. 5.

Table 2 Properties of the frame models

Table 3 Steel sections of the frame models

Fig. 5

Elevation model of the steel frames

The nonlinear behavior of columns and beams for dynamic analyses were assigned based on FEMA356 (2000) and it is depicted in Fig. 6.

Fig. 6

Bilinear model of FEMA beam and column (D: end rotation or axial deformation, F: end moment or axial force, K_e: initial elastic slope, K_h: strain hardening slope, K_h/K_e = 0.02)

4 Description of selected earthquake ground motions

In this study, a total of 244 earthquake acceleration time histories from 122 earthquake events (longitudinal (LN) and transverse (TR) components) were employed for the dynamic analysis of the SDOF systems. A set of 30 acceleration time histories selected from the aforementioned ensemble were also utilized for the analysis of two MDOF planar steel frames.

Record selection was performed in a way that can be representative of a wide variety of peak ground acceleration (PGA), peak ground velocity (PGV) as well as PGA/PGV ratios as the indicator of frequency content (Zhu et al. 1988) and strong motion duration (T_d). Figure 7 depicts the dispersion of aforementioned parameters for selected earthquake ground motions.

Fig. 7

Descriptor parameters of selected records

All the earthquake ground motions were adopted from the Pacific Earthquake Engineering Research (PEER) center database. Earthquake records were selected in a way that the following criteria were satisfied: (i) magnitude (${M}_{w}$) of the ground motions varies between 6 and 7.62; (ii) the shortest distance from the site to the rupture surface (${R}_{rup}$) is less than or equal to 10 km (i.e., the selected records are near fault events); (iii) the average shear wave velocity of top 30 m of the site (${V}_{s30}$) which corresponds to the soil type and site condition varies between 375 m/s and 750 m/s conforming to site class C according to ASCE site classification.

The list of the considered earthquakes is shown in Table 4. Ground motions which were utilized for the analyses of MDOF steel frames are highlighted and signed with star mark. The term T_d in last column of the Table 4 indicates the interval of 5–95% of squared ground acceleration cumulative integral which is identified as the most suitable duration metric (Deierlein et al. 2012).

Table 4 Earthquake ground motions employed for the analyses of SDOF systems

5 Analysis procedure and results

5.1 Response of the SDOF systems

In this section, the implemented methodology and resulted outcomes are discussed. At first, all of the 244 acceleration time histories were scaled record by record so that their maximum acceleration value was equal to 1.0 g (i.e. each record was divided by its PGA). The 5–95% significant duration (${T}_{d}$) of each time history along with 2.0 s of the time history before the ${T}_{d}$ range was considered as total range of each time history. Then, a time interval of sufficient length with zero acceleration was inserted at the end of each mainshock time history.

It is worth noting that the aforementioned time interval was embedded at the end of the time histories in order to monitor the velocity response of the systems during free vibration. In fact, when successive ground motions (i.e., mainshock-aftershock seismic sequences) occur, there is often a time gap between the mainshock and the subsequent aftershocks which may last from a few minutes to even several days. Since the cost of analysis is of a great importance specially in the nonlinear time history analysis, an optimized estimation of the required time gap (i.e., a specified interval of the time with zero acceleration during which the structural model’s velocity response approaches a value close to zero or the time needed for the structure to stop free vibration.) is necessary to be determined. For this purpose, a sufficient time gap was applied at the end of the acceleration time histories to make sure that the velocity response of the SDOF systems reaches a value very close to zero ($V_{zero}$). In the current study, it is assumed that if the free vibration velocity response of the system becomes less than or equal to 0.1% of the maximum free vibration velocity response ($V_{max. f}$) of the system and it does not increase anymore, the structural model stops free vibration (Eq. (2)). In this study, the upper limit $V_{zero}$ in Eq. (2), was set to 0.1% of the $V_{max. f}$.

$$V_{system} \le V_{zero}$$

(2)

The time required for the free vibrations velocity of system to reach $V_{zero}$ was extracted using trial and error procedure. Zero acceleration interval of 50 s was initially considered. If the assumed interval was not enough for approaching zero velocity, the interval would be increased to 100 s. This procedure was applied iteratively until the required rest time was extracted with acceptable accuracy.

After performing dynamic time history analyses on SDOF systems, the velocity responses were processed and the required time for each SDOF system to stop free vibration (rest time) was extracted following the method discussed above. It should be noted that the same procedure was implemented for the MDOF systems supposing that the velocity responses of the roof level were considered for rest time estimation. Rest time of the SDOF systems were plotted against the 5–95% significant duration (${T}_{d}$) of ground motions. Figure 8 shows the resulted plots for the SDOF systems with fundamental period (T) of 1.0 s and 4.0 s.

Fig. 8

Calculated rest time for the SDOF systems versus strong motion duration: a SDOF system with fundamental period (T) of 1.0 s, b SDOF system with T = 4.0 s

In another try, rest time of the SDOF systems were normalized by 5–95% significant duration of the corresponding record and a comparison was carried out between the normalized rest time data series (R_T) and the significant duration (${T}_{d}$) of the earthquake records to observe the changing trend. Corresponding plots for the SDOF systems with T = 1.0 s and T = 4.0 s are illustrated in Fig. 9a, b, respectively.

Fig. 9

Normalized rest time (R_T) of the SDOF systems versus strong motion duration: a SDOF system with T = 1.0 s, b SDOF system with T = 4.0 s

Referring to Fig. 9a, b, it is obvious that the normalized rest time (R_T) of an SDOF system is strongly correlated with the strong motion duration of applied ground motions and as the strong motion duration increases, the normalized rest time decreases in a regular nonlinear trend, but results of the mere rest time (non-normalized data), versus strong motion duration (see Fig. 8) seem less encouraging. It seems that the rest time is not straightly related to the strong motion duration as it is depicted in Fig. 8, but by normalizing the evaluated rest time with respect to the corresponding strong motion duration of each earthquake record, the negative nonlinear correlation of the normalized rest time and the strong motion duration data series becomes evident.

The strong emerged relationship between the parameters R_T and T_d for the SDOF systems with fundamental period (T) ranging from 0.05 to 7.0 s, leads to curve fitting of data series. This way, evaluated normalized rest time of the SDOF systems (R_T) is expressed as the function of strong motion duration (T_d) and the fundamental vibration period (T) of the SDOF systems. Details on the computational tools and mathematical operations on data series are explained in the following section.

5.2 Proposed formulation and related mathematical computation

As mentioned in the earlier section, for each of the SDOF systems with a given vibrational period (T), the normalized rest time (R_T) data series were plotted against the strong motion duration (T_d) for all the 244 applied earthquake components. Therefore, 22 (number of SDOF systems) graphs illustrating R_T against T_d for each SDOF system such as the one in Fig. 9a were extracted. The observations showed that the normalized rest time data series (R_T) and the strong motion duration data series (T_d) are strongly correlated in a nonlinear reverse manner for all the cases. Accordingly, regression analyses were performed on each of the outcome graphs so as to find the curve that best fits to obtained graphs. In this study, the curve fitting technique utilizing the nonlinear least squares method was employed to extract the aforementioned curves or functions (Hansen et al. 2013). The general form of the function for the fitted curve is in the form of Eq. (3):

$$y = ax^{b} + c$$

(3)

where x indicates the strong motion duration of each earthquake (T_d), y is the estimated normalized rest time (R_{T, estimate}) with respect to T_d data. Constant parameters a, b and c are the coefficient of the equation which are obtained by fitting the assumed function to the observed data points. Thus Eq. (3) is converted to the following form in Eq. (4):

$$R_{T. estimate} = a(T_{d} )^{b} + c$$

(4)

By fitting the curve of the assumed form to each of the 22 observed datasets for SDOF systems, the coefficients a, b and c were determined. Examples of the fitted curve versus the observed data (obtained from the time history analyses) are shown in Fig. 10. It can be seen that the fitted curve matches well with the observed data points. A similar trend was resulted for other examined SDOF systems.

Fig. 10

Curves fitted to the normalized rest time (R_T) plotted versus the strong motion duration (T_d): a for T = 1.0 s, b for T = 4.0 s

In order to evaluate the robustness of the curve fitting, the percentage of error, defined in Eq. (5) is calculated:

$$Error \% = (( R_{T. estimate} - R_{T} )/ R_{T} ) \times 100$$

(5)

where $R_{T.estimate}$ represents the normalized rest time estimated from the fitted function and $R_{T}$ is the normalized required rest time obtained from the SDOF analysis.

As shown in Fig. 11, the absolute value of the error percentage is no more than the 5% meaning that the assumed curve is fitted well enough. Results of the remaining SDOF models are also analogous. Implementation of the curve fitting process resulted in the constant coefficients a, b and c for each of the SDOF systems.

Fig. 11

The percentage of difference between the rest time calculated from analysis and the rest time estimated using the fitted curve’s formula: a for T = 1.0 s, b for T = 4.0 s

By tracking the changes of the ‘a’ coefficient with regard to the changes of the fundamental vibration period of the SDOF systems, a linear relation between the two parameters was figured out that is illustrated in Fig. 12a. But variation of two other coefficients ‘b’ and ‘c’ with respect to changes of the vibrational period are nearly around zero value as shown in Fig. 12b, c, respectively. Hence, conservatively the upper limit of data was considered for these two coefficients.

Fig. 12

Curves fitted to the coefficients of the Eq. (3) plotted along with the obtained coefficients as a function of fundamental vibration period of SDOF systems: a for “a” coefficient, b for “b” coefficient, c for “c” coefficient

The curve fitting coefficients for SDOF systems with damping ratio ($\xi$) of 5% and hardening slope (h) of 3% is expressed in Eq. (6), Eq. (7) and Eq. (8):

$$a\left( T \right) = 21.8559\left( T \right) + 0.0258$$

(6)

$$b = - 0.9982$$

(7)

$$c = 0.0214$$

(8)

in which, T represents the fundamental vibration period of the SDOF system; $a\left( T \right)$ represents the ‘a’ coefficient as a function of the vibration period for an SDOF system. Now, Eq. (4) along with Eqs. (6), (7) and (8) can be combined and be rewritten in form of Eq. (9):

$$R_{T. estimate} = \left( {21.8559 T + 0.0258} \right)(T_{d} )^{ - 0.9982} + 0.0214$$

(9)

The proposed equation (Eq. (9)), estimates the optimum normalized rest time for a structure as a function of the vibration period (T) and the strong motion duration of the applied earthquake component (T_d). The Estimated normalized rest time ($R_{T. estimate}$), should finally be multiplied by T_d to obtain the required rest time for the structure (R) as follows:

$$R = T_{d} [ \left( {21.8559 T + 0.0258} \right)\left( {T_{d} )^{ - 0.9982} + 0.0214} \right]$$

(10)

The proposed formulation estimates the minimum required rest time for a nonlinear system with $\xi = 5\%$ and hardening slope (h) of 3% when subjected to the scaled ground motions. In order to develop the proposed formulation for application in a more general term, influences of the linearity of modeling, ground motion scaling, different hardening slope and the effect of various damping ratios were investigated. Results are explained comprehensively in the following sections.

5.3 Linearity versus nonlinearity

In addition to the nonlinear SDOF systems, a group of linear SDOF systems having only the linear part of the bilinear behavior and the same vibrational periods, were also modeled and analyzed. Results of the linear models as well as the nonlinear systems under scaled ground motions (assuming the damping ratio of 5%) are illustrated in Fig. 13a, b for instances.

Fig. 13

Normalized rest time (R_T) plotted against strong motion duration (T_d) for the linear SDOF system as well as the nonlinear SDOF system: a for an SDOF with T = 0.05 s, b for an SDOF with T = 7.0 s

It is inferred that no matter systems behave linearly or nonlinearly, the required rest time is identical. Therefore, the proposed formulation for the rest time calculation [Eq. (10)], is applicable for both the linear systems as well as the nonlinear systems.

5.4 Influence of ground motion scaling

Ground motion components were once applied as the free field records and in another try, they were scaled such that their peak ground acceleration (PGA) be equal to 1.0 time the ground acceleration (g or 9.806 m/s²). Rest time values for both the scaled and the free field record were extracted using analyses. A comparison between the normalized rest time of the nonlinear SDOF systems while subjected to the scaled ground motions and the same systems in case they were analyzed under the free field ground motions was conducted.

As is shown in Fig. 14, the effect of ground motion scaling can be ignored since the rest time obtained using scaled ground motion is same as the one yielded by the free field earthquake record. It should be noted that results shown in Fig. 13 (for nonlinear SDOF systems with 3% hardening slope and the 5% damping ratio) were confirmed for the remaining SDOF systems.

Fig. 14

Normalized rest time (R_T) plotted against strong motion duration (T_d) using scaled ground motions versus free field ground motions: a for T = 1.0 s, b for T = 4.0 s

5.5 Influence of hardening slope

Impact of defining different hardening slopes for nonlinear behavior of systems on the required rest time has also been investigated. Observing Fig. 15, it is readily figured out that the rest time outputs for the assumed hardening slope of 3% conforms to the results for the 1% hardening slope. Therefore, assuming other values for the hardening slope (h) parameter in the nonlinear description of models, is not going to influence on the required rest time for the system.

Fig. 15

Normalized rest time (R_T) plotted against the strong motion duration (T_d) assuming various hardening slopes for nonlinear behavior: a for T = 1.0 s, b for T = 4.0 s

5.6 Influence of damping ratio

A key factor that affects the required rest time of a system is damping ratio since this parameter is directly concerned with the energy dissipation in a system. It is expected that as the damping ratio increases, the free vibration of structural system after mainshock would be damped more rapidly.

Hence, the effect of above-mentioned parameter was examined for three groups of SDOF systems having damping ratio of 2.5%, 5% and 7.5% respectively. Rest time results for the three values of damping ratio are presented in Fig. 16. As the damping ratio decreases, the rest time curve moves upward meaning that the rest time demand rises up. Therefore, required rest time for system is correlated with the damping ratio conversely.

Fig. 16

Normalized rest time (R_T) plotted against the strong motion duration (T_d) data series using different damping ratios: a for T = 1.0 s, b for T = 4.0 s

To deal with the damping ratio effect on the rest time response of a system, ratio of normalized rest time of the SDOF systems while $\xi$ = 2.5% ($R_{T.2.5\% }$) to the normalized rest time of the systems while $\xi$ = 5% ($R_{T.5\% }$), was calculated and compared with $\xi_{5\% } /\xi_{2.5\% }$ ratio (which is equal to 0.05/0.025) for a sample SDOF system with T = 1.0 s and the result is shown in Fig. 16. It is shown that $R_{T.2.5\% } /R_{T.5\% }$ values are almost entirely close to the continuous line of data representing the $\xi_{5\% } /\xi_{2.5\% }$ value. For instance, R_T ratios mostly vary between 1.95 and 2.05 in Fig. 17a which means that the R_T ratios approach the $\xi_{5\% } /\xi_{2.5\% }$ value of that is equal to 2.0.

Fig. 17

Ratio of normalized rest time (R_T) versus strong motion duration (T_d) for an SDOF system with two different damping ratios: a for ${\varvec{\xi}}$ = 2.5%, b for ${\varvec{\xi}}$ = 7.5%

It was demonstrated that the following relation in Eq. (11) applies for all other examined SDOF systems:

$$\frac{{R_{T.\xi } }}{{R_{T.5\% } }} \cong \frac{{\xi_{5\% } }}{\xi }$$

(11)

in which $R_{T.\xi }$ represents the normalized rest time for damping ratio of interest ($\xi$), $R_{T.5\% }$ is the normalized rest time for $\xi$ = 5% and the parameters $\xi_{5\% }$ and $\xi$ are damping ratio of 5% and target damping, respectively.

The proposed formulation was extracted assuming the commonly used damping ratio of 5%. In order to generalize the application for any desired damping ratio and considering the damping effect, Eqs. (9), (10) and (11) were assembled and resulted in Eq. (12):

$$R_{\xi } = T_{d} \left( { \frac{{\xi_{5\% } }}{\xi }} \right)\left[ {\left( {21.8559 T + 0.0258} \right)\left( {T_{d} } \right)^{ - 0.9982} + 0.0214} \right]$$

(12)

where $R_{\xi }$ is the required rest time of the system for the arbitrary damping ratio of $\xi$. Therefore, Eq. (10) was modified in a way that it could deal with the damping ratio effect. Finally, the proposed formulation in Eq. (12) estimates the required rest time of a system as a function of input parameters: $T$ or fundamental vibration period of structure, $\xi$ or damping ratio of structure and $T_{d}$ or strong motion duration.

Regarding Eq. (12), if the term $T_{d}$ outside the brackets is multiplied by terms inside the brackets, the result would be:

$$R_{\xi } = \left( { \frac{{\xi_{5\% } }}{\xi }} \right)\left[ {\left( {21.8559 T + 0.0258} \right)\left( {T_{d} } \right)^{0.0018} + 0.0214 T_{d} } \right]$$

(13.1)

Since the power of term $T_{d}$ is infinitesimal, $(T_{d} )^{0.0018}$ can be assumed equal to 1.0 without loss of accuracy. As a result, Eq. (13.1) can be replaced by the simpler form of equation as expressed in Eq. (13.2):

$$R_{\xi } = \left( { \frac{{\xi_{5\% } }}{\xi }} \right)\left[ { \left( {21.8559 T + 0.0258} \right) + 0.0214 T_{d} } \right]$$

(13.2)

Since coefficient of $T$ in Eq. (13.2) is comparatively larger than the coefficient of $T_{d}$, sensitivity of Eq. (13.2) was investigated with respect to $T_{d}$ parameter. Upper limit for $T_{d}$ parameter was set to 120 s as was recommended by Xie et al. (2012a) in their study. Results of sample structures with fundamental period of 1.0 and 4.0 s (assuming 5% damping ratio) are illustrated in Fig. 18a, b, respectively. Figure 18c depicts the push curve fitted to the maximum values of $R_{\xi }$ which were achieved through Eq. (13.2) for all SDOF systems with various vibration periods. The above-mentioned curve is formulated in Eq. (13.3):

$$R_{\xi } = \left( { \frac{{\xi_{5\% } }}{\xi }} \right) \left( {22.0451 T + 2.594} \right)$$

(13.3)

While reliability of Eq. (12) would not be hurt by offering Eq. (13.3) based on results of sensitivity analyses, Eq. (13.3) can offer a simple as well as an easy-to-use formula, yet not highly conservative. In fact, Eq. (12) can be utilized in case a more accurate estimation is demanded. It is worth noting that for lower values of $T_{d}$, the difference between estimated values from Eqs. (13.3) and (12) goes up specially for structures with higher fundamental period ($T$). However, higher $T_{d}$ values lead to the minimized difference. Consequently, both Eqs. (12) and (13.3) can be employed confidently for estimating required rest time between earthquake sequences in dynamic analyses on a case-by-case basis (depending on targeted accuracy).

Fig. 18

Required rest time values estimated based on Eq. (12) versus Eqs. (13.2) and(13.3); a for a SDOF system with vibration period of 1.0 s, b for a SDOF system with vibration period of 4.0 s, c push curve fitted to maximum rest time values of SDOF systems with various fundamental periods

5.7 Response of MDOF steel frames and validation

Promising results of the SDOF systems encouraged the authors to investigate the proposed formulation for the MDOF systems. For this purpose, two steel moment resisting frames with 3 and 12 number of stories representing low-rise and mid-rise frames respectively were modeled. Design details and other considerations of structural models were explained previously in Sect. 3.

A set of 30 scaled ground motions were applied to each of the steel frames. The ground motions were multiplied by a scale factor to match the average response spectrum for the 10% probability of exceedance in 50 years (10/50) hazard level. Also, damping ratio of 5% was assumed for nonlinear dynamic analyses of MDOF systems.

Required rest time for each of the frames were calculated based on the procedure discussed earlier in Sect. 5.1. Obtained rest time values were then compared to the estimated rest time determined using the proposed formulation in this paper [Eq. (12) ]. Figure 19 illustrates the required rest time values for each of the frames versus the estimated rest time values extracted from the proposed formulation.

Fig. 19

Required rest time obtained from the analysis versus the estimated rest time using the proposed formulation: a for the 3-story steel frame, b for the 12-story steel frame

It is observed that the proposed formula offers a reliable estimation for the required rest time and the differences between the estimated values and the calculated values are almost negligible especially in the low-rise frame. In fact, the proposed formula estimates the rest time conservatively.

The agreement between the rest time data obtained from the nonlinear analyses of frames and the rest time data estimated using the proposed formula was also investigated. As the results in Fig. 20 reveal, there is a satisfactory agreement between calculated values and the estimated ones. Therefore, the proposed formulation gives a reliable estimation both for SDOF systems as well as MDOF systems.

Fig. 20

Normalized rest time (R_T) plotted against the strong motion duration (T_d) data series using different damping ratios: a for T = 1.0 s, b for T = 4.0 s

6 Discussion

6.1 Detailed examination of required rest time against system period and strong motion duration

To better understand the influence of strong motion duration on the required rest time of structures with different vibration periods, maximum and minimum rest time for each of the vibration periods considering different strong motions (Td), were calculated. Rest time data is displayed as a function of vibration periods (T) for the maximum and minimum rest time values in Fig. 21. From Fig. 21, it is readily observed that the rest time is generally increases as the system’s vibration period increases.

Fig. 21

Maximum and minimum rest time plotted against the vibration period

Figure 21 also points out to the difference between maximum and minimum required rest time in short periods compared to the long periods.

It is shown that the difference between the maximum and minimum rest times would be more apparent in long periods. In fact, for systems with vibration period of less than 1.0 s, the differences are almost negligible. Since the maximum and minimum rest time values were calculated considering different strong motion durations, it is inferred that the influence of strong motion duration (Td) on the required rest time of a system with vibrating period of less than 1.0 s (short periods), is slight and can be ignored but as the period increases (over 1.0 s), the impact of strong motion duration appears to be more effective. As an example, for the vibration period of a system being equal to 7.0 s, the difference between the maximum rest time and minimum rest time (which were calculated for two different values of T_d), is around 20 s but the difference for a system with vibrating period of 1.0 s is close to zero value. Therefore, rest time of a system depends strongly on the vibrating period. Figure 21, also gives a general insight into the required rest time for an applicable range of vibrating periods. It is worth mentioning that the proposed formula conservatively estimates the upper limit value for the rest time.

6.2 Scope of the study

It is valuable to clearly explain the limitations and scope of this study. This would greatly help better understanding the main goal of this work, meanwhile it can make future development of this study easier.

As stated earlier, the prime objective of this work was developing a framework to estimate the time gap that is required to be considered between mainshock-aftershock sequences in dynamic analyses of structures. Results showed that the time gap between mainshock-aftershock sequence can be efficiently estimated as a function of fundamental period of system and strong motion duration of earthquakes. Future developments of this study could address the following criteria so that the proposed formulation could be generalized for any type of application.

In this work, a large number of near fault records belonging to site class C (according to ASCE site classification) have been utilized. Including mid and far fault events recorded on other type of sites would be of future interest.

The effect of stiffness degradation and strength deterioration was not considered in structural modeling. Analyzing structures by taking this phenomenon into account is recommended.

Finally, performing analyses on structures of different heights with various lateral force resisting systems would be strongly recommended for future development of this study.

The above-mentioned developments can be the subject of future studies which may lead to generation of a more comprehensive formula for estimating required time gap between earthquake sequences in dynamic analyses.

7 Conclusions

In this paper, a novel formulation is introduced to estimate the required rest time between mainshock and aftershock in nonlinear dynamic analyses of structures. The proposed formula estimates the required rest time to be considered between sequences as a function of structural system’s properties (vibrational period) and the ground motions’ feature (strong motion duration). A set of 244 ground motion components were utilized for the nonlinear dynamic analyses of SDOF systems. 30 earthquake records were also used for the analyses of steel frames as well as investigating the validity and reliability of proposed formulation in MDOF systems. In order to generalize the proposed formulation, influences of different factors including structural behavior (linearity or nonlinearity), ground motion scaling, hardening slope in bilinear behavior and damping ratio were investigated. Finally, the proposed formulation was validated for low-height and mid-rise MDOF steel frames. Important conclusions accomplished in this study are outlined:

• Required rest time is strongly correlated with strong motion duration and vibration period of the structure. Thus, the proposed formulation expresses the required rest time as a function of the aforementioned parameters.

• Rest time results for linear models were analogous to the rest time results of the nonlinear models. Hence, the required rest time for a system does not depend on the level of nonlinearity that a system experiences. Consideration of stiffness degradation and strength deterioration is recommended to be investigated in future studies.

• Whether using the scaled earthquake ground motions or the free field ones, the required rest time remains identical. Therefore, the effect of ground motion scaling on the required rest time is ignored.

• Application of different hardening slopes in the bilinear modeling of structural behavior demonstrated that the required rest time of a structure is not affected by this parameter.

• Investigation of the damping ratio impact on the required rest time has shown that as the damping ratio decreases, rest time demand increases. The ratio of rest time demand of a system (with arbitrary damping ratio) to the rest time of a system with 5% damping was proved to be proportioned to reverse ratio of damping percentages. In this regard, the proposed formula was modified to be generalized for an arbitrary damping ratio.

• A great agreement was observed between the estimated rest time from the proposed formula and the required rest time computed using the nonlinear analyses of the steel frames. So, the proposed formula can be confidently applied for estimating the required rest time of MDOF systems.