Introduction

In the history of structural engineering, some of the methods have been developed to reduce structural responses to control vibrations under lateral forces (Chang & Soong, 1980; Cheng et al., 2008; Dyke et al., 1996; Kaveh et al., 2020a; Sadek et al., 1995; Singh & Moreschi, 2001). These methods are used to improve structural performance and reduce structural damage. The tuned mass damper is one of the passive control tools that, consists of mechanical details including mass, spring, and viscous damper to reduce the structure response. The main idea of vibration control using the TMD was developed by Den Hartog and studied the response of the undamped structures under harmonic loading by adding a tuned mass with spring (Den Hartog 1956).

Considering the effect of TMD parameters on the seismic behavior of controlled structures, some studies have different approaches to optimally use the capacity of the control system (Fujino & Abe, 1993; Luft, 1979; Warburton, 1982). Hadi and Arfiadi (1998) used a genetic algorithm to optimize the TMDs parameters. Lee et al. (2006) presented a new method for optimization of the components of TMDs. In recent decades, many meta-heuristic methods have been proposed inspired by the phenomena of physics and nature to optimize engineering problems. Many of these algorithms were used to optimum design of the TMDs (Bekdas & Nigdei, 2011; Farzam & Kaveh, 2020; Farzam et al., 2020; Kaveh et al., 2015a, 2015b, 2020b).

Various types of uncertainties are traceable and identifiable in all steps of the design, construction, and maintenance of structural systems. These uncertainties can be evaluated using probabilistic models, and reliability analysis can be used to assess the safety levels of structural systems based on the probability of failure (Ditlevsen, 1982). In general, for estimating the probability of failure based on the probabilistic model and reliability analysis in the structure, various analytical methods such as the first-order reliability method (FORM) (Liu & Der Kiureghian, 1991), second-order reliability method (SORM) (Der Kiureghian & Stefano, 1991), optimization algorithms (Kaveh et al., 2014) simulation methods (Azar et al., 2015; Rashki et al., 2012), response surfaces (Chakraborty & Chowdhury, 2016; Goswami et al., 2016; Hadidi et al., 2017) and neural networks (Vazirizade et al., 2017) are used.

Because of the existence of uncertainty in structural control systems, the probability of their instability can be investigated (Spencer et al., 1992). Based on probabilistic optimal control methods, the uncertainties of the structural parameters are considered to increase the safety and reliability of the structure (Spencer et al., 1994). In some studies, the effect of uncertainty in control devices on the reliability of the structure has been investigated (Gavin & Zaicenco, 2007; Guo et al., 2002).

Recently, design methods under uncertainty have been widely developed. The reliability-based design optimization is used to minimization of the probability of failure considering uncertainties that exist in the system. Several studies have been proposed for reliability-based optimization (Doan et al., 2018; Keshtegar & Hao, 2018; Lehky et al., 2018; Tu et al., 1999). To achieve a reliable and economical design, the RBDO is widely used in structural optimization problems (Huu et al., 2016; Le et al., 2017; Liu & Paavola, 2015; Zhao et al., 2016). Also, some others studied reliability-based optimization in structures equipped with passive control devices (Altieri et al., 2018; Chakraborty & Roy, 2011; Hadidi et al., 2016; Leger et al., 2017; Mrabet et al., 2015).

Another reliability-based method is the inverse reliability method, which is classified in the category of optimization methods with probabilistic constraints. An inverse reliability analysis strategy is defined based on the reliability analysis that, uses percentile performance to satisfy probabilistic constraints. Der Kiureghian et al. (1994) proposed an iterative algorithm based on the modified HL-RF scheme. In some studies, this method is used to optimize for target reliability (Cheng et al., 2007; Du et al., 2004; Li & Foschi, 1998).

In this paper, according to various methods in optimization problems, the optimization of a structure equipped with a passive tuned mass damper in deterministic and uncertainty conditions is examined. In the deterministic case, the optimal design of the tuned mass damper is done using the meta-heuristic algorithm. Then, by using the reliability analysis method, the reliability index for this structure is calculated, and sensitivity analysis is performed for the structure based on the damper parameters. Also, in uncertainty cases, optimum design of the TMD is done with reliability-based design optimization and inverse reliability methods. In reliability-based methods, the optimum design is performed based on different target reliability, and the exploration ability of these methods in the design search space is evaluated.

Reliability analysis

Reliability is defined as the probability of a limit state function g(X) greater than zero, P{g(X) > 0} (Du, 2005). In other words, reliability equals the probability of random variables X, falling into the safe region, defined by g(X) > 0. The probability of failure is defined as the probability P{g(X) < 0}, and equals to the probability of random variables X, which existed in the fracture region defined by g(X) < 0. If the probability distribution function of the random variables X is \(f_{x} \left( x \right)\), then the probability of failure can be calculated using the following integral (Du, 2005):

$$ P_{{\text{f}}} = P\{ g\left( X \right) < 0\} = \mathop \smallint \limits_{g\left( X \right) < 0}^{ } f_{x} \left( X \right){\text{d}}x $$
(1)

and reliability can be calculated as follows:

$$ {\text{Reliability}} = 1 - P_{{\text{f}}} = P\left\{ {g\left( X \right) > 0} \right\} = \mathop \smallint \limits_{g\left( X \right) > 0}^{ } f_{x} \left( X \right){\text{d}}x. $$
(2)

The probability of failure can be determined approximately according to the reliability index (β) in first-order reliability method (FORM) as follows (Der Kiureghian, 2005):

$$ P_{{\text{f}}} = \mathop \smallint \limits_{g\left( X \right) \le 0}^{ } \ldots \smallint f_{X} \left( x \right){\text{d}}X \approx {\Phi }\left( { - \beta } \right), $$
(3)

where \(P_{{\text{f}}}\) is failure probability, \(f_{x} \left( X \right)\) is the probability distribution function and \(g\left( X \right)\) is the limit state function that divides design regions into failure and safe as \(g\left( X \right) < 0\) and \(g\left( X \right) > 0\), respectively, by using the basic random variables X. In many engineering problems, the limit state function g(X) is a complex and implicit function. Also, \(\Phi \left( . \right)\) is the cumulative distribution function.

To simplify the calculation, all random variables \(X = \left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right)\) with desired distributions are transferred to \(U = \left( {u_{1} ,u_{2} , \ldots ,u_{n} } \right)\) variables with standard normal distribution. So, the probability integral can be written as follows:

$$ p_{{\text{f}}} = P\left\{ {g\left( U \right) < 0} \right\} = \mathop \smallint \limits_{g\left( U \right) < 0}^{ } \phi_{u} \left( u \right){\text{d}}u. $$
(4)

where \(\phi_{u} \left( u \right)\) is probability distribution function (PDF) in U space.

Also, in the FORM analysis Taylor's first expansion is used to linearization of limit state function \(g\left( U \right)\) as follows (Der Kiureghian, 2005):

$$ g\left( U \right) \approx g\left( {u^{*} } \right) + \nabla g\left( {u^{*} } \right)\left( {U - u^{*} } \right)^{{\text{T}}} , $$
(5)

where \(u^{*}\) is the expansion point and \(\nabla g\left( {u^{*} } \right)\) is the gradient of the \(g\) function at \(u^{*}\).

In the standard normal space which the random variables are statistically independent and the limit state function \(g\left( {\mathbf{u}} \right)\) is linear, the reliability index (\(\beta\)), can be defined as the shortest distance from the failure surface (\(g\left( {\mathbf{u}} \right) = 0\)) to the origin. So, the probability of failure (\(P_{{\text{f}}}\)) is calculated by:

$$ P_{{\text{f}}} = \Phi \left( { - \beta } \right) = 1 - \Phi \left( \beta \right), $$
(6)

where

$$ \Phi \left( \beta \right) = \mathop \smallint \limits_{ - \infty }^{\beta } \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{1}{2}u^{2} } \right){\text{d}}u. $$
(7)

Thus, the reliability index may be described by Lee et al., (2002):

$$ {\text{find}}\;{\mathbf{u}};{\text{ which minimizes}}\;\;\beta = \left| u \right| = \sqrt {u^{{\text{T}}} u} . $$
$$ {\text{subjected to}}\;g\left( {\mathbf{u}} \right) = 0. $$

The primary goal in the FORM is to search for the most probable point (MPP, i.e., \(U^{*}\)), that is a point located closest to the origin in transformed standard normal space, consequently, \(\beta = U^{*}\) (Lee et al., 2002).

Hasofer and Lind introduced an iterative algorithm to find the MPP (Hasofer & Lind, 1974). This method is used for variables with normal distribution, then Rackwitz and Flessler (Rackwitz & Flessler 1978) developed this algorithm for random variables with any desired distribution. Liu and Der Kiureghian (Liu & Der Kiureghian, 1991) improved the HL-RF method to enhance the convergence rate using a merit function. Santosh et al. (2006) improved the HL-RF method based on the Armijo rule. Recently for searching the MPP, there are various FORM algorithms such as finite-step length (Gong & Yi, 2011), non-gradient-based algorithm (Gong et al., 2014), conjugate gradient (Farsani & Keshtegar, 2015), chaotic conjugate search direction (Keshtegar, 2016), and stability transformation method (Meng et al., 2017). The improved HL-RF method is formularized by using the steepest descent search direction to find the MPP.

Modified HL-RF method

The iterative equation of the HL-RF algorithm for FORM can be defined according to:

$$ U_{k + 1} = U_{k} + s_{k} d_{k} , $$
(8)

where \(s_{k}\) is the step size. In the standard HL-RF method, the step size is assumed as 1. \(d_{k}\) is search direction vector, that can be calculated as follows Makhduomi et al., (2017):

$$ d_{k} = \frac{{\nabla^{{\text{T}}} g\left( {U_{k} } \right)U_{k} - g\left( {U_{k} } \right)}}{{\nabla^{{\text{T}}} g\left( {U_{k} } \right)\nabla g\left( {U_{k} } \right)}}\nabla g\left( {U_{k} } \right) - U_{k} , $$
(9)

in which \(\nabla g\left( {U_{k} } \right)\) is gradient vector of the limit state function g() at point \(U_{k}\), and for random variables with normal distribution:

$$ \nabla g\left( {U_{k} } \right) = \left\{ {\frac{\partial g}{{\partial u_{1} }},\frac{\partial g}{{\partial u_{2} }}, \ldots ,\frac{\partial g}{{\partial u_{n} }}} \right\} = \left\{ {\sigma_{1} \frac{\partial g}{{\partial x_{1} }}, \sigma_{2} \frac{\partial g}{{\partial x_{2} }}, \ldots ,\sigma_{n} \frac{\partial g}{{\partial x_{n} }}} \right\}. $$
(10)

According to Eq. (8), the step size and search direction are two effective components in the iterative HL-RF equation. This iterative equation can be controlled based on the step size to find MPP. Therefore, the iterative equation of improved HL-RF (iHL-RF) can be obtained from Eq. (8), where \(\alpha_{k}\) is the adjusted step size. The step size is regulated using the merit function as follows:

$$ m\left( {U_{k} } \right) = \left\| {U_{k} - \frac{{\nabla^{{\text{T}}} g\left( {U_{k} } \right)U_{k} }}{{\nabla^{{\text{T}}} g\left( {U_{k} } \right)\nabla g\left( {U_{k} } \right)}}} \right\|\nabla g\left( {U_{k} } \right)^{2} + \frac{{g\left( {U_{k} } \right)^{2} }}{{g\left( {U_{0} } \right)^{2} }}. $$
(11)

As it is known, the merit function has a positive value \(m\left( {U_{k} } \right) \ge 0\), and it is calculated based on the previous results as well as the HL-RF method. Therefore, the step size can be calculated as follows Makhduomi et al., (2017):

$$ s_{k + 1} = \left\{ {\begin{array}{*{20}c} {\frac{{m\left( {U_{k - 1} } \right)}}{{m\left( {U_{k} } \right)}}s_{k} m\left( {U_{k} } \right) \ge m\left( {U_{k - 1} } \right)} \\ {s_{k} m\left( {U_{k} } \right) < m\left( {U_{k - 1} } \right).} \\ \end{array} } \right. $$
(12)

The first step size is assumed as 1.5 (i.e., \(s_{0} = 1.5\)). According to the adaptive step size in Eq. (12), it can be concluded that, \(s_{k + 1} \le s_{k}\).

In the HL-RF algorithm, similar to other optimization methods, the convergence criterion is used. First, the design point should be placed close to the limit state surface (Du, 2005):

$$ \left| {\frac{{g\left( {U^{*} } \right)}}{{g_{0} }}} \right| \le e_{1} . $$
(13)

That, \(g_{0}\) is a scale factor, usually, the initial step value of the limit state function, and \(e_{1}\) is a threshold that is assumed to be about 0.001. Secondly, the design point should be the closest point to the origin on the limit state surface. For this case, this should be the gradient projection point. For example, the gradient vector of the limit state function just has to pass the origin. This convergence criterion is defined as:

$$ \left\| {U^{*} - \left( {\alpha^{{\text{T}}} U^{*} } \right)\alpha } \right\| \le e_{2} , $$
(14)

that \(e_{2}\) is a threshold of about 0.001. \(\alpha\) is the importance vector that is a unit vector, so by a scaling to \(U^{*}\) this criterion is expressed as:

$$ 1 - \frac{{\alpha^{{\text{T}}} U^{*} }}{{\left\| {U^{*} } \right\|}} \le e_{2} . $$
(15)

In FORM analysis, the \(\alpha\) vector can be defined by the negative and normalized version of the gradient vector:

$$ \alpha = - \frac{\nabla g}{{\left\| {\nabla g} \right\|}}. $$
(16)

As the reliability index equals to \(\beta = \alpha^{T} U^{*}\). Thus,

$$ \alpha = \frac{\partial \beta }{{\partial U^{*} }}. $$
(17)

This vector is used to display the relative importance of variables. This is the primary importance vector for the variables that define in the U-space. The higher absolute value of α is the most important variable.

Inverse reliability problem

The definition of an inverse reliability problem is that an unknown parameter in a reliability problem is determined in such a way that the reliability index equals a predetermined amount. An inverse reliability problem is introduced to determine the value of a design variable for a certain value of the reliability index. Der Kiureghian et al. proposed an iterative algorithm based on the modified HL-RF method for solving inverse reliability problems (1994). The limit state function was defined as a function of random variables vector and a deterministic design parameter θ.

It is assumed that, \(\theta\) is a parameter of the limit state function \(G\left( {u,\theta } \right) = g\left( {x,\theta } \right)\), so \(\theta\) is determined in such a way that the reliability index is equal to a target value \(\beta = \beta_{t}\). In engineering problems, θ can be selected as one of the structural design variables for achieving specific reliability.

Inverse reliability problem is defined as follows:

$$ \begin{aligned} \left\| u \right\| - \beta_{t} & = 0 \\ u + \frac{\left\| u \right\|}{{\left\| {\nabla_{u} G\left( {u,\theta } \right)} \right\|}}\nabla_{u} G\left( {u,\theta } \right) & = 0 \\ G\left( {u,\theta } \right) & = 0, \\ \end{aligned} $$
(18)

where \(\nabla_{u}\) is the gradient operator relative to u. The proposed algorithm for solving this equation is similar to the modified HL-RF algorithm used to solve FORM. Similar to Eq. (8) in the FORM problems, the inverse reliability problem-solving algorithm is as follows:

$$ \left[ {\begin{array}{*{20}c} {u_{k + 1} } \\ {\theta_{k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {u_{k} } \\ {\theta_{k} } \\ \end{array} } \right] + s_{k} d_{k} \;{\text{with}}\;0 < s_{k} \le 1, $$
(19)

which \(d_{k}\) is direction search, \(s_{k}\) is a step length, and the merit function is defined as:

$$ f\left( {u,\theta } \right) = f^{\left( 1 \right)} \left( {u,\theta } \right) + f^{\left( 2 \right)} \left( {u,\theta } \right). $$
(20)

The merit function f consists of two subsets \(f^{\left( 1 \right)}\) and \(f^{\left( 2 \right)}\). The \(f^{\left( 1 \right)}\) confirms that the search point converges to a point on the boundary of limit state surface, and the \(f^{\left( 2 \right)}\) confirms the reliability index converges to the target reliability index at the search point as follows:

$$ f^{\left( 1 \right)} \left( {u,\theta } \right) = \frac{1}{2}\left\| {u - \frac{{\nabla_{u} G\left( {u,\theta } \right)^{{\text{T}}} .u}}{{\nabla_{u} G\left( {u,\theta } \right)^{2} }}\nabla_{u} G\left( {u,\theta } \right)} \right\|^{2} + \frac{1}{2}c_{1} G\left( {u,\theta } \right)^{2} $$
(21)
$$ f^{\left( 2 \right)} \left( {u,\theta } \right) = \frac{1}{2}c_{2} \left( {\left\| u \right\| - \beta_{t} } \right)^{2} $$
(22)

To determine the search direction \(d_{k}\), similar to the FORM analysis, the linear expansion of the limit state function at the design point can be written:

$$ G\left( {u,\theta } \right) = G\left( {u_{k} ,\theta_{k} } \right) + \left( {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right),u - u_{k} } \right) + \frac{{\partial G\left( {u_{k} ,\theta_{k} } \right)}}{\partial \theta }\left( {\theta - \theta_{k} } \right) $$
(23)

so:

$$ u = - \beta_{t} \frac{{\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)}}{{\left\| {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)} \right\|}} $$
(24)
$$ \theta = \theta_{k} + \frac{{\left[ {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right),u_{k} } \right] - G\left( {u_{k} ,\theta_{k} } \right) + \beta_{t} \left\| {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)} \right\|}}{{\frac{{\partial G\left( {u_{k} ,\theta_{k} } \right)}}{\partial \theta }}} $$
(25)

the search direction is as follows:

$$ d_{k}^{\left( 2 \right)} = \left[ \begin{gathered} - \beta_{t} \frac{{\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)}}{{\left\| {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)} \right\|}} - u_{k} \hfill \\ \frac{{\left[ {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right),u_{k} } \right] - G\left( {u_{k} ,\theta_{k} } \right) + \beta_{t} \left\| {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)} \right\|}}{{\frac{{\partial G\left( {u_{k} ,\theta_{k} } \right)}}{\partial \theta }}} \hfill \\ \end{gathered} \right]. $$
(26)

Intuitively, a combination of directions \(d_{k}^{\left( 1 \right)}\) and \(d_{k}^{\left( 2 \right)}\) can provide a more balanced search path. The expansion of \(d_{k}^{\left( 1 \right)}\) is as follows:

$$ d_{k}^{\left( 1 \right)} = \left[ {\begin{array}{*{20}c} {\frac{{\left[ {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right),u_{k} } \right] - G\left( {u_{k} ,\theta_{k} } \right)}}{{\left\| {\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right)} \right\|^{2} }}\nabla_{u} G\left( {u_{k} ,\theta_{k} } \right) - u_{k} } \\ 0 \\ \end{array} } \right], $$
(27)

the new direction search vector is as follows:

$$ d_{k} = a_{1} d_{k}^{\left( 1 \right)} + a_{2} d_{k}^{\left( 2 \right)} \;{\text{with}}\;a_{1} + a_{2} = 1. $$
(28)

An appropriate choice for \(a_{1}\) and \(a_{2}\) is as follows:

$$ a_{1} = \frac{{f^{\left( 1 \right)} \left( {u_{k} ,\theta_{k} } \right)}}{{f\left( {u_{k} ,\theta_{k} } \right)}} $$
(29)
$$ a_{2} = \frac{{f^{\left( 2 \right)} \left( {u_{k} ,\theta_{k} } \right)}}{{f\left( {u_{k} ,\theta_{k} } \right)}} $$
(30)

Colliding bodies optimization algorithm (CBO)

The Colliding bodies optimization algorithm is defined based on a collision between some pair of bodies, and after the collision, these bodies move toward minimum energy level (Kaveh & Mahdavi, 2014). Consider two moving bodies with masses of \(m_{1}\) and \(m_{2}\) and velocities of \(v_{1}\) and \(v_{2}\), in which one object collides with another object. According to the laws of physics, the total momentum and energy of the system after and before the collision are conserved. It can be expressed as:

$$ m_{1} v_{1} + m_{2} v_{2} = m_{1} v_{1}^{^{\prime}} + m_{2} v_{2}^{^{\prime}} $$
(31)

and

$$ \frac{1}{2}m_{1} v_{1}^{2} + \frac{1}{2}m_{2} v_{2}^{2} = \frac{1}{2}m_{1} v_{1}^{^{\prime} 2} + \frac{1}{2}m_{2} v_{2}^{^{\prime} 2} + Q $$
(32)

where \(v_{1}\), \(v_{2}\), \(v_{1}^{^{\prime}}\) and \(v_{2}^{^{\prime}}\) are the velocities of the bodies before and after the collision respectively. \(m_{1}\) and \(m_{2}\) are the masses of the first and second body, respectively; also Q is the kinetic energy loss due to collision.

After a collision, the velocities of bodies pair can be determined as:

$$ v_{1}^{^{\prime}} = \frac{{\left( {m_{1} - \varepsilon m_{2} } \right)v_{1} + \left( {m_{2} + \varepsilon m_{2} } \right)v_{2} }}{{m_{1} + m_{2} }} $$
(33)
$$ v_{2}^{^{\prime}} = \frac{{\left( {m_{2} - \varepsilon m_{1} } \right)v_{2} + \left( {m_{1} + \varepsilon m_{1} } \right)v_{1} }}{{m_{1} + m_{2} }} $$
(34)

where \(\varepsilon\) is coefficient of restitution (COR) of two colliding bodies, which defined as:

$$ \varepsilon = \frac{{\left| {v_{2}^{^{\prime}} - v_{1}^{^{\prime}} } \right|}}{{\left| {v_{2} - v_{1} } \right|}} = \frac{{v^{\prime}}}{v} $$
(35)

for realistic objects, \(\varepsilon\) is in the range of 0 and 1.

In the CBO algorithm, the agents \(X_{i}\) are assumed to be the Colliding Bodies (CB). The particles set are divided into two same groups including stationary and moving particles, where the particles move towards each other, and a collision occurs between pairs of particles. After this event, the positions of the particles are updated according to their new velocities.

A summary of the steps in the CBO algorithm is as follows:

Step 1. The initial positions of CBs are generated randomly in the search space:

$$ X_{i}^{0} = X_{\min } + {\text{rand}}\left( {X_{\max } - X_{\min } } \right) i = 1,2, \ldots , 2n $$
(36)

where \(X_{i}^{0}\) is the initial value of the ith CB; \(X_{\min }\) and \(X_{\max }\) are the lower and upper bound of the variables; rand is a random value in the range of 0 to 1, and 2n is the number of CBs.

Step 2. The mass of the body for each CB is determined as:

$$ m_{k} = \frac{{\frac{1}{fit\left( k \right)}}}{{\mathop \sum \nolimits_{i = 1}^{n} \frac{1}{fit\left( i \right)}}} k = 1,2, \ldots , 2n $$
(37)

where fit(i) illustrates the cost of the ith agent. It is clear that a CB with a large mass displays a good performance than the lightest ones.

Step 3. The CBs sorted based on the cost in increasing order. The sorted CBs are divided into two same groups. The good CBs are stationary bodies with zero velocity before the collision. So:

$$ v_{i} = 0 i = 1,2, \ldots , n. $$
(38)

The bad CBs are moving agents, that move toward the stationary agents. These moving bodies have a velocity of before collision as follows:

$$ v_{i} = x_{i} - x_{i - n} i = n + 1, \ldots , 2n $$
(39)

where \(x_{i}\) and \(x_{i - n}\) are the position vectors of the i-th CB in the moving group and its pair in the stationary group, respectively.

Step 4. After the collision, the velocity of particles in each group is determined as follows:

After the collision the moving CBs have velocity as follows:

$$ v_{i}^{^{\prime}} = \frac{{\left( {m_{i} - \varepsilon m_{i - n} } \right)v_{i} }}{{m_{i} + m_{i - n} }} i = n + 1, \ldots , 2n $$
(40)

and, the velocity of stationary CBs is:

$$ v_{i}^{^{\prime}} = \frac{{\left( {m_{i + n} + \varepsilon m_{i + n} } \right)v_{i + n} }}{{m_{i} + m_{i + n} }} i = 1, \ldots , n $$
(41)

where \(\varepsilon\) is COR that controls the exploration and exploitation rates. So The COR decreases linearly from unit value to zero and is defined as:

$$ \varepsilon = 1 - \frac{{{\text{iter}}}}{{{\text{iter}}_{\max } }} $$
(42)

where iter and \({\text{iter}}_{{{\text{max}}}}\) are the numbers of current and maximum iterations respectively.

Step 5. The new positions of CBs are determined based on the velocities of CBs after the collision. So, the new positions of moving CBs are:

$$ X_{i}^{{{\text{new}}}} = X_{i - n} + {\text{rand}}^{o} v_{i}^{^{\prime}} i = n + 1, \ldots , 2n. $$
(43)

Also, the new position of each stationary CB is:

$$ X_{i}^{{{\text{new}}}} = X_{i} + {\text{rand}}^{o} v_{i}^{^{\prime}} i = 1, \ldots , n. $$
(44)

where \(X_{i}^{{{\text{new}}}}\) is the new position of the i-th moving and stationary CB after the collision.

Step 6. The solution route is repeated from Step 2 until the termination criterion is satisfied.

Passive structural control: tuned mass dampers

The equation of motion for an N-degree of freedom structural model with shear frame system equipped with tuned mass damper that, installed at the top floor can be written as:

$$ M\ddot{X} + C\dot{X} + KX = P\left( t \right) $$
(45)

where M, C, K are mass, stiffness and damping matrices with the formulations as follow:

$$ M = \left[ {\begin{array}{*{20}c} {m_{1} } & & & & \\ & {m_{2} } & & & \\ & & {::} & & \\ & & & {m_{N} } & \\ & & & & {m_{d} } \\ \end{array} } \right] $$
(46)
$$ K = \left[ {\begin{array}{*{20}c} {k_{1} + k_{2} } & { - k_{2} } & & & & \\ { - k_{2} } & {k_{2} + k_{3} } & { - k_{3} } & & & \\ & { - k_{3} } & . & . & & \\ & & . & . & {k_{N} + k_{d} } & {k_{d} } \\ & & & & {k_{d} } & {k_{d} } \\ \end{array} } \right] $$
(47)
$$ C = \left[ {\begin{array}{*{20}c} {c_{1} + c_{2} } & { - c_{2} } & & & & \\ { - c_{2} } & {c_{2} + c_{3} } & { - c_{3} } & & & \\ & { - c_{3} } & . & . & & \\ & & . & . & {c_{N} + c_{d} } & {c_{d} } \\ & & & & {c_{d} } & {c_{d} } \\ \end{array} } \right] $$
(48)
$$ X\left( t \right) = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \ldots & {x_{N} } & {x_{d} } \\ \end{array} } \right] $$
(49)

where \(m_{i}\), \(k_{i}\) and \(c_{i}\) is the mass, stiffness and damping of the i-th floor (i = 1, 2, …, N) respectively; and \(m_{d}\), \(k_{d}\) and \(c_{d}\) are the mass, stiffness and damping of tuned mass damper, respectively. Also, \(x_{i}\) represent the lateral displacement of i-th floor.

The equation of motion can be solved by state-space equation as:

$$ \dot{Z}\left( t \right) = AZ\left( t \right) + BP\left( t \right) $$
(50)
$$ Y\left( t \right) = RZ\left( t \right) + QP\left( t \right) $$
(51)

where Z(t) is the state vector, and A and B are the system states. Also, R and Q are the system matrices where defined based on the type of the expected output Y.

$$ Z\left( t \right) = \left[ {\begin{array}{*{20}c} {X\left( t \right)} \\ {\dot{X}\left( t \right)} \\ \end{array} } \right] $$
(52)
$$ A = \left[ {\begin{array}{*{20}c} 0 & I \\ { - M^{ - 1} .K} & { - M^{ - 1} .C} \\ \end{array} } \right] $$
(53)
$$ B = \left[ {\begin{array}{*{20}c} 0 \\ {M^{ - 1} } \\ \end{array} } \right] $$
(54)

It should be noted that, if the external loading is the base acceleration (earthquake loading), vector P(t) can be defined as:

$$ P\left( t \right) = M\left\{ 1 \right\}_{N + 1} \ddot{x}\left( t \right)_{g} $$
(55)

Formulation of problem

The performance of a structure equipped with a tuned mass damper is influenced by the values of damper parameters. Therefore, by solving an optimization problem, the tuned mass damper can be optimally designed. In this section, the strategies used to optimize the tuned mass damper parameters are described.

Optimization strategy 1, meta-heuristic optimization method

Meta-heuristic methods are generally used to optimal design of tuned mass dampers. These methods are population-based approaches that, try to solve the optimization problem by sampling in the search space. In this method, unknown parameters are selected as design variables, and an objective function is used to minimize. Also, the constraints of the problem are defined for design variables that, should be within the acceptable domain.

The formulation of this strategy defined as:

$$ {\text{Find:Design Variables}}\, = \,\left\{ {m_{d} , k_{d} {\text{and}} c_{d} } \right\}. $$
$$ {\text{To minimize}}:{\text{ Objective Function}}\, = \,\left( {\frac{{{\text{Max}}. {\text{ Controlled Drif}}t}}{{{\text{Max}}. {\text{Uncontrolled Drift}}}}} \right) $$
$$ {\text{Subject to}}:\left\{ {\begin{array}{*{20}c} {m_{{d_{\min } }} \le m_{d} \le m_{{d_{\max } }} } \\ {k_{{d_{\min } }} \le k_{d} \le k_{{d_{\max } }} } \\ {c_{{d_{\min } }} \le c_{d} \le c_{{d_{\max } }} } \\ \end{array} } \right.. $$

The objective function is defined based on the ratio of maximum controlled structural inter-story drift to maximum drift in an uncontrolled structure. In this strategy, the CBO algorithm is used to solve the optimization problem. All parameters of the structure and the damper parameters are assumed to be deterministic. Also, after the optimum design of the TMD, the reliability index is calculated for the structure by using FORM.

Optimization strategy 2, inverse reliability-based optimization

In this strategy, the seismic behavior of the structure is expressed using probabilistic modeling. As a result, structural parameters such as mass, stiffness, and damping of the floors are selected as random variables. The damper parameters, such as mass (\(m_{d}\)), stiffness (\(k_{d}\)), and damping (\(c_{d}\)) of TMD, are selected as unknown parameters and are optimized by using the inverse reliability method for target reliability (\(\beta_{t}\)).

$$ {\text{Find}}\;\theta = \left\{ {m_{d} , k_{d} \;{\text{and}}\; c_{d} } \right\}. $$
$$ {\text{Subject to}}:\left\{ \begin{gathered} \beta = \beta_{t} \hfill \\ g\left( {u,\theta } \right) = 0 \hfill \\ u + \frac{u}{{\nabla_{u} G\left( {u,\theta } \right)}}\nabla_{u} G\left( {u,\theta } \right) = 0. \hfill \\ \end{gathered} \right. $$

Optimization strategy 3, efficient reliability-based optimization

The metaheuristic methods in solving an optimization problem have a high convergence rate, however, the reliability of the structure is not considered in the optimal design. Also, the inverse reliability methods are gradient-based and need to calculate the gradient relative to random variables and unknown parameters so, with an increase of the unknowns, the complexity of the problem increases. As a result, combining these two methods can increase the efficiency of the strategy.

This method can be defined as follow:

$$ {\text{Find}}:{\text{ Design Variables}}\, = \,\left\{ {m_{d} , k_{d} \; {\text{and}} \;c_{d} } \right\} $$
$$ {\text{To minimize}}:{\text{ Objective Function}}\, = \,\left| {u^{*} - \beta_{t} } \right| $$
$$ {\text{Subject to:}}\left\{ {\begin{array}{*{20}c} {m_{{d_{\min } }} \le m_{d} \le m_{{d_{\max } }} } \\ {k_{{d_{\min } }} \le k_{d} \le k_{{d_{\max } }} } \\ {c_{{d_{\min } }} \le c_{d} \le c_{{d_{\max } }} } \\ \end{array} } \right., $$

where \(u\) is the vector of random variables, and \(u^{*}\) is the MPP.

To solve this optimization problem, the combination of two CBO and FORM methods is used as a double loop. Figure 1 illustrates the problem-solving flowchart for this strategy. Also, considering that the value of the reliability index is calculated using the FORM for each particle of CBO, Constraints of inverse reliability problem in Eq. (16) will be satisfied.

Fig. 1
figure 1

Double-loop flowchart of the efficient reliability-based optimization algorithm

Full size image

Numerical study

There exist several benchmark examples in the literature for comparative studies of the optimization of tuned mass dampers. Here, in this study one example with two cases has been selected, and applied three strategies for optimization of tuned mass dampers, for decreasing the response of the structure based on target reliability.

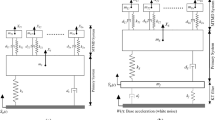
The case study selected for evaluating the application of the design strategies consists of a planer model of an 11 story shear frame structure. This structure has already been employed in several projects investigating the efficiency of seismic control (Azar et al., 2011; Pourzeynali et al., 2007; Rahbari et al., 2013; Shayeghi et al., 2009). A representation of the structural model equipped with a tuned mass damper is shown schematically in Fig. 2. Table 1 shows some properties of the system such as mass and stiffness of stories. The damping ratio for the first two modes of this building is taken 5%, and Rayleigh’s damping matrix can be then calculated from Eq. (56):

$$ C = a_{1} M + a_{2} K $$
(56)

where

$$ a_{1} = \xi \frac{{2\omega_{1} \omega_{2} }}{{\omega_{1} + \omega_{2} }} $$
(57)
$$ a_{2} = \xi \frac{2}{{\omega_{1} + \omega_{2} }}, $$

where \(\omega_{1}\) and \(\omega_{2}\) are the frequency of the first and second modes.

Fig. 2
figure 2

Structural model equipped with a tuned mass damper

Full size image
Table 1 Properties of the building for case study
Full size table

The structural model in uncontrolled and controlled cases has been analyzed numerically under El-Centro 1940 NS earthquake horizontal component with peak ground acceleration PGA = 0.349 g. It should be noted that this record has been selected as an external excitation to evaluate the presented method. It is clear that to design a control system for a specific site, the desired record can be selected with a proper acceleration scale factor in the analysis and optimization.

In Example 1 the mass of TMD was taken constant and equal to 3% of total mass (\(m_{d} = 66 \;{\text{tons}}\)). The lower bound and upper bound values of the stiffness are 0 and 5000 kN/m, while the lower bound and upper bound of damping are 0 and 40 kN-s/m, respectively. In Example 2 the mass of TMD is assumed as a design variable.

The maximum drift of stories are taken as a target, so the objective function can be written as:

$$ {\text{Objective function}} = \frac{{\text{Max controlled drift}}}{{\text{Max uncontrolled drift}}}. $$
(58)

Then the limit state function can be selected as:

$$ g\left( x \right) = \left( {{\text{Max controlled drif}}t} \right) - \left( {{\text{Max uncontrolled drif}}t} \right). $$
(59)

To describe the uncertainty and reliability analysis, the parameters of structure such as mass, stiffness, and damping of each story are selected as random variables. The random variables are used with the lognormal distribution that, the deterministic value of parameters (Table 1) is assumed as the mean value, and the standard deviation is 10% of the mean value.

To better compare all three optimization strategies results, firstly, the damper is optimized using the CBO method, and the reliability index is calculated based on these designed parameters. The obtained reliability index is selected as the target reliability for the other two strategies. Therefore, the results obtained from all three design methods can be compared for the same level of reliability.

Results and discussion

As the first case, the problem of optimum design of TMD using CBO and reliability analysis of structure equipped with TMD is presented. For this case, the convergence history of objective function based on maximum inter-story drift using CBO algorithm and the convergence history of reliability index using FORM are given in Fig. 3a, where the minimum objective function is 0.6774, and the optimum designed TMD parameters are presented in Table 2. According to Fig. 3b, the reliability index for this optimum designed TMD with the uncertainty of structural parameters and drift-based limit state function is 2.741. This value is selected as the target reliability index for RBDO and IR strategies.

Fig. 3
figure 3

a Convergence history of the objective function in CBO algorithm. b Convergence history of reliability index in FORM

Full size image
Table 2 Importance of TMD parameters in the reliability of the structure
Full size table

As mentioned, the behavior of a structure equipped with TMD is influenced by the damper parameters. Using the importance vector, it is possible to determine the relative importance and effect of each parameter of the TMD. The importance vector is calculated by reliability analysis based on the limit state functions of the maximum drift and the maximum lateral displacement. In this reliability analysis, TMD parameters were selected as random variables. Table 2 shows the components of the importance vector for the TMD parameters. According to these results, the mass of TMD is the most effective parameter in controlling maximum drift, and its damping has the least effect. Also, to control maximum lateral displacement, the mass of TMD has the greatest effect, and the stiffness and the damping of TMD have almost the same effect on the damper performance.

A sensitivity analysis has been carried out by using a limit state function based on the maximum drift to evaluate the effect of uncertainty in structural parameters and TMD parameters on the reliability of seismic behavior of the structure. Results concerning the influence of the structural and TMD parameters on the reliability of structure are shown in Fig. 4.

Fig. 4
figure 4

Effect of structural and TMD parameters on reliability index based on max. drift

Full size image

Also, a sensitivity analysis has been carried out by using different values of mass, stiffness, and damping of TMD, and the variation of reliability of structure has been also investigated. Figure 5a presents the sensitivity of the seismic reliability of the controlled structure relative to TMD parameters. From Fig. 5a one can notice that the reliability index in a structure equipped with a TMD has a high sensitivity to the damper mass. This is while the damping has the least effect on the reliability of structure based on the maximum drift. Each parameter changes around the optimal values determined by the CBO strategy. It is observed that the highest reliability index does not necessarily occur in optimal amounts of this strategy. This event can be related to the lack of the reliability concept in this optimization strategy.

Fig. 5
figure 5

Sensitivity analysis versus of TMD parameters. a Reliability Index. b Displacement. c Drift. d Acceleration

Full size image

Figures 5b–d present the sensitivity of the maximum seismic responses such as acceleration, drift, and lateral displacement of the controlled structure relative to TMD parameters variation. As can be seen, the maximum seismic responses of the structure are sensitive to the mass and stiffness of TMD. Given that, the objective function is defined based on the drift, the minimum inter-story drift and lateral displacement occur for optimal values, while the acceleration of stories is minimized for other values.

As the second case, the optimal design of TMD is done using reliability-based methods and compared with the meta-heuristic optimization method. For this purpose, the reliability-based design optimization (RBDO) and inverse reliability (IR) strategies are used. To compare the results of design strategies, the target reliability is selected equal with the reliability index of the structural model equipped with TMD that, designed by CBO algorithms. For this case study, two numerical examples have been used.

Example 1 In this example, the mass of TMD was taken constant (\(m_{d}\) = 66 ton), and the parameters of damping (\(c_{d}\)) and stiffness (\(k_{d}\)) were selected as design variables in the CBO algorithm (strategy 1). The lower bound and upper bound values of the stiffness are 0 and 5000 kN/m, while the lower bound and upper bound of damping are 0 and 40 kN-s/m, respectively. After performing the CBO, optimum values for damping and stiffness of TMD are found. For estimated optimal values, the reliability index based on the maximum drift is calculated and selected as the target reliability index for strategies 2 and 3. In the following, the optimal value of each parameter is calculated using RBDO and IR strategies for the target reliability. Table 3 presents the TMD parameters designed by all three strategies. Also, the maximum seismic responses of the structure for optimal values of each optimization strategy are shown in Fig. 6. Comparing the results of each three strategies shows that, the RBDO method has a good ability to explore the search space. Also, by using the inverse reliability (IR) method, the target reliability is obtained for a smaller amount of damping (\(c_{d}\)), but it does not lead to appropriate seismic behavior.

Table 3 TMD optimum parameters calculated by CBO, RBDO and IR for example 1
Full size table
Fig. 6
figure 6

Comparison of peak story responses for Example 1. a Displacement. b Drift. c Acceleration

Full size image

Example 2: in this example, the design is done for a higher level of reliability. So, to find the optimum parameters of TMD, use three design variables including mass (\(m_{d}\)), stiffness (\(k_{d}\)), and damping (\(c_{d}\)). The lower bound and upper bound values are 0 and 100 tons for the mass, 0 and 8000 kN/m for the stiffness, and 0 and 75 kN-s/m for the damping, respectively. Table 4 presents the TMD parameters designed by all three strategies. Also, the maximum seismic responses of the structure for optimal values of each optimization strategy are shown in Fig. 7. Comparison of the results of the CBO and RBDO methods show that, for the same combination of TMD parameters and the same reliability index, optimal design in the RBDO method leads to a further reduction in the seismic responses. The results obtained by the IR method for target reliability, reduce the seismic responses of the structure compared with the CBO method. However, due to the lack of the constraints defined for design variables, the TMD parameters are not within the defined range. This method is a gradient-based algorithm, and it does not have the ability to explore the entire search space.

Table 4 TMD optimum parameters calculated by CBO, RBDO and IR for example 2
Full size table
Fig. 7
figure 7

Comparison of peak story responses for Example 2. a Displacement. b Drift. c Acceleration

Full size image

Using the CBO algorithm, the percentage of reductions in maximum story displacements are between 22.24 and 38.44% with mean value of 31.45%. The maximum displacement of the top story is reduced to 0.1238 m from 0.1593 m (22.24% reduction). That's while using the RBDO strategy, the percentage of reductions in maximum story displacements is between 33.56 and 36.99% with mean value of 35.44%, and the maximum displacement of the top story is reduced to 0.1035 m from 0.1593 m (35.01% reduction). Also, using the IR strategy, the percentage of reductions in maximum story displacements are between 33.30 and 38.02% with mean value of 35.76%, and the maximum displacement of the top story is reduced to 0.1005 m from 0.1593 m (36.90% reduction).

For drift response of stories, using the CBO algorithm, the maximum and mean of reductions in maximum story drifts are 38.24% and 16.02% respectively. The maximum drift of the first story is reduced to 0.01388 m from 0.02235 m (37.87% reduction). Using the RBDO algorithm, the maximum and mean of reductions in maximum story drifts are 36.99% and 22.16% respectively. The maximum drift of the first story is reduced to 0.01408 m from 0.02235 m (36.99% reduction). Using the IR algorithm, the maximum and mean of reductions in maximum story drifts are 38.02% and 23.13% respectively. The maximum drift of the first story is reduced to 0.01385 m from 0.02235 m (38.02% reduction). For acceleration response of stories, using the CBO algorithm, the maximum and mean of reductions in maximum story acceleration are 28.68% and 14.23%, respectively. Using the RBDO algorithm, the maximum and mean of reductions in maximum acceleration are 29.37% and 15.94%, respectively. Using the IR algorithm, the maximum and mean of reductions in maximum story acceleration are 31.44% and 17.80%, respectively.

It should be noted that, although the percentage of reduction in some stories is less than those of the other works, the mean value of this parameter is more than that of the other ones. Therefore, one can conclude that the performance of TMD optimized with the present approach, in absorbing seismic energy and reducing total story displacement, is better than those of the previous works.

Conclusion

The overall objective of this paper was to study the effect of uncertainty on the behavior of structures equipped with TMD and determine the optimum parameters of TMD that result in utmost reduction in the structural response to earthquake loading in uncertainty conditions. The CBO, a good operation optimization algorithm in engineering problems, is used to estimate optimum parameters of TMD in deterministic conditions. Also, reliability-based design optimization and inverse reliability methods are used in uncertainty conditions. The objective function used in this study is based on the maximum drift of stories. However, to make the results comparable for all strategies, the target reliability index was used. In the numerical studies, an 11-story shear building is considered.

In the first case study, TMD parameters were optimized using the CBO algorithm, and reliability was calculated using the FORM algorithm. To investigate the importance of each damper parameter in reducing seismic responses, important vector analysis was used. The results show that the mass and damping of TMD, respectively, have the most and least importance in reducing the drift of structure. Also, to reduce the lateral displacement, the damper mass has the most effect, and the damper stiffness and damping have the same importance for reducing the maximum displacement of the structure. Then, sensitivity analysis was performed to investigate the effect of each damper parameter on the reliability of the structure based on the drift. The results show that the reliability index in the structures equipped with TMD is sensitive to the mass and stiffness of the TMD and is not sensitive to damping. Also, sensitivity analysis of seismic responses of structures such as displacement, drift, and acceleration of stories compared to TMD parameters shows that the structural responses are sensitive to the mass, stiffness, and damping, respectively.

In the second case study, the optimal design of TMD was evaluated based on the target reliability. In Example 1, the design of the TMD was performed with two design variables (stiffness and damping of TMD). The results showed that the RBDO strategy has a good ability to explore the search space. In Example 2, the design of the TMD was performed with three design variables (mass, stiffness, and damping of TMD). The results showed that the designed TMD with RBDO method has a good performance in the reduction of seismic responses. However, due to the lack of constraints for the design variables domain, the IR strategy results are unacceptable.