Introduction

Cylindrical tanks are among the strategic structures in daily human life. These facilities are used to store petroleum products, water, oil and chemicals, etc.

According to various reports and observations on the structural behavior of the reservoirs during the recent earthquakes, steel tanks are more susceptible to damage than others. Among the past earthquakes that can be listed according to those reports are 1933 Long Beach, 1952 Kern County, 1964 Alaska, 1964 Niigata, 1966 Parkfield, 1971 San Fernando, 1978 Miyagi prefecture, 1979 Imperial County, 1983 Coalinga, 1994 Northridge, 1999 Kocaeli, 1999 Turkey (Virella et al. 2006), and 2003 Boumerdès earthquakes. Boumerdès earthquake (2003) occurred in the Algerian state of Boumerdès. It was a terrible earthquake and many victims. Evidence of damage to silos Korso during this earthquake, because it was designed as not a seismic zone.

Types of failure reported for these structures are diamond or elephant’s foot buckling, uplift of their bases, pipe damage, etc. Among these negative phenomena, dynamic buckling of tank walls remains the most common and more dangerous one (AWWA 1996). The loss of tank contents can contaminate drinking-water supplies and soil, thus resulting in serious threat to human health and environment, and substantial cleanup costs.

Elephant foot buckling (EFB)—which is an outward bulge located just above the tank base—results from the combined action of vertical compressive stress, exceeding the critical stress, and hoop tension close to the yield limit (Djermane et al. 2014). Elephant foot buckling bulge usually extends completely around the bottom of tanks due to the reverse in the direction of the seismic excitation (Djermane et al. 2014). Diamond buckling is an elastic instability phenomenon due to the presence of high axial compressive stresses (Djermane et al. 2014).

The manufacturing process of shell production is associated with geometrical imperfection. Because of that, this production of cylindrical shell without imperfections is very difficult or sometimes even impossible.

The present study is also motivated by the need for the enhancement of the Algerian seismic code RPA, which has not contained any provisions for liquid storage tank design yet (Djermane et al. 2014).

The buckling behavior of steel tanks under seismic excitation

Generally, identifying the buckling behavior of steel tank under seismic excitation is done by computational and experimental studies. This is classified as elastic buckling and elastic–plastic buckling. Elephant’s foot buckling is classified as elasto-plastic buckling behavior, which is an outward bulge located just above the tank base. Hamdan (2000) described diamond shape buckling at the bottom of the tank as elastic buckling. Furthermore, buckling of the top part of the cylindrical tank and shear buckling of the shell have been classified in the elastic buckling range. Teng and Rotter (2014) reported shear buckling for tanks in the elastic range.

Many researchers described buckling modes with deflections at the top of the cylindrical part, such as: Liu and Lam (1983), Natsiavas and Babcock (1987), Nagashima et al. (1987), Redekop et al. (2002) and Morita et al. (2003).

Natsiavas and Babcock (1987) developed an analysis for dynamic buckling studies of the open-top tank under horizontal ground excitation and the results are compared with experimental work. Nagashima et al. (1987) performed the experimental studies of the dynamic and static buckling for small plastic cylindrical tanks under harmonic excitation. In addition, an experimental study as developed by Morita et al. (2003) for tall storage tanks with a roof subjected to horizontal and vertical harmonic and simulated earthquake excitation.

Shaw et al. (1993) analyzed dynamic buckling of an imperfect composite circular cylindrical shell under both excitations axial and torsional impulsive load.

Frequently, the buckling at the top of a tank is attributed to the sloshing component of the hydrodynamic response of the tank fluid (Malhotra 2000). However, in the buckling at the top of a tank considered by Morita et al. (2003) and Natsiavas and Babcock (1987), the sloshing action is not depicted as the main cause. They attribute this kind of buckling to the impulsive component of the hydrodynamic pressure.

Historical presentation of dynamic buckling criteria and applications

The dynamic stability analysis is treated by many works. Researchers in the field of dynamic instability mainly use three criteria in the investigation of the critical conditions of dynamically loaded structures. These three criteria are practical applications of instability theorems; it will be discussed in detail later. The three criteria are: the criterion by Budiansky and Roth (1962), which is the most used throughout the literature to determine the critical buckling load of dynamical impacted structures; total energy-phase plane criterion (Hoff and Bruce 1954); and the criterion of the total potential energy (Simitses and Kounadis).

The first analytical work on dynamic buckling problems was carried out by Volmir (1958) for the cylindrical shells subject to longitudinal dynamic loads. He used Galerkin’s method for obtaining the solutions of a two degree of freedom system.

The potential energy method for studying the dynamic buckling with a limited degree system has been used by many authors, such as Coppa and Nash (1964) and Roth and Klosner (1964).

The Hamilton’s principle to study the dynamic buckling of an imperfect cylindrical shell was used by Tamura and Babcock (1975).

The statistical approach to study the effect of the initial imperfection on the dynamic buckling of the cylindrical shell was performed by Maymon and Libai (1977). Zimcik and Tennyson (1980) also studied the dynamic stability of cylindrical shells. The dynamic stability of stiffened cylindrical shells under step loading was studied by Fisher and Bert (1973) and Lakshmikantham and Tsui (1974, 1975).

An experimental study of the dynamic buckling of a nuclear steel container subjected to a horizontal excitation was performed by Babcock et al. (1984). They used the Budiansky–Roth criterion for determining the dynamic instability. Tanami et al. (1988) used the Budiansky–Roth and the Fourier spectrum criteria for estimating the dynamic buckling of a reticulated single-layer dome under up and down earthquake excitation. Shaw et al. (1993) compared the dynamic buckling loads obtained using the Simitses criteria the Budiansky and Roth criteria; they obtained conservative results with Simitses criteria.

Other studies used a phase plane criterion or Hoff and Bruce, such as Auli and Ramerstorfer (1986) and Natsiavas (1987) and Hjelmstad and Williamson (1998).

The first numerical research estimation of the critical PGA that causes the dynamic buckling is by Virella et al. (2006). Using the technique of the added mass modeled by the ABAQUS code, they examined the PGA which induces the buckling of a set of anchored cylindrical tanks. The Budiansky and Roth (1962) criterion is employed in this study.

A fully nonlinear fluid–structure interaction algorithm of finite element method is employed by Ozdemir et al. (2010) for the seismic analysis of anchored and unanchored steel liquid storage tanks. Other studies used a fluid–structure interaction such as those by Shekari et al. (2009) and Zingoni (2015).

Djermane et al. (2014) presented a contribution to evaluate the PGA values compared with standard code previsions using a numerical model. This finite element developed locally is exposed in Djermane et al. (2014). The three instability criterions cited above are performed in this work for identifying the critical PGA. Jerath and Lee (2015) have presented the stability static and dynamic analysis of cylindrical tanks. The fluid–structure interaction (FSI) is modeled with ANSYS finite element code. The buckling loads were a finding by the Budiansky and Roth procedure.

More recently, in the study presented by Chikhi and Djermane (2017), three criteria were used to estimate the critical peak ground acceleration that caused tank instability. The liquid inside the tank was modeled using specific Ansys’s finite elements and fluid–structure interaction. The calculation includes modal and time history analysis as well as material and geometric nonlinearity.

Imperfection sensitivity

The importance of initial geometrical imperfections is addressed by the study of Singer and Abramovich (1995) on the development of measurement techniques of imperfection. Initial geometrical imperfections were not considered in the earlier estimation studies of buckling of shells, and this affected the buckling strength.

Many researchers such as Simitses (1986), Teng (1996) and Arbocz and Starnes (2002) explained that the buckling strength of shell structures was affected by the following significant factors classified into three major groups: geometrical imperfections (such as out-of-straightness, initial ovality, geometrical eccentricities, dents, swells, circularity, cylindricity); structural imperfections (such as residual stresses and material inhomogeneities, constructional defects, such as small holes, cut outs, rigid inclusions, and delaminations); and loading imperfections (such as non-uniform edge load distribution, unintended edge moments, load eccentricities, and load misalignments as well as imperfect boundary conditions). They also concluded that the most dominant factors belonged to the geometrical imperfection group. Prabu (2007) divided the modeling of geometrical imperfections on the surface of the cylindrical shell into two groups: distributed geometrical imperfections and localized geometrical imperfections.

The manufacturing process of shell production is associated with geometrical imperfection, because the production of cylindrical shell without imperfections is very difficult or sometimes even impossible.

The manufacturing process is detailed in Fig. 1. Cold rolled flat plates are welded one by one to from the first layer of cylindrical shell, and several cylindrical shells are welded together to build the entire tank structure (Yu et al. 2012) (see Fig. 1).

Fig. 1
figure 1

Typical manufacturing process of welded steel cylindrical shells

Full size image

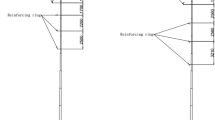
Circumferential welds produce a residual deformation at the shell surface considered as initial geometric imperfections. This type is named axisymmetric imperfection and is formed between different layers of the cylindrical shell. Asymmetrical imperfection are formed at the vertical welding lines between the various panels of the same layers (Da Silva 2011) (see Fig. 2).

Fig. 2
figure 2

Axisymmetric and asymmetric imperfections

Full size image

Welding geometric imperfection is shaped as an inward radial depression or outward radial deformation (see Fig. 3c). Rotter and Teng (1989) proposed two axisymmetric depression shapes of circumferential weld as shown in Fig. 3a, b.

Fig. 3
figure 3

Schematic diagram of three typical shapes of circumferential weld (Yu et al. 2012). a Type A. b Type B. c Circumferential weld reinforcement

Full size image

Chen et al. (2011) developed an FEM analysis to explain the effect of welding geometric imperfections on axial buckling of welded steel tank with local geometric imperfections, and the results showed the change in axial buckling deformation characteristics of steel tanks and the existence of additional damage to axial buckling critical load. The shape of local geometric imperfections of the welded steel tank observed during this study had polyhedron diamond shape as investigated by Yoshimura (1955).

Objective of the present investigation

Most of the previous works on the subject have focused on the dynamic buckling of aboveground steel tanks, subjected to the horizontal component of real earthquake records. Recently, some studies have dealt with the estimation of the critical peak ground acceleration (critical PGA), a deterministic method that causes tank instability using the added mass approach (Virella et al. 2006; Djermane et al. 2014), the fluid–structure interaction (FSI) approach and some criteria to evaluate the critical PGA (Jerath and Lee 2015). In our opinion, the most previous research to study the geometrical imperfection in the shell of steel tanks using various methods did not touch the fluid–structure interaction and the dynamic loads.

In the present study, the FSI numerical model is used to estimate the effect of geometrical imperfection with dynamic buckling of fluid-filled tanks, which will lead to a better understanding of the response and, consequently, the buckling failure of storage tanks.

For these tanks, the modeling of nonlinear fluid–structure interaction (FSI) associated with dynamic analysis is difficult and complicated. Then, a typical cylindrical tank is analyzed by the application of three different stability criteria to estimate the critical PGA. The results of the analyses are next presented and compared. Finally, conclusions are made.

Numerical model

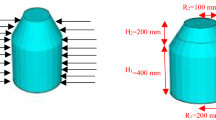
In this work, the tank used has been studied by several authors (Djermane et al. 2014; Virella et al. 2006). The tall tank has a height to a radius ratio (H/R) of 2. In the three-dimensional tank, the most developed models use shell element for the wall, the roof and the tank bottom, beam elements for the roof rafters, and fluid element for the liquid-containing cylindrical tank.

As mentioned earlier, the model of the fluid and the shell structure was done using ANSYS software.

In the numerical analysis, we used two shell elements for tank structure, the SHELL63 element for modal analysis and the SHELL181 for time history analysis. This last element is suitable for nonlinear application. The liquids inside this structure are modeled by the FLUID80 element. The roof rafters are modeled by the BEAM4 element. The material properties of the studied tank are presented in Table 1.

Table 1 Material properties
Full size table

Figure 4 shows the different shell thicknesses of the tank model.

Fig. 4
figure 4

Tank model with different shell thicknesses (Chikhi and Djermane 2017)

Full size image

Fluid–structure interaction

The fluid–tank interface is modeled by the coupling equation; the coincident nodes at the common areas between the fluid element and the shell elements are attached in the normal direction (ANSYS Inc. 2000); see Fig. 5.

Fig. 5
figure 5

Fluid–structure models (Chikhi and Djermane 2017). a Empty tank; b Fluid–structure interaction system; c Details of the fluid–structure model

Full size image

Boundary conditions

The tank studied in this work is assumed to have a completely fixed base (all the nodes at the base are assumed to be fixed).

Dynamic analysis

Modal analysis

Modal analysis is used to determine the vibration characteristics of this model. The important parameters in the design of a structure for dynamic loading conditions are the natural frequencies and mode shapes (ANSYS Inc. 2000). The equation of motion for the undamped system vibrating is freely given as:

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left[ K \right]\left\{ u \right\} = 0, $$
(1)

where [M] is the structural mass matrix, [K] is the structural stiffness matrix, \( \left\{ {{\ddot{\text{u}}}} \right\} \) is the nodal acceleration vector, and {u} is the nodal displacement vector. For a linear system, free vibration will be expressed as:

$$ u \, = \phi_{i} \cos \omega_{i} t, $$
(2)

where ϕ i is the eigenvector representing the mode shape of the ith natural frequency, ω i is the ith natural circular frequency in radians per unit time, and t is the time in seconds. Substitution of Eq. (2) in Eq. (1) gives:

$$ - \left[ M \right] + \left[ K \right]\phi_{i} = 0. $$
(3)

Nonlinear time history analysis

According to various reports (AWWA 1996; (Eurocode 2006), the damage in the thin tank walls in seismic areas shows large displacements and relatively large deformations. For these reasons, the material and geometric nonlinearities are considered in this work.

The elasto-plastic stress–strain curve is used for steel. The software offers several options, among which we have chosen the simplest consisting of a bilinear kinematic hardening curve, taking into account the Bauschinger effect. To obtain a satisfactory solution, the loads are applied incrementally at each time step through a series of smaller sub-steps (ANSYS Inc. 2000).

The transient dynamic analysis solves the basic equation of motion:

$$ \left[ M \right]\left\{ {\ddot{u}} \right\} + \left[ C \right]\left\{ {\dot{u}} \right\} + \left[ K \right]\left\{ u \right\} = \left\{ {F\left( t \right)} \right\}, $$
(4)

where [C] is the damping matrix, \( \left\{ {\dot{u}} \right\} \) is the nodal velocity vector and \( \left\{ {F(t)} \right\} \) is the load vector.

The earthquake record selection

The present study used earthquake record of El Centro with a maximum acceleration of 0.349g. A record is considered interesting in the sense of this study, because the maximum amplitudes are recorded during the first few seconds, which are also essential for the frequency content (see Fig. 6) (Djermane et al. 2014; Yaser 2013).

Fig. 6
figure 6

Selected accelerogram of El Centro 1940

Full size image

Presentation of stability criteria

Total energy-phase plane criterion (Hoff and Bruce 1954)

The curve representing the movement is traced in a phase plane (\( U \); \( \dot{U} \)) as shown in Fig. 7. The stable movements are characterized by limited trajectories and do not move too much away from the solution of the static equilibrium which plays the role of the center of attraction. When the load reaches the critical value, the trajectory moves away from this pole without any oscillation around it (Djermane 2008).

Fig. 7
figure 7

Phase plane diagram before and after the Pcr (Djermane 2008)

Full size image

Equation of motion criterion (Budiansky and Roth 1962)

The first and most used criterion of stability is by Budiansky and Roth (1962). It was formulated as an engineering application of the Lyapunov stability criteria. In this criterion, the time displacement curve is plotted for several values of PGA. The PGA value corresponding to a curve which gives a ‘‘jump’’, relative to its neighboring curves indicates the dynamic buckling critical value (see Fig. 8a).

Fig. 8
figure 8

Critical load: a criteria of Budiansky and Roth; b criteria of Ari Gur and Simonetta

Full size image

Criteria of Ari-Gur and Simonetta (1997)

This curve has been proposed originally by Budiansky and Roth (1962) and generalized later by Ari-Gur and Simonetta (1997). In the case of seismic excitation, this strong increase is less pronounced and is rather replaced by a change of the slope of the pseudo dynamic curve relating the PGA intensity and the maximum radial displacement at a fixed monitored node (several nodes are considered especially in the potential buckling zones) as shown in Fig. 8b. This criterion offers an estimation which must be confirmed with the above criteria (Djermane 2008).

One of the disadvantages of the most common stability criteria such as that of Budiansky-Ruth, the phase plane energy witch ‘‘watch’’ the dynamic bifurcation is very time consuming CPU (Djermane et al. 2014).

The local geometrical imperfections modeling

In the previous section “Imperfection sensitivity”, it is shown that the production of cylindrical shell without imperfections is very difficult or sometimes even impossible. Circumferential welds produce a residual deformation at the shell surface considered as initial geometric imperfections. The type of axisymmetric imperfection (inward horizontal dimple) formed between different layers of cylindrical shell is considered in our study. This local imperfection of the inward horizontal dimple is shown in Fig. 9. The three-variable dimple parameter is chosen for modeling this kind of imperfection; the depth and wave length parameters of initial dimple “\( \Delta w_{\text{ox}} \)”, “lgx” are, respectively, shown in Fig. 10. The height position parameter of initial dimple “λ” in the wall of the tank is shown in Fig. 11.

Fig. 9
figure 9

The shape of the of initial dimple

Full size image
Fig. 10
figure 10

Measurement of depths of initial dimples on a meridian (ENV 1993)

Full size image
Fig. 11
figure 11

The variation of the height position of the dimple: \( \lambda = 0.25 H(a);\,0.5 H(b) \,{\text{and}} \,0.75 H\,(c) \)

Full size image

The dimple parameters

The depth of initial dimple “\( \Delta w_{\text{ox}} \)”

The varying depth of the dimple: \( \Delta w_{\text{ox}} = 1t;2t;3t\, {\text{and}} 4t \) (see Fig. 10 and Table 2) (Prabu 2007).

Table 2 Recommended values given by EC3 for dimple imperfection amplitude parameters Un1 and Un2 (ENV 1993)
Full size table

The recommended values given by EC3 for dimple imperfection amplitude parameters are presented in Table 2.

The wave length of initial dimple “l gx”

The varying wave length of the dimple: \( l_{\text{gx}} = 0.5 l_{\text{gx}} ; 0.75 l_{\text{gx}} \,{\text{and}}\,1 l_{\text{gx}} \) (see Fig. 10).

The height position of initial dimple “λ” in the shell of tank

The varying height position of the dimple is shown in Fig. 11: \( \lambda = 0.25 {\text{H}};0.5 {\text{H}} \,{\text{and }}\,0.75 {\text{H}} \).

Modal analysis results

The validation of used tank model

To ensure the validity of the used model, modal analysis for the tank with the FSI system was performed. The results were compared with previous research and standard code provisions. The results are summarized in the Table 4. The excellent agreements indicate the validity of the used model.

Participation factor

The selection of significant modes is based on the criterion of effective mass participation; Fig. 12 represents the actual participation factor and the number of modes.

Fig. 12
figure 12

Modal participating mass ratio

Full size image

We can see that the impulsive modal mass is greater than the convective modal mass.

The significant convective and impulsive modes are summarized in Table 3:

Table 3 The significant convective and impulsive modes
Full size table

Table 4 compares the obtained results versus those given by the EC8, API 650 standard and the attached masses model (Virella et al.). This table indicates that the estimated values for structural periods of vibration are reasonable. The obtained fundamental impulsive mode is a column mode type as shown in Fig. 13b.

Table 4 Modal period comparison (Redekop et al. 2002) (Volmir 1958) (Coppa and Nash 1964)
Full size table
Fig. 13
figure 13

Fundamental modes’ shapes of a tank model: a The first convective mode. b The first impulsive mode. a shows the first convective mode shape of the tank model

Full size image

Results of dynamic buckling for geometrical imperfections modeling

Effect of local imperfection on dynamic buckling

Figure 14 shows the pseudo equilibrium path for El Centro excitation for inward local imperfection with dimple parameters \( \lambda = 0.5{\text{H}} \,{\text{and}} \,\Delta w_{\text{ox}} = 4t \). The discontinuity on the curve indicates that the critical value PGA (PGAcr) occurs at 0. 349g. Figure 15 shows several history curves corresponding to different excitation levels. The Budiansky–Ruth criterion is shown in Fig. 16. At the level 0.349g, a disproportionate increase in displacements is distinguished.

Fig. 14
figure 14

El Centro pseudo dynamic path for the tank model with inward local imperfection. (\( \lambda = 0.5\,H\,{\text{and}}\,\Delta w_{ox} = 4t \))

Full size image
Fig. 15
figure 15

Time history curves before and after PGAcr for the imperfect tank model (\( \lambda = 0.5H\,{\text{and}}\, \Delta w_{ox} = 4t \)) under the El Centro earthquake

Full size image
Fig. 16
figure 16

Phase plane before and after PGAcr for the imperfect tank model (\( \lambda = 0.5\,H\,{\text{and}}\,\Delta w_{ox} = 4t \)) under the El Centro earthquake

Full size image

The nature of the obtained dynamic buckling response can be evaluated by studying the deformation and the iso-stresses around the excitation critical level at 2.64 s (see Fig. 17).

Fig. 17
figure 17

mon Mises stress for the imperfect tank (\( \lambda = 0.5\,H\,{\text{and}}\,\Delta w_{ox} = 4t \)) at time = 2.64 s under the El Centro earthquake at PGA = 0.349g under PGAcr

Full size image

Comparison of the obtained dynamic buckling results with perfect and imperfect tank

Figure 18 shows the several pseudo equilibrium paths of El Centro excitation for the perfect and imperfect tank models. In this Figure, the effect of geometrical imperfection on dynamic buckling is clearly shown. The curve of the perfect tank model indicates that the critical value PGA (PGAcr) occurs at 0.384g. Unlike the curve of the imperfect tank models, the PGAcr occurs at level 0.349g and decreases by 09.11% compared to the tank model without imperfection.

Fig. 18
figure 18

El Centro pseudo dynamic path for the perfect and imperfect tank models

Full size image

Figure 19 shows the comparison of several history curves corresponding to different excitation levels with imperfect and perfect tank models.

Fig. 19
figure 19

Comparison of the time history curves at PGAcr of the three imperfect tanks and the perfect tank under the El Centro earthquake

Full size image

Using an estimation given by the pseudo dynamic paths, the Budiansky–Ruth and phase plane criteria are then used to confirm the obtained value of the tank model without imperfection at their PGAcr = 0.384g and compared with several imperfect tank models in the same PGA (Figs. 20, 21, 22).

Fig. 20
figure 20

Phase plane at PGAcr = 0.348g for the perfect and imperfect (\( \lambda = 0.75\,H\,{\text{and}}\,\Delta w_{ox} = 4t \)) tank model under the El Centro earthquake

Full size image
Fig. 21
figure 21

Phase plane at PGAcr = 0.348g for the perfect and imperfect (\( \lambda = 0.5\,H\,{\text{and}}\,\Delta w_{ox} = 4t \)) tank model under the El Centro earthquake

Full size image
Fig. 22
figure 22

Phase plane at PGAcr = 0.348g for the perfect and imperfect (\( \lambda = 0.25\,H\,{\text{and}}\,\Delta w_{ox} = 4t \)) tank model under the El Centro earthquake

Full size image

Table 5.12 shows the critical values under the El Centro earthquake at PGA of 0.384g for the four imperfect tanks and perfect tank.

Table 5 Comparison of the wall displacement, von Mises stresses and sloshing height at PGAcr of the four imperfect tanks and perfect tank under the El Centro earthquake
Full size table

In inward local imperfection, the varying height position of the dimple is considered for \( \lambda = 0.25 {\text{H}};\,0.5 {\text{H}}\; {\text{and}}\; 0.75 {\text{H}} \), depth varied as \( \Delta w_{\text{ox}} = 1t, \, 2t, \, 3t,\,{\text{ and}}\, \, 4t \), and wave length varied as 0.5 lgx, 0.75 lgx and 1 lgx.

The local geometrical imperfections are dominant compared to the perfect case in reducing the dynamic buckling of the cylindrical shell. The pseudo dynamic paths curves, for inward local imperfection with \( \lambda = 0.25 {\text{H}} \) and \( \lambda = 0.75 {\text{H}} \) are similar.

Inward local imperfection with \( \varvec{ }\lambda = 0.5 H \), \( \Delta w_{\text{ox}} = 4t \) and 1 \( l_{\text{gx}} \)

In this case, the height position of the dimple is at the middle height of the tank, and the curve of the pseudo dynamic paths indicates that the inward local imperfection with λ = 0.5 H is more dominant compared to two other types of local imperfection (see Fig. 18).

The value of wall displacement increases by 41% more than the value obtained with the perfect tank model (see Table 5). The values of von Mises stress and sloshing height are not dominant compared to wall displacement in the instability of the tank.

Inward local imperfection with \( \varvec{ }\lambda = 0.25 \), \( \Delta w_{\text{ox}} = 4t \) and 1 \( l_{\text{gx}} \)

In this case, the change is clearly shown with the decrease of non Mises stress value by 4.61% (see Table 5) compared to the perfect model tank.

Inward local imperfection with \( \varvec{ }\lambda = 0.75 \), \( \Delta w_{\text{ox}} = 4t \) and 1 \( l_{\text{gx}} \)

In this case, the sloshing height increases by 8.20% (see Table 5) compared to the obtained value of the perfect model tank, because the height position of the inward dimple is closer to the free surface.

Conclusion

Cylindrical steel storage tanks are commonly used in all major industrial facilities (e.g., refineries and nuclear power plants). They are critical structures because the loss of tank contents resulting by their buckling failures usually extremely contaminates drinking water supplies and soil. This results in serious threat to human health and environment as will as substantial cleanup costs. In this work, our investigation was focused on the search for the value of critical PGA that can lead to instability of the tank. We have used three different instability criteria. The results obtained by modal analysis confirm the validity of our model.

The primary goal of this study is to undertake an investigation through a numerical approach to simulate tank behavior as close as possible to the actual behavior, considering the coupling fluid–structure interactions. Other objectives, as mentioned in the introduction, are:

  • to create the numerical FSI model using for an estimate the critical PGA;

  • to create the models of local geometrical imperfections also investigated for estimating the dynamic buckling of fluid-filled tanks.

The obtained dynamic buckling results with perfect and imperfect tanks (local imperfections) are as follows:

  • The effect of geometrical imperfection on dynamic buckling is clearly shown. The PGAcr of the imperfect tank models decreases by 09.11% compared to the tank model without imperfection.

  • In the cases of inward local imperfection with \( \lambda = 0.5 {\text{H}} \), the values of von Mises stress and sloshing height are not dominant compared to wall displacement in the instability of the tank.

  • The pseudo dynamic paths curves for inward local imperfection with \( \lambda = 0.25 H \) and \( \lambda = 0.75 H \) are similar.

  • The inward local imperfection at the middle height of the tank is more dominant compared to the other two types of local imperfection.

In the case of inward local imperfection with λ = 0.25, \( \Delta w_{ox} = 4t \) and 1 lgx, von Mises stress value decreases by 4.61% compared to the perfect model tank.

In the case of inward local imperfection with \( \lambda = 0.75 \), \( \Delta w_{\text{ox}} = 4t \) and 1 lgx, the sloshing height increases by 8.20% compared to the obtained value of the perfect model tank, because the height position of the inward dimple is closer to the free surface.