Complex Fracture Nucleation and Evolution with Nonlocal Elastodynamics

Abstract

A mechanical model is introduced for predicting the initiation and evolution of complex fracture patterns without the need for a damage variable or law. The model, a continuum variant of Newton’s second law, uses integral rather than partial differential operators where the region of integration is over finite domain. The force interaction is derived from a novel nonconvex strain energy density function, resulting in a nonmonotonic material model. The resulting equation of motion is proved to be mathematically well-posed. The model has the capacity to simulate nucleation and growth of multiple, mutually interacting dynamic fractures. In the limit of zero region of integration, the model reproduces the classic Griffith model of brittle fracture. The simplicity of the formulation avoids the need for supplemental kinetic relations that dictate crack growth or the need for an explicit damage evolution law.

1 Introduction

Simulation of dynamic fracture is a challenging problem because of the extremes of strain and strain-rate experienced by the material near a crack tip, and because of the inherent instabilities such as branching that characterize many applications. These considerations, as well as the incompatibility of partial differential equations (PDEs) with discontinuities, have led to the formulation of specialized methods for the simulation of crack growth, especially in finite element analysis. These techniques include the extended finite element [4, 21], cohesive element [5], and phase field [2, 3, 20] methods and have met with notable successes.

The peridynamic theory of solid mechanics [24] has been proposed as a generalization of the standard theory of solid mechanics that predicts the creation and growth of cracks. In this formulation, crack dynamics is given directly by evolution equations for the deformation field eliminating the need for supplemental kinetic relations describing crack growth. The balance of linear momentum takes the form

$$ \rho(x)u_{tt}(x,t) = {\int}_{{\mathcal{H}}_{{\epsilon}}(x)} f(y,x) dy + b(x,t) $$

(1.1)

where ${\mathcal {H}}_{{\epsilon }}(x)$ is a neighborhood of x, ρ is the density, u is the displacement field, b is the body force density field, and f is a material-dependent function that represents the force density (per unit volume squared) that point y exerts on x as a result of the deformation. The radius 𝜖 of the neighborhood is referred to as the horizon. The motivation for peridynamics is that all material points are subject to the same basic field equations, whether on or off of a discontinuity; the equations also have a basis in nonequilibrium statistical mechanics [15]. This paradigm, to the extent that it is successful, liberates analysts from the need to develop and implement supplementary equations that dictate the evolution of discontinuities.

Standard practice in peridynamics dictates that the nucleation and propagation of cracks requires the specification of a damage variable within the functional form of f that irreversibly degrades or eliminates the pairwise force interaction between x and its neighbor y. This is referred to as breaking the bond between x and y. Here, the term “bond” is used only to indicate a force interaction between two material points x and y through some potential, whose value can depend on the deformations of other bonds as well. A wide variety of damage laws in peridynamics are possible, and often they contain parameters that can be calibrated to important experimental measurements such as critical energy release rate [22] or the Eshelby-Rice J-integral [13]. Damage evolution in peridynamic mechanics can be cast in a consistent thermodynamic framework [24], including appropriate restrictions derived from the Second Law of thermodynamics. This general approach of using bond damage has met with notable successes in the simulation of dynamic fracture [8, 12]. Because of the large number of bonds in a discrete formulation of (1.1), there can be a memory cost associated with keeping track of bond damage, as well as the need to specify a bond damage evolution law.

In the present paper, we report on recent efforts to model cracks in peridynamics without a bond damage variable. The main innovation in the present paper is a nonconvex elastic material model for peridynamic mechanics that, under certain conditions, nucleates and evolves discontinuities spontaneously. This approach is rigorously shown to reproduce the most salient experimentally observed characteristic of brittle fracture—the nearly constant amount of energy consumed by a crack per unit area of crack growth (the Griffith crack model). Our results further show that in spite of the strong nonlinearity of the material model, the resulting equation of motion is well-posed within a suitable function space, providing a mathematical context for which multiple interacting cracks can grow without recourse to supplemental kinetic relations. In the limit of small horizon 𝜖, the nonconvex peridynamic model recovers a limiting fracture evolution characterized by the classical PDE of linear elasticity away from the cracks. The evolving fracture system for the limit dynamics is shown to have bounded Griffith fracture energy described by a critical energy release rate obtained directly from the nonconvex peridynamic potential. These results bring the field of peridynamic mechanics closer to the goal of generalizing the conventional theory to model both continuous and discontinuous deformation using the same balance laws.

2 Nonconvex Material Model

Let S denote the bond strain, defined to be the change in the length of a bond as a result of deformation divided by its initial length. We assume that the displacements u are small (infinitesimal) relative to the size of the body D. Under this hypothesis, the strain between two points x and y under the displacement field u is given by

$$ S_{u}=\frac{u(y,t)-u(x,t)}{|y-x|} \cdot e , \qquad e=\frac{y-x}{|y-x|} , $$

(2.1)

where e is the unit vector in the direction of the bond and ⋅ is the dot product between two vectors. To describe the material response, assume that the force interaction between points x and y reversibly stores potential (elastic) energy, and that this energy depends only on the bond strain and the bond’s undeformed length. The elastic energy density at a material point x is assumed to be given by

$$ W(x)=\frac{1}{V_{{\epsilon}}}{\int}_{{\mathcal{H}}_{{\epsilon}}(x)} |y-x|{\mathcal{W}}^{{\epsilon}}\left( S_{u},y-x\right) dy $$

(2.2)

where ${\mathcal {W}}^{{\epsilon }}(S,y-x)$ is the pairwise force potential per unit length between x and y and V_𝜖 is the area (in 2D) or the volume (in 3D) of the neighborhood ${\mathcal {H}}_{{\epsilon }}(x)$.

The nonconvexity of the potential ${\mathcal {W}}^{{\epsilon }}$ with respect to the strain S distinguishes this material model from those previously considered in the peridynamic literature. By Hamilton’s principle applied to a bounded body $D\subset \mathbb {R}^{d}$, d = 2, 3, the equation of motion describing the displacement field u(x, t) is

$$ \rho u_{tt}(x,t)=\frac{2}{V_{{\epsilon}}}{\int}_{\mathcal{H}_{\epsilon}(x)} \left( \partial_{S} \mathcal{W}^{\epsilon}(S_{u},y-x)\right)e dy+b(x,t), $$

(2.3)

which is a special case of (1.1). The evolution described by (2.3) and its relation to classic linear elastic fracture mechanics is investigated in detail in the papers [16, 17]. A-priori estimates for convergence rates of finite difference and finite element schemes are developed for this model in [9, 10].

We assume the general form

$$ {\mathcal{W}}^{\epsilon}(S,y-x)=\frac{J^{\epsilon}(|y-x|)}{\epsilon|y-x|} {\Psi}(|y-x|S^{2}) $$

(2.4)

where J^𝜖(|y − x|) = J(|y − x|/𝜖) > 0 is a weight function and ${\Psi }:[0,\infty )\rightarrow \mathbb {R}^{+}$ is a continuously differentiable function such that Ψ(0) = 0, Ψ^′(0) > 0, and ${\Psi }_{\infty }:=\lim _{r\rightarrow \infty }{\Psi }(r) <\infty$. The pairwise force density is then given by

$$ \partial_{S}\mathcal{W}^{\epsilon}(S,y-x)=\frac{2J^{\epsilon}(|y-x|)}{\epsilon}{\Psi}^{\prime}\left( |y-x|S^{2}\right)S. $$

(2.5)

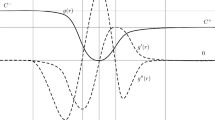
For fixed x and y, there is a unique maximum in the curve of force versus strain (Fig. 1). The location of this maximum can depend on the distance between x and y and occurs at the bond strain S_c such that $\partial ^{2}\mathcal {W}^{{\epsilon }}/\partial S^{2}(S_{c},y-x)=0$. This value is $S_{c}=\sqrt {r_{c}/|y-x|}$, where r_c is the unique number such that Ψ^′(r_c) + 2r_cΨ^″(r_c) = 0.

Fig. 1

Relation between force and strain for x and y fixed

We introduce Z(x), the maximum value of bond strain relative to the critical strain S_c among all bonds connected to x:

$$ Z(x)=\max_{y\in{\mathcal{H}}_{{\epsilon}}(x)}\frac{S_{u}(x,y)}{S_{c}(x,y)}. $$

(2.6)

The fracture energy $\mathcal {G}$ associated with a crack is stored in the bonds corresponding to points x for which Z(x) ≫ 1. It is associated with bonds so far out on the the curve in Fig. 1 that they sustain negligible force density. This set contains the jump set $\mathcal {J}_{u}$, along which the displacement u has jump discontinuities.

Consider an initial value problem for the body D with bounded initial displacement field u₀, bounded initial velocity field v₀, and a nonlocal Dirichlet condition u = 0 for x within a layer of thickness 𝜖 external to D containing the domain boundary ∂D. The initial displacement u₀ can contain a jump set $\mathcal {J}_{u_{0}}$ associated with an initial network of cracks.

This initial value problem for (2.3) is well posed provided we frame the problem in the space of square integrable displacements satisfying the nonlocal Dirichlet boundary conditions. This space is written ${L^{2}_{0}}(D;\mathbb {R}^{d})$. The body force b(x, t) is prescribed for 0 ≤ t ≤ T and belongs to $C^{1}([0,T];{L^{2}_{0}}(D;\mathbb {R}^{d}))$. The papers [16, 17] establish that if the initial data u₀, v₀ are in ${L^{2}_{0}}(D;\mathbb {R}^{d})$, and if u₀ has bounded total strain energy, then there exists a unique solution u(x, t) of (2.3) belonging to $C^{2}([0,T];{L^{2}_{0}}(D;\mathbb {R}^{d}))$ taking on the initial data u₀, v₀.

3 Crack Nucleation as a Material Instability

Normally, we expect an elastic spring to “harden,” that is, force increases with strain. If instead the spring “softens” and the force decreases, then it is unstable: under constant load, its extension will tend to grow without bound over time. A material model of the type shown in Fig. 1 has this type of softening behavior for sufficiently large strains. Yet the instability of a bond between a single pair of points x and y does not necessarily imply that the entire body is dynamically unstable. Here, we present a condition on the material stability with regard to the growth of infinitesimal jumps in displacement across surfaces.

Let γ(x, t) denote the volume fraction of points $y\in {\mathcal {H}}_{{\epsilon }}(x)$ such that S_u > S_c.¹ We apply a linear perturbation analysis of (2.3) to show that small scale jump discontinuities in the displacement can become unstable and grow under certain conditions.

Consider a time-independent body force density b and a smooth solution u^∗ of (2.3). Let x be a fixed point in D. We investigate the evolution of a small jump in displacement of the form

$$ u(y,t)=u^{\ast}(y,t)+\left\{\begin{array}{ll} 0 & {\text{if}} (y-x)\cdot n<0, \\ \bar us(t) & {\text{otherwise}}. \end{array} \right. $$

where $\bar u$ is a vector, s(t) is a scalar function of time, and n is a unit vector. Geometrically, the surface of discontinuity passes through x and has normal n. The vector $\bar u$ gives the direction of motion of points on either side of the surface as they separate.

We give conditions for which the jump perturbation is exponentially unstable. The stability tensor${\mathcal A}_{n}(x)$ is defined by

$$ {\mathcal A}_{n}(x)={\int}_{{\mathcal{H}}^{-}_{\epsilon}(x)}\frac{1}{|y-x|}{\partial^{2}_{S}}\mathcal{W}^{\epsilon}(S_{u^{\ast}},y-x) e\otimes e dy , $$

(3.1)

where ${\mathcal {H}}_{\epsilon }^{-}(x) = \{ y\in {\mathcal {H}}_{\epsilon }(x) \vert (y-x)\cdot n <0 \}$. A sufficient condition for the rapid growth of small jump discontinuity is derived in [16, 17, 25]. If the stability matrix ${\mathcal A}_{n}(x)$ has at least one negative eigenvalue then (1) γ(x) > 0, and (2) there exist a nonnull vector $\bar u$ and a unit vector n such that s(t) grows exponentially in time. The significance of this result is that the nonconvex bond strain energy model can spontaneously nucleate cracks without the assistance of supplemental criteria for crack nucleation. This is an advantage over conventional approaches because crack initiation is predicted by the fundamental equations that govern the motion of material particles. A negative eigenvalue of ${\mathcal A}_{n}(x)$ can occur only if a sufficient fraction of the bonds connected to x have strains $S_{u^{\ast }}>S_{c}$.

4 Small Horizon Limit: Dynamic Fracture

For finite horizon 𝜖 > 0, the elastic moduli and critical energy release rate are recovered directly from the strain potential $\mathcal {W}^{\epsilon }(S,y-x)$ given by (2.4). First suppose the displacement inside $\mathcal {H}_{\epsilon }(x)$ is affine, that is, u(x) = Fx where F is a constant matrix. For small strains, i.e., S = Fe ⋅ e ≪ S_c, the strain potential is linear elastic to leading order and characterized by elastic moduli μ and λ associated with a linear elastic isotropic material

$$ \begin{array}{@{}rcl@{}} W(x)&=&\frac{1}{V_{d}}{\int}_{H_{\epsilon}(x)}|y-x|\mathcal{W}^{\epsilon}(S_{u},y-x) dy\\ &=&2\mu |F|^{2}+\lambda |Tr\{F\}|^{2}+O(\epsilon|F|^{4}). \end{array} $$

(4.1)

The elastic moduli λ and μ are calculated directly from the strain energy density (2.4) and are given by

$$ \mu=\lambda=M\frac{1}{d+2} {\Psi}^{\prime}(0) , $$

(4.2)

where the constant $M={{\int }_{0}^{1}}r^{d}J(r)dr$ for dimensions d = 2,3. In regions of discontinuity, the same strain potential (2.4) is used to calculate the amount of energy consumed by a crack per unit area of crack growth, i.e., the critical energy release rate ${\mathcal {G}}$. Calculation applied to (2.4) shows that $\mathcal {G}$ equals the work necessary to eliminate force interaction on either side of a fracture surface per unit fracture area and is given in three dimensions by

$$ \mathcal{G}=\frac{4\pi}{V_{d}}{\int}_{0}^{\epsilon}{\int}_{z}^{\epsilon}{\int}_{0}^{\cos^{-1}(z/\zeta)} \mathcal{W}^{\epsilon}(\infty,\zeta)\zeta^{2}\sin{\phi} d\phi d\zeta dz $$

(4.3)

where ζ = |y − x|. (See Fig. 2 for an explanation of this computation.) In d dimensions, the result is

Fig. 2

Evaluation of the critical energy release rate $\mathcal {G}$. For each point, x along the dashed line, 0 ≤ z ≤ 𝜖, the work required to break the interaction between x and y in the spherical cap is summed up in (4.3) using spherical coordinates centered at x, which depends on z

$$ \mathcal{G}=M\frac{2\omega_{d-1}}{\omega_{d}} {\Psi}_{\infty} , $$

(4.4)

where ω_d is the volume of the d dimensional unit ball, ω₁ = 2, ω₂ = π, ω₃ = 4π/3.

In the limit of small horizon 𝜖 → 0 peridynamic solutions converge in mean square to limit solutions that are linear elastodynamic off the crack set; that is, the PDEs of the local theory hold at points off of the crack. The elastodynamic balance laws are characterized by elastic moduli μ, λ. The evolving crack set possesses bounded Griffith surface free energy associated with the critical energy release rate $\mathcal {G}$. We prescribe a small initial displacement field u₀(x) and small initial velocity field v₀(x) with bounded Griffith fracture energy given by

$$ \begin{array}{@{}rcl@{}} {\int}_{D} 2\mu |\mathcal{E} u_{0}|^{2}+\lambda |\text{div} u_{0}|^{2} dx+\mathcal{G}|\mathcal{J}_{u_{0}}|\leq C \end{array} $$

(4.5)

for some C < ∞. Here, $\mathcal {J}_{u_{0}}$ is the initial crack set across which the displacement u₀ has a jump discontinuity. This jump set need not be geometrically simple; it can be a complex network of cracks. $|\mathcal {J}_{u_{0}}|=H^{d-1}(J_{u_{0}})$ is the d − 1 dimensional Hausdorff measure of the jump set. This agrees with the total surface area (length) of the crack network for sufficiently regular cracks for d = 3(2). The strain tensor associated with the initial displacement u₀ is denoted by $\mathcal {E} u_{0}$. Consider the sequence of solutions u^𝜖 of the initial value problem associated with progressively smaller peridynamic horizons 𝜖. The peridynamic evolutions u^𝜖 converge in mean square uniformly in time to a limit evolution u⁰(x, t) in $C([0,T];{L_{0}^{2}}(D,\mathbb {R}^{d} )$ and ${u_{t}^{0}}(x,t)$ in $L^{2}([0,T]\times D;\mathbb {R}^{d})$ with the same initial data, i.e.,

$$ \begin{array}{@{}rcl@{}} \lim_{\epsilon\rightarrow 0}\max_{0\leq t\leq T}{\int}_{D}|u^{\epsilon}(x,t)-u^{0}(x,t)|^{2} dx=0, \end{array} $$

(4.6)

see [16, 17]. It is found that the limit evolution u⁰(t, x) has bounded Griffith surface energy and elastic energy given by

$$ \begin{array}{@{}rcl@{}} {\int}_{D} 2\mu |\mathcal{E} u^{0}(t)|^{2}+\lambda |\text{div} u^{0}(t)|^{2} dx+\mathcal{G}|\mathcal{J}_{u^{0}(t)}|\leq C, \end{array} $$

(4.7)

for 0 ≤ t ≤ T, where $\mathcal {J}_{u^{0}(t)}$ denotes the evolving fracture surface inside the domain D, [16, 17]. The limit evolution u⁰(t) is found to lie in the space of functions of bounded deformation SBD (see [17]). For functions in SBD, the bond strain S_u defined by (2.1) is related to the strain tensor $\mathcal {E}u$ by

$$ \lim_{\epsilon\rightarrow 0}\frac{1}{V_{\epsilon}}{\int}_{\mathcal{H}_{\epsilon}(x)}|S_{u}-\mathcal{E}u(x) e\cdot e| dy, $$

(4.8)

for almost every x in D. The jump set ${\mathcal J}_{u^{0}(t)}$ is the countable union of rectifiable surfaces (arcs) for d = 3(2) (see [1]).

In domains away from the crack set, the limit evolution satisfies local linear elastodynamics (the PDEs of the standard theory of solid mechanics). Fix a tolerance τ > 0. If for subdomains D^′⊂ D and for times 0 < t < T the associated strains $S_{u^{\epsilon }}$ satisfy $|S_{u^{\epsilon }}|<S_{c}$ for every 𝜖 < τ then it is found that the limit evolution u⁰(t, x) is governed by the PDE

$$ \begin{array}{@{}rcl@{}} \rho u^{0}_{tt}(t,x)= \text{div}\sigma(t,x)+b(t,x), \text{ on } [0,T]\times D^{\prime}, \end{array} $$

(4.9)

where the stress tensor σ is given by

$$ \begin{array}{@{}rcl@{}} \sigma =\lambda I_{d} Tr(\mathcal{E} u^{0})+2\mu \mathcal{E}u^{0}, \end{array} $$

(4.10)

I_d is the identity on $\mathbb {R}^{d}$, and $Tr(\mathcal {E} u^{0})$ is the trace of the strain (see [17]). (See [16] for a similar conclusion associated with an alternative set of hypotheses.) The convergence of the peridynamic equation of motion to the local linear elastodynamic equation away from the crack set is consistent with the convergence of peridynamic equation of motion for convex peridynamic potentials as seen in [6, 19, 23].

5 Numerical Examples

We present numerical results that showcase the features of the nonlocal model. The first three numerical simulations involve loading of samples with an existing pre-crack with different orientations and boundary loads using the numerical code developed by one of us (P. Jha). The results qualitatively agree with the experiments and the nonlocal fracture energy compares well with the classical Griffith’s fracture energy. The fourth example shows crack nucleation about a semicircular notch for a specimen loaded on the boundary and is carried out using EMU courtesy of Stewart Silling.

The material is described by the pairwise potential ${\mathcal {W}}^{\epsilon }(S,y-x)$ (see (2.4)) with Ψ(p) = c(1 − e^−βp) and J(q) = 1 − q, where c and β are positive constants. For dimension d = 2, using relation (4.2) and (4.4), we find that

$$ \begin{array}{@{}rcl@{}} c = 3\pi{\mathcal{G}}, \qquad \beta = \frac{16 \lambda}{\pi {\mathcal{G}}}, \qquad \bar{r} = \frac{1}{\sqrt{2\beta}}. \end{array} $$

(5.1)

Here, λ is the lamé parameter and ${\mathcal {G}}$ is the critical energy release rate. The maximum in the bond force curve occurs at $S_{c}=\bar {r}/\sqrt {|y-x|}$. The density ρ = 1200kg/m³, the bulk modulus k= 25GPa, and the critical energy release rate is ${\mathcal {G}}=500$J/m². The relation in (5.1) gives the values of c and β for any choice of k and ${\mathcal {G}}$.

5.1 Crack Propagation and Comparison of Fracture Energies

We present three simulation results with different orientations of the pre-crack inside the specimen. For the first three simulations, we set the horizon to be 𝜖 = 0.0005 m and the mesh size to be h = 𝜖/4 = 0.000125 m. The total time of simulation is T = 140 μ s and the time step is Δt = 0.004 μ s.

We employ a finite difference approximation on a uniform square grid of size h. For the time integration, we consider an explicit scheme and use central difference approximation for the second order time derivative of the displacement. To handle the so called surface effects in the peridynamic theory, we could introduce a no-fail region near the boundary where the boundary conditions are prescribed. However, in the current implementation, we have not applied a no-fail region near the boundary.

Example 1

Vertical crack propagation We consider a 2-d material D = [0,0.1m]² with a pre-crack of length 0.02 m extending vertically from the mid point of the bottom edge. The velocity v = ± 1m/s directed parallel to horizontal axis is specified on the bottom collar (see Fig. 3a). All points in the top collar are kept fixed throughout the simulation. In Fig. 3b, the X component of the displacement field is shown at 58μ s. At the same time, the damage profile is shown in Fig. 3c and d. To highlight the crack, we have scaled displacement by a factor 100 in all the simulations results. We note that for this crack propagation problem, the numerical convergence as h → 0 for fixed 𝜖 is carried out in [11] and it is shown that approximation converges at rate above 1.

Fig. 3

a For the first example, the top and bottom collars are of the thickness given by the horizon 𝜖 = 0.0005m. b The X component of displacement at 58μ s. c Plot of the damage Z at t = 58μ s. d The damage profile near the crack tip. We see region of points with Z ≈ 1 near the tip. During the course of deformation, the bonds in this region break causing crack to grow upwards

Example 2

Inclined crack subjected to axial loading In this example, we consider a material D = [0,0.2m]² with inclined pre-crack at the center of material (see Fig. 4a). The sample is subjected to a constant velocity parallel to horizontal axis on the left and right collars. On the left collar the velocity is 1 m/s and on the right its − 1 m/s. We find that the crack grows vertically (see Fig. 4b). This behavior has been observed experimentally as well [26]. The damage profile at t = 60μ s is shown in Fig. 4c and d.

Fig. 4

a Setup of example 2. Mid point of the crack is at the center of a domain. b X component of displacement at 60μ s. c The damage Z at 60μ s. d The damage profile near the crack tip

Example 3

Inclined crack subjected to loading along the diagonal We consider a material D = [0,0.1m]² with inclined pre-crack and subject it to a boundary force along the diagonal (see Fig. 5a). Similar experiments with a Plexiglass material show crack growth along the opposite diagonal (see [27]). This has been shown numerically in [28] using Peridynamics theory. Our results agree with the experiment result (see Fig. 5b). The damage profile and x and y components of the displacement after 102μ s are plotted in Fig. 5b, c, and d respectively.

Fig. 5

a Setup: A linear in time force with slope 5.0 × 10¹³N/s is applied along the x and y direction over the boundary points inside the red square. A similar force in the opposite direction is applied on all points inside the blue square. b Plot of damage at 102μ s. c X component of displacement at 102μ s. d Y component of displacement at 102μ s

Comparing nonlocal fracture energy and Griffith’s fracture energy

For this peridynamic material model, the softening zone (or fracture zone) is defined as the set of material points for which Z > 1. The total peridynamic fracture energy for this model is given by

$$ \begin{array}{@{}rcl@{}} P.E. := {\int}_{x\in D, Z(x) > 1} W(x) dx, \end{array} $$

(5.2)

where W(x) is the energy density of nonlocal material and is defined in (2.2). For a crack of length l, the Griffith’s fracture energy is simply $G.E. = l \times {\mathcal {G}}$ where ${\mathcal {G}}$ is the critical energy release rate. For three examples described above, the plot of peridynamic fracture energy as a function of crack length l is shown in Fig. 6. For example 1, the difference between peridynamic fracture energy and the Griffith’s fracture energy remains below 5% for crack lengths below 0.07 m. For examples 2 and 3, the difference is below 5% for crack lengths less or equal to 0.052 m and 0.064 m respectively.

Fig. 6

Peridynamic fracture energy (P.E.) and Griffith’s fracture energy (G.E.) vs crack length

5.2 Crack Nucleation and Crack Branching

In the fourth numerical example, the material occupies a 0.2 m × 0.1 m rectangle in the plane and has a semicircular notch as shown in Fig. 7. The horizon is set to 𝜖 = 0.00075 m and the mesh size is set to h = 𝜖/3 = 0.00025 m. The material has an initial velocity field v_x= 40 m/s along horizontal axis and v_y=− 13.3 m/s along vertical axis throughout. The rectangular region has constant velocity boundary conditions on the left and right boundaries that are consistent with the initial velocity field. As time progresses, the strain concentration near the notch causes some bonds to exceed Z = 1. The resulting material instability nucleates cracks at the notch that rapidly accelerate and branch. The points x associated with Z(x) > 1 are illustrated in Fig. 7 and correspond to the crack paths. Many microbranches are visible in the crack paths. For most of these microbranches, the strain energy is not sufficient to sustain growth, and they arrest. Such microbranches are frequently seen in experiments on dynamic brittle fracture, for example [7].

Fig. 7

Example 4: Computed paths of dynamic fractures nucleated at a circular notch soon after nucleation (left) and after progression through the plate (right)

6 Observations and Discussion

In this article, we describe a theoretical and computational framework for analysis of complex brittle fracture based upon Newtons Second Law. This is enabled by recent advances in nonlocal continuum mechanics that treat singularities such as cracks according to the same field equations and material model as points away from cracks. This approach is different from other contemporary approaches that involve the use of a phase field or cohesive zone elements to represent the fracture set (see [2,3,4, 14, 20]).

The key aspect of the elastic peridynamic material model that leads to crack growth is the nonconvexity of the bond energy density function. In the classical theory of solid mechanics, nonconvex strain energy densities are related to the emergence of features such as martensitic phase boundaries and crystal twinning associated with the loss of ellipticity, a type of material instability. As shown in the present paper, nonconvexity in peridynamic mechanics leads to crack nucleation and growth through an analogous material instability within the nonlocal mathematical description. We have generalized this model to state-based peridynamics in [11, 18]. The state-based potential models the response of the material to both shear and hydrostatic strain at a material point. It is shown that the resulting nonlinear model can model the material with any admissible Poisson ratio.

The benefit of using the nonconvex potential is that we no longer have to declare a damage variable which stores the state (fractured or un-fractured) of each of the bonds in the simulation. This results in less memory consumption. A typical number of bonds is 150N where N is the number of nodes. For 10⁶ nodes, one has 1.5 × 10⁸ bonds and 8 × 1.5 × 10⁸ bytes where 8 is the number of bytes per floating point number. This is 1.2Gb to store bond damage. It is noted that the Emu code stores bond breakage as a binary number and this brings the memory cost down. The theoretical model presented in this work allows for a bond stretched beyond critical to return to a stable state. However, for the dynamic problems treated in the numerical experiments in Section 5.1 , we see that bonds with a sufficiently high strain never heal, and in these cases, the nonconvex potential without irreversibly bond breaking is seen to be appropriate for monotonic loading.