A Fractional Approach to Non-Newtonian Blood Rheology in Capillary Vessels

Abstract

In small arterial vessels, fluid mechanics involving linear viscous fluid does not reproduce experimental results that correspond to non-parabolic profiles of velocity across the vessel diameter. In this paper, an alternative approach is pursued introducing long-range interactions that describe the interactions of non-adjacent fluid volume elements due to the presence of red blood cells and other dispersed cells in plasma. These non-local forces are defined as linearly dependent on the product of the volumes of the considered elements and on their relative velocity. Moreover, as the distance between two volume elements increases, the non-local forces decay with a material distance-decaying function. Assuming that decaying function belongs to a power-law functional class of real order, a fractional operator of the relative velocity appears in the resulting governing equation. It is shown that the mesoscale approach involving Hagen-Poiseuille law is able to reproduce experimentally measured profiles of velocity with a great accuracy. Additionally as the dimension of the vessel increases, non-local forces become negligible and the proposed model reverts to the classical Hagen-Poiseuille model.

1 Introduction

The rheological behavior of blood has been investigated from the nineteenth century and it is still an open debate. Indeed, the characteristic of blood flow inside vessels strongly affects stresses that are transmitted to the vessels wall, thus affecting the prediction of the wall shear stress related to the insurgence of arterial wall diseases as aneurysms and stenosis. For these reasons, analytical models capable to accurately predict the main features of blood flow inside human arteries are essential in order to better understand mechanism of appearance of aneurysms and consequence in blood supply downstream the aneurysm or stenosis. The first model for blood flow inside arterial vessels is the well-known Hagen-Poiseuille (HP) law [1], that is used for large arterial vessels [2], derived assuming Newtonian fluid and providing parabolic profile of velocity along the diameter of a circular vessel. For capillary arterial vessels, experimentally measured profiles of velocity are not parabolic [3]; hence, the HP model is not suitable for this kind of problems. In case of capillary vessels, the Casson model is certainly more reliable of the HP [2]; since this law considers a non-linear relationship between shear stress and shear rate, it leads to a non-linear governing equation and piece-wise profile of velocity across the vessel diameter. In a such a way, it has been shown that the results are in good agreement with experimental observations, to the price to deal with a non-linear model. In the context of recent advanced mechanical modelling, the presence of apparent non-linearity among state variables is considered among the constitutive relations in the cause-effect relations. However, in several problems involving inherent material heterogeneity with length scale similar to the geometry of the considered problem, the use of mesoscale approaches in linear context, yields satisfactory prediction of experimental data [4]. In this context, the non-local mechanics, defined in terms of gradients [5,6,7] or integrals [8, 9] of the state variables of the problem, provides interesting forecast of wave dispersion and shear bands as well as strain localization in mechanical interfaces [10, 11]. Non-local approaches result into mesoscale applications of continuum mechanics theory involving non-homogeneous media introducing the non-local terms to account for the heterogeneity of the representative volume elements of the considered problem. Non-local theories in fluid mechanics context have been proposed to represent the motion of fluids in microvessels [12,13,14,15,16,17]. These approaches are used in order to capture non-local contributions by means of additional state variables (such as relative displacements) in the transport equations of the problems but without specific physical representation.

This approach has been recently overcome by some of the authors introducing a mechanically based model of material long-range interactions [18] that generalizes the peridynamics approach presented at the beginning of the century [19], in the sense that it involves both local and non-local interactions. Several studies of the mechanically based non-local mechanics have been presented in recent scientific literature [20,21,22,23,24] also involving fractional-order calculus, that is a generalization of the well-known classical differential calculus in terms of real (or complex) order of differintegration [25, 26].

For the abovementioned reasons, in this paper, an alternative mesoscale approach is proposed. The model is based on the HP law that is enriched with non-local forces mutually exerted by non-adjacent fluid elements, that are elements that contain all the phases of the fluid and then may be considered representative of the whole fluid domain. These forces are transmitted to relatively long distance by relatively large cells, mainly Red Blood Cells (RBC). These long-range interactions are constructed as volume viscous forces scaled by an attenuation function that decreases the forces mutually exerted by two non-adjacent volume elements as the distance between them increases; the approach is analogous of that successfully used in various micro/nanomechanics problems [20,21,22,23,24]. It is shown that if the attenuation function is chosen as a power law of the distance between two volume elements, the integral representing non-local forces reverts to a fractional derivative operator. The advantage of this formulation is that the governing equation remains linear and comparison with experimentally observed velocity profiles along capillary vessels diameter shows very good agreement, with lower root mean square error in comparison with Casson model. Finally, as the diameter of the vessel increases, non-local term becomes negligible and the proposed model reverts to the classical HP model. The paper is organized as follows: in Section 2, the problem of Poiseuille flow is introduced; Section 3 introduces the proposed model and best fitting of mechanical parameters is presented; in Section 4, some conclusions are outlined.

2 The Non-local Approaches to Microstructured Fluid Flow

In this section, we discuss the governing equation of the 1D axial symmetric flow in stationary conditions. First, the Poiseuille flow for Newtonian fluid is discussed, then in Section 2.1, the Casson model is used for deriving the flow pattern in small capillary vessels and in Section 2.2, non-local approaches for blood flow are briefly discussed.

Let us consider a cylindrical volume V = AL where L and A are the length and the cross-sectional area, respectively, of the cylinder. Volume V is referred to a cylindrical coordinate system (r, 𝜃, z) as reported in Fig. 1 and let us assume that a pressure drop of Δp = p(r, 𝜃,0) − p(r, 𝜃, L) is applied at the two sides of the cylinder. In such circumstances, the fluid flow in the considered cylinder is axi-symmetric and linear momentum balance on a volume element Fig. 1b along the flux direction reads

Fig. 1

Blood vessel model

$$ \begin{array}{@{}rcl@{}} &&\left[t_{zz}(r,\theta,z+{\Delta} z)-t_{zz}(r,\theta,z)\right]r{\Delta}\theta{\Delta} r\\ &&\quad+ \left[t_{\theta z}(r,\theta+{\Delta} \theta,z)-t_{\theta z}(r,\theta,z)\right]{\Delta} r{\Delta}z\\ &&\quad + t_{rz}(r+{\Delta} r,\theta,z)(r+{\Delta} r){\Delta} z{\Delta}\theta\\ &&\quad-t_{rz}(r,\theta,z)r{\Delta} z{\Delta}\theta=\frac{\mathrm{D}\rho v_{z}}{\mathrm{D}t}r{\Delta} z{\Delta}\theta{\Delta} r \end{array} $$

(1)

where ρ is the fluid density ρ(r, 𝜃, z, t) and $\frac {\mathrm {D}}{\mathrm {D}t}$ denotes total derivative. Equation 1 may be rewritten, after some straightforward manipulations, as

$$ \frac{\partial t_{rz}}{\partial r}+\frac{ t_{rz}}{ r}+\frac{1}{r}\frac{\partial t_{\theta z}}{\partial \theta}+\frac{\partial t_{zz}}{\partial z}=\frac{\mathrm{D}\rho v_{z}}{\mathrm{D}t} $$

(2)

Equation 2 is the balance of linear momentum in z direction and, under the assumption of axi-symmetric flow, with the additional assumptions of stationary flow (Dρv_z/Dt = 0) the balance equation in Eq. 2 yields

$$ \frac{\partial t_{rz}}{\partial r}+\frac{ t_{rz}}{ r}=-\frac{\partial t_{zz}}{\partial z}=-\frac{{\Delta} p}{L} $$

(3)

where we assumed that a constant pressure gradient Δp/L is applied at z = 0 and z = L along the cylindrical domain. Equation 3 is a differential equation for the shear stress t_rz(r); in order to be solved, it is necessary to introduce the rheological behavior, that in the case of Newtonian fluid reads:

$$ t_{rz}=\mu \frac{\partial v_{z}}{\partial r}=\mu\frac{\partial}{\partial t}\frac{\partial u_{z}}{\partial r}=\mu \dot\gamma_{rz} $$

(4)

where $\dot \gamma _{rz}$ is the rate of the change of the displacement u_z = u_z(r) of the generic particle inside the control volume and μ is the viscosity parameter. Equation 4 is a constitutive equation that relates the shear stress to the shear velocity in the actual configuration of the fluid, and, after substitution, we get

$$ \mu \frac{d^{2}v_{z}}{dr^{2}}+\frac{\mu}{r}\frac{dv_{z}}{dr}=-\frac{{\Delta} p}{L} $$

(5a)

$$ v_{z}(-R)= 0; v_{z}(R)= 0 $$

(5b)

being R the diameter of the cylinder, that may be solved with the additional boundary conditions in Eq. 5b for the velocity at the border of the domain to yield

$$ v_{z}(r)=\frac{R^{2}-r^{2}}{4\mu}\frac{{\Delta} p}{L} $$

(6)

that represents a parabolic velocity profile along the diameter of the considered circular cross-section.

2.1 The Non-Newtonian Model of Blood Flow in Small Diameter Vessels

The experimental evidences of the velocity profile in small-diameter vessels show a strong deviation from the parabolic profile predicted by Newton constitutive equation. Such a drawback, observed at the beginning of the fifties of last century is known to be due to Fahreius-Lindqvist effect and Rouleaux formations and involves a self-organization of the RBCs in a microstructure. The phenomenological constitutive model capable to handle this effect is the so-called Casson model, that reads

$$ \sqrt{t_{rz}(r)}=\sqrt{\tau_{0}}+\sqrt{\mu}\left( \dot\gamma_{rz}\right)^{1/2} $$

(7)

where τ₀ is a yield shear stress and μ is a viscosity parameter as in the Newtonian model. Equation 7 is a non-linear constitutive law that, by the introduction in the balance equation in Eq. 3, leads to a non-linear governing equation

$$ \begin{array}{@{}rcl@{}} \frac{{\Delta} p}{L}&=&\frac{1}{r}\left[\tau_{0}+\mu\frac{du_{z}}{dr}+ 2\sqrt{\tau_{0} \mu}\left( \frac{du_{z}}{dr}\right)^{\frac{1}{2}}\right]\\&&+ \frac{d^{2}u_{z}}{dr^{2}} \left[\mu + 2\sqrt{\tau_{0} \mu}\left( \frac{du_{z}}{dr}\right)^{-\frac{1}{2}}\right] \end{array} $$

(8)

The solution to Eq. 8 is a piecewise velocity profile that may be expressed in the form

$$ \begin{array}{@{}rcl@{}} u_{z}(r)&=&\frac{R^{2}}{4\mu}\left\{\frac{{\Delta} p}{L}\left[1-\left( \frac{r}{R}\right)^{2}\right]-\frac{8}{3}\left( \frac{2\tau_{0}}{R}\frac{{\Delta} p}{L}\right)^{\frac{1}{2}}\times\right.\\ &&\left.\left[\left( 1-\frac{r}{R}\right)^{\frac{3}{2}}\right]+\frac{4\tau_{0}}{R}\left( 1-\frac{r}{R}\right)\right\} |r|>r_{y} \end{array} $$

(9a)

$$ \begin{array}{@{}rcl@{}} u_{z}(r)&=&u_{z}(r_{y}) |r|\leq r_{y} \end{array} $$

(9b)

where r_y = (2τ₀L)/Δp. Close inspection of Eq. 9 reveals that in the central part of the vessel, the velocity is constant; this is related to the fact that in the region − r_y ≤ r ≤ r_y the yield stress τ₀ is not reached, hence the velocity gradient is zero. Although the Casson model is satisfying in the reproduction of experimentally measured velocity profiles, it has the disadvantage to be non-linear, hence mathematical manipulations are not straightforward except that for problems with simple geometry and in stationary conditions; moreover, the concept of shear yield stress is an idealization that, in the authors opinion, does not reflect the real mechanics of the blood. For these reasons, in the next sections, alternative approaches are discussed.

2.2 Gradient and Integral Non-local Approaches to Microstructured Blood Flow

The idea that in the presence of microstructure some non-linear effects observed at the macroscale may be due to linear microstructural effects is not new and it traces back at the beginning of the seventies [8]. Recently, microstructured fluids have been investigated in the context of gradient models of mechanics [13, 14, 27] introducing a non-local model of Herschal-Bulkey relation that reads in our particular study

$$ <|t_{rz}|-{l_{c}^{2}}\frac{d^{2}|t_{rz}|}{dr^{2}}-\tau_{0}>=\mu^{1/n}|\dot\gamma_{rz}|^{n} $$

(10)

where $<x>=\frac {x+|x|}{2}$ is the positive operator, l_c is a specific internal scale that governs the magnitude of the non-local forces modelled with the second order gradient of t_rz, n is a parameter ruling the non-linearity between stress and shear rate and τ₀ is the initial yield stress. The flow transport equation in Eq. 10 is a non-local gradient generalization of linear non-local approach ([28]) with the introduction of a non-local stress as (τ₀ = 0, n = 1)

$$ t_{rz}-{l_{c}^{2}} \frac{d^{2}t_{rz}}{dr^{2}}-\tau_{0}=\mu\dot\gamma_{rz}=\mu \frac{dv_{z}}{dr} $$

(11)

that can be compared with the well-known stress gradient approaches to non-local solid mechanics in 1D reading [29]:

$$ t_{rz}^{(l)}+t_{rz}^{(nl)}=E\gamma_{rz} $$

(12)

where the non-local stresses $t_{rz}^{(nl)}=-{l_{c}^{2}}\frac {d^{2}t_{rz}}{dz^{2}}$ is related to the local contribution by the second order gradient operator. The constitutive assumption in Eq. 11 may be considered in the balance equation to yield, upon the integration, the velocity profile of the microstructured fluid [13, 14, 27].

A different approach to non-local fluid mechanics is provided by the integral approach [8]. Integral approach to fluids with dilute polymers and aggregates have been proposed in recent papers (see, e.g., [17]) assuming that the relations among the shear stress and shear strain is provided as:

$$ t_{rz}(r)={\int}_{-\infty}^{\infty} \eta(r-r_{1})\dot \gamma(r_{1})dr_{1} $$

(13)

where η(r − r₁) is the so-called non-local viscosity kernel and that reverts to the well-known Newtonian case as η(r − r₁) = η₀δ(r − r₁) with δ(⋅) the Dirac delta function.

The aforementioned integral relation are formally analogous to the integral non-local elasticity that, in the uniaxial case, reads:

$$ \sigma(x)={\int}_{-\infty}^{\infty} g_{k}(|x-\xi|)\varepsilon(\xi)d\xi $$

(14)

where the elastic kernel g_k(⋅) is a material dependent attenuation function, σ is the stress and ε is the Euclidean strain function.

Despite the wide diffusion of integral non-local elastic models and, as a consequence, of the non-local viscosity model in Eq. 13, some drawbacks exist as bounded domains are considered. Indeed, in presence of boundary conditions, strain dependent and strain rate dependent non-local integral models shows mathematical inconsistencies [18].

These considerations push toward a different approach to non-local viscosity model as proposed in the next section.

3 The Fractional-Order Approach to Blood Circulation in Small-Size Arterial Vessels

In this section, the non-local blood flow model is introduced starting from simple observation regarding the mechanics of blood. In particular, two main facts are taken into account:

• the blood is multiphase material, which contain a fluid part, the plasma, and many different solid parts, such as RBCs that are the larger and more influent cells;

• the blood is strongly heterogeneous, indeed the Rouleaux and the Fahraues-Lindqviust effects make the concentration of RBCs larger at the center of the vessels than at the sides (see Fig. 2); as a consequence if the dimensions and the position of a representative volume are changed, different situations may be found.

  Fig. 2

  

  Heterogeneity and multiphase nature of blood. In the circle, two non-adjacent fluid elements mutually exchange forces because of the presence of the RBC

In order to take into account of these peculiarities without really modelling all the phases contained in the blood, it is possible to adopt a mesoscale approach. In this manner, the blood is considered as a homogeneous fluid and the presence of RBCs and fibrinogen is taken into account by inserting in the governing equations long range forces mutually exerted by non-adjacent fluids elements. The reason to introduce these forces is readily understandable if Fig. 2 is closely inspected.

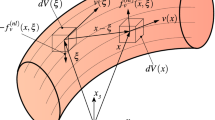
Indeed when the dimension of the vessel is comparable to the average dimension of RBCs, that is about 8μm, it is difficult to define the representative volume element (RVE) that is a volume element that contains all features and blood and then may be considered representative of all the blood domain. More specifically, a volume element representative of the blood has dimensions comparable with that of the domain, but with such dimensions of volume elements, it is not possible to describe the blood flow in a continuous fashion along the domain. On the other hand, if we consider volume elements small in comparison with the dimension of the domain they are not fully representative of the blood. Then, in the framework of a mesoscale approach, if two very small volume elements are taken on the boundary of a RBC, it is reasonable to think that they interact because of the presence of the RBC itself, and their interaction is modelled here as non-local viscous forces. Starting from this concept in the following, the proposed non-local model will be derived, for the sake of clarity, from considerations related to two finite volume elements, then contributions coming from all the volume were considered and at the end by taking the limit for the volumes that go to zero the governing equation is obtained. Non-local forces are thought as linearly depending on the product between the two interacting volumes and their relative velocity; moreover, the long-range forces are weighted by an attenuation function that decreases the force magnitude as the distance between the two elements increases. Under these assumptions, the force mutually exerted by two non-adjacent volume elements may be written as follows for a one-dimensional problem (see Fig. 3):

Fig. 3

Non-local forces mutually exerted by the two volume elements i and k in a one-dimensional problem

$$ F_{ki}=\mu_{ki} {\Delta} V_{k} {\Delta} V_{i} (v_{i}-v_{k}) $$

(15)

where ΔV_k and ΔV_i are the volume of the two fluid elements, while v_k and v_i are the velocities of the fluid elements; μ_ki is a viscous coefficient that varies with the distance d_ki through an appropriate attenuation function g(⋅), that is μ_ki = μ_NLg(d_ki), being μ_NL a non-local viscosity parameter of the model.

The resultant of non-local forces on the element k may be written as follows:

$$ F_{k}=\mu_{NL} {\Delta} V_{k} \sum\limits_{i = 1}^{N} {\Delta} V_{i} g(d_{ki})(v_{i}-v_{k}) $$

(16)

If we refer to the two-dimensional domain of Fig. 4 in axial symmetric conditions, the resultant of non-local forces on the k − th volume element may be written as

Fig. 4

Two-dimensional axial symmetric domain (cross-section of the circular vessel)

$$ F_{k}=\mu_{NL} {\Delta} V_{k} \sum\limits_{i = 1}^{N_{r}} \sum\limits_{j = 1}^{N_{\theta}} {\Delta} V_{ij} g(d_{k,ij})(v_{ij}-v_{k}) $$

(17)

where

$$ {\Delta} V_{k}=r_{k} {\Delta} r {\Delta}\theta L {\Delta} V_{ij}=\rho_{ij} {\Delta} \rho {\Delta}\varphi L $$

(18)

are the volumes of the two considered fluid elements and N_r and N_𝜃 are the number of elements in which the radial and circumferential directions have been discretized, respectively. By taking the limits for ΔV_k → 0 and ΔV_ij → 0 , the double sum reverts to a double integral as

$$ F(r)=\mu_{NL} {{\int}_{0}^{R}} {\int}_{0}^{2\pi} g(d_{r\theta,\rho\varphi})\left( v(r)-v(\rho)\right)\rho d\varphi d\rho $$

(19)

where the dependence of F, v(r) and v(ρ) from the angular coordinates 𝜃 and φ has intentionally been omitted because the problem is axial-symmetric, while for obvious geometric reasons the same can not be done for g(d_{r𝜃, ρφ}). By considering both non-local forces and Newtonian local forces and selecting a power law attenuation function in the form

$$ g(d_{r\theta,\rho\varphi})=\frac{1}{(d_{r\theta,\rho\varphi})^{2+\alpha}} $$

(20)

where d_{r𝜃, ρφ} = ρ² + r² − 2rρ cosφ, the governing equation is obtained as

$$ \begin{array}{@{}rcl@{}} \frac{{\Delta} p}{L}&=&\mu \left( \frac{1}{r}\frac{dv(r)}{dr}+\frac{d^{2}v(r)}{dr^{2}}\right)\\&& +\mu_{NL} L{{\int}_{0}^{R}} {\int}_{0}^{2\pi} \frac{\left( v(r) - v(\rho)\right)}{(\rho^{2} + r^{2} - 2r\rho\cos\varphi)^{2+\alpha}}\rho d\varphi d\rho \\ \end{array} $$

(21)

which may be labelled as fractional Hagen-Poiseuille (FHP) law. Indeed, although the integral term in polar coordinates in Eq. 21 does not seem to be a fractional derivative, in the paper [30] an operator analogous to that in Eq. 21 has been proved to be a fractional derivative labelled as Central Marchaud Fractional Derivative (CMFD). More specifically, if the problem is written in cartesian coordinates, the two-dimensional CMFD is obtained in the governing equation as the power law attenuation function is chosen; however, in the case the problem is expressed in polar coordinates and if the problem is axi-symmetric, the CMFD reduces to a classical (truncated) Marchaud fractional derivative in bounded domain. More details can be found in the I.

The solution of such a problem in analytical form is not straightforward and it may only be found for some special cases (very simple geometries and unbounded domain which imply the possibility to use the Fourier/Laplace transform method). However, accurate solutions may be easily found by discretizing the domain and the governing equation with a finite difference approximation that the authors have implemented in a custom routine of the software Matlab [31]. The computational cost associated with the non-local Poiseuille flow is not a significant issue, since the solution of the system with a finite difference scheme involves only the construction of a coefficient matrix and its inversion. Convergence of the solution is obtained with less than 200 elements in 0.77 s in the analysis with the custom routine in the software Matlab. On the other hand for the Poiseuille flow using the Casson model analytical solution is available. However, the proposed non-local model may be convenient when complex geometries and nonstationary conditions are studied: indeed, while the proposed model is linear and involves only matrix inversion for a step-by-step solution, the adoption of Casson model implies the use of iterative algorithm in order to find the solution at each step of the analysis. The advantage on the use of the proposed approach compared with the gradient or Eringen integral approaches is that the boundary conditions can be enforced as in a problem involving a classical local fluid. This is due to the fact that, as it has been demonstrated in the paper [18] considering the equilibrium equation of the volume elements at the domain boundary, the long-range resultants are infinitesimal of higher order with respect to the local stress resultant. This fact is true independently of the selected attenuation function. Then the boundary conditions are exactly the same of those in Eq. 5b that in the context of a finite difference approximation are enforced in a straightforward manner. In the next section, Eq. 21 is used in order to fit experimental data and the simulate velocity profiles in a small arterial vessel.

3.1 Best Fitting of Model Parameters

In [3], velocity profiles have been measured on arterioles of rabbit mesentery. The measurement has been performed on arterioles with diameter size in the range 17–32 μm. In this paper, a measurement on a 32-μm diameter vessels (Fig. (3) of ref. [3]) has been taken into consideration in order to tune parameters of the HP model, the Casson model and the proposed fractional model. For the Casson and Newtonian models, least-squares method has been adopted in order to set the parameters. For the proposed model, since analytical solution is not available, the best fitting has been performed by means of an iterative procedure with a custom routine in the generic purpose software Matlab. The procedure consists in solving the discretized system several times varying the mechanical parameters and to assume those set of parameters that minimize the root mean square error (RMSE) between experimental data and analytical results. Results of the best fitting are reported in Table 1 and theoretical curves are contrasted with experimental data in Fig. 5.

Table 1 Parameters obtained by the best-fitting procedure for the HP, Casson, and FHP model

Fig. 5

Comparison between theoretical velocity profile and experimental data (black dots). HP model black dashed line, Casson model blue thin line, FHP model red thick line

From Fig. 5, it is evident that the classical Hagen-Poiseuille model is not suitable to model behavior of blood in small arterial vessels; the Casson and the proposed non-local model are capable of reproducing the characteristics flattened velocity profiles that are experimentally observed. Comparison between the Casson and the non-local model shows that while the former has two different behaviors along the diameter, the latter provides a velocity profile that varies very gradually. In order to assess the accuracy of the three models, the RMSE is used; the RMSE is defined as

$$ RMSE=\sqrt{\frac{{{\sum}_{i}^{r}}\left( v_{T}(x_{i})-v_{m,i}\right)^{2}}{r}} $$

(22)

where r is the number of velocity data along the diameter, v_T is the theoretical velocity and v_m is the measured velocity. In Table 2, the RMSEs of the three models are compared.

Table 2 Comparison of the RMSEs obtained with the three models HP, Casson and FHP

From Table 2, it can concluded that the proposed non-local model represents an improvement of results obtained with the Casson model. The proposed non-local model is a linear model that is able to capture an apparent non-linearity in the blood behavior. Moreover, it can be easily verified that another desirable feature of the proposed model is that as the diameter of the vessel increases, non-local forces become negligible and the model reverts to the classical Hagen-Poiseuille model.

4 Conclusion

In this paper, a non-local model for the blood behavior in small arterial vessels has been introduced. The model is based on a mesoscale approach in which the presence of RBCs and other cells dispersed in the blood plasma is neglected but taken into account in the rheological behavior of blood by adding long-range interactions between non-adjacent fluid elements in the equilibrium equations. The use of a power law attenuation function leads to governing equations involving fractional derivatives. The model has proved to be very efficient in reproducing experimental velocity profiles without the need of non-linearity in the rheological behavior. In comparison with other non-local model, the proposed approach has the advantage that boundary conditions can be enforced as in a problem involving a local rheological behavior of the fluid. Moreover, the model is linear and this ensure that in case of problems with non-simple geometries the computational effort is lower compared with the use of non-linear models. In the future, the model may be applied to more complicated problems and implemented in a CFD context.

Appendix:: Recalls on fractional calculus

In this section, a brief introduction to the fundamentals of fractional calculus will be given.

Consider the function f(x), $x\in \mathbb {R}$, the left the right Riemann-Liouville (RL) fractional integral are defined as [25]:

$$ \left( I_{+}^{\alpha} f\right)(x)=\frac{1}{{\Gamma}(\alpha)}{\int}_{-\infty}^{x} \frac{f(\xi)}{(x-\xi)^{1-\alpha}}d\xi $$

(23a)

$$ \left( I_{-}^{\alpha} f\right)(x)=\frac{1}{{\Gamma}(\alpha)}{\int}_{x}^{\infty} \frac{f(\xi)}{(\xi-x)^{1-\alpha}}d\xi $$

(23b)

while the RL fractional derivative are defined as

$$ \left( D_{+}^{\alpha} f\right)(x)=\frac{1}{{\Gamma}(1-\alpha)}\frac{d}{dx}{\int}_{-\infty}^{x} \frac{f(\xi)}{(x-\xi)^{\alpha}}d\xi $$

(24a)

$$ \left( D_{-}^{\alpha} f\right)(x)=-\frac{1}{{\Gamma}(1-\alpha)}\frac{d}{dx}{\int}_{x}^{\infty} \frac{f(\xi)}{(\xi-x)^{\alpha}}d\xi $$

(24b)

where $\alpha \in \mathbb {R}$, 0 ≤ α ≤ 1 and Γ(⋅) is the Euler gamma function. If f(x) is a continuous function with continuous first derivative, the left and right RL fractional derivatives are coincident with the Marchaud fractional derivatives, that may be written as follows:

$$ \left( \textbf{D}_{+}^{\alpha} f\right)(x)=\frac{\alpha}{{\Gamma}(1-\alpha)}{\int}_{-\infty}^{x} \frac{f(x)-f(\xi)}{(x-\xi)^{\alpha}}d\xi $$

(25a)

$$ \left( \textbf{D}_{-}^{\alpha} f\right)(x)=\frac{\alpha}{{\Gamma}(1-\alpha)}{\int}_{x}^{\infty} \frac{f(x)-f(\xi)}{(\xi-x)^{\alpha}}d\xi $$

(25b)

The Marchaud fractional derivatives may be defined also for a bounded domain 0 ≤ x ≤ L as

$$ \begin{array}{@{}rcl@{}} \left( \textbf{D}_{0^{+}}^{\alpha} f\right)(x)\!&=&\!\frac{\alpha}{{\Gamma}(1 - \alpha)}{{\int}_{0}^{x}} \frac{f(x) - f(\xi)}{(x - \xi)^{1+\alpha}}d\xi + \frac{f(x)}{{\Gamma}(1 - \alpha)x^{\alpha}} \end{array} $$

(26a)

$$ \begin{array}{@{}rcl@{}} \left( \textbf{D}_{L^{-}}^{\alpha} f\right)(x)\!&=&\!\frac{\alpha}{{\Gamma}(1 - \alpha)}{{\int}_{x}^{L}} \frac{f(x) - f(\xi)}{(\xi - x)^{1+\alpha}}d\xi + \frac{f(x)}{{\Gamma}(1 - \alpha)(L - x)^{\alpha}} \\ \end{array} $$

(26b)

The definitions of Marchaud fractional derivatives related to a single-variable scalar function may be extended to a multi-variable scalar function. The extension is more readable if referred to the Riesz fractional operators. Then it is necessary to introduce Riesz fractional integral $\left (\bar {I}^{\alpha } f\right )(x)$ and derivative $\left (\bar {D}^{\alpha } f\right )(x)$:

$$ \begin{array}{@{}rcl@{}} \left( \bar I^{\alpha} f\right)(x)&=&\!\nu(\alpha){\int}_{-\infty}^{\infty} \frac{f(\xi)}{|x-\xi|^{1-\alpha}}d\xi \\&=&\!\nu(\alpha)\left[\left( I_{+}^{\alpha} f\right)(x)+\left( I_{-}^{\alpha} f\right)(x)\right] \end{array} $$

(27a)

$$ \begin{array}{@{}rcl@{}} \left( \bar D^{\alpha} f\right)(x)&=&\!\nu(-\alpha){\int}_{-\infty}^{\infty} \frac{f(x-\xi)-f(x)}{|\xi|^{1+\alpha}}d\xi\\ &=&\!{\Gamma}(1 - \alpha)\nu(-\alpha)\left[\left( \textbf{D}_{+}^{\alpha} f\right)(x) + \left( \textbf{D}_{-}^{\alpha} f\right)(x)\right] \\ \end{array} $$

(27b)

where ν(±α) = [2 cos(απ/2)Γ(±α)]^− 1. The Riesz fractional operator may be generalized to multivariate scalar function f(x), with $\textbf {x}\in \mathbb {R}^{n}$:

$$ \begin{array}{@{}rcl@{}} \left( \bar D^{\alpha} f\right)(\textbf{x})&=&\frac{1}{d_{n,\bar l}(\bar\alpha)}{\int}_{\mathbb{R}^{n}} \frac{f({\boldsymbol \xi})-f(\textbf{x})}{||{\boldsymbol \xi}-\textbf{x}||^{n+\alpha}}d{\boldsymbol \xi}\\&=& \frac{\chi(\bar\alpha)}{d_{n,\bar l}(\bar\alpha)}\left[\left( \textbf{D}_{+}^{\alpha} f\right)(\textbf{x})+\left( \textbf{D}_{-}^{\alpha} f\right)({\boldsymbol x})\right] \end{array} $$

(28)

where

$$ d_{n,l}(\alpha)=\beta_{n}(\alpha)\frac{A_{l}(\alpha)}{\sin(\alpha\pi/2)} $$

(29a)

$$ \beta_{n}(\alpha)=\frac{\pi^{1+n/2}}{2^{\alpha} {\Gamma}(1+\alpha/2){\Gamma}(n+\alpha/2)} $$

(29b)

$$ A_{l}(\alpha)=\sum\limits_{k = 0}^{l}(-1)^{k-1}{l\choose k}k^{\alpha} $$

(29c)

and χ(α) = −A_l(α)Γ(α), $\bar \alpha =n-1+\alpha$, $\bar l=n-1+l$, l = {α} + 1 and {α} is the integer part of α. The complete demonstration of Eq. 28 is omitted here for the sake of brevity; more information can be found in [26].

Finally, we briefly introduce the n-dimensional CMFD as

$$ \left( \textbf{D}_{-}^{\alpha} f\right)({\boldsymbol x})=\frac{\alpha}{{\Gamma}(1-\alpha)}{\int}_{\mathbb{R}^{n}} \frac{f({\boldsymbol x})-f({\boldsymbol \xi})}{({\boldsymbol \xi}-{\boldsymbol x})^{n+\alpha}}{\boldsymbol J}_{kj}d{\boldsymbol \xi} $$

(30)

where J_kj = i_ki_j is a Jacoby directional tensor, being i_k the unit vector associated with the direction x −ξ. In the specific problem treated in this paper, the governing equation written in polar coordinates and in axial-symmetric conditions is basically a scalar governing equation, then the Jacoby tensor reduce to unity; this is equivalent to say that the attenuation function, that is responsible for the appearance of fractional operator, reduces in this case to a scalar function. As a consequence, in the governing equation in Eq. 21, the integral term may be recognized as the integral part of the Marchaud fractional derivative defined in bounded domain and reported in Eq. 21. More details can be found in [30].