Spatio-temporal modeling of global ozone data using convolution

Abstract

Large spatial data are becoming more and more popular in environmental science and other related fields. Observations are often made over a substantial fraction of the surface of the Earth over a long period of time. It is necessary to model spatio-temporal random processes on the sphere which is challenging both conceptually and computationally. Convolution modeling method can be utilized to generate a random field with valid covariance structure on spheres. A latent dynamic process is defined on a grid covering the globe. The data vector is first projected onto the low-dimensional space spanned by those grids at each available time point. The resulting time series are fitted with seasonal ARIMA models. Forecasting is made by convolving the latent dynamic processes at all grid points using von Mises–Fisher kernel function. The procedure is illustrated by the total ozone data collected by Total Ozone Mapping Spectrometer during a 12-year period of time.

1 Introduction

Large-scale spatial data are becoming more and more popular recently due to the wide use of high-tech instruments and accumulation of observed data over time. It is not uncommon that the data contain a huge amount of observations, and may be collected within a large region on the surface of the Earth, sometimes even around the globe. There has been a substantial body of literature on modeling and analyzing spatial data. See Cressie (1993), Gelfand et al. (2010) for references. If the size of the region where the data are collected is not very large, the distance between any two points within the region can be accurately approximated to be Euclidean. Traditional spatial analysis relies on this assumption to guarantee valid covariance functions on $\mathbb {R}^d$, where d is in general equal to 2 for spatial processes on a two-dimensional plane. As the size of the data collection region gets larger, the curvature of the Earth can not be simply ignored and the distance is no longer Euclidean.

Many valid covariance functions in $\mathbb {R}^d$ are no longer valid on the unit sphere $\mathbb {S}^2$, including Gaussian and some Matérn models (Huang et al. 2011). Gneiting showed that a Matérn covariance function is valid on spheres if and only if its smoothness parameter is no greater than 1/2 (Gneiting 2013). Generally, valid covariance functions on spheres can be obtained by constraining covariance functions in $\mathbb {R}^3$. If a function $C_0(h)$ is a valid covariance function in $\mathbb {R}^3$, a new function defined as $C(\theta )=C_0(2\sin (\theta /2))$ is a valid covariance function on $\mathbb {S}^2$. Recently, the construction of valid covariance functions on spheres directly using great circle distance instead of chordal distance was discussed in some literature. For example, Jeong and Jun discussed a way to produce Matérn-like covariance functions for smooth processes on the surface of a sphere that are valid with great circle distance (Jeong and Jun 2015).

Some approaches designed specifically to model spatial random fields on spheres have emerged recently. Heaton et al. (2014) considered constructing valid spatial processes on spheres using kernel convolutions. They used Kent distribution with interpretable parameters and established a link between kernels and covariance function using spherical harmonic decomposition. Cressie and Johannesson (2008) proposed a fixed rank kriging formula in which a flexible family of nonstationary covariance functions is defined by a group of basis functions. The number of these basis functions are fixed (a few hundreds) so the difficulty of inverting the covariance matrix in kriging can be alleviated. Castruccio and Genton (2015) introduced a flexible class of models by relaxing the assumption of longitudinal stationarity in the context of regularly gridded climate model output for global data. Li and Zhu (2016) also used kernel convolution to construct valid covariance functions which may be nonstationary on spheres. By allowing the parameters of the kernel to be a function of the latitudes, they were able to generate axially symmetric spatial random processes. Jeong et al. (2017) reviewed several approaches to building process models on spheres.

For spatio-temporal global data, Jun and Stein (2007) proposed to consider a sum of independent processes which are obtained by applying a first-order differential operator to a fully symmetric process on sphere and time. Rodrigues and Diggle (2010) proposed a parametric family of models for spatio-temporal stochastic processes. Porcu et al. (2016) presented methods of construction of stationary covariance functions using great circle distance and provided closed-form expressions for both spatio-temporal and multivariate cases. Castruccio and Genton (2016) proposed a method of compressing the ensemble and had the computational advantage that they were able to fit a non-trivial model to a data set of one billion data points. For other recent approaches to model spatio-temporal data, we refer the readers to Porcu et al. (2018), White and Porcu (2018), De Iaco et al. (2019) and Heaton et al. (2019).

In this paper, the general concept and formula of kernel convolution method is first introduced along with some generalization in analyzing spatial data. We then apply the idea to model a spatio-temporal total ozone data. A global forecasting is made followed by some comments and discussions.

2 Convolution method

A Gaussian process Z(s) over a spatial region $\mathcal {D}$ can be constructed by convolving a continuous white noise process X(s) $(s\in \mathcal {D})$ using kernel smoothing as

$$\begin{aligned} Z(s)=\int _{\mathcal {D}} k(s,u)X(u)\mathrm{{d}}u \end{aligned}$$

(1)

at an arbitrary location $s\in \mathcal {D}$ (Higdon 1998). Here $k(\cdot )$ is a kernel function and X(u) is an infinitely dense Gaussian white noise process at $u \in \mathcal {D}$ (continuous) such that

$$\begin{aligned} E(X(u)) = 0, \text { and } \int _{\mathcal {A}} X(u)\mathrm{{d}}u \sim N(0, \sigma ^2 \times \mathrm {Area}(\mathcal {A})) , \end{aligned}$$

(2)

where $\mathcal {A}$ is a subregion in $\mathcal {D}$ and $\sigma ^2$ is the variance of the white noise process.

Since Z(s) at two different locations involve the white noise process at some common locations, it is a correlated spatial process whose covariance function is

$$\begin{aligned} \text {Cov}(Z(s_1), Z(s_2))=\int _{\mathcal {D}}k(s_1,u)k(s_2,u)\mathrm{{d}}u . \end{aligned}$$

(3)

This covariance function is non-negative definite, since

$$\begin{aligned} \sum _{i=1}^{m}\sum _{j=1}^{m}a_i a_j \text {Cov}(Z(s_i), Z(s_j))&= \sum _{i=1}^{m}\sum _{j=1}^{m}a_i a_j \int _{\mathcal {D}}k(s_i,u)k(s_j,u)\mathrm{{d}}u\\&=\int _{\mathcal {D}}\left( \sum _{i=1}^{m}a_i k(s_i,u)\right) ^2\mathrm{{d}}u\ge 0 , \end{aligned}$$

where m is any positive integer and $\{a_i: i =1, \dots , m\}$ are any real numbers.

Convolution approach is essentially a continuous version of the moving average process in time series. It is powerful to generate valid covariance function in domain $\mathcal {D}$ because of the flexibility in choosing the kernel function $k(\cdot )$. There is a one to one relationship between the smoothing kernel $k(\cdot )$ and the covariance function for isotropic process (Higdon 2002). Integrals in (1) and (3), however, pose some serious obstacles to apply the convolution procedure in practice. For computational convenience, some analytically tractable kernel functions are preferred, for example, two-dimensional Gaussian kernel $k(s)=\frac{1}{2\pi }\exp \{-\frac{1}{2}s^T s\}$ even though it may not be the appropriate one depending on the nature of the data in hand (Stein 1999).

In many cases, convolution-based models are implemented using discretized versions, because the integral has to be evaluated numerically and is computationally intensive. A white noise processes X (also called latent processes) located at a set of discrete locations $\{u_i:i=1, 2, \dots , m\}$ are first defined. They are essentially a collection of m independent random variables with mean zero and variance $\sigma ^2$. These means and variances may be homogeneous or vary with locations. The spatial process is generated by convolving these m white noise processes $\{X(u_1), X(u_2), \dots , X(u_m)\}$ through

$$\begin{aligned} Z(s)=\sum _{i=1}^{m}k(s, u_i)X(u_i) , \end{aligned}$$

(4)

which serves as an approximation to (1). Discretization may result in edge effects such that the evaluation of the field close to the boundary of $\mathcal {D}$ may be unstable due to the fact the number of latent processes close to the boundary is lower than the central region (Ripley 2005).

The flexibility of the kernel convolution approach comes from the fact that one only needs to model the smoothing kernel $k(\cdot )$ rather than the covariance function which has to be positive definite. Barry and Ver Hoef (1996) proposed a nonparametric specification of the variogram by taking the kernels to be piecewise constant functions. Similar ideas were also explored in other literature, for example, Kern (2000).

Kernel convolution models can be generalized in several different ways to accommodate various spatial structures in the data. Firstly, instead of being homogeneous across all locations in the study region $\mathcal {D}$, the kernel function k(s, u) in (1) can depend on some parameter set $\eta$ such that $k(s,u)=k(s,u; \eta )$, where $\eta$ varies spatially depending on the location s at which the kernel function is evaluated. The resulting spatial process is nonstationary whose dependence structure can vary with location (Higdon 1998; Higdon et al. 1999). In Li and Zhu (2016), a global data set is considered, where the parameters of the kernel function is taken to be a function of the latitude to create an axially symmetric spatial process on spheres.

Secondly, modeling based on the discretized representation (4) is a dimension reduction procedure. Instead of working directly on the n-dimensional data vector $\mathbf {Z}=\{Z(s_1), \dots , Z(s_n)\}$, where the number of observations n may be huge, a sparse support set for the latent processes $\mathbf {X}=\{X(u_1), \dots , X(u_m)\}$ is used which makes the computation easier to deal with. This projection of the n-dimensional vector $\mathbf {Z}$ onto a lower-dimension space $\mathbf {X}$ can be modeled by a linear regression model with mixed-effects

$$\begin{aligned} \mathbf {Z}=\mu \mathbf {1}_n + \mathbf {K}\mathbf {X} + \varvec{\epsilon } , \end{aligned}$$

(5)

and the computational burden can be greatly alleviated if $m\ll n$. Here $\mathbf {1}_n$ is an n-dimensional vector of 1s, $\mathbf {K}$ is an $n\times m$ matrix with $(i,j)^{\text {th}}$ entry $k(s_i, u_j)$, and $\varvec{\epsilon }$ is an n-dimensional independent random vector $\varvec{\epsilon } \sim N(\mathbf {0}, \sigma ^2_{\epsilon } \mathbf {I}_n)$.

Thirdly, kernel convolution formulas can also be generalized to model spatio-temporal random processes evolving in the domain of $\mathcal {D} \times \mathcal {T}$, where $\mathcal {T}$ is the time span of the process. Higdon (1998) used a three-dimensional kernel (two dimensions in space and one dimension in time) to convolve a three-dimensional white noise process in the study of temperatures in the North Atlantic Ocean. However, time series data in environmental science and climatology almost always show dynamic features including seasonality and directional space-time dependence. Thus, it is easier to spatially convolve a dynamic random process evolving with time (Calder et al. 2002). In this framework, the spatio-temporal random process Z(s, t) is modeled as a moving average of discrete uncorrelated dynamic latent processes located on a grid,

$$\begin{aligned} Z(s,t)=\sum _{i=1}^{m}k(s-u_i)X(u_i,t) , \end{aligned}$$

(6)

where kernel k is purely spatial and X(u, t) is a time series at a specified location u. Sansó et al. (2008) considered convolving independent processes with a discrete kernel that is represented by a lower triangular matrix. Spatio-temporal dependence can be introduced by either convolving spatial processes with isotropic correlations using a temporal kernel, or convolving $\text {AR}(p)$ processes using a spatial kernel. For nonstationary spatial process, the kernel function can be specified to be dependent on the location instead of being homogeneous.

3 Data analysis

Total Ozone Mapping Spectrometer (TOMS) is a satellite instrument which was flown on NASA-satellites for measuring ozone values on a global scale. Nimbus-7 and Meteor-3 satellites carried several TOMS instruments and provided global measurements of total column ozone on a daily basis from the period of November 1978 to December 1994. TOMS Level 2 data give spatial and temporal irregular measurements following the satellite scanning tracks (Jun and Stein 2008). Since the instrument relies on backscattered light, there are a lot of missing observations in Level 2 data. A post-processed Level 3 data are obtained by averaging Level 2 data pixel by pixel and are on a spatially regular lattice. The number of missing values are thus greatly reduced. The data can be found from NASA ozone and air quality site (NASA Goddard Ozone & Air Quality).

In this paper, we use the total ozone data collected by Nimbus-7 satellites from January 1, 1981 to May 6, 1993. The time span is about 4500 days. On each day, the measurements are on a regular grid in terms of latitudes and longitudes. Latitudes are from $-89.5^{\circ }$ (south) to $89.5^{\circ }$ (north) with spacing $1^{\circ }$. Longitudes are from $-179.375^{\circ }$ (west) to $179.375^{\circ }$ (east) with spacing $1.25^{\circ }$. There are 180 latitudes and 288 longitudes, and observations are available at each lattice point. Therefore, there are 51,840 collected measurements each day. Total ozone values are often reported in Dobson units denoted as “DU”. Typical values vary between 200 and 600 DU over the globe.

We first notice that, even though Level 3 data are processed from Level 2 data, missing values are still present, especially at high latitudes. The daily proportion of missing values is less than 10% for most of the days. Missing values are first imputed by an ad hoc procedure. For each location with missing value, we use inverse distance interpolation to impute using its 10 nearest neighbors with available measurement. We have tried other imputation methods but there is little effect on the results.

We use the TOMS data on the first day of each month from January 1981 to December 1992. There are in total 144 time points, each with 51,840 observed values on a regular latitude–longitude grid on the surface of the Earth. Figures 1 and 2 display the heat maps of the observed ozone data on March 1st (early spring) and September 1st (early fall) of 1981. In Fig. 1, the maximum values at high latitudes in the Northern Hemisphere can be as high as 550 DU, which is more than twice the values in regions close to the equator. Figure 2 shows that in early fall, total ozone is low in the Northern Hemisphere, while a pronounced maximum in the Southern Hemisphere is observed. In the tropics, the total ozone changes through the progression of the seasons are much weaker than in the polar regions due to the fact that seasonal changes in both sunlight and ozone transport are smaller in the tropics than those in the polar regions (Hegglin et al. 2014).

Fig. 1

Heat map of the observed total ozone data on March 01 (early spring), 1981

Fig. 2

Heat map of the observed total ozone data on September 01 (early fall), 1981

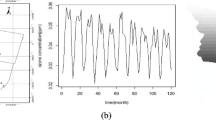
This pattern of seasonality is more apparent if we look at the time series at fixed locations. In Fig. 3, three sequences of observations made at three locations in the Northern Hemisphere are plotted. These locations share the same longitude but different latitudes. The seasonal pattern is obvious from the plot. The peaks occur around March and valleys are often associated with September or October. The magnitude of the oscillation increases with latitudes. For low latitude ($0.5^{\circ }$ N), the oscillation is between 230 and 300 DU. Total ozone shows a maximum at high latitudes during spring as a result of increased transport of ozone from its source region in the tropics toward the polar regions during late fall and winter. This ozone transport is much weaker during the summer and early fall periods and is weaker overall in the Southern Hemisphere (Hegglin et al. 2014). This comparison becomes obvious in Fig. 4 which shows three sequences at mirror sites of those in Fig. 3 in the Southern Hemisphere.

Fig. 3

Three sequences of observations made at three different locations which have the same longitude ($79.375^{\circ }$ W) but different latitudes in the Northern Hemisphere. The magnitude of the oscillation increases with latitude. Peaks and valleys occur around March and September, respectively

Fig. 4

Three sequences of observations made at three different locations which have the same longitude ($79.375^{\circ }$ W) but different latitudes in the Southern Hemisphere. The magnitude of the oscillation also increases with latitude. Peaks and valleys occur in September and March, respectively

To model this spatio-temporal data set containing almost 7.5 million ($51{,}840\times 144)$ observations, a latent dynamic random process is defined at 685 distinct locations scattered around the globe. Thirty seven latitudes are selected between two poles with spacing $5^{\circ }$ ($\{90^{\circ }$ S, $85^{\circ }$ S, ..., $85^{\circ }$ N, $90^{\circ }$ N$\}$). At each latitude, equally-spaced locations are chosen in a way such that the longitudinal spacing is roughly homogeneous across latitudes. Figure 5 shows the distribution of the locations for the latent process. At each location $\{u_i: i = 1, 2, \dots , 685\}$, there is a dynamic random process $X(u_i, t)$ whose evolution is governed by some underlying temporal models. Processes at different locations are assumed to be uncorrelated.

Fig. 5

685 Locations for the latent process are labeled by $\times$. They are distributed around the globe with latitudinal spacing of $5^{\circ }$

At each time point $t_i$ $(i=1,2,\dots , 144)$, we first project the observed data vector of length 51,840 onto a subspace of dimension 685 spanned by the latent processes. This idea of dimension reduction is also used in the fixed random kriging (Cressie and Johannesson 2008) which is more computationally attractive. This project can be done by fitting a multiple linear regression model in which the latent processes are essentially basis functions. That is,

$$\begin{aligned} \mathbf {Z}(t_i)=\mu _0(t_i) + \mathbf {G}\mathbf {X}(t_i)+\varvec{\epsilon }(t_i) , \end{aligned}$$

(7)

where $\mathbf {Z}(t_i)$ is the data vector at time $t_i$; $\mu _0(t_i)$ is the overall trend function at $t_i$ which is assumed to be homogeneous around the globe; $\varvec{\epsilon }(t_i)$ is the vector of independent random errors; $\mathbf {G}$ is a matrix of dimension $51{,}840\times 685$ with $(j,k){\text {th}}$ entry being some kernel function $k(s_j, u_k)$. A natural choice of the kernel density function on a three-dimensional sphere is the von Mises–Fisher distribution

$$\begin{aligned} k(x; \mu , \kappa )=\frac{\kappa }{2\pi ({\text {e}}^{\kappa }-{\text {e}}^{-\kappa })} {\text {e}}^{\kappa \mu \cdot x} , \end{aligned}$$

(8)

where concentration parameter $\kappa \ge 0$ and mean direction $\mu$ is a vector on the unit sphere. $k(x; \mu , \kappa )$ has a mode in the direction of $\mu$ and monotonically decreases as x moves further away from $\mu$. The greater the value of $\kappa$, the higher the concentration of the distribution around the $\mu$. The distribution is unimodal for $\kappa > 0$, and is uniform on the sphere for $\kappa =0$.

It is to be expected that a climatic phenomena on the global scale can rarely be entirely stationary and homogeneous due to the dissimilar conditions resulted from the Earth’s rotation. Measurements on total column ozone are no exception. It is found that they can be modeled as axially symmetric, where the first two moments are invariant to rotations about the Earth’s axis and the covariance function only depends on the longitude difference (Jones 1962). Similar to the estimation procedure in Li and Zhu (2016), we fit the empirical variogram using observations at each latitude L to get the estimated range $r_L$. Here we use the exponential variogram function $\gamma (h)=\sigma ^2_L[1-\exp (-h/r_L)]$ but other parametric forms can also be adopted. After getting the estimated range for all available latitudes, we apply a locally weighted polynomial regression to obtain a smooth curve for any latitude. The concentration parameter $\kappa$ in (8) is chosen to match the estimated range at each latitude.

Model (7) can be fitted with least squares at each time point $t_i$. As a result of that, 686 vectors of time series, corresponding to one trend $\mu _0(t)$ and 685 uncorrelated dynamic random processes $X_j(t)$ $(j=1, 2, \dots , 685)$ are obtained. Figure 6 shows four of these time series. The seasonality structure is apparent in all of them. The sign and magnitude of latent processes $X_j(t)$ can be rather different depending on the location $u_j$.

Fig. 6

Time series plot of the fitted processes from model (7). The top left panel is the trend sequence, while the other three are latent processes at different locations. A seasonal pattern with seasonality of 12 is obvious in all these plots

A time series process with seasonality is applied to model each temporal random process. Specifically, a seasonal ARIMA (autoregressive integrated moving average) model $\text {ARIMA}(p,d,q)\times (P,D,Q)$ with seasonality of 12 is fitted (Shumway and Stoffer 2017). The auto.arima function in forecast package in R is able to search for the best ARIMA model according to either AIC, AICc, or BIC value (Hyndman and Khandakar 2008). For example, the trend $\mu _0(t)$ is fitted with an $\text {ARIMA}(1,0,1)\times (1,1,1)$ with a slight negative drift. The forecast value at a future time point $t_0$ along with the prediction uncertainty can be obtained which is shown for the same four time series in Fig. 7. Since latent processes are assumed to be uncorrelated, we do allow them to follow different ARIMA models without any constraint. Different random processes can evolve differently over time. Alternatively, some patterns could be implemented, for example, latent processes at the same latitude might follow the same ARIMA model.

Fig. 7

Forecast of the trend function and latent temporal processes at three locations. The blue line is the forecasting line. Uncertainty is shown as the gray band, where light gray is 95% confidence interval and dark gray is 80% confidence interval

The predicted value of ozone measurement at an arbitrary location $s_0$ on the Earth at a future time $t_0$ is given by a kernel convolution of the dynamic latent processes at $t_0$, that is,

$$\begin{aligned} Z(s_0, t_0)=\mu _0(t_0) + \sum _{j=1}^{m} k(s_0, u_j) X(u_j, t_0). \end{aligned}$$

(9)

Figures 8, 9 and 10 show the heat maps of forecasting future total ozone at three different time points. Figure 8 is for January 1993 which is 1 time lag into the future. Figure 9 is for March 1993 when total ozone is at its peak for the Northern Hemisphere. Figure 10 is for September 1993 when total ozone in the Southern Hemisphere is high. It is clear that the general seasonal distribution (variations with season) and global distribution (variations with location) of total ozone can be captured. The heat map of the prediction variance:

$$\begin{aligned} \text {Var}[Z(s_0, t_0)]=\text {Var}[\mu _0(t_0)]+\sum _{j=1}^{m}k^2(s_0;u_j)\text {Var}[X(u_j, t_0)] \end{aligned}$$

for January 1993 is shown in Fig. 11. The prediction variance is higher at high latitudes due to the fact that ozone measurements are more variable at high latitudes than the regions closer to the equator.

To assess the effects of the number of the basis functions on the prediction performance, we carry out a sensitivity analysis, where we vary m, the number of $X_i$. The performance is evaluated using root mean squared prediction error (RMSPE) which is calculated using $\sqrt{\frac{1}{n}\sum _{i=1}^{n}(\hat{z}_i-z_i)^2}$, and the correlation between the predicted and observed values. The results are shown in Table 1. As expected, the prediction performance improves when m becomes larger. In practice, however, m is usually limited to be in the hundreds due to the computataional complexity (Cressie and Johannesson 2008).

Table 1 Comparison of the prediction performance for four different numbers of basis functions

Fig. 8

Forecast heat map of total ozone for January 1993

Fig. 9

Forecast heat map of total ozone for March 1993

Fig. 10

Forecast heat map of total ozone for September 1993

Fig. 11

Heat map of prediction variance for January 1993

4 Summary and conclusions

In this paper, we introduce a simple method of modeling spatio-temporal data which are observed around the globe. The original data is first projected onto a lower dimensional space spanned by a set of latent dynamic processes. These processes are assumed to evolve independently over time. The forecast time series are then convolved with kernel function to get a complete prediction on the globe. In doing this, temporal evolution and spatial evolution are considered separately. Therefore, this method essentially corresponds to a separable spatio-temporal model. The advantage of the current procedure is that both temporal and spatial covariance structure can be modeled in a very flexible way. Each latent process is allowed to follow its own ARIMA model independent of others. There is also the freedom to select the appropriate spatial kernel function when convolving the latent processes. The current method also has lower computational burden by dimension reduction.

Possible generalization to the current method includes the usage of multi-resolution spatial kernel functions. Fixed rank kriging (Cressie and Johannesson 2008) uses three different sets of basis functions with different scales of variations to capture the spatial structures at various resolutions. Also, the assumption of independent evolution of latent dynamic processes may be improved by taking the spatial information into consideration. The variations in total ozone are caused by large-scale movements of stratospheric air and the chemical production and destruction of ozone (Hegglin et al. 2014). Two latent processes defined at locations close in space are likely to be influenced by comparable environmental factors and thus should follow similar temporal models.