1 Introduction

There are numerous motivations for delving into the study of approximation theory and methods. These range from the necessity of representing functions in computer calculations to a keen interest in the mathematical aspects of a given subject. The application of approximation algorithms is widespread across various scientific domains, further underscoring the significance of exploring approximation theory. It is well-established that linear positive operators occupy a crucial position in the examination of approximation theory. One of the most well-known operators among these is the Szász operators, which are an extension of the Bernstein polynomials given below to the infinite range [35],

$$\begin{aligned} S_{\eta }(\psi ;\tau )=e^{-\eta \tau }\sum _{k=0}^{\infty }\psi \left( \frac{k}{\eta }\right) \frac{\tau ^{k}\eta ^{k}}{k!},{ \ \ \ \ \ }\tau \in \left[ 0,\infty \right) ,{ \ \ \ \ }\eta \in \mathbb {N}. \end{aligned}$$

The investigation of operators \(S_{\eta }\) has consistently been a focal point of research. Numerous authors have introduced modifications and generalizations of this operator, and approximation properties have been thoroughly investigated (see [1,2,3,4,5,6, 8, 9, 13, 14, 16, 17, 21,22,23, 26, 29, 31,32,33, 35, 40, 42]). As these operators unsuitable for approximating discontinuous functions within the scope of achieving an approximation process in spaces of integrable functions on unbounded intervals, Butzer [37] introduced and investigated an integral modification of the operators denoted as the Szász–Mirakyan–Kantorovich operators, as defined by

$$\begin{aligned} K_{\eta }(\psi ;\tau )=e^{-\eta \tau }\sum _{k=0}^{\infty }\frac{\left( \eta k\right) ^{k}}{k!}\overset{1}{\underset{0}{ {\displaystyle \int } }}\psi \left( \frac{k+t}{\eta }\right) dt,\ \ \ \ \ \tau \in \left[ 0,\infty \right) ,\ \ \ \ \eta \in \mathbb {N}. \end{aligned}$$

Totik [38] studied the approximations properties of the Szász–Mirakjan-Kantorovich operators. In this context, numerous researchers have proposed various modifications and generalizations for this operator, and their approximation properties have been examined as can be seen in [7, 11, 18, 20, 24, 28, 30, 34, 36, 41]. Very recently, in [10], Aral introduced a new modulus of continuity for locally integrable function spaces, influenced by the inherent structure of \(L_{p}\) spaces. This work included a quantitative theorem on the rate of convergence for convolution-type integral operators and their iterates. Another important study was done by Finta [43]. In this study, author proved the existence of the functions \(r_{n}\left( n=1,2,\ldots \right) \) on \(\left[ 0,1\right] \) such that the corresponding sequence of King operators approximates each continuous function on \(\left[ 0,1\right] \) and preserves the functions \(e_{0}(x)=1\) and \(e_{j}(x)=x^{j}\), where \(j\in \left\{ 2,3,\ldots \right\} \) is fixed. In addition, Kara [25] introduced the following modification of Szász–Mirakjan operators and studies approximation properties such as asymptotic formulas, weighted approximation a rate of convergence.

$$\begin{aligned} M_{\eta }^{*}(\psi ;\tau )=\sum _{k=0}^{\infty }s_{\eta ,k}(\tau )\psi \left( \frac{k}{\eta }\right) , \end{aligned}$$
(1.1)

where \(s_{\eta ,k}(\tau )=\eta e^{-\eta \tau }\frac{\tau ^{k-1}\eta ^{k}}{k!}\left( \frac{k}{\eta }-\tau \right) ^{2},\tau \in \left( 0,1\right) \) and \(\psi \in C\left( 0,1\right) .\)

The intention of this article is to present and explore new Kantorovich Szász–Mirakjan operators, derived from the generalization provided in (1.1). The remaining sections of this study are organized as follows. In section, we compute the moments \(K_{\eta }^{*}\left( t^{\mu };\tau \right) \) for \(\mu =0,1,2,3,4\) and central moments \(K_{\eta }^{*}\left( \left( t-\tau \right) ^{\mu };\tau \right) \) \(\left( \mu =1,2,4\right) \) using the derived recurrence formula. In Sect. 3, an examination of the local approximation properties of these operators is conducted employing Peetre’s K-functional. In Sect. 4, we compute the convergence rate using the standard modulus of continuity. Furthermore, to see the smoothness of approximation for Lipschitz-type maximal functions, we obtained the degree of convergence for these operators. In Sect. 5, we prove Voronovskaja type theorem. In Sect. 6, we explore weighted approximation properties of the new Szász–Mirakjan operators in terms of the modulus of continuity. In Sect. 7, we introduce the bivariate extension of these operators and investigate some approximation properties. Finally, in Sect. 8, some numerical illustrative examples are provided.

2 The New Szász–Mirakjan Operators

Definition 2.1

Let \(\psi :\left( 0,\infty \right) \rightarrow R\) and \(\eta \in \mathbb {N} \), new modification of Kantorovich-type Szász–Mirakjan operator can be defined by

$$\begin{aligned} K_{\eta }^{*}\left( \psi ;\tau \right) :=\sum _{k=0}^{\infty }s_{\eta ,k} (\tau )\overset{1}{\underset{0}{ {\displaystyle \int } }}\psi \left( \frac{k+t}{\eta }\right) dt, \end{aligned}$$
(2.1)

where \(s_{\eta ,k}(\tau )=\eta e^{-\eta \tau }\frac{\tau ^{k-1}\eta ^{k}}{k!}\left( \frac{k}{\eta }-\tau \right) ^{2}.\)

It is evident that the operator \(K_{\eta }^{*}\) possesses linearity and positivity. The role of moments in positive operators is pivotal for proving our main theorems. Therefore, the next lemma gives the iterative formula utilized to compute the moments of the new operators. It should be mentioned that if \(\psi \) does not depend on t, that is, \(\psi \left( \frac{k+t}{\eta }\right) =\psi \left( \frac{k}{\eta }\right) ,\) we get operator (1.1) studied by Kara in [25].

Lemma 2.2

The equality presented below is applicable for all \(\tau \in \left( 0,\infty \right) \) and \(\mu \in \mathbb {N};\)

$$\begin{aligned} K_{\eta }^{*}\left( t^{\mu };\tau \right) =\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}M_{\eta }^{*}\left( t^{\rho };\tau \right) , \end{aligned}$$

where

$$\begin{aligned} M_{\eta }^{*}(\psi ;\tau )=\sum _{k=0}^{\infty }s_{\eta ,k}(\tau )\psi \left( \frac{k}{\eta }\right) . \end{aligned}$$
(2.2)

Proof

According to the definition of \(K_{\eta }^{*}(\psi ;\tau )\) (2.1), we have

$$\begin{aligned} K_{\eta }^{*}\left( t^{\mu };\tau \right)&=\sum _{k=0}^{\infty }s_{\eta ,k}(\tau )\frac{1}{\eta ^{\mu }}\underset{0}{\overset{1}{ {\displaystyle \int } }}\left( k+t\right) ^{\mu }dt\\&=\sum _{k=0}^{\infty }s_{\eta ,k}(\tau )\sum _{\rho =0}^{\mu }\frac{1}{\eta ^{\mu } }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \underset{0}{\overset{1}{ {\displaystyle \int } }}k^{\rho }t^{\mu -\rho }dt\\&=\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\eta ^{\mu -\rho }\left( \mu -\rho +1\right) }\sum _{k=0}^{\infty }s_{\eta ,k}(\tau )\frac{k^{\rho }}{\eta ^{\rho }}\\&=\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\eta ^{\mu -\rho }\left( \mu -\rho +1\right) }M_{\eta }^{*}(t^{\rho };\tau ). \end{aligned}$$

\(\square \)

Lemma 2.3

[25] For all \(\tau \in \left( 0,\infty \right) \) and \(\eta \in \mathbb {N} \), we have

$$\begin{aligned} M_{\eta }^{*}\left( 1;\tau \right)&=1,\\ M_{\eta }^{*}\left( t;\tau \right)&=\frac{1}{\eta }+\tau ,\\ M_{\eta }^{*}\left( t^{2};\tau \right)&=\frac{1}{\eta ^{2}}+\frac{5}{\eta }\tau +\tau ^{2},\\ M_{\eta }^{*}\left( t^{3};\tau \right)&=\frac{1}{\eta ^{3}}+\frac{13}{\eta ^{2}}\tau +\frac{12}{\eta }\tau ^{2}+\tau ^{3},\\ M_{\eta }^{*}\left( t^{4};\tau \right)&=\frac{1}{\eta ^{4}}+\frac{29}{\eta ^{3}}\tau +\frac{61}{\eta ^{2}}\tau ^{2}+\frac{22}{\eta }\tau ^{3} +\tau ^{4}. \end{aligned}$$

By employing Lemmas 2.2 and 2.3, the next lemma follows immediately.

Lemma 2.4

For all \(\tau \in \left( 0,\infty \right) \) and \(\eta \in \mathbb {N} \), we have

$$\begin{aligned} \mathrm{(a)}\text K_{\eta }^{*}\left( 1;\tau \right)&=1,\\ \mathrm{(b)}\text K_{\eta }^{*}\left( t;\tau \right)&=\frac{3}{2\eta }+\tau ,\\ \mathrm{(c)}\text K_{\eta }^{*}\left( t^{2};\tau \right)&=\frac{5}{3\eta ^{2} }+\frac{6}{\eta }\tau +\tau ^{2},\\ \mathrm{(d)}\text K_{\eta }^{*}\left( t^{3};\tau \right)&=\frac{15}{4\eta ^{3} }+\frac{43}{2\eta ^{2}}\tau +\frac{27}{2\eta }\tau ^{2}+\tau ^{3},\\ \mathrm{(e)}\text K_{\eta }^{*}\left( t^{4};\tau \right)&=\frac{31}{\eta ^{4} }+\frac{67}{\eta ^{3}}\tau +\frac{87}{\eta ^{2}}\tau ^{2}+\frac{24}{\eta }\tau ^{3}+\tau ^{4}. \end{aligned}$$

Proof

Since the same method is used to prove the above inequalities, we only provide the proof for the last two inequalities. From Lemma 2.2,

$$\begin{aligned} K_{\eta }^{*}\left( t^{3};\tau \right)= & \left( {\begin{array}{c}3\\ 0\end{array}}\right) \frac{1}{4\eta ^{3} }M_{\eta }^{*}\left( 1;\tau \right) +\left( {\begin{array}{c}3\\ 1\end{array}}\right) \frac{1}{3\eta ^{2}} M_{\eta }^{*}\left( t;\tau \right) \\ & +\left( {\begin{array}{c}3\\ 2\end{array}}\right) \frac{1}{3\eta ^{2}}M_{\eta }^{*}\left( t^{2};\tau \right) +\left( {\begin{array}{c}3\\ 3\end{array}}\right) M_{\eta }^{*}\left( t^{3};\tau \right) . \end{aligned}$$

Using Lemma 2.3, we obtain

$$\begin{aligned} K_{\eta }^{*}\left( t^{3};\tau \right) =\frac{15}{4\eta ^{3}}+\frac{43}{2\eta ^{2}}\tau +\frac{27}{2\eta }\tau ^{2}+\tau ^{3}. \end{aligned}$$

Secondly,

$$\begin{aligned} K_{\eta }^{*}\left( t^{4};\tau \right)= & \left( {\begin{array}{c}4\\ 0\end{array}}\right) \frac{1}{5\eta ^{4} }M_{\eta }^{*}\left( 1;\tau \right) +\left( {\begin{array}{c}4\\ 1\end{array}}\right) \frac{1}{4\eta ^{3}} M_{\eta }^{*}\left( t;\tau \right) +\left( {\begin{array}{c}4\\ 2\end{array}}\right) \frac{1}{3\eta ^{2}}M_{\eta }^{*}\left( t^{2};\tau \right) \\ & +\left( {\begin{array}{c}4\\ 3\end{array}}\right) \frac{1}{2\eta }M_{\eta }^{*}\left( t^{3};\tau \right) +\left( {\begin{array}{c}4\\ 4\end{array}}\right) M_{\eta }^{*}\left( t^{3};\tau \right) . \end{aligned}$$

Using Lemma 2.3, we obtain

$$\begin{aligned} K_{\eta }^{*}\left( t^{4};\tau \right) =\frac{31}{\eta ^{4}}+\frac{67}{\eta ^{3}}\tau +\frac{87}{\eta ^{2}}\tau ^{2}+\frac{24}{\eta }\tau ^{3}+\tau ^{4}. \end{aligned}$$

\(\square \)

Now, utilizing Lemma 2.4, we give explicit formulas for the first, second, and fourth central moments.

Lemma 2.5

For every \(\tau \in \left( 0,\infty \right) \) and \(\eta \in \mathbb {N} \), we have

$$\begin{aligned} A_{\eta }(\tau )&=K_{\eta }^{*}\left( \left( t-\tau \right) ;\tau \right) =\frac{3}{2\eta },\end{aligned}$$
(2.3)
$$\begin{aligned} B_{\eta }(\tau )&=K_{\eta }^{*}\left( \left( t-\tau \right) ^{2} ;\tau \right) =\frac{5}{3\eta ^{2}}+\frac{3}{\eta }\tau ,\end{aligned}$$
(2.4)
$$\begin{aligned} C_{\eta }(\tau )&=K_{\eta }^{*}\left( \left( t-\tau \right) ^{4} ;\tau \right) =\frac{11}{\eta ^{2}}\tau ^{2}+\frac{52}{\eta ^{3}} \tau +\frac{31}{\eta ^{4}}. \end{aligned}$$
(2.5)

Proof

Through the property of linearity, we can compute the second-order and fourth-order central moments as follows:

$$\begin{aligned} K_{\eta }^{*}\left( \left( t-\tau \right) ^{2};\tau \right)&=K_{\eta }^{*}\left( t^{2};\tau \right) -2\tau K_{\eta }^{*}\left( t;\tau \right) +\tau ^{2}K_{\eta }^{*}\left( 1;\tau \right) \\&=\frac{5}{3\eta ^{2}}+\frac{6}{\eta }\tau +\tau ^{2}-2\tau \left( \frac{3}{2\eta }+\tau \right) +\tau ^{2}\\&=\frac{5}{3\eta ^{2}}+\frac{3}{\eta }\tau \end{aligned}$$

and

$$\begin{aligned}&K_{\eta }^{*}\left( \left( t-\tau \right) ^{4};\tau \right) \\&\quad =K_{\eta }^{*}\left( t^{4};\tau \right) -4\tau K_{\eta }^{*}\left( t^{3};\tau \right) +6\tau ^{2}K_{\eta }^{*}\left( t^{2};\tau \right) -4\tau ^{3}K_{\eta }^{*}\left( t;\tau \right) +\tau ^{4}\\&\quad =\frac{31}{\eta ^{4}}+\frac{67}{\eta ^{3}}\tau +\frac{87}{\eta ^{2}}\tau ^{2}+\frac{24}{\eta }\tau ^{3}+\tau ^{4}-4\tau \left( \frac{15}{4\eta ^{3}} +\frac{43}{2\eta ^{2}}\tau +\frac{27}{2\eta }\tau ^{2}+\tau ^{3}\right) \\&\qquad +6\tau ^{2}\left( \frac{5}{3\eta ^{2}}+\frac{6}{\eta }\tau +\tau ^{2}\right) -4\tau ^{3}\left( \frac{3}{2\eta }+\tau \right) +\tau ^{4}\\&\quad =\frac{11}{\eta ^{2}}\tau ^{2}+\frac{52}{\eta ^{3}}\tau +\frac{31}{\eta ^{4}}. \end{aligned}$$

\(\square \)

Lemma 2.6

For every \(\tau \in \left( 0,\infty \right) \) and \(\eta \in \mathbb {N} \), we have

$$\begin{aligned} \mathrm{(i)}\underset{\eta \rightarrow \infty }{\lim }\eta K_{\eta }^{*}\left( t-\tau ;\tau \right)&=\frac{3}{2},\\ \mathrm{(ii)}\underset{\eta \rightarrow \infty }{\lim }\eta K_{\eta }^{*}\left( \left( t-\tau \right) ^{2};\tau \right)&=3\tau ,\\ \mathrm{(iii)}\underset{\eta \rightarrow \infty }{\lim }\eta ^{2}K_{\eta }^{*}\left( \left( t-\tau \right) ^{4};\tau \right)&=11\tau ^{2}. \end{aligned}$$

3 Local Approximation Results for \(K_{\eta }^{*}(\psi ;\tau )\)

In this section, we investigate the local approximation properties of \(K_{\eta }^{*}(\psi ;\tau )\). Let \(C\left( 0,\infty \right) \) be the set of all continuous functions \(\psi \) defined on \(\left( 0,\infty \right) \) and \(C_{B}\left( 0,\infty \right) \) denote the space of bounded real-valued continuous, endowed with the norm \(\left\| \psi \right\| =\sup _{\tau \in \left( 0,\infty \right) }\left| \psi (\tau )\right| .\) Further, we consider the following Peetre’s K-functional,

$$\begin{aligned} K_{2}(\psi ,\delta ):=\underset{\hslash \in C_{B}^{2}\left( 0,\infty \right) }{\inf }\left\{ \left\| \psi -\hslash \right\| +\delta \left\| \hslash ^{\prime \prime }\right\| \right\} , \end{aligned}$$

where \(\delta >0\) and \(C_{B}^{2}\left( 0,\infty \right) =\left\{ \hslash \in C_{B}\left( 0,\infty \right) :\hslash ^{^{\prime }},\hslash ^{^{\prime \prime } }\in C_{B}\left( 0,\infty \right) \right\} .\)Taking into account [15], there exists an absolute positive constant C such that

$$\begin{aligned} K_{2}(\psi ,\delta )\le C\omega _{2}\left( \psi ,\sqrt{\delta }\right) , \end{aligned}$$
(3.1)

where

$$\begin{aligned} \omega _{2}(\psi ,\delta ):=\sup _{0<h\le \sqrt{\delta }}\sup _{\tau \pm h\in \left( 0,\infty \right) }\left| \psi (\tau +2h)-2\psi (\tau +h)+\psi (\tau )\right| \end{aligned}$$

is the second-order modulus of smoothness of \(\psi \in C_{B}\left( 0,\infty \right) \) and \(C>0.\) Additionally, the usual modulus of continuity of \(\psi \in C_{B}\left( 0,\infty \right) \) can be defined as:

$$\begin{aligned} \omega (\psi ,\delta )=\sup _{0<h\le \delta }\sup _{\tau \in \left( 0,\infty \right) }\left| \psi (\tau +h)-\psi (\tau )\right| . \end{aligned}$$

Theorem 3.1

For all \(\psi \in C_{B}\left( 0,\infty \right) \) and \(\tau \in \left( 0,\infty \right) \), we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi )-\psi \right| _{C\left( 0,\infty \right) }\le 2w\left( \psi ;\sqrt{B_{\eta }(\tau )}\right) . \end{aligned}$$
(3.2)

Proof

For any \(\delta >0,\) we have

$$\begin{aligned} \left| \psi (u)-\psi (\tau )\right| \le w\left( \psi ;\left| u-\tau \right| \right) \le \left( 1+\frac{\left| u-\tau \right| }{\delta }\right) w\left( \psi ;\delta \right) . \end{aligned}$$

Applying \(K_{\eta }^{*}\) to both ends, we can obtain

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le K_{\eta }^{*}(\left| \psi (u)-\psi (\tau )\right| ;\tau )\\&\le \left( 1+\frac{1}{\delta }K_{\eta }^{*}\left( \left| u-\tau \right| ;\tau \right) \right) w\left( \psi ;\delta \right) . \end{aligned}$$

By using the Cauchy–Schwarz inequality and taking \(\delta =\sqrt{B_{\eta } (\tau )},\) we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le \left( 1+\frac{1}{\delta }\sqrt{K_{\eta }^{*}\left( \left( u-\tau \right) ^{2};\tau \right) }\right) w\left( \psi ;\delta \right) \\&\le 2w\left( \psi ;\sqrt{B_{\eta }(\tau )}\right) . \end{aligned}$$

\(\square \)

Theorem 3.2

For all \(\psi \in C_{B}\left( 0,\infty \right) \) and \(\tau \in \left( 0,\infty \right) \), there exist absolute constant \(C>0\) such that

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right| \le Cw_{2} (\psi ;\sqrt{\delta _{\eta }(\tau )})+w\left( \psi ;\theta _{\eta }(\tau )\right) \end{aligned}$$

where \(\theta _{\eta }(\tau )=A_{\eta }(\tau )\) and \(\delta _{\eta }(\tau )=B_{\eta }(\tau )+A_{\eta }^{2}(\tau )\).

Proof

First, we define the following auxiliary operator as

$$\begin{aligned} \overset{\sim }{K}_{\eta }^{*}(\psi ;\tau )=K_{\eta }^{*}(\psi ;\tau )+\psi (\tau )-\psi (\mu _{\eta }(\tau )). \end{aligned}$$
(3.3)

where \(\mu _{\eta }(\tau )=\frac{3}{2\eta }+\tau \). Note that, from Lemmas 2.4 and 2.5, we have

$$\begin{aligned} \overset{\sim }{K}_{\eta }^{*}(1;\tau )=1\text { and }\overset{\sim }{K}_{\eta }^{*}((t-\tau );\tau )=0. \end{aligned}$$

For \(\hslash \) \(\in C_{B}^{2}\left( 0,\infty \right) \), making use of Taylor’s expansion,

$$\begin{aligned} \hslash (t)=\hslash (\tau )+\hslash ^{\prime }(\tau )(t-\tau )+\int _{\tau } ^{t}(t-s)\hslash ^{\prime \prime }(s)ds. \end{aligned}$$

Applying \(\overset{\sim }{K}_{\eta }^{*}\) to both sides of the above equation, we have

$$\begin{aligned} \overset{\sim }{K}_{\eta }^{*}(\hslash ;\tau )-\hslash (\tau )&=\overset{\sim }{K}_{\eta }^{*}((t-\tau )\hslash ^{\prime }(\tau );\tau )+\overset{\sim }{K}_{\eta }^{*}\left( \int _{\tau }^{t}(t-s)\hslash ^{\prime \prime } (s)ds;\tau \right) \\&=\hslash ^{\prime }(\tau )\overset{\sim }{K}_{\eta }^{*}((t-\tau );\tau )+K_{\eta }^{*}\left( \int _{\tau }^{t}(t-s)\hslash ^{\prime \prime }(s)ds;\tau \right) \\&\quad -\int _{\tau }^{\mu _{\eta }(\tau )}\left( \mu _{\eta } (\tau )-s\right) \hslash ^{\prime \prime }(s)ds\\&=K_{\eta }^{*}\left( \int _{\tau }^{t}(t-s)\hslash ^{\prime \prime }(s)ds;\tau \right) -\int _{\tau }^{\mu _{\eta }(\tau )}\left( \mu _{\eta } (\tau )-s\right) \hslash ^{\prime \prime }(s)ds. \end{aligned}$$

On the other hand,

$$\begin{aligned} \left| \int _{\tau }^{t}(t-s)\hslash ^{\prime \prime }(s)ds\right|&\le \int _{\tau }^{t}\left| t-s\right| \left| \hslash ^{\prime \prime }(s)\right| ds\\&\le \left\| \hslash ^{\prime \prime }\right\| \int _{\tau }^{t}\left| t-s\right| ds\le \left\| \hslash ^{\prime \prime }\right\| (t-s)^{2} \end{aligned}$$

and

$$\begin{aligned} \left| \int _{\tau }^{\mu _{\eta }(\tau )}\left( \mu _{\eta }(\tau )-s\right) \hslash ^{\prime \prime }(s)ds\right|&\le \int _{\tau }^{\mu _{\eta }(\tau )}\left| \mu _{\eta }(\tau )-s\right| \left| \hslash ^{\prime \prime }(s)\right| ds\\&\le \left\| \hslash ^{\prime \prime }\right\| (\mu _{\eta }(\tau )-\tau )^{2}\\&=\left\| \hslash ^{\prime \prime }\right\| \left( K_{\eta }^{*}(t-\tau ;\tau )\right) ^{2}, \end{aligned}$$

which implies

$$\begin{aligned} \left| \overset{\sim }{K}_{\eta }^{*}(\hslash ;\tau )-\hslash (\tau )\right|&\le \left| K_{\eta }^{*}\left( \int _{\tau } ^{t}(t-s)\hslash ^{\prime \prime }(s)ds;\tau \right) \right| +\left| \int _{\tau }^{\mu _{\eta ,k}(\tau )}\left( \mu _{\eta }(\tau )-s\right) \hslash ^{\prime \prime }(s)ds\right| \nonumber \\&\le \left\| \hslash ^{\prime \prime }\right\| \left\{ K_{\eta }^{*}((t-\tau )^{2};\tau )+(K_{\eta }^{*}\left( t-\tau \right) ;\tau )^{2}\right\} \nonumber \\&=\left\| \hslash ^{\prime \prime }\right\| \delta _{\eta }(\tau ). \end{aligned}$$
(3.4)

Using Lemma 2.4 and (3.3), we have

$$\begin{aligned} \left| \overset{\sim }{K}_{\eta }^{*}(\psi ;\tau )\right| & \le \left| K_{\eta }^{*}(\psi ;\tau )\right| +\left| \psi (\tau )\right| +\left| \psi (\mu _{\eta }(\tau ))\right| \le \left\| \psi \right\| K_{\eta }^{*}\left( 1;\tau \right) +2\left\| \psi \right\| \\ & \le 3\left\| \psi \right\| . \end{aligned}$$

Using (3.4) and the uniform boundedness of \(\overset{\sim }{K}_{\eta }^{*},\) we get

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le \left| \overset{\sim }{K}_{\eta }^{*}(\psi -\hslash ;\tau )\mathbf {-(} \psi -\hslash )(\tau )\right| \mathbf {+}\left| \overset{\sim }{K}_{\eta }^{*}(\hslash ;\tau )-\hslash (\tau )\right| \mathbf {+}\left| \psi (\tau ) \right. \\&\quad \ \left. -\psi \left( \mu _{\eta }(\tau )\right) \right| \\&\le 4\left\| \psi -\hslash \right\| +\left\| \hslash ^{\prime \prime }\right\| \delta _{\eta }(\tau )+\omega \left( \psi ,\theta _{\eta } (\tau )\right) \text {.} \end{aligned}$$

Taking infimum on the right hand side over all \(\hslash \in C_{B}^{2}\left( 0,\infty \right) \), we obtain following inequality

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right| \le 4K_{2}\left( \psi ;\delta _{\eta }(\tau )\right) +\omega \left( \psi ,\theta _{\eta } (\tau )\right) , \end{aligned}$$

which together with (3.1) gives the proof of the theorem. \(\square \)

Theorem 3.3

For all \(\psi ^{^{\prime }}\in C_{B}\left( 0,\infty \right) \) and \(\tau \in \left( 0,\infty \right) \), we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right| \le \left| \psi ^{^{\prime }}(t)\right| \left| A_{\eta }(\tau )\right| +2\sqrt{B_{\eta }(\tau )}w\left( \psi ^{^{\prime }};\sqrt{B_{\eta }(\tau )}\right) , \end{aligned}$$

where \(B_{\eta }(\tau )=K_{\eta }^{*}\left( \left( u-\tau \right) ^{2};\tau \right) .\)

Proof

Applying \(M_{\eta }^{*}\) to both sides of the equality \(\psi (u)=\psi (\tau )+\psi ^{^{\prime }}(t)(u-\tau )+\psi (u)-\psi (t)-\psi ^{^{\prime }} (\tau )(u-\tau ),\) using mean value theorem and the Cauchy–Schwarz inequality and taking \(\delta =\sqrt{B_{\eta }(\tau )},\) we can obtain

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le \left| \psi ^{^{\prime }}(\tau )\right| \left| K_{\eta }^{*}(u-\tau ;\tau )\right| +K_{\eta }^{*}\left( \left| \psi (u)-\psi (\tau )-\psi ^{^{\prime }}(\tau )(u-\tau )\right| ;\tau \right) \\&\le \left| \psi ^{^{\prime }}(\tau )\right| \left| K_{\eta }^{*}(u-\tau ;\tau )\right| +K_{\eta }^{*}\left( \left| u-\tau \right| \left( 1+\frac{\left| u-\tau \right| }{\delta }\right) w\left( \psi ^{^{\prime }};\delta \right) ;\tau \right) \\&\le \left| \psi ^{^{\prime }}(\tau )\right| \left| A_{\eta } (\tau )\right| +w\left( \psi ^{^{\prime }};\delta \right) \left( K_{\eta }^{*}(\left| u-\tau \right| ;\tau )+\frac{K_{\eta }^{*}\left( \left( u-\tau \right) ^{2};\tau \right) }{\delta }\right) \\&\le \left| \psi ^{^{\prime }}(\tau )\right| \left| A_{\eta } (\tau )\right| \\&\quad +w\left( \psi ^{^{\prime }};\delta \right) \sqrt{K_{\eta }^{*}\left( \left( u-\tau \right) ^{2};\tau \right) }\left( 1+\frac{\sqrt{K_{\eta }^{*}\left( \left( u-\tau \right) ^{2};\tau \right) }}{\delta }\right) \\&\le \left| \psi ^{^{\prime }}(\tau )\right| \left| A_{\eta } (\tau )\right| +2\sqrt{B_{\eta }(\tau )}w\left( \psi ^{^{\prime }} ;\sqrt{B_{\eta }(\tau )}\right) . \end{aligned}$$

\(\square \)

Corollary 3.4

For each \(\psi \in C_{B}\left( 0,\infty \right) \), the sequence of the operators \(K_{\eta }^{*}(\psi ;\tau )\) convergence to uniformly on \(\left( 0,A\right] .\)

4 Rate of Convergence

In this section, we determine the rate of convergence by utilizing the standard modulus of continuity and functions within the Lipschitz class. Let’s consider the Lipschitz class as follows

where M is a positive constant depending only on \(\varsigma \) and \(\psi \).

Let

\(C_{\mu }\left( 0,\infty \right) :=\left\{ \psi :\psi \in B_{\mu }\left( 0,\infty \right) \cap C\left( 0,\infty \right) ,\left\| \psi \right\| _{\mu }:=\frac{\left| \psi (\tau )\right| }{1+\tau ^{2}}\le \infty \right\} ,\)

\(C_{\mu }^{*}\left( 0,\infty \right) :=\left\{ \psi :\psi \in C_{\mu }\left( 0,\infty \right) ,\underset{\tau \rightarrow \infty }{\lim }\frac{\left| \psi (\tau )\right| }{1+\tau ^{2}}\le \infty \right\} \). On \(C_{\mu }^{*}\left( 0,\infty \right) \), the norm and usual modulus of continuity of \(\psi \) on the closed interval \(\left( 0,A\right] \) are given respectively as follows:

$$\begin{aligned} \left\| \psi \right\| _{\mu }:=\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{\left| \psi (\tau )\right| }{1+\tau ^{\mu }} \end{aligned}$$

and

$$\begin{aligned} \omega _{A}(\psi ,\delta )=\underset{\left| t-\tau \right| \le \delta }{\sup }\underset{{ \ \ \ }\tau ,t\in \left( 0,A\right] }{\sup }\left| \psi (t)-\psi (\tau )\right| . \end{aligned}$$

Theorem 4.1

Let \(\psi \in C_{2}\left( 0,\infty \right) \). Then, we have

$$\begin{aligned} \left\| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right\| _{C\left( 0,A\right] } & \le 6 M_{\psi }\left( 1+A^{2}\right) \left[ \frac{5}{3\eta ^{2} }+\frac{3}{\eta }A\right] \\ & \quad \ +2\omega _{A+1}\left( \psi ,\frac{5}{3\eta ^{2}} +\frac{3}{\eta }A\right) , \end{aligned}$$

where \(\omega _{A+1}\) is the modulus of continuity on the interval \(\left( 0,A+1\right] .\)

Proof

For \(\tau \in \left( 0,A\right] \) and \(t>A+1,\) we can get (see [20, eqn. 3.3])

$$\begin{aligned} \left| \psi (t)-\psi (\tau )\right| \le 6M_{\psi }\left( 1+A^{2}\right) (t-\tau )^{2}+\left( 1+\frac{\left| t-\tau \right| }{\delta }\right) \omega _{A+1}\left( \psi ,\delta \right) . \end{aligned}$$
(4.1)

Thus, applying the operators \(K_{\eta }^{*}(.;\tau )\) to both sides of (4.1), we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le K_{\eta }^{*}\left( \left| \psi (t)-\psi (\tau )\right| ;\tau \right) \\&\le 6M_{\psi }\left( 1+A^{2}\right) K_{\eta }^{*}\left( (t-\tau )^{2};\tau \right) \\&\quad +\left( 1+\frac{\left| t-\tau \right| }{\delta }\right) \omega _{A+1}\left( \psi ,\delta \right) \left( 1+\frac{1}{\delta }K_{\eta }^{*}\left( (t-\tau )^{2};\tau \right) \right) ^{1/2}. \end{aligned}$$

Using the Cauchy–Schwarz’s inequality and Lemma 2.5, we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le 6M_{\psi }\left( 1+A^{2}\right) \left[ \frac{5}{3\eta ^{2}}+\frac{3}{\eta }\tau \right] \\&\quad +\omega _{A+1}\left( \psi ,\delta \right) \left( 1+\frac{1}{\delta }\left( \frac{5}{3\eta ^{2}}+\frac{3}{\eta }\tau \right) \right) ^{1/2}. \end{aligned}$$

So,

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|\le & 6M_{\psi }\left( 1+A^{2}\right) \left[ \frac{5}{3\eta ^{2}}+\frac{3}{\eta }A\right] \\ & +\omega _{A+1}\left( \psi ,\delta \right) \left( 1+\frac{1}{\delta }\left( \frac{5}{3\eta ^{2}}+\frac{3}{\eta }A\right) \right) ^{1/2}. \end{aligned}$$

By taking \(\delta =\sqrt{\left( \frac{5}{3\eta ^{2}}+\frac{3}{\eta }A\right) } \), we get the desired result. \(\square \)

Theorem 4.2

Let S be any subset of the interval \(\left( 0,\infty \right) \), if \(\psi \in \) Lip\(_{M}\left( \varsigma ,T\right) ,\) then, for any \(\tau \in \left( 0,\infty \right) ,\) we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right| \le M\left( B_{\eta }^{\frac{\varsigma }{2}}(\tau )+2d^{\varsigma }(\tau ,T)\right) , \end{aligned}$$

where \(B_{\eta }(\tau )=K_{\eta }^{*}\left( \left( t-\tau \right) ^{2};\tau \right) \), M is a constant depending on \(\varsigma \), \(\psi \) and \(d(\tau ,T)=\inf \left\{ \left| t-\tau \right| :t\in T\right\} \) denotes the distance between \(\tau \) and T.

Proof

Let \(\overline{T}\) be the closure of T in \(\left( 0,\infty \right) .\) Then, there exists a point \(\tau _{0}\in \overset{-}{T}\) such that \(\left| \tau -\tau _{0}\right| =d(\tau ,T)\). By the triangle inequality, we have

$$\begin{aligned} \left| \psi (t)-\psi (\tau )\right| \le \left| \psi (t)-\psi (\tau _{0})\right| +\left| \psi (\tau )-\psi (\tau _{0})\right| . \end{aligned}$$

Applying the operators \(K_{\eta }^{*}(.;\tau )\) to both sides of above inequality, we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le K_{\eta }^{*}\left( \left| \psi (t)-\psi (\tau _{0})\right| ;\tau \right) +K_{\eta }^{*}\left( \left| \psi (\tau )-\psi (\tau _{0})\right| ;\tau \right) \\&\le M\left\{ K_{\eta }^{*}\left( \left| t-\tau _{0}\right| ^{\varsigma };\tau \right) +\left| \tau -\tau _{0}\right| ^{\varsigma }\right\} \\&\le M\left\{ K_{\eta }^{*}\left( \left| t-\tau \right| ^{\varsigma }+\left| \tau -\tau _{0}\right| ^{\varsigma };\tau \right) +\left| \tau -\tau _{0}\right| ^{\varsigma }\right\} \\&\le M\left\{ K_{\eta }^{*}\left( \left| t-\tau \right| ^{\varsigma };\tau \right) +2\left| \tau -\tau _{0}\right| ^{\varsigma }\right\} . \end{aligned}$$

Finally, applying the Hölder inequality with \(p=\frac{2}{\varsigma }\) and \(q=\frac{2}{2-\varsigma },\) we get

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le M\left\{ \left[ K_{\eta }^{*}\left( \left| t-\tau \right| ^{\varsigma } ;\tau \right) \right] ^{\frac{1}{p}}\left[ K_{\eta }^{*}\left( 1^{q} ;\tau \right) \right] ^{\frac{1}{q}}+2d^{\varsigma }(\tau ,T)\right\} \\&=M\left\{ \left[ K_{\eta }^{*}\left( \left| t-\tau \right| ^{2};\tau \right) \right] ^{\frac{\varsigma }{2}}+2\left( d(\tau ,T)\right) ^{\varsigma }\right\} \\&=M\left\{ (B_{\eta }(\tau ))^{\frac{\varsigma }{2}}+2d^{\varsigma } (\tau ,T)\right\} \end{aligned}$$

and the proof is completed. \(\square \)

5 Weighted Approximation by \(K_{\eta }^{*}\)

Weighted approximation involving positive operators is a topic of interest in mathematical analysis. In this section, we investigate approximation properties of the operators \(M_{\eta }^{*}\) within the weighted space of continuous functions on \(\left( 0,\infty \right) \). Firstly, to obtain some results, we need to following lemma which can be found in [12].

Lemma 5.1

[25] For all \(\tau \in \left( 0,\infty \right) \) and \(\mu \in \mathbb {N} \), we have

$$\begin{aligned} M_{\eta }^{*}\left( t^{\mu };\tau \right) =\frac{\eta }{\tau }S_{\eta }\left( t^{\mu +2};\tau \right) -2\eta S_{\eta }\left( t^{\mu +1};\tau \right) +\eta \tau S_{\eta }\left( t^{\mu };\tau \right) , \end{aligned}$$
(5.1)

where \(S_{\eta }(\psi ;\tau )=e^{-\eta \tau }\sum _{k=0}^{\infty }\psi \left( \frac{k}{\eta }\right) \frac{\tau ^{k}\eta ^{k}}{k!}.\)

Lemma 5.2

[12]For all \(\mu \in \mathbb {N},\) we have

$$\begin{aligned} S_{\eta }\left( t^{\mu };\tau \right) \sum _{i=0}^{\mu }a_{\mu ,k}\frac{\tau ^{i} }{\eta ^{\mu -i}} \end{aligned}$$
(5.2a)

where

$$\begin{aligned} a_{\mu +1,k}&=ka_{\mu ,k}+a_{\mu ,k-1},{ \ \ \ }\mu \ge 0,k\ge 1,\\ a_{0,0}&=1,{ \ \ }a_{\mu ,0}=0{ \ \ \ \ \ }\mu >0,\\ a_{\mu ,k}&=0,{ \ \ \ \ }\mu <k. \end{aligned}$$

Lemma 5.3

For the operators \(K_{\eta }^{*}\), we have

$$\begin{aligned} K_{\eta }^{*}\left( t^{\mu };\tau \right)&=\frac{\eta }{\tau }\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}\underset{k=1}{\overset{\rho +2}{ {\displaystyle \sum } }}a_{\rho +2,k}\frac{\tau ^{k}}{\eta ^{\rho +2-k}}\\&\quad -2\eta \sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}\underset{k=1}{\overset{\rho +1}{ {\displaystyle \sum } }}a_{\rho +1,k}\frac{\tau ^{k}}{\eta ^{\rho +1-k}}\\&\quad +\eta \tau \sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}\underset{k=1}{\overset{\rho }{ {\displaystyle \sum } }}a_{\rho ,k}\frac{\tau ^{k}}{\eta ^{\rho -k}}. \end{aligned}$$

Proof

From Lemma 2.2, we have

$$\begin{aligned} K_{\eta }^{*}\left( t^{\mu };\tau \right) =\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}M_{\eta }^{*}\left( t^{\rho };\tau \right) . \end{aligned}$$

Then, using recurrence formula (5.1), we obtain

$$\begin{aligned} K_{\eta }^{*}\left( t^{\mu };\tau \right)&=\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho }}\left\{ \frac{\eta }{\tau }S_{\eta }\left( t^{\mu +2};\tau \right) \right. \\&\quad \left. -2\eta S_{\eta }\left( t^{\mu +1};\tau \right) +\eta \tau S_{\eta }\left( t^{\mu };\tau \right) \right\} . \end{aligned}$$

The proof is easily concluded by using formula 5.2a given in Lemma 5.2. \(\square \)

Lemma 5.4

Let \(\psi \in C_{\mu }^{*}\left( 0,\infty \right) \). Then there exists a positive constant C such that

$$\begin{aligned} \left\| K_{\eta }^{*}\left( 1+t^{\mu };\tau \right) \right\| \le C_{\mu }{, \ \ \ }\eta \in \mathbb {N}. \end{aligned}$$
(5.3)

Moreover, for every \(\psi \in C_{\mu }^{*}\left( 0,\infty \right) \), we have

$$\begin{aligned} \left\| K_{\eta }^{*}\left( \psi ;\tau \right) \right\| \le C_{\mu }\left\| \psi \right\| _{\mu }{, \ \ \ }\eta \in \mathbb {N}. \end{aligned}$$
(5.4)

Thus \(M_{\eta }^{*}\) is a linear positive operator from \(C_{\mu }^{*}\left( 0,\infty \right) \) in to \(C_{\mu }^{*}\left( 0,\infty \right) \).

Proof

Inequality (5.3) is obvious for \(\mu =0\). Let \(\mu \ge 1\). Then, by Lemma 5.3, we have

$$\begin{aligned}&\frac{1}{1+\tau ^{\mu }}K_{\eta }^{*}\left( 1+t^{\mu };\tau \right) \\ &\quad =\frac{1}{1+\tau ^{\mu }} +\frac{1}{1+\tau ^{\mu }}\left\{ \sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho -1}}\underset{k=1}{\overset{\rho +2}{ {\displaystyle \sum } }}a_{\rho +2,k}\frac{\tau ^{k-1}}{\eta ^{\rho +2-k}}\right. \\&\qquad \left. -2\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho -1}}\underset{k=1}{\overset{\rho +1}{ {\displaystyle \sum } }}a_{\rho +1,k}\frac{\tau ^{k}}{\eta ^{\rho +1-k}}\right. \\&\qquad \left. +\sum _{\rho =0}^{\mu }\left( {\begin{array}{c}\mu \\ \rho \end{array}}\right) \frac{1}{\left( \mu -\rho +1\right) \eta ^{\mu -\rho -1}}\underset{k=1}{\overset{\rho }{ {\displaystyle \sum } }}a_{\rho ,k}\frac{\tau ^{k+1}}{\eta ^{\rho -k}}\right\} . \end{aligned}$$

Thus

$$\begin{aligned} \frac{1}{1+\tau ^{\mu }}K_{\eta }^{*}\left( 1+t^{\mu };\tau \right) \le 1+K_{\mu }\le C_{\mu }, \end{aligned}$$

the positive constant \(C_{\mu }\) is contingent on the parameter \(\mu \). On the other hand,

$$\begin{aligned} \left\| K_{\eta }^{*}\left( \psi ;\tau \right) \right\| _{\mu } \le \left\| \psi \right\| _{\mu }\left\| K_{\eta }^{*}\left( 1+t^{\mu };\tau \right) \right\| _{\mu } \end{aligned}$$

for every \(\psi \in C_{\mu }^{*}\left( 0,\infty \right) \). Using (5.3), we get (5.4). \(\square \)

Theorem 5.5

For all \(\psi \in C_{2}^{*}\left( 0,\infty \right) \) and \(\tau \in \left( 0,\infty \right) \), we have

$$\begin{aligned} \underset{\eta \rightarrow \infty }{\lim }\left\| K_{\eta }^{*}\left( \psi ;\tau \right) -\psi (\tau )\right\| _{2}=0. \end{aligned}$$

Proof

In accordance with Korovkin’s theorem, as presented by [19], it is adequate to confirm the fulfillment of the subsequent three conditions:

$$\begin{aligned} \underset{\eta \rightarrow \infty }{\lim }\left\| K_{\eta }^{*}\left( t^{\mu };\tau \right) -\tau ^{\mu }\right\| _{2}=0,{ \ \ \ \ \ \ } \mu =0,1,2. \end{aligned}$$
(5.5)

By Lemma 2.4-(a), it is clear that

$$\begin{aligned} \underset{\eta \rightarrow \infty }{\lim }\left\| K_{\eta }^{*}\left( 1;\tau \right) -1\right\| _{2}=0. \end{aligned}$$

For \(\mu =1\) and \(\mu =2,\) we have

$$\begin{aligned} \left\| K_{\eta }^{*}\left( t;\tau \right) -\tau \right\| _{2}&=\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{\left| K_{\eta }^{*}\left( t;\tau \right) -\tau \right| }{1+\tau ^{2}}\\&=\frac{3}{2\eta }\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{1}{1+\tau ^{2}}\\&\le \frac{2}{\eta } \end{aligned}$$

and

$$\begin{aligned} \left\| K_{\eta }^{*}\left( t^{2};\tau \right) -\tau ^{2}\right\| _{2}&=\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{\left| K_{\eta }^{*}\left( t^{2};\tau \right) -\tau ^{2}\right| }{1+\tau ^{2}}\\&=\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{1}{1+\tau ^{2} }\left| \frac{5}{3\eta ^{2}}+\frac{6}{\eta }\tau +\tau ^{2}-\tau ^{2}\right| \\&=\frac{5}{3\eta ^{2}}\underset{\tau \in \left( 0,\infty \right) }{\sup } \frac{1}{1+\tau ^{2}}+\frac{6}{\eta }\underset{\tau \in \left( 0,\infty \right) }{\sup }\frac{\tau }{1+\tau ^{2}}\\&\le \frac{2}{\eta ^{2}}+\frac{6}{\eta }. \end{aligned}$$

Hence

$$\begin{aligned} \underset{\eta \rightarrow \infty }{\lim }\left\| K_{\eta }^{*}\left( t;\tau \right) -\tau \right\| _{2}=0\text { and }\underset{\eta \rightarrow \infty }{\lim }\left\| K_{\eta }^{*}\left( t^{2};\tau \right) -\tau ^{2}\right\| _{2}=0. \end{aligned}$$

which ends the proof. \(\square \)

For \(\psi \in C_{\mu }^{*}\left[ 0,\infty \right) ,\) the weighted modulus of continuity is defined as

$$\begin{aligned} \Omega _{\mu }(\psi ,\delta )=\underset{\tau \ge 0,\text 0<h\le \delta }{\sup }\frac{\left| \psi (\tau +h)-\psi (\tau )\right| }{1+(\tau +h)^{\mu }}. \end{aligned}$$

Lemma 5.6

[27]If \(\psi \in C_{\mu }^{*}\left[ 0,\infty \right) ,\mu \in \mathbb {N} \), then

$$\begin{aligned} & \mathrm{(i)}\quad \Omega _{\mu }(\psi ,\delta ) \hbox {is a monotone increasing function of} \ \delta ,\\ & \mathrm{(ii)} \quad \underset{\delta \rightarrow \infty }{\lim }\Omega _{\mu }(\psi ,\delta )=0,\\ & \mathrm{(iii)} \quad \hbox {for any }\rho \in \left[ 0,\infty \right) ,\Omega _{\mu }(\psi ,\rho \delta )\le (1+\rho )\Omega _{\mu }(\psi ,\delta ). \end{aligned}$$

Theorem 5.7

If \(\psi \in C_{\mu }^{*}\left[ 0,\infty \right) ,\)then

$$\begin{aligned} \left\| K_{\eta }^{*}(\psi )-\psi \right\| _{\mu +1}\le k\Omega _{\mu }\left( \psi ,\frac{1}{\sqrt{\eta }}\right) \end{aligned}$$

where k is a constant independent of \(\psi \) and \(\eta .\)

Proof

From the definition of \(\Omega _{\mu }(\psi ,\delta )\) and Lemma 5.6, we may write

$$\begin{aligned} \left| \psi (t)-\psi (\tau )\right|&\le \left( 1+\left( \tau +\left| t-\tau \right| \right) ^{\mu }\right) \left( \frac{\left| t-\tau \right| }{\delta }+1\right) \Omega _{\mu } (\psi ,\delta )\\&\le \left( 1+\left( 2\tau +t\right) ^{\mu }\right) \left( \frac{\left| t-\tau \right| }{\delta }+1\right) \Omega _{\mu }(\psi ,\delta ). \end{aligned}$$

Then, we have

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le K_{\eta }^{*}\left| (\psi (t)-\psi (\tau )\right| ;\tau )\\&\le \Omega _{\mu }(\psi ,\delta )K_{\eta }^{*}\left( 1+(2\tau +t)^{\mu } ;\tau \right) +K_{\eta }^{*}\left( \left( 1+(2\tau +t)^{\mu }\right) ;\tau \right) \\&=\Omega _{\mu }(\psi ,\delta )K_{\eta }^{*}\left( 1+(2\tau +t)^{\mu } ;\tau \right) +I_{1}. \end{aligned}$$

Applying the Cauchy–Schwarz inequality to \(I_{1}\), we get

$$\begin{aligned} I_{1}\le K_{\eta }^{*}\left( (1+(2\tau +t)^{\mu }\right) ^{2};\tau ))^{1/2}\left( K_{\eta }^{*}\left( \frac{\left| t-\tau \right| ^{2}}{\delta ^{2}};\tau \right) \right) ^{1/2}. \end{aligned}$$

Therefore,

$$\begin{aligned} & \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right| \le \Omega _{\mu }(\psi ,\delta )K_{\eta }^{*}(1+(2\tau +t)^{\mu };\tau )\\ & \quad +K_{\eta }^{*}\left( (1+(2\tau +t)^{\mu }\right) ^{2};\tau ))^{1/2}\left( K_{\eta }^{*}\left( \frac{\left| t-\tau \right| ^{2}}{\delta ^{2}};\tau \right) \right) ^{1/2}. \end{aligned}$$

From Lemma 5.4, we have

$$\begin{aligned} & K_{\eta }^{*}(1+(2\tau +t)^{\mu };\tau )\le C_{\mu }\left( 1+\tau ^{\mu }\right) , \\ & K_{\eta }^{*}\left( (1+(2\tau +t)^{\mu }\right) ^{2};\tau ))^{1/2}\left( K_{\eta }^{*}\left( \frac{\left| t-\tau \right| ^{2}}{\delta ^{2} };\tau \right) \right) ^{1/2}\le C_{\mu }^{1}\left( 1+\tau ^{\mu }\right) . \end{aligned}$$

Also, from Lemma 2.4, we have

$$\begin{aligned} \left( K_{\eta }^{*}\left( \frac{\left| t-\tau \right| ^{2}}{\delta ^{2}};\tau \right) \right) ^{1/2}&\le \frac{1}{\delta }\sqrt{\frac{5}{3\eta ^{2}}+\frac{3}{\eta }\tau }\\&\le \frac{(2+3\tau )}{\delta \sqrt{\eta }}. \end{aligned}$$

So if we combine all these results, we get

$$\begin{aligned} \left| K_{\eta }^{*}(\psi ;\tau )-\psi (\tau )\right|&\le \Omega _{\mu }(\psi ,\delta )\left( C_{\mu }\left( 1+\tau ^{\mu }\right) +C_{\mu }^{1}\frac{\left( 1+\tau ^{\mu }\right) (2+3\tau )}{\delta \sqrt{\eta }}\right) \\&=\Omega _{\mu }(\psi ,\delta )\left( C_{\mu }\left( 1+\tau ^{\mu }\right) +C_{\mu }^{1}C_{1}\frac{\left( 1+\tau ^{\mu +1}\right) }{\delta \sqrt{\eta } }\right) \end{aligned}$$

where

$$\begin{aligned} C_{1}=\underset{\tau >0}{\sup }\frac{2+2\tau ^{\mu }+3\tau +3\tau ^{\mu +1}}{1+\tau ^{\mu +1}}. \end{aligned}$$

In the above inequality, if we substitute \(\frac{1}{\sqrt{\eta }}\) instead of \(\delta \), we obtain the desired result. \(\square \)

6 Voronovskaja Theorem for \(K_{\eta }^{*}\)

Voronovskaja’s theorem is a significant result in approximation theory, focusing on the convergence properties of certain approximation operators. The theorem offers an estimate for the rate of convergence of a sequence of approximation operators to a given function. Named after the Soviet mathematician Tamara Voronovskaja, the theorem often involves expressing the difference between the function being approximated and its approximation in terms of a remainder term. This theorem is foundational in understanding the behavior and efficiency of approximation methods in mathematical analysis.In this section, we give Voronovskaja type theorem for \(K_{\eta }^{*}.\)

Theorem 6.1

For any \(\psi \in C_{2}^{*}\left( 0,\infty \right) \) such that \(\psi ^{^{\prime }},\psi ^{^{\prime \prime }}\in C_{2}^{*}\left( 0,\infty \right) \), we get

$$\begin{aligned} \lim _{\eta \rightarrow \infty }\eta \left( K_{\eta }^{*}\left( \psi ;\tau \right) -\psi \left( \tau \right) \right) =\frac{3}{2}\psi ^{^{\prime } }(\tau )+\left( \frac{5}{3\eta }+3\tau \right) \psi ^{\prime \prime }\left( \tau \right) \end{aligned}$$

uniformly on the interval \(\left( 0,A\right] \).

Proof

Let \(\tau \in \left( 0,\infty \right) \) be fixed. By the Taylor formula we may write

$$\begin{aligned} \psi \left( t\right) =\psi \left( \tau \right) +\psi ^{\prime }\left( \tau \right) \left( t-\tau \right) +\frac{1}{2}\psi ^{\prime \prime }\left( \tau \right) \left( t-\tau \right) ^{2}+r\left( t;\tau \right) \left( t-\tau \right) ^{2}, \end{aligned}$$
(6.1)

where \(r\left( t;\tau \right) \) is the Peano form of the remainder, \(r\left( \cdot ;\tau \right) \in C_{B}\left( 0,\infty \right) \) and \(\lim _{t\rightarrow \tau }r\left( t;\tau \right) =0\). Applying \(K_{\eta }^{*}\) to (6.1), then we get

$$\begin{aligned} \eta \left( K_{\eta }^{*}\left( \psi ;\tau \right) -\psi \left( \tau \right) \right)&=\eta \psi ^{\prime }\left( \tau \right) K_{\eta }^{*}\left( t-\tau ;\tau \right) +\frac{1}{2}\eta \psi ^{\prime \prime }\left( \tau \right) K_{\eta }^{*}\left( \left( t-\tau \right) ^{2};\tau \right) \nonumber \\&\quad +\eta K_{\eta }^{*}\left( r\left( t;\tau \right) \left( t-\tau \right) ^{2};\tau \right) . \end{aligned}$$
(6.2)

Utilizing the Cauchy–Schwarz inequality to last part of (6.2), we get

$$\begin{aligned} \eta K_{\eta }^{*}\left( r\left( t;\tau \right) \left( t-\tau \right) ^{2};\tau \right) \le \sqrt{K_{\eta }^{*}\left( r^{2}\left( t;\tau \right) ;\tau \right) }\sqrt{\eta ^{2}K_{\eta }^{*}\left( \left( t-\tau \right) ^{4};\tau \right) }. \end{aligned}$$
(6.3)

We observe that \(r^{2}\left( \tau ;\tau \right) =0\) and \(r^{2}\left( .,\tau \right) \in \) \(C_{B}\left( 0,\infty \right) \).

Then, from Theorem 5.5,

$$\begin{aligned} \lim _{\eta \rightarrow \infty }K_{\eta }^{*}\left( r^{2}\left( t;\tau \right) ;\tau \right) =r^{2}\left( \tau ;\tau \right) =0 \end{aligned}$$
(6.4)

uniformly for \(\tau \in \left( 0,A\right] \) .

Hence, from (6.3), (6.4) and Lemma 2.6 we get immediately

$$\begin{aligned} \lim _{\eta \rightarrow \infty }\eta \left( K_{\eta }^{*}\left( \psi ;\tau \right) -\psi \left( \tau \right) \right) =\frac{3}{2}\psi ^{^{\prime } }(\tau )+\left( \frac{5}{3\eta }+3\tau \right) \psi ^{\prime \prime }\left( \tau \right) . \end{aligned}$$

\(\square \)

7 New Generalization of Bivariate Szász–Mirakjan Operator

In this section, we present the bivariate extension of the operators as referenced in (2.1). The bivariate extension of the \(K_{\eta }^{*}\left( \psi ;\tau \right) \) can be defined by

$$\begin{aligned} K_{\eta _{1},\eta _{2}}^{*}\left( \psi ;\tau ,\gamma \right) :=\sum _{k_{1} =0}^{\infty }\sum _{k_{2}=0}^{\infty }s_{\eta _{1},k_{1}}(\tau )s_{\eta _{2},k_{2} }(\gamma )\overset{1}{\underset{0}{ {\displaystyle \int } }}\overset{1}{\underset{0}{ {\displaystyle \int } }}\psi \left( \frac{k_{1}+t_{1}}{\eta _{1}},\frac{k_{2}+t_{2}}{\eta _{2} }\right) dt_{1}dt_{2} \end{aligned}$$

where \(\tau ,\gamma \in I^{2}=\left( 0,\infty \right) \times \left( 0,\infty \right) .\)

The new generalization of Bivariate Szász–Mirakjan operators can be rewritten as

$$\begin{aligned} K_{\eta _{1},\eta _{2},k_{1},k_{2}}^{*}\left( ;\tau ,\gamma \right) =K_{\eta _{1},k_{1}}^{*}\left( ;\tau \right) K_{\eta _{2},k_{2}}^{*}\left( ;\gamma \right) . \end{aligned}$$

Lemma 7.1

Let \(e_{i\rho }\left( \tau ,\gamma \right) =\tau ^{i} \gamma ^{\rho }\), \(0\le i+\rho \le 2.\) For \(\left( \tau ,\gamma \right) \in I^{2}=\left( 0,\infty \right) \times \left( 0,\infty \right) \), we have

$$\begin{aligned} K_{\eta _{1},\eta _{2}}^{*}(e_{00};\tau ,\gamma )&=1,\\ K_{\eta _{1},\eta _{2}}^{*}(e_{10};\tau ,\gamma&=\frac{3}{2\eta _{1}} +\tau ,\\ K_{\eta _{1},\eta _{2}}^{*}(e_{01};\tau ,\gamma )&=\frac{3}{2\eta _{1} }+\gamma ,\\ K_{\eta _{1},\eta _{2}}^{*}(e_{20};\tau ,\gamma )&=\frac{5}{3\eta _{1}^{2} }+\frac{6}{\eta _{1}}\tau +\tau ^{2},\\ K_{\eta _{1},\eta _{2}}^{*}(e_{02};\tau ,\gamma )&=\frac{5}{3\eta _{2}^{2} }+\frac{6}{\eta _{2}}\gamma +\gamma ^{2}. \end{aligned}$$

Remark 7.2

According to above Lemma 7.1, we get

$$\begin{aligned} K_{\eta _{1},\eta _{2}}^{*}(e_{10}-\tau ;\tau ,\gamma )&=\frac{3}{2\eta _{1} },\\ K_{\eta _{1},\eta _{2}}^{*}(e_{01}-\gamma ;\tau ,\gamma )&=\frac{3}{2\eta _{2}},\\ K_{\eta _{1},\eta _{2}}^{*}(\left( e_{10}-\tau \right) ^{2};\tau ,\gamma )&=\frac{5}{3\eta _{1}^{2}}+\frac{3}{\eta _{1}}\tau =\delta _{\eta _{1}}(\tau ),\\ K_{\eta _{1},\eta _{2}}^{*}(\left( e_{01}-\gamma \right) ^{2};\tau ,\gamma )&=\frac{5}{3\eta _{2}^{2}}+\frac{3}{\eta _{2}}\gamma =\delta _{\eta _{2}}(\gamma ) \end{aligned}$$

In the next theorem, we obtain the uniform convergence of new generalization of bivariate Bernstein–Kantorovich operators to the bivariate functions defined on \(I^{2}=\left( 0,\infty \right) \times \left( 0,\infty \right) \).

Theorem 7.3

Let \(C(I_{A,B}^{2})\) be the space of continuous bivariate function on \(I_{A,B}^{2}=\left( 0,A\right] \times \left( 0,B\right] \in I^{2}.\) Then for any \(\psi \in C(I_{A,B}^{2})\), we have

$$\begin{aligned} \underset{\eta _{1},\eta _{2}\rightarrow \infty }{\lim }\left\| K_{\eta _{1},\eta _{2}}^{*}\psi -\psi \right\| =0. \end{aligned}$$

Proof

Using Lemma 7.2, we get

$$\begin{aligned} \left\| K_{\eta _{1},\eta _{2}}^{*}e_{00}-e_{00}\right\|&=0,\left\| K_{\eta _{1},\eta _{2}}^{*}e_{10}-e_{10}\right\| \rightarrow 0\\ \left\| K_{\eta _{1},\eta _{2}}^{*}e_{01}-e_{01}\right\|&\rightarrow 0,\left\| K_{\eta _{1},\eta _{2}}^{*}\left( e_{20} +e_{02}\right) -\left( e_{20}+e_{02}\right) \right\| \rightarrow 0\text { as }\eta _{1},\eta _{2}\rightarrow \infty \end{aligned}$$

Hence, by Volkov’s theorem [39], we deduce

$$\begin{aligned} \underset{\eta _{1},\eta _{2}\rightarrow \infty }{\lim }\left\| K_{\eta _{1},\eta _{2}}^{*}\psi -\psi \right\| =0. \end{aligned}$$

\(\square \)

For bivariate real functions, we use the following continuity module:

$$\begin{aligned} w\left( \psi ;\delta _{\eta },\delta _{\mu }\right) =\sup \left\{ \left| \psi (t,s)-\psi (\tau ,\gamma )\right| :\left( t,s\right) ,\left( \tau ,\gamma \right) \in I^{2},\left| t-\tau \right| \le \delta _{\eta },\left| s-\gamma \right| \le \delta _{\mu }\right\} . \end{aligned}$$

Theorem 7.4

Let \(\psi \in C(I^{2})\). Then for all \(\left( \tau ,\gamma \right) \in I^{2}\), the inequality

$$\begin{aligned} \left| K_{\eta _{1},\eta _{2}}^{*}\left( \psi ;\tau ,\gamma \right) -\psi \left( \tau ,\gamma \right) \right| \le 4w\left( \psi ;\delta _{\eta _{1}}(\tau ),\delta _{\eta _{2}}(\gamma )\right) \end{aligned}$$

holds, where \(\delta _{\eta _{1}}(\tau ),\delta _{\eta _{2}}(\gamma )\) are as in Remark 7.2.

Proof

By the linearity and positivity properties of the \(K_{\eta _{1},\eta _{2}} ^{*}\), we can write

$$\begin{aligned} \left| K_{\eta _{1},\eta _{2}}^{*}\left( \psi ;\tau ,\gamma \right) -\psi \left( \tau ,\gamma \right) \right|&\le K_{\eta _{1},\eta _{2} }^{*}\left( \left| \psi (t,s)-\psi \left( \tau ,\gamma \right) \right| ;\tau ,\gamma \right) \\&\le w\left( \psi ;\delta _{1},\delta _{2}\right) \left[ K_{\eta _{1}} ^{*}\left( 1;\tau \right) +\frac{1}{\delta _{1}}K_{\eta _{1}}^{*}\left( \left| t-\tau \right| ;\tau \right) \right] \\&\quad \times \left[ K_{\eta _{2}}^{*}\left( 1;\gamma \right) +\frac{1}{\delta _{2}}K_{\eta _{2}}^{*}\left( \left| s-\gamma \right| ;\gamma \right) \right] . \end{aligned}$$

Applying Cauchy–Schwarz inequality, we obtain

$$\begin{aligned} K_{\eta _{1}}^{*}\left( \left| t-\tau \right| ;\tau \right) \le K_{\eta _{1}}^{*}\left( \left( t-\tau \right) ^{2};\tau \right) ^{\frac{1}{2}} \end{aligned}$$

and

$$\begin{aligned} K_{\eta _{2}}^{*}\left( \left| s-\gamma \right| ;\gamma \right) \le K_{\eta _{2}}^{*}\left( \left( s-\gamma \right) ^{2};\gamma \right) ^{\frac{1}{2}}. \end{aligned}$$

Choosing \(\delta _{1}=\delta _{\eta _{1}}(\tau )\) and \(\delta _{2}=\delta _{\eta _{2}}(\gamma )\), we have desired result. \(\square \)

8 Graphical Simulations

Example 8.1

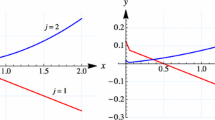
Let \(f(x)=2x^{4}+14x^{3}-20x^{2}+8x-1\) with \(x\in \left[ 0.1,1\right] \). Here we take the value of \(n\in \left\{ 250,350,850\right\} \). Figure 1 illustrates the convergence of operators to f(x) as the values of n increase. Secondly, The absolute error function \(E_{n}\left( \psi ;x\right) =\left| K_{n}^{*}(f;x)-f(x)\right| \) is illustrated in Fig. 2. Finally, we give the absolute error between \(K_{n}^{*}(f;x)\) and f(x) for varying n values, considering specific x entries outlined in Table 1.

Fig. 1
figure 1

Approximation to f by \(K_{n}^{*}(f;x)\) for \(n\in \left\{ 250,350,850\right\} \) and \(f(x)=2x^{4}+14x^{3}-20x^{2}+8x-1\)

Full size image
Fig. 2
figure 2

Absolute error function \(E_{n}\left( f;x\right) \) for \(n\in \left\{ 250,350,850\right\} \) and \(f(x)=2x^{4}+14x^{3}-20x^{2}+8x-1\)

Full size image

Example 8.2

Let \(f(x)=x^{3}+y\) with \(\left( x,y\right) \in \left[ 0.1,1\right] \times \left[ 0.1,1\right] .\) Here we take the value of \(n_{1},n_{2} \in \left\{ 200,400\right\} \). The Fig. 3 illustrates the convergence of operators to f(x, y) as the values of increase \(n_{1}\) and \(n_{2}\). Secondly, The absolute error function \(E_{n_{1},n_{2}}\left( f;x,y\right) =\left| K_{n_{1},n_{2}}^{*}(f;x,y)-f(x,y)\right| \) is illustrated in Fig. 4. Finally, we give the absolute error between \(K_{n_{1},n_{2}}^{*}(f;x,y)\) and f(x, y) for varying \(n_{1}\) and \(n_{2}\) values, considering specific \(\left( x,y\right) \) entries outlined in Tables 1 and 2.

Table 1 \(E_{n}\left( f;x\right) \) with \(f(x)=2x^{4} +14x^{3}-20x^{2}+8x-1\) for some values of x in \(\left[ 0.1,0.5\right] \) and \(n\in \left\{ 250,350,850\right\} \)
Full size table
Fig. 3
figure 3

Approximation to f by \(K_{n_{1}n_{2}}^{*}(f;x,y)\) for \(n_{1},n_{2}\in \left\{ 200,400\right\} \) and \(f(x,y)=x^{3}+y.\)

Full size image
Fig. 4
figure 4

Absolute error function \(E_{n_{1},n_{2}}\left( f;x,y\right) \) for \(n_{1},n_{2}\in \left\{ 200,400\right\} \) and \(f(x,y)=x^{3}+y.\)

Full size image
Table 2 \(E_{n_{1},n_{2}}\left( f;x,y\right) \) with \(f(x,y)=x^{3}+y\) for some values of \(\left( x,y\right) \) in \(\left[ 0.1,0.5\right] \times \left[ 0.1,0.5\right] \) and \(n_{1},n_{2}\in \left\{ 200,400\right\} \)
Full size table

9 Conclusion

This paper introduced a novel generalization of Szász–Mirakjan operators. Subsequently, we scrutinized the local approximation properties of these operators employing Peetre’s K-function. Additionally, we delved into the analysis of the convergence rate, utilizing both the ordinary modulus of continuity and Lipschitz-type maximal functions. Following this, we formally prove theorems related to weighted approximation and Voronoskaja-type specific to these innovative operators. Finally, we supplemented our findings with several numerical illustrative examples.