n-Jordan Homomorphisms into Fields and Integral Domains

Abstract

We investigate under what conditions an n-Jordan homomorphism between rings or algebras is an n-homomorphism. More specifically, if R and S are rings and S is of characteristic greater than n, along with some other results for an n-Jordan homomorphism $\psi :R \rightarrow S$, we prove the following results: If S is a field and either $char \, S = 0$ or $char \, S > 2 \, card \, \{ \alpha \in S: {\alpha }^{n - 1} = 1 \}$, then $\psi$ is an n-homomorphism, where $char \, S$ and $card \,$ denote the characteristic of S and the cardinal number (of a set), respectively. If S is an integral domain, then $\psi$ is an n-homomorphism if S is an algebra, or either one of the conditions $char \, S = 0$, $char \, S > 2(n - 1)$, $n = 3$, holds.

1 Introduction

In the sequel we always assume that $n \in {\mathbb {N}}$, $n \ge 2$. An additive map (operator) $\psi :R \rightarrow S$ between rings R and S is called an n-homomorphism if

$$\begin{aligned} \psi (a_1a_2 \cdots a_n)=\psi (a_1)\psi (a_2) \cdots \psi (a_n), \end{aligned}$$

for every $a_1, a_2,..., a_n \in R$. A 2-homomorphism is simply called a homomorphism. In particular, if $\psi :R \rightarrow S$ is an additive map such that $\psi (a^n)=\psi (a)^n$ for every $a\in R$, it is called an n-Jordan homomorphism and a 2-Jordan homomorphism is simply called a Jordan homomorphism .

In the definitions above, whenever R and S are algebras, the map (operator) $\psi$ is assumed to be either additive or linear, which will be specified in each case.

In 1956, I. N. Herstein introduced the concept of additive n-Jordan homomorphisms on rings [10]. In 1968, for $n=2$, W. Żelazko proved that every complex linear n-Jordan homomorphism (Jordan homomorphism) on an algebra is a homomorphism [20]. This result can be easily extended as follows, which is known as the Żelazko Theorem:

Let A be an algebra, which is not necessarily commutative, and let B be a semisimple commutative Banach algebra. Then every linear Jordan homomorphism $\psi :A\rightarrow B$ is a homomorphism.

The study of connections of Jordan homomorphisms with homomorphisms dates back to the 1940’s. The notion of linear n-homomorphisms on algebras was introduced in 2005 by Sh. Hejazian et al. [9]. For the early works in this field, one may refer to [1, 2, 10, 15, 17, 18] and [20].

It is a long-standing question that under what conditions an n-Jordan homomorphism between rings or algebras is an n-homomorphism.

During the recent years, some authors have presented certain conditions to establish this property. In this paper, along with some other results on n-Jordan homomorphisms, we will extend some of the known results in this field to more general cases, by some new techniques.

We first review some definitions and elementary results, which will be useful in the sequel.

Definition 1.1

Let R be a ring and ${\mathcal {N}} = \{ n \in {\mathbb {N}}: na = 0 \, (a \in R) \}$. The characteristic of R, which we denote by $char \, R$, is defined as follows:

$$\begin{aligned} char \, R {\mathop {=}\limits ^{\textrm{def}}}\left\{ \begin{array}{ll} \min {\mathcal {N}}, &{}\quad {\mathcal {N}} \ne \emptyset ; \\ 0, &{}\quad {\mathcal {N}} = \emptyset . \end{array} \right. \end{aligned}$$

Note that $char \, R = 1$ if and only if $R = \{ 0 \}$.

Definition 1.2

Let R be a ring and $n \in {\mathbb {N}}$.

• 1. R is said to be not of characteristic n if for each $a \in R$, $na = 0$ implies $a = 0$.

• 2. R is said to be of characteristic greater than n if R is not of characteristic k for any $k \in \{ 1, 2, \ldots , n \}$.

Obviously, if $R\ne \{0\}$ then R is not of characteristic 1. Moreover, if $n \in {\mathbb {N}}$, then it is easy to show that R is of characteristic greater than n if and only if R is not of characteristic $n!$.

Remark 1.3

Definitions 1.1 and 1.2 are not compatible with each other. More specifically, assume that $n \in {\mathbb {N}}$. Then the phrase “R is not of characteristic n”, in the sense of Definition 1.2, is not equivalent to $char \, R \ne n$. Similarly, the phrase “R is of characteristic greater than n” is not equivalent to $char \, R > n$.

To avoid ambiguity, from now on we will follow the convention that the phrases “R is not of characteristic n” and “R is of characteristic greater than n” are to be understood in the sense of Definition 1.2.

Definition 1.4

A ring R is called a prime ring if for any $a,b \in R$, whenever $aRb=0$ then either $a=0$ or $b=0$. A non-zero commutative ring R is called an integral domain if for all $a, b \in R$, the equality $ab = 0$ implies that either $a = 0$ or $b = 0$ (some authors require an integral domain to have an identity, but we don’t).

Note that whenever R is an integral domain in the Definition 1.1, ${\mathcal {N}}$ is, in fact, equal to $\{ n \in {\mathbb {N}}: na =0$ for some non-zero $a \in R\}$.

For the convenience of the reader we recall the following known result, which will be used in the sequel. For part 1 of the theorem, one may refer to [11, Section 3.2, problem 6], or [16, Chapter III, Theorem 1.9(iii)]. The other parts of the theorem are immediate consequences of part 1.

Theorem 1.5

Assume that R is an integral domain.

• 1. The characteristic of R is either zero or a prime number.

• 2. The characteristic of R is the unique non-negative integer number with the following property:

  

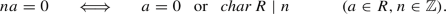
• 3. If $n \in {\mathbb {N}}$, then we have:

  • (i) R is not of characteristic n if and only if $char \, R \not \mid n$.

  • (ii) R is of characteristic greater than n if and only if $char \, R = 0$ or $char \, R > n$.

To define the Field of Fractions of a ring R, which is an integral domain, we consider the relation $\sim$ on $R \times (R {\setminus } \{ 0 \})$ as follows:

Clearly $\sim$ is an equivalence relation on $R \times (R {\setminus } \{ 0 \})$. For all $(a, b) \in R \times (R {\setminus } \{ 0 \})$, define $a / b$ as the equivalence class of $(a, b)$ with respect to $\sim$.

An addition and a multiplication is defined on $F = \{ a / b: a, b \in R, b \ne 0 \}$ as follows:

$$\begin{aligned}\left\{ \! \! \begin{array}{l} + :F \times F \rightarrow F \\ (a / b) + (c / d) = (ad + bc) / (bd), \end{array} \right. \qquad \left\{ \! \! \begin{array}{l} \cdot :F \times F \rightarrow F \\ (a / b) \cdot (c / d) = (ac) / (bd). \end{array} \right. \end{aligned}$$

These operations are well-defined and $(F, +, \cdot )$ is a field, which is called the field of fractions of R.

Now we take $\varphi :R \rightarrow F$, $a {\mathop {\mapsto }\limits ^{\varphi }} a^2 / a \ (a \ne 0)$ and $0 {\mathop {\mapsto }\limits ^{\varphi }} 0$. It is easy to see that $\varphi$ is a one-to-one homomorphism. Therefore, we usually consider R and $\varphi (R)$ to be the same and so we may take $R\subseteq F$. In particular, for all $a \in R$, we usually denote $\varphi (a)$ by a.

Proposition 1.6

$char \, F = char \, R$.

Proof

By Theorem 1.5, $char \, F$ is the unique non-negative integer number with the following property:

Since $R \subseteq F$,

(1.1)

By Theorem 1.5, $char \, R$ is the unique non-negative integer number with the following property:

(1.2)

By (1.1) and (1.2), it follows that $char \, F = char \, R$. $\square$

2 Some Properties of n-Jordan Homomorphisms

We first present some known results, which we intend to extend them somehow in the next sections.

One of the old and interesting results in this field is due to I. N. Herstein, which is stated as follows:

Theorem 2.1

[10, Theorem   K] Let $\varphi : R\rightarrow S$ be an n-Jordan homomorphism from a ring R onto a prime ring S of characteristic larger than n, where $n\ge 3$. Suppose further that R has a unit element. Then $\varphi =\alpha \psi$, where $\psi$ is either a homomorphism or an anti-homomorphism and where $\alpha$ is an $(n-1)$st root of unity lying in the center of S.

Since $\alpha ^n=\alpha$ in the theorem above, it is easy to see that $\varphi$ turns out to be either an n-homomorphism or an anti n-homomorphism. Moreover, Herstein at the end of his article, states that “One might conjecture that an appropriate variant of Theorem K would hold even if R does not have a unit element". This conjecture was proved by M. Bresar, W. S. Martindale and R. C. Miers in 1998, as the main theorem of [5], while they prove several results in this long paper to conclude the main theorem of this article.

Let $3 \le n \le 4$ and R, S be commutative algebras. If $\psi :R \rightarrow S$ is an additive n-Jordan homomorphism, then $\psi$ is an n-homomorphism [7, Theorem 2.2].

Let R be a unital ring and S be a ring with characteristic greater than n. If every Jordan homomorphism is either a homomorphism, or an anti-homomorphism, then every n-Jordan homomorphism is either an n-homomorphism, or an anti n-homomorphism, respectively [3, Theorem 2.4].

The following result is due to E. Gselmann [8, Theorem 2.1], which has also been proved in [13, Theorem 2.3] with a different method.

Theorem 2.2

If R and S are commutative rings, S is of characteristic greater than n, and $\psi :R \rightarrow S$ is an n-Jordan homomorphism, then $\psi$ is an n-homomorphism. Moreover, if R is unital with the unit $1_R$, then $\psi (1_R)=\psi (1_R)^n$ and the function $\varphi$ defined by

$$\begin{aligned} \varphi (x)=\psi ^{n-2}(1_R)\psi (x) \quad (x\in R), \end{aligned}$$

is a homomorphism between R and S.

Note that the result above has also been proved in [4, Theorem 2.2] when R and S are commutative algebras and $\psi :R \rightarrow S$ is an additive n-Jordan homomorphism. However, recently it has also been proved in [6, Theorem 2.3], whenever R and S are commutative algebras and $\psi :R \rightarrow S$ is a linear n-Jordan homomorphism.

We would like to indicate that in [8], there are some other interesting results for the non-commutative case, which are somehow related to this subject. In fact, it is shown that under certain conditions an additive map turns out to be an n-Jordan homomorphism.

We now recall the following result [21, Theorem 2.4]:

Let R be a unital Banach algebra, which is not necessarily commutative, and let S be a unital commutative semisimple Banach algebra. Then every 3-Jordan homomorphism $f: R\rightarrow S$ is a 3-homomorphism

The next result is an extension of the result above, which also extends the Żelazko Theorem.

Let R be a ring, which is not necessarily commutative, and let S be a unital commutative semisimple Banach algebra. Then every n-Jordan homomorphism $f: R\rightarrow S$ is an n-homomorphism. In particular, if R is a Banach algebra and moreover, f is linear, then f is automatically continuous [13, Corollary 2.10].

The following related result is an extension of [22, Theorem 3.4].

Theorem 2.3

[14, Theorem  3.2] Suppose that R and S are rings, where $char S>n$ and $T:R\rightarrow S$ is an n-Jordan homomorphism such that T(R) is commutative and $T(ab)=T(ba)$ for every $a,b\in R$. Then T is an n-homomorphism if $\ker T$ is an ideal in R.

In the case that R and S are topological algebras equipped with separating sequences of submultiplicative seminorms, it has been investigated in the article [14] that under some conditions an almost n-Jordan homomorphism $T:R\rightarrow S$ is an almost n-homomorphism. In particular, it has been shown that whenever R and S are commutative, then T turns out to be an almost n-homomorphism [14, Corollary 2.7]. Moreover, the automatic continuity of such maps has also been studied in this article.

In the following we assume that R and S are rings.

Definition 2.4

An additive map (operator) $\varphi :R \rightarrow S$ is called a weak n-Jordan homomorphism if

$$\begin{aligned} \varphi \left( \sum _{\pi : \, \text{ permutation }} a_{\pi (1)} a_{\pi (2)} \ldots a_{\pi (n)} \right) = \sum _{\pi : \, \text{ permutation }} \varphi (a_{\pi (1)}) \varphi (a_{\pi (2)}) \ldots \varphi (a_{\pi (n)}), \end{aligned}$$

(2.1)

for all $a_1, a_2, \ldots , a_n \in R$. A weak 2-Jordan homomorphism is simply called a weak Jordan homomorphism.

Theorem 2.5

• 1. If the map $\varphi :R \rightarrow S$ is an n-Jordan homomorphism, then it is a weak n-Jordan homomorphism.

• 2. If the map $\varphi :R \rightarrow S$ is a weak n-Jordan homomorphism and S is of characteristic greater than n, then $\varphi$ is an n-Jordan homomorphism.

Proof

The first statement of the theorem has been mentioned in the proof of [10, Theorem K]. However, for a different proof of this result one may refer to [13, Theorem 2.2].

To prove the second statement, assume that $\varphi :R \rightarrow S$ is a weak n-Jordan homomorphism and S is of characteristic greater than n. If we take $a_1 = a_2 = \cdots = a_n = a \in R$ in (2.1), it follows that $n! \varphi (a^n) = n! {\varphi (a)}^{n}$. Since S is of characteristic greater than n, we have $\varphi (a^n) = {\varphi (a)}^{n}$ for all $a \in R$. Hence $\varphi$ is an n-Jordan homomorphism.

$\square$

Proposition 2.6

Let S be of characteristic greater than n and $\varphi :R \rightarrow S$ be an n-Jordan homomorphism. Then $\varphi$ is an $(n + k(n - 1))$-Jordan homomorphism for all $k \ge 0$.

Proof

We use induction. The conclusion is obvious for $k = 0$. Assume that $k \ge 0$ and $\varphi$ is an $(n + k(n - 1))$-Jordan homomorphism. We must show that $\varphi$ is an $(n + (k + 1)(n - 1))$-Jordan homomorphism. Since $\varphi$ is an n-Jordan homomorphism, we have

$$\begin{aligned} \varphi \left( \sum _{\pi : \, \text{ permutation }} a_{\pi (1)} a_{\pi (2)} \ldots a_{\pi (n)} \right) = \sum _{\pi : \, \text{ permutation }} \varphi (a_{\pi (1)}) \varphi (a_{\pi (2)}) \ldots \varphi (a_{\pi (n)}), \end{aligned}$$

for all $a_1, a_2, \ldots , a_n \in R$. If we put $a_1 = a_2 = \cdots = a_{n - 1} = a$ and $a_n = b$, then

$$\begin{aligned}{} & {} {(n -1)!\varphi (a^{n - 1} b + a^{n - 2} b a + \cdots + b a^{n - 1})} \\{} & {} \quad = (n -1)!(\varphi (a)^{n - 1} \varphi (b) + \varphi (a)^{n - 2} \varphi (b) \varphi (a) + \cdots + \varphi (b) \varphi (a)^{n - 1}). \end{aligned}$$

Since S is of characteristic greater than n, it follows that

$$\begin{aligned}{} & {} \varphi (a^{n - 1} b + a^{n - 2} b a + \cdots + b a^{n - 1})\\{} & {} \quad = \varphi (a)^{n - 1} \varphi (b) + \varphi (a)^{n - 2} \varphi (b) \varphi (a) + \cdots + \varphi (b) \varphi (a)^{n - 1}. \end{aligned}$$

Now we take $b = a^{n + k(n - 1)}$. Then

$$\begin{aligned} {n \varphi (a^{n + (k + 1)(n - 1)})}= & {} \varphi (a)^{n - 1} \varphi (a^{n + k(n - 1)}) + \varphi (a)^{n - 2} \varphi (a^{n + k(n - 1)}) \varphi (a) \\{} & {} + \cdots + \varphi (a^{n + k(n - 1)}) \varphi (a)^{n - 1} \\= & {} \varphi (a)^{n - 1} \varphi (a)^{n + k(n - 1)} + \varphi (a)^{n - 2} \varphi (a)^{n + k(n - 1)} \varphi (a) \\{} & {} + \cdots + \varphi (a)^{n + k(n - 1)} \varphi (a)^{n - 1} \\= & {} n \varphi (a)^{n + (k + 1)(n - 1)}. \end{aligned}$$

Since S is of characteristic greater than n, we have $\varphi (a^{n + (k + 1)(n - 1)}) = \varphi (a)^{n + (k + 1)(n - 1)}$. $\square$

Corollary 2.7

If R and S are rings such that S is not of characteristic 2 and $\varphi :R \rightarrow S$ is a Jordan homomorphism, then $\varphi$ is an n-Jordan homomorphism.

3 n-Jordan Homomorphisms into Fields

In this section we assume that R and S are rings. Before introducing a new terminology, we state the following result, which is easy to verify and can also be found in [12, Example 2.4].

Proposition 3.1

Assume that S is not of characteristic 2, $\varphi :R \rightarrow S$ is a Jordan homomorphism (homomorphism), $\alpha \in S$, ${\alpha }^n = \alpha$, and $\alpha \varphi (a) = \varphi (a) \alpha$ for all $a \in R$. Then the map $\psi :R \rightarrow S$, defined by $\psi (a) = \alpha \varphi (a)$, is an n-Jordan homomorphism (n-homomorphism).

In contrast with the proposition above, we bring the following definition:

Definition 3.2

An n-homomorphism (n-Jordan homomorphism) $\psi :R \rightarrow S$ is called decomposable if there exist a homomorphism (Jordan homomorphism) $\varphi :R \rightarrow S$ and $\alpha \in S$ such that ${\alpha }^n = \alpha$, $\alpha \varphi (a) = \varphi (a) \alpha$ for all $a \in R$, and $\psi = \alpha \varphi$. The ordered pair $(\alpha , \varphi )$ is called a decomposition of $\psi$.

The following result is due to Herstein in 1956:

If S is an integral domain and is not of characteristic 2, then every Jordan homomorphism $\psi :R \rightarrow S$ is a homomorphism [10, Lemma 4].

It is easy to see that the above result of Herstein can be extended to n-Jordan homomorphisms as follows:

Proposition 3.3

Let S be an integral domain, which is not of characteristic 2 and let $\psi :R \rightarrow S$ be a decomposable n-Jordan homomorphism. Then $\psi$ is a decomposable n-homomorphism.

Proposition 3.4

Assume that R and S are rings, S is of characteristic greater than n and $\psi :R \rightarrow S$ is an n-Jordan homomorphism. In the case that R has a non-zero identity, say $1_R$, it has been shown in [12, Theorem 2.5] that

• (i) $\psi (a^2) = {\psi (1_R)}^{n - 2} {\psi (a)}^2$ for all $a \in R$;

• (ii) $\psi$ is decomposable.

If we drop the assumption that R has an identity and let $S = {\mathbb {C}}$, then

• (a) there exists $\lambda \in {\mathbb {C}}$ such that $\lambda ^{n-1}=1$ and $\psi (a^2) = \lambda {\psi (a)}^2$ for all $a \in R$ [13, Theorem   2.6];

• (b) $\psi$ is an n-homomorphism [13, Theorem   2.8].

In the sequel we always assume that $\psi :R \rightarrow S$ is an n-Jordan homomorphism.

The following lemma is due to T. G. Honary et al. [13, Theorem 2.5], which will be used in the sequel.

Lemma 3.5

If S is an integral domain which is of characteristic greater than n, then ${\psi (a^2)}^{n - 1} = {\psi (a)}^{2n - 2}$ for all $a \in R$. In particular, for every $a \in R$, $\psi (a) = 0$ if and only if $\psi (a^2) = 0$.

We now present the main results of this section, which are somehow extensions of the results above.

Theorem 3.6

Assume that S is a field, which is of characteristic greater than n and $\psi \ne 0$. Then $\psi$ is decomposable if and only if there exists $\lambda \in S$ such that $\psi (a^2) = \lambda {\psi (a)}^2$ for all $a \in R$. Moreover, in this case

1.:

$\lambda$ is unique and ${\lambda }^{n - 1} = 1_S$.

2.:

$\psi$ is uniquely decomposable and $\lambda \psi$ is a Jordan homomorphism.

3.:

$\psi$ is a uniquely decomposable n-homomorphism.

Proof

Let $\psi$ be decomposable. Then there exist a Jordan homomorphism $\varphi :R \rightarrow S$ and $\alpha \in S$ such that ${\alpha }^n = \alpha$ and $\psi = \alpha \varphi$. Since $\psi \ne 0$ and S is a field, it follows that $\alpha \ne 0$, $\varphi = {\alpha }^{-1} \psi$, and ${\alpha }^{n - 1} = 1_S$. If we take $\lambda = {\alpha }^{-1}$, then

$$\begin{aligned} \psi (a^2) = \alpha \varphi (a^2) = \alpha {\varphi (a)}^2 = \alpha {({\alpha }^{-1} \psi (a))}^2 = {\alpha }^{-1} {\psi (a)}^2 = \lambda {\psi (a)}^2. \quad ( a \in R ) \end{aligned}$$

Conversely, assume that there exists $\lambda \in S$ such that $\psi (a^2) = \lambda {\psi (a)}^2$ for all $a \in R$.

If $\varphi = \lambda \psi$ then $\varphi$ is additive and moreover,

$$\begin{aligned} \varphi (a^2) = \lambda \psi (a^2) = {\lambda }^2 {\psi (a)}^2 = {(\lambda \psi (a))}^2 = {\varphi (a)}^2. \quad ( a \in R ) \end{aligned}$$

Hence, $\varphi$ is a Jordan homomorphism. Since S is an integral domain, by Lemma  3.5 and the hypothesis, we have

$$\begin{aligned} {\psi (a)}^{2n-2} = {\psi (a^2)}^{n - 1} = {(\lambda {\psi (a)}^2)}^{n - 1} = {\lambda }^{n - 1} {\psi (a)}^{2n-2} \quad ( a \in R ). \end{aligned}$$

Since S is a field and $\psi \ne 0$, it follows that ${\lambda }^{n - 1} = 1_S$. If $\alpha = {\lambda }^{-1}$ then ${\alpha }^{n - 1} = 1_S$ and hence ${\alpha }^n = \alpha$. Since $\varphi = \lambda \psi$, it follows that $\psi = \alpha \varphi$. Therefore, $\psi$ is decomposable.

Now suppose that $\psi$ is decomposable, $\lambda \in S$, and $\psi (a^2) = \lambda {\psi (a)}^2$ for all $a \in R$.

For the proof of 1, assume that there exists another ${\lambda }' \in S$ such that $\psi (a^2) = {\lambda }' {\psi (a)}^2$ for all $a \in R$. Hence, $\lambda {\psi (a)}^2 = {\lambda }' {\psi (a)}^2$ for every $a \in R$. Since S is a field and $\psi \ne 0$, it follows that $\lambda = {\lambda }'$. Therefore, $\lambda$ is unique. Moreover, we have already shown that ${\lambda }^{n - 1} = 1_S$.

For the proof of 2, let $\psi$ be decomposable with the decomposition $\psi = \alpha \varphi$, where $\alpha = {\lambda }^{-1}$ and $\varphi = \lambda \psi$. To show that $\psi$ is uniquely decomposable, assume that $\psi = {\tilde{\alpha }} {\tilde{\varphi }}$ is another decomposition of $\psi$. We must show that ${\tilde{\alpha }} = \alpha$ and ${\tilde{\varphi }} = \varphi$. By the argument above, ${\tilde{\varphi }} = {{\tilde{\alpha }}}^{-1} \psi$ and $\psi (a^2) = {{\tilde{\alpha }}}^{-1} {\psi (a)}^2$ for all $a \in R$. Hence, ${{\tilde{\alpha }}}^{-1} = \lambda$ and consequently we have

$$\begin{aligned} {\tilde{\alpha }}= & {} {\lambda }^{-1} \ = \ \alpha , \\ {\tilde{\varphi }}= & {} {{\tilde{\alpha }}}^{-1} \psi \ = \ {\alpha }^{-1} \psi \ = \ \lambda \psi \ = \ \varphi . \end{aligned}$$

Finally, for the proof of 3, let $\psi$ be a decomposable n-Jordan homomorphism. Since S is a field, it is an integral domain and hence, by Proposition  3.3, $\psi$ is a decomposable n-homomorphism. $\square$

Corollary 3.7

Assume that S is a field, which is of characteristic greater than n and $\psi \ne 0$. Then the following statements are equivalent:

1.:

$\psi$ is a decomposable n-Jordan homomorphism.

2.:

$\psi$ is a uniquely decomposable n-Jordan homomorphism.

3.:

$\psi$ is a uniquely decomposable n-homomorphism.

Remark 3.8

Assume that S is a field and $Z = \{ \alpha \in S: {\alpha }^{n - 1} = 1_S \}$. For all $\alpha \in S$,

$$\begin{aligned} {\alpha }^{n - 1} - 1_S = (\alpha - 1_S)({\alpha }^{n - 2} + {\alpha }^{n - 3} + \cdots + \alpha + 1_S). \end{aligned}$$

Therefore, $Z = \{ 1_S \} \cup \{ \alpha \in S: {\alpha }^{n - 2} + {\alpha }^{n - 3} + \cdots + \alpha + 1_S = 0 \}$ (if $n = 2$ then $Z = \{ 1_S \}$). Note that Z has at most $n - 1$ distinct elements, even if S is an integral domain [19, Corollary 2.8.4].

The following theorem is an extension of [13, Theorem 2.8].

Theorem 3.9

Let S be a field, which is of characteristic greater than n and let $Z = \{ \alpha \in S: {\alpha }^{n - 1} = 1_S \}$. If $\psi \ne 0$, then $\psi$ is a uniquely decomposable n-homomorphism if one of the following cases holds:

1.:

$char \, S = 0$.

2.:

$p {\mathop {=}\limits ^{\textrm{def}}} char \, S > 2 \, card \, Z$.

Note that in case 2, p is a prime number, by Theorem 1.5.

Proof

Let $\lambda :\{ a \in R: \psi (a) \ne 0 \} \rightarrow Z$, $a \mapsto {\lambda }_a {\mathop {=}\limits ^{\textrm{def}}}{\psi ({a}^{2})}/{{\psi (a)}^{2}}$. By Lemma 3.5, the map $\lambda$ is well defined. By Theorem 3.6, $\psi$ is decomposable if and only if the map $\lambda$ is constant. To show that the map $\lambda$ is constant, let $a, b \in R$ such that $\psi (a), \psi (b) \ne 0$. We must show that ${\lambda }_a = {\lambda }_b$. On the contrary, assume that ${\lambda }_a \ne {\lambda }_b$ and define the sets M and $M_0$ as follows:

$$\begin{aligned} M = \left\{ \begin{array}{ll} {\mathbb {N}}, &{} \text{ in } \text{ case } \text{1; } \\ \{ 1, 2, \ldots , p \}, &{} \text{ in } \text{ case } \text{2; } \end{array} \right. \qquad M_0 = \{ m \in M: \psi (ma + b) = 0 \}. \end{aligned}$$

Obviously, for all $m \in M_0$,

$$\begin{aligned} m\psi (a) = -\psi (b). \end{aligned}$$

(3.1)

Now we show that $M_0$ has at most one element. Let $m_1, m_2 \in M_0$ and $m_1\ge m_2$. By (3.1), $(m_1 - m_2) \psi (a) = 0$. Since S is an integral domain and $\psi (a) \ne 0$, in case 1 $( char \, S = 0 )$, it follows that $m_1 = m_2$. In case 2, since $char \, S=p$, we have $p \mid m_1 - m_2$; but $m_1, m_2 \in \{ 1, 2, \ldots , p \}$ and hence $m_1 = m_2$.

We now define ${\lambda }_m = {\lambda }_{(ma + b)}$ for $m \in M {\setminus } M_0$. Then,

$$\begin{aligned} \psi ({(ma + b)}^2)= & {} {\lambda }_m {\psi (ma + b)}^2, \end{aligned}$$

(3.2)

$$\begin{aligned} \psi ({(ma + b)}^2)= & {} m^2 {\lambda }_a {\psi (a)}^2 + {\lambda }_b {\psi (b)}^2 + m \psi (ab + ba), \end{aligned}$$

(3.3)

$$\begin{aligned} {\lambda }_m {\psi (ma + b)}^2= & {} {\lambda }_m m^2 {\psi (a)}^2 + {\lambda }_m {\psi (b)}^2 + 2 {\lambda }_m m \psi (a) \psi (b). \end{aligned}$$

(3.4)

Combining (3.2), (3.3), and (3.4), we conclude that

$$\begin{aligned}{} & {} m^2 ({\lambda }_a - {\lambda }_m) {\psi (a)}^2 + m (\psi (ab + ba) \nonumber \\{} & {} \quad - 2 {\lambda }_m \psi (a) \psi (b)) + {\psi (b)}^2 ({\lambda }_b - {\lambda }_m) = 0. \end{aligned}$$

(3.5)

For $\alpha \in Z$, take $M_{\alpha } = \{ m \in M {\setminus } M_0: {\lambda }_m = \alpha \}$. Then $\{ M_{\alpha }: \alpha \in Z, M_{\alpha } \ne \emptyset \}$ is a partition for $M {\setminus } M_0$. Now we show that $M_{{\lambda }_a}$ has at most one element. By (3.5), for $m \in M_{{\lambda }_a}$ we have

$$\begin{aligned} m (\psi (ab + ba) - 2 {\lambda }_a \psi (a) \psi (b)) = -({\lambda }_b - {\lambda }_a) {\psi (b)}^2. \end{aligned}$$

(3.6)

Let $m_1$ and $m_2$ be two distinct elements of $M_{{\lambda }_a}$. By (3.6), it follows that

$$\begin{aligned} (m_1 - m_2) (\psi (ab + ba) - 2 {\lambda }_a \psi (a) \psi (b)) = 0. \end{aligned}$$

Since $(m_1 - m_2) \ne 0$ and in case 1, $char \, S = 0$, it follows that $\psi (ab + ba) - 2 {\lambda }_a \psi (a) \psi (b) = 0$. In case 2, since $char \, S = p$ and $p \not \mid (m_1 - m_2)$, we have $\psi (ab + ba) - 2 {\lambda }_a \psi (a) \psi (b) = 0$. Thus in both cases,

$$\begin{aligned} \psi (ab + ba) - 2 {\lambda }_a \psi (a) \psi (b) = 0. \end{aligned}$$

By (3.6), we see that $({\lambda }_b - {\lambda }_a) {\psi (b)}^2 = 0$. Therefore, either $\psi (b) = 0$ or ${\lambda }_b = {\lambda }_a$. This contradiction shows that $M_{{\lambda }_a}$ has at most one element.

Now assume that $\alpha \in Z {\setminus } \{ {\lambda }_a \}$. We show that $M_{\alpha }$ has at most two elements. Let $m_1$, $m_2$, $m_3$ be three distinct elements of $M_{\alpha }$. By (3.5), we see that for $m \in M_{\alpha }$,

$$\begin{aligned} m^2 ({\lambda }_a - \alpha ) {\psi (a)}^2 + m (\psi (ab + ba) - 2 \alpha \psi (a) \psi (b)) = -({\lambda }_b - \alpha ) {\psi (b)}^2. \end{aligned}$$

Therefore,

$$\begin{aligned} ({m_1}^2 - {m_2}^2) ({\lambda }_a - \alpha ) {\psi (a)}^2 = -(m_1 - m_2) (\psi (ab + ba) - 2 \alpha \psi (a) \psi (b)). \end{aligned}$$

With a similar argument as in the above, we have

$$\begin{aligned} (m_1 + m_2) ({\lambda }_a - \alpha ) {\psi (a)}^2 = -(\psi (ab + ba) - 2 \alpha \psi (a) \psi (b)). \end{aligned}$$

(3.7)

Similarly, we have

$$\begin{aligned} (m_1 + m_3) ({\lambda }_a - \alpha ) {\psi (a)}^2 = -(\psi (ab + ba) - 2 \alpha \psi (a) \psi (b)). \end{aligned}$$

(3.8)

By (3.7) and (3.8), it follows that $(m_2 - m_3) ({\lambda }_a - \alpha ) {\psi (a)}^2 = 0.$

Again with a similar argument as before, we have $({\lambda }_a - \alpha ) {\psi (a)}^2 = 0$. Therefore, either $\psi (a) = 0$ or ${\lambda }_a = \alpha$. This contradiction shows that $M_{\alpha }$ has at most two elements.

We know that

$$\begin{aligned} M = M_0 \cup M_{{\lambda }_a} \cup \bigg (\bigcup _{\alpha \in Z \setminus \{ {\lambda }_a \}} M_{\alpha }\bigg ). \end{aligned}$$

In case 1, $M={\mathbb {N}}$. Hence

$$\begin{aligned} card \, {\mathbb {N}} \le 1 + 1 + 2 \, card \, (Z {\setminus } \{ {\lambda }_a \}) = 2 + 2 \, ( card \, Z - 1) = 2 \, card \, Z. \end{aligned}$$

Therefore, Z must be infinite, whereas $card \, Z \le n - 1$.

In case 2, since $card \, \{ 1, 2, \ldots , p \} \le 2 \, card \, Z,$ it follows that $p \le 2 \, card \, Z$, whereas $p > 2 \, card \, Z$.

Therefore, in both cases, we get a contradiction. $\square$

Corollary 3.10

Let S be a field and $\psi \ne 0$. If $char \, S > 2 (n - 1)$, then $\psi$ is a uniquely decomposable n-homomorphism.

Proof

Take $Z = \{ \alpha \in S: {\alpha }^{n - 1} = 1_S \}$. Since $card \, Z \le n - 1$ and $char \, S > 2 (n - 1)$, it follows that $char \, S > 2 \, card \, Z$. By Theorem 3.9, $\psi$ is a uniquely decomposable n-homomorphism. $\square$

Example 3.11

Let $S = {\mathbb {C}}$ and $\psi \ne 0$. Then there exist a unique homomorphism $\varphi :R \rightarrow {\mathbb {C}}$ and a unique $k \in \{ 0, 1, \ldots , n - 2 \}$ such that

$$\begin{aligned} \psi = \exp \left( \frac{2 k \pi i}{n - 1}\right) \varphi . \end{aligned}$$

Example 3.12

Let $S = {\mathbb {R}}$ and $\psi \ne 0$.

• 1. If n is odd, then either $\psi$ or $-\psi$ is a homomorphism.

• 2. If n is even, then $\psi$ is a homomorphism.

Example 3.13

Let $n = 4$ and $S = {{\mathbb {Z}}}_{p}$, where p is a prime number, $p \ge 5$, and ${{\mathbb {Z}}}_{p} = {\mathbb {Z}}/(p {\mathbb {Z}}) = \{ k + p {\mathbb {Z}}: k \in {\mathbb {Z}} \}$. Then S is a field and $char \, S = p$. Since $p \ge 5$, it follows that S is of characteristic greater than $n = 4$.

Since $Z = \{ \alpha \in S: {\alpha }^{n - 1} = 1_S \} = \{ k + p {\mathbb {Z}}: k \in {\mathbb {Z}}, k^3 - 1 \in p {\mathbb {Z}} \}$, for $p = 5$, it follows that $Z = \{ 1 + p {\mathbb {Z}} \}$ and hence $p > 2 = 2 \, card \, Z$. If $p \ge 7$, then $p > 6 = 2 (n - 1) \ge 2 \, card \, Z$. Therefore, for all prime numbers $p \ge 5$, a 4-Jordan homomorphism $\psi :R \rightarrow {{\mathbb {Z}}}_{p}$ is a uniquely decomposable 4-homomorphism by Theorem 3.9.

4 n-Jordan Homomorphisms into Integral Domains

In this section, R and S are rings and $\psi :R \rightarrow S$ is an n-Jordan homomorphism. Before presenting our main results of this section, we bring the following known result, which is due to T. G. Honary in 2020 [12, Corollary 2.9].

Proposition 4.1

If R is unital and S is an integral domain, which is of characteristic greater than n, then $\psi :R \rightarrow S$ is an n-homomorphism.

In contrast with the result above we present the following result:

Theorem 4.2

Let S be an integral domain and $\psi \ne 0$. Then $\psi$ is an n-homomorphism if one of the following cases holds:

• (i) $char \, S = 0$.

• (ii) $char \, S > 2 (n - 1)$.

Proof

Let F be the field of fractions of S. Since $\psi :R \rightarrow S$ is an n-Jordan homomorphism, so is $\psi :R \rightarrow F$. On the other hand, from Proposition 1.6, it follows that $char \, F = char \, S$ and hence, in case (i), $char \, F = 0$. Therefore, by Theorem 3.9, $\psi :R \rightarrow F$ is a uniquely decomposable n-homomorphism. Since in case (ii), $char \, F > 2 (n - 1)$, it follows from Corollary 3.10, that $\psi :R \rightarrow F$ is a uniquely decomposable n-homomorphism. Thus, in both cases $\psi :R \rightarrow F$ is an n-homomorphism and hence $\psi :R \rightarrow S$ is also an n-homomorphism. $\square$

It is interesting to note that, whenever R is unital in the theorem above, it is shown in [12, Corollary 2.9] that $\psi$ is an n-homomorphism, without imposing any of the conditions (i) or (ii).

The following result is an extension of [21, Theorem 2.4] and [12, Theorem 2.13].

Theorem 4.3

Let $n = 3$ and S be an integral domain, which is of characteristic greater than 3. Then either $\psi$ or $-\psi$ is a homomorphism and hence $\psi$ is a 3-homomorphism.

Proof

If $\psi = 0$, then the claim is obviously true. So we assume that $\psi \ne 0$.

Let F be the field of fractions of S and $Z = \{ a/b \in F: {(a/b)}^{2} = 1_F \}$. Since S is of characteristic greater than $n = 3$, so is F. By Theorem 1.5,

$$\begin{aligned} \text{ either } ~~ char \, F = 0 ~~ \text{ or } ~~ char \, F > 3. \end{aligned}$$

(4.1)

By (4.1), we see that $1_F \ne -{1_F}$. Since $card \, Z \le 2$ and $\{ 1_F, -{1_F} \} \subseteq Z$, it follows that $Z = \{ 1_F, -{1_F} \}$.

Since $char \, F$ is a prime number, $char \, F \ge 5$ whenever $char \, F > 3$. Therefore, it is clear from (4.1), that

$$\begin{aligned} \text{ either } ~~ char \, F = 0 ~~ \text{ or } ~~ char \, F > 2 \, card \, Z. \end{aligned}$$

(4.2)

Since $\psi :R \rightarrow S$ is an n-Jordan homomorphism, so is $\psi :R \rightarrow F$. By (4.2) and Theorem 3.9, $\psi :R \rightarrow F$ is a uniquely decomposable 3-homomorphism. So there exist a unique $\alpha \in Z$ and a unique homomorphism $\varphi :R \rightarrow F$ such that $\psi = \alpha \varphi$.

If $\alpha = 1_F$, then $(\psi :R \rightarrow F) = (\varphi :R \rightarrow F)$ and hence $\varphi (R) \subseteq S$ and $(\psi :R \rightarrow S) = (\varphi :R \rightarrow S)$. Therefore, $\psi :R \rightarrow S$ is a homomorphism.

If $\alpha = -{1_F}$, then $(\psi :R \rightarrow F) = (-\varphi :R \rightarrow F)$ and hence $\varphi (R) \subseteq S$ and $(-\psi :R \rightarrow S) = (\varphi :R \rightarrow S)$. Therefore, $-\psi :R \rightarrow S$ is a homomorphism.

Consequently, either $\psi :R \rightarrow S$ or $-\psi :R \rightarrow S$ is a homomorphism and hence $\psi :R \rightarrow S$ is a 3-homomorphism. $\square$

Finally, if S is an algebra then ${\mathcal {N}} = \{ k \in {\mathbb {N}}: ka = 0 ~ (a \in S) \}=\phi$. Hence $char \, S = 0$ and so we obtain the following result, which is an easy consequence of Theorem 4.2.

Theorem 4.4

If R is a ring and S is an algebra, which is an integral domain, then every n-Jordan homomorphism $\psi :R \rightarrow S$ is an n-homomorphism.