A Generalized Self-Adaptive Algorithm for the Split Feasibility Problem in Banach Spaces

Abstract

In this paper, we propose a generalized self-adaptive method for solving the multiple-set split feasibility problem in the framework of certain Banach spaces. Under some suitable conditions, we prove the strong convergence of the sequence generated by our method with a new way to select the step-sizes without prior knowledge of the operator norm. Several numerical experiments to illustrate the convergence behavior are presented. The results presented in this paper improve and extend the corresponding results in the literature.

1 Introduction

Let E and F be two real p-uniformly convex Banach spaces which are also uniformly smooth. Let $C_i$, $i = 1,2,\ldots ,M$ and $Q_j$, $j =1,2,\ldots ,N$ be nonempty, closed and convex subsets of E and F, respectively. Let $A : E\rightarrow F$ be a bounded linear operator with its adjoint $A^*:F^*\rightarrow E^*$. We consider the following so-called multiple-set split feasibility problem (MSFP):

$$\begin{aligned} \text {find}~~x^*\in \bigcap _{i=1}^{M}C_i~~\text {such~that}~~Ax^*\in \bigcap _{j=1}^{N}Q_j. \end{aligned}$$

(1.1)

We denote by $\Omega :=\Big (\bigcap _{i=1}^{M}C_i\Big )\cap A^{-1}\Big (\bigcap _{j=1}^{N}Q_j\Big )$ the solution set of Problem (1.1). This problem was first introduced in finite-dimensional Hilbert spaces by Censor et al. [10]. The MSFP has broad applicability in many areas of mathematics and the physical and engineering sciences, for example, it can be applied in fields of image reconstruction and signal processing (see [33]) and in the inverse problem of intensity-modulated radiation therapy (IMRT) in the field of medical care (see [10, 13, 14]). Moreover, this problem is a generalization of convex feasibility problem (CFP) and as a generalization of the split feasibility problem. In particular, if $M=N=1$, then the MSFP becomes the following well-known split feasibility problem (SFP) [12]:

$$\begin{aligned} \text {find}~~x^*\in C~~\text {such~that}~~Ax^*\in Q. \end{aligned}$$

(1.2)

There are many modification methods have been proposed for solving the MSFP and the SFP in different styles (see for instance [6, 9, 16, 19, 29,30,31,32, 34,35,36,37,38,39,40,41,42,43,44,45,46, 50]).

A one efficient method for solving the SFP in Hilbert spaces is known as Byrne’s CQ algorithm [9] which is defined in the following manner: for given $x_1\in C$, compute the sequences $\{x_n\}$ generated iteratively by

$$\begin{aligned} x_{n+1} = P_{C}(x_{n} - \tau _n A^*(I-P_Q)Ax_n),~~\forall n\ge 1, \end{aligned}$$

(1.3)

where $P_{C}$ and $P_{Q}$ are the metric projections onto C and Q, respectively. It was proved that the sequence $\{x_{n}\}$ defined by (1.3) converges weakly to a solution of the SFP provided the step-size $\tau _n\in (0,\frac{2}{\Vert A\Vert ^{2}})$.

Note that the choice of the step-size $\tau _n$ of above work and other corresponding results depend on the operator norm $\Vert A\Vert$. In general, the implementation of such algorithms is not an easy work in practice. As a result the implementation of the iteration process inefficient when the computation of the operator norm is not explicit. To overcome this difficulty, López et al. [21] constructed a new choice to select the following step-size so that without prior knowledge of the operator norm:

$$\begin{aligned} \tau _n=\frac{\rho _n f(x_n)}{\Vert \nabla f(x_n)\Vert ^2}, \end{aligned}$$

(1.4)

where $f(x)=\frac{1}{2}\Vert (I-P_Q)Ax\Vert ^2$ with its gradient $\nabla f(x)= A^*(I-P_Q)Ax$ and $\{\rho _n\}\subset (0,4)$ satisfies $\liminf _{n\rightarrow \infty }\rho _n(4-\rho _n)>0$. They established the weak convergence of the Byrne’s CQ algorithm (1.3) to a solution of SFP with the step-size $\tau _n$ defined by (1.4).

Let C and Q be nonempty, closed and convex subsets of E and F, respectively. Schöpfer et al. [34] first introduced the following algorithm for solving SFP in Banach spaces: for given $x_{1}\in E$ and

$$\begin{aligned} x_{n+1} = \Pi _{C}J_{q}^{E^{*}}(J_{p}^{E}(x_{n})-\tau _n A^*J_{p}^{F}(I-P_Q)Ax_n),~~\forall n\ge 1, \end{aligned}$$

(1.5)

where $\Pi _C$ is the generalized projection onto C, $P_Q$ is the metric projection onto Q. They considered more general Bregman distance functions for its solution and proved that the sequence ${\{x_{n}}\}$ generated by (1.5) converges weakly to a solution of the SFP provided the duality mappings are weak-to-weak continuous and the step-size $\tau _n$ satisfies $0<\tau _n<\Big (\frac{q}{c_q\Vert A\Vert ^q}\Big )^{\frac{1}{q-1}}$, where $\frac{1}{p}+\frac{1}{q}=1$ and $c_q$ is the uniform smoothness coefficient of E (see [48]). Clearly, the algorithm (1.5) covers the Byrne’s CQ algorithm as a special case.

To obtain the strong convergence result, Shehu [35] proposed the following algorithm for solving the SFP in p-uniformly convex Banach spaces which are also uniformly smooth: for given $u,x_1\in E$ and

$$\begin{aligned} x_{n+1}=\Pi _{C}J_{q}^{E^{*}}(\alpha _n J_{p}^{E}(u)+(1-\alpha _n)(J_{p}^{E}(x_n)-\tau _nA^*J_{p}^{F}(I-P_Q)Ax_n)),~~\forall n\ge 1, \end{aligned}$$

(1.6)

where $\{\alpha _n\}$ and $\{\beta _n\}$ are sequences in (0, 1) and the step-size $\tau _n$ satisfies $0<a\le \tau _n\le b<\big (\frac{q}{\kappa _q\Vert A\Vert ^q}\big )^{\frac{1}{q-1}}$ for some $a,b>0$. He proved that the sequence $\{x_n\}$ generated by (1.6) converges strongly to a solution of the SFP under some mild conditions.

Very recently, Alsulami and Takahashi [6] introduced an algorithm for solving the SFP between Hilbert space and strictly convex, reflexive and smooth Banach space. To be more precise, they obtained the following result.

Theorem 1.1

Let H be a Hilbert space and E be a strictly convex, reflexive and smooth Banach space. Let $J_E$ be the duality mapping on E. Let C and Q be nonempty, closed and convex subsets of H and E, respectively. Let $P_C$ and $P_Q$ be the metric projections of H onto C and E onto Q, respectively. Let $A:H\rightarrow E$ be a bounded linear operator with its adjoint $A^*$ such that $A \ne 0$. Suppose that the solution set $\Omega$ of the SFP (1.2) is nonempty. Let $\{u_n\}$ be a sequence in H such that $u_n\rightarrow u$. For given $x_1\in H$, let $\{x_n\}$ be a sequence generated by

$$\begin{aligned} x_{n+1}=\beta _nx_n+(1-\beta _n)(\alpha _nu_n+(1-\alpha _n)P_C(x_n-\tau A^*J_E(I-P_Q)Ax_n)),~~\forall n\ge 1, \end{aligned}$$

(1.7)

where $\{\alpha _n\}\subset (0,1)$ and $\{\beta _n\}\subset (0,1)$ satisfy the following conditions:

• (i) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$;

• (ii) $0<a\le \beta _n\le b<1$ for some $a,b\in (0,1)$;

• (iii) $0<\tau \Vert A\Vert ^2<2$, where $\tau >0$.

Then $\{x_n\}$ converges strongly to $x^*\in \Omega$, where $x^*=P_{\Omega }u$.

There are some open questions which are posed as follows:

• (1) Can we extend Theorem 1.1 for solving the MSFP in two Banach spaces?

• (2) It is possible to remove the conditions $0<\tau \Vert A\Vert ^2<2$ and $0<a\le \beta _n$?

In this paper, we propose a new iterative method to answer two above open questions. We prove the strong convergence of the sequence generated by our method under some suitable conditions. Finally, we give some numerical examples to illustrate for the main result and showing its performance in finite and infinite dimensional spaces.

2 Preliminaries

Let E and $E^*$ be real Banach spaces and the dual space of E, respectively. We write $\langle x,j\rangle$ for the value of a functional j in $E^*$ at x in E. We shall use the notations $x_n\rightarrow x$ means that $\{x_n\}$ converges strongly to x and $x_n\rightharpoonup x$ means that $\{x_n\}$ converges weakly to x. Let $S_E=\{x\in E:\Vert x\Vert =1\}$ and $B_E=\{x\in E:\Vert x\Vert \le 1\}$. The modulus of convexity of E is the function $\delta _E:[0,2]\rightarrow [0,1]$ defined by

$$\begin{aligned} \begin{array}{lcl} \delta _E(\epsilon )=\inf \Big \{1-\frac{\Vert x+y\Vert }{2}:x,y\in B_E, \Vert x-y\Vert \ge \epsilon \Big \}. \end{array} \end{aligned}$$

Let $1<q\le 2\le p<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$. The space E is called uniformly convex if $\delta _E(\epsilon )>0$ for all $\epsilon \in (0,2]$ and p-uniformly convex if there is a $c_p > 0$ such that $\delta _E(\epsilon )\ge c_p\epsilon ^p$ for all $\epsilon \in (0,2]$. The modulus of smoothness of E is the function $\rho _E:{\mathbb {R}}^{+}:=[0,\infty )\rightarrow {\mathbb {R}}^{+}$ defined by

$$\begin{aligned} \begin{array}{lcl} \rho _E(\tau )=\sup \Big \{\frac{\Vert x+\tau y\Vert +\Vert x- \tau y\Vert }{2}-1:x,y\in S_E\Big \}. \end{array} \end{aligned}$$

The space E is called uniformly smooth if $\lim _{\tau \rightarrow 0}\frac{\rho _{E}(\tau )}{\tau }=0$ and called q-uniformly smooth if there exists a $c_q > 0$ such that $\rho _E(\tau )\le c_q\tau ^q$ for all $\tau >0$. It is known that every p-uniformly convex (q-uniformly smooth) space is uniformly convex (uniformly smooth) space and E is p-uniformly convex (q-uniformly smooth) if and only if its dual $E^*$ is q-uniformly smooth (p-uniformly convex) (see [1]). Furthermore, $L_p$ (or $\ell _p$) and the Sobolev spaces are $\min \{p,2\}$-uniformly smooth for every $p> 1$ while Hilbert space is uniformly smooth (see [48]).

Definition 2.1

A continuous strictly increasing function $\varphi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$ is said to be a gauge function if $\varphi (0)=0$ and $\lim _{t\rightarrow \infty }\varphi (t)=\infty$.

Definition 2.2

The mapping $J_{\varphi }:E\rightarrow 2^{E^*}$ associated with a gauge function $\varphi$ defined by

$$\begin{aligned} J_{\varphi } (x)=\{f\in E^*:\langle x,f\rangle =\Vert x\Vert \varphi (\Vert x\Vert ),~\Vert f\Vert =\varphi (\Vert x\Vert )\},~~x\in E \end{aligned}$$

is called the duality mapping with gauge $\varphi$, where $\langle \cdot ,\cdot \rangle$ denotes the duality pairing between E and $E^*$.

In the particular case $\varphi (t)=t$, the duality mapping $J_{\varphi }=J$ is called the normalized duality mapping. In the case $\varphi (t)=t^{p-1}$, where $p>1$, the duality mapping $J_{\varphi }=J_{p}$ is called the generalized duality mapping which is defined by

$$\begin{aligned} \begin{array}{lcl} J_{p}(x)=\{f\in E^*:\langle x,f\rangle =\Vert x\Vert ^p,\Vert f\Vert =\Vert x\Vert ^{p-1}\}. \end{array} \end{aligned}$$

It follows from the definition that $J_{\varphi }(x)=\frac{\varphi (\Vert x\Vert )}{\Vert x\Vert }J(x)$ and $J_p(x)=\Vert x\Vert ^{p-2}J(x)$, $p>1$. It is well-known that if E is uniformly smooth, the generalized duality mapping $J_{p}$ is norm-to-norm uniformly continuous on bounded subsets of E (see [27]). Furthermore, $J_{p}$ is one-to-one, single-valued and satisfies $J_{p}=J^{-1}_{q}$, where $J_{q}$ is the generalized duality mapping of $E^*$ (see [15, 26] for more details).

Lemma 2.3

[48] Let E be a q-uniformly smooth Banach space. Then there exists a constant $c_q>0$ which is called the q-uniform smoothness coefficient of E such that

$$\begin{aligned} \begin{array}{lcl} \Vert x-y\Vert ^q\le \Vert x\Vert ^q-q\langle y,J_q(x)\rangle +c_q\Vert y\Vert ^q, \end{array} \end{aligned}$$

for all $x,y\in E$.

Let C be a nonempty, closed and convex subset of a strictly convex, smooth and reflexive Banach space E. Then we know that for any $x\in E$, there exists a unique element $z\in C$ such that

$$\begin{aligned} \Vert x-z\Vert \le \inf _{y\in C}\Vert x-y\Vert . \end{aligned}$$

The mapping $P_C:E\rightarrow C$ defined by $z=P_Cx$ is called the metric projection of E onto C. It is well-known that $P_C x$ is the unique minimizer of the norm distance, which can be characterized by the variational inequality:

$$\begin{aligned} \langle y-P_{C}x,J_\varphi (x-P_{C}x)\rangle \le 0,~~\forall y\in C. \end{aligned}$$

(2.1)

For a gauge function $\varphi$, the function $\Phi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}$ defined by

$$\begin{aligned} \Phi (t)=\int _{0}^{t}\varphi (s)ds \end{aligned}$$

is a continuous, convex and strictly increasing differentiable function on ${\mathbb {R}}^{+}$ with $\Phi '(t)=\varphi (t)$ and $\lim _{t\rightarrow \infty }\frac{\Phi (t)}{t}=\infty$. Therefore, $\Phi$ has a continuous inverse function $\Phi ^{-1}$.

Let E be a real smooth Banach space. The Bregman distance $D_\varphi :E\times E\rightarrow {\mathbb {R}}^{+}$ [7] is defined by

$$\begin{aligned} D_\varphi (x,y)=\Phi (\Vert y\Vert )-\Phi (\Vert x\Vert )-\langle y-x,J_\varphi (x)\rangle \end{aligned}$$

for all $x,y\in E$. We note that $D_\varphi (x,y)\ge 0$ and $D_\varphi (x,y)=0$ if and only of $x=y$. In general, the Bregman distance is not a metric due to the fact that it is not symmetric. The Bregman distance has the following important properties:

$$\begin{aligned} D_{\varphi }(x,y)+D_{\varphi }(y,x)=\langle x-y,J_{\varphi }(x)-J_{\varphi }(y)\rangle \end{aligned}$$

and

$$\begin{aligned} D_{\varphi }(x,y)+D_{\varphi }(y,z)-D_{\varphi }(x,z)=\langle x-y,J_{\varphi }(z)-J_{\varphi }(y)\rangle \end{aligned}$$

for all $x,y,z\in E$.

In the case $\varphi (t)=t^{p-1}$, $p > 1$, we have $\Phi (t)=\int _{0}^{t}\varphi (s)ds=\frac{t^p}{p}$. So we have the distance $D_\varphi =D_p$ is called the p-Lyapunov function which was studied in [8] and it is given by

$$\begin{aligned} D_{p}(x,y) = \frac{\Vert x\Vert ^p}{p}-\langle x,J_{p}(y)\rangle +\frac{\Vert y\Vert ^p}{q}, \end{aligned}$$

where $\frac{1}{p}+\frac{1}{q}=1$. If $p=2$, then the Bregman distance becomes the Lyapunov function $\phi :E\times E\rightarrow {\mathbb {R}}^+$ [2, 3] defined as

$$\begin{aligned} \phi (x,y)=\Vert x\Vert ^2-2\langle x,Jy\rangle +\Vert y\Vert ^2. \end{aligned}$$

Let E be a strictly convex, smooth and reflexive Banach space. Following [2, 11], we make use of the function $V_p:E\times E^*\rightarrow {\mathbb {R}}^{+}$ which is given by

$$\begin{aligned} V_p(x,{\bar{x}}) = \frac{\Vert x\Vert ^{p}}{p}-\langle x,{\bar{x}}\rangle +\frac{\Vert {\bar{x}}\Vert ^{q}}{q} \end{aligned}$$

for all $x\in E$ and ${\bar{x}}\in E^*$. Then $V_p$ is nonnegative and $V_p$ satisfies the following properties:

$$\begin{aligned} V_p(x,{\bar{x}})=D_p(x,J_{q}({\bar{x}})),~~\forall x\in E,~{\bar{x}}\in E^* \end{aligned}$$

(2.2)

and

$$\begin{aligned} V_p(x,{\bar{x}})+\langle J_{q}({\bar{x}})-x,{\bar{y}}\rangle \le V_p(x,{\bar{x}}+{\bar{y}}),~~\forall x\in E,~{\bar{x}},{\bar{y}}\in E^*. \end{aligned}$$

(2.3)

Moreover, $V_p$ is convex in the second variable. Then for all $z\in E$,

$$\begin{aligned} D_p\Big (z,J_{q}\Big (\sum _{i=1}^{M}t_iJ_{p}(x_i)\Big )\Big )\le \sum _{i=1}^{M}t_iD_p(z,x_i), \end{aligned}$$

where $\{x_i\}_{i=1}^{M}\subset E$ and $\{t_i\}_{i=1}^{M}\subset (0,1)$ with $\sum _{i=1}^{M}t_i=1$.

The Bregman projection, denoted by $\Pi _{C}^{\varphi }$, is defined as the unique solution of the following minimization problem:

$$\begin{aligned} \Pi _{C}^{\varphi }x=\text {argmin}_{y\in C}D_{\varphi }(x,y),~~x\in E. \end{aligned}$$

It can be characterized by the variational inequality [20]:

$$\begin{aligned} \langle z-\Pi _{C}^{\varphi }x,J_{\varphi }(x)-J_{\varphi }(\Pi _{C}^{\varphi }x)\rangle \le 0,~~\forall z\in C. \end{aligned}$$

Moreover, we have

$$\begin{aligned} D_{\varphi }(y,\Pi _{C}^{\varphi }x)+D_{\varphi }(\Pi _{C}^{\varphi }x,x)\le D_{\varphi }(y,x),~~\forall y\in C. \end{aligned}$$

(2.4)

When $\varphi (t)=t$, we have $\Pi _{C}^{\varphi }$ coincides with the generalized projection which studied in [2]. When $\varphi (t)=t^{p-1}$, where $p>1$, we have $\Pi _{C}^{\varphi }$ becomes the Bregman projection with respect to p and denoted by $\Pi _C$.

Lemma 2.4

[28] Let E be a smooth and uniformly convex real Banach space. Suppose that $x\in E$, if $\{D_{p}(x,x_n)\}$ is bounded, then the sequence $\{x_n\}$ is bounded.

Lemma 2.5

[25] Let E be a smooth and uniformly convex Banach space. Suppose that $\{x_n\}$ and $\{y_n\}$ are two sequences in E. Then $\lim _{n\rightarrow \infty }D_{p}(x_n,y_n)=0$ if and only if $\lim _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0$.

Lemma 2.6

[22] Let $\{ a_{n}\}$ and $\{ c_{n}\}$ be nonnegative real sequences such that

$$\begin{aligned} a_{n+1}\le (1-\delta _{n})a_{n}+b_{n}+c_{n},~~\forall n\ge 1, \end{aligned}$$

where $\{\delta _{n}\}$ is a sequence in (0,1) and $\{ b_{n}\}$ is a real sequence. Assume that $\sum _{n=1}^{\infty } c_{n}<\infty$. Then the following results hold:

• (i) If $\frac{b_{n}}{\delta _{n}}\le M$ for some $M\ge 0$, then $\{a_{n}\}$ is a bounded sequence.

• (ii) If $\sum _{n=1}^{\infty } \delta _{n}=\infty$ and $\limsup _{n \rightarrow \infty }\frac{b_{n}}{\delta _{n}}\le 0$, then $\lim _{n \rightarrow \infty }a_{n}=0$.

Lemma 2.7

[23] Let $\{\Gamma _n\}$ be a nonnegative real sequence that does not decrease at infinity in the sense that there exists a subsequence $\{\Gamma _{n_k}\}$ of $\{\Gamma _n\}$ which satisfies $\Gamma _{n_k}<\Gamma _{n_{k}+1}$ for all $k\in {\mathbb {N}}$. For each $n\ge n_0$, define an integer sequence $\{\tau (n)\}$ as follows:

$$\begin{aligned} \tau (n)=\max \{n_0\le k\le n:\Gamma _k<\Gamma _{k+1}\}. \end{aligned}$$

Then the following results hold:

• (i) $\tau (n)\rightarrow \infty$ as $n\rightarrow \infty$;

• (ii) $\max \{\Gamma _{\tau (n)},\Gamma _n\}\le \Gamma _{\tau (n)+1}$ for all $n\ge n_0$.

3 Main Result

In this section, we propose a new self-adaptive algorithm to solve the multiple-set split feasibility problem in Banach spaces E and prove a convergence theorem of the generated sequences by the proposed method. Throughout this paper, we denote by $J_{p}^{E}$ and $J_{q}^{E^*}$ the duality mappings of E and its dual space, respectively, where $1<q\le 2\le p<\infty$ with $\frac{1}{p}+\frac{1}{q}=1$.

Theorem 3.1

Let E be a p-uniformly convex and uniformly smooth Banach space and F be a reflexive, strictly convex and smooth Banach space. Let $C_i$, $i=1,2,\ldots ,M$ and $Q_j$, $j=1,2,\ldots ,N$ be nonempty, closed and convex subsets of E and F, respectively. Let $A : E \rightarrow F$ be a bounded linear operator and $A^{*}:F^{*}\rightarrow E^{*}$ be an adjoint of A. Suppose that the solution set $\Omega$ of the MSFP (1.1) is nonempty. Let $\{u_n\}$ be a sequence in E such that $u_n\rightarrow u$. For given $x_1\in E$, let $\{x_n\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} v_{n,1}=J_{q}^{E^{*}}(J_{p}^{E}(x_n)-\tau _{n,1}\nabla f(x_n)),\\ v_{n,2}=J_{q}^{E^{*}}(J_{p}^{E}(v_{n,1})-\tau _{n,2}\nabla f(v_{n,1})),\\ ~~\vdots \\ v_{n,N}=J_{q}^{E^{*}}(J_{p}^{E}(v_{n,N-1})-\tau _{n,N}\nabla f(v_{n,N-1})),\\ y_n=J_{q}^{E^{*}}(a_{n,0}J_{p}^{E}(v_{n,N})+\sum _{i=1}^{M}a_{n,i}J_{p}^{E}(\Pi _{C_i}v_{n,N})),\\ x_{n+1}=J_{q}^{E^{*}}(\beta _nJ_{p}^{E}(x_n)+(1-\beta _n)(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n))),~~\forall n\ge 1, \end{array} \end{array}\right. } \end{aligned}$$

where $\{\alpha _n\}\subset (0,1)$, $\{a_{n,i}\}_{i=1}^{M}\subset (0,1)$, $\{\beta _n\}\subset [0,1)$, $f(v_{n,j})=\frac{1}{p}\Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert ^p$ for $j=1,2,\ldots ,N-1$ and $f(x_n)=\frac{1}{p}\Vert (I-P_{Q_{1}})Ax_n\Vert ^p$ with the step-sizes $\tau _{n,1}$ and $\tau _{n,j}$, $j=1,2,\ldots ,N-1$ are chosen self-adaptively as

$$\begin{aligned} \tau _{n,1}= \left\{ \begin{array}{ll} \frac{\rho _n f^{p-1}(x_n)}{\Vert \nabla f(x_n)\Vert ^p},&{}\qquad \quad \text {if}~f(x_n)\ne 0; \\ 0,&{}\qquad \quad \text {otherwise} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \tau _{n,j+1}= \left\{ \begin{array}{ll} \frac{\rho _n f^{p-1}(v_{n,j})}{\Vert \nabla f(v_{n,j})\Vert ^p},&{}\qquad \quad \text {if}~f(v_{n,j})\ne 0; \\ 0,&{}\qquad \quad \text {otherwise}, \end{array}\right. \end{aligned}$$

respectively, where $\{\rho _n\}\subset \big (0,(\frac{pq}{c_q})^\frac{1}{q-1}\big )$. Suppose that the following conditions hold:

• (C1) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$;

• (C2) $\liminf _{n\rightarrow \infty }\rho _n\Big (p-\frac{\rho _{n}^{q-1}c _q}{q}\Big )>0$;

• (C3) $\sum _{i=0}^{M}a_{n,i}=1$ and $\liminf _{n\rightarrow \infty }a_{n,i}>0$ for $i=1,2,\ldots ,M$;

• (C4) $\limsup _{n\rightarrow \infty }\beta _n<1$.

Then $\{x_n\}$ converges strongly to $x^*=\Pi _\Omega u$, where $\Pi _\Omega$ is the Bregman projection from E onto $\Omega$.

Proof

For each $j=1,2,\ldots ,N-1$, we note that $\nabla f(v_{n,j})=A^*J_{p}^{F}(I-P_{Q_{j+1}})Av_{n,j}$ (see [17], Proposition 5.7]). Let $z\in \Omega$, that is, $z\in \bigcap _{i=1}^{M}C_i$ and $Az\in \bigcap _{j=1}^{N}Q_j$. Then for each $j=1,2,\ldots ,N-1$, we have from (2.1) that

$$\begin{aligned} \Vert v_{n,j}-z\Vert \Vert \nabla f(v_{n,j})\Vert\ge & {} \langle v_{n,j}-z,\nabla f(v_{n,j})\rangle \nonumber \\= & {} \langle v_{n,j}-z, A^*J_{p}^{E}(I-P_{Q_{j+1}})Av_{n,j}\rangle \nonumber \\= & {} \langle Av_{n,j}-Az,J_{p}^{E}(I-P_{Q_{j+1}})Av_{n,j}\rangle \nonumber \\\ge & {} \langle Av_{n,j}-Az,J_{p}^{E}(I-P_{Q_{j+1}})Av_{n,j}\rangle \nonumber \\&+\langle Az-P_{Q_{j+1}}Av_{n,j},J_{p}^{E}(I-P_{Q_{j+1}})Av_{n,j}\rangle \nonumber \\= & {} \langle Av_{n,j}-P_{Q_{j+1}}Av_{n,j},J_{p}^{E}(I-P_{Q_{j+1}})Av_{n,j}\rangle \nonumber \\= & {} \Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert ^p=pf(v_{n,j}). \end{aligned}$$

(3.1)

We see that $\Vert \nabla f(v_{n,j})\Vert >0$, when $f(v_{n,j})\ne 0$. This implies that $\Vert \nabla f(v_{n,j})\Vert \ne 0$ for each $j=1,2,\ldots ,N-1$. Hence, $\tau _{n,j+1}$ is well defined. In the same manner, we also have $\tau _{n,1}$ is well defined. For each $j=1,2,\ldots ,N-1$, it follows from Lemma 2.3 and (3.1) that

$$\begin{aligned} D_p(z,v_{n,j+1})= & {} D_p(z,J_{q}^{E^{*}}(J_{p}^{E}(v_{n,j})-\tau _{n,j+1}\nabla f(v_{n,j})))\nonumber \\= & {} V_p(z,J_{p}^{E}(v_{n,j})-\tau _{n,j+1}\nabla f(v_{n,j}))\nonumber \\= & {} \frac{\Vert z\Vert ^p}{p}-\langle z,J_{p}^{E}(v_{n,j})\rangle +\tau _{n,j+1}\langle z,\nabla f(v_{n,j})\rangle \nonumber \\&+\frac{1}{q}\Vert J_{p}^{E}(v_{n,j})-\tau _{n,j+1}\nabla f(v_{n,j})\Vert ^q\nonumber \\\le & {} \frac{\Vert z\Vert ^p}{p}-\langle z,J_{p}^{E}(v_{n,j})\rangle +\tau _{n,j+1}\langle z,\nabla f(v_{n,j})\rangle \nonumber \\&+\frac{1}{q}\Vert J_{p}^{E}(v_{n,j})\Vert ^q-\tau _{n,j+1}\langle v_{n,j},\nabla f(v_{n,j})\rangle \nonumber \\&+\frac{c_q\tau _{n,j+1}^{q}}{q}\Vert \nabla f(v_{n,j})\Vert ^q\nonumber \\= & {} \frac{\Vert z\Vert ^p}{p}-\langle z,J_{p}^{E}(v_{n,j})\rangle +\frac{1}{q}\Vert v_{n,j}\Vert ^p-\tau _{n,j+1}\langle v_{n,j}-z,\nabla f(v_{n,j})\rangle \nonumber \\&+\frac{c_q\tau _{n,j+1}^{q}}{q}\Vert \nabla f(v_{n,j})\Vert ^q\nonumber \\= & {} D_p(z,v_{n,j})-\tau _{n,j+1}p f(v_{n,j})+\frac{c_q\tau _{n,j+1}^{q}}{q}\Vert \nabla f(v_{n,j})\Vert ^q\nonumber \\= & {} D_p(z,v_{n,j})-\frac{\rho _n p f^{p}(v_{n,j})}{\Vert \nabla f(v_{n,j})\Vert ^p}+\frac{\rho _{n}^{q}c_q}{q}\frac{f^{p}(v_{n,j})}{\Vert \nabla f(v_{n,j})\Vert ^p}\nonumber \\= & {} D_p(z,v_{n,j}) -\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}. \end{aligned}$$

(3.2)

In the same manner, we can see that

$$\begin{aligned} D_p(z,v_{n,1})\le & {} D_p(z,x_n)-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}. \end{aligned}$$

(3.3)

It follows from (3.2) and (3.3) that

$$\begin{aligned}&D_p(z,v_{n,N})\nonumber \\&\quad \le D_p(z,v_{n,N-1})-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,N-1})}{\Vert {\nabla f(v_{n,N-1})\Vert ^p}}\nonumber \\&\quad \vdots \nonumber \\&\quad \le D_p(z,v_{n,1})-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,1})}{\Vert {\nabla f(v_{n,1})\Vert ^p}}-\ldots \nonumber \\&\qquad -\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,N-1})}{\Vert {\nabla f(v_{n,N-1})\Vert ^p}}\nonumber \\&\quad \le D_p(z,x_n)-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,1})}{\Vert {\nabla f(v_{n,1})\Vert ^p}}\nonumber \\&\quad -\ldots -\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\frac{f^{p}(v_{n,N-1})}{\Vert {\nabla f(v_{n,N-1})\Vert ^p}}\nonumber \\&\quad =D_p(z,x_n)-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\Big [\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}+\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\Big ]. \end{aligned}$$

(3.4)

From (2.4) and (3.4), we see that

$$\begin{aligned} D_p(z,y_n)= & {} D_p(z,J_{q}^{E^{*}}(a_{n,0}J_{p}^{E}(v_{n,N})+\sum _{i=1}^{M}a_{n,i}J_{p}^{E}(\Pi _{C_i}v_{n,N})))\nonumber \\\le & {} a_{n,0}D_p(z,v_{n,N})+\sum _{i=1}^{M}a_{n,i}D_p(z,\Pi _{C_i}v_{n,N})\nonumber \\\le & {} a_{n,0}D_p(z,v_{n,N})+\sum _{i=1}^{M}a_{n,i}D_p(z,v_{n,N})-\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\nonumber \\= & {} D_p(z,v_{n,N})-\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\nonumber \\\le & {} D_p(z,x_n)-\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\Big [\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}+\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\Big ]\nonumber \\&-\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N}), \end{aligned}$$

(3.5)

which implies by the assumption of $\{\rho _n\}$ that

$$\begin{aligned} D_p(z,y_n)\le D_p(z,x_n). \end{aligned}$$

Put $w_n=J_{q}^{E^{*}}(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n))$ for all $n\ge 1$, we have

$$\begin{aligned} D_p(z,w_n)= & {} D_p(z,J_{q}^{E^{*}}(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n)))\\\le & {} \alpha _n D_p(z,u_n)+(1-\alpha _n)D_p(z,y_n)\\\le & {} \alpha _n D_p(z,u_n)+(1-\alpha _n)D_p(z,x_n). \end{aligned}$$

It follows that

$$\begin{aligned} D_p(z,x_{n+1})= & {} D_p(z,J_{q}^{E^{*}}(\beta _nJ_{p}^{E}(x_n)+(1-\beta _n)J_{p}^{E}(w_n)))\\\le & {} \beta _n D_p(z,x_n)+(1-\beta _n)D_p(z,w_n)\\\le & {} \beta _n D_p(z,x_n)+(1-\beta _n)(\alpha _n D_p(z,u_n)+(1-\alpha _n)D_p(z,x_n))\\= & {} (1-(1-\beta _n)\alpha _n)D_p(z,x_n)+(1-\beta _n)\alpha _nD_p(z,u_n). \end{aligned}$$

Since $\{u_n\}$ is bounded, we also have $\{D_p(z,u_n)\}$ is bounded. By induction, we have $\{D_p(z,x_n)\}$ is bounded. Hence, by Lemma 2.6, we have $\{x_n\}$ is bounded, so are $\{v_{n,j}\}$ and $\{y_n\}$ for each $j=1,2,\ldots ,N-1$. Let $x^*= \Pi _\Omega u$. From (2.3) and (3.5), we have

$$\begin{aligned} D_p(x^*,w_n)= & {} D_p(x^*,J_{q}^{E^{*}}(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n)))\\= & {} V_p(x^*,\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n))\\\le & {} V_p(x^*,\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n)-\alpha _n(J_{p}^{E}(u_n)-J_{p}^{E}(x^*))\\&+\alpha _n\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(x^*)\rangle \\= & {} V_p(x^*,\alpha _nJ_{p}^{E}(x^*)+(1-\alpha _n)J_{p}^{E}(y_n))\\&+\alpha _n\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(x^*)\rangle \\= & {} \alpha _nD_p(x^*,x^*)+(1-\alpha _n)D_p(x^*,y_n)\\&\quad +\alpha _n\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(x^*)\rangle \\\le & {} (1-\alpha _n)\left\{ D_p(x^*,x_n)-\rho _n\left( p-\frac{\rho _{n}^{q-1}c_q}{q}\right) \left[ \frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}\right. \right. \\&\quad \left. \left. +\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\right] \right. \\&\quad \left. -\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\right\} +\alpha _n\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(x^*)\rangle . \end{aligned}$$

It follows that

$$\begin{aligned}&D_p(x^*,x_{n+1})\nonumber \\&\quad \le \beta _n D_p(x^*,x_n)+(1-\beta _n)D_p(x^*,w_n)\nonumber \\&\quad \le (1-(1-\beta _n)\alpha _n)D_p(x^*,x_n)\nonumber \\&\qquad -(1-\alpha _n)(1-\beta _n)\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\Big [\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}+\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\Big ]\nonumber \\&\qquad -(1-\alpha _n)(1-\beta _n)\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\nonumber \\&\qquad +\alpha _n(1-\beta _n)\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(u)\rangle \nonumber \\&\qquad +\alpha _n(1-\beta _n)\langle w_n-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle . \end{aligned}$$

(3.6)

Put $\Gamma _n=D_p(x^*,x_n)$ for all $n\ge 1$. From (3.6), we have

$$\begin{aligned}&(1-\alpha _n)(1-\beta _n)\rho _n\Big (p-\frac{\rho _{n}^{q-1}c_q}{q}\Big )\Big [\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}+\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\Big ]\nonumber \\&\qquad +(1-\alpha _n)(1-\beta _n)\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\nonumber \\&\quad \le \Gamma _n-\Gamma _{n+1}+\alpha _n(1-\beta _n)\langle w_n-x^*,J_{p}^{E}(u_n)\nonumber \\&\qquad -J_{p}^{E}(u)\rangle +\alpha _n(1-\beta _n)\langle w_n-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle . \end{aligned}$$

(3.7)

We now show that $\Gamma _n\rightarrow 0$ as $n\rightarrow \infty$ by the following two possible cases:

Case 1. Suppose that there exists $n_0\in {\mathbb {N}}$ such that $\Gamma _{n+1}\le \Gamma _n$ for all $n\ge n_0$. Then we have

$$\begin{aligned} \Gamma _{n}-\Gamma _{n+1}\rightarrow 0. \end{aligned}$$

By our assumptions, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Big [\frac{f^{p}(x_n)}{\Vert {\nabla f(x_n)\Vert ^p}}+\sum _{j=1}^{N-1}\frac{f^{p}(v_{n,j})}{\Vert {\nabla f(v_{n,j})\Vert ^p}}\Big ]=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})=0. \end{aligned}$$

Since $\{\Vert \nabla f(x_n)\Vert ^p\}$ and $\{\Vert \nabla f(v_{n,j})\Vert ^p\}$ for all $j=1,2,\ldots ,N-1$ are bounded, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }f(x_n)=\lim _{n\rightarrow \infty }\Vert (I-P_{Q_{1}})Ax_n\Vert =0 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }f(v_{n,j})=\lim _{n\rightarrow \infty }\Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert =0~~\text {for~each}~~j=1,2,\ldots ,N-1.\nonumber \\ \end{aligned}$$

(3.8)

Moreover, we also have

$$\begin{aligned} \lim _{n\rightarrow \infty }D_p(\Pi _{C_i}v_{n,N},v_{n,N})=0~~\text {for~each}~~i=1,2,\ldots ,M \end{aligned}$$

and hence

$$\begin{aligned} D_p(y_n,v_{n,N})\le & {} a_{n,0}D_p(v_{n,N},v_{n,N})+\sum _{i=1}^{M}a_{n,i}D_p(\Pi _{C_i}v_{n,N},v_{n,N})\nonumber \\\rightarrow & {} 0. \end{aligned}$$

By Lemma 2.5, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{n,N}-\Pi _{C_i}v_{n,N}\Vert =0~~\text {for~each}~~i=1,2,\ldots ,M \end{aligned}$$

(3.9)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert y_n-v_{n,N}\Vert =0. \end{aligned}$$

From (3.8), we see that

$$\begin{aligned} \Vert J_{p}^{E}(v_{n,j+1})-J_{p}^{E}(v_{n,j})\Vert= & {} \tau _{n,j+1}\Vert \nabla f(v_{n,j})\Vert \nonumber \\\le & {} \tau _{n,j+1}\Vert A^*\Vert \Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert ^{p-1}\nonumber \\\rightarrow & {} 0 \end{aligned}$$

for each $j=1,2,\ldots ,N-1$. In a similar way, we can see that

$$\begin{aligned} \Vert J_{p}^{E}(v_{n,1})-J_{p}^{E}(x_n)\Vert= & {} \tau _{n,1}\Vert \nabla f(x_n)\Vert \nonumber \\\le & {} \tau _{n,1}\Vert A^*\Vert \Vert (I-P_{Q_{1}})Ax_n\Vert ^{p-1}\nonumber \\\rightarrow & {} 0. \end{aligned}$$

Since $J_{q}^{E^{*}}$ is norm-to-norm uniformly continuous on bounded subsets of $E^{*}$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{n,j+1}-v_{n,j}\Vert =0~~\text {for each}~~j=1,2,\ldots ,N-1 \end{aligned}$$

(3.10)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{n,1}-x_n\Vert =0. \end{aligned}$$

(3.11)

From (3.10) and (3.11), we have

$$\begin{aligned} \Vert y_n-x_n\Vert\le & {} \Vert y_n-v_{n,N}\Vert +\Vert v_{n,N}-v_{n,N-1}\Vert +\ldots +\Vert v_{n,1}-x_n\Vert \nonumber \\\rightarrow & {} 0. \end{aligned}$$

(3.12)

It follows that

$$\begin{aligned} \Vert x_n-v_{n,N}\Vert\le & {} \Vert x_n-y_n\Vert +\Vert y_n-v_{n,N}\Vert \nonumber \\\rightarrow & {} 0. \end{aligned}$$

(3.13)

From (3.12), we see that

$$\begin{aligned} D_p(w_n,x_n)\le & {} \alpha _n D_p(u_n,x_n)+(1-\alpha _n)D_p(y_n,x_n)\nonumber \\\rightarrow & {} 0 \end{aligned}$$

and hence

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n-w_n\Vert =0. \end{aligned}$$

(3.14)

Since $\{x_n\}$ is bounded, without loss of generality, we may assume there exists a subsequence $\{x_{n_{k}}\}$ of $\{x_n\}$ such that $x_{n_{k}}\rightharpoonup v\in E$ as $k\rightarrow \infty$. Also, we have a subsequence $\{v_{n_k,N}\}$ of $\{v_{n,N}\}$ such that $v_{n_k,N}\rightharpoonup v\in E$ as $k\rightarrow \infty$.

We next show that $v\in \Omega$. From (2.1) and (3.9), we have

$$\begin{aligned} D_p(v,\Pi _{C_i}v)\le & {} \langle v-\Pi _{C_i}v,J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\= & {} \langle v-v_{n_{k},N},J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\&+\langle v_{n_{k},N}-\Pi _{C_i}v_{n_{k},N},J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\&+\langle \Pi _{C_i}v_{n_{k},N}-\Pi _{C_i}v,J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\\le & {} \langle v-v_{n_{k},N},J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\&+\langle v_{n_{k},N}-\Pi _{C_i}v_{n_{k},N},J_{p}^{E}(v)-J_{p}^{E}(\Pi _{C_i}v)\rangle \\\rightarrow & {} 0. \end{aligned}$$

This gives $v\in C_i$ for $i=1,2,\ldots ,M$ and so $v\in \bigcap _{i=1}^{M}C_i$. Form (3.10) and (3.13), for each $j=1,2,\ldots ,N-1$, we have

$$\begin{aligned} \Vert x_n-v_{n,j}\Vert\le & {} \Vert x_n-v_{n,N}\Vert +\Vert v_{n,N}-v_{n,N-1}\Vert +\ldots +\Vert v_{n,j+1}-v_{n,j}\Vert \nonumber \\\rightarrow & {} 0. \end{aligned}$$

Since $x_{n_{k}}\rightharpoonup v$, we also have $v_{n_k,j}\rightharpoonup v$ as $k\rightarrow \infty$. For each $j=1,2,\ldots ,N-1$, we note that

$$\begin{aligned}&\Vert Av-P_{Q_{j+1}}Av\Vert ^p\nonumber \\&\quad =\langle Av-P_{Q_{j+1}}Av,J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle \nonumber \\&\quad =\langle Av-Av_{n_k,j},J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle \nonumber \\&\qquad +\langle Av_{n_k,j}-P_{Q_{j+1}}Av_{n_k,j},J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle \nonumber \\&\qquad +\langle P_{Q_{j+1}}Av_{n_k,j}-P_{Q_{j+1}}Av,J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle \nonumber \\&\quad \le \langle Av-Av_{n_k,j},J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle \nonumber \\&\qquad +\langle Av_{n_k,j}-P_{Q_{j+1}}Av_{n_k,j},J_{p}^{F}(Av-P_{Q_{j+1}}Av)\rangle . \end{aligned}$$

(3.15)

By the continuity of A, we have $Av_{n_k,j}\rightharpoonup Av$ and $Av_{n_k,j}-P_{Q_{j+1}}v_{n_k,j}\rightarrow 0$. Letting $k\rightarrow \infty$ in (3.15), we have $\Vert Av-P_{Q_{j+1}}Av\Vert =0$ for each $j=1,2,\ldots ,N-1$. In a similar way, we can see that $\Vert Av-P_{Q_{1}}Av\Vert =0$. Hence, we have $Av\in Q_j$ for $j=1,2,\ldots ,N$ and so $Av\in \bigcap _{j=1}^{N}Q_j$. Therefore, $v\in \Omega$.

We next show that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle w_n-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle \le 0. \end{aligned}$$

To get this inequality, we can choose a subsequence $\{w_{n_k}\}$ of $\{w_n\}$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle w_n-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle =\lim _{k\rightarrow \infty }\langle w_{n_k}-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle . \end{aligned}$$

Since $x_{n_k} \rightharpoonup v$ and by (3.14), we also have $w_{n_k} \rightharpoonup v$. Then we have

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle w_n-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle =\langle v-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle \le 0.\nonumber \\ \end{aligned}$$

(3.16)

Since $u_n\rightarrow u$, it follows that $\lim _{n\rightarrow \infty }\langle w_n-x^*,J_{p}^{E}(u_n)-J_{p}^{E}(u)\rangle =0$. This together with (3.6) and (3.16), we conclude by Lemma 2.6 that $\Gamma _n\rightarrow 0$ as $n\rightarrow \infty$. Therefore, $x_n\rightarrow x^*$ as $n\rightarrow \infty$.

Case 2. Suppose that there exists a subsequence $\{\Gamma _{n_i}\}$ of $\{\Gamma _n\}$ such that $\Gamma _{n_i}< \Gamma _{n_i+1}$ for all $i\in {\mathbb {N}}$. Then by Lemma 2.7, we can define an integer sequence $\{\tau (n)\}$ for all $n\ge n_0$ by

$$\begin{aligned} \tau (n)=\max \{k\le n:\Gamma _k<\Gamma _{k+1}\}. \end{aligned}$$

Moreover, $\{\tau (n)\}$ is a non-decreasing sequence such that $\tau (n)\rightarrow \infty$ as $n\rightarrow \infty$ and $\Gamma _{\tau (n)}\le \Gamma _{\tau (n)+1}$ for all $n\ge n_0$. From (3.7), we can show that

$$\begin{aligned}&\lim _{n\rightarrow \infty }\Vert (I-P_{Q_{1}})Ax_{\tau (n)}\Vert =0, \\&\lim _{n\rightarrow \infty }\Vert (I-P_{Q_{j+1}})Av_{\tau (n),j}\Vert =0~~\text {for~each}~~j=1,2,\ldots ,N-1 \end{aligned}$$

and

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{\tau (n),N}-\Pi _{C_i}v_{\tau (n),N}\Vert =0~~\text {for~each}~~i=1,2,\ldots ,M. \end{aligned}$$

By the similar argument as in Case 1, we can show that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle w_{\tau (n)}-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle \le 0. \end{aligned}$$

Also, from (3.6) and the assumptions of $\{\alpha _{\tau (n)}\}$ and $\{\beta _{\tau (n)}\}$, we have

$$\begin{aligned} \Gamma _{\tau (n)}\le \langle w_{\tau (n)}-x^*,J_{p}^{E}(u_{\tau (n)})-J_{p}^{E}(u)\rangle +\langle w_{\tau (n)}-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle .\nonumber \\ \end{aligned}$$

(3.17)

Hence, $\limsup _{n\rightarrow \infty }\Gamma _{\tau (n)}\le 0$ and so $\lim _{n\rightarrow \infty }\Gamma _{\tau (n)}=0$. Again from (3.6), we see that

$$\begin{aligned} \Gamma _{\tau (n)+1}-\Gamma _{\tau (n)}\le & {} \alpha _{\tau (n)}(1-\beta _{\tau (n)})\langle w_{\tau (n)}-x^*,J_{p}^{E}(u_{\tau (n)})-J_{p}^{E}(u)\rangle \nonumber \\&+\alpha _{\tau (n)}(1-\beta _{\tau (n)})\langle w_{\tau (n)}-x^*,J_{p}^{E}(u)-J_{p}^{E}(x^*)\rangle \nonumber \\\rightarrow & {} 0. \end{aligned}$$

This together with (3.17) implies that $\lim _{n\rightarrow \infty }\Gamma _{\tau (n)+1}=0$. Thus, we have

$$\begin{aligned} 0\le \Gamma _{n}\le \max \{\Gamma _{\tau (n)},\Gamma _{n}\}\le \Gamma _{\tau (n)+1}\rightarrow 0, \end{aligned}$$

which implies that $D_p(x^*,x_n)\rightarrow 0$. Therefore, $x_n\rightarrow x^*\in \Omega$. We thus complete the proof. $\square$

Remark 3.2

We note that Theorem 3.1 improves and extends the main results of López et al. [21] and Alsulami and Takahashi [6] in the following ways:

(i) Our result extends the result of López et al. [21] (from SFP in Hilbert spaces to MSFP in Banach spaces) and Alsulami and Takahashi [6] (from SFP between Hilbert and Banach spaces to MSFP in two Banach spaces).

(ii) The step-sizes of our method are very different from Alsulami and Takahashi [6] because they do not depend on the operator norm of the bounded linear operators, while the step-size of those work depends on the operator norm.

(iii) Our result is proved with a new assumption on the control condition $\{\beta _n\}$. However, the assumption that $\liminf _{n\rightarrow \infty }\beta _n>0$ of our result can be removed.

Taking $\beta _n = 0$ for all $n\ge 1$, we obtain the following Halpern-type iteration process in Banach spaces immediately.

Corollary 3.3

Let E be a p-uniformly convex and uniformly smooth Banach space and F be a reflexive, strictly convex and smooth Banach space. Let $C_i$, $i=1,2,\ldots , M$ and $Q_j$, $j=1,2,\ldots ,N$ be nonempty, closed and convex subsets of E and F, respectively. Let $A : E \rightarrow F$ be a bounded linear operator and $A^{*}:F^{*}\rightarrow E^{*}$ be the adjoint of A. Suppose that $\Omega \ne \emptyset$. Let $\{u_n\}$ be a sequence in E such that $u_n\rightarrow u$. For given $x_1\in E$, let $\{x_n\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} v_{n,1}=J_{q}^{E^{*}}(J_{p}^{E}(x_n)-\tau _{n,1}\nabla f(x_n)),\\ v_{n,2}=J_{q}^{E^{*}}(J_{p}^{E}(v_{n,1})-\tau _{n,2}\nabla f(v_{n,1})),\\ ~~\vdots \\ v_{n,N}=J_{q}^{E^{*}}(J_{p}^{E}(v_{n,N-1})-\tau _{n,N}\nabla f(v_{n,N-1})),\\ y_n=J_{q}^{E^{*}}(a_{n,0}J_{p}^{E}(v_{n,N})+\sum _{i=1}^{M}a_{n,i}J_{p}^{E}(\Pi _{C_i}v_{n,N})),\\ x_{n+1}=J_{q}^{E^{*}}(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n)),~~\forall n\ge 1, \end{array} \end{array}\right. } \end{aligned}$$

where $\{\alpha _n\}\subset (0,1)$, $\{a_{n,i}\}_{i=1}^{M}\subset (0,1)$, $f(v_{n,j})=\frac{1}{p}\Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert ^p$ for $j=1,2,\ldots ,N-1$ and $f(x_n)=\frac{1}{p}\Vert (I-P_{Q_{1}})Ax_n\Vert ^p$ with the step-sizes $\tau _{n,1}$ and $\tau _{n,j}$, $j=1,2,\ldots ,N-1$ are chosen self-adaptively as

$$\begin{aligned} \tau _{n,1}= \left\{ \begin{array}{ll} \frac{\rho _n f^{p-1}(x_n)}{\Vert \nabla f(x_n)\Vert ^p},&{}\qquad \quad \text {if}~f(x_n)\ne 0; \\ 0,&{}\qquad \quad \text {otherwise} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \tau _{n,j+1}= \left\{ \begin{array}{ll} \frac{\rho _n f^{p-1}(v_{n,j})}{\Vert \nabla f(v_{n,j})\Vert ^p},&{}\qquad \quad \text {if}~f(v_{n,j})\ne 0; \\ 0,&{}\qquad \quad \text {otherwise}, \end{array}\right. \end{aligned}$$

respectively, where $\{\rho _n\}\subset \big (0,(\frac{pq}{c_q})^\frac{1}{q-1}\big )$. Suppose that the following conditions hold:

• (C1) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$;

• (C2) $\liminf _{n\rightarrow \infty }\rho _n\Big (p-\frac{\rho _{n}^{q-1}c _q}{q}\Big )>0$;

• (C3) $\sum _{i=0}^{M}a_{n,i}=1$ and $\liminf _{n\rightarrow \infty }a_{n,i}>0$ for $i=1,2,\ldots ,M$.

Then $\{x_n\}$ converges strongly to $x^*=\Pi _\Omega u$, where $\Pi _\Omega$ is the Bregman projection from E onto $\Omega$.

We consequently obtain the following result in Hilbert spaces.

Corollary 3.4

Let $H_1$ and $H_2$ be two real Hilbert spaces. Let $C_i$, $i=1,2,\ldots ,M$ and $Q_j$, $j=1,2,\ldots ,N$ be nonempty, closed and convex subsets of $H_1$ and $H_2$, respectively. Let $A : H_1 \rightarrow H_2$ be a bounded linear operator and $A^{*}:H_2\rightarrow H_1$ be the adjoint of A. Suppose that $\Omega \ne \emptyset$. Let $\{u_n\}$ be a sequence in $H_1$ such that $u_n\rightarrow u$. For given $x_1\in H_1$, let $\{x_n\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} v_{n,1}=x_n-\tau _{n,1}\nabla f(x_n),\\ v_{n,2}=v_{n,1}-\tau _{n,2}\nabla f(v_{n,1}),\\ ~~\vdots \\ v_{n,N}=v_{n,N-1}-\tau _{n,N}\nabla f(v_{n,N-1}),\\ y_n=a_{n,0}v_{n,N}+\sum _{i=1}^{M}a_{n,i}P_{C_i}v_{n,N},\\ x_{n+1}=\beta _n x_n+(1-\beta _n)(\alpha _n u_n+(1-\alpha _n)y_n),~~\forall n\ge 1, \end{array} \end{array}\right. } \end{aligned}$$

(3.18)

where $\{\alpha _n\}\subset (0,1)$, $\{a_{n,i}\}_{i=1}^{M}\subset (0,1)$, $\{\beta _n\}\subset [0,1)$, $f(v_{n,j})=\frac{1}{2}\Vert (I-P_{Q_{j+1}})Av_{n,j}\Vert ^2$ for $j=1,2,\ldots ,N-1$ and $f(x_n)=\frac{1}{2}\Vert (I-P_{Q_{1}})Ax_n\Vert ^2$ with the step-sizes $\tau _{n,1}$ and $\tau _{n,j}$, $j=1,2,\ldots ,N-1$ are chosen self-adaptively as

$$\begin{aligned} \tau _{n,1}= \left\{ \begin{array}{l} \frac{\rho _n f(x_n)}{\Vert \nabla f(x_n)\Vert ^2},~~~~~~~~~~~~\text {if}~f(x_n)\ne 0; \\ 0,~~~~~~~~~~~~~~~~~~~~~~~~~\text {otherwise} \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \tau _{n,j+1}= \left\{ \begin{array}{l} \frac{\rho _n f(v_{n,j})}{\Vert \nabla f(v_{n,j})\Vert ^2},~~~~~~~~~~\text {if}~f(v_{n,j})\ne 0; \\ 0,~~~~~~~~~~~~~~~~~~~~~~~~~\text {otherwise}, \end{array}\right. \end{aligned}$$

respectively, where $\{\rho _n\}\subset (0,4)$. Suppose that the following conditions hold:

• (C1) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$;

• (C2) $\liminf _{n\rightarrow \infty }\rho _n(4-\rho _n)>0$;

• (C3) $\sum _{i=0}^{M}a_{n,i}=1$ and $\liminf _{n\rightarrow \infty }a_{n,i}>0$ for $i=1,2,\ldots ,M$;

• (C4) $\limsup _{n\rightarrow \infty }\beta _n<1$.

Then $\{x_n\}$ converges strongly to $x^*=P_\Omega u$, where $P_\Omega$ is the metric projection from $H_1$ onto $\Omega$.

We obtain the following result for the SFP in Banach spaces.

Corollary 3.5

Let E be a p-uniformly convex and uniformly smooth Banach space and F be a reflexive, strictly convex and smooth Banach space. Let C and Q be nonempty, closed and convex subsets of E and F, respectively. Let $A : E \rightarrow F$ be a bounded linear operator and $A^{*}:F^{*}\rightarrow E^{*}$ be the adjoint of A. Suppose that $\Omega \ne \emptyset$. Let $\{u_n\}$ be a sequence in E such that $u_n\rightarrow u$. For given $x_1\in E$, let $\{x_n\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} y_n=\Pi _{C}J_{q}^{E^{*}}(J_{p}^{E}(x_n)-\tau _{n}\nabla f(x_n)),\\ x_{n+1}=J_{q}^{E^{*}}(\beta _nJ_{p}^{E}(x_n)+(1-\beta _n)(\alpha _n J_{p}^{E}(u_n)+(1-\alpha _n)J_{p}^{E}(y_n))),~~\forall n\ge 1, \end{array} \end{array}\right. } \end{aligned}$$

where $\{\alpha _n\}\subset (0,1)$, $\{\beta _n\}\subset [0,1)$ and $f(x_n)=\frac{1}{p}\Vert (I-P_Q)Ax_n\Vert ^p$ with the step-size $\tau _{n}$ is chosen self-adaptively as

$$\begin{aligned} \tau _{n}= \left\{ \begin{array}{l} \frac{\rho _n f^{p-1}(x_n)}{\Vert \nabla f(x_n)\Vert ^p},~~~\text {if}~f(x_n)\ne 0; \\ 0,~~~~~~~~~~~~~~\text {otherwise}, \end{array}\right. \end{aligned}$$

where $\{\rho _n\}\subset \big (0,(\frac{pq}{c_q})^\frac{1}{q-1}\big )$. Suppose that the following conditions hold:

• (C1) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$;

• (C2) $\liminf _{n\rightarrow \infty }\rho _n\Big (p-\frac{\rho _{n}^{q-1}c _q}{q}\Big )>0$;

• (C3) $\limsup _{n\rightarrow \infty }\beta _n<1$.

Then $\{x_n\}$ converges strongly to $x^*=\Pi _\Omega u$, where $\Pi _\Omega$ is the Bregman projection from E onto $\Omega$.

4 Numerical Examples

In this section, we give some numerical examples to support our main result.

4.1 Numerical Example in Finite Dimensional Spaces

Example 4.1

We consider MSFP (1.1) with $C_i\subset {\mathbb {R}}^{{\mathcal {N}}}$ and $Q_j\subset {\mathbb {R}}^{{\mathcal {M}}}$, which are defined by

$$\begin{aligned}&C_i = \{x\in {\mathbb {R}}^{\mathcal {N}}:\ \langle a^C_i,x\rangle \le b^C_i\},\\&Q_j = \{x\in {\mathbb {R}}^{\mathcal {M}}:\ \langle a^Q_j,x\rangle \le b^Q_j\}, \end{aligned}$$

where $a^C_i\in {\mathbb {R}}^{\mathcal {N}}, a^Q_j\in {\mathbb {R}}^{\mathcal {M}}$, $b^C_i, b^Q_j\in {\mathbb {R}}$ for all $i=1,2,\ldots ,M$ and all $j=1,2,\ldots ,N$, and A is a bounded linear operator from ${\mathbb {R}}^{\mathcal {N}}$ into ${\mathbb {R}}^{\mathcal {M}}$ the elements of the representing matrix of which are randomly generated in the closed interval [5, 10]. Next, we use randomly generated values of the coordinates of $a^C_i$, $a^Q_j$ in the closed interval [3, 5] and of $b^C_i$, $b^Q_j$ in the closed interval [1, 10], respectively. It is clear that $\Omega := \Big (\bigcap _{i=1}^{M}C_i\Big )\cap A^{-1}\Big (\bigcap _{j=1}^{N}Q_j\Big )\ne \emptyset$ because $0\in \Omega$.

Remark 4.2

In this example, we define the function $\text {TOL}_n$ by

$$\begin{aligned} \text {TOL}_n=\dfrac{1}{M}\sum _{i=1}^M\Vert x_n-P_{C_i}x_n\Vert ^2+\dfrac{1}{N} \sum _{j=1}^N\Vert Ax_n-P_{Q_j}Ax_n\Vert ^2,~~\forall n\ge 1. \end{aligned}$$

We use the stopping rule $\text {TOL}_n<\text {err}$ to stop the iterative process. Note that if at the nth step $\hbox {TOL}_n=0$, then $x_n\in \Omega$, that is, $x_n$ is a solution to this problem.

Applying iterative method (3.18) in Corollary 3.4 with ${\mathcal {N}}=40$, ${\mathcal {M}}=50$, $M=30$, $N=40$, $\beta _{n}=\dfrac{3}{4}$, $\alpha _n=\dfrac{1}{n+1}$, $\rho _n =0.25$ and $u_n=u$ for all $n\ge 1$. Take the initial values $u, x_1\in {\mathbb {R}}^{{\mathcal {N}}}$ where its coordinates are also randomly generated in the closed interval [10, 50], we arrive at the following table of numerical results (Table 1).

Table 1 Table of numerical results for Example 4.1

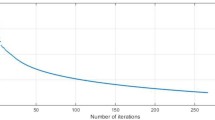
The behavior of $\text {TOL}_n$ in the case $\hbox {TOL}_n<10^{-9}$ is described in Fig. 1.

Fig. 1

The behavior of $\hbox {TOL}_n$ with the stop condition $\hbox {TOL}_n<10^{-9}$

4.2 Numerical Examples in Infinite Dimensional Spaces

Example 4.3

In this example, we take $E=F=L_2([0,\pi ])$ with the inner product

$$\begin{aligned} \langle f,g\rangle =\int _0^\pi f(t)g(t)\mathrm{d}t \end{aligned}$$

and the norm

$$\begin{aligned} \Vert f \Vert =\Big (\int _0^\pi f^2(t)\mathrm{d}t\Big )^{1/2}, \end{aligned}$$

for all $f,g\in L_2([0,\pi ]).$

Now, let

$$\begin{aligned} C_i=\{x\in L_2([0,\pi ]):\ \langle a_i,x\rangle =b_i\}, \end{aligned}$$

where $a_i(t)=\sin (2it)$, $b_i=\dfrac{4i}{4i^2-1}$ for all $i=1,2,\ldots , M$ and $t\in [0,\pi ]$,

$$\begin{aligned} Q_j=\{x\in L_2([0,\pi ]):\ \langle c_j,x\rangle \le d_j\}, \end{aligned}$$

in which $c_j(t)=\exp (jt)$, $d_j=\dfrac{\exp (j\pi )-1}{j}$ for all $j=1,2,\ldots ,N$ and $t\in [0,\pi ]$.

Let us assume that

$$\begin{aligned} A:\ L_2([0,\pi ])\rightarrow L_2([0,\pi ]),\ (Ax)(t)=\dfrac{x(t)}{2}. \end{aligned}$$

We consider the Problem (1.1) with $C_i$, $Q_j$ and A are defined as the above. It is easy to check that $x(t)=\cos t +c\in \bigcap _{i=1}^M C_i$, with c is an arbitrary real number. Moreover, if the constant $c\in [0,1]$, then we have

$$\begin{aligned} \int _0^\pi \exp (jt)\dfrac{\cos t+c}{2}\mathrm{d}t\le \int _0^\pi \exp (jt)\mathrm{d}t=\dfrac{\exp (j\pi )-1}{j}, \end{aligned}$$

for all $j=1,2,\ldots ,N$. So, we obtain that $A(\cos t +c)\in \bigcap _{j=1}^NQ_j$. Thus, we arrive that

$$\begin{aligned} x(t)=\cos t +c\in \Bigg (\bigcap _{i=1}^MC_i\Bigg ) \cap A^{-1}\Bigg (\bigcap _{j=1}^NQ_j\Bigg ),\ \forall c\in [0,1]. \end{aligned}$$

So, the set of the solutions of the Problem (1.1) is a nonempty set.

When $M=50$, $N=100$, with the same initial guess elements $x_1(t)=t^2+1$ and $u_n(t)=u(t)=t$ for all $n\ge 1$ and $t\in [0,\pi ]$, we now consider the convergence of iterative method (3.18) with $\rho _n=0.05$, $\beta _n=0.25$, $\alpha _n=1/n$, $a_{n,i}=1/(M+1)$ for all $n\ge 1$, $i=0,1,\ldots , M$, and iterative method (27) in [38, Theorem 4.1] with $\rho _n=0.05$, $\beta _{i,n}=1.5$, $\lambda _{j,n}=0.5$, $\alpha _n=1/n$ for all $n\ge 1$, $i=1,2,\ldots , M$, and $j=1,2,\ldots ,N$. Note that, we define the function $\hbox {TOL}_n$ as in Example 4.1 and use the stopping rule $\text {TOL}_n<\text {err}$ to stop the iterative process.

Table 2 Table of numerical results for Example 4.3

The behaviors of the approximation solution $x_n(t)$ in Table 2 (with $\hbox {TOL}_n<10^{-3}$ and $\hbox {TOL}_n<10^{-4}$) are presented in Figs. 2 and 3.

Fig. 2

The behavior of $x_n(t)$ with the stop condition $\hbox {TOL}_n<10^{-3}$

Fig. 3

The behavior of $x_n(t)$ with the stop condition $\hbox {TOL}_n<10^{-4}$

Finally, we provide some connection between the MSFP and the Fredholm integral equations.

Example 4.4

Let us consider the Fredholm integral equation of the first kind as considered in [4],

$$\begin{aligned} \int _{a}^{b}K(s,t)x(t)\mathrm{d}t=g(s),~~a\le s\le b, \end{aligned}$$

(4.1)

where $K :[a,b]^2\rightarrow {\mathbb {R}}$ is the continuous kernel and $g :[a,b]\rightarrow {\mathbb {R}}$ is the continuous free term. Consider the computing $L_p$-solutions of the Problem (4.1): find $x^*\in \bigcap _{i=1}^{M}C_i$, where

$$\begin{aligned} C_i=\{x\in L_p([a,b]):\langle a_{i},x\rangle =b_i\}, \end{aligned}$$

with $a_i(t)=K(s_i,t)\in L_q([a,b])$ and $b_i=g(s_i)\in {\mathbb {R}}$ for $i=1,2,..,M$, while $a=s_1<s_2<\cdot \cdot \cdot <s_M=b$ (see [18, 49]). Under some hypothesis, (4.1) has solutions [24], then approximating an $L_p$-solution of (4.1) equivalent to solving the MSFP with $E=F=L_p([a,b])$, $A=I$ and $Q_j=L_p([a,b])$ for all $j=1,2,\ldots ,N$.

We consider the following the Fredholm integral equations of the first kind [47, Example 2]:

$$\begin{aligned} \dfrac{\pi }{2}\cos s=\int _0^\pi \cos (t-s)x(t)\mathrm{d}t, \ 0\le s\le \pi . \end{aligned}$$

(4.2)

It follows from [47], Example 2] that the set of solutions of the Problem (4.2) is a nonempty set. Moreover, $x(t)=\cos t$ or $x(t)=\cos t+\sin (2n+1)t$, $n=1,2,\ldots$ are solutions of this problem.

We now approximate the solution of the Problem (4.2) in $L_2([0,\pi ])$ by solving the MSFP, that is, find $x^*\in \bigcap _{i=1}^{M}C_i$, where

$$\begin{aligned} C_i=\{x\in L_2([0,\pi ]):\langle a_{i},x\rangle =b_i\}, \end{aligned}$$

with $a_i(t)=\cos (t-s_i)$ and $b_i=\dfrac{\pi }{2}\cos s_i$ for $i=1,2,..,M$, while $0=s_1<s_2<\cdot \cdot \cdot <s_M=\pi .$

In this case, the sequence $\{x_n\}$ is defined by (see, iterative method (3.18) in Corollary 3.4) $x_1,u\in L_2([0,\pi ])$, and

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} y_n=a_{n,0}x_n+\sum _{i=1}^Ma_{n,i}P_{C_i}x_n,\\ x_{n+1}=\beta _n x_n +(1-\beta _n)(\alpha _n u_n+(1-\alpha _n)y_n),\ \forall n\ge 1. \end{array} \end{array}\right. } \end{aligned}$$

(4.3)

Applying iterative method (4.3) with $a_{n,i}=1/(M+1)$, $\beta _n=0.05$, $\alpha _n=1/n$ for all $n\ge 1$ and for all $i=0,1,\ldots , M$. Take the initial values $x_1(t)=1$, $u_n(t)=u(t)=\sin 3t$ for all $n\ge 1$ and $t\in [0,\pi ]$, we obtain the following table of numerical results (Table 3).

Table 3 Table of numerical results for Example 4.4

Remark 4.5

Note that, in this example when $u_n(t)=u(t)=\sin 3t$ for all $n\ge 1$, then $x^*(t)=\cos t +\sin 3t$ is the projection of u onto the set of solutions of Problem (4.2).