A Linear Unconditionally Stable Scheme for the Incompressible Cahn–Hilliard–Navier–Stokes Phase-Field Model

Abstract

In this paper, we propose a linear, unconditional energy-stable time-discretization scheme for Cahn–Hilliard–Navier–Stokes model, which is a phase-field model for two-phase incompressible flow. Based on a Lagrange multiplier approach and pressure projection method, our proposed scheme is linearized. Error analyses are carried out under the finite element frame; numerical experiments are done to demonstrate the effectiveness for the proposed scheme.

1 Introduction

Recently, numerical simulation and analysis of multiphase flow have bcome very common in scientific research and practical application, such as hydraulic machinery, underwater launching, aeronautical and chemical engineering and so on. Among them, the phase-field approach, whose origin can be traced back to [1, 2], has been used extensively with much successes and has become one of the major tools to study a variety of interfacial phenomena. As well as avoiding interface tracking, a special advantage of the phase field approach is that the governing system can be obtained from the energy-based variational form. This usually leads to the law of energy dissipation, which allows us to establish a coupled nonlinear system. For two fluids with matched density, the Cahn–Hilliard–Navier–Stokes system (CHNS) is a well-accepted phase field model. The difficulty in the numerical approximation of phase-field models is how to construct efficient and easy-to-implement numerical schemes which perserve a discrete energy law. Some existing numerical methods can be seen in related literatures; two typical stable numerical methods have been developed: the stabilization method [11,12,13,14, 19] and the convex splitting method [15,16,17,18,19]. There are other ideas to design numerical schemes for NSCH problem, such as the following : Taylor expansion [24], SAV (Lagrange multiplier) [27], Secant method [26], decoupling method [28].

In addition, an adaptive energy-stable scheme is formulated in [20] and two decoupling of energy stable numerical schemes are provided in [21]. In [22], the author proposed several second-order in time, fully discrete, linear and nonlinear numerical schemes for solving the phase field model of two-phase incompressible flows in the framework of finite element method. In [23] a novel second-order in time numerical scheme is proposed, in which second-order convex-splitting method for the Cahn–Hilliard equation and pressure-projection method for the Navier–Stokes equation are used. In [24], by introducing Lagrange multiplier method to the Cahn–Hilliard equation, a linear scheme is obtained. In [25], the main purpose is to provide a rigorous error analysis for these given schemes in semi-discrete (in time) form for CHNS system.

The main objective of this paper was to construct a linear, decoupled energy stable scheme for Cahn–Hilliard–Navier–Stokes model. By introducing a new variable q in the double potential function $F(\phi )$, the whole model is linearized due to the treatment for $\phi$ and q implicitly or explicitly. We show that the scheme is mass conservative, unconditionally stable.

The rest of this paper is organized as follows: In Sect. 2, the Cahn–Hilliard phase- field model that we consider is described. In Sect. 3, a coupled linearized numerical scheme is provided, and unconditionally energy stable is proven. In Sect. 4, a rigorous error analysis for our semi-discrete scheme in time is provided. In Sect. 5, some numerical simulations are presented to validate our scheme.

2 Cahn–Hilliard Phase-Field Model

To introduce the underlying model, we introduce a phase function (macroscopic labeling function) $\phi$ such that

$$\begin{aligned} \phi (x,t)= {\left\{ \begin{array}{ll} 1 &{} fluid 1,\\ -1 &{} fluid 2, \end{array}\right. } \end{aligned}$$

(2.1)

with a thin, smooth transition region of width ${O}(\eta )$, and consider the following Ginzburg–Landau type of Helmholtz free energy functional:

$$\begin{aligned} W(\phi ,\nabla \phi )=\int _{\varOmega }{}\lambda (\frac{1}{2}|\nabla \phi |^{2}+F(\phi )){}\mathrm{d}x, \end{aligned}$$

(2.2)

where $\lambda$ is the mixing energy density, where the first term leads to the hydrophilic (tendency of mixing) of interactions between the materials and the second part, the double-well bulk energy $F(\phi )=\frac{1}{4\eta ^2}(\phi ^2-1)^2, \phi \in [-1,1]$, represents the hydrophobic type (tendency of separation) of interactions. Parameter $\eta$ represents a thin smooth transition layer of thickness connecting the two fluids.

The Cahn–Hilliard–Navier–Stokes model confined in a domain $\varOmega \in R^d(d=2,3)$ can be written as follows:

where M is the relaxation or mobility parameter of the phase function, $\nu$ is the viscosity parameter, $\mathbf{u }$ is the fluid velocity field, and p is the pressure. The above system (2.3)–(2.6) should be supplemented with a set of appropriate boundary conditions:

$$\begin{aligned} \mathbf{u }|_{\partial \varOmega }=0, \frac{\partial \phi }{\partial n}|_{\partial \varOmega }=0, \frac{\partial \omega }{\partial n}|_{\partial \varOmega }=0. \end{aligned}$$

(2.7)

By taking the inner product of (2.3)–(2.5) with $-\omega$, $\phi _t$ and $\mathbf{u }$, respectively, and adding the three relations, we find that the system (2.3)–(2.6) satisfies the following energy law:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _{\varOmega }{\Big (}\frac{1}{2}|\mathbf{u }|^{2}+\frac{\lambda }{2}|\nabla \phi |^2+\lambda F(\phi ){\Big )}\mathrm{d}x=-\int _{\varOmega }{\Big (}\nu |\nabla \mathbf{u }|^{2}+M|\nabla \omega |^2{\Big )}\mathrm{d}x. \end{aligned}$$

(2.8)

3 Energy-Stable Numerical Scheme for Cahn–Hilliard Phase-Field Model

We introduce a linear scheme based on a Lagrange multiplier approach in [24], where it is first developed to solve the Cahn–Hilliard equation without flow. A function $q=\frac{\phi ^2-1}{\eta ^2}$ is introduced such that one can write $f(\phi )=q\phi$. It then follows that $q_t=\frac{2}{\eta ^2}\phi \phi _t$. By using the variable q, the total energy can be written as

$$\begin{aligned} E=\int _{\varOmega }{\Big (}\frac{1}{2}|\mathbf{u }|^{2}+\frac{\lambda }{2}|\nabla \phi |^2+\frac{\lambda \eta ^2}{4}q^2{\Big )}\mathrm{d}x. \end{aligned}$$

(3.1)

Given the initial conditions $\phi ^0,\mathbf{u }^0,q^0=\frac{(\phi ^0)^2-1}{\eta ^2}$ and $p^0=0$, for this numerical scheme that we consider, we solve for $(\phi ^{n+1},\omega ^{n+1},q^{n+1},\tilde{\mathbf{u }}^{n+1})$, and then we solve for $(\mathbf{u }^{n+1},p^{n+1})$; the scheme is expressed as follows:

Remark 3.1

If $(\tilde{\mathbf{u }}^{n+1}\cdot \nabla )\phi ^n$ of (3.2) will be substituted by $\nabla \cdot (\mathbf{u }_*^n\phi ^n)$, where $\mathbf{u }_*^n=\mathbf{u }^n-\tau \phi ^n\nabla \omega ^{n+1}$. $-\omega ^{n+1}\nabla \phi ^n$ of (3.5) will be substituted by $\phi ^n\nabla \omega ^{n+1}$, computations of $(\phi ^{n+1},\omega ^{n+1},q^{n+1})$,$\tilde{\mathbf{u }}^{n+1}$, $(\mathbf{u }^{n+1},p^{n+1})$ are totally decoupled, as can be seen in [28].

For the above scheme, we can establish the following theorem:

Lemma 3.2

The scheme (3.2)–(3.9) is uniquely solvable.

Proof

Let $(\phi _1^{n+1},\omega _1^{n+1},q_1^{n+1},\tilde{\mathbf{u }}_1^{n+1})$ and $(\phi _2^{n+1},\omega _2^{n+1},q_2^{n+1},\tilde{\mathbf{u }}_2^{n+1})$ be two solutions of (3.2)-(3.6) and denoting $\phi =\phi _1^{n+1}-\phi _2^{n+1},\omega =\omega _1^{n+1}-\omega _2^{n+1},q=q_1^{n+1}-q_2^{n+1},\tilde{\mathbf{u }}=\tilde{\mathbf{u }}_1^{n+1}-\tilde{\mathbf{u }}_2^{n+1}$; then

By taking the inner product of (3.10)–(3.13) with $\omega$, $\frac{\phi }{\tau }$, $\lambda q$ and $\tilde{\mathbf{u }}$, respectively, and adding the four resulting relations, we get the following:

$$\begin{aligned} M\Vert \nabla \omega \Vert ^2+\frac{\lambda }{\tau }\Vert \nabla \phi \Vert ^2+\frac{\lambda \eta ^2}{2\tau }\Vert q\Vert ^2+\frac{\Vert \tilde{\mathbf{u }}\Vert ^2}{\tau }+\nu \Vert \nabla \tilde{\mathbf{u }}\Vert ^2=0. \end{aligned}$$

Hence the proof of the unicity of the scheme (3.2)–(3.6) holds, because the scheme (3.7)–(3.9) consists of a linear elliptic equation, and the scheme (3.2)–(3.9) is uniquely solvable. $\square$

Theorem 3.3

The solution of (3.2)–(3.9) satisfies the following discrete energy law:

$$\begin{aligned}&E(\mathbf{u }^{n+1},\phi ^{n+1},q^{n+1})+\frac{\tau ^2}{2}\Vert \nabla p^{n+1}\Vert ^2+\nu \tau \Vert \nabla \tilde{\mathbf{u }}^{n+1}\Vert ^2+M\tau \Vert \nabla \omega ^{n+1}\Vert ^2 \\ {}&\quad \le E(\mathbf{u }^{n},\phi ^{n},q^{n})+\frac{\tau ^2}{2}\Vert \nabla p^{n}\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} E(\mathbf{u },\phi ,q)=\frac{1}{2}\Vert \mathbf{u }\Vert ^2 +\frac{\lambda }{2}\Vert \nabla \phi \Vert ^2+\frac{\lambda \eta ^2}{4}\Vert q\Vert ^2; \end{aligned}$$

thus the scheme is unconditionally stable.

Proof

Taking the inner product of (3.5) with $2\tau \tilde{\mathbf{u }}^{n+1}$, using the well-known property

$$\begin{aligned} (\mathbf{u }\cdot \nabla \mathbf{v },\mathbf{v })=0, \forall \mathbf{u }\in H,\mathbf{v }\in (H_0^1(\varOmega ))^d, \end{aligned}$$

where $H=\{{\mathbf{u }}\in (L^2(\varOmega ))^d:\nabla \cdot \mathbf{u }=0,\mathbf{u }\cdot n=0\}$, we derive

$$\begin{aligned}&\Vert \tilde{\mathbf{u }}^{n+1}\Vert ^2-\Vert \mathbf{u }^n\Vert ^2+\Vert \tilde{\mathbf{u }}^{n+1}-\mathbf{u }^n\Vert ^2+2\nu \tau \Vert \nabla \tilde{\mathbf{u }}^{n+1}\Vert ^2\nonumber \\&\quad +2\tau (\nabla p^n,\tilde{\mathbf{u }}^{n+1})-2\tau (\omega ^{n+1}\nabla \phi ^n,\tilde{\mathbf{u }}^{n+1})=0 \end{aligned}$$

(3.14)

To deal with $(\omega ^{n+1}\nabla \phi ^n,\tilde{\mathbf{u }}^{n+1})$ in (3.14), we first take the inner product of (3.7) with $2\tau \nabla p^n$ to obtain

$$\begin{aligned} \tau ^2(\Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^{n}\Vert ^2-\Vert \nabla p^{n+1}-\nabla p^{n}\Vert ^2)=2\tau (\tilde{\mathbf{u }}^{n+1},\nabla p^n); \end{aligned}$$

(3.15)

We also derive from (3.7) that

$$\begin{aligned} \tau ^2\Vert \nabla p^{n+1}-\nabla p^{n}\Vert ^2=\Vert \tilde{\mathbf{u }}^{n+1}-\mathbf{u }^{n+1}\Vert ^2; \end{aligned}$$

(3.16)

Then we take the inner product of (3.7) with $\mathbf{u }^{n+1}$ to get

$$\begin{aligned} \Vert \mathbf{u }^{n+1}\Vert ^2+\Vert \tilde{\mathbf{u }}^{n+1} -\mathbf{u }^{n+1}\Vert ^2=\Vert \tilde{\mathbf{u }}^{n+1}\Vert ^2; \end{aligned}$$

(3.17)

Combining (3.14)–(3.17), we find

$$\begin{aligned}&\Vert \mathbf{u }^{n+1}\Vert ^2-\Vert \mathbf{u }^n\Vert ^2+\Vert \tilde{\mathbf{u }}^{n+1}-\mathbf{u }^n\Vert ^2+2\nu \tau \Vert \nabla \tilde{\mathbf{u }}^{n+1}\Vert ^2\nonumber \\ {}&\quad +\tau ^2(\Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^{n}\Vert ^2)-2\tau (\omega ^{n+1}\nabla \phi ^n,\tilde{\mathbf{u }}^{n+1})=0. \end{aligned}$$

(3.18)

It now remains to deal with the last term in (3.18); taking the inner product of (3.2) with $2\tau \omega ^{n+1}$, we get

$$\begin{aligned} 2(\phi ^{n+1}-\phi ^{n},\omega ^{n+1})+2\tau (\tilde{\mathbf{u }}^{n+1} \nabla \phi ^n,\omega ^{n+1})+2M\tau \Vert \nabla \omega ^{n+1}\Vert ^2=0; \end{aligned}$$

(3.19)

Taking the inner product of (3.3) with $-2(\phi ^{n+1}-\phi ^n)$, we get

$$\begin{aligned}&-2(\omega ^{n+1},\phi ^{n+1}-\phi ^n)+\lambda (\Vert \nabla \phi ^{n+1}\Vert ^2-\Vert \nabla \phi ^{n}\Vert ^2+\Vert \nabla \phi ^{n+1}-\nabla \phi ^{n}\Vert ^2) \nonumber \\&\qquad + 2\lambda (\phi ^n q^{n+1},\phi ^{n+1}-\phi ^n)=0 \end{aligned}$$

(3.20)

Taking the inner product of (3.4) with $2\lambda \tau q^{n+1}$, we have

$$\begin{aligned} \frac{\eta ^2\lambda }{2}(\Vert q^{n+1}\Vert ^2-\Vert q^n\Vert ^2+\Vert q^{n+1}-q^n\Vert ^2)=2\lambda (\phi ^n(\phi ^{n+1}-\phi ^n),q^{n+1}) \end{aligned}$$

(3.21)

Combining all the above equations, we find

$$\begin{aligned}&\Vert \mathbf{u }^{n+1}\Vert ^2-\Vert \mathbf{u }^n\Vert ^2+\Vert \tilde{\mathbf{u }}^{n+1}-\mathbf{u }^n\Vert ^2+2\nu \tau \Vert \nabla \tilde{\mathbf{u }}^{n+1}\Vert ^2\nonumber \\ {}&\quad +\tau ^2(\Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^{n}\Vert ^2)+2M\tau \Vert \nabla \omega ^{n+1}\Vert ^2\nonumber \\ {}&\quad +\lambda (\Vert \nabla \phi ^{n+1}\Vert ^2-\Vert \nabla \phi ^{n}\Vert ^2+\Vert \nabla \phi ^{n+1}-\nabla \phi ^{n}\Vert ^2)\nonumber \\ {}&\quad + \frac{\eta ^2\lambda }{2}(\Vert q^{n+1}\Vert ^2-\Vert q^n\Vert ^2+\Vert q^{n+1}-q^n\Vert ^2)=0 \end{aligned}$$

(3.22)

Thus, we derive

$$\begin{aligned}&\frac{1}{2}\Vert \mathbf{u }^{n+1}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \phi ^{n+1}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert q^{n+1}\Vert ^2+\frac{\tau ^2}{2}\Vert \nabla p^{n+1}\Vert ^2+\nu \tau \Vert \nabla \tilde{\mathbf{u }}^{n+1}\Vert ^2\nonumber \\ {}&+M\tau \Vert \nabla \omega ^{n+1}\Vert ^2 \le \frac{1}{2}\Vert \mathbf{u }^{n}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \phi ^{n}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert q^{n}\Vert ^2+\frac{\tau ^2}{2}\Vert \nabla p^n\Vert ^2 \end{aligned}$$

(3.23)

The desired result is then a direct consequence of the above inequality. $\square$

4 Error Estimates

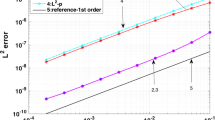
4.1 First-Order Error Estimates

Assumption We assume that the exact solutions $(u,\phi ,\omega ,p)$ are sufficiently smooth. More precisely,

$$\begin{aligned}&\phi \in L^\infty (0,T;H^3(\varOmega ))\cap W^{1,\infty }(0,T;H^2(\varOmega )) \\&\cap W^{2,\infty }(0,T;H^1(\varOmega ))\cap W^{3,\infty }(0,T;L^2(\varOmega )) \\&\mathbf{u }\in L^\infty (0,T;H^3(\varOmega )^d)\cap W^{1,\infty }(0,T;H^2(\varOmega )^d) \\&\cap W^{2,\infty }(0,T;H^1(\varOmega )^d)\cap W^{3,\infty }(0,T;L^2(\varOmega )^d) \\&\omega \in L^\infty (0,T;H^3(\varOmega ))\cap L^\infty (0,T;H^2(\varOmega )) \\&p\in W^{2,\infty }(0,T;H^1(\varOmega )) \\&q\in L^\infty (0,T;H^2(\varOmega ))\cap L^\infty (0,T;H^3(\varOmega )) \end{aligned}$$

Let $(\mathbf{u }^n,p^n,q^n,\omega ^n,\phi ^n,\tilde{\mathbf{u }}^n)$ be the numerical solution obtained from the scheme (3.2)–(3.9), and $(\mathbf{u }(t^n),p(t^n),q(t^n),\omega (t^n),\phi (t^n))$ be the exact solution; we define the error function for $n=0,1,2,....,N$ as

$$\begin{aligned} {\tilde{e}}_u^n= & {} \mathbf{u }(t^n)-\tilde{\mathbf{u }}^n,\qquad e_u^n=\mathbf{u }(t^n)-\mathbf{u }^n,\qquad e_q^n=q(t^n)-q^n, \\ e_p^n= & {} p(t^n)-p^n,\qquad e_\phi ^n=\phi (t^n)-\phi ^n,\qquad e_\omega ^n=\omega (t^n)-\omega ^n. \end{aligned}$$

Theorem 4.1

Under the Assumption, there exists some $\tau _0>0$ such that when $\tau <\tau _0$ the solution $(\mathbf{u }^n,p^n,\phi ^n,\omega ^n)(0\le n\le \frac{T}{\tau })$ of scheme (3.2)–(3.9) satisfies the following error estimates:

$$\begin{aligned}&\Vert e_{\phi ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert e_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}+\Vert e_{\omega ,\tau }\Vert _{l^2(H^1(\varOmega ))}\le c\tau ,\nonumber \\&\Vert e_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}+\Vert e_{\omega ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}\le c\tau ^{\frac{1}{2}},\nonumber \\&\Vert e_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}+\Vert e_{q,\tau }\Vert _{l^\infty (L^2(\varOmega ))}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}\le c\tau ,\Vert \nabla e_p^n\Vert _{(L^2(\varOmega )^d)}\lesssim 1. \end{aligned}$$

(4.1)

Proof

To analyze the error for the stabilized scheme (3.2)–(3.9), we define the local truncation error $R_\phi ^{n+1}(n=0,1,...,N-1)$ for the equation (3.2)as follows:

$$\begin{aligned} R_\phi ^{n+1}=\frac{\phi (t^{n+1})-\phi (t^n)}{\tau }+(\mathbf{u }(t^{n+1})\cdot \nabla )\phi (t^n)-M\varDelta \omega (t^{n+1}) \end{aligned}$$

(4.2)

the local truncation error $R_\omega ^{n+1}(n=0,1,...,N-1)$ for the following equation (3.3):

$$\begin{aligned} R_\omega ^{n+1}=\omega (t^{n+1})+\lambda (\varDelta \phi (t^{n+1})-\phi (t^n)q(t^{n+1})) \end{aligned}$$

(4.3)

the local truncation error $R_q^{n+1}(n=0,1,...,N-1)$ for the equation (3.4):

$$\begin{aligned} R_q^{n+1}=\frac{\eta ^2}{2}\frac{q(t^{n+1})-q(t^n)}{\tau }-\phi (t^n)\frac{\phi (t^{n+1})-\phi (t^n)}{\tau } \end{aligned}$$

(4.4)

the local truncation error $R_u^{n+1}(n=0,1,...,N-1)$ for the equation (3.5):

$$\begin{aligned} R_u^{n+1}&=\frac{\mathbf{u }(t^{n+1})-\mathbf{u }(t^n)}{\tau }-\mu \varDelta \mathbf{u }(t^{n+1})+\nabla p(t^{n})\nonumber \\&\quad +(\mathbf{u }(t^n)\cdot \nabla )\mathbf{u }(t^{n+1})-\omega (t^{n+1})\nabla \phi (t^n) \end{aligned}$$

(4.5)

the local truncation error $R_p^{n+1}(n=0,1,...,N-1)$ for the equation (3.7):

$$\begin{aligned} R_p^{n+1}= & {} \frac{\mathbf{u }(t^{n+1})-\mathbf{u }(t^{n+1})}{\tau }+\nabla (p(t^{n+1})-p(t^n))\nonumber \\= & {} \nabla (p(t^{n+1})-p(t^n)) \end{aligned}$$

(4.6)

It is easy to establish the following estimates for the truncation errors, provided that the exact solution are sufficiently smooth:

Lemma 4.2

Under Assumption, the truncation errors satisfy

$$\begin{aligned}&\Vert R_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}+\Vert R_{\phi ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert R_{\omega ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}\nonumber \\&\quad +\Vert R_{p,\tau }\Vert _{l^\infty (L^2(\varOmega ))}+\Vert R_{q,\tau }\Vert _{l^\infty (L^2(\varOmega ))}\le c\tau , \end{aligned}$$

(4.7)

where c is independent of $\tau$.

Proof

We sketch the proof for $R_{\phi ,\tau }$(4.2) and omit the rest error terms. Recalling (4.2) and the original equation (3.2), by Taylor expansion, we have

$$\begin{aligned} R_\phi ^{n+1}&=\frac{\phi (t^{n+1})-\phi (t^n)}{\tau }-\partial _t\phi (t^{n+1}) +\mathbf{u }(t^{n+1})\cdot \nabla \phi (t^n)-\mathbf{u }(t^{n+1})\cdot \nabla \phi (t^{n+1})\nonumber \\&=-\frac{\tau }{2}\partial _{tt}\phi (t^*)-\tau \mathbf{u }(t^{n+1})\cdot \nabla \partial _t \phi (t^{**}), \end{aligned}$$

(4.8)

where $t^*,t^{**}\in (t^n,t^{n+1})$. The error bound for $R_{\phi ,\tau }$ is then implied by the regularity Assumption. $\square$

Next,we derive the equations governing the error growth. Define

$$\begin{aligned} \dot{{\tilde{e}}}_u^{n+1}=\frac{{\tilde{e}}_u^{n+1}-e_u^n}{\tau }+(\mathbf{u }(t^n)\cdot \nabla )\mathbf{u }(t^{n+1})-(\mathbf{u }^n\cdot \nabla )\tilde{\mathbf{u }}^{n+1} \end{aligned}$$

(4.9)

Subtracting (4.2)–(4.6) from (3.2), (3.3), (3.4), (3.5) and (3.7), respectively, we get the following error equations for $n\ge 0:$

with the boundary conditions

$$\begin{aligned} {\tilde{e}}_u^{n+1}|_{\partial \varOmega }=0,\partial _n e_\phi ^{n+1}|_{\partial \varOmega }=0,\partial _n e_\omega ^{n+1}|_{\partial \varOmega }=0. \end{aligned}$$

(4.15)

Taking inner product of (4.10) with $\lambda \tau e_\phi ^{n+1}$ and $\tau e_\omega ^{n+1}$, we obtain

$$\begin{aligned}&\frac{\lambda }{2}(\Vert e_\phi ^{n+1}\Vert ^2-\Vert e_\phi ^n\Vert ^2+ \Vert e_\phi ^{n+1}-e_\phi ^n\Vert ^2)+\lambda \tau (\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{e}}_u^{n+1}\cdot \nabla \phi ^n,e_\phi ^{n+1})\nonumber \\&\quad +M\tau \lambda (\nabla e_\omega ^{n+1},\nabla e_\phi ^{n+1})=(R_\phi ^{n+1},\lambda \tau e_\phi ^{n+1}) \end{aligned}$$

(4.16)

$$\begin{aligned}&(e_\phi ^{n+1}-e_\phi ^n,e_\omega ^{n+1}) +\tau (\mathbf{u }(t^{n+1})\cdot \nabla \phi (t^n) -\tilde{\mathbf{u }}^{n+1}\cdot \nabla \phi ^{n}, e_\omega ^{n+1})\nonumber \\&\quad +M\tau \Vert \nabla e_\omega ^{n+1}\Vert ^2=(R_\phi ^{n+1},\tau e_\omega ^{n+1}) \end{aligned}$$

(4.17)

Taking inner product of (4.11) with $M\tau e_\omega ^{n+1}$ and $-(e_\phi ^{n+1}-e_\phi ^n)$, respectively, we have

$$\begin{aligned}&M\tau \Vert e_\omega ^{n+1}\Vert ^2-\lambda \tau M(\nabla e_\phi ^{n+1},\nabla e_\omega ^{n+1})\nonumber \\&\quad -\lambda \tau M(\phi (t^n)q(t^{n+1})-\phi ^n q^{n+1},e_\omega ^{n+1})=(R_\omega ^{n+1},M \tau e_\omega ^{n+1}) \end{aligned}$$

(4.18)

$$\begin{aligned}&-(e_\phi ^{n+1}-e_\phi ^n,e_\omega ^{n+1})+\frac{\lambda }{2}(\Vert \nabla e_\phi ^{n+1}\Vert ^2-\Vert \nabla e_\phi ^n\Vert ^2+\Vert \nabla e_\phi ^{n+1}-\nabla e_\phi ^n\Vert ^2)\nonumber \\&\quad +\lambda (\phi (t^n)q(t^{n+1})-\phi ^n q^{n+1},e_\phi ^{n+1}-e_\phi ^n)=-(e_\phi ^{n+1}-e_\phi ^n,R_\omega ^{n+1}) \end{aligned}$$

(4.19)

Taking inner product of (4.12) with $\lambda \tau e_q^{n+1}$, we have

$$\begin{aligned}&\frac{\lambda \eta ^2}{4}(\Vert e_q^{n+1}\Vert ^2-\Vert e_q^n\Vert ^2+\Vert e_q^{n+1}-e_q^n\Vert ^2) \nonumber \\&\quad -\lambda (\phi (t^n)(\phi (t^{n+1})-\phi (t^n))-\phi ^n(\phi ^{n+1}-\phi ^n),e_q^{n+1})=\lambda \tau (R_q^{n+1},e_q^{n+1}) \end{aligned}$$

(4.20)

Taking inner product of (4.13) with $\tau {\tilde{e}}_u^{n+1}$, we have

$$\begin{aligned}&\frac{1}{2}(\Vert {\tilde{e}}_u^{n+1}-e_u^n\Vert ^2+\Vert {\tilde{e}}_u^{n+1}\Vert ^2-\Vert e_u^n\Vert ^2)+\mu \tau \Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2+\tau ({\tilde{e}}_u^{n+1},\nabla e_p^n)+\nonumber \\ {}&\quad \tau ((\mathbf{u }(t^n)\cdot \nabla )\mathbf{u }(t^{n+1})-(\mathbf{u }^n\cdot \nabla )\tilde{\mathbf{u }}^{n+1},{\tilde{e}}_u^{n+1})\nonumber \\ {}&-\tau (\omega (t^{n+1})\nabla \phi (t^n)-\omega ^{n+1}\nabla \phi ^n,{\tilde{e}}_u^{n+1})=\tau (R_u^{n+1},{\tilde{e}}_u^{n+1}) \end{aligned}$$

(4.21)

In addition, we know

$$\begin{aligned}&\lambda (\phi (t^n)q(t^{n+1})-\phi ^n q^{n+1},e_\phi ^{n+1}-e_\phi ^n) \nonumber \\ {}&\qquad -\lambda (\phi (t^n)(\phi (t^{n+1})-\phi (t^n))-\phi ^n(\phi ^{n+1}-\phi ^n),e_q^{n+1}) \nonumber \\ {}&\quad =\lambda (e_\phi ^n q(t^{n+1})+\phi ^n e_q^{n+1},e_\phi ^{n+1}-e_\phi ^n)\nonumber \\&\qquad -\lambda (e_\phi ^n(\phi (t^{n+1})-\phi (t^n))+\phi ^n(e_\phi ^{n+1}-e_\phi ^n),e_q^{n+1}) \nonumber \\ {}&\quad =\lambda (e_\phi ^n q(t^{n+1}),e_\phi ^{n+1}-e_\phi ^n)-\lambda (e_\phi ^n(\phi (t^{n+1})-\phi (t^n)),e_q^{n+1}) \end{aligned}$$

(4.22)

Combining (4.16)–(4.21) and using (4.22), we obtain

$$\begin{aligned}&\frac{\lambda }{2}(\Vert e_\phi ^{n+1}\Vert ^2-\Vert e_\phi ^n\Vert ^2+\Vert e_\phi ^{n+1}-e_\phi ^n\Vert ^2)+M\tau \Vert \nabla e_\omega ^{n+1}\Vert ^2+M\tau \Vert e_\omega ^{n+1}\Vert ^2\nonumber \\&\qquad +\frac{\lambda }{2}(\Vert \nabla e_\phi ^{n+1}\Vert ^2-\Vert \nabla e_\phi ^n\Vert ^2+\Vert \nabla e_\phi ^{n+1}-\nabla e_\phi ^n\Vert ^2)\nonumber \\&\qquad +\frac{\lambda \eta ^2}{4}(\Vert e_q^{n+1}\Vert ^2-\Vert e_q^n\Vert ^2+\Vert e_q^{n+1}-e_q^n\Vert ^2)+\lambda \tau (\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n,e_\phi ^{n+1}) \nonumber \\&\qquad +\frac{1}{2}(\Vert {\tilde{e}}_u^{n+1}-e_u^n\Vert ^2+\Vert {\tilde{e}}_u^{n+1}\Vert ^2-\Vert e_u^n\Vert ^2)+\nu \tau \Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2\nonumber \\&\qquad +\lambda \tau ({\tilde{e}}_u^{n+1}\cdot \nabla \phi ^n,e_\phi ^{n+1}) -\lambda \tau M(\phi (t^n)q(t^{n+1})-\phi ^n q^{n+1},e_\omega ^{n+1})\nonumber \\&\qquad +\lambda (e_\phi ^n q(t^{n+1}),e_\phi ^{n+1}-e_\phi ^n)-\lambda (e_\phi ^n(\phi (t^{n+1})-\phi (t^n)),e_q^{n+1})+\tau ({\tilde{e}}_u^{n+1},\nabla e_p^n)\nonumber \\ {}&\qquad +\tau (e_u^n\nabla \mathbf{u }(t^{n+1}),{\tilde{e}}_u^{n+1})+\tau (\mathbf{u }(t^{n+1})\nabla e_\phi ^n,e_\omega ^{n+1})-\tau (\omega (t^{n+1})\nabla e_\phi ^n,{\tilde{e}}_u^{n+1}) \nonumber \\&\quad =\tau (R_u^{n+1},{\tilde{e}}_u^{n+1})+(R_\phi ^{n+1},\lambda \tau e_\phi ^{n+1})+(R_\phi ^{n+1},\tau e_\omega ^{n+1})+(R_\omega ^{n+1},M \tau e_\omega ^{n+1})\nonumber \\&\qquad +(e_\phi ^{n+1}-e_\phi ^n,R_\omega ^{n+1})+\lambda \tau (R_q^{n+1},e_q^{n+1}) \end{aligned}$$

(4.23)

We now control each term in (4.23) as follows: First, it is easy to estimate

$$\begin{aligned} |(R_\phi ^{n+1},\lambda \tau e_\phi ^{n+1})|&\le c\tau \Vert R_\phi ^{n+1}\Vert \Vert e_\phi ^{n+1}\Vert \le c\tau ^3+c\tau \Vert e_\phi ^{n+1}\Vert ^2\nonumber \\ |(R_\phi ^{n+1},\lambda \tau e_\omega ^{n+1})|&\le c\tau \Vert R_\phi ^{n+1}\Vert \Vert e_\omega ^{n+1}\Vert \le c\tau ^3+\frac{M\tau }{16}\Vert e_\omega ^{n+1}\Vert ^2\nonumber \\ |(R_\omega ^{n+1},M \tau e_\omega ^{n+1})|&\le M\tau \Vert R_\omega ^{n+1}\Vert \Vert e_\omega ^{n+1}\Vert \le c\tau ^3+\frac{M\tau }{16}\Vert e_\omega ^{n+1}\Vert ^2\nonumber \\ |\lambda \tau (R_q^{n+1},e_q^{n+1})|&\le c\tau \Vert R_q^{n+1}\Vert \Vert e_q^{n+1}\Vert \le c\tau ^3+c\tau \Vert e_q^{n+1}\Vert ^2\nonumber \\ |\tau (R_u^{n+1},{\tilde{e}}_u^{n+1})|&\le \tau \Vert R_u^{n+1}\Vert \Vert {\tilde{e}}_u^{n+1}\Vert \le c\tau ^3+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2 \\ \nonumber \end{aligned}$$

(4.24)

$$\begin{aligned} |\lambda \tau (\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n,e_\phi ^{n+1})|&\le c\tau \Vert \nabla e_\phi ^n\Vert \Vert e_\phi ^{n+1}\Vert \le c\tau \Vert \nabla e_\phi ^n\Vert ^2+c\tau \Vert e_\phi ^{n+1}\Vert ^2\nonumber \\ |\lambda \tau (\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n,e_\omega ^{n+1})|&\le c\tau \Vert \nabla e_\phi ^n\Vert \Vert e_\omega ^{n+1}\Vert \le c\tau \Vert \nabla e_\phi ^n\Vert ^2+\frac{M\tau }{16}\Vert e_\omega ^{n+1}\Vert ^2\nonumber \\ |\tau (\omega (t^{n+1})\nabla e_\phi ^n,{\tilde{e}}_u^{n+1})|&\le c\tau \Vert \nabla e_\phi ^n\Vert \Vert {\tilde{e}}_u^{n+1}\Vert \le c\tau \Vert \nabla e_\phi ^n\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla e_u^{n+1}\Vert ^2\nonumber \\ |\tau ((e_u^n\cdot \nabla )\mathbf{u }(t^{n+1}),{\tilde{e}}_u^{n+1})|&\le c\tau \Vert e_u^n\Vert \Vert {\tilde{e}}_u^{n+1}\Vert \le c\tau \Vert e_u^n\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2 \\ \nonumber \end{aligned}$$

(4.25)

$$\begin{aligned} |\lambda \tau ({\tilde{e}}_u^{n+1}\nabla \phi ^n,e_\phi ^{n+1})|&\le c\tau \Vert {\tilde{e}}_u^{n+1}\Vert _1\Vert \nabla \phi ^n\Vert \Vert e_\phi ^{n+1}\Vert _1\nonumber \\ {}&\le c\tau (\Vert e_\phi ^{n+1}\Vert ^2+\Vert \nabla e_\phi ^{n+1}\Vert ^2)+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2 \end{aligned}$$

(4.26)

$$\begin{aligned}&|-\lambda \tau M(\phi (t^n)q(t^{n+1})-\phi ^n q^{n+1},e_\omega ^{n+1})|\nonumber \\ {}&\quad =|-\lambda \tau M(\phi (t^n)e_q^{n+1}+e_\phi ^n q^{n+1},e_\omega ^{n+1})|\nonumber \\ {}&\quad \le c\tau \Vert e_q^{n+1}\Vert \Vert e_\omega ^{n+1}\Vert + c\tau \Vert e_\phi ^n\Vert _{1}\Vert e_\omega ^{n+1}\Vert _{1}\Vert q^{n+1}\Vert _{L^2}\nonumber \\ {}&\quad \le c\tau \Vert e_q^{n+1}\Vert ^2+\frac{M\tau }{16}\Vert e_\omega ^{n+1}\Vert ^2+c\tau \Vert e_\phi ^n\Vert ^2+c\tau \Vert \nabla e_\phi ^n\Vert ^2+\frac{M\tau }{16}\Vert \nabla e_\omega ^{n+1}\Vert ^2. \end{aligned}$$

(4.27)

$$\begin{aligned}&|\lambda (e_\phi ^n q(t^{n+1}),e_\phi ^{n+1}-e_\phi ^n)|\nonumber \\ {}&\quad =|\lambda \tau (e_\phi ^n q(t^{n+1}),\frac{e_\phi ^{n+1}-e_\phi ^n}{\tau })|\nonumber \\ {}&\quad \le |\lambda \tau (e_\phi ^n q(t^{n+1}),-(\mathbf{u }(t^{n+1})\nabla e_\phi ^n+{\tilde{e}}_u^{n+1}\nabla \phi ^n))|\nonumber \\ {}&\qquad +|\lambda \tau (e_\phi ^n q(t^{n+1}),M\varDelta e_\omega ^{n+1}+R_\phi ^{n+1})|\nonumber \\ {}&\quad \le c\tau \Vert e_\phi ^n\Vert \Vert R_\phi ^{n+1}\Vert +|M\lambda \tau (\nabla e_\phi ^n q(t^{n+1})+e_\phi ^n\nabla q(t^{n+1}),\nabla e_\omega ^{n+1})|\nonumber \\ {}&\qquad +c\tau \Vert e_\phi ^n\Vert \Vert \nabla e_\phi ^n\Vert +c\tau \Vert e_\phi ^n\Vert _1\Vert {\tilde{e}}_u^{n+1}\Vert _1\Vert \nabla \phi ^n\Vert \nonumber \\ {}&\quad \le c\tau \Vert e_\phi ^n\Vert \Vert R_\phi ^{n+1}\Vert +c\tau \Vert \nabla e_\phi ^n\Vert \Vert \nabla e_\omega ^{n+1}\Vert +c\tau \Vert \nabla e_\phi ^n\Vert \Vert \nabla e_\omega ^{n+1}\Vert \nonumber \\ {}&\qquad +c\tau \Vert e_\phi ^n\Vert \Vert \nabla e_\phi ^n\Vert +c\tau \Vert e_\phi ^n\Vert _1\Vert {\tilde{e}}_u^{n+1}\Vert _1\Vert \nabla \phi ^n\Vert \nonumber \\ {}&\quad \le c\tau \Vert e_\phi ^n\Vert ^2+c\tau ^3+c\tau \Vert \nabla e_\phi ^n\Vert ^2+\frac{M\tau }{8}\Vert \nabla e_\omega ^{n+1}\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2. \end{aligned}$$

(4.28)

The boundedness of $\Vert \nabla \phi ^n\Vert$ in (4.26), (4.28) and $\Vert q^{n+1}\Vert _{L^2}$ in (4.27) is obtained from Theorem 3.3.

$$\begin{aligned}&|\lambda ^2(e_\phi ^n(\phi (t^{n+1})-\phi (t^n)),e_q^{n+1})|\nonumber \\&\quad \le \lambda ^2\tau |(e_\phi ^n \phi _t(\xi ),e_q^{n+1})| \le c\tau \Vert e_\phi ^n\Vert \Vert e_q^{n+1}\Vert \le c\tau \Vert e_\phi ^n\Vert ^2+c\tau \Vert e_q^{n+1}\Vert ^2 \end{aligned}$$

where $\xi \in (t^n,t^{n+1})$.

Following (4.28), we estimate

$$\begin{aligned}&|(e_\phi ^{n+1}-e_\phi ^n,R_\omega ^{n+1})|\nonumber \\&\quad =|\tau (R_\omega ^{n+1},\frac{e_\phi ^{n+1}-e_\phi ^n}{\tau })|\nonumber \\ {}&\quad =|\tau (R_\omega ^{n+1},-(\mathbf{u }(t^{n+1})\nabla e_\phi ^n+{\tilde{e}}_u^{n+1}\nabla \phi ^n))| +|\tau (R_\omega ^{n+1},M\varDelta e_\omega ^{n+1}+R_\phi ^{n+1})|\nonumber \\ {}&\quad \le \frac{M\tau }{16}\Vert \nabla e_\omega ^{n+1}\Vert ^2+c\tau ^3+c\tau \Vert \nabla e_\phi ^n\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2. \end{aligned}$$

It remains to estimate the term involving pressure. Using (4.15), $e_u^{n+1}\cdot n| _{\partial \varOmega }=0$, and $\nabla \cdot e_u^{n+1}=0$, we get

$$\begin{aligned}&\tau ({\tilde{e}}_u^{n+1},\nabla e_p^n)\nonumber \\ {}&\quad =\tau (e_u^{n+1}-\tau R_p^{n+1}+\tau (\nabla e_p^{n+1}-\nabla e_p^n),\nabla e_p^n)\nonumber \\ {}&\quad =-\tau ^2(R_p^{n+1},\nabla e_p^n)+\frac{\tau ^2}{2}(\Vert \nabla e_p^{n+1}\Vert ^2-\Vert \nabla e_p^n\Vert ^2-\Vert \nabla e_p^{n+1}-\nabla e_p^n\Vert ^2) \end{aligned}$$

(4.29)

and

$$\begin{aligned} \Vert \frac{e_u^{n+1}}{\tau }+(\nabla e_p^{n+1}-\nabla e_p^n)\Vert ^2=\Vert R_p^{n+1}+\frac{{\tilde{e}}_u^{n+1}}{\tau }\Vert ^2, \end{aligned}$$

(4.30)

which implies

$$\begin{aligned}&\Vert \nabla e_p^{n+1}-\nabla e_p^n\Vert ^2 =\frac{1}{\tau ^2}(\Vert {\tilde{e}}_u^{n+1}\Vert ^2-\Vert e_u^{n+1}\Vert ^2)+\Vert R_p^{n+1}\Vert ^2+\frac{2}{\tau }(R_p^{n+1},{\tilde{e}}_u^{n+1}) \end{aligned}$$

(4.31)

Hence, from (4.29) and (4.31), we find

$$\begin{aligned} \tau ({\tilde{e}}_u^{n+1},\nabla e_p^n)&=\frac{\tau ^2}{2}(\Vert \nabla e_p^{n+1}\Vert ^2-\Vert \nabla e_p^n\Vert ^2)+\frac{1}{2}(\Vert e_u^{n+1}\Vert ^2-\Vert {\tilde{e}}_u^{n+1}\Vert ^2) -\frac{\tau ^2}{2}\Vert R_p^{n+1}\Vert ^2\nonumber \\&\quad -\tau (R_p^{n+1},{\tilde{e}}_u^{n+1})-\tau ^2(R_p^{n+1},\nabla e_p^n), \end{aligned}$$

(4.32)

where

$$\begin{aligned} |\tau (R_p^{n+1},{\tilde{e}}_u^{n+1})|&\le \tau \Vert R_p^{n+1}\Vert \Vert {\tilde{e}}_u^{n+1}\Vert \le c\tau ^3+\frac{\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{n+1}\Vert ^2. \\ \tau ^2|(R_p^{n+1},\nabla e_p^n)|&\le \tau ^2\Vert R_p^{n+1}\Vert \Vert \nabla e_p^n\Vert \le \tau ^3\Vert \nabla e_p^n\Vert ^2+c\tau ^3 \end{aligned}$$

Last, with $\Vert e_\phi ^{0}\Vert =0,\Vert \nabla e_\phi ^{0}\Vert =0,\Vert e_u^{0}\Vert =0,\Vert e_q^{0}\Vert =0,\Vert \nabla e_p^{0}\Vert =0$, summing (4.23) together for time steps 1 to n, and combining the results above, we derive that for $1\le n\le [T/\tau ]-1$,

$$\begin{aligned}&\frac{\lambda }{2}\Vert e_\phi ^{n+1}\Vert ^2+\frac{\lambda }{2}\Vert \nabla e_\phi ^{n+1}\Vert ^2+\frac{1}{2}\Vert e_u^{n+1}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert e_q^{n+1}\Vert ^2 \nonumber \\&\qquad +\frac{\tau ^2}{2}\Vert \nabla e_p^{n+1}\Vert ^2+ \sum ^n_{k=1}[\frac{\lambda }{2}\Vert \nabla e_\phi ^{k+1}-\nabla e_\phi ^k\Vert ^2+\frac{1}{2}\Vert {\tilde{e}}_u^{k+1}-e_u^k\Vert ^2\nonumber \\&\qquad +\frac{9\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{k+1}\Vert ^2 +\frac{3M\tau }{4}\Vert \nabla e_\omega ^{k+1}\Vert ^2+\frac{3M\tau }{4}\Vert e_\omega ^{k+1}\Vert ^2]\nonumber \\ {}&\quad \le c\tau ^3(n+1)+c\tau \sum ^{n+1}_{k=0}(\frac{\lambda }{2}\Vert e_\phi ^{k}\Vert ^2+\frac{\lambda }{2}\Vert \nabla e_\phi ^{k}\Vert ^2+\frac{1}{2}\Vert e_u^{k}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert e_q^{k}\Vert ^2+\frac{\tau ^2}{2}\Vert \nabla e_p^{k}\Vert ^2)\nonumber \\ {}&\quad \le cT\tau ^2+c\tau \sum ^{n+1}_{k=0}(\frac{\lambda }{2}\Vert e_\phi ^{k}\Vert ^2+\frac{\lambda }{2}\Vert \nabla e_\phi ^{k}\Vert ^2+\frac{1}{2}\Vert e_u^{k}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert e_q^{k}\Vert ^2+\frac{\tau ^2}{2}\Vert \nabla e_p^{k}\Vert ^2). \end{aligned}$$

Since the constants appearing in the above inequalities are independent of $\tau$, we derive from Gronwall’s inequality that there exist some constant c such that

$$\begin{aligned}&\frac{\lambda }{2}\Vert e_\phi ^{n+1}\Vert ^2+\frac{\lambda }{2}\Vert \nabla e_\phi ^{n+1}\Vert ^2+\frac{1}{2}\Vert e_u^{n+1}\Vert ^2+\frac{\lambda \eta ^2}{4}\Vert e_q^{n+1}\Vert ^2\nonumber \\&\qquad +\frac{\tau ^2}{2}\Vert \nabla e_p^{n+1}\Vert ^2+ \sum ^n_{k=1}[\frac{\lambda }{2}\Vert \nabla e_\phi ^{k+1}-\nabla e_\phi ^k\Vert ^2+\frac{1}{2}\Vert {\tilde{e}}_u^{k+1}-e_u^k\Vert ^2\nonumber \\&\qquad +\frac{9\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{k+1}\Vert ^2 +\frac{3M\tau }{4}\Vert \nabla e_\omega ^{k+1}\Vert ^2+\frac{3M\tau }{4}\Vert e_\omega ^{k+1}\Vert ^2]\nonumber \\&\quad \le c\tau ^2,\qquad 1\le n\le [T/\tau ]-1 \end{aligned}$$

According to the inequality $1\le n\le [T/\tau ]-1$

$$\begin{aligned} \Vert e_\phi ^{n+1}\Vert ^2+\Vert \nabla e_\phi ^{n+1}\Vert ^2+\Vert e_u^{n+1}\Vert ^2+\Vert e_q^{n+1}\Vert ^2+\tau ^2\Vert \nabla e_p^{n+1}\Vert ^2\le c\tau ^2, \end{aligned}$$

we get

$$\begin{aligned} \Vert e_{\phi ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert e_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}+\Vert {\tilde{e}}_{q,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}\le \tau , \Vert \nabla e_p^n\Vert _{(L^2(\varOmega )^d)}\lesssim 1. \end{aligned}$$

From $1\le n\le [T/\tau ]-1$

$$\begin{aligned} \sum ^n_{k=1}[\frac{9\nu \tau }{16}\Vert \nabla {\tilde{e}}_u^{k+1}\Vert ^2 +\frac{3M\tau }{4}\Vert \nabla e_\omega ^{k+1}\Vert ^2+\frac{3M\tau }{4}\Vert e_\omega ^{k+1}\Vert ^2]\le c\tau ^2, \end{aligned}$$

we obtain

$$\begin{aligned} \Vert e_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}+\Vert e_{\omega ,\tau }\Vert _{l^2(H^1(\varOmega ))}\le c\tau . \end{aligned}$$

Using

$$\begin{aligned} \sum ^n_{k=1}[\Vert \nabla {\tilde{e}}_u^{k+1}\Vert ^2+\Vert \nabla e_\omega ^{k+1}\Vert ^2+\Vert e_\omega ^{k+1}\Vert ^2]\le c\tau ,\quad 1\le n\le [T/\tau ]-1, \end{aligned}$$

we know

$$\begin{aligned} \max _{1\le k\le n}\Vert \nabla {\tilde{e}}_u^{k+1}\Vert ^2+ \max _{1\le k\le n}\Vert \nabla e_\omega ^{k+1}\Vert ^2+\max _{1\le k\le n}\Vert e_\omega ^{k+1}\Vert ^2\le c\tau , \end{aligned}$$

so

$$\begin{aligned} \Vert e_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}+\Vert e_{\omega ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}\le c\tau ^{\frac{1}{2}}. \end{aligned}$$

where the estimate for $\Vert e_{u,\tau }\Vert _{H^1(\varOmega )^d}$ can be derived from the inequality $\Vert e_u^{n+1}\Vert _1 \le c\Vert {\tilde{e}}_u^{n+1}\Vert _1$. Thus (4.1) holds. $\square$

Lemma 4.3

Under the Assumption, for the stabilized scheme (3.2)-(3.9), we have

$$\begin{aligned} \Vert e_\phi ^{n+1}\Vert _2\le c\tau ^{\frac{1}{2}},\qquad 1\le n\le [T/\tau ]-1 \end{aligned}$$

Proof

Applying $H^2$ theory to (4.11), we have

$$\begin{aligned} \Vert e_\phi ^{n+1}\Vert _2\le c(\Vert R_\omega ^{n+1}\Vert +\Vert e_\omega ^{n+1}\Vert +\Vert e_\phi ^n\Vert +\Vert e_q^{n+1}\Vert )\le c\tau ^{\frac{1}{2}} \end{aligned}$$

$\square$

4.2 Improved Pressure Estimates

Combining with Theorem 4.1, we now establish a sub-optimal error bound for the pressure. we define some notation, for a sequence of function $\{\phi ^k,k=0,1,2,...\}$

$$\begin{aligned} \delta _t\phi ^k=\phi ^k-\phi ^{k-1} \end{aligned}$$

Lemma 4.4

Under the assumption of Assumption, for the stabilized scheme (3.2)–(3.9), we have the following estimate for the pressure

$$\begin{aligned} \Vert e_{p,\tau }\Vert _{l^2(L^2(\varOmega ))}\le c\tau ^{\frac{1}{2}} \end{aligned}$$

Proof

Form Theorem 4.1, we know

$$\begin{aligned} \Vert (\delta _t e_u)_\tau \Vert _{l^\infty (L^2(\varOmega )^d)}\le c\tau ,\qquad \Vert (\delta _t e_u)_\tau \Vert _{l^2(L^2(\varOmega )^d)}\le c\tau ^{\frac{3}{2}}. \end{aligned}$$

Adding (4.14) to (4.13), we get

$$\begin{aligned}&-\nu \varDelta {\tilde{e}}_u^{n+1}+\nabla e_p^{n+1}=h^{n+1}\nonumber \\ {}&\nabla \cdot {\tilde{e}}_u^{n+1}=g^{n+1},\qquad {\tilde{e}}_u^{n+1}|_{\partial \varOmega }=0, \end{aligned}$$

(4.33)

where

$$\begin{aligned} h^{n+1}&={\tilde{h}}^{n+1}-\frac{e_u^{n+1}-e_u^n}{\tau }\nonumber \\ {\tilde{h}}^{n+1}&=R_u^{n+1}+R_p^{n+1}-e_u^n\cdot \nabla \mathbf{u }(t^{n+1})-\mathbf{u }^n\cdot \nabla {\tilde{e}}_u^{n+1}\nonumber \\ {}&\qquad +\lambda (\omega (t^{n+1})\nabla e_\phi ^n+e_\omega ^{n+1}\nabla \phi ^n)\nonumber \\ g^{n+1}&=\tau \varDelta (p^{n+1}-p^n) \end{aligned}$$

Due to

$$\begin{aligned} \Vert g^{n+1}\Vert =\Vert \nabla \cdot {\tilde{e}}_u^{n+1}\Vert \le \Vert \nabla {\tilde{e}}_u^{n+1}\Vert \le c\tau ^{\frac{1}{2}},\qquad \Vert {\tilde{h}}^{n+1}\Vert _{-1}\le c\tau ^{\frac{1}{2}} \end{aligned}$$

Then, we get

$$\begin{aligned} \Vert h^{n+1}\Vert _{-1}&\le \Vert {\tilde{h}}^{n+1}\Vert _{-1}+\Vert \frac{e_u^{n+1}-e_u^n}{\tau }\Vert _{-1}\nonumber \\ \Vert h_\tau \Vert _{l^2(H^{-1}(\varOmega )^d)}&\le \Vert {\tilde{h}}_\tau \Vert _{l^2(H^{-1}(\varOmega )^d)}+\frac{1}{\tau }\Vert (\delta _t e_u)_\tau \Vert _{l^2(L^2(\varOmega )^d)}\le c\tau ^{\frac{1}{2}}. \end{aligned}$$

Applying stand stability result for inhomogeneous Stokes system to (4.33), it turns out

$$\begin{aligned} \Vert {\tilde{e}}_u^{n+1}\Vert _1+\Vert {e}_p^{n+1}\Vert \lesssim \Vert h^{n+1}\Vert _{-1}+\Vert g^{n+1}\Vert \end{aligned}$$

we get

$$\begin{aligned} \Vert e_{p,\tau }\Vert _{l^2(L^2(\varOmega ))}\le c\tau ^{\frac{1}{2}}, \end{aligned}$$

the sub-optimal error estimate for pressure is derived. $\square$

Lemma 4.5

Under the assumption of Assumption, for the scheme (3.2)–(3.9), we have

$$\begin{aligned} \Vert (\delta _t e_u)_\tau \Vert _{l^\infty (L^2(\varOmega )^d)}\le c\tau ^{\frac{3}{2}},\qquad \Vert (\delta _t e_u)_\tau \Vert _{l^2(L^2(\varOmega )^d)}\le c\tau ^2. \end{aligned}$$

Proof

Denote time increment operator as

$$\begin{aligned} \epsilon _u^n=\delta _t e_u^n,\quad {\tilde{\epsilon }}_u^n=\delta _t {\tilde{e}}_u^n,\quad \epsilon _\phi ^n=\delta _t e_\phi ^n,\quad \epsilon _\omega ^n=\delta _t e_\omega ^n,\quad \epsilon _p^n=\delta _t e_p^n,\quad \epsilon _q^n=\delta _t e_q^n, \end{aligned}$$

applying time increment operator $\delta _t$ to (4.10)–(4.14), we have for $n\ge 1$

where

$$\begin{aligned} {\tilde{R}}_\phi ^{n+1}&={\tilde{e}}_u^n\cdot \nabla \delta _t\phi ^n+\delta _t\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{\epsilon }}_u^{n+1}\cdot \nabla \phi ^n+\mathbf{u }(t^{n})\cdot \nabla \epsilon _\phi ^n, \\ {\tilde{R}}_\omega ^{n+1}&=e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\phi ^n\epsilon _q^{n+1}+\delta _t\phi ^n e_q^n, \\ {\tilde{R}}_q^{n+1}&=e_\phi ^n\frac{\delta _t\phi (t^{n+1})-\delta _t\phi (t^n)}{\tau }+\epsilon _\phi ^n\frac{\phi (t^n)-\phi (t^{n-1})}{\tau } \nonumber \\ {}&\qquad +\phi ^n\frac{\epsilon _\phi ^{n+1}-\epsilon _\phi ^n}{\tau }+\delta _t\phi ^n\frac{e_\phi ^n-e_\phi ^{n-1}}{\tau }, \\ {\tilde{R}}_{u,u}^{n+1}&=\delta _t \mathbf{u }^n\cdot \nabla {\tilde{e}}_u^n+e_u^n\cdot \nabla \delta _t\mathbf{u }(t^{n+1})+\mathbf{u }^n\cdot \nabla {\tilde{\epsilon }}_u^{n+1}+\epsilon _u^n\cdot \nabla \mathbf{u }(t^n), \\ {\tilde{R}}_{u,\phi }^{n+1}&=-e_\omega ^n\nabla \delta _t\phi -\delta _t\omega (t^{n+1})\nabla e_\phi ^n-\omega (t^{n})\nabla \epsilon _\phi ^n-\epsilon _\omega ^{n+1}\nabla \phi ^n. \end{aligned}$$

Taking inner product of (4.51) with $\lambda \tau \epsilon _\phi ^{n+1}$, we obtain

$$\begin{aligned}&\frac{\lambda }{2}(\Vert \epsilon _\phi ^{n+1}\Vert ^2-\Vert \epsilon _\phi ^n\Vert ^2+\Vert \epsilon _\phi ^{n+1}-\epsilon _\phi ^n\Vert ^2) +\lambda M\tau (\nabla \epsilon _\phi ^{n+1},\nabla \epsilon _\omega ^{n+1})\nonumber \\&\quad = \lambda \tau (\delta _t R_\phi ^{n+1},\epsilon _\phi ^{n+1})-\lambda \tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\phi ^{n+1}) \end{aligned}$$

(4.39)

Taking inner product of (4.51) with $\tau \epsilon _\omega ^{n+1}$, we obtain

$$\begin{aligned} (\epsilon _\phi ^{n+1}-\epsilon _\phi ^n,\epsilon _\omega ^{n+1})+M\tau \Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2=\tau (\delta _t R_\phi ^{n+1},\epsilon _\omega ^{n+1})-\tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\omega ^{n+1}) \end{aligned}$$

(4.40)

Taking inner product of (4.52) with $\frac{M\tau }{2}\epsilon _\omega ^{n+1}$ and $-(\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)$, we get

$$\begin{aligned}&\frac{M\tau }{2}\Vert \epsilon _\omega ^{n+1}\Vert ^2-\frac{M\lambda \tau }{2}(\nabla \epsilon _\phi ^{n+1},\nabla \epsilon _\omega ^{n+1})- \frac{M\tau }{2}({\tilde{R}}_\omega ^{n+1},\epsilon _\omega ^{n+1})=\frac{M\tau }{2}(\delta _t R_\omega ^{n+1},\epsilon _\omega ^{n+1}) \end{aligned}$$

(4.41)

$$\begin{aligned}&\quad -(\epsilon _\phi ^{n+1}-\epsilon _\phi ^n,\epsilon _\omega ^{n+1})+\frac{\lambda }{2}(\Vert \nabla \epsilon _\phi ^{n+1}\Vert ^2- \Vert \nabla \epsilon _\phi ^n\Vert ^2+\Vert \nabla \epsilon _\phi ^{n+1}-\nabla \epsilon _\phi ^n\Vert ^2)\nonumber \\&\quad + ({\tilde{R}}_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)=-(\delta _t R_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n) \end{aligned}$$

(4.42)

Taking inner product of (4.52) with $\frac{\lambda M\tau }{2}\varDelta \epsilon _\phi ^{n+1}$, we get

$$\begin{aligned}&-\frac{M\lambda \tau }{2}(\nabla \epsilon _\phi ^{n+1},\nabla \epsilon _\omega ^{n+1})+\frac{M\lambda ^2\tau }{2}\Vert \varDelta \epsilon _\phi ^{n+1}\Vert ^2 \nonumber \\&-\frac{M\lambda \tau }{2}({\tilde{R}}_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1})=\frac{M\lambda \tau }{2}(\delta _tR_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1}) \end{aligned}$$

(4.43)

Taking inner product of (4.53) with $\tau \epsilon _q^{n+1}$, we get

$$\begin{aligned} \frac{\eta ^2}{4}(\Vert \epsilon _q^{n+1}\Vert ^2-\Vert \epsilon _q^n\Vert ^2+\Vert \epsilon _q^{n+1}-\epsilon _q^n\Vert ^2)- \tau ({\tilde{R}}_q^{n+1},\epsilon _q^{n+1})=\tau (\delta _t R_q^{n+1},\epsilon _q^{n+1}) \end{aligned}$$

(4.44)

Taking inner product of (4.54) with $\tau {\tilde{\epsilon }}_u^{n+1}$, we get

$$\begin{aligned}&\frac{1}{2}(\Vert {\tilde{\epsilon }}_u^{n+1}-\epsilon _u^n\Vert ^2+\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2-\Vert \epsilon _u^n\Vert ^2) +\nu \tau \Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2+\tau (\nabla \epsilon _p^n,{\tilde{\epsilon }}_u^{n+1})\nonumber \\&\quad =\tau (\delta _t R_u^{n+1},{\tilde{\epsilon }}_u^{n+1})-\tau ({\tilde{R}}_{u,u}^{n+1}+{\tilde{R}}_{u,\phi }^{n+1},{\tilde{\epsilon }}_u^{n+1}) \end{aligned}$$

(4.45)

Then, summing up (4.39)–(4.45), we derive

$$\begin{aligned}&\frac{\lambda }{2}(\Vert \epsilon _\phi ^{n+1}\Vert ^2-\Vert \epsilon _\phi ^n\Vert ^2+\Vert \epsilon _\phi ^{n+1}-\epsilon _\phi ^n\Vert ^2) +M\tau \Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2+\frac{M\tau }{2}\Vert \epsilon _\omega ^{n+1}\Vert ^2\nonumber \\&\qquad +\frac{M\lambda ^2\tau }{2}\Vert \varDelta \epsilon _\phi ^{n+1}\Vert ^2+\frac{\lambda }{2}(\Vert \nabla \epsilon _\phi ^{n+1}\Vert ^2- \Vert \nabla \epsilon _\phi ^n\Vert ^2+\Vert \nabla \epsilon _\phi ^{n+1}-\nabla \epsilon _\phi ^n\Vert ^2)\nonumber \\ {}&\qquad +\frac{\eta ^2}{4}(\Vert \epsilon _q^{n+1}\Vert ^2-\Vert \epsilon _q^n\Vert ^2+\Vert \epsilon _q^{n+1}-\epsilon _q^n\Vert ^2)+\nu \tau \Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2\nonumber \\ {}&\qquad + \frac{1}{2}(\Vert {\tilde{\epsilon }}_u^{n+1}-\epsilon _u^n\Vert ^2+\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2-\Vert \epsilon _u^n\Vert ^2) +\tau (\nabla \epsilon _p^n,{\tilde{\epsilon }}_u^{n+1})\nonumber \\ {}&\quad =\lambda \tau (\delta _t R_\phi ^{n+1},\epsilon _\phi ^{n+1})-\lambda \tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\phi ^{n+1}) +\tau (\delta _t R_\phi ^{n+1},\epsilon _\omega ^{n+1})-\tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\omega ^{n+1})\nonumber \\ {}&\qquad +\frac{M\tau }{2}({\tilde{R}}_\omega ^{n+1},\epsilon _\omega ^{n+1})+\frac{M\tau }{2}(\delta _t R_\omega ^{n+1},\epsilon _\omega ^{n+1}) -(\delta _t R_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)\nonumber \\ {}&\qquad -({\tilde{R}}_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n) +\tau ({\tilde{R}}_q^{n+1},\epsilon _q^{n+1})+\tau (\delta _t R_q^{n+1},\epsilon _q^{n+1})\nonumber \\ {}&\qquad +\tau (\delta _t R_u^{n+1},{\tilde{\epsilon }}_u^{n+1})-\tau ({\tilde{R}}_{u,u}^{n+1}+{\tilde{R}}_{u,\phi }^{n+1},{\tilde{\epsilon }}_u^{n+1}) +\frac{M\lambda \tau }{2}({\tilde{R}}_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1}) \nonumber \\ {}&\qquad +\frac{M\lambda \tau }{2}(\delta _tR_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1}) =\sum _{i=1}^{14}B_i \end{aligned}$$

(4.46)

Together with the assumptions on the exact solution, we have

$$\begin{aligned}&\Vert \delta _t\phi ^n\Vert _1\le \Vert \delta _t\phi (t^n)\Vert _1+\Vert \delta _t e_\phi ^n\Vert _1\lesssim \tau \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \nonumber \\&\Vert \phi ^n\Vert _2\le \Vert \phi (t^n)\Vert _2+\Vert e_\phi ^n\Vert _2\le c\nonumber \\&\Vert \delta _t \mathbf{u }^n\Vert _1\le \Vert \delta _t \mathbf{u }(t^n)\Vert _1+\Vert \epsilon _u^n\Vert _1\lesssim \tau +\Vert {\tilde{\epsilon }}_u^n\Vert _1\nonumber \\&\Vert \delta _t\phi ^n\Vert _{L^\infty }\le \Vert \delta _t\phi (t^n)\Vert _{L^\infty }+\Vert \epsilon _\phi ^n\Vert _{H^2}, \end{aligned}$$

where these conclusions will be used in the behind of theoretical analysis. We now estimate the right-hand terms in (4.46) as follows:

$$\begin{aligned} B_1&\le |\lambda \tau (\delta _t R_\phi ^{n+1},\epsilon _\phi ^{n+1})|\le c\tau \Vert \delta _t R_\phi ^{n+1}\Vert \Vert \epsilon _\phi ^{n+1}\Vert \le c\tau \Vert \epsilon _\phi ^{n+1}\Vert ^2+c\tau ^5,\qquad \\ B_2&\le |\lambda \tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\phi ^{n+1})|\nonumber \\&=|\lambda \tau ({\tilde{e}}_u^n\cdot \nabla \delta _t\phi ^n+\delta _t\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{\epsilon }}_u^{n+1}\cdot \nabla \phi ^n+\mathbf{u }(t^{n})\cdot \nabla \epsilon _\phi ^n,\epsilon _\phi ^{n+1})|\nonumber \\ {}&\le c\tau [\Vert \nabla \delta _t\phi ^n\Vert \Vert {\tilde{e}}_u^n\Vert _1\Vert \epsilon _\phi ^{n+1}\Vert _1+\Vert \delta _t\mathbf{u }(t^{n+1})\Vert _1\Vert \nabla e_\phi ^n\Vert \Vert \epsilon _\phi ^{n+1}\Vert _1\nonumber \\&\quad +\Vert \nabla \phi ^n\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1\Vert \epsilon _\phi ^{n+1}\Vert _1+ \Vert \mathbf{u }(t^{n})\Vert _2\Vert \nabla \epsilon _\phi ^n\Vert \Vert \epsilon _\phi ^{n+1}\Vert ]\nonumber \\ {}&\le c\tau (\tau ^2\Vert {\tilde{e}}_u^n\Vert _1^2+\tau ^4+\Vert \epsilon _\phi ^{n+1}\Vert _1^2+\Vert \epsilon _\phi ^{n}\Vert _1^2)+\frac{\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2, \end{aligned}$$

$$\begin{aligned}B_3\le |\tau (\delta _t R_\phi ^{n+1},\epsilon _\omega ^{n+1})|&\le c\tau \Vert \delta _t R_\phi ^{n+1}\Vert \Vert \epsilon _\omega ^{n+1}\Vert \le \frac{M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2+c\tau ^5.\qquad \qquad \end{aligned}$$

$$\begin{aligned}B_4&\le |\tau ({\tilde{R}}_\phi ^{n+1},\epsilon _\omega ^{n+1})|\nonumber \\ {}&=|\tau ({\tilde{e}}_u^n\cdot \nabla \delta _t\phi ^n+\delta _t\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{\epsilon }}_u^{n+1}\cdot \nabla \phi ^n+\mathbf{u }(t^{n})\cdot \nabla \epsilon _\phi ^n,\epsilon _\omega ^{n+1})|\nonumber \\ {}&\le \tau [\Vert \nabla \delta _t\phi ^n\Vert \Vert {\tilde{e}}_u^n\Vert _1\Vert \epsilon _\omega ^{n+1}\Vert _1+\Vert \delta _t\mathbf{u }(t^{n+1})\Vert _1\Vert \nabla e_\phi ^n\Vert \Vert \epsilon _\omega ^{n+1}\Vert _1\nonumber \\ {}&\qquad +\Vert \nabla \phi ^n\Vert _1\Vert {\tilde{\epsilon }}_u^{n+1}\Vert \Vert \epsilon _\omega ^{n+1}\Vert _1+\Vert \mathbf{u }(t^{n})\Vert _2\Vert \nabla \epsilon _\phi ^n\Vert \Vert \epsilon _\omega ^{n+1}\Vert ]\nonumber \\ {}&\le c\tau (\tau ^2\Vert {\tilde{e}}_u^n\Vert _1^2+\tau ^4+\Vert \epsilon _\phi ^n\Vert _1^2+\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2) +\frac{M\tau }{16}\Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2+\frac{M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2 \\ B_5&\le |\frac{M\tau }{2}({\tilde{R}}_\omega ^{n+1},\epsilon _\omega ^{n+1})|\nonumber \\&=|M\tau (e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\phi ^n\epsilon _q^{n+1}+\delta _t\phi ^n e_q^n,\epsilon _\omega ^{n+1})|\nonumber \\&\le c\tau \Vert \delta _t q(t^{n+1})\Vert _{L^\infty }\Vert e_\phi ^n\Vert \Vert \epsilon _\omega ^{n+1}\Vert +c\tau \Vert q(t^{n})\Vert _{L^\infty }\Vert \epsilon _\phi ^n\Vert \Vert \epsilon _\omega ^{n+1}\Vert \nonumber \\&\quad +c\tau \Vert \phi ^n\Vert _{L^\infty }\Vert \epsilon _q^{n+1}\Vert \Vert \epsilon _\omega ^{n+1}\Vert +c\tau \Vert \delta _t \phi ^n\Vert _1\Vert e_q^n\Vert _1\Vert \epsilon _\omega ^{n+1}\Vert \nonumber \\&\le \frac{M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2+c\tau ^5+c\tau \Vert \epsilon _\phi ^n\Vert ^2+c\tau \Vert \epsilon _q^{n+1}\Vert ^2, \end{aligned}$$

where we have used the following inequality:

In fact, (3.4) can be rewritten as

$$\begin{aligned} q^{n+1}-\frac{(\phi ^{n+1})^2-1}{\eta ^2}=q^{n}-\frac{(\phi ^{n})^2-1}{\eta ^2}-\frac{(\phi ^{n+1}-\phi ^n)^2}{\eta ^2} \end{aligned}$$

Noting that $(\phi ^{n+1}-\phi ^n)^2\sim O(\tau ^2)$, therefore, $q^{n+1}$ is formally a second order approximation to $\frac{(\phi ^{n+1})^2-1}{\eta ^2}$.

$$\begin{aligned} \Vert e_q^n\Vert _1&=\Vert e_q^n\Vert +\Vert \nabla e_q^n\Vert \le c\tau +\Vert \nabla e_q^n\Vert \nonumber \\ \Vert \nabla e_q^n\Vert&=\Vert \nabla q(t^n)-\nabla q^n\Vert + O(\tau ^2)=\Vert \frac{2}{\eta ^2}(\phi (t^n)\nabla \phi (t^n)-\phi ^n\nabla \phi ^n)\Vert + O(\tau ^2)\nonumber \\&=\Vert \frac{2}{\eta ^2}(e_\phi ^n\nabla \phi (t^n)+\phi ^n\nabla e_\phi ^n)\Vert + O(\tau ^2) \le c\Vert e_\phi ^n\Vert \nonumber \\&\quad +\Vert \phi ^n\Vert _{L^\infty }\Vert \nabla e_\phi ^n\Vert + O(\tau ^2)\le c\tau \nonumber \\ \Vert e_q^n\Vert _1&=\Vert e_q^n\Vert +\Vert \nabla e_q^n\Vert \le c\tau \end{aligned}$$

For the remaining terms, we have

$$\begin{aligned} B_6&\le |\frac{M\tau }{2}(\delta _t R_\omega ^{n+1},\epsilon _\omega ^{n+1})|\le c\tau \Vert \delta _t R_\omega ^{n+1}\Vert \Vert \epsilon _\omega ^{n+1}\Vert \le c\tau ^5+\frac{M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2\qquad \nonumber \\ B_7&\le |(\delta _t R_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)|\nonumber \\ {}&=|\tau (\delta _t R_\omega ^{n+1},M\varDelta \epsilon _\omega ^{n+1}+\delta _t R_\phi ^{n+1}-{\tilde{R}}_\phi ^{n+1})|\nonumber \\ {}&\le c\tau \Vert \nabla \delta _t R_\omega ^{n+1}\Vert \Vert \nabla \epsilon _\omega ^{n+1}\Vert +c\tau \Vert \nabla \delta _t R_\omega ^{n+1}\Vert \Vert \nabla \delta _t R_\phi ^{n+1}\Vert +\tau (\delta _t R_\omega ^{n+1},{\tilde{R}}_\phi ^{n+1})\quad \,\nonumber \\ {}&\le \frac{M\tau }{16}\Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2+c\tau ^5+\tau (\delta _t R_\omega ^{n+1},{\tilde{R}}_\phi ^{n+1}) \end{aligned}$$

(4.47)

Next, we estimate the last term $\tau (\delta _t R_\omega ^{n+1},{\tilde{R}}_\phi ^{n+1})$ of (4.47)

$$\begin{aligned}&\tau |(\delta _t R_\omega ^{n+1},{\tilde{R}}_\phi ^{n+1})|\nonumber \\ {}&\quad =\tau |(\delta _t R_\omega ^{n+1},{\tilde{e}}_u^n\cdot \nabla \delta _t\phi ^n+\delta _t\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{\epsilon }}_u^{n+1}\cdot \nabla \phi ^n+\mathbf{u }(t^{n})\cdot \nabla \epsilon _\phi ^n)|\nonumber \\ {}&\quad \le \tau \Vert \delta _t R_\omega ^{n+1}\Vert _1\Vert {\tilde{e}}_u^n\Vert \Vert \delta _t\phi ^n\Vert _{L^\infty }+\tau \Vert \delta _t R_\omega ^{n+1}\Vert \Vert \delta _t\mathbf{u }(t^{n+1})\Vert _{L^\infty }\Vert \nabla e_\phi ^n\Vert \nonumber \\ {}&\qquad +\tau \Vert \delta _t R_\omega ^{n+1}\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1\Vert \nabla \phi ^n\Vert _1 +\tau \Vert \delta _t R_\omega ^{n+1}\Vert \Vert \mathbf{u }(t^{n})\Vert _{L^\infty }\Vert \nabla \epsilon _\phi ^n\Vert \nonumber \\ {}&\quad \le \frac{\lambda ^2M\tau }{32}\Vert \triangle \epsilon _\phi ^n\Vert ^2+\tau ^5+\frac{\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2 +c\tau \Vert \nabla \epsilon _\phi ^n\Vert ^2 \end{aligned}$$

$$\begin{aligned} B_8&=-({\tilde{R}}_\omega ^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n) \nonumber \\&=-(e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\phi ^n\epsilon _q^{n+1}+\delta _t\phi ^n e_q^n,\epsilon _\phi ^{n+1}-\epsilon _\phi ^n), \end{aligned}$$

(4.48)

Where $(\phi ^n\epsilon _q^{n+1},\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)$ will cancel out with (4.49). Therefore, we only need to analyze the remaining three terms of (4.48)as follows:

$$\begin{aligned}&-(e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\delta _t\phi ^n e_q^n,\epsilon _\phi ^{n+1}-\epsilon _\phi ^n)\nonumber \\ {}&\quad =-\tau (e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\delta _t\phi ^n e_q^n,M\varDelta \epsilon _w^{n+1}+\delta _t R_\phi ^{n+1}-{\tilde{R}}_\phi ^{n+1}); \end{aligned}$$

then, we have

$$\begin{aligned}&|\tau (e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\delta _t\phi ^n e_q^n,M\varDelta \epsilon _w^{n+1})|\nonumber \\ {}&\quad =|M\tau (\nabla e_\phi ^n\delta _t q(t^{n+1})+e_\phi ^n\nabla \delta _t q(t^{n+1})+ \nabla \epsilon _\phi ^n q(t^n)\nonumber \\&\qquad +\epsilon _\phi ^n \nabla q(t^n) +\nabla \delta _t\phi ^n e_q^n+\delta _t\phi ^n \nabla e_q^n,\nabla \epsilon _w^{n+1})|\nonumber \\ {}&\quad \le c\tau \Vert \nabla e_\phi ^n\Vert \Vert \delta _t q(t^{n+1})\Vert _{L^\infty }\Vert \nabla \epsilon _w^{n+1}\Vert +c\tau \Vert e_\phi ^n\Vert \Vert \nabla \delta _t q(t^{n+1})\Vert _{L^\infty }\Vert \nabla \epsilon _w^{n+1}\Vert \nonumber \\ {}&\qquad +c\tau \Vert \nabla \epsilon _\phi ^n\Vert \Vert q(t^{n})\Vert _{L^\infty }\Vert \nabla \epsilon _w^{n+1}\Vert +c\tau \Vert \epsilon _\phi ^n\Vert \Vert \nabla q(t^{n})\Vert _{L^\infty }\Vert \nabla \epsilon _w^{n+1}\Vert \nonumber \\ {}&\qquad +c\tau \Vert \nabla \delta _t\phi ^n\Vert _1\Vert e_q^n\Vert _1\Vert \nabla \epsilon _w^{n+1}\Vert +c\tau \Vert \delta _t\phi ^n\Vert _{L^\infty }\Vert \nabla e_q^n\Vert \Vert \nabla \epsilon _w^{n+1}\Vert \nonumber \\ {}&\quad \le \frac{M\tau }{16}\Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2+c\tau ^5+\frac{\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{n}\Vert ^2+c\tau \Vert \nabla \epsilon _\phi ^n\Vert ^2 +c\tau \Vert \epsilon _\phi ^n\Vert ^2 \nonumber \\&|\tau (e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\delta _t\phi ^n e_q^n,\delta _t R_\phi ^{n+1})|\nonumber \\ {}&\quad \le c\tau \Vert e_\phi ^n\Vert _1\Vert \delta _t q(t^{n+1})\Vert _1\Vert \delta _t R_\phi ^{n+1}\Vert +c\tau \Vert \epsilon _\phi ^n\Vert \Vert q(t^{n})\Vert _{L^\infty }\Vert \delta _t R_\phi ^{n+1}\Vert \nonumber \\ {}&\qquad +c\tau \Vert \delta _t\phi ^n\Vert _1\Vert e_q^n\Vert _1\Vert \delta _t R_\phi ^{n+1}\Vert \nonumber \\ {}&\quad \le c\tau ^5+c\tau \Vert \epsilon _\phi ^n\Vert ^2 \nonumber \\&|\tau (e_\phi ^n\delta _t q(t^{n+1}),{\tilde{R}}_\phi ^{n+1})|\nonumber \\ {}&\quad =|\tau (e_\phi ^n\delta _t q(t^{n+1}),{\tilde{e}}_u^n\cdot \nabla \delta _t\phi ^n+\delta _t\mathbf{u }(t^{n+1})\cdot \nabla e_\phi ^n+{\tilde{\epsilon }}_u^{n+1}\cdot \nabla \phi ^n+\mathbf{u }(t^{n})\cdot \nabla \epsilon _\phi ^n)|\nonumber \\ {}&\quad \le \tau \Vert \delta _t q(t^{n+1})\Vert _{L^\infty }(\Vert e_\phi ^n\Vert _1\Vert {\tilde{e}}_u^n\Vert \Vert \delta _t\phi ^n\Vert _{L^\infty } +\Vert e_\phi ^n\Vert \Vert \delta _t\mathbf{u }(t^{n+1})\Vert _{L^\infty }\Vert \nabla e_\phi ^n\Vert )\nonumber \\ {}&\qquad +\tau \Vert e_\phi ^n\Vert _1\Vert \delta _t q(t^{n+1})\Vert _{L^\infty }\Vert {\tilde{\epsilon }}_u^{n+1}\Vert \Vert \nabla \phi ^n\Vert _1 +\tau \Vert e_\phi ^n\Vert _1\Vert \delta _t q(t^{n+1})\Vert _1\Vert \mathbf{u }(t^{n})\Vert _{L^\infty }\Vert \nabla \epsilon _\phi ^n\Vert \nonumber \\ {}&\quad \le c\tau ^5+\frac{\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{n}\Vert ^2+c\tau \Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2 +c\tau \Vert \epsilon _\phi ^n\Vert _1^2. \nonumber \\&B_9=\tau ({\tilde{R}}_q^{n+1},\epsilon _q^{n+1})\nonumber \\ {}&\quad =\tau (e_\phi ^n\frac{\delta _t\phi (t^{n+1})-\delta _t\phi (t^n)}{\tau }+\epsilon _\phi ^n\frac{\phi (t^n)-\phi (t^{n-1})}{\tau } \nonumber \\ {}&\qquad +\phi ^n\frac{\epsilon _\phi ^{n+1}-\epsilon _\phi ^n}{\tau }+\delta _t\phi ^n\frac{e_\phi ^n-e_\phi ^{n-1}}{\tau },\epsilon _q^{n+1})\nonumber \\ {}&\quad =(e_\phi ^n(\delta _t\phi (t^{n+1})-\delta _t\phi (t^n))+\epsilon _\phi ^n(\phi (t^n)-\phi (t^{n-1}))\nonumber \\ {}&\qquad +\phi ^n(\epsilon _\phi ^{n+1}-\epsilon _\phi ^n) +\delta _t\phi ^n(e_\phi ^n-e_\phi ^{n-1}),\epsilon _q^{n+1}), \end{aligned}$$

(4.49)

where $(\phi ^n(\epsilon _\phi ^{n+1}-\epsilon _\phi ^n),\epsilon _q^{n+1})$ can be cancelled out with (4.48). Therefore, we only need to analyze the remaining three terms of (4.49):

$$\begin{aligned} (e_\phi ^n(\delta _t\phi (t^{n+1})-\delta _t\phi (t^n)),\epsilon _q^{n+1})&\le c\tau ^2\Vert e_\phi ^n\Vert \Vert \epsilon _q^{n+1}\Vert \le c\tau \Vert \epsilon _q^{n+1}\Vert ^2+c\tau ^5. \\ (\epsilon _\phi ^n(\phi (t^{n})-\phi (t^{n-1})),\epsilon _q^{n+1})&\le c\tau \Vert \epsilon _\phi ^n\Vert \Vert \epsilon _q^{n+1}\Vert \le c\tau \Vert \epsilon _q^{n+1}\Vert ^2+c\tau \Vert \epsilon _\phi ^n\Vert ^2. \nonumber \\ (\delta _t\phi ^n(e_\phi ^n-e_\phi ^{n-1}),\epsilon _q^{n+1})&=(\delta _t\phi ^n\epsilon _\phi ^n,\epsilon _q^{n+1}) \le \Vert \delta _t\phi ^n\Vert _1\Vert \epsilon _\phi ^n\Vert _1\Vert \epsilon _q^{n+1}\Vert \nonumber \\ {}&\le c\tau \Vert \epsilon _\phi ^n\Vert _1\Vert \epsilon _q^{n+1}\Vert \le c\tau \Vert \epsilon _q^{n+1}\Vert ^2+c\tau \Vert \epsilon _\phi ^n\Vert _1^2 \nonumber \\ B_{10}=\tau (\delta _t R_q^{n+1},\epsilon _q^{n+1})&\le c\tau \Vert \delta _t R_q^{n+1}\Vert \Vert \epsilon _q^{n+1}\Vert \le c\tau \Vert \epsilon _q^{n+1}\Vert ^2+c\tau ^5 \nonumber \\ B_{11}=\tau (\delta _t R_u^{n+1},{\tilde{\epsilon }}_u^{n+1})&\le c\tau \Vert \delta _t R_u^{n+1}\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert \le c\tau ^5+\frac{\mu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2 \end{aligned}$$

$$\begin{aligned} B_{12}&\le |-\tau ({\tilde{R}}_{u,u}^{n+1}+{\tilde{R}}_{u,\phi }^{n+1},{\tilde{\epsilon }}_u^{n+1})|\nonumber \\ {}&\le c\tau (\Vert \delta _t \mathbf{u }^n\Vert _1\Vert \nabla {\tilde{e}}_u^n\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1+\Vert e_u^n\Vert _1\Vert \nabla \delta _t \mathbf{u }(t^{n+1})\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1\nonumber \\ {}&\quad +c\tau (\Vert e_\omega ^n\Vert _1\Vert \delta _t\phi ^n\Vert _1\Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1+\Vert \omega (t^n)\Vert _{L^3}\Vert \nabla \epsilon _\phi ^n\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1 +\Vert \epsilon _u^n\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1)\nonumber \\ {}&\quad +\Vert \delta _t\omega (t^{n+1})\Vert _1\Vert \nabla e_\phi ^n\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert _1 +\Vert \epsilon _\omega ^{n+1}\Vert \Vert \phi ^n\Vert _{W^{1,2d}}\Vert {\tilde{\epsilon }}_u^{n+1}\Vert _{L^\frac{2d}{d-1}})\nonumber \\ {}&\le c\tau (\tau ^2\Vert {\tilde{e}}_u^{n+1}\Vert _1^2+\tau ^2\Vert {\tilde{e}}_u^{n}\Vert _1^2+\tau ^2\Vert e_u^{n}\Vert _1^2+\Vert \epsilon _u^{n}\Vert ^2 +\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2+\Vert \nabla \epsilon _\phi ^n\Vert ^2\nonumber \\ {}&\quad +\tau ^2\Vert e_\omega ^n\Vert _1^2+\tau ^4) +\frac{M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n}\Vert ^2 +\frac{\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2 \nonumber \\ B_{13}&\le |\frac{M\lambda \tau }{2}({\tilde{R}}_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1})|\nonumber \\ {}&\le |\frac{M\lambda \tau }{2}(e_\phi ^n\delta _t q(t^{n+1})+\epsilon _\phi ^n q(t^n)+\phi ^n\epsilon _q^{n+1}+\delta _t\phi ^n e_q^n,\varDelta \epsilon _\phi ^{n+1})|\nonumber \\ {}&\le c\tau \Vert e_\phi ^n\Vert _1\Vert \delta _t q(t^{n+1})\Vert _1\Vert \varDelta \epsilon _\phi ^{n+1}\Vert +c\tau \Vert \epsilon _\phi ^n\Vert \Vert q(t^n)\Vert _{L^\infty }\Vert \varDelta \epsilon _\phi ^{n+1}\Vert \nonumber \\ {}&\quad +c\tau \Vert \phi ^n\Vert _{L^\infty }\Vert \epsilon _q^{n+1}\Vert \Vert \varDelta \epsilon _\phi ^{n+1}\Vert +c\tau \Vert \delta _t\phi ^n\Vert _1\Vert e_q^n\Vert _1\Vert \varDelta \epsilon _\phi ^{n+1}\Vert \nonumber \\ {}&\le \frac{\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{n+1}\Vert ^2+c\tau ^5+c\tau \Vert \epsilon _\phi ^n\Vert ^2+c\tau \Vert \epsilon _q^{n+1}\Vert ^2,\qquad \nonumber \\ B_{14}&\le |\frac{M\lambda \tau }{2}(\delta _tR_\omega ^{n+1},\varDelta \epsilon _\phi ^{n+1}| \le \frac{\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{n+1}\Vert ^2+c\tau ^5.\qquad \qquad \end{aligned}$$

To control $\tau (\nabla \epsilon _p^n,{\tilde{\epsilon }}_u^{n+1})$ in (4.46), we have the following result similar to (4.32):

$$\begin{aligned} \tau (\nabla \epsilon _p^n,{\tilde{\epsilon }}_u^{n+1})&=\frac{\tau ^2}{2}(\Vert \nabla \epsilon _p^{n+1}\Vert ^2-\Vert \nabla \epsilon _p^n\Vert ^2)+\frac{1}{2}(\Vert \epsilon _u^{n+1}\Vert ^2-\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2) -\frac{\tau ^2}{2}\Vert \delta _t R_p^{n+1}\Vert ^2\nonumber \\&\quad -\tau (\delta _tR_p^{n+1},{\tilde{\epsilon }}_u^{n+1})-\tau ^2(\delta _tR_p^{n+1},\nabla \epsilon _p^n). \end{aligned}$$

$$\begin{aligned} |\tau (\delta _tR_p^{n+1},{\tilde{\epsilon }}_u^{n+1})|&\le \tau \Vert \delta _tR_p^{n+1}\Vert \Vert {\tilde{\epsilon }}_u^{n+1}\Vert \le \frac{\mu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2+c\tau ^5 \\ |\tau ^2(\delta _tR_p^{n+1},\nabla \epsilon _p^n)|&\le \tau ^2\Vert \delta _tR_p^{n+1}\Vert \Vert \nabla \epsilon _p^n\Vert \le \tau ^3\Vert \nabla \epsilon _p^n\Vert ^2+c\tau ^5. \end{aligned}$$

Inserting the above estimates into (4.46), we obtain

$$\begin{aligned}&\frac{\lambda }{2}(\Vert \epsilon _\phi ^{n+1}\Vert ^2-\Vert \epsilon _\phi ^n\Vert ^2+\Vert \epsilon _\phi ^{n+1}-\epsilon _\phi ^n\Vert ^2) +M\tau \Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2+\frac{M\tau }{2}\Vert \epsilon _\omega ^{n+1}\Vert ^2 \nonumber \\&\qquad +\frac{7\lambda ^2 M\tau }{16}\Vert \varDelta \epsilon _\phi ^{n+1}\Vert ^2+\frac{\lambda }{2}(\Vert \nabla \epsilon _\phi ^{n+1}\Vert ^2- \Vert \nabla \epsilon _\phi ^n\Vert ^2+\Vert \nabla \epsilon _\phi ^{n+1}-\nabla \epsilon _\phi ^n\Vert ^2)\nonumber \\ {}&\qquad +\frac{\eta ^2}{4}(\Vert \epsilon _q^{n+1}\Vert ^2-\Vert \epsilon _q^n\Vert ^2+\Vert \epsilon _q^{n+1}-\epsilon _q^n\Vert ^2)+\frac{\tau ^2}{2}(\Vert \nabla \epsilon _p^{n+1}\Vert ^2-\Vert \nabla \epsilon _p^n\Vert ^2)\nonumber \\ {}&\qquad + \frac{1}{2}(\Vert {\tilde{\epsilon }}_u^{n+1}-\epsilon _u^n\Vert ^2+\Vert \epsilon _u^{n+1}\Vert ^2-\Vert \epsilon _u^n\Vert ^2) +\upsilon \tau \Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2\nonumber \\ {}&\quad \le c\tau (\Vert \epsilon _\phi ^{n+1}\Vert ^2+\tau ^2\Vert \nabla \epsilon _p^n\Vert ^2+\Vert \epsilon _\phi ^n\Vert ^2+\Vert \nabla \epsilon _\phi ^{n+1}\Vert ^2+\Vert \epsilon _u^n\Vert ^2+\Vert \epsilon _q^{n+1}\Vert ^2+\Vert {\tilde{\epsilon }}_u^{n+1}\Vert ^2)\nonumber \\ {}&\qquad +\frac{5\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n+1}\Vert ^2+\frac{\nu \tau }{16}\Vert \nabla {\tilde{\epsilon }}_u^{n}\Vert ^2+\frac{3\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{n}\Vert ^2+\frac{3M\tau }{16}\Vert \nabla \epsilon _\omega ^{n+1}\Vert ^2\nonumber \\ {}&\qquad +\frac{5M\tau }{16}\Vert \epsilon _\omega ^{n+1}\Vert ^2+c\tau ^3(\tau ^2+\Vert {\tilde{e}}_u^n\Vert _1^2+\Vert e_\omega ^n\Vert _1^2). \end{aligned}$$

(4.50)

Together with

$$\begin{aligned} \Vert \nabla {\tilde{\epsilon }}_u^1\Vert ^2=0,\Vert \epsilon _u^1\Vert ^2=0,\Vert \epsilon _\phi ^1\Vert ^2=0, \Vert \nabla \epsilon _p^1\Vert ^2=0,\Vert \nabla \epsilon _\phi ^1\Vert ^2=0,\Vert \epsilon _q^{1}\Vert ^2=0; \end{aligned}$$

Summing up (4.50) from 0 to n, we obtain

$$\begin{aligned}&\frac{\lambda }{2}\Vert \epsilon _\phi ^{n+1}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \epsilon _\phi ^{n+1}\Vert ^2+ \frac{\eta ^2}{4}\Vert \epsilon _q^{n+1}\Vert ^2+\frac{1}{2}\Vert \epsilon _u^{n+1}\Vert ^2+\frac{\tau ^2}{2}\Vert \nabla \epsilon _p^{n+1}\Vert ^2\nonumber \\&\qquad +\frac{1}{8}\sum _{k=2}^{n+1}(\lambda \Vert \epsilon _\phi ^{k}-\epsilon _\phi ^{k-1}\Vert ^2 +\Vert \nabla \epsilon _\phi ^{k}-\nabla \epsilon _\phi ^{k-1}\Vert ^2+\eta ^2\Vert \epsilon _q^{k}-\epsilon _q^{k-1}\Vert ^2+ \Vert {\tilde{\epsilon }}_u^{k}-\epsilon _u^{k-1}\Vert ^2)\nonumber \\ {}&\qquad +\sum _{k=2}^{n+1}(\frac{13M\tau }{16}\Vert \nabla \epsilon _\omega ^{k}\Vert ^2+\frac{3M\tau }{16}\Vert \epsilon _\omega ^{k}\Vert ^2 +\frac{5\mu \tau }{8}\Vert \nabla {\tilde{\epsilon }}_u^{k}\Vert ^2+\frac{11\lambda ^2 M\tau }{32}\Vert \varDelta \epsilon _\phi ^{k}\Vert ^2)\nonumber \\ {}&\quad \le c\tau ^3\sum _{k=1}^{n+1}(\tau ^2+\Vert {\tilde{e}}_u^k\Vert _1^2+\Vert e_\omega ^k\Vert _1^2)+c\tau \sum _{k=1}^{n+1}(\Vert \epsilon _\phi ^k\Vert ^2+\Vert \nabla \epsilon _\phi ^k\Vert ^2+\Vert \epsilon _q^k\Vert ^2 +\Vert \epsilon _u^k\Vert ^2) \end{aligned}$$

Then, applying Gronwall inequality, and using Theorem 4.1, we derive the desired result. $\square$

Theorem 4.6

Under the Assumption, there exists a constant $\tau _0>0$ such that when $\tau <\tau _0$ the solution $(\mathbf{u }^n,p^n,\phi ^n,\omega ^n)(0\le n\le \frac{T}{\tau })$ of scheme (3.2)–(3.9) satisfies the following error be cancelled out with the following estimates:

$$\begin{aligned}&\Vert e_{\phi ,\tau }\Vert _{l^\infty (H^1(\varOmega ))}+\Vert e_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^2(H^1(\varOmega )^d)}\nonumber \\ {}&\quad +\Vert e_{\omega ,\tau }\Vert _{l^2(H^1(\varOmega ))}+\Vert e_{p,\tau }\Vert _{l^2(L^2(\varOmega ))}\le c\tau ,\nonumber \\&\Vert e_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}+\Vert e_{\omega ,\tau }\Vert _{l^\infty (H^1(\varOmega ))} +\Vert {\tilde{e}}_{u,\tau }\Vert _{l^\infty (H^1(\varOmega )^d)}+\Vert e_{p,\tau }\Vert _{l^\infty (L^2(\varOmega ))}\le c\tau ^{\frac{1}{2}},\nonumber \\&\Vert e_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}+\Vert {\tilde{e}}_{u,\tau }\Vert _{l^\infty (L^2(\varOmega )^d)}\le c\tau , \end{aligned}$$

Proof

$$\begin{aligned} \Vert (\delta _t e_u)_\tau \Vert _{l^\infty (L^2(\varOmega )^d)}\le c\tau ^{\frac{3}{2}},\qquad \Vert (\delta _t e_u)_\tau \Vert _{l^2(L^2(\varOmega )^d)}\le c\tau ^2. \end{aligned}$$

Then,we get

$$\begin{aligned} \Vert h^{n+1}\Vert _{-1}&\le \Vert {\tilde{h}}^{n+1}\Vert _{-1}+\Vert \frac{e_u^{n+1}-e_u^n}{\tau }\Vert _{-1} \nonumber \\ \Vert h_\tau \Vert _{l^2(H^{-1}(\varOmega )^d)}&\le \Vert {\tilde{h}}_\tau \Vert _{l^2(H^{-1}(\varOmega )^d)}+\frac{1}{\tau }\Vert (\delta _t e_u)_\tau \Vert _{l^2(L^2(\varOmega )^d)}\le c\tau . \end{aligned}$$

Applying stand stability result for inhomogeneous Stokes system, it turns out that

$$\begin{aligned} \Vert {\tilde{e}}_u^{n+1}\Vert _1+\Vert {e}_p^{n+1}\Vert \lesssim \Vert h^{n+1}\Vert _{-1}+\Vert g^{n+1}\Vert , and \end{aligned}$$

we get

$$\begin{aligned} \Vert e_{p,\tau }\Vert _{l^2(L^2(\varOmega ))}\le c\tau . \end{aligned}$$

The proof is completed. $\square$

5 Numerical Results

In this section, we will present some numerical experiments to verify the efficiency of our method. In the following simulation, for the phase field $\phi$, chemical potential $\omega$, variable q, and the pressure p, we take the P1 finite element space(continuous piecewise linear), for the fluid velocity $\mathbf{u }$, we take the P1b finite element space(piecewise linear continuous function plus bubble function). All experiments are implemented in Freefem++.

5.1 Convergence Tests

In this section,convergence tests are done using our scheme. We use $P1b-P1$ finite element spaces, and we choose the domain $[0,1]^2$ and fix $\eta =0.1,M=0.01,\lambda =0.001,\nu =0.1,T=1$. We set the initial condition as

$$\begin{aligned} \phi _0&=0.24\cos (2\pi x)\cos (2\pi y)+0.4\cos (\pi x)\cos (3\pi y)\\ \mathbf{u }_0&=(-sin(\pi x)^2\sin (2\pi y),sin(\pi y)^2\sin (2\pi x)). \end{aligned}$$

In this test, consider that exact solution cannot be founded; we provide a more accurate approach to test the convergence orders with respect to $\varDelta t$. We use the difference between results on different time step size to derive the error $e_\phi ^\tau :=\phi ^\tau (x,T)-\phi ^{\frac{\tau }{2}}(x,T)$. The rate of convergence is defined as the ratio of errors: $\log _2(\Vert e_\phi ^\tau \Vert /\Vert e_\phi ^{\frac{\tau }{2}}\Vert )$. The error and the rate of convergence in $H^1$ norm and $L^2$ norm are calculated, respectively. The results are presented in Table 1, 2, 3 and 4. We observe that the results is consist with theoretical analysis.

Table 1 Numerical results with (P1b, P1) element

Table 2 Numerical results with (P1b, P1) element

Table 3 Numerical results with (P1b, P1) element

Table 4 Numerical results with (P1b, P1) element

Table 5 Numerical results of (3.9a)–(3.9e)

Table 6 Numerical results of (3.9a)–(3.9e)

Fig. 1

The modified energy evolution

Fig. 2

The modified energy E1 and the exact energy E2

Fig. 3

Snapshots of coarsening of a binary fluid during spinodal decomposition

Using the scheme (3.9a)–(3.9e) in [19]for inhomogeneous Stokes system and our proposed scheme, some numerical results are presented in Tables 5 and 6 to make a comparison. The error and convergence rate of $L^2$ norm of $\phi$, $\mathbf{u }$ and p are calculated; parameters are the same as Table 1.

5.2 Energy Stability

To demonstrate the stability of the proposed scheme, the energy functional (2.8) can be discretized as

$$\begin{aligned} E(\mathbf{u },\phi ,q)=\frac{1}{2}\Vert \mathbf{u }\Vert ^2 +\frac{\lambda }{2}\Vert \nabla \phi \Vert ^2+\lambda F(\phi ), \end{aligned}$$

where the modified energy of discrete scheme (3.2)–(3.9) is defined as

$$\begin{aligned} E(\mathbf{u },\phi ,q)=\frac{1}{2}\Vert \mathbf{u }\Vert ^2+\frac{\lambda }{2}\Vert \nabla \phi \Vert ^2+\frac{\lambda \eta ^2}{4}\Vert q\Vert ^2 \end{aligned}$$

we can observe that the energy is non-increasing. There are two curves in the Fig.  1. The red line represents $\lambda =0.001$ and the green line represents $\lambda =0.01$, where we choose $h=\frac{1}{64},\tau =0.001$ and other parameters are the same as in Table 1. The picture in Fig. 2 shows both of the modified energy E1 and the exact energy E2.

5.3 The Process of Coarsening

In this experiment, we study the phase separation behavior; we simulate the process of spinodal decomposition in Cahn–Hilliard–Navier–Stokes system. The simulation is done in the domain $[0,1]\times [0,1]$ with the parameters $h=1/64$ and $\tau =0.001$. We fixed $\eta =0.005,M=0.01,\lambda =0.001,\nu =0.1$. The initial condition is taken as a random field value. The process of coarsening is shown in the following figures:

6 Conclusion

In this paper, we established the theoretical analysis for solving Cahn–Hilliard–Navier–Stokes phase-field model. Based on Lagrange multiplier approach, the proposed scheme is linearized. By observing the numerical tests, the scheme are of first-order accuracy for $\phi , \mathbf{u }$ in $L^2$ norm, the rate of covergence for pressure p appears to be only half-order which is known for the pressure projection scheme, and our scheme is energy-dissipative. These results show that our scheme is effective.