1 Introduction

The California Bearing Ratio \(({\text{CBR}})\) is a critical index in earth structures and geotechnical engineering, such as highway embankments, earth dams, the fills behind retaining walls, and bridge abutments. CBR tests can be conducted on compacted soil in the lab or on the ground surface. In practice (Ho and Tran 2022), since CBR tests are time-consuming and expensive to do, only a limited number of them can be conducted, for example, over a road construction project (Karunaprema 2002; Yildirim and Gunaydin 2011; Ho and Tran 2022). Therefore, artificial-based methods can be logical to be used in the CBR prediction procedures (Varol et al. 2021; Salehi et al. 2022; Xiao-xia 2022).

In predicting CBR value, validation of its correlation with other soil properties similar to the study conducted by Roy et al. (2006) can be helpful. In another study, Shukla and Kukalyekar (2004) developed a relationship between the compaction properties and CBR for compacted fly ash. Recently, Srinivasa Rao (2004) developed a relationship between the Group index and CBR. He developed tests on 150 soil samples, including various soil types. Additionally, Karunaprema and Edirisinghe (2002) and Nuwaiwu et al. (2006) conducted investigations to estimate the California Bearing Ratio from the Dynamic Cone Penetration (DCP) value and plasticity modulus.

The artificial neural network (ANN) is an extensively accepted simulation that can be used in various civil engineering branches. Therefore, the ANN is a precise solution for predicting in engineering fields (Masoumi et al. 2020; Nurlan 2022; behnam Sedaghat et al. 2023). It can be applied in various branches of geotechnical engineering (Cheng et al. 2022), such as the prediction of the bearing capacity of the pile (Das and Basudhar 2006) and slope stability (Erzin and Cetin 2013). Although ANNs are used widely in geotechnical engineering, research with the aim of CBR prediction is few, such as which estimated the California Bearing Ratio of stabilized soil by Si Ho and Quan Tran (2022) or single and multiple regression applications in CBR estimation of soil using a dataset from highways of Turkey located in different regions. The findings demonstrate that the neural network outperforms the statistical models (Yildirim and Gunaydin 2011). In a separate investigation, ANN and multiple regression approaches were employed to predict the CBR of soil mixed with lime and quarry (Sabat 2013).

Radial basis function (RBF) can be considered one of the widely used artificial neural networks to estimate the unconfined compressive strength of a soil–stabilizer mix (Bors and Pitas 1996; Heshmati et al. 2009; Yin et al. 2021). Heshmati et al. (2009) confirmed data from the results of previously published stabilization tests with previous laboratory tests. Also, they compared the RBF-based predictions with the numerical and experimental results of other researchers and found them more accurate. Sabour and Movahed (2017) developed a radial basis function neural network model to predict the soil sorption partition coefficient for about 800 organic varied and even unknown compounds. The obtained results indicated that the performance of the model is excellent.

Moreover, Shahani et al. (2021) developed four gradient-based machine learning algorithms to estimate the uniaxial compressive strength of soft sedimentary rocks at Thar Coalfield, Pakistan. They allocated a 106-point dataset identically for each algorithm into 30% for the testing and 70% for the training models. Also, Shangguan et al. (2010) applied the classical gradient-based optimization algorithm for estimating model parameters of conditioned soils in an EBP shield. They trained the neural network weights using a fast convergent approximation, namely the Levenberg–Marquardt. Comparing results from the model with simulated observations illustrates that the proposed neural network has better identification accuracy and higher computing efficiency. Chen et al. (2023) studied various advanced versions of this optimizer. Then, they sorted this algorithm’s application domains and analyzed its shortcomings, development status, and role in each research domain. This review not only suggested possible future research directions in this field but also provided a complete source of information about the slime mold algorithm and its advanced versions.

In this current research investigation, three distinct hybrid models have been developed, employing the radial basis function (RBF) neural network approach and integrating three different optimizers: the adaptive opposition slime mold algorithm (AOSMA), the gradient-based optimizer (GBO), and the sine cosine algorithm (SCA). The primary aim of these models is to predict the CBR value with precision. The efficacy of these newly devised models in forecasting CBR values was rigorously assessed using a comprehensive set of five input variables. These variables encompassed essential parameters, such as optimum moisture content, lime percentage, maximum dry density, curing period, and lime sludge percentage. The combined power of these variables facilitated robust predictions of the CBR value. To validate the predictive prowess of the models, a comparison was made between the estimated CBR values and observed values. This comparison was performed in two distinct categories: training and testing models. Subsequently, the model demonstrating the most remarkable performance in CBR value estimation is presented as the optimal choice for practical applications. This research venture not only advances the understanding of CBR value prediction but also offers a reliable and potent tool for real-world applications in the field.

2 Materials and methodology

2.1 Dataset description

Experimental records presented in Table 1 were used to assess lime sludge’s and lime’s impact on CBR in different curing periods (Ikeagwuani 2021). Input parameters considered in measuring CBR values included five effective variables: curing period \((\mathrm{CP }({\text{day}})),\) lime sludge percentage \((\mathrm{LS }(\mathrm{\%})),\) lime percentage \((\mathrm{LI }(\mathrm{\%})),\mathrm{ maximum dry density }(\mathrm{MDD }({\text{g}}/{\text{cc}}))\mathrm{ and}\), optimum moisture content [\({\text{OMC}}\) \((\mathrm{\%})]\). Statistical properties of these variables in the dataset are reported in Table 1. Moreover, Fig. 1 shows the histogram and the cumulative plot of inputs and output.

Table 1 The variables contained in the dataset and their statistical properties
Full size table
Fig. 1
figure 1

Histogram cumulative plot for the input and output variables

Full size image

The division of data into training and testing sets was identified as a crucial step in ensuring robust model evaluation in our study. To preserve statistical consistency and guarantee the representativeness of both sets, a random stratified sampling approach was employed. Consistency in the distribution of key variables between the training and testing sets is ensured by this method, thus, creating a reliable basis for evaluating the model’s performance. This process has been clarified in the manuscript for improved transparency and understanding.

Stabilizing soil with lime enhances both physical and chemical properties. Physically, it increases density, reduces porosity, strengthens the soil, improves workability, and minimizes shrinkage. Chemically, lime raises pH, influences cation exchange capacity, stabilizes minerals, and reduces swelling potential. These modifications result in improved soil stability, reduced erosion, and enhanced nutrient availability. The effectiveness of lime stabilization depends on factors like soil type, lime dosage, and curing time, with testing required to determine optimal conditions for achieving desired results.

In this study, Python programming language was employed for data analysis and coding purposes. The choice of Python was driven by its versatility, extensive libraries, and robust capabilities in handling diverse data sets, ensuring the accuracy and efficiency of the analyses. In addition, the codes of model and optimizers mentioned in Appendix.

2.2 Radial basis function (RBF)

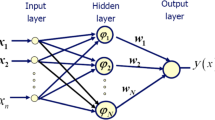
Artificial neural networks \(({\text{ANNs}})\), such as radial basis function \(({\text{RBF}})\) networks, are powerful tools for estimating nonlinearities by employing a modeling philosophy that does not rely on mathematical equations to define the relationship between model inputs and corresponding outputs, use the data alone to determine the structure of the model and unknown parameters. These methods can learn and upgrade as more data becomes accessible without repeating from the beginning. Thus, they outweigh the conventional methods (Alavi et al. 2009).

RBF consists of an input layer, a linear output layer, and a hidden layer. The hidden layer A Gaussian distribution based on a function that is utilized as an activation function is used to transform input vectors into \(RBF\). Width and center are two important parameters that are associated with the Gaussian basis function (\({\psi }_{j})\) (Heshmati et al. 2009). This function is given in the following form:

$${\psi }_{j}(x)=exp\left(\frac{{\left|x-{\lambda }_{j}\right|}^{2}}{2{\sigma }_{j}^{2}}\right)$$
(1)

where \(x\) is the input pattern, and \({\sigma }_{j}\) and \({\lambda }_{j}\) are the spread and center of the Gaussian basis function, respectively. The output neuron is written as:

$$y\left( x \right) = \mathop \sum \limits_{{j = 1}}^{n} \upsilon _{j} \psi _{j} \left( x \right) + a$$
(2)

Here, \(n\) is the number of hidden neurons, \({\upsilon }_{j}\) is the weight between \({jth}\) hidden and the output neuron, and \(a\) is the bias term. Figure 2 shows the flowchart of RBF.

Fig. 2
figure 2

Flowchart of RBF

Full size image

2.3 Adaptive opposition slime mold algorithm (AOSMA)

The SMA is inspired by the plasmodial SM’s oscillation mode, which employs positive-negative feedback to find the best path and oscillation to reach its nutrition source (Naik et al. 2021). In Li et al. (2020), the AOSMA is proposed, which enhances the SM’s foraging behavior by incorporating adaptive decision-making based on the opposition.

To create a mathematical representation of AOSMA, it is postulated that a certain search area is inhabited by N slime molds bounded by a lower limit (LB) and an upper limit (\(UB\)). Then \({X}_{i}= ({x}_{i}^{1}, {x}_{i}^{2}, \ldots ,{x}_{i}^{d}), \forall i \in [1, N]\) is the position of \(i{\text{th}}\) slime mold in d-dimensions and \(F({X}_{i}), \forall i = [1, N]\) represents the fitness of the \(i{\text{th}}\) slime. Therefore, the fitness and the position of N slime molds at the iteration t are presented in Eqs. (3) and (4):

$$X\left(x\right)=\left[\begin{array}{c}{x}_{1}^{1} {x}_{1}^{2} \cdots {x}_{1}^{d}\\ {x}_{2}^{1} {x}_{2}^{2} \cdots {x}_{2}^{d}\\ \vdots \vdots \vdots \vdots \\ {x}_{N}^{1} {x}_{N}^{2} \cdots {x}_{N}^{d}\end{array}\right]=\left[\begin{array}{c}{X}_{1}\\ {X}_{2}\\ \vdots \\ {X}_{N}\end{array}\right]$$
(3)
$$F\left(X\right)=\left[F\left({X}_{1}\right),F\left({X}_{2}\right), \ldots , F\left({X}_{N}\right)\right]$$
(4)

The upgraded position of the slime mold in the \((t+1)\) iteration is as follows:

$${X}_{i}\left(t+1\right)=\left\{\begin{array}{c}{X}_{LB}\left(t\right)+{V}_{d}\left(W. {X}_{A}\left(t\right)-{X}_{B}\left(t\right)\right) {p}_{1}\ge \delta \quad and \quad {p}_{2}<{m}_{i}\\ {V}_{e}. {X}_{i}\left(t\right) {p}_{1}\ge \delta and {p}_{2}\ge {m}_{i},\quad \forall i\in [1,N] \\ rand. \left(UB-LB\right)+LB {p}_{1}<z\end{array}\right.$$
(5)

\({X}_{LB}\) is the best local slime mold, \({X}_{A}\) and \({X}_{B}\) are pooled individuals by random, \(W\) is the weight factor, and \({V}_{d}\) and \({V}_{e}\) are the random velocities. \({p}_{1}\) and \({p}_{2}\) are randomly chosen numbers in [0,1]. The chance of the slime mold, which is fixed at \(\delta =0.03\), refers to the initial search location that is selected randomly.

\({m}_{i}\) is the threshold value of \(ith\) member in the population that helps opt for the position of slime mold using itself or the best alternative for the next iteration, which is evaluated in Eqs. (6–8):

$${m}_{i}= tanh\left|F\left({X}_{i}\right)-{F}_{G}\right|, \forall i\in [1,N]$$
(6)
$${F}_{G}=F({X}_{G})$$
(7)
$$W\left({SortInd}_{F}\left(i\right)\right)=\left\{\begin{array}{c}1+rand.{\text{log}}\left(\frac{{F}_{LB}-F({X}_{i})}{{F}_{LB}-{F}_{Lw}}+1\right) 1\le i\le \frac{N}{2}\\ 1-rand.{\text{log}}\left(\frac{{F}_{LB}-F({X}_{i})}{{F}_{LB}-{F}_{Lw}}+1\right) \frac{N}{2}<i\le N\end{array}\right.$$
(8)

Here, \({F}_{G}\) and \({X}_{G}\) are the value of global best fitness and global best position, respectively. The variable \(rand\) represents a randomly generated number within the interval [0,1]. \({F}_{LB}\) and \({F}_{Lw}\) are local best and worst fitness values. In a minimization problem in Eq. (9), an ascending order as follows can be used for sorting fitness values:

$$\left[{Sort}_{F},{SortInd}_{F} \right]=sort(F)$$
(9)

Now, the local best and worst fitness also the local best slime mold \({X}_{LB}\) can be extracted in Eqs. (10) to (12):

$${F}_{LB}=F\left({Sort}_{F}\left(1\right)\right)$$
(10)
$${F}_{LW}=F\left({Sort}_{F}\left(N\right)\right)$$
(11)
$${X}_{LB}=X\left({SortInd}_{F}\left(1\right)\right)$$
(12)

\({V}_{d}\) and \({V}_{e}\) as random velocities are defined as follows:

$${V}_{d}\in [-d,d]$$
(13)
$${V}_{e}\in [-e,e]$$
(14)
$$d={\text{arctanh}}\left(-\left(\frac{t}{T}\right)+1\right)$$
(15)
$$e=1-\frac{t}{T}$$
(16)

In Eq. (16), \(T\) is the maximum iteration, and the algorithm converges to a solution. In the context of engineering design problems and optimizations, the Slime Mold Algorithm (SMA) has shown potential for both exploration and exploitation. Several key factors determine the improvement of the slime mold rules in SMA:

Case 1: When \({p}_{1}\) ≥ z and \({p}_{2}\) < \({m}_{i}\), the search guided by the slime mould’s local best, denoted as \({X}_{LB}\) and two random individuals \({X}_{A}\) and \({X}_{B}\) with velocity \({V}_{d}\). This stage aids in maintaining a balance between exploitation and exploration.

Case 2: When \({p}_{1}\) ≥ z and \({p}_{2}\) \(\ge\) \({m}_{i}\), the search is guided by the position of slime mold with a velocity \({V}_{e}\). This case assists in the exploiting process.

Case 3: where \({p}_{1}\) \(<\) z, the individual undergoes reinitialization within a defined search space. This step contributes to the exploration process.

In Case 1, it is demonstrated that when \({X}_{A}\) and \({X}_{B}\) represent two random slime molds, the probability of achieving optimal solutions through exploration and exploitation is not effectively controlled. To overcome this shortcoming, local best individual \({X}_{LB}\) can be replaced by\({X}_{A}\). Therefore, the \(ith (i = \mathrm{1,2}, \ldots , N)\) member’s position upgrading rule of Eq. (5) is remodeled as Eq. (17).

$${Xn}_{i}\left(t\right)=\left\{\begin{array}{c}{X}_{LB}\left(t\right)+{V}_{d}\left(W. {X}_{LB}\left(t\right)-{X}_{B}\left(t\right)\right) {p}_{1}\ge \delta \quad and \quad {p}_{2}<{m}_{i}\\ {V}_{e}. {X}_{i}\left(t\right) {p}_{1}\ge \delta \quad and \quad {p}_{2}\ge {m}_{i} \\ rand. \left(UB-LB\right)+LB {p}_{1}<\delta \end{array}\right.$$
(17)

Case 2 illustrates that slime mold exploits a place in the neighborhood. Thus, a path of lower fitness may be followed by that. To address this issue, opting for an adaptive decision mechanism proves to be a more effective alternative.

Case 3 demonstrates that although SMA provides criteria for exploration, the limited value of \(\delta =0.03\) restricts the level of exploration. To address this issue, an additional exploration supplement for SMA is required. A combined solution to Case 2’s and Case 3’s limitations involves using an adaptive decision strategy for determining if further exploration is necessary through opposition-based learning (OBL) [28]. OBL utilizes a defined \({Xop}_{i}\) in the search space that is precisely opposite of the Xni for each member (\(i = \mathrm{1,2},\cdots ,N\)) and compares it to improve the position of the following iterations. This approach helps improve convergence and prevent the likelihood of getting trapped in local minima. Therefore, the \({Xop}_{i}\) for the ith individual in the jth (\(j =\mathrm{1,2},\cdots ,s\)) dimension is defined in Eq. (18):

$${Xop}_{i}^{j}={\text{min}}\left({Xn}_{i}\left(t\right)\right)+max\left({Xn}_{i}\left(t\right)\right)-{Xn}_{i}^{j}\left(t\right)$$
(18)

In Eq. (19), \({Xr}_{i}\) represents the ith member’s position in the minimization problem and is formulated as:

$${Xr}_{i}=\left\{\begin{array}{c}{Xop}_{i}\left(t\right) F({Xop}_{i}\left(t\right))<F\left({Xn}_{i}\left(t\right)\right)\\ {Xn}_{i}\left(t\right) F({Xop}_{i}\left(t\right))\ge F\left({Xn}_{i}\left(t\right)\right)\end{array}\right.$$
(19)

When a descendant nutrient path is detected, an adaptive decision is made based on the old fitness value f(Xi(t)) and the current fitness value f(Xni(t)). This decision helps provide additional exploration when necessary. Subsequently, the next iteration’s position undergoes an update as follows:

$${X}_{i}\left(t+1\right)=\left\{\begin{array}{c}{Xn}_{i}\left(t\right) F({Xn}_{i}\left(t\right))\le F\left({X}_{i}\left(t\right)\right)\\ {Xr}_{i}\left(t\right) F({Xn}_{i}\left(t\right))>F\left({X}_{i}\left(t\right)\right)\end{array}\right. , \forall i\in [1,N]$$
(20)

Related pseudocode is presented as follows and code of hybrid RBF-AOSMA is mentioned in Appendix.

2.4 Gradient-based optimizer (GBO)

GBO merges the population and GB approaches and the search direction to explore the search area using a pair of primary operators, namely the local escaping operators and gradient search rule specified by Newton’s technique (Ahmadianfar et al. 2020), alongside a vector collection. In optimization problems, the aim is to minimize the objective function.

figure a

2.4.1 Gradient search rule (GSR)

Generally, the GBO originates a speculated initial strategy and moves toward the following situation through a gradient-specified direction. The Taylor series related to \(f\left( {x + \Delta x} \right)\) and \(f\left( {x - \Delta x} \right)\) are definable in Eqs. (21) and (22):

$$f\left(x + \Delta x\right)=f\left(x\right)+{f}{^\prime}\left({x}_{0}\right)\Delta x+\frac{f{^\prime}{^\prime}\left({x}_{0}\right){\Delta x}^{2}}{2!}+\frac{{f}^{(3)}\left({x}_{0}\right){\Delta x}^{3}}{3!}+\cdots$$
(21)
$$f\left(x- \Delta x\right)=f\left(x\right)+{f}^{\mathrm{^{\prime}}}\left({x}_{0}\right)\Delta x+\frac{f\mathrm{^{\prime}}\mathrm{^{\prime}}\left({x}_{0}\right){\Delta x}^{2}}{2!}-\frac{{f}^{(3)}\left({x}_{0}\right){\Delta x}^{3}}{3!}+\cdots$$
(22)

Then, the following central differencing equation defines the first-order derivative as follows:

$$f^{\prime \prime } \left( x \right) = \frac{{f\left( {x + \Delta x} \right) - f\left( {x - \Delta x} \right)}}{2\Delta x}$$
(23)

So, the new position is as follows:

$$x_{n + 1} = x_{n} - \frac{{2\Delta x \times f\left( {x_{n} } \right)}}{{f\left( {x_{n} + \Delta x} \right) - f\left( {x_{n} - \Delta x} \right)}}$$
(24)

As justified in (Ahmadianfar et al. 2020), Eq. (25) must be rewritten as follows:

$$GSR=randn\times \frac{2\Delta x\times {x}_{n}}{({x}_{worst}-{x}_{best}+\delta )}$$
(25)

Here \(randn\) is a randomly chosen number, and \(\delta\) determines a small value ranging between [0, 0.1].

To keep a balance between the local and global explorations for exploring promising regions within the search space and consequently to meet the optimal solution at the global level, in Eqs. (26–28), the GSR could be altered by utilizing an adaptive coefficient such as \({\sigma }_{1}\).

$${\sigma }_{1}=2\times {\text{rand}}\times \beta -\beta$$
(26)
$$\beta =\left|\alpha \times {\text{sin}}\left(\frac{3\pi }{2}+{\text{sin}}\left(\alpha \times \frac{3\pi }{2}\right)\right)\right|$$
(27)
$$\alpha ={\alpha }_{{\text{min}}}+({\alpha }_{{\text{max}}}-{\alpha }_{{\text{min}}})\times {\left(1-{\left(\frac{m}{M}\right)}^{3}\right)}^{2}$$
(28)

Here \({\alpha }_{{\text{min}}}=0.2\) and \({\alpha }_{{\text{max}}}=1.2\). \(m\) represent the iterations’ number, and M represents the total amount. The maximum value for \(m\) is 1000.

In Eqs. (29) and (30), the motion’s direction (M) is presented for exploiting the neighborhood area properly \({x}_{n}\):

$$M={\text{rand}}\times \lambda \times ({x}_{{\text{best}}}-{x}_{n})$$
(29)
$$\lambda =2\times {\text{rand}}\times \beta -\beta$$
(30)

Finally, based on the GSR and M, the following equation can be used to obtain an updated position (\({x^{\prime}}_{n}^{m})\) of the current vector (\({x}_{n}^{m}\)):

$${x^{\prime}}_{n}^{m}={x}_{n}^{m}-GSR+M$$
(31)

2.4.2 Local escaping operator (LEO)

The LEO enhances the efficiency of the offered method in handling complicated issues as it assists in the rising diversity of the population in search space and goes far from local optimal solutions. For more details, see (Ahmadianfar et al. 2020).

In addition, the code of hybrid RBF-GBO is mentioned in the Appendix.

2.5 Sine cosine algorithm (SCA)

The Sine cosine algorithm (SCA) utilizes the rules of trigonometric sine and cosine to update the individuals’ position toward the ideal solution. Updating equations in \(SCA\) are presented in Eq. (32) (Mirjalili 2016):

$${x}_{ij}^{t+1}=\left\{\begin{array}{c}{x}_{ij}^{t}+{p}_{1}*cos\left({p}_{2}\right)*\left|{p}_{3}{b}_{ij}^{t}-{x}_{ij}^{t}\right| ,{p}_{4}\ge 0.5\\ {x}_{ij}^{t}+{p}_{1}*sin\left({p}_{2}\right)*\left|{p}_{3}{b}_{ij}^{t}-{x}_{ij}^{t}\right| ,{p}_{4}<0.5\end{array}\right.$$
(32)

where \({b}_{ij}^{t}\) represents the best individual’s position and \({p}_{1}\), \({p}_{2}\), \({p}_{3}\), \({p}_{4}\) are random to avoid trapping into local optima. These parameters can be described in Eq. (33) (Gabis et al. 2021):

  • \({p}_{1}\) decides whether an updated position is the best solution (\({p}_{1}\) < 1) or outwards it (\({p}_{1}\) > 1).

    $${p}_{1}=b-t\frac{b}{{T}_{max}}$$
    (33)

    where t is the present iteration, b is a constant, and \({T}_{max}\) represents the maximum iterations.

  • \({p}_{2}\) is set in \([0, 2\pi ],\) which dictates if the movement of a solution is toward the destination or outward it.

  • \({p}_{3}\) assigns a weight to the terminus randomly. This permits \(de-\) emphasizing (\({p}_{3}\) < 1) or emphasizing (\({p}_{3} > 1)\) the influence of the terminus of the position updating of other answers. This parameter is in the range of \([0, 2]\).

  • \({p}_{4}\) is in the range of [0, 1]. It acts as a switch to opt between the trigonometric functions of sine or cosine.

Related pseudocode is presented as follows, and the code of hybrid RBF-SCA is mentioned in the Appendix.

figure b

2.6 Performance evaluation methods

The metrics for evaluation of model performance are:

  • The coefficient of determination (R2) indicates the extent to which the estimated values match the observed values, and it can be calculated using Eq. (34).

    $${R}^{2}={\left(\frac{{\sum }_{i=1}^{n}({t}_{i}-\overline{t })({e}_{i}-\overline{e })}{\sqrt{\left[{\sum }_{i=1}^{n}{({e}_{i}-t)}^{2}\right]\left[{\sum }_{i=1}^{n}{({e}_{i}-\overline{e })}^{2}\right]}}\right)}^{2}$$
    (34)

  • The RMSE is explained in Eq. (35):

    $${\text{RMSE}}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{({e}_{i}-{t}_{i})}^{2}}$$
    (35)

  • Normalized Root Mean Square Error (NRMSE) is as follows in Eq. (36):

    $${\text{NRMSE}}=\frac{\sqrt{\frac{1}{n}\sum_{i=1}^{n}{({e}_{i}-{t}_{i})}^{2}}}{\frac{1}{n}\sum_{i=1}^{n}({t}_{i})}$$
    (36)

  • The Mean Absolute Error (MAE) represents the mean of the absolute differences between the predicted and observed values, as shown in Eq. (37):

    $${\text{MAE}}=\frac{1}{n}\sum_{i=1}^{n}\left|{e}_{i}-{t}_{i}\right|$$
    (37)

  • The scatter index (SI) is defined as a function of RMSE in Eq. (38):

    $${\text{SI}}=\frac{{\text{RMSE}}}{\overline{t} }$$
    (38)

In all the five equations, n is the number of samples, \({e}_{i}\) represents the estimated value and \(\overline{e }\) is the average of the estimated value. \({t}_{i}\) and \(\overline{t }\) represent the experimental value and the average of the practical value, respectively. In the introduced metrics, except for R2, which is the highest desired value, the rest of the metrics should have the lowest value.

2.7 Hybridization

In this study, a novel hybrid architecture is proposed, wherein the Radial Basis Function (RBF) is combined with three distinct optimization algorithms: the adaptive opposition slime mold algorithm (AOSMA), gradient-based optimizer (GBO), and sine cosine algorithm (SCA). The unique strengths of each component are aimed to be leveraged for the enhancement of overall performance and robustness. The steps of integration are as follows:

  • Identification of components: Identify the radial basis function (RBF) as the primary modeling component and the three chosen optimizers: Adaptive opposition slime mold algorithm (AOSMA), gradient-based optimizer (GBO), and sine cosine algorithm (SCA).

  • Understanding characteristics of components: Attain a comprehensive understanding of the characteristics, strengths, and weaknesses inherent in each optimizer (AOSMA, GBO, and SCA) and the RBF within the specific problem domain.

  • Definition of integration strategy: Ascertain the manner in which the RBF will be coupled with each optimizer. Consider whether the integration will follow a sequential, parallel, or hierarchical approach. Define how the optimization process will influence the parameters of the RBF.

  • Adjustment of parameters: Modify the parameters of each optimizer and the RBF to ensure compatibility and optimal performance within the hybrid system. Fine-tune parameters based on the characteristics of the data and the specific requirements of the problem.

  • Implementation of integration: Execute the defined integration strategy by combining the RBF with each optimizer. Develop interfaces or connectors to facilitate communication and ensure seamless interaction between the RBF and the optimizers.

  • Evaluation of performance: Evaluate the performance of each hybrid model (RBF-AOSMA, RBF-GBO, RBF-SCA) using appropriate evaluation metrics. Assess how well the integrated components operate together and determine whether the hybridization achieves improvements over the standalone RBF.

  • Refinement through iteration: Based on the performance evaluation, iteratively refine the hybrid models. Adjust integration parameters, revisit the selection of optimizers, and fine-tune the hybridization strategy to enhance overall performance and convergence.

  • Documentation process: Thoroughly document the hybridization process. Include details about the RBF and each optimizer, the integration strategy, parameter settings, and any insights gained during the iterative refinement. This documentation is crucial for transparency and replicability.

  • Testing procedures: Conduct thorough testing of each hybrid model to ensure robustness and generalizability. Verify the performance on both training and unseen data, ensuring that the hybrid models effectively leverage the optimizers for improved results.

  • Guidelines for application: Provide clear guidelines on how each hybrid model (RBF-AOSMA, RBF-GBO, RBF-SCA) can be applied in practical scenarios. Specify input requirements, steps for obtaining predictions, and any considerations for real-world applications, taking into account the integration with the respective optimizers.

3 Results and discussion

This work presents three kinds of hybrid models that compare the observed experimental findings with anticipated values of \(CBR\) using \(RBF\) in conjunction with \(AOSMA, GBO\), and \(SCA\). The coupled models were created in the framework of RBF + AOSMA (RBAO), RBF + GBO (RBGB), and RBF + SCA (RBSC). In these hybrid models, data are split into training and test sets, which make up \(70\%\) and \(30\%\) of the final models, respectively. In order to ascertain if one version works better than another, this part compares statistical identifiers created for the produced research.

Table 2’s R2 values may be compared to see which method produces the greatest results. RBAO, for example, has the highest R2 values (0.994 and 0.977, respectively) in both the training and testing phases. All three models’ test portion R2 values are greater than the train portion, indicating inadequate training. It is clear by comparing values of the scatter Index (SI), where lower SI denotes the maximum model accuracy, that RBAO again yields the best results in both the training and testing stages. Comparing three types of errors, including RMSE, MAE, and NRMSE, in all three criteria, testing and training RBAO with smaller values of errors show the best results.

Table 2 Evaluation of introduced models
Full size table

Figure 3 depicts the scatter plot of the relationship between CBR’s measured and predicted values regarding RMSE and R2 evaluators reported for each data point. The RMSE is used as a measure of dispersal, with lower values indicating higher density and less variation in the results. However, the validation and learning points are brought closer to the centerline by the R2. A linear fit, two lines above and below the centerline at \(Y=0.9X\) and \(Y=1.1X\), and the centerline at \(Y=X\) are among the other variables shown in the picture. The intersection of the upper and lower lines indicates overestimation and underestimation. Figure 3 depicts three models generated by combining three optimizers during the testing and training frameworks. The R2 of RBAO and RBSC models are satisfactory, particularly in the training phase, where the points are clustered close to the centerline and aligned in the same direction.

Fig. 3
figure 3

Scatter plot depicting measured and predicted values

Full size image

The excellent match between the observed and projected CBR values in each of the three models is clearly seen in Fig. 4, indicating the viability of the established algorithms that have been suggested for CBR value estimation. The RBAO model’s training section is where this agreement is most noticeable, while the RBGB training models are linked to the largest discrepancy between anticipated and observed values. Overall, it can be inferred that the suggested models demonstrate accurate performance with minimal error in predicting CBR, thereby demonstrating their potential effectiveness for practical applications.

Fig. 4
figure 4

Line-symbol plot for contrasting the measured values with the predicted ones

Full size image

Discrete training and testing stages of three generated models are shown in Fig. 5‘s histogram-distribution plot as the normal distribution of errors. Less precision in the outcome is associated with a wider tendency of spreading error. After training and testing, the narrow bell-shaped normal distribution diagram is the result of the improved performance of the RBAO hybrid model. Errors are in the 0 percent range in all three models, with RBAO being the most accurate. Through diagram comparison, it is evident that, with the exception of RBGB, where the training phase diagram has a spreading error trend that has covered a broader range than the testing diagram, the training has a spreading error trend that is as wide as the testing phase diagram’s covered range.

Fig. 5
figure 5

Histogram-distribution plot for the error percentage of presented models

Full size image

Across all three models that were developed, it is notable that the highest prediction errors seen in the testing process are either equivalent to or less than the maximum errors encountered in the training phase. This consistency between the training and testing phases is a positive indicator of model robustness. When comparing the prediction errors of these models, as depicted in Fig. 6, it becomes evident that in the case of the RBAO model, the errors exhibit a relatively narrow range, staying consistently below the 20% threshold. In contrast, the RBGB and RBSC models display prediction errors that fluctuate at significantly higher levels, with RBGB around 60% and RBSC around 40%. This analysis leads to the conclusion that the RBAO model outperforms the other two models in accurately estimating the CBR value in practical applications. Its more stable and lower error range suggests that RBAO is the most suitable choice for accurate CBR value predictions, which can be crucial in various engineering and construction scenarios.

Fig. 6
figure 6

Line-symbol plot for error percentage of developed hybrid models

Full size image

4 Conclusion

In the present research, three different hybrid models using the radial basis function (RBF) neural network are developed along with three optimizers containing adaptive opposition slime mold algorithm (AOSMA), gradient-based optimizer (GBO), and sine cosine algorithm (SCA). The performance of the models was assessed based on five input variables: maximum dry density, optimum moisture content, lime percentage, curing period, and lime sludge percentage. Finally, through some evaluators, the predicted values of CBR in two categories of training and testing models have been compared between the developed models, and the best-proposed model is presented for practical applications. Generally, RBAO had the best performance, with lower errors in training (\({\text{RMSE}}=2.658\), \({\text{MAE}}=2.10\), and \({\text{NRMSE}}=0.052\)), and testing models (\({\text{RMSE}}=4.195\), \({\text{MAE}}=2.863\), and \({\text{NRMSE}}=0.242\)). Furthermore, this model prepares accurate results with high density as it has lower values of SI in both the training and testing phases. The predicted CBR values by all of the developed models agree well with the predicted values, which demonstrates the offered hybrid algorithms’ workability in the CBR estimation procedure. Therefore, all models, especially RBAO, conclude the exact anticipation having the smallest error in the CBR forecasting procedure, making them efficient for practical applications. The combination of the RBF with Adaptive AOSMA, GBO, and SCA offers a range of advantages for predicting CBR. This synergy holds the potential to significantly improve the accuracy, adaptability, and robustness of predictive models. Firstly, it enhances prediction accuracy by efficiently optimizing model parameters, leading to highly accurate forecasts. The versatility of this approach allows for the selection of different optimizers based on specific dataset characteristics, adapting to various scenarios. Moreover, it expedites model training and convergence, saving computational resources and time. The risk of overfitting is reduced through fine-tuning, ensuring the model performs well on unseen data. Optimal parameter selection and adaptability to diverse data contribute to improved robustness, making the model resilient to data variations and outliers. Lastly, this approach efficiently utilizes available data, even with noise or limited datasets, resulting in more meaningful predictions.