Estimating the ultra-high-performance concrete compressive strength with a machine learning model via meta-heuristic algorithms

Abstract

In recent years, many experimental articles have been conducted to study ultra-high-performance concrete (UHPC). Thus, the relationship between its blend composition and the mechanical properties of UHPC is highly non-linear and challenging to utilize conventional statistical approaches. A robust and sophisticated method is needed to rationalize the variety of relevant experimental datasets, provide insight into aspects of non-linear materials science, and make estimative tools of desirable accuracy. Machine learning (ML) is a potent strategy that can reveal underlying patterns in complex datasets. This study aims to employ state-of-the-art ML methods for predicting the UHPC compressive strength (CS) by operating 165 previously published samples with 8 input characteristics via support vector regression (SVR). In addition, a novel approach has been used based on meta-heuristic algorithms to enhance accuracy, including Dynamic Arithmetic Optimization Algorithm (DAOA), Arithmetic Optimization Algorithm (AOA), and Black Widow Optimization (BWO). Furthermore, the models evaluated the prediction input dataset by some criteria indicators. The results indicated that the represented models obtained suitable estimative efficiency and can be reliable on ML methods in saving time and energy. In general, in comparing hybrid models, SVDA has a more acceptable performance than other hybrid models.

1 Introduction

In recent years, Ultra High-Performance Concrete (UHPC) has been a new class of concrete generated. UHPC has superior compressive, tensile behavior, and durability properties compared to High-Performance Concrete (HPC) (Graybeal 2007). UHPC demonstrates excellent durability, ductility, and strength as an alternative to new construction. This material has been produced over the last decades, and UHPC has various illustrations according to different classifications. The French Association of Civil Engineers (AFGC) specifications define UHPC as concrete with a compressive strength (CS) greater than 150 MPa and up to 250 MPa (Shafieifar et al. 2018). The properties of UHPC enable the development of long-span bending structures, lightweight bridge decks, and structural construction projects that demand high-strength material (Wille et al. 2012).

Compressive and tensile strength and Young’s modulus are the effective properties of the UHPC structural performance. Hence, it is difficult to precisely determine the above mechanical properties due to the complex microstructures shaped when cementitious composites' hydration occurs (Mattei et al. 2007). Investigators searching for the complex microstructural interactions and properties of these complex cementitious composites have mainly turned to exploratory examinations. Other advantages of utilizing UHPC include decreasing the number of concretes required for the structure. This improves the total net space equipment required, decreases labor to assemble precast units, and shortens structure time (Abellán García et al. 2020; Yin et al. 2021; Cheng et al. 2022). UHPC has a complex mixture design, and applying experimental approaches to obtain CS is labor-intensive, time-consuming, and expensive equipment materials. Some investigators use machine learning (ML) techniques to make concrete predictions to overcome test approach limitations. Choosing the suitable algorithm can enhance the estimation accuracy of models while ensuring training speed (Huang et al. 2022; Akbarzadeh et al. 2023).

A support vector machine (SVM) is an ML that implements the inductive principle of structural risk minimization to generalize well to a limited set of learning designs. Support vector regression (SVR) endeavors to minimize the bounded development error to obtain developed performance. SVR uses a loss function to penalize errors higher than a threshold. These loss functions result in sparse representations of decision rules. It provides algorithmic and representative advantages. SVMs have been used in different design recognition applications like image recognition and text classification and have been observed to be expanded to regression investigation. SVM has proven successful in various areas of engineering (Vapnik 1999; Ye et al. 2005; Mukherjee et al. 1997; Masoumi et al. 2020; behnam Sedaghat et al. 2023).

The study conducted by Awodiji and colleagues (Awodiji et al. 2018) investigate a. sequences of. artificial neural network (ANN) employing various modeling techniques to explore the correlation between CS and the ratio of material mass to establish the age of a range of hydrated lime-cement concrete specimens’ mixtures. Their model obtained correlation coefficients ranging from 90.1 to 98.4 percent. This indicates that the model successfully predicted the CS of different concrete mixes. Samui (2008) employed SVM to specify the subsidence of shallow scaffolds in non-cohesive soils and found that SVM could be a helpful and practical tool for predicting subsidence. Shi et al. (2011) used SVMs to predict cement strength. The SVM results were compared with those of an ANN model, and it was found that SVM achieves more suitable precision than the ANN approach. Kasperkiewicz et al. (1995) utilized ANN. to. enhance cement, superplasticizer, silica, small and large granular components, and water in (HPC)., irrespective of the intricacy, data gaps, and reliability issues, forecasted a good blending proportion. Their model shows a strong association between the recorded real and. estimated standards, and artificial neural network (ANN). models offer a means to estimate ideal combinations. Maity et al. (2010) confirmed the potential of SVR to predict monthly current flow using intrinsic features. Chen et al. (2009) used SVM to estimate the exposure temperature of fire-damaged concrete. They have been obtained that the accuracy of the SVM model estimation improves as the effective parameters increase, and the ratio of training to total samples was assumed when analyzing the SVM method. Lee et al. (2007) used the SVR method and neural network (NN) on experimental results to successfully predict the strength of concrete according to mixed data. The SVR approach showed higher estimation accuracy and shorter calculation time. Ghafari et al. (2012) explored the application of a (BPNN). and a statistical blending technique created to predict the ultra-high performance concrete demeanor presentation. Their goal was applying a BPNN in combination with a statistical mix plan approach to forecast both the compressive strength (CS) and uniformity of UHPC. across two. different curative styles, mostly steam curing and. wet curative. Fifty-three concrete. specimens were created using a statistical blending design medium. The elements that make up the. combination were. taken by way of autonomous variables within the BPNN. framework. The outcomes indicated that the BPNN. can anticipate compressive strength and workability with higher accuracy than. a statistically blended design.

Table 1 summarizes several published articles to measure ML models' accuracy.

Table 1 Summary of several published articles for predicting CS of UHPC

The primary objective of this study is to leverage SVR, a subset of SVM, for the precise prediction of CS in UHPC. CS prediction in UHPC holds immense importance in civil engineering and material science, aiding in optimizing structural designs and material compositions. The prediction process is approached in two integral phases: training and testing, utilizing a dataset of 165 experimental samples extracted from published studies. Accurate prediction of CS in UHPC is essential for ensuring the structural integrity and durability of construction projects. By employing the SVR model, a powerful and versatile machine learning technique, this study aims to improve the accuracy of CS prediction and enhance the overall efficiency of UHPC applications.

A novel approach is proposed to enhance prediction accuracy and minimize errors by integrating meta-heuristic algorithms with the SVR model, forming hybrid models. Specifically, the Dynamic Arithmetic Optimization Algorithm (DAOA), Arithmetic Optimization Algorithm (AOA), and Black Widow Optimization (BWO) are selected for their potential to fine-tune the SVR model and improve prediction outcomes.

In the subsequent section, these meta-heuristic algorithms will be thoroughly introduced, elucidating their mathematical foundations and principles. The specifics of the hybrid models also delve into SVDA, SVAO, and SVBW, which represent the amalgamation of the SVR model with DAOA, AOA, and BWO, respectively. These hybrid models are designed to leverage the strengths of the SVR model and the meta-heuristic algorithms, aiming for superior prediction accuracy while considering computational efficiency.

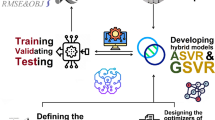
Furthermore, an evaluation framework will be established to assess the performance of the hybrid models, utilizing appropriate evaluation metrics to quantify prediction errors. This rigorous evaluation process is vital in selecting the most effective hybrid model, optimizing the prediction accuracy, and ultimately contributing to efficient resource utilization by saving energy and time in UHPC prediction processes. In addition, the process of the present study is mentioned in Fig. 1.

Fig. 1

Process of the present study

2 Materials and methodology

2.1 Data gathering

The paper used 165 experimental samples published in previous studies (Abuodeh et al. 2020; Chang and Zheng 2020). Table 2 shows the fed variables feature of models. As it is clear in the table, the concrete mixing design has eight inputs, which include all cement (C), sand–cement ratio (S/C), silica fume–cement ratio (SF/C), fly ash–cement ratio (FA/C), steel fiber–cement ratio (STF/C), quartz powder–cement ratio (QP/C), water–cement ratio (W/C), and admixture–cement ratio (Ad/C), in addition, CS is the output. The specified unit for the inputs except for (C), which is in $\left(\frac{\mathrm{Kg}}{{\mathrm{m}}^{3}}\right)$, the rest are in (percent) because of showing the ratio with (C). In addition, the output, i.e., CS, is expressed in terms of (MPa). In addition, Fig. 2 shows the histogram distribution of variables.

Table 2 The fed variables feature of models

Fig. 2

The histogram distribution of inputs and output

The presented Figure and Table offer a comprehensive overview of vital variables central to the study of UHPC. These variables encompass critical components and ratios significantly influencing the material's properties, specifically its CS, a key performance indicator. C demonstrates variability from a minimum of 383 units to a maximum of 1600 units. This variation signifies the diverse compositions of concrete mixtures used in the study. Moreover, ratios have a pivotal role in determining the material's characteristics. FA/C ranges from 0 to 0.332, highlighting the varying proportions of fine aggregate, while SF/C exhibits a range of 0 to 1.011, emphasizing the diverse use of silica fume. Other ratios, for instance QP/C,S/C., Ad/C, STF/C., W/C, and, also demonstrate noteworthy variations. For instance, the W/C ranges from 0.0375 to 0.514, showcasing different water-cement proportions employed. CS, the target variable crucial for assessing concrete performance, ranges from 95 to 240 MPa. This indicates the spectrum of strengths observed in the dataset, emphasizing the influence of these variables on the ultimate compressive strength of the UHPC.

2.2 Support vector regression (SVR)

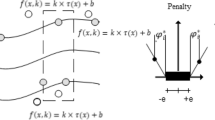
For use in many civil engineering problems, a support vector machine (SVM) was proposed by Vapnik et al. (1996) to use a non-linear fitting (mapping) of input data to a larger D-dimensional feature space (An et al. 2007; Çevik et al. 2015). Customization is common in kernel functions, including sigmoidal, Linear, Gaussian radial basis functions (RBF), and polynomials (Vapnik 2013). A linear model in feature space is a mathematical notation as:

$$f\left(x,w\right)=\sum_{j=1}^{D}{w}_{j}{v}_{j}\left(x\right)+c.$$

(1)

In Eq. (1), ${v}_{j}\left(x\right)$, $j=\mathrm{1,2},\dots ,D$ indicates a vector of weight in which the choice of kernel function parameters often relies on the execution kernel and software type used. Nevertheless, the selection of function parameters and kernel sort should consider the distribution of the training datasets.

Some non-linear regression models define the relationship between outcome factors and two or more illustratives via fitting a linear equation to a sample dataset. The use of linear regression models is the first attempt due to their wide acceptance and ease of use in predictive modeling (Chou et al. 2014; Liang and Song 2009). Non-linear regression fits a hyperplane into a D-dimensional space when solving computer modeling issues. Where D determines the illustrative components' number. Provided a system with variable x describing D and components y of the result, the general least-squares problem is for determine the unknown parameters ${P}_{i}$ of a linear model. A common equation is:

$$Y={P}_{0}+\sum_{i=1}^{n}{P}_{i}{v}_{i}\left(x\right)+c.$$

(2)

Here, $Y$ determines the output, i.e., CS, ${P}_{i}$ shows the regression coefficient, $x$ shows the specific descriptive component, and $c$ indicates the error term. The non-linear regression model usage has been commonly utilized in civil engineering issues. Furthermore, Fig. 3 indicates the flowchart of SVR.

Fig. 3

The SVR flowchart

2.3 Black widow optimization (BWO)

The problem variables’ values should be put into desirable structures to solve the problem. This structure is called a “widow”. BWA saw Black Widow Spider as a powerful solution to any problem. Each Black Widow spider specifies the values of task variables. The document should assume the structure to resolve the benchmark function as an array. The widow is a $1\times {N}_{v}$ array determined by solving the problem for ${N}_{v}$-dimensional optimization problems. The array can be calculated in Eq. (3):

$$A=\left[{x}_{1},{x}_{2}, \dots , {x}_{{N}_{v}}\right].$$

(3)

Each component value $\left[{x}_{1},{x}_{2}, \dots , {x}_{{N}_{v}}\right]$ indicates a floating-point number. The fitness of a widow is $\left({x}_{1},{x}_{2}, \dots , {x}_{{N}_{v}}\right)$ and can be calculated in Eq. (4):

$$f\left(A\right)=\left({x}_{1},{x}_{2}, \dots , {x}_{{N}_{v}}\right).$$

(4)

A potential widows matrix of size N_pop × N_var is produced in the initial population of spiders at the start of the optimization algorithm. Parent pairs are then randomly selected, and a mating reproduction step is implemented.

At this stage, black male widows are eaten by females. Pairs initiate mating independently of each other and replicate new development in parallel. In addition, each pair on the web mates independently with other pairs in nature. A single mating will produce about 1000 eggs, but some more powerful spider babies can survive in the real world. With x₁ and x₂ as parents and y₁ and y₂ as $\varepsilon$, the following formula produces children:

$$\left\{\begin{array}{c}{y}_{1}=\varepsilon \times {x}_{1}+(1-\varepsilon )\times {x}_{2}\\ {y}_{2}=\varepsilon \times {x}_{2}+(1-\varepsilon )\times {x}_{1}\end{array}\right..$$

(5)

The strategy involved is repeated N_var/2 times, but the randomly selected digits are not copied. Finally, mothers and children were sorted by fitness value and added to an array. Some of the best individuals are added to the newly generated population according to cannibalism ratings. Instructions are used in all pairs. Figure 4 illustrates the flowchart of BWO.

Fig. 4

The BWO flowchart

2.4 Arithmetic optimization algorithm (AOA)

AOA was suggested by Abualigah et al. in 2020 using some mathematical equations and operators (Castelli et al. 2013). This algorithm starts with a set of random solutions. Target values for each solution are calculated at each iteration. Before updating the solution position, AOA has two control parameters named $F$ and $V$ that must be updated as:

$$F\left(i\right)=\mathrm{Min}+c\times \left(\frac{{b}_{\mathrm{max}}-{b}_{\mathrm{min}}}{{\mathrm{Max}}_{\mathrm{iter}}}\right),$$

(6)

$$V\left(i\right)=1-{\left(\frac{c}{{\mathrm{Max}}_{\mathrm{iter}}}\right)}^\frac{1}{s}.$$

(7)

In the above equations, $F\left(i\right)$ indicates the function value at iteration ith, $c$ is the current iteration, ${\mathrm{Max}}_{\mathrm{iter}}$ indicates the maximum iteration and ${b}_{\mathrm{max}},{b}_{\mathrm{min}}$ indicate the maximum and minimum values for bonding $F$. Also, $V$ is the coefficient, which is the probability of the mathematical optimizer, $V\left(i\right)$ defines the function at the value of the ith iteration, and $s$ shows the constant value. After updating $V$ and $F$, it develops a random number, namely ${r}_{2}$ to switch between mining and discovery. The exploration and exploitation are utilized in Eqs. (8) and (9), respectively:

$${x}_{i,j}\left(t+1\right)=\left\{\begin{array}{l}\frac{\mathrm{best}({x}_{j})}{(V+g)}\times \left({ub}_{j}-{lb}_{j}\right)\times m+{lb}_{j} \,if\, {r}_{1}<0.5 (a)\\ best\left({x}_{j}\right)\times V\times \left({ub}_{j}-{lb}_{j}\right)\times m+{lb}_{j} \,if\, otherwise\, (b)\end{array}\right.,$$

(8)

$${x}_{i,j}\left(t+1\right)=\left\{\begin{array}{l}best\left({x}_{j}\right)-V\times \left({ub}_{j}-{lb}_{j}\right)\times m+{lb}_{j} \,if\, {r}_{2}<0.5 (a)\\ best\left({x}_{j}\right)+V\times \left({ub}_{j}-{lb}_{j}\right)\times m+{lb}_{j}\, if \,otherwise\, (b)\end{array}.\right.$$

(9)

where $best\left({x}_{j}\right)$ shows the jth position in the best-achieved solution so far, $m$ indicates the parameter of controlling, $g$ defines a small number for avoiding division with zero, and ${ub}_{j},{lb}_{j}$ indicate the upper and lower value of the jth bound position, alternatively. Figure 5 indicates the AOA flowchart.

Fig. 5

The flowchart of AOA

2.5 Dynamic arithmetic optimization algorithm (DAOA)

Two dynamic properties with new accelerator features have been implemented in the basic version of the arithmetic optimization algorithm to improve performance (Khodadadi et al. 2022). The dynamic version modifies solution candidates during optimization techniques and examines sections simplifying exploitation and exploration methods. The most notable attribute of DAOA is that it does not need prior fine-tuning of parameters associated with the most commonly utilized meta-heuristics.

Arithmetic Optimization Algorithms’ Dynamic Acceleration Functions for Dynamics play an important role in the exploring phase. AOA needs to adjust the maximum and minimum values for the initial stats of the acceleration ability. As a new downward function replaces the dynamically accelerated function, employing an algorithm without tunable internal parameters is suggested. The improvement factor in the algorithm is given as follows:

$$C={\left(\frac{{\mathrm{Max}}_{\mathrm{iter}}}{c}\right)}^{s}.$$

(10)

The noteworthy point is that the parameters mentioned in Sect. 2.4 are related to AOA, some of them are repeated in this section, so they have an explanation similar to the explanation of AOA metrics. The function is reduced with each iteration of the algorithm.

Furthermore, the two main sections of metaheuristic algorithms are exploration and exploitation; a proper balance between them is essential for the algorithm. During the optimization strategy to emphasize exploration and exploitation, each solution dynamically updates its position from the best solution achieved in this dynamic version in the following:

$${x}_{i,j}\left(t+1\right)=\left\{\begin{array}{l}best({x}_{j})\div (D+s)\times (({ub}_{j}-{lb}_{j})\times M+{lb}_{j})), {r}_{1}<0.5\\ best({x}_{j})\times D\times (({ub}_{j}-{lb}_{j})\times M+{lb}_{j})), otherwise\end{array},\right.$$

(11)

$${x}_{i,j}\left(t+1\right)=\left\{\begin{array}{l}best\left({x}_{j}\right)-(D+s)\times (({ub}_{j}-{lb}_{j})\times m+{lb}_{j})), {r}_{2}<0.5\\ best\left({x}_{j}\right)+D\times (({ub}_{j}-{lb}_{j})\times m+{lb}_{j})), otherwise\end{array}.\right.$$

(12)

The value decreases during each iteration, and a dynamic candidate solution function $(D)$ is given by the effect of reducing the percentage of candidate solutions as:

$$D\left(0\right)=1-\sqrt{\frac{c}{{\mathrm{Max}}_{\mathrm{iter}}}},$$

(13)

$$D\left(t+1\right)=D(t)\times 0.99.$$

(14)

Many exploration agents and iterations suggest that using candidate solutions in DAOA will accelerate AOA’s convergence. Also, the improvements enhance the quality of the solution. The algorithm’s ability is often considered an advantage of these algorithms to work without parameters. The use of dynamic functions varies between DAOA and AOA. The DAOA algorithm has the advantage of being parameter adaptive so that the number of parameters is minimal to be adjusted. This contrasts competing algorithms that need parameter tuning for different problems. One of the drawbacks of the algorithm can be mentioned in that the adaptive mechanism depends on the number of iterations rather than improving fitness. The pseudocode of DAOA is illustrated in Algorithm 1.

Algorithm 1 The dynamic form of AOA

2.6 Performance evaluation methods

This section has introduced the metrics that have the role of evaluating the models. Evaluators included weight absolute percentage error (WAPE), correlation coefficient $({R}^{2})$, mean absolute percentage error (MAPE), root mean square error (RMSE), and median absolute percentage error (MDAPE). In addition, the mathematical equations are represented in the following:

$${R}^{2}={\left(\frac{{\sum }_{i=1}^{N}({E}_{i}-\overline{E })({M}_{i}-\overline{M })}{\sqrt{\left[{\sum }_{i=1}^{N}{({E}_{i}-\overline{E })}^{2}\right]\left[{\sum }_{i=1}^{N}{({M}_{i}-\overline{M })}^{2}\right]}}\right)}^{2},$$

(15)

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}{({E}_{i}-{M}_{i})}^{2}},$$

(16)

$$\mathrm{MAPE}=\frac{100}{N}\sum_{i=1}^{N}\frac{\left|{E}_{i}\right|}{\left|{M}_{i}\right|},$$

(17)

$$\mathrm{WAPE}=\mathrm{max}\left[\frac{\left|{E}_{i}-{M}_{j}\right|}{{M}_{j}}\right],$$

(18)

$$\mathrm{MDAPE}=100\times \mathrm{median}\left(\frac{\left|{M}_{i}\right|}{\left|{E}_{i}\right|}\right).$$

(19)

In the above equations, $N$ is the sample number, ${M}_{i}$ indicates the measured value, ${E}_{i}$ determine the estimated value, and $\overline{E },\overline{M }$ are the mean value of the estimated and measured samples, alternatively.

2.7 Hyperparameter

Table 3 presents the hyperparameters for the Support Vector Regression (SVR) model in the context of the proposed hybrid models: SVDA, SVAO, and SVBW. Hyperparameters are crucial in determining the SVR model's behavior and performance, allowing customization based on the specific dataset and prediction goals. Optimal selection of hyperparameters is crucial to achieve the best performance of the SVR model. These values have been carefully tuned to maximize prediction accuracy and are essential in achieving the study's objectives of precise CS prediction in UHPC.

Table 3 The hyperparameters of SVR

3 Results and discussion

The results of hybrid models are examined in two training and testing phases. In this evaluation, 70% of the samples were related to the training phase, and the remaining 30% were related to the test. Table 4 determines the results calculated by models to make a statistical assessment. In the related table, it should be noted that except for R², the rest of the metrics should have their lowest value due to showing the errors in the models. In R², the highest value belonged to SVDA in the training and testing phases, equal to 0.987 and 0.991. The lowest value and, in other words, the weakest performance in R² was related to the SVBW model, equal to 0.967 in training and 0.970 in the test. In RMSE, the most suitable value in training has been achieved by SVDA = 4.98 MPa, which obtained the best value in the test phase via SVAO = 5.25 MPa. In MAPE, the lowest value obtained in training and testing was 2.02 MPa and 2.36 MPa, respectively, which belonged to SVDA. For MDAPE, the lowest value was obtained by SVDA, equal to 1.32 in the training phase and 1.53 MPa in the test. Like other evaluators, alternatively, the SVDA model obtained the lowest value in WAPE, equal to 0.020 and 0.024 MPa. On the other hand, the SVBW model obtained the poorest values in all evaluators and both phases. Broadly speaking, one could infer that DAOA succeeded in achieving a better combination with SVR to obtain CS of UHPC prediction results. In addition, compared to the other two models, BWO has not obtained acceptable values by combining them with SVR. Furthermore, it should be noted that the SVDA and SVAO models have obtained the most appropriate values in the test phase, which indicates that the samples have learned well in the training phase. As a result, they obtained satisfactory values in the testing phase.

Table 4 The results calculated by models to make a statistical assessment

Figure 6 illustrates the scatter plot for hybrid presented models. The scatter of points is related to two evaluators, R² and RMSE, the highest and lowest value of the result is the most appropriate performance, respectively. The points have been analyzed in two phases, including training and testing. For each corresponding phase, the linear fit has been determined, whose angle difference with the midpoint denotes the. proper presentation of. the. model. The. two specified axes are based on the predicted and measured that the middle point has determined the X = Y. organizes. As a result, the. closer the. points are to these coordinates is accepted the more accurately the prediction. In addition, two axes of 1.1 × and 0.9 × specify the overestimated and underestimated predictions of the models, respectively. In SVDA, it can be seen that the points are concentrated on the center line in both phases and are not observed over or under-estimated points. SVAO also performed almost the same as SVDA but with more dispersion than SVDA. On the other hand, for SVBW, there are scattered points and underestimated in some samples.

Fig. 6

The scatter plot for hybrid presented models

Figure 7 shows the comparison bar chart of measured and predicted values. The ideal state of Fig. 7 is that the predicted and measured bar charts should be superimposed, which results in the low error percentage shown in Fig. 8. In SVDA, it can be seen that in some examples, there was a difference between the predicted and the measured, so that the highest error was equal to 7% in the training phase, which with the improvement of itself performance, the difference has been reduced and reached 7.5%. For SVAO, the difference between predicted and measured was more significant in the training phase than SVDA, which was an error equal to 12%. This difference was equal to 4.5%, with an acceptable reduction in the testing phase. On the other hand, for BWO, which had the weakest performance compared to the other two models, it can be seen that in the training phase, there were many differences between the predicted and measured bar charts, which resulted in a 29% error. In addition, the error has reduced to under 10% in the test, which determines that the samples have not been trained well in the training phase. In general, the SVDA, SVAO, and SVBW models were from the most appropriate to the poorest performances in both the comparison bar chart and error percentage, respectively.

Fig. 7

The comparison bar chart of measure and predicted values

Fig. 8

The error percentage of developed models

Figure 9 shows the error percentage based on the violin with a stick plot for the presented models. In the section related to SVDA, it can be seen that in the training phase, the dispersion of errors was low, and most of the density was in the near zero percent range. Moreover, the same behavior is repeated in the test phase, with the difference that the error percentage has decreased. For SVAO, even though the prediction error went up to 14% in the training phase, they can be called outliers, and most of the errors were below 10%. Also, the errors were obtained below 5% by improving the performance in the test phase of the corresponding model. Finally, for SVBW in the training phase, the dispersion of errors has gone up to 12%, although almost 75% of the errors were below 10%. On the other hand, SVBW has observed a weakening performance in the test where the dispersion and increase of errors are evident. Generally, the most desirable performance and the least error were related to SVDA in both phases.

Fig. 9

The error percentage based on violin with stick plot for presented models

4 Conclusion

In recent years, many experimental studies have been conducted to study ultra-high-performance concrete (UHPC). Regardless, the relationship between mixture variables and the engineering properties of UHPC is highly challenging and non-linear to design employing a conventional statistical approach. A robust and sophisticated method is needed to rationalize the variety of relevant experimental data available for creating estimative methods of reasonable accuracy and provide insight into aspects of non-linear materials science. Machine learning (ML) is a potent strategy that can reveal underlying patterns in complex datasets. Therefore, this study seeks to use state-of-the-art ML techniques consisting of support vector regression (SVR) to estimate the UHPC compressive strength (CS) utilizing a comprehensive published literature observed dataset containing 165 experiment samples and eight input characteristics. In addition, three meta-heuristic algorithms have been used to enhance the performance of the related model, which include the Dynamic Arithmetic Optimization Algorithm (DAOA), Arithmetic Optimization Algorithm (AOA), and Black Widow Optimization (BWO). The results of the developed hybrid models were as follows:

• In RMSE, SVDA and SVAO have obtained the best values in the training and testing phases, respectively, so they have a difference of almost 41% with SVBW.

• For R², the highest value was equal to 0.99 MPa, which belonged to SVDA, so it had a very small difference with SVAO and a difference of 2% with SVBW.

• The lowest value in MAPE = 1.35 MPa was associated with SVDA, which. obtained a variance of. 27 to 90 percent within SVAO and. SVBW, alternatively.

• In. MDAPE and other metrics, SVDA obtained the most appropriate value, with a. variance of. 71% with SVAO and 51% with SVBW.

• Finally, for WAPE, the SVDA could obtain the lowest value equal to 0.0135 MPa, with a difference of 23% and 46% by SVAO and SVBW, respectively.