An explanatory machine learning model for forecasting compressive strength of high-performance concrete

Abstract

High-performance concrete (HPC) is one of the concrete types with high strength, good performance, and high durability, which has been considered in the structural industry. Testing and sampling this type of concrete to determine its mechanical properties is daunting and complex. In addition, human and environmental factors were significant in the preparation of samples, which was also time-consuming and energy-consuming. Artificial intelligence (AI) can be used to eliminate and reduce these factors. This article intends to use the machine learning (ML) method to forecast one of the HPC mechanical properties: compressive strength (CS). The experimental data set used from the published article includes 168 samples, of which 70% (118) of the sample belonged to training and 30% (50) to the testing phase. Least square support vector regression (LSSVR) is one of the ML models used for forecasting in this article. In addition, meta-heuristic algorithms have been utilized to obtain the target to improve the accuracy and reduce the error. Algorithms include Honey Badger algorithm (HBA), COOT optimization algorithm (COA), and generalized normal distribution optimization (GNDO). Combining the algorithms with the introduced model forms a hybrid format evaluated by metrics in the training and testing phases. By evaluating the hybrid models, it has been determined that they can forecast with high accuracy and are reliable. In general, the LSHB hybrid model obtained the highest R² and the lowest error compared to other models.

1 Introduction

High-performance concrete (HPC) is the material of a building defined as concrete that satisfies high durability, strength, and workability (Aïtcin 1998). The American Concrete Institute (ACI) identifies HPC with specific combinations of uniformity and performance needs that are not always routinely achievable, operating normal mixing, established ingredients, placement, and curing practices (Russell 1999). While normal concrete combines water, coarse and fine aggregates, and Portland cement, HPC uses silica fume, fly ash, and superplasticizer as mineral and chemical admixtures (Bharatkumar et al. 2001; Lim et al. 2004). Using mineral admixtures as partial cement substitutes increases concrete behaviour via acting as pozzolanic materials and mineral admixtures. Conversely, chemical admixtures improve the HPC compressive strength (CS) by decreasing the porosity and water content within the hydrated cement paste (Larrard and Malier 2018; Huang et al. 2022).

Compressive strength (CS) is an important mechanical property, perhaps the most important quality of concrete, and is usually achieved by measuring concrete samples after standard curing for 28 days (Ni and Wang 2000). Therefore, developing forecasting models for the early specification of CS has received much attention. CS values can be forecasted using nonlinear and linear regression models for conventional concrete. However, for HPC, the relationship between input factors and CS is highly nonlinear; it gets complicated as the number of input factors enhancements. Therefore, regression models are improper for HPC’s estimation of CS values. Hence, models according to artificial intelligence (AI) are attracting attention (Benemaran and Esmaeili-Falak 2020; Sarkhani Benemaran et al. 2022; Yin et al. 2021; Cheng et al. 2022). Forecasting the nonlinear relationship between concrete composition and strength based on machine learning (ML) demands complete, large, consistent data sets. However, data sets are often incomplete due to missing data corresponding to various input characteristics, making it difficult to develop robust ML-based forecast models, so the availability of such data sets is critical. Moreover, as the complexity of these ML models improves, the results become more difficult to interpret. Interpreting these results is important for developing efficient material design processes to improve material performance (Lyngdoh et al. 2022; Yaltaghian and Khiabani 2023; Masoumi et al. 2020).

Yeh (1998) suggested a new neural network architecture and studied its efficiency and precision in modelling concrete CS. Sobhani et al. (2010) investigated some adaptive neuro-fuzzy inference systems (ANFIS), artificial neural networks (ANN), and regression models for estimating 28-day CS of concrete. They indicated that ANFIS and ANN could estimate CS with satisfactory performance, but regression models are unreliable. Prasad et al. (Prasad et al. 2009) employed ANN for forecasting 28-day CS of normal, HPC, and high-strength self-compacting concrete (SCC) with large amounts of fly ash. Alshihri et al. (Alshihri et al. 2009) studied a method to forecast the CS of lightweight concrete (LWC) utilizing backpropagation (BP) and cascade correlation (CC) neural networks. Their identification demonstrated that the ANN model was sufficient to forecast the LWC CS.

Topcu and Saridemir (2008) investigated a fuzzy logic model with ANN to forecast 7-, 28-, and 90-day concrete CS, including low- and high-lime fly ash. Their conclusions indicated that fuzzy logic models and ANN are practical models to forecast concrete CS. Chen et al. (2012) suggested a hybrid for estimating CS of HPC by incorporating fast, chaotic genetic algorithms in an evolutionary fuzzy support vector machine inference model (EFSIMT), weighted support vector machines (SVM), and fuzzy logic for time series data. They showed that the EFSIMT approach obtained higher performance goals compared to SVM. In addition, they determined that SVM performed the worst compared to ANN and EFSIMT. Zhang et al. (2020a) used the random forest (RF) algorithm to calculate variable importance in their study, and they imputed the data using kNN-10. In a separate study, Nguyen et al. (2021) used XGBoost to generate feature importance for concrete tensile strength. Both studies assessed feature importance by directly examining the data or observing the decrease in model performance. However, there has been no effort to integrate data interpretation algorithms with machine learning (ML)-based models. Therefore, there is a need for a more efficient integration of a robust data interpretation algorithm with ML-based models for concrete strength prediction, to develop a powerful and interpretable predictive tool.

The novelty of this article is to enhance the SVM model’s accuracy in estimating the HPC CS. Despite the many advantages of SVMs, the theory of SVMs only covers parameter specification and kernel selection for specific values of regularization and kernel parameters. In addition, the existing SVM method has a very complex algorithm and requires much memory. This study proposed the least square support vector regression (LSSVR) model, a lower calculation cost conversion of the support vector regression (SVR) model. Nevertheless, like SVR, the LSSVR’s effectiveness model relies on kernel parameter settings and proper regularization, which can be defined as optimization issues.

Moreover, the meta-heuristic algorithm has been combined with LSSVR to improve the efficiency and accuracy of forecasting CS and optimize the output. The algorithms are included Honey Badger algorithm (HBA), COOT optimization algorithm (COA), and generalized normal distribution optimization (GNDO). The models were in hybrid form and framework of LSSVR + HBA (LSHB), LSSVR + COA (LSCO), and LSSVR + GNDO (LSGN). The hybrid models have been evaluated with several indicators for choosing the most suitable model. In addition, the models’ performance compared via the experimental data set used from the published article include 168 samples, of which 70% (118) of the sample belonged to training and 30% (50) to the testing phase.

2 Materials and methodology

2.1 Data gathering

This study used the experimental data set published in Lam et al. (1998). The main concrete variables are water, coarse and fine aggregates and binders. In addition to these main ingredients, other additives, such as fly ash (FA), micro-silica (MS), and superplasticizer (SP), can be added to the mixture to improve concrete properties. On the other side, it is clear that the longer the time of the curing, the higher the CS. Hence, considering to use all these components as inputs for improving the completeness of the model. Eight components were chosen as input components based on their impact on CS forecasting using FA and MS in samples of different ages. The input variables consisted of sample age (age), superplasticizer to total binder ratio (SP/B), micro-silica to total binder ratio (MS/B), fly ash to total binder ratio (FA/B), water to total binder ratio (W/B), the ratio of coarse aggregate to total binder (CA/B), coarse aggregate to the total aggregate ratio (CA/TA), and total binder content (B), which the output variable is CS. Tables 1 and 2 indicate 70% (118) of training and 30% (50) of testing samples, respectively. Furthermore, the minimum (min), standard deviation (St. dev.), maximum (max), and average (avg) values of variables.

Table 1 Statistical attributes of inputs and CS in the train phase

Table 2 Statistical attributes of inputs and CS in the test phase

2.2 Least square support vector regression (LSSVR)

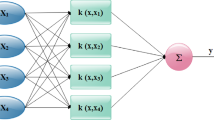
The least squares support vector machine algorithm (LS-SVM) is a refinement of the standard SVM, which is computationally more computationally efficient than the standard SVM by transforming the quadratic optimization issues into a transformed, more linear system of equations. Instead of solving the quadratic programming issues in standard SVM, the LS-SVM algorithm solves a linear set of equations. LS-SVM is able to be utilized for both regression and classification troubles. The present work uses LS-SVR to predict the CS of HPC in regression form. Here is an overview of LS-SVR:

Input x_i (experimental variable) and output y_i (forecasted value: local precipitation). Based on the LS-SVR approach, the nonlinear LS-SVR function is able to be presented in the following equation:

$$f\left(x\right)={w}^{\mathrm{^{\prime}}}m+t$$

(1)

here $f$ represents the relationship between local precipitation and experimental variables, and $w$ is m-dimensional weight vectors, $m$ and $t$ show mapping functions and bias terms, alternatively (Kisi 2015).

The regression issue employing the function forecasting error for the structure minimization principle can be presented in the following:

$$\mathrm{min}G\left(w,r\right)=\frac{1}{2}{w}^{\mathrm{^{\prime}}}w+\frac{p}{2}\sum_{i=1}^{n}{r}_{i}^{2}$$

(2)

It has the following limitations:

$${y}_{i}={w}^{\mathrm{^{\prime}}}m\left({x}_{i}\right)+t+{r}_{i},\quad i=1, 2, \dots , n$$

(3)

where ${r}_{i}$ represents the training error of ${x}_{i}$ and p is the penalty term.

For solving for $w$ and $r$, use Lagrange multiplier optimal programming for solving Eq. (2). The objective function can be defined by transforming the constrained issue into an unconstrained one. The Lagrange function F is able to be determined in the following equation:

$$F\left(w,t,r,a\right)=G\left(w,r\right)-\sum_{i=1}^{n}{a}_{i}\left\{{w}^{\mathrm{^{\prime}}}m\left({x}_{i}\right)+t+{r}_{i}-{y}_{i}\right\}$$

(4)

Here ${a}_{i}$ is the multipliers’ Lagrange. Considering the Karush–Kuhn–Tucker (KKT) condition, the partial results of Eq. (5) for $w$, $t$, $r$, and $a$, alternatively are

$$\left\{\begin{array}{c}w=\sum_{i=1}^{n}{a}_{i}m({x}_{i})\\ \sum_{i=1}^{n}{a}_{i}=0\\ {a}_{i}=p{r}_{i}\\ {w}^{\mathrm{^{\prime}}}m\left({x}_{i}\right)+t+{r}_{i}-{y}_{i}=0\end{array}\right.$$

(5)

Then the linear equation can be derived after removing ${r}_{i}$ and $w$ in the following equation:

$$\left[\begin{array}{cc}0& {Y}^{\mathrm{^{\prime}}}\\ Y& {ZZ}^{\mathrm{^{\prime}}}+\frac{H}{p}\end{array}\right]\left[\begin{array}{c}t\\ a\end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

(6)

here $Y=\left({y}_{1}, \dots , {y}_{n}\right),Z=\left({m\left({x}_{1}\right)}^{\mathrm{^{\prime}}}{y}_{1}, \dots , {m\left({x}_{n}\right)}^{\mathrm{^{\prime}}}{y}_{n}\right)$, $H=(1, \dots , n)$, $a=({a}_{1}, \dots , {a}_{n})$.

The function of kernel $C\left(x,{x}_{i}\right)={m\left({x}_{1}\right)}^{\mathrm{^{\prime}}}m\left({x}_{i}\right), i=1, \dots , n$, satisfied with the condition of Mercer (Suykens et al. 2002). Consequently, LS-SVR can be expressed in the following equation:

$$f\left(x\right)=\sum_{i=1}^{n}{a}_{i}C\left(x,{x}_{i}\right)+t$$

(7)

2.3 Honey Badger algorithm (HBA)

The Honey Badger algorithm (HBA) mimics the Honey Badgers searching manner (Hashim et al. 2022). To find food sources, honeyguide birds are sniffed and dug or followed by honey badgers. The first case is named digging mode, and the second is named honey mode. In the previous mode, it utilizes scent capability to get closer to the location of prey. Once there, it moves around its prey to choose a suitable spot to dig and capture it. In the latter mode, honey badgers use honeyguide bird guides for locating hives directly.

Initialize each location based on the badgers’ number (N) and Eq. (8):

$${x}_{i}={lb}_{i}+{r}_{1}\times ({ub}_{i}-{lb}_{i})$$

(8)

where ${r}_{1}$ shows a random number between 0 and 1, ${x}_{i}$ shows the ith honey badger’s position associated with the candidate solution for the N population, and ${ub}_{i}$ and ${lb}_{i}$ show the explore region’s upper and lower bounds, respectively.

The intensity was the distance between the honey badger and the prey and prey concentration. ${L}_{i}$ shows the prey odour severity. When the smell is powerful, the movement is fast and vice versa, represented by the inverse square law (Kapner et al. 2007) as given by the following equation:

$$\begin{gathered} L_{i} = r_{2} \times \frac{C}{{4\pi d_{i}^{2} }} \hfill \\ C = \left( {x_{i} - x_{i + 1} } \right)^{2} \hfill \\ d_{i} = x_{{{\text{prey}}}} - x_{i} \hfill \\ \end{gathered}$$

(9)

Here ${r}_{2}$ is the random number between 0 and 1, $C$ shows the strength of concentration, ${d}_{i}$ is the distance between the ith badger and the prey.

The factor of density (f) manages the time-varying randomness to provide a smooth transition from exploration to exploitation. In addition, updating the factor of the density (d), which reduces with repetition, to reduce the randomness over time utilizing the following equation:

$$a=S\times exp\left(\frac{-t}{{t}_{\mathrm{max}}}\right)$$

(10)

where ${t}_{\mathrm{max}}$ is a maximum iteration number, and $S$ shows a constant $\ge 1$ (default = 2).

Escaping from the local optimum step and the position of agents’ phases are employed for exiting the optimal local region. The presented algorithm operates an indicator (I) that alterations the explore direction to take advantage of large opportunities for agents to traverse the search space closely.

As previously mentioned, the HBA (${x}_{\mathrm{new}}$) location update strategies are split into two parts, the "honey phase" and the “digging phase”. Here is a suitable illustration.

A badger shows an action resembling the Cardioid shape (Akopyan 2015) during the digging phase. Cardioid motion can be simulated by the following equation:

$${x}_{\mathrm{new}}={x}_{\mathrm{prey}}+I\times b\times L\times {x}_{\mathrm{prey}}+I\times {r}_{3}\times a\times {d}_{i}\times \left|\mathrm{cos}(2\pi {r}_{4})\times \left[1-\mathrm{cos}(2\pi {r}_{5})\right]\right|$$

(11)

here ${x}_{\mathrm{prey}}$ shows the position of the prey; this is the finest position found thus far—that is to say, the finest overall position. b ≥ 1 (default = 6) is the capability of the badger to get food, ${r}_{3}$, ${r}_{4}$, and ${r}_{5}$ shows 3 various accidental numbers among 0 and 1, and $I$ acts as a explore direction change flag, which is defined by the following equation:

$$\mathrm{I}=\left\{\begin{array}{l}1\, if \,\quad {r}_{6}\le 0.5\\ -1 \quad else\end{array}\right.$$

(12)

A honey badger is highly dependent on the odour intensity of its prey, the distance between the badger and the prey ${d}_{i}$ and the time-varying foraging influence factor $a$ during the digging phase. In addition, a badger can pick up on any F-noise, allowing it to find its prey’s location even better during foraging.

If the honey badger follows the honey leader to attain the hive, it is given by the following equation:

$${x}_{\mathrm{new}}={x}_{\mathrm{prey}}+I\times {r}_{7}\times a\times {d}_{i}$$

(13)

where ${x}_{\mathrm{new}}$ refers to the new position of the honey badger and ${x}_{prey}$ shows the position of the prey. $I$ and $a$ indicate calculated employing Eqs. (12) and (10), alternatively. Based on the distance information ${d}_{i}$, can observe how the badger explores near the prey position ${x}_{prey}$ found so far in Eq. (13). The exploration is subject to time-varying search behaviour. Honey badgers can also find $I$ obstacles. In addition, Algorithm 1 has shown the pseudo-code of HBA (Hashim et al. 2022).

2.4 COOT optimization algorithm (COA)

Coots are small waterfowl belonging to the Rallidae family. They form the genus Fulica, Latin for “coot” (Paillisson and Marion 2001).

The algorithm starts with x = {x₁, x₂,…, x_n} primary random populations (Naruei and Keynia 2021). For determining target values $V=\left\{{V}_{1},{V}_{2}, \dots ,{V}_{n}\right\}$, the random population is frequently assessed by the target function. Furthermore, this is powered by a rules’ set that form the optimization method’s core. Population-based optimization methods search an optimal set of optimization issues, so it is not guaranteed that a solution will be found in a single pass. Thus, using sufficient optimization steps and random solutions increases the likelihood of finding the global optimum. The population is accidentally developed in visible space according to the following equation:

$$P\left(i\right)=r\left(1,d\right)\times \left(ub-lb\right)+lb$$

(14)

here $P\left(i\right)$ shows the Coot’s position, $lb$, $ub$ are the lower and upper bound of exploring space, $d$ is the dimensions of the trouble.

In addition, we need to compute each solution’s fitness utilizing the objective function Oi = f(x) after specifying the location of each agent and producing the initial population. Select several coots as the group leader. Leader selection is random.

We have implemented the four motions of the Coot on the water surface described in the earlier section.

To assume a random location based on Eq. (15) in the explore space and move the Coot toward the accidental location for achieving random motion.

$$G=r\left(1,d\right)\times \left(ub-lb\right)+lb$$

(15)

The Coot’s movements explore various parts of the explore space. This move will bring the algorithm out of the local optimum if the algorithm is blocked in a local optimum. The new position of Coot is calculated on the basis of the following equation:

$$P\left(i\right)=P\left(i\right)+E\times r\times (G-P\left(i\right))$$

(16)

where $r$ demonstrates a random number among 0 and 1, and $E$ is determined in the following equation:

$$E=1-T\times \left(\frac{1}{{\mathrm{Max}}_{\mathrm{Iter}}}\right)$$

(17)

where ${\mathrm{Max}}_{\mathrm{Iter}}$ shows the maximum iteration, and $T$ show the present iteration.

Chain movement can be implemented using the two coots’ average position. Another way to achieve chain motion is to compute the distance vector among the two coots, then move the Great Coot closer to the other by about half the vector distance. Using the first method, Coot’s new position is computed based on the following equation:

$$P\left(i\right)=0.5\times (P\left(i-1\right)+P\left(i\right))$$

(18)

here $P\left(i-1\right)$ shows the second Coot.

Sometimes, the remaining coots should control their location according to the group’s leader and approach them, and a few coots in the face of the group manage the group. The idea is to control its location according to the leader. The leader’s average location can be considered, and the Coot can update its location according to this average location. Assuming the average location leads to premature convergence. For implementing the move, a can be chosen a leader using the mechanism based on the following equation:

$$L=1+(nN)$$

(19)

where L indicates the index number of the leader, n shows the present coot number, and $N$ shows the number of leaders.

According to the leader’s location, the Coot must update its position. The Coot’s next location according to chosen leader can be computed in the following equation:

$$P\left(i\right)=l+2\times r\times \mathrm{cos}(2\pi {r}_{1})\times (l-P\left(i\right))$$

(20)

here $P\left(i\right)$ shows the Coot’s present location, $l$ shows the location of chosen leader, and ${r}_{1}$ indicates a random number in the interval [− 1, 1].

The group needs to align itself toward the purpose, so the leader needs to update his position toward the goals. Equation (21) recommends updating the leader’s location as the equation searches the suitable locations around the present suite spot. Leaders must pull away from their present optimal location to find a suitable position. The equation delivers a great way to get away from or near the optimal location.

$$l=\left\{\begin{array}{l}D\times r\times \mathrm{cos}\left(2\pi {r}_{1}\right)\times \left(B-l\right) \quad if \quad r<0.5 (a)\\ D\times r\times \mathrm{cos}\left(2\pi {r}_{1}\right)\times \left(B-l\right)-B \quad if \quad r\ge 0.5 (b)\end{array}\right\}$$

(21)

Here $B$ shows the finest location found so far, and $D$ is computed based on the following equation:

$$D=1-T\times \left(\frac{1}{{\mathrm{Max}}_{\mathrm{Iter}}}\right)$$

(22)

Moreover, the COA pseudo-code has been indicated in Algorithm 2.

2.5 Generalized Normal distribution optimization (GNDO)

Generalized normal distribution optimization (GNDO) mimics the normal distribution theory (Zhang et al. 2020b). The normal distribution is a very important tool for explaining natural phenomena called Gaussian distribution. The normal distribution can be determined by assuming a random variable x follows a contingency distribution with position parameter μ and scale parameter δ, whose contingency density function is able to be stated as

$$f\left(x\right)=\frac{1}{\sqrt{2\pi \delta }}.\mathrm{exp}\left(-\frac{{(x-\mu )}^{2}}{2\delta }\right)$$

(23)

where x shows a normal random variable and the distribution is normal, µ is the location parameter, and δ is the scale parameter used to determine the mean and standard variance of the random variable, respectively. Local exploitation refers to finding the finest solution in the exploration space that contains everyone’s present location. Can construct a generalized normal distribution model for optimization based on the relationship between the normal distribution and the distribution of individuals in the population in the following equation:

$${v}_{i}^{t}={\mu }_{i}+{\delta }_{i}\times \eta , i=1, 2, 3, \dots , N$$

(24)

where ${v}_{i}^{t}$ denotes the ith individuals’ tracking vector at time t, ${\mu }_{i}$ denotes the ith individual’s generalized mean position, ${\delta }_{i}$ denotes the generalized standard variance, and $\eta$ is the penalty that shows the coefficient. Furthermore, ${\mu }_{i}$, ${\delta }_{i}$, and $\eta$ can be determined in the following:

$${\mu }_{i}=\frac{1}{3}({x}_{i}^{t}+{x}_{\mathrm{best}}^{t}+M)$$

(25)

$${\delta }_{i}=\sqrt{\frac{1}{3}[{({x}_{i}^{t}-\mu )}^{2}+{({x}_{\mathrm{best}}^{t}-\mu )}^{2}+{(M-\mu )}^{2}]}$$

(26)

$$\eta =\left\{\begin{array}{l}\sqrt{-\mathrm{log}\left({\lambda }_{1}\right)}\times \mathrm{cos}\left(2\pi {\lambda }_{2}\right), \quad if \quad a\le b\\ \sqrt{-\mathrm{log}\left({\lambda }_{1}\right)}\times \mathrm{cos}\left(2\pi {\lambda }_{2}+\pi \right), \quad if \quad a>b\end{array}\right.$$

(27)

where $a$, $b$, ${\lambda }_{1}$, and ${\lambda }_{2}$ denote random numbers between 0 and 1, ${x}_{\mathrm{best}}^{t}$ denotes the present finest position, and $M$ denotes the present population means position. In addition, M can be computed in the following equation:

$$M=\frac{\sum_{i=1}^{N}{x}_{i}^{t}}{N}$$

(28)

Global exploration is searching language zones around the world to find hopeful zones. The global scan on GNDO assumes 3 accidentally elected persons, which can be expressed as

$${v}_{i}^{t}={x}_{i}^{t}+\beta \times \left(\left|{\lambda }_{3}\right|\times {v}_{1}\right)+(1-\beta )\times \left(\left|{\lambda }_{4}\right|\times {v}_{2}\right)$$

(29)

where ${\lambda }_{3}$ and ${\lambda }_{4}$ denote two random numbers following a standard normal distribution, $\beta$ is a tuning parameter denoting a random number between 0 and 1, and ${v}_{1}$ and ${v}_{2}$ denote two tracking vectors. In addition, ${v}_{1}$ and ${v}_{2}$ can be computed in the following:

$${v}_{1}=\left\{\begin{array}{l}{x}_{i}^{t}-{x}_{p1}^{t}, \quad if \quad f\left({x}_{i}^{t}\right)<f\left({x}_{p1}^{t}\right)\\ {x}_{p1}^{t}-{x}_{i}^{t}, \quad otherwise\end{array}\right.$$

(30)

$${v}_{2}=\left\{\begin{array}{l}{x}_{p2}^{t}-{x}_{p3}^{t}, \quad if \quad f\left({x}_{p2}^{t}\right)<f\left({x}_{p3}^{t}\right)\\ {x}_{p3}^{t}-{x}_{p2}^{t}, \quad otherwise\end{array}\right.$$

(31)

where $p1$, $p2$, and $p3$ indicate 3 random integers chosen from 1 to n.

2.6 Performance evaluation methods

Five performance indicators are commonly employed in concrete estimative evaluations. In addition, they were used for assessing the machine learning method proposed in this paper. The correlation coefficient (R²) determines an amount of how acceptable the explanatory variables explain the variable’s measured response. Provides the virtue of fit of the model. The suitable estimative potential of such a model is defined with a higher R² value. Root mean squared error (RMSE) shows a forecast accuracy’s statistical measure. RMSE calculates a response variable’s variance, which can be described via models. Mean absolute error (MAE) indicates a statistic that computes the average error size of the model’s forecasting. Furthermore, variance account factor (VAF) and mean absolute percentage error (MAPE) are presented in the following:

$${R}^{2}={\left(\frac{{\sum }_{i=1}^{n}\left({p}_{i}-\overline{p }\right)\left({r}_{i}-\overline{r }\right)}{\sqrt{\left[{\sum }_{i=1}^{n}{\left({p}_{i}-p\right)}^{2}\right]\left[{\sum }_{i=1}^{n}{\left({r}_{i}-\overline{r }\right)}^{2}\right]}}\right)}^{2}$$

(32)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\sum }_{i=1}^{n}{\left({r}_{i}-{p}_{i}\right)}^{2}}$$

(33)

$$\mathrm{MAE}=\frac{1}{n}\sum_{i=1}^{n}\left|{p}_{i}-{r}_{i}\right|$$

(34)

$$\mathrm{MAPE}=\frac{100}{n}\sum_{i}^{n}\frac{\left|{t}_{i}\right|}{\left|{p}_{i}\right|}$$

(35)

$$\mathrm{VAF}=\left(1-\frac{var({r}_{i}-{p}_{i})}{var({r}_{i})}\right)\times 100$$

(36)

where ${p}_{i}$ and ${r}_{i}$ determine the forecasted and measured values, $\overline{r }$ and $\overline{p }$ show the mean values of measured and forecasted, respectively; also, $n$ is the sample number.

3 Results and discussion

3.1 Hyperparameter

LSSVR is a type of support vector machine (SVM) that is used for regression tasks. Like other machine learning algorithms, LSSVR has hyperparameters that must be set before training the model (Kovačević et al. 2016, 2021). Table 3 shows the important hyperparameters of LSSVR. For each optimization algorithm, the table shows the values of C and Gamma that were found to give the best performance on the data set being used. Specifically, for LSHB, the optimal hyperparameters were found to be $C=938.505$ and $\mathrm{Gamma}=917.994$; for LSCO, the optimal hyperparameters were C = 895.8666 and Gamma = 801.9936; and for LSGN, the optimal hyperparameters were $C=980.1297$ and $\mathrm{Gamma}=793.2765$. These hyperparameters were likely found through a process of hyperparameter tuning, where the optimization algorithms were used to search through a range of possible hyperparameter values to find the combination that resulted in the best performance on a held-out validation set. The specific range of searched hyperparameter values and the performance metric used to evaluate the models are not shown in the table but would be important to consider for a full understanding of the hyperparameter tuning process.

Table 3 Results of hyperparameters

In addition, Table 4 displays the initiation parameters for three optimization algorithms (HBA, COA, and GNDO) in the context of a practical implementation. The initiation parameters are used to set up the optimisation algorithms’ initial conditions, including the population size, the range of variable values, and the maximum number of iterations. For HBA, the population size is 50, and the maximum number of iterations is 100. The beta and C parameters are also specified, with beta set to 6 and C set to 2. The lower and upper bounds are set to 0 and 1000, respectively. For COA, the population size is also set to 50, and the maximum number of iterations is set to 100. In addition, the number of leaders and COOTS are specified, with n_leader set to 5, and n_COOT set to 45. The lower and upper bounds are set to 0 and 1000, respectively. For GNDO, the population size and maximum number of iterations are as same as other optimizers. The lower and upper bounds are set to 0 and 1000, respectively. It is worth noting that these initiation parameters are specific to the problem being addressed and may need to be adjusted for different problems or optimization algorithms.

Table 4 Initiation parameter HBA

3.2 Comparing the performance

This section examines the present models according to the metrics explained in the previous section. In evaluating the models, the highest value of R² and VAF and the lowest value of RMSE, MAE, and MAPE are considered. Table 5 demonstrates the obtained model values in the evaluators in two testing and training phases. 70% and 30% of the samples are assigned to the training and testing phase. According to Table 5, the highest R² value equal to 0.999 was obtained for LSHB_Train, and the lowest value was obtained by LSGN_Test equal to 0.982. For RMSE, the lowest value was for LSHB_Train = 0.377, and the highest was for LSGN_Test = 2.579. In MAE, LSHB_Train = 0.234 had the finest performance, while LSGN_Test = 1.979 had the worst performance. The noteworthy point in evaluating the models is that all the models have obtained the highest value in the training section, and their performance has weakened in the testing section, which indicates that the models are not well trained in the training section. In MAPE, the most appropriate value was obtained by LSGB_Train = 0.428, while the poorest value belonged to LSGN_Test = 3.165. Finally, for VAF, which, like R², is the highest value of the finest performance criterion, the most satisfactory value is LSHB_Train = 99.95, and the lowest value is obtained by LSGN_Test = 79.66. From the strongest to the weakest performance, LSHB, LSCO, and LSGN have generally performed. In addition, it was shown that combining HBA with LSSVR can provide a suitable model with high accuracy for forecasting.

Table 5 Results obtained from the proposed models

Figure 1 shows the Scatter plot of forecasted and measured CS in two testing and training phases. The corresponding shape is determined based on two evaluators, R² and RMSE, which determine being in a series and dispersion or density, respectively. In addition, the center line component, which is based on X = Y coordinates, and the linear fit component have been in two phases of training and testing. The difference in the angle of these two lines indicates the appropriate or poor performance of the models. In LSHB, due to the high value of R² and the lower RMSE in training compared to testing; as a result, it can be seen that there is less dispersion in training compared to testing, and the difference between the angle of linear fit and the center line is smaller. On the other hand, LSCO and LSGN models have similar performance in the two phases of training and testing. However, considering that LSGN has the highest RMSE and the lowest R² in both the testing and training phases, it can be seen that the scatter of points in this model is more than the other two models.

Fig. 1

Scatter plot of forecasted and measured CS

Figure 2 compares forecasted and measured CS in two training and testing phases. The ideal situation is such that the forecasted and measured behaviour is similar. The models performed almost the same in the training phase, but with a closer look at samples 100–109, it can be seen that LSHB had a smaller difference with the measured than the other two models. In addition, it can be seen in the test phase that LSHB has the most appropriate performance, and LSGN has shown a relatively weak performance. In general, it is able to be deduced that the models performed more satisfactorily in the training phase than the test, and the combined LSHB model had higher accuracy in both phases compared to the LSCO and LSGN models.

Fig. 2

Comparison between forecasted and measured CS

Figure 3 shows the error percentage in the train and test phases. As mentioned, 70% of the samples were related to the training section and 30% to the testing section. The LSHB model recorded the highest error percentage in the training at almost 3%, which increased to 5.5% as the performance weakened. In LSCO, the highest percentage of error in training was equal to 6.2%, which, like LSHB, was obtained by increasing the error in testing equal to 9.2%. Finally, for LSGN, the highest error percentage was equal to 9%, the highest among the models, and the error in the test reached almost 12%. In general, it can be seen that the LSHB model had the least error in the two phases of training and testing, and the other two models were also reliable for forecasting.

Fig. 3

Error percentage in the train and test phase

Figure 4 shows the box normal for the error percentage of the presented models. In LSHB, it can be seen that in the training phase, the average error was 0%, and its normal distribution was sharp and normal, showing this less dispersion. In addition, the errors were good in the dispersion test, below 10%. In LSCO, the dispersion of samples has been evident in both phases, and a flatter normal distribution has been registered, but despite this, the highest error below 10% has been obtained. Finally, for LSGN, which had the highest and most scattered error, only in the test phase was a sample above 10% obtained, which can be called outlier data. The normal distribution of LSGN is also flatter than the other two models and has a lower frequency close to zero. In general, it can be concluded that all three models performed well, but LSHB recorded the finest output.

Fig. 4

Box-normal for the error percentage of the presented models

4 Conclusion

Due to its durability and workability, high-performance concrete (HPC) has performed better than ordinary concrete in special structures. However, obtaining the values of the mechanical properties of this type of concrete in a laboratory has been a time-consuming and energy-consuming task. For this reason, learning machines have replaced human experiments. This study’s novelty is introducing one of the machine learning methods, including LSSVR, to forecast HPC compressive strength (CS). In addition, to increase the accuracy and get the least errors, the corresponding model was combined with three meta-heuristic algorithms and formed a hybrid model, which the algorithms include Honey Badger algorithm (HBA), COOT optimization algorithm (COA), and generalized normal distribution optimization (GNDO). In addition, in this article, several metrics were used to evaluate the performance of the models, including R², RMSE, MAE, MAPE, and VAF. In evaluating the models, it was observed that HBA obtained a better combination with LSSVR. According to the obtained outputs, it was observed that in R², the models obtained close results and did not differ much from each other. In RMSE, the most appropriate value obtained by LSHB with LSCO and LSGN has a difference of 62 and 72 per cent and 59 and 69 per cent recorded in MAE, respectively. The difference is obtained for MAPE with LSCO = 61.5% and LSGN = 71%. In VAF, the highest value obtained by LSHB in the training phase had values close to each other, but in the testing phase, the better performance of the models with each other was evident. In general, it can be concluded that machine learning methods are reliable for forecasting, and algorithms can increase the performance of models in terms of accuracy and error reduction.