Risk analysis of earthen embankment considering cross-correlated spatially variable soil parameters subjected to pore pressure and seismic loadings

Abstract

The deterministic slope stability analysis does not consider uncertainties that originate due to various factors such as spatial variability in properties of soil, mechanical and human measurement errors, etc. In this study, a probabilistic slope stability analysis (PSSA) is performed, considering effective cohesion, effective angle of internal friction and unit weight of soil as spatially variable parameters subjected to pore pressure and seismic loadings. Furthermore, the cross-correlation between the soil parameters is taken into consideration while performing PSSA using Monte Carlo and Subset Simulation methods with UPSS 3.0 module, developed in an MS-Excel spreadsheet environment. Detailed discussions have been presented on the choice of cross-correlation coefficients between soil parameters, namely effective cohesion, effective angle of internal friction and unit weight. The results of PSSA are represented in the form of complementary cumulative distribution function (CCDF) plots, and these plots are helpful for determining the condition in which failure occurs. It is observed that when spatial variability of correlated soil parameters is considered along with seismic and pore pressure loadings, the chances of slope failure increases. Furthermore, the probabilistic output response is also plotted in the form of major and minor principal stresses observed on the failure/slip surface of the slope at the moment when the failure is initiated.

1 Introduction

Earthen embankments are important engineering structures for managing water, such as storing and supplying water for irrigation, generating hydroelectric power, protecting the community during floods, etc. (Liang et al. 1999). The stability of an embankment is majorly affected by external loadings such as pore-pressure loading and seismic loading (Johari et al. 2015a, b). Thus, geotechnical engineers need to ensure that an embankment is safe against all types of loading against all possible failure modes, including slope failure. The stability of the slope can be analysed with various techniques such as the limit equilibrium method (Fellenius 1936; Bishop 1955; Janbu 1954, 1968; Morgenstern and Price 1965; Spencer 1967; Sarma 1973), finite element method (Griffiths and Lane 1999) and finite difference method (Soren et al. 2014). It is a common knowledge that the properties of soil vary from one location to another in both horizontal and vertical directions (Hamrouni et al. 2022). The soil properties, such as effective cohesion $\left( {c^{\prime}} \right)$, effective angle of internal friction $\left( {\varphi^{\prime}} \right)$, and unit weight $\left( \gamma \right)$ are correlated with each other. The experimental results suggest that $c^{\prime}$−$\varphi^{\prime}$ is negatively cross-correlated, whereas $\varphi^{\prime}$−$\gamma$ and $c^{\prime}$−$\gamma$ are positively cross-correlated. If there is considerable variation in the soil properties, it cannot be said for sure that an embankment is safe against slope failure even when the deterministic estimation of the factor of safety (FS) is more than 1.0. Thus, for safe and economic stability estimates of embankments, it is necessary to account for the various uncertainties arising due to geological anomalies, human errors, assumptions, and spatial variation in soil parameters that can adversely affect the stability of the slope of the embankment (Ramly et al. 2002; Guo et al. 2019; Johari et al. 2019; Hamrouni et al. 2021). Usually, the soil parameters ($c^{\prime}$, $\varphi^{\prime}$ and $\gamma$) are considered as random variables while performing probabilistic analysis of geotechnical problems. However, while conducting probabilistic slope stability analysis (PSSA) using pseudo-static approach, the horizontal seismic coefficient $\left( {k_{h} } \right)$ was also considered as a random variable by a few researchers (Guo et al. 2019; Johari et al. 2015a, b). The parameter $k_{h}$ was considered to be exponentially distributed by Johari et al. (2015a, b), while conducting stochastic seismic slope stability analysis of natural and man-made slopes. On the other hand, Hamrouni et al. (2019) considered $k_{h}$ as lognormally distributed while investigating the ultimate dynamic bearing capacity of shallow strip foundations. The other parameters i.e., $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ were assumed to follow both normal and lognormal distributions, and the stochastic responses were investigated for each case.

The concept of probability was first incorporated with LEM to perform the slope stability analysis (Alonso 1976; Tang et al. 1976; Harr 1977). Approximate methods like first-order reliability method (FORM) and second-order reliability method (SORM) have been used by several researchers to perform probabilistic slope stability analysis (Low and Tang 1997; Griffiths et al. 2007). In both methods, non-normal variables are converted into standard normal variables with mean $\left( \mu \right)$ and variance $\left( \sigma \right)$ equal to 0.0 and 1.0. A marker called the reliability index $\left( \beta \right)$ is determined on the limit state failure surface (Shinozuka 1983; Madsen et al. 1986) that indicates the safety level of the system under consideration. The SORM method is better than FORM because it gives better accuracy by simulating the real field problem considering the limit state failure surface as quadratic (Zhao and Ono 1999; Huang et al. 2018). A random variable approach is a probabilistic approach which is used to quantify the uncertainties of soil properties as input variables to perform the slope stability analysis. In the random variable approach, the input soil parameters are assumed to have the same value within the domain, even though it has been chosen randomly from given probability distribution (Mbarka et al. 2010). The investigators did not consider spatial variation of soil properties in this approach. The jointly distributed random variable (JDRV) method is another analytical probabilistic method in which probability density functions (PDF) of independent input variables are mathematically defined and linked with statistical relationships (Johari and Javadi 2012; Johari and Khodaparast 2013; Johari et al 2013, 2015a, b, 2018). In JDRV method, the probability of failure $\left( {P_{f} } \right)$ is computed by integrating the expressions of PDF over the entire domain. Random finite element method (RFEM), proposed by Fenton and Griffiths (2008), is an excellent choice for carrying out probabilistic analysis of any engineering structure. In this method, the finite element method (FEM) is associated with random field theory to simulate and analyse actual field problems, and finally, the probability of failure is computed with the help of Monte Carlo Simulation (MCS) method (Griffiths et al. 2015, 2016; Hamade and Mitri 2013; Huang et al. 2017; Zhu et al. 2019). The probabilistic analysis of any system using MCS involves analysing the system repeatedly with all possible combinations of the input variables and reporting $P_{f}$ by counting how many times the system has failed during such trials. However, MCS often fails to produce failure samples leading to theoretically impossible prediction of $P_{f}$ = 0.0. Some researchers also used an advanced version of MCS, i.e., Subset Simulation (SS), to perform probabilistic slope stability analysis (Au et al. 2010; Wang et al. 2011). SS has higher precision, and accuracy and requires smaller samples to perform probabilistic analysis than MCS.

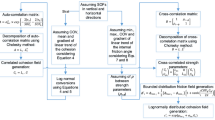
Previously, the researchers did not consider the effect of cross-correlation between different parameters and spatial variation of parameters together with the application of seismic and pore pressure loading to execute probabilistic slope stability analysis with MCS and SS techniques. In this work, firstly, a deterministic approach is developed for slope stability analysis by considering the seismic and pore-pressure loading with modified ordinary method of slices according to these external loading. Amongst various available methods for dynamic analysis such as pseudo-static method (Seed 1979; Siyahi 1998), Newmark’s sliding block approach (Newmark 1965), experimental methods based on shake table and centrifuges (Hong et al. 2011; Martakis et al. 2017), the pseudo-static approach is a very popular method where the effects of dynamic earthquake loading can be easily simulated by subjecting the embankment to an equivalent horizontal static load in a limit equilibrium analysis framework (Johari et al. 2015a, b). The ordinary method of slices is combined with pseudo-static method to perform slope stability with seismic loading. The soil properties such as effective cohesion $\left( {c^{\prime}} \right)$, effective angle of internal friction $\left( {\varphi^{\prime}} \right)$ and unit weight $\left( \gamma \right)$ are considered as spatially random variables. Furthermore, the dependencies of the soil parameters (i.e., $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$) on each other is also taken into account by considering the correlation between these parameters. Random fields of related soil parameters i.e., $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are developed considering cross-correlation between these variables as well as their spatial variation using Markov correlation function. The soil parameters $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are lognormally distributed within the embankment domain in the present study. The UPSS 3.0 module developed in MS-Excel spreadsheet environment by eminent researchers (Au and Wang 2014) for executing probabilistic seismic slope stability analysis by MCS and SS techniques has been used to conduct the probabilistic slope stability analysis (PSSA). The results prove that the pore pressure and seismic loading severely impact an earthen embankment's stability. It is noticed that the cross-correlation and spatial correlation of different soil parameters have a major impact on the stability of slope. There has been very limited study on the probabilistic response of an earthen embankment considering the cross-correlation of the involved soil parameters as well as the spatial variation of these parameters. In this context, the current study provides important insight in the response of the embankment where the cross-correlation between the soil parameters and their spatial variation has been taken into consideration. It is noticed that SS is a very accurate and precise method for performing probabilistic analysis with a smaller number of samples. The probabilistic response of the slope is investigated at the precise moment when the failure initiates by plotting graphs between major and minor effective principal stresses developed on the slip surface of slope.

2 Methodology

This section briefly describes the theories involved in probabilistic slope stability analysis of an embankment. In this work, the factor of safety $\left( {FS} \right)$ against slope failure is determined by ordinary method of slices in presence of self-weight, seismic and pore-pressure loading. The strength parameters such as $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are considered as spatially random variables which are also cross-correlated to each other. The probabilistic slope stability is finally performed with MCS and SS techniques considering the spatial variation of these cross-correlated random variables within the embankment domain.

2.1 Deterministic slope stability analysis

The deterministic response of the embankment is determined using the ordinary method of slices based on limit equilibrium method in the presence of seismic and pore-pressure loadings. The pore-pressure loading is simulated by considering different values of pore-pressure ratio $\left( {r_{u} } \right)$ considering saturated embankment. The seismic forces are expressed in terms of seismic coefficient $\left( {k_{h} } \right)$ and weight as per pseudo-static method. In this approach the critical failure surface is considered as circular failure surface and the failure surface is divided into several numbers of vertical slices. The free-body diagram of ith slice is shown in Fig. 1 with all forces acting on it. The forces acting on the i^th slice are resisting and driving forces.

Fig. 1

Free body diagram of ith slice

It is necessary to evaluate the resisting and driving moment for the entire failure mass by summing the respective quantities for all the slices in which the failure mass is subdivided. These are:

$${\text{Total resisting moment}}\;(M_{R} ) = \sum\limits_{i = 1}^{i = n} {\left( {c^{\prime}_{i} l_{i} + (N - k_{h} W_{i} \sin \beta_{i} - u_{i} )\tan \phi^{\prime}} \right)r}$$

(1)

$${\text{Total driving moment}}\left( {M_{D} } \right) = \sum\limits_{i = 1}^{i = n} {\left( {W_{i} \sin \beta_{i} + k_{h} W_{i} \cos \beta_{i} } \right)r}$$

(2)

The normal component of weight of ith slice $\left( N \right)$ and the pore-water pressure $\left( u \right)$ are computed using Eq. (3) and Eq. (4), respectively, which are given below:

$$N = W\cos \beta_{i}$$

(3)

$$u = r_{u} \gamma h.$$

(4)

When the seismic and pore-pressure loadings are considered simultaneously, the embankment's slope stability is expressed in terms of safety factor $\left( {{\text{FS}}} \right)$, which is determined by taking the ratio of resisting moment $(M_{R} )$ and driving moment $\left( {M_{D} } \right)$. The final expression of factor of safety $\left( {{\text{FS}}} \right)$ against slope failure is shown in Eq. (5) (Kramer 1996).

$${\text{FS}} = \frac{{\sum\limits_{i = 1}^{i = n} {\left( {c^{\prime}_{i} l_{i} + (W_{i} \cos \beta_{i} - k_{h} W_{i} \sin \beta_{i} - r_{u} \gamma_{i} h_{i} )\tan \varphi_{i}^{\prime } } \right)} }}{{\sum\limits_{i = 1}^{i = n} {\left( {W_{i} \sin \beta_{i} + k_{h} W_{i} \cos \beta_{i} } \right)} }},$$

(5)

where $c^{\prime}_{i} =$ effective cohesion of soil in ith slice, $\varphi_{i}{\prime} =$ effective angle of internal friction in ith slice, $\gamma_{i} =$ unit weight in ith slice, $l_{i} =$ length of ith slice, $b_{i} =$ width of ith slice, $W_{i} =$ weight of ith lice, $\beta_{i} =$ base angle of ith slice, $h_{i} =$ mid-height of ith slice, $k_{h} =$ horizontal seismic coefficient, $r_{u} =$ pore pressure ratio.

An MS-Excel spreadsheet called deterministic model (D.M.) worksheet is developed to determine the FS of slope of earthen embankment using the above equations.

2.2 Probabilistic slope stability analysis

To conduct the probabilistic analysis of the embankment against slope failure, it is necessary to generate random fields of the related variables. For the present analysis, the variables of interest are $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$. In the following section, the random field generation procedure considering the correlation between the soil strength parameters and their spatial variation is discussed in a brief manner.

2.2.1 Cross-correlation between soil parameters

It is well known that the input strength parameters such as $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$ are cross-correlated with each other. Various researchers (Nguyen and Chowdhary 1985; Javankhoshdel and Bathurst 2015) investigated the effects of correlation between strength parameters while determining $P_{f}$ of the slope. These correlations are quantified by the cross-correlation coefficient $\left( \rho \right)$. Drained triaxial tests proves that negative correlations exist between $c^{\prime}$ and $\varphi^{\prime}$(Lumb 1970; Yucemen et al. 1973; Cherubini 1997, 2000; Forrest and Orr 2010; Hata et al. 2012). The negative cross-correlation between $c^{\prime}$ and $\varphi^{\prime}$ indicates that when the values of $c^{\prime}$ increases the values of $\varphi^{\prime}$ decreases. According to many researchers (Chowdhury and Xu 1993; Low and Tang 1997; Sivakumar Babu and Srivastava 2007), a positive cross-correlation occurs between ($\varphi^{\prime}$ and $\gamma$) and ($c^{\prime}$ and $\gamma$). The maximum possible range of cross-correlation coefficient is $- 1.0 < \rho < 1.0$(Javankhoshdel and Bathurst 2015). It is necessary to consider all possible combinations of cross-correlation coefficient $\rho$ between the related random parameters, and the $\rho$ value for which $P_{f}$ of the system is highest should be found out. In the present work, the influence of cross-correlation between different strength parameters on probability of failure of slope is analysed. The detailed procedure of computing cross-correlation between different strength parameters are discussed below:

• $\rho_{1}$ = cross-correlation coefficient between $c^{\prime}$ and $\varphi^{\prime}$.

• $\rho_{2}$ = cross-correlation between $c^{\prime}$ and $\gamma$.

• $\rho_{3}$ = cross-correlation between $\varphi^{\prime}$ and $\gamma$.

The strength parameters $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$ are correlated and normally distributed random variables. In this case, the cross-correlation coefficient between these parameters can be expressed as below:

$$\rho_{1} = \frac{{c{\text{var}}_{{c^{\prime},\varphi^{\prime}}} }}{{\sigma_{{c^{\prime}}} \sigma_{{\varphi^{\prime}}} }}$$

(6)

$$c{\text{var}}_{{c^{\prime},\varphi^{\prime}}} = \rho_{1} \sigma_{{c^{\prime}}} \sigma_{{\varphi^{\prime}}} ,$$

(7)

where $c{\text{var}}_{{c^{\prime},\varphi^{\prime}}}$ = covariance between $c^{\prime}$ and $\varphi^{\prime}$, $\sigma_{{c^{\prime}}}$ = standard deviation of $c^{\prime}$, $\sigma_{{\varphi^{\prime}}}$ = standard deviation of $\varphi^{\prime}$

In this work, there are three random strength parameters which are considered to be correlated to each other. Therefore, the covariance between these random parameters is expressed in terms of covariance matrix with 3 $\times$ 3 elements which is expressed in Eq. (8).

$$\Lambda = \left[ {\begin{array}{*{20}c} {\sigma_{{c^{\prime}}}^{2} } & {\rho_{1} \sigma_{{c^{\prime}}} \sigma_{{\varphi^{\prime}}} } & {\rho_{1} \sigma_{{c^{\prime}}} \sigma_{{\gamma^{\prime}}} } \\ {\rho_{1} \sigma_{{\varphi^{\prime}}} \sigma_{{c^{\prime}}} } & {\sigma_{{\varphi^{\prime}}}^{2} } & {\rho_{2} \sigma_{{\varphi^{\prime}}} \sigma_{{y^{\prime}}} } \\ {\rho_{2} \sigma_{{\gamma^{\prime}}} \sigma_{{c^{\prime}}} } & {\rho_{3} \sigma_{{\gamma^{\prime}}} \sigma_{{\varphi^{\prime}}} } & {\sigma_{{\gamma^{\prime}}}^{2} } \\ \end{array} } \right].$$

(8)

The correlated random variables are expressed using the relationship expressed below

$$X = \sigma Z + \mu ,$$

(9)

where $X$ = random variable, $\sigma$ = standard deviation, $Z$ standard variable, $\mu$ = mean.

Now, the correlated random variable can be computed with the help of Eq. (8) and Eq. (9) which is expressed below in Eqs. (10–12).

$$c^{\prime} = \sigma_{{c^{\prime}}} Z_{1} + \mu_{{c^{\prime}}}$$

(10)

$$\varphi^{\prime} = \rho_{1} \sigma_{{\varphi^{\prime}}} Z_{1} + \sigma_{{\varphi^{\prime}}} \sqrt {1 - \rho_{1}^{2} } Z_{2} + \mu_{{\varphi^{\prime}}}$$

(11)

$$\gamma = \rho_{2} \sigma_{\gamma } Z_{1} + \frac{{\sigma_{{\gamma^{\prime}}} \left( {\rho_{3} - \rho_{1} \rho_{2} } \right)}}{{\sqrt {1 - \rho_{1}^{2} } }}Z_{2} + \sigma_{\gamma } \sqrt {1 - \rho_{2}^{2} + \frac{{\left( {\rho_{3} - \rho_{1} \rho_{2} } \right)^{2} }}{{1 - \rho_{1}^{2} }}} Z_{3} + \mu_{\gamma } ,$$

(12)

where $\sigma_{{c^{\prime}}}$ = standard deviation of $c^{\prime}$, $\sigma_{{\varphi^{\prime}}}$ = standard deviation of $\varphi^{\prime}$, $\sigma_{\gamma }$ = standard deviation of $\gamma$, $\mu_{{c^{\prime}}}$ = mean of $c^{\prime}$,$\mu_{{\varphi^{\prime}}}$ = mean of $\varphi^{\prime}$, $\mu_{\gamma }$ = mean of $\gamma$

2.2.2 Spatial variability of soil parameters

The soil strength parameters $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$ are spatial variable within the embankment domain. The random values of strength parameters at different locations within the domain are required for probabilistic analysis. Firstly, the embankment domain is divided into n layers. The Markov correlation function is used to illustrate the spatial correlation $\left( \xi \right)$ between one location and another location, which can be expressed as below.

$$\xi \left( {Z_{i} ,Z_{j} } \right) = \exp \left\{ {\frac{ - 2}{\theta }\left| {Z_{i} - Z_{j} } \right|} \right\}.$$

(13)

If n locations are selected within the embankment domain, then the spatial correlation between all n locations with each other is expressed in the form of spatial correlation matrix $\left[ \xi \right]$ using the Eq. (13). The spatial correlation matrix $\left[ \xi \right]$ is developed in such a way that satisfies the relationship given below:

$$\left[ \xi \right] = \left[ L \right]\left[ L \right]^{T} ,$$

(14)

where $\left[ \xi \right]$ = spatial correlation matrix, $\left[ L \right]$ = lower triangular matrix of $\left[ \xi \right]$.

The lower triangular matrix $\left[ L \right]$ of spatial correlation matrix $\left[ \xi \right]$ is computed using Cholesky factorisation of the spatial correlation matrix $\left[ \xi \right]$. For n locations within the embankment domain, “n” numbers of uniform i.i.d (independent and identically distributed) random variables are generated between 0 and 1 by using the built-in function “RAND()” in MS Excel. These n uniform i.i.d. are converted into standard Gaussian variables $\left\{ X \right\}$ by using another built-in function, “NORMINV()”. The values of probability distribution function of these Gaussian variables are computed by the function “NORMDIST()”. The correlation for strength parameters is simulated by taking the product of $\left[ L \right]\left\{ X \right\}$. The product $\left[ L \right]\left\{ X \right\}$ is a vector composed of correlated Gaussian distribution variables. In this way, lognormally distributed random values of the soil strength parameters can be created at different locations within the embankment domain using the following equations.

$$\ln c^{\prime} = \mu_{{\ln c^{\prime}}} + \sigma_{{\ln c^{\prime}}} \left[ L \right]\left\{ X \right\}$$

(15)

$$\ln \varphi^{\prime} = \mu_{{\ln \varphi^{\prime}}} + \sigma_{{\ln \varphi^{\prime}}} \left[ L \right]\left\{ X \right\}$$

(16)

$$\ln \gamma = \mu_{\ln \gamma } + \sigma_{\ln \gamma } \left[ L \right]\left\{ X \right\},$$

(17)

where,$\ln c^{\prime}$ = log normal distribution effective cohesion, $\ln \varphi^{\prime}$ = lognormal distribution of effective angle of internal friction, $\ln \gamma$ = lognormal distribution of unit weight, $\mu_{{\ln c^{\prime}}}$ = Mean of $\ln c^{\prime}$,$\sigma_{{\ln c^{\prime}}}$ = Standard deviation of $\ln c^{\prime}$, $\mu_{{\ln \varphi^{\prime}}}$ = Mean of $\ln \varphi^{\prime}$, $\sigma_{{\ln \varphi^{\prime}}}$ = Standard deviation of $\ln \varphi^{\prime}$, $\mu_{\ln \gamma }$ = Mean of $\ln \gamma$,$\sigma_{\ln \gamma }$ = Standard deviation of $\ln \gamma$.

The cross-correlated random values of $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$ obtained from Eqs. (10–12) are further used in Eqs. (15–17) to generate random fields of soil strength parameters. In this way, spatially distributed random fields of $c^{\prime}$, $\varphi^{\prime}$, and $\gamma$ can be generated which are also cross-correlated with each other. Now, the target random values of strength parameters at selected location within the domain is computed with the help of equations given below.

$$c^{\prime} = \exp \left\{ {\ln c^{\prime}} \right\}$$

(18)

$$\varphi^{\prime} = \exp \left\{ {\ln \varphi^{\prime}} \right\}$$

(19)

$$\gamma = \exp \left\{ {\ln \gamma } \right\}.$$

(20)

The overall procedure of computing random values of strength parameters at different location within the embankment domain is simulated in a MS-Excel spreadsheet usually called as Uncertainty Model (UM) worksheet. The DM and UM worksheet are interlinked together by setting the cell references for nominal values of strength parameters in the DM worksheet with the cell references of the random values of strength parameters in UM worksheet. After interlinking of the DM and UM worksheets, the probabilistic slope stability analysis is performed with MCS and SS techniques using the UPSS 3.0 module, which is a suite of Excel Visual Basic application (VBA) designed as an Excel Add-in. The UPSS-3.0 was originally developed by Au and Wang (2014). Additional Excel functions are enhanced with “Add-in” for implementing direct Monte Carlo and Subset Simulation procedures, and compiled as an independent file with an extension of “. Xla” in Excel (Au and Wang 2014; Shekhar et al. 2022). After installation, the “UPSS 3.0 Add-in” launches with Excel by default, and then “Add-in” can be used similarly to Excel's built-in functionalities. More details about UPSS-3.0 Add-in can be found in an excellent description given by Au and Wang (2014).

2.2.2.1 Monte Carlo simulation (MCS)

MCS is an efficient technique for execution of computer-based simulations of probabilistic analysis of any stochastic system where $N$ fields are generated considering random variations of input variables to determine the system response. The probability of failure is expressed simply by computing the ratio of the number of trials in which the system response has exceeded a threshold limit to the total number of trial runs. The required input data for executing PSSA with MCS are the number of runs, number of samples per run $\left( {N} \right)$, random variables $\left\{ X \right\}$ and the system response $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$. $N$ number of system responses $\left( {y_{1} ,y_{2} , \ldots ,y_{N} } \right)$ are generated as an output variable in MCS worksheet. The random values of strength parameters and $FS$ values are also recorded at different locations with help of this analysis. A MCS chart is generated after performing probabilistic analysis by MCS technique. MCS chart is basically a CCDF plot between the probability of system and various threshold values of system response. The probability of failure is the probability of the system when the threshold value of system response is just greater than 1.0.

2.2.2.2 Subset simulation (SS)

Subset simulation is an enhanced version of MCS based on Bayes theorem, which can compute the probability of failure $\left( {P_{f} } \right)$ lower than 0.001 (Wang et al. 2011). SS technique requires fewer samples than MCS to determine the probability of failure with the desired accuracy level. Markov Chain Monte Carlo (MCMC) technique is used to generate random samples as per specified probability distribution function (PDF). More details of the MCMC algorithm can be found in the works (Au and Wang 2014). The event with the low failure probability is known to be expressed using a series of intermediate failure probabilities in the circumstances with higher conditional failure probability. In this method, probability of failure $\left( {P_{f} } \right)$ is computed as follows:

$$P_{f} = P\left( {Y > y_{1} } \right)P\left( {Y > y_{2} |Y > y_{1} } \right) \times \ldots \times P\left( {Y > y_{n} |Y > y_{N - 1} } \right),$$

(21)

where $Y$ = Event, and $y_{1} ,y_{2} ,....,y_{N}$ = threshold values of system response.

PSSA using subset simulation is executed by “UPSS 3.0 ADD-IN”, with given general inputs such as number of runs, number of samples per level $\left( N \right)$, conditional probability $\left( {p_{0} } \right)$, number of simulation levels $\left( m \right)$, random variables $\left\{ X \right\}$, probability distribution function (PDF) and driving variable $\left( {Y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$. While performing probabilistic analysis using SS, the variable $\left( {y_{1} } \right)$ is the same as the conditional probability of failure $\left( {p_{0} } \right)$. $N$ number of threshold values of system response $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$ are generated as the output of this analysis corresponds to a particular conditional probability value, and 0.10 is the appropriate value of conditional probability $\left( {p_{0} } \right)$ is because SS achieves the highest precision and accuracy in computing $P_{f}$ of the system. Au and Wang (2014) also recommended the value $p_{0}$ is 0.10 (Au et al. 2010; Wang et al. 2011; Au and Wang 2014).

2.2.3 Probabilistic major and minor principal stress

It would be interesting to observe the probabilistic response of the embankment when the failure is initiated. For this purpose, the authors chose to report the variation of effective major principal stress $\left( {\sigma^{\prime}_{1} } \right)$ and effective minor principal stress $\left( {\sigma^{\prime}_{3} } \right)$ that develops on the slip surface of the embankment. Slip surface represents the failure plane, the normal stress $\left( {\sigma^{\prime}} \right)$ and shear stress $\left( {\tau^{\prime}} \right)$ generated at the base of the slices should lie on the Mohr–Coulomb failure envelope. Figure 3 shows a Mohr–Coulomb failure envelope where the straight-line envelope touches the Mohr’s circle at M $\left( {\sigma^{\prime},\tau^{\prime}} \right)$. The centre of the Mohr’s circle is at C. Effective major principal stress $\left( {\sigma^{\prime}_{1} } \right)$ = OH, effective minor principal stress $\left( {\sigma^{\prime}_{3} } \right)$ = OQ, effective normal stress $\left( {\sigma^{\prime}} \right)$ = ON, and effective shear stress $\left( {\tau^{\prime}} \right)$ = MN are represented on Mohr circle in Fig. 2.

Fig. 2

Mohr–Coulomb failure envelope

The major and minor effective principal stress is computed in terms of $\sigma^{\prime}$ and $\tau^{\prime}$. Since, ∆QMN is a right-angle triangle (refer to Fig. 2), and therefore, we have $\angle QMN = 45^{^\circ } - \frac{{\varphi^{\prime}}}{2}$. Therefore,

$$\frac{QN}{{MN}} = \tan \left( {45^{^\circ } - \frac{{\varphi^{\prime}}}{2}} \right)$$

(22)

$$QN = MN\tan \left( {45^{^\circ } - \frac{{\varphi^{\prime}}}{2}} \right) = \tau^{\prime}\tan \left( {45^{^\circ } - \frac{{\varphi^{\prime}}}{2}} \right)$$

(23)

$$OQ = ON - QN$$

(24)

$$\sigma^{\prime}_{3} = \sigma^{\prime} - \tau^{\prime}\tan \left( {45^{^\circ } - \frac{{\varphi^{\prime}}}{2}} \right).$$

(25)

Once the minor principal stress $\left( {\sigma^{\prime}_{3} } \right)$ is found out, the major principal stress $\left( {\sigma^{\prime}_{1} } \right)$ can be obtained from the well-known relationship (Das 2010):

$$\sigma^{\prime}_{1} = \sigma^{\prime}_{3} N_{{\varphi^{\prime}}} + 2c^{\prime}\sqrt {N_{{\varphi^{\prime}}} } ,$$

(26)

where $N_{{\varphi^{\prime}}}$ = flow value = $\tan^{2} \left( {45^{^\circ } + \frac{{\varphi^{\prime}}}{2}} \right)$

3 Results and discussion

Figure 3 shows a 12.0 m high saturated earthen embankment with 8.0 m crest width and 68.0 m base width having 2.50 H:1.0 V upstream and downstream slope rested on a 12.0 m depth foundation. The dimensions of the embankment as well as the centre of rotation “O”$\left( {x_{c} ,y_{c} } \right)$ and radius $\left( {r_{c} } \right)$ of critical slip circle are also displayed in the figure. The mean values of spatially variable soil strength parameters i.e., effective cohesion $\left( {c^{\prime}} \right)$, effective angle of friction $\left( {\varphi^{\prime}} \right)$ and unit weight $\left( \gamma \right)$ are shown in Table 1. The influence of spatial variation of cross-correlated soil parameters $c^{\prime}$,$\varphi^{\prime}$ and $\gamma$ with the effects of various types of loading such as pore pressure and seismic loading on the stability of the embankment is considered.

Fig. 3

Dimension of earthen embankment

Table 1 Properties of soil of earthen embankment

The slope stability analysis of the earthen embankment is performed using ordinary method of slices based on limit equilibrium method. The probabilistic slope stability analysis (PSSA) is performed by creating spatially variable random fields of the related strength parameters $\left( {c^{\prime},\varphi^{\prime},{\text{and }}\gamma } \right)$ which are also correlated to each other using Eqs. (14–17). The seismic loading on the embankment is simulated using pseudo-static method where horizontal seismic coefficient $\left( {k_{h} } \right)$ has been varied from 0.0, 0.05, 0.10, 0.15–0.20. Melo and Sharma (2004) presented an excellent treatise on the topic of choosing $k_{h}$ for seismic slope stability analysis following Pseudo-static method. Pseudo-static method was originally proposed by Terzaghi (1950) for conducting seismic slope stability analysis, and it still remains very popular among the practising engineers and researchers because of the methods simplicity and robustness in assessing the stability of the slope under earthquake loadings. Table 2 shows the various $k_{h}$ values used by the researchers in the past. It can be seen that $k_{h}$ = 0.05–0.20 have been used to represent mild to violent, destructive earthquakes based on this information, $k_{h}$ value considered in the present study are 0.0, 0.05, 0.10, 0.15 and 0.20.

Table 2 Recommended horizontal seismic coefficients $\left( {k_{h} } \right)$.

The pore pressure loading is generated by considering different values of pore pressure ratio $\left( {r_{u} } \right)$ = 0.0, 0.25 and 0.50, respectively. It is necessary to understand that in the present analysis, the pore pressure loading is simulated by constant $r_{u}$ values (refer to Eq. 4). However, $r_{u}$ is also dependent on $\gamma$ which is considered to be a random parameter in the present analysis. Ideally, the correlation between $c^{\prime},\;\varphi^{\prime},\;\gamma$ and $r_{u}$ should be considered and all these four parameters should be treated as random variables. However, it should also be appreciated that the specification of pore pressure ratio $r_{u}$ is a simple way to consider the effect of pore water pressure for a fully saturated embankment domain when the exact location of phreatic surface within the embankment is unknown. In order to simplify the analysis procedure, the pore pressure loading is imposed through constant $r_{u}$ values.

Figure 4 shows the deterministic model (DM) worksheet that performs slope analysis of an embankment following the ordinary slice method. The various input parameters i.e. height of slope $\left( H \right)$, centre of critical slip circle $\left( {x_{c} ,y_{c} } \right)$, radius of critical slip circle $\left( {r_{c} } \right)$, effective cohesion $\left( {c^{\prime}} \right)$, effective angle of internal friction $\left( {\varphi^{\prime}} \right)$, and unit weight $\left( \gamma \right)$ are considered to compute $FS$ of slope. The strength parameters of the embankment’s soil i.e., $c^{\prime}$, $\varphi^{\prime}$ and unit weight $\gamma$ are arranged along the depth of the embankment that is sub-divided into 12 layers of 1.0 m depth each. The slope analysis procedure is shown in detail in Fig. 3 where various terms are: $T_{Lx} =$ top left $x$ co-ordinate of slice, $T_{Ly} =$ top left $y$ co-ordinate of slice, $B_{Lx} =$ bottom left $x$ co-ordinate of slice, $B_{Ly} =$ bottom left $y$ co-ordinate of slice, $T_{Rx} =$ top right $x$ co-ordinate of slice, $T_{Ry} =$ top right $y$ co-ordinate of slice, $B_{Rx} =$ bottom right $x$ co-ordinate of slice, $B_{Ry} =$ bottom right $y$ co-ordinate of slice. The driving moment $\left( {M_{D} } \right)$ and resisting moment $\left( {M_{R} } \right)$ are then computed to determine $FS$ of slope.

Fig. 4

Deterministic model worksheet

The covariance matrix $\left[ \Lambda \right]$ for cross-correlated $c^{\prime}$,$\varphi^{\prime}$ and $\gamma$ with input values $\mu_{{C^{\prime}}}$, $\mu_{{\varphi^{\prime}}}$,$\mu_{\gamma }$,$\rho_{1}$,$\rho_{2}$,$\rho_{3}$,$\upsilon_{{c^{\prime}}}$,$\upsilon_{{\varphi^{\prime}}}$ and $\upsilon_{\gamma }$ is calculated using Eq. (8). The earthen embankment is subdivided into 12 layers of 1.0 m depth horizontally and 2.0 m is taken as the correlation length $\left( \theta \right)$ to develop the correlation matrix $\left[ \xi \right]$ using Eq. (13). The developed correlation matrix $\left[ \xi \right]$ is a 13 × 13 matrix. The lower triangular matrix $\left[ L \right]$ is computed using Cholesky decomposition of the correlation matrix $\left[ \xi \right]$ using MATLAB. The correlation matrix helps to find the spatial correlation of random variables $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ within the embankment domain. Both correlation matrix $\left[ \xi \right]$ and the corresponding lower triangular matrix $\left[ L \right]$ are shown in Fig. 5. Also, the covariance matrix $\left[ \Lambda \right]$ is also shown in Fig. 5 for different choices of $\upsilon_{{c^{\prime}}}$, $\upsilon_{{\varphi^{\prime}}}$ and $\upsilon_{\gamma }$.

Fig. 5

Covariance matrix $\left[ \Lambda \right]$, Correlation matrix $\left[ \xi \right]$ and the lower matrix $\left[ L \right]$ for the embankment domain

Figure 6 shows the uncertainty modelling (U.M.) worksheet which demonstrates the spatial distribution of cross-correlated random variables $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ within the embankment domain. To develop the U.M. worksheet, values of $\mu_{{C^{\prime}}}$, $\mu_{{\varphi^{\prime}}}$, $\mu_{\gamma }$, $\rho_{1}$, $\rho_{2}$, $\rho_{3}$, $\upsilon_{{c^{\prime}}}$, $\upsilon_{{\varphi^{\prime}}}$ and $\upsilon_{\gamma }$ are given as input parameter. Initially, the soil strength parameters are considered normally distributed and the three-standard normal i.i.d.$Z_{1}$, $Z_{2}$ and $Z_{3}$ are recorded in the cells D9:F9, respectively. Then, the cross-correlated random values of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are recorded in cell J7, J8 and J9, respectively, using Eqs. (10–12). The generated values of uniform I.I.D., std. normal i.i.d.$\left\{ X \right\}$, probability density function $\left( {p\left\{ X \right\}} \right)$ are recorded in cells “D13:P13”, “D14:P14”, and “D15:P15”, respectively, in the U.M. worksheet on the selected locations. The lognormal distribution of random variables $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are recorded in cells “D17:P17”, “D18:P18” and “D19:P19”. The lognormally distributed random variables are then converted into normally distributed random variables $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ in cells “D21:P21”, “D22:P22”and “D23:P23”, respectively, at the selected locations within the embankment domain. The recommended range of variations for different soil parameters are shown in Table 3 (Branco et al. 2014). Probabilistic analyses are carried out considering different values of coefficient of variation $\upsilon_{{c^{\prime}}}$ = 0.25 and 0.50 respectively. Similarly, the values of $\upsilon_{{\varphi^{\prime}}}$ = 0.05 and 0.10 and $\upsilon_{\gamma }$ = 0.05 have been used in the present analyses.

Fig. 6

Uncertainty modelling (UM) worksheet

Table 3 Coefficients of variation in properties of soils

The DM and UM worksheet are interlinked together by setting the cells “D8:P8”, “D9:P9” and “D10:P10” for mean values of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ in the DM worksheet with the cells “D21:P21”, “D22:P22” and “D23:P23” for the random values of strength parameters in the UM worksheet. The resulting worksheet contains the random values of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ in cells “D8:P8”, “D9:P9” and “D10:P10” as shown in Fig. 7. In this worksheet, the probabilistic value of ${\text{FS}}$ of the slope of earthen embankment and the system response $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$ are recorded in cells “P4” and “Q4”, respectively. The outcomes of PSSA using MCS and SS techniques are presented next.

Fig. 7

Probabilistic modelling (PM) worksheet

3.1 Choice of cross-correlation coefficients

In this study, the probabilistic slope stability analysis is performed considering that the strength parameters $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are correlated to each other. Here, $\rho_{1}$ is the cross-correlation coefficient between $c^{\prime}$ and $\varphi^{\prime}$, $\rho_{2}$ is the cross-correlation between $c^{\prime}$ and $\gamma$ and $\rho_{3}$ is the cross-correlation between $c^{\prime}$ and $\gamma$. The inter-dependencies between these parameters have been considered to generate the cross-correlated values of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ using Eq. (10–12). The cross-correlation coefficients vary between − 1.0 and 1.0. Sivakumar Babu and Srivastava (2007) considered the range of correlation coefficient from $- 0.7 < \rho < 0.7$ for the soil parameters $c^{\prime}$ and $\varphi^{\prime}$. Javankhoshdel and Bathurst (2015) studied the influence of different combinations of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on slope stability analysis while representing the correlated behaviours of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$. Javankhoshdel and Bathurst (2015) considered the maximum range of cross-correlation coefficient $- 0.5 < \rho < 0.5$ and stated that maximum $P_{f}$ occurs for the combination of cross-correlation coefficients $\rho_{1} = 0.5$, $\rho_{2} = \rho_{3} = - 0.5$. Drained triaxial tests proves that negative correlations exist between $c^{\prime}$ and $\varphi^{\prime}$(Lumb 1970; Yucemen et al. 1973; Cherubini 1997, 2000; Forrest and Orr 2010; Hata et al. 2012). The negative cross-correlation between $c^{\prime}$ and $\varphi^{\prime}$ indicates that when the values of $c^{\prime}$ increases, the values of $\varphi^{\prime}$ decreases. According to many researchers (Chowdhury and Xu 1993; Low and Tang 1997; Sivakumar Babu and Srivastava 2007), a positive cross-correlation behaviour exists between ($\varphi^{\prime}$ and $\gamma$) and ($c^{\prime}$ and $\gamma$). Based on the experimental results, it can be inferred that $\rho_{1}$ should be negative whereas $\rho_{2}$ and $\rho_{3}$ should be positive. Though Javankhoshdel and Bathurst (2015) checked probability of failure of clayey soil slopes for both positive and negative values of $\rho_{1}$, they also mentioned that positive $\rho_{1}$ values were considered out of academic interest only. In the present work, positive $\rho_{1}$ values and negative $\rho_{2}$ and $\rho_{3}$ have not been considered as theses correlation trends are not supported by physical data. In the present work, the considered ranges of the $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ values are $- 1.0 < \rho_{1} < 0.0$, $0.0 > \rho_{2} > 1.0$ and $0.0 > \rho_{3} > 1.0$ respectively. Following the works of Sivakumar Babu and Srivastava (2007), the combinations of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ values have been considered are (i) $\rho_{1} = - 0.7,\rho_{2} = \rho_{3} = 0.7$ (ii) $\rho_{1} = - 0.5,\rho_{2} = \rho_{3} = 0.5$ (iii) $\rho_{1} = - 0.3,\rho_{2} = \rho_{3} = 0.3$ and (iv) $\rho_{1} = - 0.1,\rho_{2} = \rho_{3} = 0.1$. It is checked for which $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ combination, the maximum $P_{f}$ of the soil slope occurs, and that value is used for running the subsequent probabilistic slope stability analyses.

Figure 8 shows the plot between $P_{f} (\% )$ and $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ to analyse the effect of different combination of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on $P_{f}$ of slope when $r_{u} = 0.25$, $k_{h} = 0.10$, $\upsilon_{{c^{\prime}}} = 0.25$,$\upsilon_{{\varphi^{\prime}}} = 0.05$ and $\upsilon_{\gamma } = 0.05$. The $P_{f}$ is reported when the system response $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$ is just greater than 1.0. When $\rho_{1} = - 0.1,\rho_{2} = \rho_{3} = 0.1$ is considered,$P_{f}$ is 11.446%. When $\rho_{1} = - 0.3,\rho_{2} = \rho_{3} = 0.3$; the $P_{f}$ is 9.246%. If $\rho_{1} = - 0.5,\rho_{2} = \rho_{3} = 0.5$, the $P_{f}$ is 7.818%, and the $P_{f}$ is 6.336% when $\rho_{1} = - 0.7,\rho_{2} = \rho_{3} = 0.7$. These data show when $P_{f} < 50\%$, the probability of failure of the slope increases when the value $\rho_{1}$ increases. Similar observations have also been made by Javankhoshdel and Bathurst (2015) for a clayey slope.

Fig. 8

Effect of different combinations of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on $P_{f}$ when $r_{u} = 0.25$, $k_{h} = 0.10$, $\upsilon_{{c^{\prime}}} = 0.25$,$\upsilon_{{\varphi^{\prime}}} = 0.05$ and $\upsilon_{\gamma } = 0.05$

Figure 9 shows the curve plotted between $P_{f} (\% )$ and $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ for analyse the effect of different combination of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on $P_{f} (\% )$ of slope when $r_{u} = 0.25$, $k_{h} = 0.20$,$\upsilon_{{c^{\prime}}} = 0.50$, $\upsilon_{{\varphi^{\prime}}} = 0.10$ and $\upsilon_{\gamma } = 0.05$. The $P_{f} (\% )$ is reported when the system response $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$ is just greater than 1.0. When $\rho_{1} = - 0.1,\rho_{2} = \rho_{3} = 0.1$ is considered, the $P_{f}$ of the slope is 73.176%. For $\rho_{1} = - 0.3,\rho_{2} = \rho_{3} = 0.3$, the $P_{f}$ is 75.838%. If $\rho_{1} = - 0.5,\rho_{2} = \rho_{3} = 0.5$, the corresponding $P_{f}$ is 76.67%, and when $\rho_{1} = - 0.7,\rho_{2} = \rho_{3} = 0.7$, the value of $P_{f}$ is 77.378%. It is noticed that $P_{f}$ of the slope of the embankment increases when the value $\rho_{1}$ decreases. These findings also corroborate the observations made by Javankhoshdel and Bathurst (2015).

Fig. 9

Effect of different combinations of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on $P_{f}$ when $r_{u} = 0.25$, $k_{h} = 0.20$,$\upsilon_{{c^{\prime}}} = 0.50$, $\upsilon_{{\varphi^{\prime}}} = 0.10$ and $\upsilon_{\gamma } = 0.05$

Table 4 shows the effect of different combinations of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ on $P_{f}$ of slope for different cases considered in the analysis. It is noticed that when the $P_{f}$ is less than 50%, then the $P_{f}$ increases with increase in the value of $\rho_{1}$. Furthermore, when the $P_{f}$ is greater than 50%, the $P_{f}$ of the slope decreases with increase in the value of $\rho_{1}$. Therefore, it is concluded that the combination $\rho_{1} = - 0.1,\rho_{2} = \rho_{3} = 0.1$ should be used as this combination of $\rho_{1}$, $\rho_{2}$ and $\rho_{3}$ values yielding maximum $P_{f}$ in case of $P_{f} < 50\%$. On the other hand, and the combination $\rho_{1} = - 0.7,\rho_{2} = \rho_{3} = 0.7$ should be used for further analyses when $P_{f} > 50\%$, as this combination results in maximum $P_{f}$ of the slope under consideration. Similar observations have also been made by previous researchers (Griffiths et al. 2009; Javankhoshdel and Bathurst 2015) for a clayey slope.

Table 4 The effects of cross-correlation coefficients on probability of failure of the embankment

3.2 Monte Carlo simulation results

The uncertainty propagation of slope failure analysis by Monte Carlo simulation is performed next with N = 50,000 samples. The system response variable $\left( {y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$ is chosen from the PM worksheet, whereas the random variables are chosen from cells “D13:P13” of the UM sheet. The probability $P(Y > y)$ of the system $\left( Y \right)$ greater than the threshold value of the system response $\left( y \right)$ can be obtained after running MCS analysis. The values of $P(Y > y)$,$y$ and $FS$ are recorded in column A, B and C of Fig. 10. Furthermore, the random values of $c^{\prime}$ are recorded from column “D to P”, random values of $\varphi^{\prime}$ are recorded in column “Q and AC” and the random values of $\gamma$ are recorded in column “AD to AP” within the embankment domain in this worksheet.

Fig. 10

PSSA using Monte Carlo simulation

Table 5 shows the variation of $P_{f} (\% )$ with number of samples for MCS analysis for the two cases namely, Case 1: $r_{u} = 0.25$, $k_{h} = 0.10$, $\upsilon_{{c^{\prime}}} = 0.25$, $\upsilon_{{\varphi^{\prime}}} = 0.05$, $\upsilon_{\gamma } = 0.05$ and Case 2: $r_{u} = 0.25$, $k_{h} = 0.20$, $\upsilon_{{c^{\prime}}} = 0.50$, $\upsilon_{{\varphi^{\prime}}} = 0.10$, $\upsilon_{\gamma } = 0.05,$ respectively. When the number of samples is less, there are some variations of ${\mathbf{P}}_{{\mathbf{f}}}$ noticed; but when the number of samples is greater than 30,000 then there is convergence in the reported $P_{f} (\% )$. Therefore, 50,000 samples are enough to perform MCS analysis for the present study. Au and Wang (2014) have recommended that when the ${\mathbf{P}}_{{\mathbf{f}}}$ is very small then for increase the accuracy of the analysis, MCS is performed with a large number of samples or the analysis is performed with subset simulation.

Table 5 Variation of $P_{f} (\% )$ with number of samples for MCS analysis

3.3 CCDF perspective for evaluation of ${\mathbf{P}}_{{\mathbf{f}}}$

The probabilistic slope analysis is carried out considering different pore pressure and seismic loading scenarios. Figure 11 presents the CCDF plot between $P(Y > y)$ vs.$y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ for $k_{h}$ values (i.e., 0.00, 0.05, 0.10, 0.15, 0.20) at $r_{u}$ = 0.0. Similarly, Figs. 12, 13 show the CCDF plot between $P(Y > y)$ vs. $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ for other $r_{u}$ values (i.e., 0.25 and 0.50). Also, different combinations of coefficient of variation $\left( \upsilon \right)$ for $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are further used in the analysis. The various combinations of $\left( {\upsilon_{{c^{\prime}}} ,\upsilon_{{\varphi^{\prime}}} {\text{and }}\upsilon_{\gamma } } \right)$ considered for stability analysis of the embankment are (0.25, 0.05, 0.05) and (0.50, 0.10, 0.05), respectively. Since, the system response is $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$, the slope failure occurs when $y > 1.0$. The probability of failure $\left( {P_{f} } \right)$ of the embankment is the probability when $y > 1.0$ i.e., $P(Y > 1.0)$. The results presented in Figs. 12, 13 reflect increased chances of slope failure when coefficient of variations of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ of the soil of embankment rises. From the results, it is clear that the probability of failure $\left( {P_{f} } \right)$ of the embankment steadily increases when higher pore water pressure loading is considered. The trend of the CCDF plot shows that $P_{f}$ increases when COV increases along with the increase in the pore-water pressure ratio. It can be further noticed that the CCDF plot developed after performing MCS analysis gives the $P(Y > y)$ up to 0.00002.

Fig. 11

CCDF plot of $P\left( {Y > y} \right){\text{ vs}}. \, y$ when $r_{u} = 0.00$ from MCS analysis

Fig. 12

CCDF plot of $P\left( {Y > y} \right)\;{\text{vs}}.y$ when $r_{u} = 0.25$ after MCS analysis

Fig. 13

CCDF plot of $P\left( {Y > y} \right)\;{\text{vs}}.y$ when $r_{u} = 0.50$ from MCS analysis

In MCS method, the $P_{f}$ is computed by taking the ratio of number of failed sample and total number of samples. Table 6 represents the $P_{f}$ with MCS technique for all the cases which are considered for analysis.

Table 6 $P_{f}$ estimation from failed sample data for MCS analyses

Figure 14 shows the histogram plot of all 50,000 samples for the analysis case $r_{u} = 0.25$,$k_{h} = 0.10$, $\upsilon_{{c^{\prime}}} = 0.25$, $\upsilon_{{\varphi^{\prime}}} = 0.05$ and $\upsilon_{\gamma } = 0.05$ from MCS analysis. The histogram clearly displays the number of samples having $FS < 1.0$ which are failed samples. It is clearly notice that 5723 samples are failed out of 50,000 samples during PSSA with MCS technique. This plot has been provided only for the purpose of illustration. Similarly, histogram plots can be shown for other analysis cases.

Fig. 14

$FS$ Histogram obtained from MCS for $r_{u} = 0.25$, $k_{h} = 0.10$, $\upsilon_{{c^{\prime}}} = 0.25$, $\upsilon_{{\varphi^{\prime}}} = 0.05$, $\upsilon_{\gamma } = 0.05$

3.4 Subset simulation results

Next, PSSA is performed with Subset Simulation (SS) technique. The UPSS-3.0 module written in Visual Basic code is used to run the SS analysis. It is necessary to specify the number of samples per level (N), number of simulation level (m), conditional probability $\left( {p_{0} } \right)$. The system response variable $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$, random values of standard normal i.i.ds $\left\{ X \right\}$, probability density function of $\left\{ X \right\}$ i.e., $P\left\{ X \right\}$ are chosen in the UM worksheet. Au and Wang (2014) suggested that the conditional probability $p_{0}$ = 0.10 is a good choice for most problems, and the same value is used in the current work. The developed worksheet with SS analysis is shown in Fig. 15. The probability $P(Y > y)$ of system $\left( Y \right)$ greater than threshold value of system response $\left( y \right)$ can be obtained after performing SS analysis. These values of $P(Y > y)$, $y$ and $FS$ are recorded in column A, B and C of Fig. 16. Furthermore, the random values of $c^{\prime}$ are recorded from column “D to P”, random values of $\varphi^{\prime}$ are recorded in column “Q to AC” and the random values of $\gamma$ are recorded in column “AD to AP” within the embankment domain in this worksheet.

Fig. 15

PSSA using subset simulation

Fig. 16

CCDF plot of $P\left( {Y > y} \right)\;{\text{vs}}.y$ when $r_{u} = 0.00$ after SS analysis

The probabilistic slope analysis is carried out considering different pore pressure and seismic loading scenarios. Figure 16 presents the CCDF plot between $P(Y > y)$ vs.$y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ for various $k_{h}$ values (i.e., 0.00, 0.05, 0.10, 0.15, 0.20) at $r_{u}$ = 0.0. Similarly, Figs. 18, 19 show the CCDF plot between $P(Y > y)$ vs. $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$ for other $r_{u}$ values (i.e., 0.25 and 0.50). Also, different combinations of coefficient of variation $\left( \upsilon \right)$ for $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ are further used in the analysis. The various combinations of $\left( {\upsilon_{{c^{\prime}}} ,\upsilon_{{\varphi^{\prime}}} {\text{and }}\upsilon_{\gamma } } \right)$ considered for stability analysis of the embankment are (0.25, 0.05, 0.05) and (0.50, 0.10, 0.05), respectively. Since, the system response is $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}$, slope failure occurs when $y > 1.0$. The probability of failure $\left( {P_{f} } \right)$ of the embankment is the probability when $y > 1.0$ i.e., $P(Y > 1.0)$. The results presented in Figs. 16, 17, 18 reflect increased chances of slope failure when coefficient of variations of $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ of the soil of embankment rises. From the results, it is clear that the probability of failure $\left( {P_{f} } \right)$ of the embankment steadily increases when higher static seismic loading is considered. The trend of the CCDF plot shows that $P_{f}$ increases when COV increases along with the increase in seismic loading. It can be further noticed that the CCDF plot developed after performing SS analysis gives the $P(Y > y)$ up to 0.00001.

Fig. 17

CCDF plot of $P\left( {Y > y} \right)\;{\text{vs}}.y$ when $r_{u} = 0.25$ after SS analysis

Fig. 18

CCDF plot of $P\left( {Y > y} \right)\;{\text{vs}}{.}y$ when $r_{u} = 0.50$ after SS analysis

Table 7 shows the $P_{f}$ of the embankment from SS analyses for different loading cases as well as the failed sampled data. SS analysis is run for $m = 3$ simulation levels. Thus, three bins of conditional samples are generated denoted by $B_{1} = \left\{ {Y \le y_{1} } \right\}$, $B_{2} = \left\{ {y_{1} < Y \le y_{2} } \right\}$ and $B_{3} = \left\{ {Y > y_{3} } \right\}$.The number of samples considered in these bins are denoted by $N_{1}$, $N_{2}$, and $N_{3}$, respectively. Here, $N_{1} = N_{2} = (1 - 0.1)N$ and $N_{3} = N$, where $N$ is the number of samples at each level. The number of failed samples in these bins are denoted by $N_{1f}$, $N_{2f}$ and $N_{3f}$ respectively. The probability of failure $\left( {P_{f} } \right)$ for SS analysis can be calculated using the equation:

$$P_{f} = \sum {P\left( {F|B_{i} } \right)P\left( {B_{i} } \right)} ,$$

(27)

where the probabilities of failure of bins of conditional samples at each simulation level $i$ can be expressed as $P(F|B_{i} ) = \frac{{N_{if} }}{{N_{i} }}$. Here, $B_{i}$ are the bins of conditional samples at each simulation level and the probabilities of failure of these bins are expressed as $P\left( {B_{i} } \right)$. Here,$P\left( {B_{1} } \right) \approx 1 - 0.1 = 0.9$, $P\left( {B_{2} } \right) \approx 0.1 - 0.1^{2} = 0.09$ and $P(B_{3} ) \approx 0.1^{2} = 0.01$ where $p_{0} = 0.1$ is the conditional probability.

Table 7 $P_{f}$ estimation from failed samples data for SS analyses

In Table 7, the $P_{f}$ values listed in the last column have been calculated using Eq. (27). For example, when $r_{u} = 0.25$, $k_{h} = 0.15$, $\upsilon_{{c^{\prime}}} = 0.25$, $\upsilon_{{\varphi^{\prime}}} = 0.05$, $\upsilon_{\gamma } = 0.05$, it is seen that $N_{1} = N_{2}$ = 450 and $N_{3}$ = 500. Furthermore,$N_{1f}$ = 145,$N_{2f}$ = 450 and $N_{3f}$ = 500. Therefore,$P_{f} (\% )$ = $\left( {0.9 \times \frac{145}{{450}}} \right)$ + $\left( {0.09 \times \frac{450}{{450}}} \right)$ + $\left( {0.01 \times \frac{500}{{500}}} \right)$ = 39.00%. In this way, the $P_{f}$ values for all loading situations are determined and shown in Table 7.

Figure 19 shows the histograms obtained from SS for the analysis case $r_{u}$ = 0.25,$k_{h}$ = 0.10, $\upsilon_{{c^{\prime}}}$ = 0.25, $\upsilon_{{\varphi^{\prime}}}$ = 0.05, and $\upsilon_{\gamma }$ = 0.05. In the SS technique, the analysis is performed in three simulation levels. Therefore, the histograms are plotted for all the three levels. Figure 19a shows that the histogram for 450 samples in level 1. The histogram plot shows the frequency of all 450 samples having different FS values. It is clearly seen that 8 samples have failed in level 1, because these eight samples have values $FS < 1.0$. Figure 19b shows the histogram of 450 samples having different FS values in level 2. It is clearly seen that all 450 samples have failed because FS values for all samples are less than 1.0. Likewise, Fig. 19c shows the histogram plot for 500 samples generated in simulation level 3. Here also, all 500 samples are seen to have failed as $FS < 1.0$.

Fig. 19

Histograms of FS values from SS analysis with $r_{u}$ = 0.25, $k_{h}$ = 0.10, $\upsilon_{{c^{\prime}}}$ = 0.25, $\upsilon_{{\varphi^{\prime}}}$ = 0.05,$\upsilon_{\gamma }$ = 0.05 for a level 1, b level 2 and c level 3

3.5 Time estimates of PSSA using MCS and SS

In the present study, PSSA has been performed with both MCS and SS technique. It is noticed that in the present study, 50,000 samples are used to perform the MCS and only 1400 samples are used in three simulation levels to achieve the accuracy to determine the $P_{f}$ of slope of the embankment with desired level of accuracy. It is self-evident that SS requires less time than MCS, because SS technique requires significantly less number of samples in comparison to required number of samples in MCS technique. It is also noticed that when the number of samples increases, the required time also increases in MCS. MCS and SS analysis time for all cases are shown in Table 8. It is noticed that the minimum analysis time occurs in the case $r_{u}$ = 0.0, $k_{h}$ = 0.20, $\upsilon_{{c^{\prime}}}$ = 0.50, $\upsilon_{{\varphi^{\prime}}}$ = 0.10, $\upsilon_{\gamma }$ = 0.05. In this case MCS analysis time is 307.45 s, whereas SS analysis time is 9.20 s. The maximum analysis time occurs in the case $r_{u}$ = 0.0, $k_{h}$ = 0.0, $\upsilon_{{c^{\prime}}}$ = 0.25, $\upsilon_{{\varphi^{\prime}}}$ = 0.05, $\upsilon_{\gamma }$ = 0.05. In this case, 492.15 s and SS analysis time is 19.12 s. From the Table 7, it is clearly observed that SS analysis time is very less than MCS analysis. Therefore, it is concluded that that SS is a more efficient technique for performing probabilistic analysis than MCS.

Table 8 MCS and SS analyses time

3.6 Probabilistic variation of $\sigma^{\prime}_{1}$ and $\sigma^{\prime}_{3}$ along the slip surface

After the probabilistic slope stability analysis of the embankment is carried out, it would be interesting to investigate the behaviour of probabilistic output variables. For this purpose, the major and minor principal stresses ($\sigma^{\prime}_{1}$ and $\sigma^{\prime}_{3}$) developing along the slip surface of the failure mass are plotted for the cases: $r_{u}$ = 0.25, $k_{h}$ = 0.10, $\upsilon_{{c^{\prime}}}$ = 0.25, $\upsilon_{{\varphi^{\prime}}}$ = 0.05, $\upsilon_{\gamma }$ = 0.05 and $r_{u}$ = 0.25, $k_{h}$ = 0.20, $\upsilon_{{c^{\prime}}}$ = 0.50, $\upsilon_{{\varphi^{\prime}}}$ = 0.10, $\upsilon_{\gamma }$ = 0.05 when the slope has just failed i.e., when $y = {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}} > 1.0$. For these cases, the probabilistic slope stability is performed with SS technique using the random values of the input variables ($c^{\prime}$, $\varphi^{\prime}$ and $\gamma$) and the variation of $\sigma^{\prime}_{1}$ vs. $\sigma^{\prime}_{3}$ along the slip surface is shown in Fig. 20. A best-fit line is also drawn representing the failure envelope in terms of $\sigma^{\prime}_{1}$ and $\sigma^{\prime}_{3}$. Though the plots are made only for the two cases to illustrate the response of probabilistic output parameters, the same exercise can be carried out for all other analyses cases. These plots are helpful in reflecting the effects of spatial randomness of cohesion and angle of internal friction on the failure envelope.

Fig. 20

Variations of $\sigma^{\prime}_{1}$ vs.$\sigma^{\prime}_{3}$ along the slip surface

4 Conclusions

The present study is primarily concerned with probabilistic slope stability analysis of an earthen embankment considering spatially variable cross-correlated soil parameters, i.e., effective cohesion $\left( {c^{\prime}} \right)$, effective angle of internal friction $\left( {\varphi^{\prime}} \right)$ and unit weight $\left( \gamma \right)$. Previous researchers did not consider the cross-correlation and spatial correlation together for performing probabilistic slope stability analysis with MCS and SS. In this study, PSSA of embankment has been performed by considering the cross-correlation and spatial variation of random variables with MCS and SS technique when seismic and pore pressure loading act simultaneously. A detailed study on the probabilistic behaviour of earthen embankment considering spatial variation of cross-correlated soil parameters with pore pressure and earthquake loadings was long overdue, and the issue is addressed in this study. The probabilistic analysis is performed with MCS and SS techniques using the UPSS 3.0 module developed in an MS-Excel spreadsheet platform by Au and Wang (2014). The following conclusions are drawn based on results obtained from the analyses:

• 1. The analysis shows that the cross-correlation between random variables and spatial distribution of random variables highly impact the stability of embankment. Therefore, it is necessary to consider both cross-correlation and spatial correlation simultaneously during probabilistic analysis.

• 2. It is found that when $P_{f} < 50\%$, $P_{f}$ increases with increase in cross-correlation coefficient of $c^{\prime}$ and $\varphi^{\prime}$ and $P_{f}$ decreases with increase in cross-correlation coefficient of $c^{\prime}$ and $\varphi^{\prime}$ when $P_{f} > 50\%$.

• 3. It is observed that the higher number of samples move towards the failure region with increase in $\upsilon_{{c^{\prime}}}$, $\upsilon_{{\varphi^{\prime}}}$ and $\upsilon_{\gamma }$ as they introduce higher uncertainty in the system. In this study, two different combinations of coefficient of variation in $c^{\prime}$, $\varphi^{\prime}$ and $\gamma$ = (0.25, 0.05, 0.05), and (0.50, 0.10, 0.05) are considered in the slope stability analysis. It is further noticed that $P_{f}$ increases with increase in $\upsilon_{{c^{\prime}}}$, $\upsilon_{{\varphi^{\prime}}}$ and $\upsilon_{\gamma }$ resulting in reduced stability of the embankment.

• 4. The analysis shows that $P_{f}$ of earthen embankment increases with an increase in horizontal seismic coefficient $\left( {k_{h} } \right)$ and pore pressure ratio $\left( {r_{u} } \right)$. The CCDF plots show that when $k_{h}$ and $r_{u}$ values are increased, the CCDF plots shift towards right indicating a movement of the samples towards the failure region. The CCDF plots help us to precisely locate the condition when the failure is initiated by observing the first random field corresponding to the system response $\left( {y > {1 \mathord{\left/ {\vphantom {1 {FS}}} \right. \kern-0pt} {FS}}} \right)$.

• 5. The most critical condition for the stability of earthen embankment when $r_{u}$ = 0.50,$k_{h}$ = 0.20, $\upsilon_{{c^{\prime}}} = 0.50$, $\upsilon_{{\varphi^{\prime}}} = 0.10$, $\upsilon_{\gamma } = 0.05$ are considered in the slope stability analysis. In this case, $P_{f}$ = 99.80% is reported.

• 6. The CCDF plot shows that MCS computes the value of $P(Y > y)$ up to ${10}^{-4}$ level but SS is able to compute the value of $P(Y > y)$ up to ${10}^{-5}$ level. Here, it is found that MCS fails to generate the failure sample in case $r_{u} = 0.0$, $k_{h} = 0.0$, $\upsilon_{{c^{\prime}}} = 0.25$, $\upsilon_{{\varphi^{\prime}}} = 0.05$, $\upsilon_{\gamma } = 0.05$ and report $P_{f}$ = 0.0 which is unrealistic but SS generates failure samples in this case and report the $P_{f}$ = 0.002%. Therefore, it is concluded that SS is the more suitable technique for the probabilistic analysis for system with low $P_{f}$ values.

• 7. The SS analysis time is very less compared to MCS analysis time. Therefore, SS is deemed as a more efficient technique than MCS for probabilistic analysis.

• 8. The probabilistic response of output parameters is shown in terms of major and minor effective principal stresses ($\sigma^{\prime}_{1}$ and $\sigma^{\prime}_{3}$) that develop along the slip surface, and the plots display the nature of variation of these parameters due to spatial randomness of the corresponding soil parameters.

• 9. Some researchers have treated $k_{h}$ as a random variable following exponential and lognormal distributions (Johari et al. 2015a, b; Hamrouni et al. 2021). It would be interesting to investigate the performance of MCS and SS simulation in probabilistic slope stability analysis considering both pore pressure ratio ($r_{u}$) and horizontal seismic coefficient ($k_{h}$) as spatially distributed random variables. In future, the authors will communicate the results of MCS and SS analysis treating $r_{u}$ and $k_{h}$ as random variable in addition to cohesion, angle of internal friction and unit weight of soil.