Estimation in generalized uniform distribution with progressively type-II censored sample

Abstract

In this paper, the two-parameter generalized uniform distribution is considered as a lifetime model and its distributional and reliability characteristics are discussed. The maximum likelihood and Bayes estimates for both parameters are derived when the lifetime data are progressively type-II censored. The asymptotic confidence intervals and highest posterior density (HPD) credible intervals for the parameters are also discussed. For carrying out the Bayes estimation, the Metropolis-Hastings algorithm is used for generating a Markov chain Monte Carlo (MCMC) sample from the posterior distribution. The performance of the derived estimates is illustrated using a Monte Carlo simulation study. Finally, two real data sets are analyzed with respect to the estimation methods discussed.

1 Introduction

In reliability estimation, the lifetime of a system or an item is assumed to follow a certain statistical distribution, which is then used for studying the reliability characteristics of the system. Various versatile statistical models have been proposed in the literature over the past years, some of them being exponential, gamma, Weibull etc. For more details see, Lawless (2003) and Sinha (1986). Once a statistical model is assumed for the lifetime of the system/unit, life-testing experiments are conducted on a random sample of items and inferences are then drawn, about the reliability characteristics, on the basis of the observed failure-time data. Generally, in reliability theory, the lifetime of a device is assumed to be a non-negative random variable with no finite upper limit. In practice, it seems very much plausible to have an upper bound to the lifetime of a system/unit, since nothing is immortal and thus there should be some maximum lifetime possible for the product. Also, as mentioned in Balakrishnan and Aggarwala (2000), the uniform distribution is one of the frequently used distributions in life studies. It is also an interesting distribution to discuss, particularly from a mathematical point of view. Of course, it is also to one’s benefit to have a wider choice of distributional results when modelling lifetime data.

Proctor (1987) introduced the four-parameter generalized uniform distribution which is a counterpart to the Burr type XII. Tiwari et al. (1996) studied the Bayes estimation for parameters in the Pareto distribution using the generalized uniform distribution. Lee (2000) derived the maximum likelihood estimator (MLE), modified MLE, minimum risk estimator (MRE) and uniformly minimum variance unbiased estimator (UMVUE) of shape and scale parameters in generalized uniform distribution and proposed several estimators for the right tail probability using the proposed estimators for shape and scale parameters. Dixit et al. (2003) studied the problem of efficient estimation of parameters of a uniform distribution in the presence of outliers. He assumed that a set of random variables $X_1,X_2\dots ,X_n$ represents the masses of roots where out of n-random variables some of these roots (say k) have different masses; therefore, those masses have different uniform distributions with unknown parameters and these k observations are distributed with generalized uniform distribution (GUD), see Bhatt (2014). Ali et al. (2005) considered independent generalized uniform distributions for the stress and strength model and obtained the minimum variance unbiased reliability estimator. Phal and Dixit (2012) obtained the MLE and the UMVUE of $P(X \le Y)$, where both X and Y follow the uniform distribution and outliers are generated from a generalized uniform distribution (GUD). It was shown that UMVUE is better than MLE when one parameter of GUD is known. When both parameters of the GUD are unknown, $P (X \le Y)$ was estimated by using a mixture estimate and was shown that the estimator of $P(X \le Y)$ is consistent. Bhatt (2014) obtained the characterization result based on the expectation of the function of a random variable for generalized uniform distribution. The uniform distribution and its generalization find various applications in practice. For the design of anchorage regions in traditional set-up, the stress on the anchorage length is commonly assumed to be uniformly distributed. Further, the force of water flow, stress on the venting valve, etc. may have generalized uniform distribution, see Pal (2022). Pal (2022) found suitable estimators of reliability function for the stress-strength model when stress and strength independently follow generalized uniform distribution and strength stochastically dominates stress.

The progressive type-II censoring has been studied extensively by numerous researchers. The foremost advantage of the above censoring scheme, that it allows for the removal of live units during the course of the life testing experiment, has made this censoring scheme applicable in various fields of study. Moreover, it results in reduced cost and time of the experiment. The progressive type-II censoring, which includes the conventional type-II censoring scheme as a special case, was first introduced by Cohen (1963), although (Herd 1956) was the first to discuss the idea of progressive censoring in his PhD thesis entitled "Estimation of the parameters of a population from a multi-censored sample" at Iowa state college (Ames, Iowa). Since then various authors have discussed inferential methods using progressive type-II right censoring for different statistical models. Hofmann et al. (2005) discussed that in many situations the type-II progressive censoring schemes significantly improve upon the conventional type-II censoring. For the recent work on the progressive censoring one can see the following references: Kumar et al. (2017) studied the Nakagami distribution as a reliability lifetime model, Chaturvedi et al. (2018) discussed the reliability estimation from a family of distributions, Almongy et al. (2021) applied transformer insulation using Weibull extended distribution (Kumar and Kumar 2022) obtained estimation for reliability from inverse Pareto distribution, Kumari et al. (2022) discussed estimation of multicomponent reliability from the inverse Pareto lifetime model, Shukla et al. (2023) studied inferential analysis of the Weibull-G family of distributions, Saini et al. (2023) discussed inference on multicomponent stress-strength reliability from Topp-Leone distribution, Kumari et al. (2024) obtained Bayesian and classical estimates of the reliability from the power Lindley distribution, Saini et al. (2024) studied statistical inference on reliability from Kumaraswamy distribution, Goel and Krishna (2024) discussed accidental breakages in progressively type-II censored lifetime experiments, Tian et al. (2024) obtained inferences and optimal censoring scheme for a competing-risks model from inverse exponentiated Rayleigh distribution and references cited therein.

The progressive type-II right censoring scheme can be described as follows: Suppose that n items are put on life test, under pre-fixed progressive censoring scheme $\mathop {R}\limits _{\sim }=(R_1,R_2,\dots ,R_m)$ and the fixed number of failures m. At the time of the first failure, $R_1$ units are removed randomly from the remaining $n-1$ live units, and after the second failure, $R_2$ units are removed randomly from the remaining $n-R_1-1$ live units and so on. This procedure is continued until remaining live units $R_m$ are removed from the life test at the time of $m^{th}$ failure. Clearly, $\sum _{i=1}^{m}R_i+m=n$. If $x_1,x_2,\dots ,x_m$ denote the observed failure times, then the likelihood function of these sample data is given as

$$\begin{aligned} L(\mathop {x}\limits _{\sim })= & {} A \prod _{i=1}^{m}f(x_i)[1-F(x_i)]^{R_i}; 0 \le x_1 \le x_2\dots \le x_m<\infty , \\ \text {where}~~ A= & {} n(n-R_1-1)(n-R_1-R_2-2)\dots (n-R_1-R_2-\dots -R_m-m+1). \end{aligned}$$

In this paper, we have considered generalized uniform distribution (GUD), with shape and scale parameters (indicating the maximum lifetime of a product), as a feasible lifetime model. The main contribution of this paper is to study the maximum likelihood and Bayesian estimation of the parameters of GUD using progressively type-II censored data. The GUD model is suitable in life testing experiments where it is desirable to have an upper limit on the maximum age of an item. In practice, it is not desirable to assume the upper limit of the lifetime of an item to be infinity, as none of the electronic, mechanical or biological units can work forever. Here, the parameter $\theta$ being the scale parameter provides an upper limit to the lifetime of an item. It also suggests the maximum lifetime of an item when the unit will need to be replaced. It will be interesting to see the effect of the progressively type-II censored data on the estimation of the parameters of GUD as it has increasing and U-shaped failure rate functions depending on the true values of the parameters.

The rest of the paper is articulated as follows: In section 2 the model and its reliability characteristics are discussed along with data generation techniques. Section 3 deals with the derivation of MLEs of the parameters and their asymptotic interval estimates. In section 4 we have derived the Bayes estimates of the parameters along with the highest posterior density (HPD) intervals using the Metropolis-Hastings (MH) algorithm. In section 5 we have discussed the details of the Monte Carlo simulation study, their results and conclusions of the study. Finally, in section 6, two real data sets are studied concerning different estimation methods discussed above.

2 Model description

In this section, we discuss some statistical properties and reliability characteristics of the GUD.

2.1 Statistical properties

The probability density function (pdf) and the corresponding cumulative distribution function (cdf) of $GUD(\alpha ,\theta$), respectively, are given by

$$\begin{aligned} {f_X}(x;\alpha ,\theta )= & {} \frac{\alpha }{\theta }\left( \frac{x}{\theta }\right) ^{\alpha -1}\,;\, 0<x<\theta<\infty \,;\, \alpha>0 \\ {F_X}(x;\alpha ,\theta )= & {} \left( \frac{x}{\theta }\right) ^{\alpha } \,;\, 0<x<\theta <\infty \,;\, \alpha >0 \end{aligned}$$

The r-th raw moment of the above distribution is given by

$$\begin{aligned} {E}[X^{r}]=\frac{\alpha \theta ^{r}}{r+\alpha } \,;\, r+\alpha >0 \end{aligned}$$

In particular,

$$\begin{aligned}{E}[X]=\frac{\alpha \theta }{1+\alpha }~~~~ \text {and}~~~~ {Var}[X]=\frac{\alpha \theta ^{2}}{(1+\alpha )^{2}(2+\alpha )}\end{aligned}$$

The mode and median of the distribution are, respectively, given by

$$\begin{aligned} M_0=\left[ \frac{3}{2^{1/\alpha }}-\frac{2\alpha }{1+\alpha }\right] \theta ~~~~ \text {and}~~~~ M_d=\frac{\theta }{2^{1/\alpha }} \end{aligned}$$

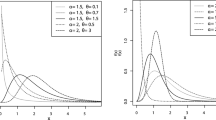
Here, $\alpha$ and $\theta$ are the shape and scale parameters, respectively. As special cases, for $\alpha =1$ the distribution reduces to uniform distribution on the interval (0, $\theta$) and power distribution for $\theta =1$. Also, this distribution is positively (negatively) skewed for $\alpha <1$ $(\alpha >1)$. Figure 1a shows plots of the above pdf for $\theta =1$ and different values of $\alpha$. GUD also has relationships with exponential and Pareto distributions in such a way:

• If $X\,\sim {}\,GUD(\alpha ,\,\theta )$ then the distribution of $Y=-\,\alpha \,ln(X/\theta )$ is standard exponential i.e $Y\,\sim \,Exp(1)$.

• If $X\,\sim \,GUD(\alpha ,\,\theta )$ then the distribution of $Z\,=\,1/X$ is Pareto with shape parameter $\alpha$ and scale parameter $\beta$ i.e $Z\,\sim \,Pa(\alpha ,\beta )$, where $\beta =1/\theta$.

Fig. 1

Plots of pdf and hazard rate function of GUD

2.2 Reliability characteristics

The reliability function of GUD ($\alpha ,\theta$) is given by

$$\begin{aligned} {R}(t)=1-F(t)=1-\left( \frac{t}{\theta }\right) ^{\alpha } \,;\, 0<t<\theta <\infty \,;\, \alpha >0 \end{aligned}$$

The hazard rate function of GUD ($\alpha ,\theta$) is given by

$$\begin{aligned} {h}(t)=\frac{f(t)}{R(t)}=\frac{\alpha \, t^{\alpha -1}}{\theta ^{\alpha }-t^{\alpha }} \,;\, 0<t<\theta <\infty \,;\, \alpha >0 \end{aligned}$$

The Mean time to system failure of GUD ($\alpha ,\theta$) is given by

$$\begin{aligned} MTSF={E}[X]=\frac{\alpha \theta }{1+\alpha } \end{aligned}$$

Figure 1 shows the plots of the pdf and hazard rate function of GUD for different values of the parameter $\alpha$ and $\theta =1$. Figure 1b shows that, for $\alpha >1$, the hazard-rate function is a monotonically increasing function of t. For $\alpha <1$ the hazard-rate decreases monotonically for $t<t_0$ and increases monotonically for $t>t_0$, where $t_0=\theta (1-\alpha )^{1/\alpha }$.

2.3 Data generation from GUD

Let $X_{1:m:n},X_{2:m:n},\dots ,X_{m:m:n}$ be a progressively type-II right censored sample obtained from a sample of size n from GUD($\alpha ,\theta$) with the pre-specified censoring scheme $\mathop {R}\limits _{\sim }= (R_1,R_2,\dots ,R_m)$. Then the likelihood function of the sample, with $X_{i:m:n}=x_{i}$ is given by

$$\begin{aligned}L(\mathop {x}\limits _{\sim })= A\left( \frac{\alpha }{\theta }\right) ^{m}\prod _{i=1}^{m}\left( \frac{x_i}{\theta }\right) \left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] ^{R_i};0< x_1\le x_2\dots \le x_m<\theta <\infty ;\,\alpha >0\end{aligned}$$

where, $A=n(n-R_1-1)(n-R_1-R_2-2)\dots (n-R_1-R_2-\dots -R_{m-1}-m+1)$.

Before giving the algorithm to generate progressively type-II right censored sample from GUD($\alpha ,\theta$) we state the following theorem from (Balakrishnan and Aggarwala, 2000, page. 18).

Theorem 1

Let $X_{1:m:n},X_{2:m:n},\dots ,X_{m:m:n}$ denote a progressively type-II right censored sample from the standard exponential distribution, with censoring scheme $(R_1,R_2,\dots ,R_m)$. Define

$Z_1=nX_{1:m:n}$

$Z_2=(n-R_1-1)(X_{2:m:n}-X_{1:m:n})$

... ...

... ...

$Z_m=(n-R_1-R_2-\dots -R_{m-1}-m+1)(X_{m:m:n}-X_{m-1:m:n})$

Then the "Progressively Type-II right censored spacings" defined above, are all independent and identically distributed as standard exponential.

2.3.1 Algorithm to generate data from GUD

For generating Progressively type-II right censored sample from GUD($\alpha ,\theta$) we make use of the following algorithm given in (Balakrishnan and Aggarwala, 2000, page.33).

• 1. Generate n iid standard uniform random variables $(u_1,u_2,\dots ,u_n)$.

• 2. Set $z_i=-log(1-u_i)\,; \,i=1,2\dots ,n$. Then $z_1,z_2,\dots ,z_n$ are iid standard exponential random variables.

• 3. Set $y_1=z_1/n$ and $y_i=y_{i-1}+\frac{z_i}{n-\sum \nolimits _{j=1}^{i-1}R_j-i+1} \,;\, i=2,3,\dots ,m$ for the given censoring   scheme $\mathop {R}\limits _{\sim }=(R_1,R_2,\dots ,R_m)$. Then $y_1,y_2\dots y_m$ is a progressively type-II right censored sample from a standard exponential distribution.

• 4. Set $x_i={F_X}^{-1}(y_i)=\theta (1-e^{-y_i})^{1/\alpha }$; $i=1,2\dots ,m$. Then $x_1,x_2\dots x_m$ is the required progressively type-II right censored sample from GUD ($\alpha ,\theta$).

3 Maximum likelihood estimation

Let $x_1,x_2\dots ,x_m$ be a progressively type-II censored sample from GUD($\alpha ,\theta$) with censoring scheme $\mathop {R}\limits _{\sim }=(R_1,R_2,\dots ,R_m)$. Then the likelihood function is;

$$\begin{aligned} L(\mathop {x}\limits _{\sim })=A\left( \frac{\alpha }{\theta }\right) ^{m}\prod _{i=1}^{m}\left( \frac{x_i}{\theta }\right) ^{\alpha -1}\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] ^{R_i};0< x_1\le x_2\dots \le x_m<\theta <\infty ;\,\alpha >0 \end{aligned}$$

(1)

where; $A=n(n-R_1-1)(n-R_1-R_2-2)\dots (n-R_1-R_2-\dots -R_m-m+1)$.

Taking the natural logarithm of the above equation we get;

$$\begin{aligned}{} & {} \log L=\log A+m \log \alpha -m \alpha \log \theta \nonumber \\{} & {} \quad +(\alpha -1)\sum _{i=1}^{m}\log x_i+\sum _{i=1}^{m}R_i\log \left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] \end{aligned}$$

(2)

Differentiating the above equation w.r.t $\alpha$ and $\theta$ we get,

$$\begin{aligned}{} & {} \frac{\partial \log L}{\partial \alpha }=\frac{m}{\alpha }-m\log \theta +\sum _{i=1}^{m}\log x_i-\sum _{i=1}^{m}\frac{R_i x_i^{\alpha }\log (\frac{x_i}{\theta })}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] \theta ^{\alpha }} \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \quad \frac{\partial \log L}{\partial \theta }=-\frac{m\alpha }{\theta }+\sum _{i=1}^{m}\frac{\alpha R_i x_i^{\alpha }}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] \theta ^{\alpha +1}} \end{aligned}$$

(4)

Also,

$$\begin{aligned}{} & {} \frac{\partial ^{2}\log L}{\partial \alpha ^2}=-\frac{m}{\alpha ^2}-\sum _{i=1}^{m}\frac{R_i\left( \frac{x_i}{\theta }\right) ^{2\alpha }\left[ \log \left( \frac{x_i}{\theta }\right) \right] ^{2}}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] ^{2}}\nonumber \\{} & {} \quad -\sum _{i=1}^{m}\frac{R_i\left( \frac{x_i}{\theta }\right) ^{\alpha }\left[ \log \left( \frac{x_i}{\theta }\right) \right] ^{2}}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] } \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \quad \frac{\partial ^{2}\log L}{\partial \theta ^2}=\frac{m\alpha }{\theta ^2}-\frac{\alpha ^2}{\theta ^{2\alpha +2}} \sum _{i=1}^{m}\frac{R_ix_i^{2\alpha }}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^\alpha \right] ^2}\nonumber \\{} & {} \quad -\frac{\alpha (\alpha +1)}{\theta ^{\alpha +2}}\sum _{i=1}^{m}\frac{R_ix_i^\alpha }{\left[ 1-\left( \frac{x_i}{\theta }\right) ^\alpha \right] } \end{aligned}$$

(6)

$$\begin{aligned} {} \begin{aligned} \frac{\partial ^{2}\log L}{\partial \alpha \partial \theta }&= -\frac{m}{\theta }+\sum _{i=1}^{m}\frac{R_i x_i^\alpha }{\left[ 1-\left( \frac{x_i}{\theta }\right) ^\alpha \right] {\theta ^{\alpha +1}}} +\alpha \sum _{i=1}^{m}\frac{R_ix_i^{2\alpha }\log \left( \frac{x_i}{\theta }\right) }{\left[ 1-\left( \frac{x_i}{\theta }\right) ^\alpha \right] ^{2}\theta ^{2\alpha +1}} \\&\quad +\alpha \sum _{i=1}^{m}\frac{R_ix_i^{\alpha }\log \left( \frac{x_i}{\theta }\right) }{\left[ 1-\left( \frac{x_i}{\theta }\right) ^\alpha \right] \theta ^{\alpha +1}} \\ \\&= \frac{\partial ^{2}\log L}{\partial \theta \partial \alpha } \end{aligned} \end{aligned}$$

(7)

Now, when both parameters are unknown the MLEs of $\alpha$ and $\theta$ can be found by simultaneously solving the following non-linear equations;

$$\begin{aligned} \frac{\partial \log L}{\partial \alpha }=\frac{m}{\alpha }+\sum _{i=1}^{m}\log x_i-m\log \theta -\sum _{i=1}^{m}\frac{R_i x_i^{\alpha }\log (\frac{x_i}{\theta })}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] \theta ^{\alpha }}=0 \end{aligned}$$

(8)

and

$$\begin{aligned} \frac{\partial \log L}{\partial \theta }=\sum _{i=1}^{m}\frac{\alpha R_i x_i^{\alpha }}{\left[ 1-\left( \frac{x_i}{\theta }\right) ^{\alpha }\right] \theta ^{\alpha +1}}-\frac{m\alpha }{\theta } =0 \end{aligned}$$

(9)

The equations (8) and (9) cannot be solved analytically, and thus we use some appropriate numerical method to solve them. The bivariate Newton-Raphson method, which involves the following iterative procedure, can be used.

$$\begin{aligned} \begin{bmatrix} \alpha ^{(k+1)} \\ \theta ^{(k+1)} \end{bmatrix} = \begin{bmatrix} \alpha ^{(k)} \\ \theta ^{(k)} \end{bmatrix} - \hat{I}^{-1}(\alpha ^{(k)},\theta ^{(k)}) \begin{bmatrix} \frac{\partial \log L}{\partial \alpha } \\ \frac{\partial \log L}{\partial \theta } \end{bmatrix}_{\alpha =\hat{\alpha },\theta =\hat{\theta }} \end{aligned}$$

(10)

where, $(\alpha ^{(k)},\theta ^{(k)})$ denotes the value of $(\alpha ,\theta )$ at the $k^{th}$ iteration and $\hat{I}(\theta ^{(k)},\alpha ^{(k)})$ is the observed fisher information matrix given by;

$$\begin{aligned} \hat{I}(\alpha ^{(k)},\theta ^{(k)}) = \begin{bmatrix} -\frac{\partial ^{2}\log L}{\partial \alpha ^2} &{} -\frac{\partial ^{2}\log L}{\partial \alpha \partial \theta } \\ -\frac{\partial ^{2}\log L}{\partial \theta \partial \alpha } &{} -\frac{\partial ^{2}\log L}{\partial \theta ^2} \end{bmatrix}_{\alpha =\alpha ^{(k)},\,\theta =\theta ^{(k)}} \end{aligned}$$

(11)

Alternatively, one can use the maxLik package of R programming language to directly maximize the log likelihood function which along with the ML estimates of the parameters, also returns the standard errors of these estimates.

3.1 Asymptotic variances and confidence intervals

Since the distribution of $\hat{\alpha }$ and $\hat{\theta }$ cannot be determined, hence it is not possible to obtain the expressions for the variances or standard errors of the estimates. So we proceed by considering the asymptotic variance-covariance matrix of $(\hat{\alpha },\hat{\theta })$ which can be computed using the inverse of Fisher’s information matrix, given by;

$$\begin{aligned} I(\alpha ,\theta )= {E}\begin{bmatrix} - \frac{\partial ^{2}\log L}{\partial \alpha ^2} &{} -\frac{\partial ^{2}\log L}{\partial \alpha \partial \theta } \\ -\frac{\partial ^{2}\log L}{\partial \theta \partial \alpha } &{} -\frac{\partial ^{2}\log L}{\partial \theta ^2} \end{bmatrix} \end{aligned}$$

(12)

where, the expressions for $\frac{\partial ^{2}\log L}{\partial \alpha ^2},\frac{\partial ^{2}\log L}{\partial \alpha \partial \theta },\frac{\partial ^{2}\log L}{\partial \theta \partial \alpha }$ and $\frac{\partial ^{2}\log L}{\partial \theta ^2}$ have been computed in equations (5), (6) and (7). The expected values of these expressions are very complicated to handle analytically and thus, for obtaining the estimate of the asymptotic variance-covariance of $(\hat{\alpha },\,\hat{\theta })$ we use the inverse of observed Fisher’s information matrix, given by;

$$\begin{aligned} \hat{I}(\hat{\alpha },\hat{\theta }) = \begin{bmatrix} -\frac{\partial ^{2}\log L}{\partial \alpha ^2} &{} -\frac{\partial ^{2}\log L}{\partial \alpha \partial \theta } \\ -\frac{\partial ^{2}\log L}{\partial \theta \partial \alpha } &{} -\frac{\partial ^{2}\log L}{\partial \theta ^2} \end{bmatrix}_{\alpha =\hat{\alpha },\,\theta =\hat{\theta }} \end{aligned}$$

(13)

i.e. the estimate of asymptotic variance-covariance matrix of $(\hat{\alpha },\,\hat{\theta })$ is given by $\hat{I}^{-1}(\hat{\alpha },\hat{\theta })$ and we can obtain the estimates of the variances, $\hat{Var}(\hat{\alpha })$ and $\hat{Var}(\hat{\theta })$, as the diagonal elements of this matrix. Using the large sample property of MLEs, which states that $(\hat{\alpha },\,\hat{\theta })$ converges in distribution to $N_{2}((\alpha ,\,\theta ),\,I^{-1}(\alpha ,\theta ))$ and the estimates of variances, we obtain the two-sided $100(1-\gamma )\%$ asymptotic confidence intervals for $\alpha$ and $\theta$ as $\hat{\alpha }\,\pm \,z_{\gamma /2}\sqrt{\hat{Var}(\hat{\alpha })}$ and $\hat{\theta }\,\pm \,z_{\gamma /2}\sqrt{\hat{Var}(\hat{\theta })}$ respectively. The coverage probabilities for both the parameters can be obtained as follows;

$$\begin{aligned} CP_{\alpha }=P\left[ \Bigg |{\frac{\hat{\alpha }-\alpha }{\sqrt{\hat{Var}(\hat{\alpha })}}}\Bigg | \le z_{\gamma /2}\right] \end{aligned}$$

and

$$\begin{aligned} CP_{\theta }=P\left[ {\Bigg |\frac{\hat{\theta }-\theta }{\sqrt{\hat{Var}(\hat{\theta })}}}\Bigg | \le z_{\gamma /2}\right] \end{aligned}$$

where, $z_{\gamma /2}$ is the upper $(\gamma /2)^{th}$ quantile of the standard normal distribution and $0<\gamma <1$.

4 Bayes estimation

In this section, we consider the estimation of parameters of the model under Bayesian setup when both of them are unknown. Due to the non-existence of conjugate prior and for the sake of similarity with the likelihood function, the prior distributions for $\alpha$ and $\theta$ are independently chosen as gamma and inverted gamma distributions, respectively, with the following pdfs

$$\begin{aligned}{} & {} g_{1}(\alpha ;a_{1},b_{1})\propto \alpha ^{b_{1}-1}e^{-a_{1}\alpha }; \alpha ,a_{1},b_{1}>0 \\{} & {} \quad g_{2}(\theta ;a_{2},b_{2})\propto \theta ^{-b_{2}-1}e^{-a_{2}/\theta }; \theta ,a_{2},b_{2}>0 \end{aligned}$$

where, $(a_{1},b_{1},a_{2},b_{2})$ are the hyper parameters of the model. The families of gamma/inverted gamma distributions are amply flexible as these can model a variety of priors information. Moreover, non-informative priors are particular cases of these priors. Also, the parameters of gamma/inverted gamma priors can be merged with model parameters, so that mathematical computations become easy. Thus, the joint prior distribution of $(\alpha ,\theta )$ can be obtained as

$$\begin{aligned}{} & {} g(\alpha ,\theta ;a_{1},b_{1},a_{2},b_{2})\propto g_{1}(\alpha ;a_{1},b_{1})g_{2}(\theta ;a_{2},b_{2}) \nonumber \\{} & {} \quad \text {i.e.}~~~~~~~~~~~~ g(\alpha ,\theta ;a_{1},b_{1},a_{2},b_{2})\nonumber \\{} & {} \propto \alpha ^{b_{1}-1}e^{-a_{1}\alpha }\theta ^{-b_{2}-1}e^{-a_{2}/\theta };\alpha ,\theta >0 \end{aligned}$$

(14)

The posterior distribution of $\alpha$ and $\theta$, given the progressively type-II censored data, can be obtained as follows;

$$\begin{aligned} \pi (\alpha ,\theta | data)\propto L(\mathop {x}\limits _{\sim }|\alpha ,\theta )g(\alpha ,\theta ) \end{aligned}$$

where $L(\mathop {x}\limits _{\sim }|\alpha ,\theta )$ denotes the likelihood function of the data $\mathop {x}\limits _{\sim }=(x_{1},x_{2},\dots ,x_{m})$.

Using equations (1) and (14) we get the posterior distribution as;

$$\begin{aligned} \begin{aligned} \pi (\alpha ,\theta | data)\propto \frac{\alpha ^{m+b_{1}-1}}{\theta ^{m+b_{2}+1}}\prod _{i=1}^{m}\left( \frac{x_{i}}{\theta }\right) ^{\alpha -1}\left[ 1-\left( \frac{x_{i}}{\theta }\right) ^{\alpha }\right] ^{R_{i}}e^{-a_{1}\alpha }e^{-a_{2}/\theta } \\;0< x_1\le \dots \le x_m<\theta <\infty ;\,\alpha >0 \end{aligned} \end{aligned}$$

(15)

For obtaining the Bayes estimates of any parametric function $\phi (\alpha ,\theta )$ under squared error loss function (SELF) we need to compute,

$$\begin{aligned} E[\phi (\alpha ,\theta )|data]=\frac{\int _{0}^{\infty }\int _{0}^{\infty }\phi (\alpha ,\theta ) \pi (\alpha ,\theta |data) d\alpha d\theta }{\int _{0}^{\infty }\int _{0}^{\infty }\pi (\alpha ,\theta |data)d\alpha d\theta }\end{aligned}$$

The solution of the above equation requires the computation of complex integrals, but, the analytic solution does not seem feasible. Hence, we propose to use approximation methods using MCMC simulation techniques. These techniques and corresponding algorithms are discussed in the following sub-sections.

4.1 Metropolis–Hastings (M–H) algorithm

Here we discuss an efficient MCMC technique called the Metropolis–Hastings (MH) algorithm to generate a sample from the above-derived posterior distribution and compute the estimate of any parametric function using the generated sample. The MH algorithm, initially proposed by Metropolis and Ulam (1949) and later extended by Hastings (1970), consists in generating a Markov chain of random samples from a probability distribution which eventually converges to the target distribution (from which we originally wanted to generate sample) using a proposal distribution.

We have considered symmetric proposal distribution of type $q(\delta ^{'}|\delta )=q(\delta |\delta ^{'})$ for generating candidate values for the parameters. Here we have considered generating candidate values for $(\alpha ,\,\theta )$ from Bivariate Normal distribution. Since, generating values from Normal distribution allows for producing negative values as well, which is not acceptable, thus we follow the approach discussed below in the algorithm for generating values.

4.1.1 Algorithm

• 1. Set the initial value of the parameters $(\alpha ^{(0)},\,\theta ^{(0)})$.

• 2. Repeat the following steps T times

  • (a) For $1 \le t \le T$, generate $(\delta ^{'},\,\psi ^{'})$ from $N_{2}\, (\,{\mathop {\mu }\limits _{\sim }}^{(t-1)},S)\,$, where ${\mathop {\mu }\limits _{\sim }}^{(t-1)}=(\,\ln (\alpha ^{(t-1)}),\,\ln (\theta ^{(t-1)})\,)$

  • (b) Set $\alpha ^{'}\,=\,exp(\delta ^{'})$ and $\theta ^{'}=exp(\psi ^{'})$.

  • (c) Compute $r=min\left[ 1,\frac{\pi \,(\,\alpha ^{'},\, \theta ^{'}\,|\,\alpha ^{(t-1)},\,\theta ^{(t-1)})}{\pi \,(\,\alpha ^{(t-1)},\,\theta ^{(t-1)})\,|\,\alpha ^{'},\,\theta ^{'})}\right]$.

  • (d) Generate u from Unif(0, 1).

  • (e) If $u<r$, update $(\alpha ^{(t)},\theta ^{(t)})$ with $(\alpha ^{'},\theta ^{'})$, else $(\alpha ^{(t)},\theta ^{(t)})=(\alpha ^{(t-1)},\theta ^{(t-1)})$.

The initial values $(\alpha ^{(0)},\theta ^{(0)})$ are chosen as the MLEs of $\alpha$ and $\theta$. The choice of the variance covariance matrix of the proposal distribution, often called as the tuning parameter, is an important issue. Here we have considered the observed Fisher’s information matrix as the initial value for S and further modified so as to improve the acceptance rate. One can refer to Natzoufras (2009) for a detailed discussion on the topic. The initial $M_0$ values out of M are discarded as the burn-in sample and the Bayes estimates for any parametric function $\phi (\alpha ,\theta )$ are computed using the following expression

$$\begin{aligned} \hat{\phi }_{B}(\alpha ,\theta \,|\,data)=\frac{1}{M-M_0}\left[ \,\,\sum _{i=M_{0}+1}^{M}{\phi (\alpha ^{(i)},\,\theta ^{(i)})}\right] \end{aligned}$$

where, $(\alpha ^{(i)},\theta ^{(i)})$ $; i=M_{0}+1$ $,M_{0}+2,\dots$, M is the generated sample of observations from the target posterior distribution $\pi$.

The Bayes estimates, under SELF, for $\alpha$ and $\theta$ can be obtained as

$$\begin{aligned}{} & {} \hat{\alpha }_{B}=\frac{1}{M-M_0}\,\,\sum _{i=M_{0}+1}^{M}\alpha ^{(i)} \\{} & {} \quad \hat{\theta }_{B}=\frac{1}{M-M_0}\,\,\sum _{i=M_{0}+1}^{M}\theta ^{(i)} \end{aligned}$$

4.2 Highest posterior density (HPD) intervals

The generated MCMC sample in the previous section can be used to construct HPD credible intervals for the parameters. Following the work by Chen and Shao (1999), we discuss the construction of HPD credible interval for $\alpha$ and the same procedure can be used for the construction of HPD credible interval for $\theta$.

Let $\alpha ^{(1)}< \alpha ^{(2)}<,\dots , < \alpha ^{(K)}\,;K=M-M_0$, represent the ordered values of the generated sample $\alpha ^{(M_{0}+1)}\,,\,\alpha ^{(M_{0}+2)}\, \dots \ \,\alpha ^{(M)}$. Then, the $\,100\,(1-\gamma )\,\%$ HPD credible interval, where $0<\gamma <1$, is given by $(\,\alpha _{(j)},\,\alpha _{(j+[(1-\gamma )\,K])}\,)$. The index j is chosen such that;

$$\begin{aligned} \,\alpha _{(j+[(1-\gamma )\,K]\,)}-\alpha _{(j)}=\, \min \limits _{1\, \le j \,\le K} \big (\alpha _{(j+[(1-\gamma )\,K]\,)}-\alpha _{(j)}\big )\,\, \end{aligned}$$

where, [x] denotes the greatest integer value of x.

5 Simulation study

In this section, we study the performances of the MLE’s and Bayes estimates of the parameters (both unknown) based on simulated data sets under two different parameter set-ups, ($\alpha =1,\,\theta =1$) and ($\alpha =2,\,\theta =1$). The study is conducted for two sample sizes viz. $n=30$ (moderate sample size) and $n=50$ (large sample size) and nine censoring schemes for each sample size with different failure information. These censoring schemes are presented in Table 1. The progressive type-II censored data from GUD is obtained using the algorithm discussed in subsection 2.3.1. For evaluating the performance of the MLE’s, the average of the estimates (AE) and average of corresponding mean squared error (MSE) are computed based on 10,000 replications for each censoring scheme. The average length (AL-95) and coverage probabilities (CP-95) of 95% asymptotic confidence intervals for parameters are also computed. The results of simulation study are reported in Tables 2 and 3.

For computing the Bayes estimates of the parameters we have used Metropolis-Hastings (MH) algorithm. The estimates are obtained under the squared error loss function using informative prior as discussed in section 4. The values of the hyperparameters in the case of informative priors are taken in such a way that the mean of the prior distributions come out equal to the true values of the parameters. The hyperparameters of the model are chosen as $(a_1=2,\,b_1=2,\,a_2=1,\,b_2=1)$. In the MH algorithm the starting values of the parameters $(\alpha ^{(0)},\,\theta ^{(0)})$ are chosen as the respective MLEs of the parameters and the tuning parameter S is chosen as the observed Fisher’s information matrix $I^{-1}(\hat{\alpha },\,\hat{\theta })$. The tuning parameter is further adjusted so as to improve the acceptance rate. We have generated 1, 00, 000 observations out of which initial $20\%$ were discarded as the burn-in sample and the remaining ones are used for computing the estimates. For evaluating the performance of these estimates the average of the estimates (AE) and average of corresponding mean squared error (MSE) are computed based on 1000 replications for each censoring scheme. Also, the coverage probability of $95\%$ HPD credible interval (HPD-95) along with the corresponding average length of the interval (AL-95) is computed. The simulation results are reported in Tables 4 and 5, respectively. From these Tables, the following conclusions are made:

• The MLEs of both parameters (shape and scale) are quite satisfactory even for censoring schemes with less failure information and seem to converge to actual values as n and m increase. It is observed that the shape parameter $\alpha$ and the scale parameter $\theta$, respectively, are consistently overestimated and underestimated by the MLEs.

• The estimates perform well as far as mean squared errors are concerned, which are much less and gradually decrease with increasing values of n and m, as expected.

• The observed coverage probability of $\alpha$ matches with the true confidence coefficient, but the same is not observed for $\theta$. In fact, even for the largest values of n and m the coverage probability does not seem to attain desired value.

• The average length of the confidence intervals for both parameters is quite small. It is therefore suggested that for the estimation of shape parameter both the point and interval estimation methods work quite well. As far as scale parameter is concerned point estimation works comparatively better.

• The average values of the Bayes estimates are close to the true values of the parameters $\alpha$ and $\theta$, respectively, even for small values of m and n.

• The mean squared error for both the parameters is much less and gradually decreases as m and n increase. As in the case of MLEs, the same trend i.e. overestimation of $\alpha$ and underestimation of $\theta$ by the estimates is observed here.

• The observed coverage probability for $\alpha$ is very good, even more than the true confidence coefficient. The same for $\theta$ is quite satisfactory and close to the true confidence coefficient for most censoring schemes and even better in cases with high failure information. As compared to the case of MLE’s the interval estimates have significantly improved here.

Thus, it is observed that both point and interval estimation methods in both of the classical and Bayesian paradigm work quite well for both parameters.

Table 1 Progressive Type-II censoring schemes used in the simulation study

Table 2 MLEs of the parameters with associated MSE, AL and CP when $\alpha =1$ & $\theta = 1$

Table 3 MLEs of the parameters with associated MSE, AL and CP when $\alpha =2$ & $\theta = 1$

Table 4 Bayes estimates of the parameters when $\alpha =1,\theta =1$

Table 5 Bayes estimates of the parameters when $\alpha =2,\theta =1$

6 Real data analysis

In this section, two real data sets are analyzed. The data provide the breaking strength of jute fibre at two different gauge lengths. These data have been taken from (Xia et al. 2009) and are also used by Pal (2022). These data sets are given below:

Data set 1: Breaking strength of jute fibre when gauge length = 10 mm.

693.73 704.66 323.83 778.17 123.06 637.66 383.43 151.48 108.94 50.16 671.49 183.16 257.44 727.23 291.27 101.15 376.42 163.40 141.38 700.74 262.90 353.24 422.11 43.93 590.48 212.13 303.90 506.60 530.55 177.25

Data set 2: Breaking strength of jute fibre when gauge length = 20 mm.

71.46 419.02 284.64 585.57 456.60 113.85 187.85 688.16 662.66 45.58 578.62 756.70 594.29 166.49 99.72 707.36 765.14 187.13 145.96 350.70 547.44 116.99 375.81 581.60 119.86 48.01 200.16 36.75 244.53 83.55

Table 6 Goodness of fit tests for the real data sets

For testing the goodness of fit of the model to the data, we have considered Kolmogorov-Smirnov (KS), Cramer-Von-Mises (CVM) and Anderson-Darling (AD) tests. The p-values of the three tests for both data sets are satisfactory and thus show that the model fits the data quite well. The value of the statistics and corresponding p-values are reported in Table 6. For the illustration of estimation methods using the given data, three values of m (failure information) and nine different censoring schemes (3 schemes corresponding to each value of m) are used, which are presented in Table 7. The point and interval estimates, both classical and Bayes, of the parameters under each data set are computed. For the Bayesian computations, MCMC method is used having a posterior sample size of 1, 00, 000 with a burn-in period 20, 000. The results are reported in Tables 8 and 9, respectively. Also, we have drawn diagnostic plots like trace and ACF plots of the MCMC samples to check the convergence for each censoring scheme. These plots are shown in Figs. 2 and 3, respectively. The trace plots show the fine mixings of the generated Markov chains in each case. Also, the ACF plots show that there is no autocorrelation present in the generated MCMC samples.

Table 7 Progressive type-II censoring schemes used in real data analysis

Table 8 Point and interval estimates for the real data set 1

Table 9 Point and interval estimates for the real data set 2

Fig. 2

Trace and ACF plots of $\alpha$ (Green) and $\theta$ (Pink) for the real data set 1

Fig. 3

Trace and ACF plots of $\alpha$ (Green) and $\theta$ (Pink) for the real data set 2

7 Conclusions and future scope

This paper deals with the classical and Bayesian estimation methods of the parameters of two-parameter generalized uniform distribution (GUD). The GUD is a very useful lifetime model in real-life situations and it can model a variety of lifetime data sets. The maximum likelihood and the associated asymptotic confidence interval estimates of the parameters were developed. The Bayes estimates and HPD credible intervals based on the MCMC method were also derived. A Monte Carlo simulation was carried out to compare various estimates developed. Simulation results showed that the Bayes estimates with some prior information outperformed the ML estimates and the HPD credible intervals gave better results than the asymptotic confidence intervals. Two different real data sets were analysed for illustrative purposes. As a future course of study, using the same methodology, we can obtain various estimates of the parameters as well as the reliability characteristics of different lifetime models.