1 Introduction

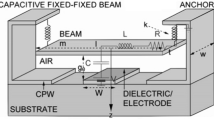
MEMS (Micro-electromechanical systems) technology is used in many fields such as the automobile industry, medical industry, optical devices, aerospace, wireless networks, and communication industry (5G, B5G, and 6G), etc. A few of mostly used MEMS technology-based devices include accelerometers, tire pressure sensors, gyroscopes, blood pressure sensors, pacemakers, MEMS tweezers, energy harvesting devices, switches, filters, and switch matrices [1,2,3,4,5,6,7,8,9,10,11]. MEMS technology used in the field of communication is called RF-MEMS (Radio Frequency Micro-electromechanical systems). RF-MEMS switch is the most basic device and used at various places in any telecommunication system. RF-MEMS switches offer good RF response (isolation and low insertion loss) as compared to solid-state switches. These devices use the physical movement of a suspended structure. Most of them use electrostatic actuation due to low power consumption and integration feasibility with silicon technology. Non-linearity in the actuation dynamics makes it necessary to use a non-linear solver for calculating the switching time [12]. Therefore, analytical expressions are needed for design intuition. Many studies have been reported in the literature for analyzing the switching time behavior of an electrostatic actuator [12,13,14,15,16,17]. However, still, the expressions as derived in [12,13,14] are used for pull-in and release times. In 2011, Shekhar et al. used the same expressions for pull-in and pull-up times [18]. Manivannan et al. [19] have calculated the pull-in time of a fixed–fixed type switching structure using the expression as derived in [12,13,14]. In 2020, Narang and Singh [20] have also done the calculation of pull-in time using the same expression. Thus, in the presented paper, new expressions have been derived for switching time calculation and analysis. Figure 1 shows a schematic representation of an RF-MEMS switch. There are two stable states of this device. Under up-state, the device remains in its un-actuated position and whereas the hanging structure snaps down to the lower electrode in the down-state of the device. The toggling between the states is achieved through the electrostatic force.

Fig. 1
figure 1

A parallel plate capacitor based RF-MEMS Switch

Full size image

2 Analytical modelling

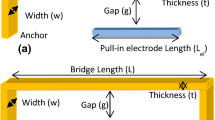
Figure 2 represents the methodology adopted for calculating the pull-in time and release times. A 1-D (One-dimensional) mass, spring, and damper equivalent model of the parallel capacitor is used for the calculation of pull-in and release times (Fig. 2). The pull-in time is calculated under the un-actuated state of the switch, whereas the release time is calculated under the actuated condition. Further, derivation of pull-in time is done under subSect. 2.1 and subSect. 2.2 is used for release time.

Fig. 2
figure 2

Algorithmic flowchart for switching time calculation

Full size image

2.1 Pull-in time

It is the time taken by a hanging structure to snap down to the lower electrode. The pull-in time is calculated from force balance equation (Eq. (1)). Further, the process cited above in Fig. 2 is used for deriving the pull-in time with damping (Fig. 3)

Fig. 3
figure 3

1- D Mass, spring, damper equivalent of the actuator

Full size image

.

$$m.\frac{{d}^{2}y}{{dt}^{2}}+ ky+b.\frac{dy}{dt}=\frac{0.5{\in }_{o}A{v}_{s}}{(d-{y)}^{2}}$$
(1)

where m is the mass of the switching structure, k = spring constant, b = damping coefficient, A = actuation area,\({\in }_{o}\)= air permittivity, d = initial gap between electrodes, y = any intermediate distance between the electrodes, and \({v}_{s}\)= source voltage.

Equation (1) can be modified to Eq. (2) if damping is insignificant. Further, Eq. (3) is used in order to get Eq. (2) in \(\frac{dy}{dt}\) form.

$$0.5m.{\left(\frac{dy}{dt}\right)}^{2}+ 0.5k{y}^{2}=\frac{0.5{\in }_{o}A{{v}_{s}}^{2}y}{d\left(d-y\right)}$$
(2)
$$\frac{dy}{dt}=\sqrt{\frac{A{\in }_{o}{{v}_{s}}^{2}y}{md\left(d-y\right)}}-\frac{k{y}^{2}}{m}$$
(3)
$${t}_{pull-in@mk}= \sqrt{\frac{md}{{\in }_{o}A{{v}_{s}}^{2}}}{\int }_{0}^{d}\sqrt{\frac{\left(d-y\right)}{y\left(1-\frac{kyd\left(d-y\right)}{{\in }_{o }A{{v}_{s}}^{2}}\right)} } dy$$
(4)

where \({t}_{pull-in@mk}\)= pull-in time expression under the acceleration-limited condition as derived in Eq. (4).

$${t}_{pullin@mk}=\sqrt{\frac{md}{{\in }_{o}A{{v}_{s}}^{2}}}{\int }_{0}^{d}\sqrt{\frac{\left(d-y\right)}{y}} {\left[1-\frac{kyd\left(d-y\right)}{{\in }_{o}A{V}_{s}^{2}}\right]}^{-\frac{1}{2}}dy$$
(5)

The Eq. (6) is achieved using the Taylor series and the putting the value of pull-in voltage \({(v}_{p})= \sqrt{\frac{8k{d}^{3}}{27{\in }_{o}A}}\) into Eq. (5).

$${t}_{pullin@mk}=\left[2.88\frac{{V}_{p}}{{V}_{s}{\omega }_{0}}+0.608\frac{{V}_{p}^{3}}{{{\omega }_{o}V}_{s }^{3}}+ 0.29\frac{{V}_{p}^{5}}{{\omega }_{o}{V}_{s}^{5}}+0.17\frac{{V}_{p}^{7}}{{\omega }_{o}{V}_{s}^{7 }}+0.11\frac{{V}_{p}^{9}}{{\omega }_{o}{V}_{s}^{79 }}+0.07\frac{{V}_{p}^{11}}{{\omega }_{o}{V}_{s}^{11}}\right]$$
(6)

where \({\omega }_{o}= \sqrt{\frac{k}{m}}\) is the natural angular frequency of the bridge. Furthermore, Eq. (1) can be modified to Eq. (7) if damping is significant.

$$b\frac{dx}{dt}=\frac{0.5{\in }_{o}A{V}^{2}}{(d-{y)}^{2}}$$
(7)
$${t}_{pullin@b}={\int }_{(10\% of d)}^{(90\% of d)} \frac{2b{(d-y)}^{2}}{{\in }_{o}{AV}_{s}^{2}}dy$$
(8)

where \({t}_{pull@b}\)= pull-in time expression under the damping-limited condition (Eq. (8)). To get Eq. (9), Eq. (8) is solved by integration, and then the pull-in voltage expression is substituted.

$${t}_{pullin@b}=1.638\frac{{bV}_{p}^{2}}{m{\omega }_{o}^{2}{V}_{s}^{2}}$$
(9)
$$b=k/Q{\omega }_{o}$$
(10)

where Q is the quality factor

$${t}_{pullin@b}=1.638\frac{{V}_{p}^{2}}{{Q\omega }_{o}{V}_{s}^{2}}$$
(11)

Further, Eq. (10) is processed in Eq. (11) using Eq. (10)

$${t}_{pull-in}={t}_{pulin@mk}+{t}_{pullin@b}$$
(12)

The Eq. (12) gives the total pull-in time expression as derived in this work, and the Eq. (13) represents the pull-in time expression as given in [12,13,14].

$${t}_{pull-in}=\frac{3.67{v}_{p}}{{v}_{s}{\omega }_{o}}$$
(13)

2.2 Release time

Release time is defined when the switching structure regains its neutral position with an applied voltage of 0 V. Equation (1) can be modified to Eq. (14) if damping is not significant and \({v}_{s}=0 V.\) Further, Eq. (15) is used to get Eq. (16) in \(\frac{dy}{dt}\) form.

$$\frac{m{d}^{2}y}{d{t}^{2}}=kd-ky$$
(14)
$$0.5m({dy/dt)}^{2}=0.5k{d}^{2}-k{y}^{2}$$
(15)
$$\frac{dy}{dt}=\sqrt{k({d}^{2}-{y}^{2})/m}$$
(16)
$${t}_{release@mk}=2\pi /4{\omega }_{o}$$
(17)

where \({t}_{release@mk}\)= release time expression under the acceleration-limited case (Eq. (17)). Equation (1) is modified to Eq. (18) considering damping is significant and \({v}_{s}=0 V.\) To get Eq. (20), Eq. (19) is solved by integration, and then Eq. (10) also is substituted.

$$b\frac{dy}{dt}+ky=0$$
(18)
$${t}_{release@b} = \frac{-b}{k}.{\int }_{d(10\% of d)}^{x(90\% of d)}\frac{1}{y}.dy$$
(19)
$${t}_{release@b}=2.2\left(b|k\right) = \frac{2.2}{Q{\omega }_{o}}$$
(20)

where \({t}_{release@b}\)= release time expression under the damping-limited condition. Equation (21) gives the total release time expression, and Eq. (17) represents release time expression as given in [12,13,14].

$${t}_{release}=\frac{2\pi }{4{\omega }_{o}}+\frac{2.2}{Q{\omega }_{o}}$$
(21)

In the next section, the accuracy of the derived expressions is verified through the simulated and measured data of switching time given in [21].

3 Case study

A case related to the study of pull-in and release times has been presented in [21]. The values used for \({v}_{p}\),\({v}_{s}\),\(Q,{\mathrm{f}}_{\mathrm{o}}\) in the above reference are given in Table 1. A comparison of the results obtained using derived expressions, and the expressions presented in references [12,13,14] are summarized in Tables 2 and 3.

Table 1 Input data for dynamic response (data is taken from reference [21])
Full size table
Table 2 Switch pull-in time
Full size table
Table 3 Switch release time
Full size table

4 Results and discussions

The FEM-simulated pull-in time of the switch as discussed in reference 21 is given under the second column of Table 2. There is a slight variation between the FEM-simulated and measured pull-in times. Further, Eq. 13 is also used for calculating the pull-in time of the same switching structure. In this case, a large mismatch exists between the calculated and measured values. This variation is reduced substantially with the expression derived in the presented work as given under column four of Table 2. This clearly shows that derived expression's pull-in time match the measured pull-in time more accurately than the expression given in reference [12,13,14]. Furthermore, Table 3 compares the release time of the same switching structure. Under release time table, columns 2 and 3 represent the FEM-simulated release time and measured release time, as discussed in reference [21]. The measured result of release time deviates more from the result obtained from Eq. (17). Furthermore, the release time as calculated from Eq. (21) of this work matches closely with the measured result.

5 Conclusion

Improved expressions for pull-in and release times have been presented for MEMS technology-based electrostatic actuators under the squeeze film damping effect. The derived expressions’ results are in close agreement compared to the existing expressions for the calculation of switch pull-in and release time as verified through a case study. The derived expressions are useful for all the MEMS technology-based devices that are based on electrostatic actuation. Thus, in the future, the researcher might use these derived expressions for obtaining the switching time results, which would closely match the simulated and measured values. Furthermore, in future work, the author will also try to explore other ways for improving the accuracy of switching time expressions.