1 Introduction

Unmanned Aerial Vehicles (UAVs) commonly called drones are aerial vehicles capable of carrying out a mission more or less autonomously [1]. These vehicles come from all sizes and shapes [2,3,4,5,6]. Their primary function is to extend human vision beyond the natural horizon, to perform risky or hostile environments works [7, 8]. They have been mostly used by military for surveillance use or reconnaissance missions [9], without the risk of loss of life. More recently, civilian applications have emerged such as forest fire prevention [10], structures inspection [11, 12], traffic monitoring [13, 14], photography and filmmaking [15], safety and security [16], mapping [17], and agriculture [18, 19].

In recent years, trajectory control has become one of the important problems in the study of the UAV. Advances in computer science and electronic technologies have facilitated development in automation control, and intelligent algorithms, some significant works have been implemented on the trajectory control of UAV. Authors of [20] studied the trajectory tracking control problem of a six-degree of freedom (6-DOF) quadrotor unmanned aerial vehicle (UAV) with input saturation by using a backstepping approach. In [21] authors proposed a robust nonlinear controller which combines the sliding-mode control technique and the backstepping control technique for UAV trajectory tracking. A robust decentralized and linear time-invariant controller is proposed [22] for quadrotors with multiple uncertainties to achieve trajectory tracking. The research [23] presents a detailed comparison between two state-of-the-art model-based control techniques for Micro Air Vehicles trajectory tracking; a linear versus nonlinear Model Predictive Controller is presented and compared. A continuous sliding-mode control strategy for quadrotor robust tracking under the influence of external disturbances and uncertainties in real-time is proposed in [24]. In [25] a continuous multivariable finite-time output feedback is developed for trajectory tracking control and attitude stabilization of quadrotor helicopters. A PD-type trajectory tracking controlling with the extended state observer is proposed [26] for the quadrotor UAV to deal with the wind disturbance.

The strongest arguments for the use of intelligence controllers is that classical controllers mentioned above require the knowledge of the controlled system in term of a set of algebraic and differential equations, which analytically relate inputs and outputs. However, these models can become complex and may contain parameters which are difficult to measure or may change significantly during operation. These problems can be overcome by using intelligence based control techniques.

Intelligent control refers to approaches to control systems design, modeling, identification, and operation that use artificial intelligence techniques, such as fuzzy logic, neural networks, machine learning, evolutionary computation, and metaheuristics. Intelligent control techniques are often capable of controlling dynamical systems that, because of their complexity, are very difficult to control by other techniques.

Generally, the following two types of intelligence based systems are used for estimation and control of drives, namely:

  • Artificial neural networks (ANNs)

  • Fuzzy logic systems (FLSs)

Neural networks suffer from the difficulty to deal with imprecise information and the "black box" syndrome that more or less has limited their applications in practice. To overcome this drawback, NNs are integrated with fuzzy inference to form Fuzzy Neural Networks (FNNs). Such hybrid systems combining fuzzy logic, neural networks, optimization techniques, and expert systems are proving their effectiveness in a wide variety of real-world problems.

In recent years, Adaptive Neuro-Fuzzy Inference System (ANFIS), developed by JANG, 1993 [27], has gained more attraction than other types of Fuzzy Inference Systems (FIS), because the results obtained from it are more robust then of the statistical methods [28,29,30,31,32,33,34,35,36,37,38,39,40].

The major problem with Neuro-Fuzzy system including ANFIS is the number of rules which increase exponentially as the number of inputs increase. Thus, the more number of rules, the more is the complexity of ANFIS architecture and its computational cost. But, it is also noteworthy that over reducing the number of rules results in the loss of accuracy. To overcome this issue, this research proposes optimization technique using Improved Particle Swarm Optimization algorithm (IPSO). IPSO algorithm is a bio-inspired swarm intelligence optimizer introduced by Kennedy and Eberhart in 1995 [41]. This algorithm has proved its effectiveness in wide range of applications. The inertia weight is an important parameter of the IPSO. It is responsible for determining the operating results. In IPSO, the model based on functional inertia weight improvement. This optimization technique is used to guarantee the convergence to the optimum ANFIS parameters that permit the controller to reproduce accurately the UAV trajectory and reduce tracking error.

This paper presents an effective method using IPSO for designing an ANFIS controller of type Takagi–Sugeno first order by optimizing the parameters of membership functions and the fuzzy rules. The remaining of this paper is organized as follows: The description of the UAV model and the problem formulation are given in Sect.2. ANFIS system with its architecture and learning algorithm are introduced in Sect. 3. The purpose of Sect. 4 is to present the IPSO algorithm that will later be used for the optimization of ANFIS parameters. Section 5 details the proposed control design and strategy. In Sect. 6, comparisons and numerical simulations results are given in order to demonstrate the optimal effectiveness of the proposed controller. Section 7 gives the conclusions.

2 Modeling of a quadrotor and problem formulation

The class of aerial vehicles considered in this work can be described as rigid bodies using a simplified dynamic model via affine parameterization for a multivariable nonlinear UAV modeled to fly in 2D space.

2.1 Dynamical model

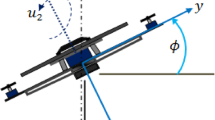
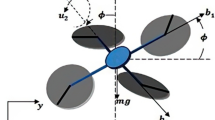
The motion of a quadrotor as a rigid body is described by the motion of a body-fixed frame of reference \(FB = \left( {OB,\left\{ {b_{1} ,b_{2} } \right\}} \right)\)with respect to an inertial reference frame \(FI = \left( {OI,\left\{ {y,z} \right\}} \right),\)as shown in Fig. 1.

Fig. 1
figure 1

Quadrotor configuration scheme

Full size image

The origin located in the center of the quadrotor. It is known that the quadrotor is a 3-DOF object. The Euler angle \(\phi \) represent the orientation of the quadrotor, where it is roll angle about the y-axis. So the quadrotor is modeled to fly in 2 dimensions \(yz\) plane with an angle \(\phi \) witch is the roll angle as shown in Fig. 1.

Therefore, the state of the quadrotor is \(\left[ {y, z, \phi } \right]^{T}\) and there are two inputs \({u}_{1}\) and \({u}_{2}\) the thrust and the moment about the x-axis respectively.

The equations of motion are described by the following system;

$$ \ddot{y} = \frac{{u_{1} }}{m}\sin \left( \phi \right) . $$
(1)
$$ \ddot{z} = g - \frac{{u_{1} }}{m}\cos \left( \phi \right) . $$
(2)
$$ \ddot{\phi } = \frac{{u_{2} }}{{I_{xx} }}. $$
(3)

where \(m\) and \({I}_{xx}\) are the mass and the moment of inertia of the rigid body, respectively.

It is assumed to be the UAV is near hover condition and commanded roll angle \(\phi \) is calculated based on desired \(y\) component and is used to calculate \({u}_{2}\) which is net moment acting on center of gravity (CoG).

The equations of motion have been rewriting as follows;

$$ \left[ {\begin{array}{*{20}c} {\ddot{y}} \\ {\ddot{z}} \\ {\ddot{\phi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ g \\ 0 \\ \end{array} } \right] + \left[ { - \begin{array}{*{20}c} {\frac{1}{m}{\sin}\phi } & 0 \\ {\frac{1}{m}{\cos}\phi } & 0 \\ 0 & {\frac{1}{{I_{{{\text{zz}}}} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] $$
(4)

The state space description of the quadrator;

$$ x = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} y \\ z \\ \varphi \\ {\dot{y}} \\ {\dot{z}} \\ {\dot{\varphi }} \\ \end{array} } \right] $$
(5)

The first derivative of the state vector is presented in Eq. (12). The first three elements of the vector represent velocities and the last three elements represent accelerations.

$$ \dot{x} = \left[ {\begin{array}{*{20}c} {\dot{y}} \\ {\dot{z}} \\ {\dot{\varphi }} \\ 0 \\ g \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{1}{m}{\sin}\phi } & 0 \\ { - \frac{1}{m}{\cos}\phi } & 0 \\ 0 & {\frac{1}{{I_{{{\text{zz}}}} }}} \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right] $$
(6)

3 Structure of the Neuro-Fuzzy controller

The structure of the Neuro-Fuzzy controller that implements a Takagi Sugeno type fuzzy inference system (FIS) is shown in Fig. 2. However, for the simplicity of the presentation, we developed an ANFIS with two inputs and only one output. The generalization for the multi-variable case is direct. The structure of the ANFIS consists of five layers:

Fig. 2
figure 2

The equivalent typical ANFIS architecture

Full size image

Layer 1 (fuzzification): In this layer, the nodes are adaptive with a function. The outputs are the fuzzy membership grade of the inputs, which are given by:

$$ O_{i}^{1} = \mu_{{A_{i} }} \left( x \right), \quad i = 1,2 $$
(7)
$$ O_{j}^{1} = \mu_{{B_{j} }} (y),\quad j = 1,2 $$
(8)

Fuzzifying the inputs is conducted by MF such as Piecewise linear, triangular, trapezoidal, Gaussian and Singleton. Among the abovementioned MFs, this paper has used the gaussian function because of its smooth and concise notation. Therefore, as \({\mu }_{{A}_{i}}(x)\), given that

$$ {\text{Triangular: }}\mu_{{A_{i} }} \left( x \right) = max\left( {min\left( {\frac{{x - a_{i} }}{{b_{i} - a_{i} }},\frac{{c_{i} - x}}{{c_{i} - b_{i} }}} \right),0} \right), i = 1,2 $$
(9)
$$ {\text{Trapezoidal: }}\mu_{{A_{i} }} \left( x \right) = max\left( {min\left( {\frac{{x - a_{i} }}{{b_{i} - a_{i} }},1,\frac{{d_{i} - x}}{{d_{i} - c_{i} }}} \right),0} \right), i = 1,2 $$
(10)
$$ {\text{Gaussian: }}\mu_{{A_{i} }} \left( x \right) = exp\left( { - \frac{{\left( {x - c_{i} } \right)^{2} }}{{\sigma_{i}^{2} }}} \right), i = 1,2 $$
(11)

where \({a}_{i}\)\({\mathrm{a}}_{\mathrm{i}}\), \({b}_{i}\),\({\mathrm{b}}_{\mathrm{i}}\)\({c}_{i}\)\({\mathrm{c}}_{\mathrm{i}}\) and \({\sigma }_{i}\) are the antecedent (premise) parameters.

Layer 2 (Weighting of fuzzy rules): The symbol M shows every fixed node in this layer. This layer calculates the firing strength \({w}_{k}\) by using membership values computed in fuzzification layer, and the outputs are computed as the following:

$$ O_{k}^{2} = w_{k} = \mu_{{(A_{i} )}} (x)*\mu_{{(B_{j} )}} (y),\quad i,j = 1,2. $$
(12)

Layer 3 (normalization): Every node is fixed node and called by N. Each node obtains the normalization by calculating the ratio of the \({k}^{th}\) rule's firing strength to the sum of all rules firing strength. The output \({O}_{i}^{3}\) at this step is given by:

$$ O_{k}^{3} = \overline{{w_{k} }} = \frac{{\overline{{w_{k} }} }}{{\overline{{\sum w_{i} }} }} = \frac{{w_{k} }}{{w_{1} + w_{2} }},\quad k = 1,2. $$
(13)

Layer 4 (defuzzification): Weighted consequent values of rules are calculated in each node of this layer as given in (20).

$$ O_{k}^{4} = \overline{{w_{k} }} f_{k} = \overline{{w_{k} }} \left( {p_{k} x + q_{k} y + r_{k} } \right), \quad k = 1,2 . $$
(14)

where \({w}_{k}\) represents the output of the third layer, and \(\left\{{p}_{k}, {q}_{k}, {r}_{k}\right\}\) are consequent parameters.

Layer 5 (summation): The actual output is obtained by summing the outputs of all incoming signals that coming from the defuzzification layer to produce the overall ANFIS output.

$$ O^{5} = \mathop \sum \limits_{k = 1}^{2} \overline{{w_{k} }} f_{k} = \frac{{\mathop \sum \nolimits_{1 = 1}^{2} w_{k} *f_{k} }}{{w_{1} + w_{2} }} $$
(15)

where \({w}_{k}\) is the output of the third layer, and \(\left\{{p}_{k}, {q}_{k}, {r}_{k}\right\}\) is the set of parameters. These parameters refer to as the consequent parameters.

4 Particle swarm optimization

Particle swarm optimization (PSO) is evolutionary algorithm belongs to the family of stochastic iterative optimization methods. An essential advantage is that these methods can be applied to both discrete and continuous variable problems. In our case, we wanted to apply the PSO method to the problem of optimizing fuzzy logic controllers that were introduced in Sect. 3 and it’s entirely described by the boundaries of fuzzy partitions introduced for each performance indicator for the database (continuous variables).

4.1 Introduction to particle swarm optimization

Swarm particle optimization is an optimization technique based on a set of fixed size agents, called particles, moving in the D-dimensional search space. The position of each particle corresponds to a setting of the fuzzy logic controller. The speed of each particle corresponds to the modifications of this parameterization between two simulations. The velocity and position of each particle are randomly initialized. The entire particles move in the search space, and the performance of each particle is regularly evaluated using cost functions. The evolution of each particle allows an intelligent exploration of the research space. All the particles form the swarm, of size S fixed at the beginning.

4.2 Principles of evolution of the particle swarm

We consider a research space of dimension \(D\). A particle \(i\) of the swarm is modeled by a vector of position \({x}_{i}=({x}_{i1}, {x}_{i2},\dots , {x}_{iD})\) and a velocity vector noted \({v}_{i}=({v}_{i1}, {v}_{i2},\dots , {v}_{iD})\). Each particle saves in memory the best position by which it has passed, noted \({Pbest}_{i}=({pbest}_{i1}, {pbest}_{i2},\dots , {pbest}_{iD})\). All the best positions reached by the swarm are noted by \({Gbest}_{i}=({gbest}_{i1}, {gbest}_{i2},\dots , {gbest}_{iD})\). At the beginning of the solution search process, all the particles in the swarm are randomly initialized in the search space. Then, at each iteration, any particle of the swarm moves, linearly combining the three components of Eq. (16).

At iteration t, the velocity vector is calculated as follows [42, 43]:

$$ v_{ij} \left( {t + 1} \right) = wv_{ij} \left( t \right) + c_{1} r_{1} \left[ {pbest_{ij} \left( t \right) - x_{ij} \left( t \right)} \right] + c_{2} r_{2} \left[ {gbest_{ij} \left( t \right) - x_{ij} \left( t \right)} \right] $$
(16)

with \(j\in \left\{1, 2, ..., D\right\}\) and \(\mathrm{w}\) a constant, called the coefficient of inertia.

The degree of attraction towards the best position of a particle and that of these informants is respectively represented by two coefficients of cognitive confidence \({c}_{1}\) and social \({c}_{2}\). The good exploration of particles in the search space is guaranteed by the coefficients \({r}_{1}\) and \({r}_{2}\) which are two random numbers drawn uniformly in the interval \(\left[\mathrm{0,1}\right]\).

Equation (16) is composed of three terms which are: \(w{v}_{ij}\left(t\right)\) a displacement physical component of which \(\mathrm{w}\) is a variable parameter allowing to control the displacement of the particle at the next iteration, \({c}_{1}{r}_{1}\left[{pbest}_{ij}\left(t\right)-{x}_{ij}(t)\right]\) a cognitive component of displacement and \({c}_{2}{r}_{2}\left[{gbest}_{ij}(t)-{x}_{ij}(t)\right]\) a social component of displacement [44]. The position at the iteration \(\left(t+1\right)\) of the particle \(i\) is then defined by the following equation:

$$ x_{ij} \left( {t + 1} \right) = x_{ij} \left( t \right) + v_{ij} \left( t \right),j \in \left\{ {1,2, \ldots ,D} \right\} $$
(17)

As already mentioned, the PSO algorithm is population-based. In fact, all the particles are randomly positioned in the D-dimensional search space. At each iteration, the particles move according to the motion Eqs. (16) and (17), as shown in Fig. 3. Once the position change has taken place, an update affects the two vectors \({Pbest}_{i}\) and \({Gbest}_{i}\). At the iteration \(t+1\), the latter two vectors will be updated according to the two Eqs. (18) and (19).

$$ Pbest_{i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {Pbest_{i} \left( t \right), \quad if \; f\left( {x_{i} \left( t \right)} \right) \ge f\left( {Pbest_{i} \left( t \right)} \right) } \\ {x_{i} \left( t \right), \qquad \quad otherwise } \\ \end{array} } \right. $$
(18)
$$ Gbest_{i} \left( {t + 1} \right) = Arg \mathop {\min }\limits_{i} \left[ {Pbest_{i} \left( {t + 1} \right)} \right] $$
(19)
Fig. 3
figure 3

Determination of the new position of a particle in a PSO process (illustration of the displacement of a particle in the research space by combining the three movement trends)

Full size image

In the literature, the stopping criterion of a PSO algorithm can be defined in different ways. The algorithm is executed as long as one of the three stops criteria, or all at once, of the following convergence criteria are verified [45]:

  1. a.

    The maximum number of iteration defined is not reached;

  2. b.

    The variation of the particle velocity is close to zero;

  3. c.

    The value of the objective is satisfactory with respect to the following relation:

$$ \left| {f\left( {gbest_{ij} \left( t \right)} \right) - f\left( {gbest_{ij} \left( {t - \alpha } \right)} \right)} \right| \le \varepsilon , with \alpha \in \left[ {1,{\Lambda }} \right] $$
(20)

The parameter \(\varepsilon \) represents a tolerance chosen most often of the order of \({10}^{-5}\) and \(\Lambda \) a number of iterations chosen of the order of \(10\).

4.3 The IPSO algorithm

In this section, the different steps of an IPSO algorithm in the case of single-objective optimization were presented in order:

  1. a.

    At the beginning, all the parameters of the algorithm are declared; the cognitive coefficients \({c}_{1}\) and social \({c}_{2}\), the inertia factor \(w\), the size of the population that is normally defined according to the optimization problem

  2. b.

    Each particle has initial position \({\mathrm{x}}_{0}\) and initial velocity \({\mathrm{v}}_{0}\) that are randomly initialized to be updated according to Eqs. (18) and (19)

  3. c.

    Evaluate all the particles of the population in the search space to be able to determine the vectors of the best initial positions \({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{0}\) and \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{0}\)

  4. d.

    Calculate the velocities and positions of the particles at each iteration according to the motion Eqs. (16) and (17). Then, evaluate the positions of the particles and update the sizes \(\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}\) and \(\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}\)

  5. e.

    Repeat the fourth step as long as the stopping criterion is not met

Inertia weight is an important parameter of the standard IPSO. It determines the operating results of IPSO. Fixed inertia weight make the particles always have the same exploration competence in flight. Currently,the conventional strategy of improving inertia weight is LDIW (Liner Decreasing Inertia Weight) [46].

5 Controller design

5.1 ANFIS modeling

In a neuro-fuzzy controller, fuzzy rules are applied to linguistic terms. These terms, which make it possible to qualify a linguistic variable, are defined through membership functions.

First, we define for each variable the discourse universe \(\left[a,b\right]\) according to the minimum and maximum values of each variable. Second, we define Gaussian-type membership functions that constitute the fuzzy partition of the linguistic variable. It can be seen that this function depends on the antecedent parameters. For example, for the variable \(z\left(t\right)\) there are two inputs \(\left({z}_{r}(t),{z}_{c}(t)\right)\) and five linguistic inputs that are partitioned on the discourse universe in each input variable. Where \({z}_{r}(t)\) is the measured trajectory and \({z}_{c}(t)\) is the reference trajectory. Therefore, a typical rule in a Sugeno fuzzy model is described as follows:

If \(x\) is \({A}_{1}\) and \(y\) is \({B}_{1}\) then \({f}_{1}={p}_{1}x+{q}_{1}y+{r}_{1}\)

If \(x\left({z}_{r}\left(t\right)\right)={A}_{1}\) and \(y\left({z}_{c}\left(t\right)\right)={B}_{1}\) then \({f}_{1}={p}_{1}x+{q}_{1}y+{r}_{1}\). Where \(x\left({z}_{r}\left(t\right)\right)\) and \(y\left({z}_{c}\left(t\right)\right)\) are linguistic variables, \({A}_{1}\) and \({B}_{1}\) are the linguistic values, \({f}_{1}\) denotes the first output value, and \({p}_{1},{q}_{1}\), and \({r}_{1}\) are the consequent parameters.

The ANFIS is optimized by adjusting the antecedent parameters (membership function parameters) and the consequent parameters (polynomial coefficients) to minimize a specified objective function. The most common and the most applicable fuzzy inference systems training algorithm is the back-propagation learning algorithm that is used to recursively solve the premise and consequent parameters optimization. This conventional optimization algorithm is likely to get stuck at local optima. To overcome this drawback, the use of evolutionary techniques is recommended. The evolutionary technique is used to optimize the antecedent and consequent parameters. In this work, we suggest to use IPSO technique for training the parameters of ANFIS.

The Mean Squared Error (MSE) and Root Mean Squared Error (RMSE) functions are used as a fitness function in order to calculate the fitness of a solution. In order to compute the MSE and RMSE errors values, the output of ANFIS and its real output are used as given in Eqs. (21) and (22):

$$ MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2} $$
(21)
$$ {\text{RMSE } = \text{ }}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{{\text{i}}} - \hat{y}_{{{\text{ii}}}} )} } $$
(22)

Here, \({y}_{i}\) is the real output, \({\stackrel{-}{y}}_{i}\) is the measured output by ANFIS and \(n\) is the number of samples.

5.2 Proposed ANFIS-IPSO

In this research work, in order to improve the training process of the ANFIS, meta-heuristic algorithm was used for optimizing the influential parameters in the ANFIS. For this reason, one of the most commonly used meta-heuristic algorithm is used which is IPSO.

In the ANFIS-IPSO approach, IPSO improves the approximation capability of ANFIS by tuning its parameters. In better words, IPSO minimizes the estimation error by tuning input and output MFs through the search space provided by ANFIS model. IPSO algorithm optimized MFs of the developed ANFIS models while minimizing both MSE and RMSE. The block diagram showing this structure is given in Fig. 4.

Fig. 4
figure 4

The block diagram of the control scheme

Full size image

Every learning step of the algorithm contains the learning of antecedent and consequent parameters. The major steps of the combined algorithm are stated as follows.

  1. (a)

    Randomly initialize particle swarm in search space, including dimension of search space, particle swarm size, learning factors, maximum number of iterations, and initial speed and position of every particle

  2. (b)

    In the first iteration, the initial position of every particle is defined as the initial individual best position. Then, the value of the best position for the whole swarm is determined and the position vector of each particle is used as the antecedent and consequent parameters of ANFIS in sequence. It is followed by calculating the value of the output based on Eqs. (7), (8), (12), (13), (14) and (15). Next, the \(\mathrm{M}\mathrm{S}\mathrm{E}\) and \(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}\) between the model output \({\widehat{\mathrm{y}}}_{\mathrm{i}}\) and the reference data for the \({\mathrm{i}}^{\mathrm{t}\mathrm{h}}\) particle is calculated, which is also the fitness value \({\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{i}}\) and \({\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{i}}\) for the ith particle. The fitness values of particles are compared; the particle which has the smallest fitness is selected as the best particle. Its position vector is defined as the initial global best position

  3. (c)

    The iterations were continued. For each iteration; the velocity vector \({\mathrm{v}}_{\mathrm{i}\mathrm{j}}\) and the position vector \({\mathrm{x}}_{\mathrm{i}\mathrm{j}}\) for each particle are updated based on Eqs. (16) and (17) initially

  4. (d)

    Then, the fitness values particles are calculated. Compare the current fitness values \(\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\right)\) with the individual best fitness value \(\mathrm{f}\left({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\right)\) for each particle; if the current fitness value is smaller than \(\mathrm{f}\left({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\right)\), the individual best fitness value \({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\) is set as \(\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\right)\), and the particle’s historical optimal position along with its new position \({\mathrm{P}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t}+1)={\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\) is updated. Comparing the particle’s current fitness value \(\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\right)\) with the global best fitness value \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\), if the current fitness value, \(\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\right)\) is smaller than \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\), the global best fitness value \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}(\mathrm{t})\) is set as \(\mathrm{f}\left({\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\right)\), the global optimal position with its new position \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}\left(\mathrm{t}+1\right)={\mathrm{x}}_{\mathrm{i}}(\mathrm{t})\) is updated, and the number of the best particle is recorded

  5. (e)

    Iterations stop when the maximum number of iterations is met. The values of \({\mathrm{G}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}_{\mathrm{i}}\left(\mathrm{t}+1\right)\) are the identified antecedent and consequent parameters. The parameter w will be changed after each iteration.

6 Simulation results

To validate the approach used, we carried out simulations for the adaptive control of a 3-DOF UAV robot moving along a specified trajectory, whose model parameters are estimated by three ANFIS networks. The adjustment of the network parameters is performed by an IPSO algorithm to obtain the optimal objective value. The UAV is commanded to track a preprogrammed trajectory through a function of time defined by the coordinates \(y\left(t\right)\) and \(z\left(t\right)\).

The control performance obtained by the proposed control system is compared with PID and ANFIS controllers to validate the superior performance of the studied controller.

The simulation results are obtained with a vertical trajectory in 2D space. The desired trajectory input is defined as:

$$ y_{d} \left( t \right) = 2{\sin}\left( t \right) $$
$$ z_{d} \left( t \right) = 5{\sin}\left( t \right) $$

The parameters of the quadrotor used in the following simulations are shown in Table 1.

Table 1 Parameters of quadrotor
Full size table

The PID-based control was used to control the UAV robot for a control purpose. The simulation results are illustrated in Figs. 5, 6, 7 and 8. The reference trajectory (blue line) is compared with the measured one (red line) as shown in Fig. 8.

Fig. 5
figure 5

Measured \(z(t)\) trajectory with PID controller

Full size image
Fig. 6
figure 6

Measured \(y(t)\) trajectory with PID controller

Full size image
Fig.7
figure 7

Measured \(\phi \)(t) trajectory with PID controller

Full size image
Fig. 8
figure 8

Measured trajectory with PID controller

Full size image

The difference between the calculated trajectory and the desired one can be measured by the mean square error showed in Fig. 9.

Fig. 9
figure 9

Trajectory Error with PID Controller

Full size image

As we can see in Fig. 9, the PID controller can reproduce the tracking trajectory with error of \(\mathrm{M}\mathrm{S}\mathrm{E}={4.6478\mathrm{*}10}^{-2}\) and \(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=0.21559.\)

The control by ANFIS has proved its worth. The results obtained clearly justify the use of artificial intelligence techniques, of which ANFIS is a part.

Based on the simulation results obtained in Figs. 10, 11, and 12, results showed indicate that respectively the measured \(z(t)\) (magenta dotted line), \(y(t)\) (green dotted line) and \(\phi \left(t\right)\) (cyan dotted line) trajectories of the quadrotor track exactly the desired \(z(t)\) (red line), \(y(t)\) (cyan line) and \(\phi \left(t\right)\) (brown line) trajectories.

Fig. 10
figure 10

Measured z(t) trajectory with ANFIS controller

Full size image
Fig. 11
figure 11

Measured \(y(t)\) trajectory with ANFIS controller

Full size image
Fig. 12
figure 12

Measured \(\phi (t)\) trajectory with ANFIS controller

Full size image

The ANFIS measured \(\left(z(t),y(t)\right)\) trajectory, in Fig. 13 (dotted red line) deviate slightly from the desired (solid blue line) trajectory. The error between the two trajectories showed in Fig. 14, indicates that the calculated mean square error with the ANFIS controller is evaluated at \(\mathrm{M}\mathrm{S}\mathrm{E}={1.7169\mathrm{*}10}^{-9}\) and \(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=4.1435\mathrm{*}{10}^{-5}\), which is too small than the MSE with PID controller which approve the effectiveness of the ANFIS controller over PID controller.

Fig. 13
figure 13

Measured trajectory with ANFIS controller

Full size image
Fig. 14
figure 14

Trajectory error with ANFIS controller

Full size image

Figures 15, 16 and 17 show the ANFIS-IPSO simulation results of the parameters \(y(t), z(t)\) and \(\phi (t)\). From the figures, it is very clear that the measured quadrotor trajectories follow accurately the desired trajectories. The tracking performance is illustrated in Fig. 18, where the measured trajectory (red dotted line) of the quadrotor and the reference trajectory (solid blue line) are shown together. The results obtained show that the performances of the ANFIS-IPSO hybrid approach are superior to those of the other models. It can be seen that the ANFIS-IPSO makes a very good approximation of the system with a mean error of \(2.25183\mathrm{*}{10}^{-16}\). The Tracking errors of different trajectories (\(\mathrm{z}\left(\mathrm{t}\right), \mathrm{y}(\mathrm{t})\), and \(\upphi (\mathrm{t}\))) of the quadrotor are illustrated in Figs. 19, 20, 21, 22, 23, and 24. It can be clearly seen that the trajectory tracking errors converge to zero.

Fig. 15
figure 15

Measured \(z(t)\) trajectory with ANFIS-IPSO controller

Full size image
Fig. 16
figure 16

Measured \(y(t)\) trajectory with ANFIS-IPSO controller

Full size image
Fig. 17
figure 17

Measured \(\phi \)(t) trajectory with ANFIS-IPSO controller

Full size image
Fig. 18
figure 18

Measured trajectory with ANFIS-ACO controller

Full size image
Fig. 19
figure 19

Error test data (\(z\) parameter)

Full size image
Fig. 20
figure 20

Error train data (\(z\) parameter)

Full size image
Fig. 21
figure 21

Error test data (\(y\) parameter)

Full size image
Fig. 22
figure 22

Error train data (\(y\) parameter)

Full size image
Fig. 23
figure 23

Error train data (\(\phi \) parameter)

Full size image
Fig. 24
figure 24

Error test data (\(\phi \) parameter)

Full size image

7 Conclusion

This research was dedicated to solving the limitations of classical control laws in the absence of model parameters. The use of control methods based on artificial intelligence techniques has become a necessity. These techniques include neural networks, fuzzy logic and evolutionary algorithms among many others.

The paper presents an Improved Particle Swarm Optimization algorithm (IPSO) applied to fitting Adaptive Neuro-Fuzzy Inference System (ANFIS) membership functions. The case study was implemented using simulations, whose main purpose is to control a quadrotor UAV trajectory tracking task.

To validate this intelligent approach, an objective function was used to optimize the ANFIS parameters via the IPSO algorithm. The results obtained were compared with a PID and ANFIS to prove the high performance of ANFIS-IPSO.