1 Introduction

Forward kinematics problem calculates the end effector’s location in the Cartesian Space using joint variables as input. Conversely, inverse kinematics problem deals with obtaining the required manipulator joint values for a given value of end effector’s position and orientation in Cartesian Space. In case of rotational joints, the joint variables are the angles between the links and in the case of prismatic joints, these are the angles between the link extensions [1, 2].

It is a quite established fact that solving the inverse kinematics problem is more challenging and complex as compared to the forward kinematics problem [1,2,3,4]. The complexity of the problem is described by the robot’s geometry and the nonlinear trigonometric equations that describe the relationship between Cartesian frame and co-ordinate frame. The fundamental methods to solve inverse kinematic problem are: geometric, algebraic and iterative methods. A closed form solution is desirable for many applications but it is difficult to find it using the traditional methods as the number of degrees of robotic manipulator increases [3, 4]. Application of neural networks in the field of image recognition, speech recognition, data fitting etc. show us their capability to work with complex functions [5, 6]. A neural network architecture with 6 sub-neural networks to solve the inverse kinematics problem for robotics manipulators with 2 or higher degrees of freedom is proposed in [7]. In Ref. [8], Jacobian Matrix is used to solve the problem of inverse kinematics with neural network. In Ref. [10], an evolutionary approach based on a real-coded genetic algorithm is used to obtain the solution of the multimodal inverse kinematics problem of industrial robots. A neural network to produce the solution to the inverse kinematics problem for a three-link robotic manipulator is investigated in [14]. The neural network is trained using the data provided by the forward kinematics to learn the inverse forward mapping of the configuration space.

This paper investigates the use of neural networks to solve the inverse kinematics problem for a two degree of freedom (DOF) robotic manipulator using unsupervised learning. We only give the end-effectors’ Cartesian coordinates as input to the neural network and expect the neural network to give us the joint angles as output. The remainder of this paper is organized as follows. Problem formulation is presented in Sect. 2. Numerical simulation results are included in Sect. 3. Final conclusion is given in Sect. 4.

2 Problem formulation and neural Network Implementation

Consider a hypothetical robotic manipulator for testing the proposed algorithm. It is a two-link planar manipulator with rotational joints and the link lengths are given by:

$$ \begin{aligned} L_{1} & = 4,\;L_{2} = 5\quad \left( {For\;Problem\,1} \right) \\ L_{1} & = 0.5,\;L_{2} = 0.5\quad \left( {For\;Problem\,2} \right) \\ \end{aligned} $$
(1)

The joint angles of the robotic manipulator have a range of [0:2π]. The workspace of the robotic arm can be given by Eq. (2)

$$ \left| {L_{1} - L_{2} } \right| \le \left( {x^{2} + y^{2} } \right)^{1/2} \le L1 + L_{2} $$
(2)

The calculation of inverse kinematic solution for any values of x-coordinate and y-coordinate satisfying the above condition is possible using the proposed algorithm. For the values of x-coordinate and y-coordinate not satisfying the above equation, the result will be ambiguous since the manipulator cannot reach that point. Figure 1 shows the representation of a two degrees of freedom robotic manipulator with OA = L1 and AB = L2. The axis of rotational joints of these links is perpendicular to their plane.

Fig. 1
figure 1

A two link planar manipulator

Full size image

Forward kinematics is the use of known parameters of a robotic manipulator along with q1 and q2 to find the x-coordinate and y-coordinate in the Cartesian coordinate system. The forward kinematic equations for the two link planar manipulator given in Fig. 1 are given as

$$ \begin{aligned} x_{e} & = L_{1} \,cos\left( {q_{1} } \right) + L_{2} \,cos\left( {q_{1} + q_{2} } \right) \\ y_{e} & = L_{1} \,sin\left( {q_{1} } \right) + L_{2} \,sin\left( {q_{1} + q_{2} } \right) \\ \end{aligned} $$
(3)

where L1 and L2 represent the link lengths and q1 and q2 represent the known joint angles.

To test the validity of the proposed algorithm, we have the following two problems.

2.1 Problem 1

The robotic arm is required to draw a circular trajectory in its workspace. The points on this trajectory is given by the parametric equation of the circle

$$ \begin{aligned} & x_{p} = x_{c} + r\,cos\,\varTheta \\ & y_{p} = y_{c} + r\,sin\,\varTheta \\ & \varTheta = \left[ {0:2\pi } \right] \\ \end{aligned} $$
(4)

where r is the radius of the circle, (x p , y p ) are the coordinates of the centre of circle and Θ is the parametric variable.

The neural network is executed for every increase in Θ by one degree in Eq. (4) till it reaches 2π, therefore forming a circular trajectory. The neural network gives the inverse kinematic solution every time Θ increases and thus we end up having the angles for a two degrees of freedom robotic manipulator which would result in a circular trajectory.

2.2 Problem 2

The robotic arm is required to catch a ball approaching in its workspace. The trajectory of the ball is supposed to be given by the following equation

$$ \begin{aligned} x_{b} & = - 2 + 0.15t^{2} - 0.01t^{3} \\ y_{b} & = - 4 + 0.6t^{2} - 0.04t^{3} - 0.0225t^{4} + 0.003t^{5} - 0.0001t^{6} \\ \end{aligned} $$
(5)

The time (t) is incremented by 0.2 till it reaches its maximum value i.e. 10. For every sample value, the slope of the line joining the ball and end-effectors’ position is calculated. The inverse of the slope is calculated which gives us the angle. The derived angle is used as a variable in Eq. (6) which acts as an input to the neural network.

$$ \begin{aligned} & x_{p} = o_{1} + v\,cos\,\beta \\ & y_{p} = o_{2} + v\,sin\,\beta \\ & v = k*d \\ & \beta = tan^{ - 1} \left( {y_{b} - o_{2} } \right)/\left( {x_{b} - o_{1} } \right) \\ \end{aligned} $$
(6)

Here (yb − o2) and (xb − o1) are always taken to be positive, v represents the velocity of the robotic arm which keeps on decreasing as the ball approaches the end-effector and k is taken to be the constant initial velocity. Once the ball is caught by the manipulator, it follows the trajectory of the ball for some time before coming to rest. For the manipulator to show good results, it is important that the ball should enter the workspace of the manipulator as early as possible.

2.3 The artificial neural network

Since there is a significant amount of research going on to develop artificial systems that can respond to environmental changes intelligently and not in a pre-programmed manner, a lot of algorithms have been proposed by different authors for the same. Fuzzy logic and PID controller based systems have already made their way into various industries but in the past decade a considerable amount of research has been done in the area of artificial neural networks [7,8,9,10]. Artificial neural networks have proved to be more feasible and accurate in complex tasks such as image processing and have yielded great results even in an undesirable situation.

In this paper we are solving the inverse kinematics problem for a two-DOF robotic manipulator using a feed-forward neural network which has two input neurons, four hidden neurons and two output neurons as shown in Fig. 2.

Fig. 2
figure 2

The architecture of neural network

Full size image

In Fig. 2, the x-coordinate and y-co-ordinate is given as an input to the neural network and the angles q1 and q2 are the outputs. The transfer function for the hidden layer is taken to be a sigmoid function.

2.4 Implementation

The training algorithm used for the neural network is unsupervised learning i.e. no prior target data set is given to the neural network. This algorithm is different from other algorithms because it gives us a method to implement neural network controller on robots with less data requirement i.e. no data is required initially [8, 9, 12]. Hence, the memory consumed by desired output matrix is eliminated. Whereas, in other algorithms we require a desired output matrix for supervised learning [11,12,13].

The unsupervised learning is implemented by considering that the neural network has an invisible layer after the output layer having two neurons each of which contains forward kinematics equation for x-coordinate and y-coordinate respectively. The input to this invisible layer is q1 and q2, respectively and the outputs are o1 and o2, respectively, given by Eq. (7).

$$ \begin{aligned} {\text{o}}1 & = {\text{L}}1*{ \cos }\,\left( {{\text{q}}1} \right) + {\text{L}}2*{ \cos }\,\left( {{\text{q}}1 + {\text{q}}2} \right) \\ {\text{o}}2 & = {\text{L}}1*{ \sin }\,\left( {{\text{q}}1} \right) + {\text{L}}2*{ \sin }\,\left( {{\text{q}}1 + {\text{q}}2} \right) \\ \end{aligned} $$
(7)

An important fact about the invisible layer is that this layer is not directly connected to the output layer using any weight and hence updating the weight is not done in this layer. This approach can be represented by the block diagram given in Fig. 3.

Fig. 3
figure 3

Block diagram representation of invisible layer

Full size image

The desired output values of the neural network are the inputs (xp, yp) only and therefore, the error of the neural network is calculated using the formula given in Eq. (8).

$$ {\text{E}} = \left[ {\left( {{\text{xp}} - {\text{o}}1} \right)^{2} + \left( {\left( {{\text{yp}} - {\text{o}}2} \right)^{2} } \right)} \right] $$
(8)

The objective is to minimize this error using artificial neural network. This is done by updating weights using delta (δ) which is the partial differentiation of error with respect to weights for which the equations are given by

$$ \updelta\left( {\text{i, j}} \right) = \partial {\text{E}}/\partial {\text{W}}\left( {\text{i,j}} \right)\quad {\text{i}} = \left[ {1:4} \right],\,{\text{j}} = \left[ {1,2} \right] $$
(9)
$$ \updelta\left( {\text{k,l}} \right) = \partial {\text{E}}/\partial {\text{W}}\left( {\text{k,l}} \right)\quad {\text{k}} = \left[ {1,2} \right],\,{\text{l}} = \left[ {1:4} \right] $$
(10)

Equation (9) calculates delta for hidden layer and Eq. (10) calculates delta for input layer. The updated weights are given by the formula

$$ {\text{W}}\left( {{\text{n}} + 1} \right) = {\text{W}}\left( {\text{n}} \right) - \left( {{\text{learning}}\,{\text{rate}}} \right)*\left(\updelta \right) $$
(11)

Here n represents the iteration number and learning rate is taken according to the problem. The maximum number of iterations is 5000 and the neural network stops processing if the error reaches below a certain threshold value set by the user.

3 Results

3.1 Problem 1

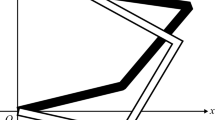
The coordinates of the points on the desired trajectory, which is a circle of radius one having center at (3, 4) are given as an input to the neural network and Θ is varied from [0:2π] in steps of one degree. We were able to obtain satisfactory results using the above proposed algorithm. Figure 4 shows the desired trajectory and the actual trajectory of the robotic manipulator.

Fig. 4
figure 4

Actual trajectory versus desired trajectory

Full size image

It is evident from Fig. 4 that there is a negligible amount of difference in both the trajectories. Figure 5 shows the value of error for each input sample.

Fig. 5
figure 5

Error/input sample

Full size image

It is evident from Fig. 5 that for every input sample, the error converged to a value less than the threshold value which was taken to be 0.0002.

Artificial neural networks are considered to be computationally complex and time consuming due to high number of iterations. But in our model, the maximum number of iterations taken to reach the threshold error value is 451, thereby proving its efficiency. The number of iteration along with input sample is given in Fig. 6.

Fig. 6
figure 6

Number of iterations versus input Sample

Full size image

The convergence of error with respect to the number of iterations for first input value (which took the maximum no. of iterations) is shown in Fig. 7. As expected from a neural network controller, the error converges to zero.

Fig. 7
figure 7

Error versus number of iterations

Full size image

3.2 Problem 2

In this problem, the coordinates of the trajectory of ball is given by Eq. (5) and the robotic manipulator trajectory is given by Eq. (6). The above proposed algorithm performed exceptionally well and gave satisfactory results. Figure 8 shows the ball trajectory and the actual trajectory of the robotic manipulator whereas Fig. 9 shows the number of iterations with respect to the input sample.

Fig. 8
figure 8

Ball trajectory versus manipulator trajectory

Full size image
Fig. 9
figure 9

No. of iterations versus input sample

Full size image

As can be seen in the above figure, some the samples stopped only when the number of iteration exceeded the threshold value which was set to be 5000. This is because of the limitation of manipulator’s workspace. The desired location of the end-effector’s was out of reach due to constrained motion and hence the neural network could not converge. But as soon as the ball enters the workspace of the robotic arm, the algorithm starts to converge within very little iteration.

Figure 10 shows that the error remained above the threshold value when the ball was outside the workspace of the robotic manipulator. But as soon as it entered the workspace of the robotic manipulator, the error fell below the threshold value. The threshold value of error in this problem is 0.0002.

Fig. 10
figure 10

Error versus input sample

Full size image

4 Conclusion

The results shown in the previous section are obtained using Microsoft Excel. The inverse kinematics problem of a robotic manipulator is solved by an artificial neural network using unsupervised learning. The solution is useful for practical purposes since the error is negligibly small. It would also be better than already used methods because of its ability to adapt itself with the change in environmental conditions. The results show promising trajectory tracking capabilities and hence the authors will try to apply this work in real world problems.