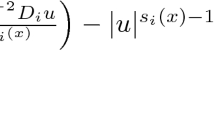Nonlinear anisotropic degenerate parabolic equations with variable exponents and irregular data

Abstract

In this paper, we prove the existence and the regularity of weak solutions for a class of nonlinear anisotropic parabolic equations with $p_i(\cdot )$ growth conditions, degenerate coercivity and $L^{m(\cdot )}$ data, with $m(\cdot )>1$ being small. The functional setting involves Lebesgue-Sobolev spaces with variable exponents.

1 Introduction

In this paper, we are interested in the existence and regularity of solutions for some nonlinear parabolic equations with principal part having degenerate coercivity:

$$\begin{aligned} \begin{aligned}&\partial _tu -\sum ^{N}_{i=1}D_i\big (b_i(t,x,u)a_i(t,x,Du)\big )+F(t,x,u)=f \quad \hbox { in}\ Q_T, \\&u=0\quad \hbox { on}\ \Sigma _T, \\&u(0,x)=u_0(x)\quad \hbox { in}\ \Omega . \end{aligned} \end{aligned}$$

(1)

where $Q_T\doteq (0,T)\times \Omega$, $\Sigma _T=(0,T)\times \partial \Omega$, $\Omega$ is a bounded open subset of $\mathbb {R}^N$, $(N\ge 2)$, $T>0$ is a real number, $f\in L^{m(\cdot )}$, and $u_0\in L^{(m(\cdot )-1)s_+(\cdot )+1}(\Omega )$, $s_+(\cdot )=\max _{1\le i\le N} s_i(\cdot )$. Here, we suppose that $b_i:Q_T\times \mathbb {R}\longrightarrow \mathbb {R}$, $a_i:Q_T\times \mathbb {R}^N\longrightarrow \mathbb {R}$, $F:Q_T\times \mathbb {R}\rightarrow \mathbb {R}$ are Carathéodory functions and satisfying for a.e.$(t,x)\in Q_{T}$, for all $u\in \mathbb {R}$, for all $\xi ,\xi '\in \mathbb {R}^N$, and for all $i=1,\dots ,N$ the following:

$$\begin{aligned}&a_i(t,x,\xi )\cdot \xi _i \ge \alpha |\xi _i|^{p_i(x)}, \end{aligned}$$

(2)

$$\begin{aligned}&|a_i(t,x,\xi )|\le \Big (g +\sum _{j=1}^N|\xi _j|^{p_j(x)}\Big )^{1-\frac{1}{p_i(x)}}, \end{aligned}$$

(3)

$$\begin{aligned}&\Big (a_i(t,x,\xi _i) - a_i(t,x,\xi _i')\Big )\cdot (\xi _i-\xi _i') > 0,\;\;\xi _i\ne \xi _i', \end{aligned}$$

(4)

$$\begin{aligned}&\frac{C_2}{(1+|u|)^{\sigma (x)}}\le b_i(t,x,u)\le C_1, \end{aligned}$$

(5)

where $\alpha >0$, $C_1>0$, $C_2>0$, $m,\;\sigma \in C({\overline{\Omega }})$, $m(\cdot )> 1$, $\sigma (\cdot )\ge 0$, $g\in L^1(Q_T)$ is non-negative function, and the variable exponents $p_i:{\overline{\Omega }}\longrightarrow (1,+\infty )$ are continuous functions.

$$\begin{aligned}&\sup _{|u|\le \lambda }|F(t,x,u) |\in L^1(Q_T),\quad \text{ for } \text{ all } \lambda >0, \end{aligned}$$

(6)

$$\begin{aligned}&F(t,x,u)\,\mathrm {sign}(u)\ge \sum _{i=1}^N|u|^{s_i(x)}, \; a.e.\;(t,x)\in Q_T, \text{ for } \text{ all } u\in \mathbb {R}, \end{aligned}$$

(7)

where $s_i:{\overline{\Omega }}\longrightarrow (1,+\infty )$ are continuous functions on ${\overline{\Omega }}$.

Let us consider for example the operator

$$\begin{aligned} Au= & {} -\sum ^{N}_{i=1}D_i\big (b_i(t,x,u)a_i(t,x,Du)\big ) \\&=-\sum ^{N}_{i=1}\left( D_i\left( \frac{ |D_{i}u|^{p_i(x)-2}D_{i}u}{\Big (\ln (e+|u|)\Big )^{\sigma (x)}}\right) \right) . \end{aligned}$$

The main difficulties in studying (1) are the fact that, due to assumption (5), the differential operator Au is not coercive if u is very large, and the problem (1) has a more complicated nonlinearity than the classical case $p_i(\cdot )=p_i$ since it is nonhomogeneous. This shows that the classical methods for the constant case [7] can’t be applied here. In the classical case $\sigma =0$ and $p_i(\cdot )=p_i$ the existence and regularity solution have been treated in [7]. It is worth pointing out that the problem (1) has been studied in [5] in the particular case $p_i(\cdot )=2$, $i\in \{1,2,\cdots ,N\}$, $m(\cdot )=m$, and $\sigma (\cdot )=\theta \in \left[ 0,1+\frac{2}{N}\right)$ with $u_0=0$, where the author have discussed the existence and regularity results based on (Lemma 2.2, [5]), but this technique do not work in the anisotropic case. In this paper, we assume that condition (7) holds true and we treat the regularity of u depending simultaneously on F and f. It is an open question to solve our problem without an additional control on u $(F=0)$. As in elliptic case [1, 9], we give also a better regularity result on Du when $s(\cdot )$ is large enough because if $\sigma (\cdot )=\sigma$, $m(\cdot )=m$, and $S_+(\cdot )>\frac{(N+1){\overline{p}}-N(1+\sigma )}{N-(m-1){\overline{p}}(\cdot )}$ we have

$$\begin{aligned} \frac{m p_i(\cdot )s_+(\cdot )}{1+s_+(\cdot ) +\sigma }>\frac{mp_i(\cdot )}{{\overline{p}}(\cdot )} \left( \frac{(N+1){\overline{p}}(\cdot )-N(1+\sigma )}{N+1-(1+\sigma )(m-1)}\right) , \;\frac{1}{{\overline{p}}(\cdot )}=\frac{1}{N}\sum _{i=1}^N\frac{1}{p_i(\cdot )}. \end{aligned}$$

So, Theorem 4 improves Theorem 3 and (Theorem 1.4, [5]).

The proof of existence and regularity results under the assumptions (2)-(5), where $p_i(\cdot )$ is assumed to be merely a continuous function (is not as in (10)), is essentially based on the approximate problems (24) with some non degenerate coercivity and regular data. To describe briefly the tools we use, firstly we have the anisotropic Sobolev inequality to overcome the difficulties of getting the regularity in the Lemma 7, secondly we introduce the Lemma 9 to facilitate the control of the term $\partial u_n$ of the regularized problem. Thirdly to prove Theorems 4, a key result about an $L^{m(\cdot )s_+(\cdot )}(Q_T)$ estimate for solution to (1) is proved. For the uniqueness of the weak solution, where f is irregular data, it is necessary to impose additional conditions on the data of the problem (1). Our regularity results are new and have not been proven before neither in the isotropic nor in the anisotropic case.

This paper is organized in the following way: In Sect. 2, we introduce the function spaces. The main Results are presented in Sect. 3. Theorems 3–5 are proved in Sect. 4.

2 Preliminaries

Let $p_i(\cdot ):\Omega \rightarrow (1,+\infty )$ be a continuous function for all $i=1,\ldots ,N$ and let $p_i^{-}=\displaystyle \min _{x\in {\overline{\Omega }}}p(x)$, $p_i^{+}=\displaystyle \max _{x\in {\overline{\Omega }}}p(x)$. The appropriate Sobolev space to study problem (1) is the anisotropic spaces

$$\begin{aligned} W^{1,p_i(\cdot )}(\Omega )=\left\{ u\in L^{p_i(\cdot )}(\Omega )\mid D_iu\in L^{p_i(\cdot )}(\Omega ) \right\} , \\ W^{1,p_i(\cdot )}_0(\Omega )=\left\{ u\in W_0^{1,1}(\Omega )\mid D_iu\in L^{p_i(\cdot )}(\Omega ) \right\} , \end{aligned}$$

which are Banach spaces under the norm

$$\begin{aligned} \Vert u\Vert _i=\Vert u\Vert _{L^{p_i(\cdot )}(\Omega )}+\Vert D_iu\Vert _{L^{p_i(\cdot )}(\Omega )},\quad i=1,\ldots ,N, \end{aligned}$$

(8)

where

$$\begin{aligned} \Vert u\Vert _{L^{p_i(\cdot )}(\Omega )}=\inf \left\{ \lambda >0\mid \int _{\Omega }\left|\frac{u(x)}{\lambda }\right|^{p_i(x)}dx \le 1 \right\} . \end{aligned}$$

The following inequality will be used later

$$\begin{aligned} \min \left\{ \Vert u\Vert ^{p_i^-}_{L^{p_i(\cdot )}(\Omega )},\Vert u\Vert ^{p_i^+}_{L^{p_i(\cdot )}(\Omega )} \right\} \le \int _\Omega |u(x)|^{p_i(x)}dx \le \max \left\{ \Vert u\Vert ^{p_i^-}_{L^{p_i(\cdot )}(\Omega )},\Vert u\Vert ^{p_i^+}_{L^{p_i(\cdot )}(\Omega )}\right\} . \end{aligned}$$

(9)

The smooth functions are in general not dense in $\bigcap _{i=1}^{i=N}W^{1,p_i(\cdot )}_0(\Omega )$, but if the exponent variable $p_i(\cdot )>1$ for each $i=1,\ldots ,N$ satisfies the log-Hölder continuity condition (10), that is $\exists M>0$:

$$\begin{aligned} |p_i(x)-p_i(y)|\le & {} -\frac{M}{\ln (|x-y|)}\; \forall x\ne y\in \Omega \; \text{ such } \text{ that } |x-y|\le \frac{1}{2}, \end{aligned}$$

(10)

then the smooth functions are dense in $\bigcap _{i=1}^{i=N}W^{1,p_i(\cdot )}_0(\Omega )$. The Poincaré type inequality is not correct in the variable anisotropic case but we have the following

Theorem 1

([4]) Let $\Omega \subset \mathbb {R}^N$ be a bounded domain and $p_i(\cdot )>1$ are continuous functions. Suppose that

$$\begin{aligned} p_i(x)<{\overline{p}}^*(x), \end{aligned}$$

(11)

where

$$\begin{aligned} {\overline{p}}^*(x)=\left\{ \begin{array}{ll} \frac{N{\overline{p}}(x)}{N-{\overline{p}}(x)}, &{} \hbox {if }{\overline{p}}(x)<N \\ +\infty , &{} \hbox {if }{\overline{p}}(x)\ge N. \end{array} \right. \end{aligned}$$

Then the following Poincaré-type inequality holds:

$$\begin{aligned} \Vert u\Vert _{L^{p_+(\cdot )}(\Omega )}\le C\sum _{i=1}^N\left\| D_iu\right\| _{L^{p_i(\cdot )}(\Omega )},\quad \forall u\in \bigcap _{i=1}^NW^{1,p_i(\cdot )}_0(\Omega ), \end{aligned}$$

where C is a positive constant independent of u. Thus, $\sum _{i=1}^N\Vert D_iu\Vert _{L^{p_i(\cdot )}(\Omega )}$ is an equivalent norm on $\bigcap _{i=1}^NW^{1,p_i(\cdot )}_0(\Omega )$.

The following embedding result for the anisotropic constant exponent Sobolev space is well-known [11, 13].

Lemma 2

Let Q be a cube of $\mathbb {R}^N$ with faces parallel to the coordinate planes. Suppose $p_i\ge 1$, $i=1,...,N$ and $u\in \bigcap _{i=1}^{N}W^{1,p_i}(Q)$. Then

$$\begin{aligned} \Vert u\Vert _{L^{s}(Q)}\le & {} K\prod _{i=1}^{N}\Big (\Vert u\Vert _{L^{p_i}(Q)}+\Vert D_i u\Vert _{L^{p_i}(Q)}\Big )^{\frac{1}{N}}, \end{aligned}$$

(12)

where $s={\overline{p}}^{*}=\frac{N{\overline{p}}}{N-{\overline{p}}}$ if ${\overline{p}}<N$ with ${\overline{p}}$ given by $\frac{1}{{\overline{p}}}=\frac{1}{N}\sum _{i=1}^{N}\frac{1}{p_i}$. The constant K depends on N and $p_i$. Furthermore, if ${\overline{p}}\ge N$ , the inequality (12) is true for all $s\ge 1$, and K depends on s and $|Q|$.

Remark 1

([3]) Let $\Omega$ be a bounded subset of  $\mathbb {R}^N$, and $p_i:\Omega \rightarrow (1,+\infty )$ be a continuous function. We have the following continuous dense embeddings

$$\begin{aligned} L^{p_i^+}(0,T;L^{p_i(\cdot )}(\Omega ))\hookrightarrow L^{p_i(\cdot )}(Q_T)\hookrightarrow L^{p_i^-}(0,T;L^{p_i(\cdot )}(\Omega )). \end{aligned}$$

Throughout the paper we suppose that $p_i(\cdot )>1$ are continuous functions satisfied the assumption (11).

3 Statements of results

Definition 1

A function u is a weak solution of problem (1) if:

$$\begin{aligned} u\in L^{1}(0,T;W^{1,1}_{0}(\Omega ))\cap \Big ( L^{s_+(\cdot )}(Q_T)\Big ), \, a_i\in L^{1}(0,T;L^{1}(\Omega )),\, F\in L^1(Q_T), \end{aligned}$$

and

$$\begin{aligned}&-\int _{0}^T\int _{\Omega }u\partial _{t} \varphi \,dx\,dt+ \sum _{i=1}^N\int _{0}^T\int _{\Omega } b_i(t,x,u)a_i(t,x,Du)D_i\varphi \,dx\,dt \nonumber \\&+\int _{0}^T\int _{\Omega }F(t,x,u) \varphi \,dx\,dt =\int _{0}^T\int _{\Omega }\varphi (t,x) f \,dx\,dt+\int _{\Omega }\varphi (0,x)u_{0}(x)\,dx, \end{aligned}$$

(13)

for all $\varphi \in C_{c}^1([0,T)\times \Omega )$, the $C^{1}_c$ functions with compact support.

Our main existence results for (1) are the following:

Theorem 3

Let $m(\cdot )=m$, $\sigma (\cdot )=\sigma$, $f\in L^{m}(Q_T)$ with $m>1$, such that

$$\begin{aligned} \frac{(N+\sigma +2){\overline{p}}(\cdot )}{(N+1){\overline{p}}(\cdot )-2N(1+\sigma ) +(N+\sigma +2){\overline{p}}(\cdot )}<m<\frac{(N+\sigma +2){\overline{p}}(\cdot )}{(N+\sigma +2){\overline{p}}(\cdot )-N(\sigma +1)}, \end{aligned}$$

(14)

$$\begin{aligned} 0\le \sigma <\min \left\{ {\overline{p}}(\cdot )-1+\frac{{\overline{p}}(\cdot )}{N}, {\overline{p}}(\cdot )-2+\frac{m{\overline{p}}(\cdot )}{N}\right\} ,\;{\overline{p}}(\cdot )\ge 2. \end{aligned}$$

(15)

Assume that $s_i(\cdot )$, $p_i(\cdot )$ are continuous functions such that for all $i=1,\dots ,N$

$$\begin{aligned} \frac{{\overline{p}}(\cdot )\Big (N+1-(1+\sigma )(m-1)\Big )}{m\Big ((N+1) {\overline{p}}(\cdot )-N(1+\sigma )\Big )}<p_i(\cdot )<\frac{{\overline{p}}(\cdot )\Big (N+1-(1+\sigma )(m-1)\Big )}{mN(1+\sigma )-(m-1)(N+\sigma +2){\overline{p}}(\cdot )}, \end{aligned}$$

(16)

and

$$\begin{aligned} s_i(\cdot )\ge p_i(\cdot ). \end{aligned}$$

(17)

Let $a_i$, F be Carathéodory functions, where $a_i$ satisfying (2)-(4) and F satisfying (6)-(7). Then, the problem (1) has at least one weak solution

$$\begin{aligned} u\in \bigcap _{i=0}^N L^{q^{-}_i}\Big (0,T;W^{1,q_i(\cdot )}_{0}(\Omega )\Big ), \end{aligned}$$

where $q_i(\cdot )$ are continuous functions on ${\overline{\Omega }}$ satisfying for all $i=1,\ldots ,N$

$$\begin{aligned} 1\le q_i(\cdot )<\frac{mp_i(\cdot )}{{\overline{p}}(\cdot )} \left( \frac{(N+1){\overline{p}}(\cdot )-N(1+\sigma )}{N+1-(1+\sigma )(m-1)}\right) . \end{aligned}$$

(18)

Remark 2

The lower bound for m in (14) is due to the fact that $q_i(\cdot )$ must not be smaller than 1. The upper bound for m in (14) implies $q_i(\cdot )<p_i(\cdot )$. In the Theorem 3, we suppose that $m>1$ because if $0\le \sigma <\frac{(N+1){\overline{p}}(\cdot )-2N}{2N}$, then $\frac{(N+\sigma +2){\overline{p}}(\cdot )}{(N+1){\overline{p}}(\cdot )-2N (1+\sigma )+(N+\sigma +2){\overline{p}}(\cdot )}<1$.

Remark 3

We note that (14) (resp. (16)) is well defined since we have (15) (resp. (14)).

Remark 4

We not that (14) implies

$$\begin{aligned} {\overline{p}}(\cdot )<\frac{N(N+\sigma +2)}{m(N+1)}. \end{aligned}$$

(19)

Therefore, by (18) we have ${\overline{q}}(\cdot )< N$.

Remark 5

Under the assumption $0\le \sigma <\frac{(N+2){\overline{p}}(\cdot )-2(N+1)}{1+N-{\overline{p}}(\cdot )}$ that is

$$\begin{aligned} \frac{(N+\sigma +2){\overline{p}}(\cdot )}{(N+\sigma +2){\overline{p}}(\cdot ) -N(\sigma +1)}<~{\overline{p}}(\cdot ), \end{aligned}$$

we can deduce that f is never in the dual space $\left( \displaystyle \bigcap _{i=1}^N L^{p^{-}_i}\Big (0,T;W^{1,p_i(\cdot )}_{0}(\Omega )\Big )\right) ^{'}$, so that the result of this paper deals with irregular data as in [2, 10]. If m tends to be 1, then $q_i(\cdot )<\frac{p_i(\cdot )}{{\overline{p}}(\cdot )} \left( {\overline{p}}(\cdot )-\frac{N(\sigma +1)}{N+1}\right)$, which is bound on $q_i(\cdot )$ obtained in [10]. Furthermore if $p_i(.)=2$ the assumption (15) is equivalent to [(1.2), [5]], and then $q_i(.)=q=\frac{m(N(1-\sigma )+2)}{N+1-(1+\sigma )(m-1)}$, which is bound on q obtained in [(1.6), [5]].

Theorem 4

Let $f\in L^{m(\cdot )}(Q_T)$, $1<m(\cdot )<p_i'(\cdot )$ $p_i'(\cdot )=\frac{p_i(\cdot )}{p_i(\cdot )-1}$, $s_i(\cdot )>0$, $i=1,\dots ,N$ and $\sigma (\cdot )\ge 0$, such that

$$\begin{aligned}&\frac{1+\sigma (\cdot )}{m(\cdot )-1}>s_+(\cdot )>(1+\sigma (\cdot )) \max \left\{ \frac{(p_i(\cdot )-1)}{(m(\cdot )-1)p_i(\cdot )+1};(p_i(\cdot )-1) \right\} \nonumber \\& \nabla s_+\in L^\infty (Q_T),\; \nabla m\in L^\infty (Q_T) \end{aligned}$$

(20)

$$\begin{aligned}&p_i(\cdot )>\frac{1}{m(\cdot )}\Big (1+\frac{1+\sigma (\cdot )}{s_+(\cdot )}\Big ). \end{aligned}$$

(21)

Let $a_i$, F be Carathéodory functions, where $a_i$ satisfying (2)-(4), and F satisfying (6)-(7). Then, the problem (1) has at least one weak solution

$$\begin{aligned} u\in \bigcap _{i=0}^N L^{q^{-}_i}\Big (0,T;W^{1,q_i(\cdot )}_{0}(\Omega )\Big ), \end{aligned}$$

where $q_i(\cdot )$ are continuous functions on ${\overline{\Omega }}$ satisfying for all $i=1,\ldots ,N$

$$\begin{aligned} q_i(\cdot )=\frac{m(\cdot ) p_i(\cdot )s_+(\cdot )}{1+s_+(\cdot ) +\sigma (\cdot )}. \end{aligned}$$

(22)

Theorem 5

Let $f\in L^{m(\cdot )}(Q_T)$, $1<m(\cdot )<p_i'(\cdot )$, $\sigma (\cdot )\ge 0$, such that

$$\begin{aligned} s_+(\cdot )\ge \frac{1+\sigma (\cdot )}{m(\cdot )-1},\quad \nabla \sigma \in L^{\infty }(\Omega ). \end{aligned}$$

(23)

Under the hypotheses (2)-(10) and (6)-(7), the problem (1) has at least one weak solution $u\in \cap _{i=1}^NL^{p_i^-}(0,T,W_0^{1,p_i(\cdot )}(\Omega ))\cap L^{1+s_+(\cdot )+\sigma (\cdot )}(Q_T)$.

Remark 6

The assumption $1<m(\cdot )<p_i'(\cdot )$ implies that (20) holds, otherwise (20) become empty. By (21) we have that $q_i(\cdot )>1$ in (22).

4 Proof of Theorems 3, 4, and 5

4.1 Approximation of (1)

Let $(f_{n})_{n\in \mathbb {N^{\star }}}\subset C^{\infty }_{c}(Q_T)$ and $(u_{0,n})_{n\in \mathbb {N^{\star }}}\subset C^{\infty }_{c}(\Omega )$ be sequences of functions satisfying

$$\begin{aligned}&|f_{n}|\le n,\;|u_{0,n}|\le n,\;\forall n \ge 1,\\&\Vert f_n\Vert _{L^{m(\cdot )}(Q_T)} \le \Vert f\Vert _{L^{m(\cdot )}(Q_T)},\; \Vert u_{0,n}\Vert _{L^{(m(\cdot )-1)s_+(\cdot )+1}(\Omega )} \le \Vert u_{0}\Vert _{L^{(m(\cdot )-1)s_+(\cdot )+1}(\Omega )}\;\forall n \ge 1. \end{aligned}$$

Then, there exists at least one weak solution (see [2])

$$\begin{aligned} \left\{ \begin{array}{lll} &{}u_n\in \bigcap _{i=1}^N L^{p^-_i}\left( 0,T;W^{1,p_i(\cdot )}_0(\Omega )\right) \cap C([0,T];L^2(\Omega )),\\ &{}\partial _t u_n\in \sum _{i=1}^N L^{{p_i^-}'}\left( 0,T;(W^{1,p_{i}(\cdot )}_0(\Omega ))'\right) +L^1(Q_T), \end{array}\right. \end{aligned}$$

of problems

$$\begin{aligned} \begin{aligned}&\partial _tu_{n} -\sum ^{N}_{i=1}D_i\big (b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\big )+F(t,x,u_{n}) =f_{n} \quad \hbox { in}\ Q_T, \\&u_{n}=0\quad \hbox { on}\ \Sigma _T, \\&u_{n}(0,x)=u_{0,n}(x)\quad \hbox { in}\ \Omega , \end{aligned} \end{aligned}$$

(24)

each of them satisfying the weak formulation

$$\begin{aligned} \begin{aligned}&\displaystyle \int _0^T <\partial _tu_{n},\varphi >\,dt +\displaystyle \sum _{i=1}^N\int _0^T \int _\Omega b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n}).D_i \varphi \,\,dx\,dt \\&+\displaystyle \int _0^T \int _\Omega F(t,x,u_n). \varphi \,\,dx\,dt=\displaystyle \int _0^T \int _\Omega f_{n}\varphi \,dx\,dt, \end{aligned} \end{aligned}$$

(25)

for all $\varphi \in \displaystyle \bigcap _{i=1}^N L^{p^{-}_i}\Big (0,T;W^{1,p_i(\cdot )}_{0}(\Omega )\Big )\cap L^{\infty }(Q_T)$. The truncation function  $T_k$ at height $k$, $k > 0$ is defined by $T_k(t)=\max\{-k,\min\{k,t\}\}$, $t\in\mathbb{R}$.

4.2 Uniform estimates

In this section, we state and prove uniform estimates for the solutions $u_n$ of problem (24). In the remainder of this paper, we denote by C or $C_{j},j\in \mathbb {N}^\star$, various positive constants depending only on the structure of $a_i, F, |\Omega |, \Vert f\Vert _{L^m(Q_T)},$ and T, never on n.

Lemma 6

([10]) There exists a constant $C > 0$ (independent of n) such that

$$\begin{aligned} \int _{0}^T\int _{\Omega }|F(t,x,u_n)|\,dx\,dt\le C. \end{aligned}$$

Lemma 7

Let m, $p_i(\cdot )$, $\sigma$, $s_i(\cdot )$ $i=1,\ldots ,N$ are restricted as in Theorem 3. Then, for all $i=1,\ldots ,N$, $(D_iu_n)$ is bounded in $L^{q_i^-}(0,T;L^{q_i(\cdot )}(\Omega ))$, furthermore $(u_n)$ is bounded in $L^{{\overline{q}}^-}(0,T,L^{{\overline{q}}^*(\cdot )}(\Omega ))$, where the exponents $q_i(\cdot )$ are defined as in (18), ${{\overline{q}}}^*(\cdot )=\frac{N{\overline{q}}(\cdot )}{N-{\overline{q}}(\cdot )}$, ${\overline{q}}(\cdot )<N$.

Proof

For all $\delta \in (0,1)$ and $\tau \in (0,T)$ using $\varphi _\delta (u_n)=\left( (1+|u_n|)^{1-\delta }-1\right) {\text {sign}}(u_n)\chi _{(0,\tau )},$ as a test function in (25), where $\chi _{(0,\tau )}$ denotes the characteristic function of $(0,\tau )$ in (0, T], one gets

$$\begin{aligned} \begin{aligned}&\displaystyle \int _0^T <\partial _tu_{n},\varphi _\delta (u_n) >\,dt +\displaystyle \sum _{i=1}^N\int _0^T \int _\Omega b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n}).D_i \varphi _\delta (u_n)\,\,dx\,dt\\ {}&+\displaystyle \int _0^T \int _\Omega F(t,x,u_n). \varphi _\delta (u_n)\,\,dx\,dt=\displaystyle \int _0^T \int _\Omega f_{n}\varphi _\delta (u_n)\,dx\,dt. \end{aligned} \end{aligned}$$

From (2) and (5), we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Omega }\,dx\int _0^{u_n(\tau ,x)}\varphi _\delta (r) \,dr+\alpha (1-\delta ) C_2\sum _{i=1}^N\int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{(\delta +\sigma (x))}}\,dx\,dt \\&+\int _{0}^T\int _{\Omega }F(t,x,u_n)\varphi _\delta (u_n)\,dx\,dt \\ {}&\le \int _{0}^T\int _{\Omega }\varphi _\delta (u_n)f_n \,dx\,dt+\int _{\Omega }\,dx\int _0^{u_n(0,x)}\varphi _\delta (r)\,dr. \end{aligned} \end{aligned}$$

(26)

Observing that there exist two positive constants $C_3$ and $C_4$ such that

$$\begin{aligned} \forall r\in \mathbb {R},\quad \int _0^r \varphi _\delta (t)dt\ge C_3|r|^{2-\delta }-C_4. \end{aligned}$$

(26) and (6), yield

$$\begin{aligned} \begin{aligned}&\Vert u_n\Vert ^{2-\delta }_{L^\infty (0,T;L^{2-\delta }(\Omega ))}+ \sum _{i=1}^N\int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{(\delta +\sigma (x))}}\,dx\,dt \\ {}&\le C_5+C_6\left( \int _{Q_T} \Big (1+|u_n|\Big )^{(1-\delta )m'}\,dx\,dt\right) ^{\frac{1}{m'}}. \end{aligned} \end{aligned}$$

(27)

Now, let $q_i^{+}=\displaystyle \max _{x\in {\overline{\Omega }}}\left\{ q_i(x)\right\}$, $i=1,...,N$ be a constant such that

$$\begin{aligned} q_i^{+}<\min _{x\in {\overline{\Omega }}}\left\{ \frac{mp_i(x)}{{\overline{p}}(x)} \left( \frac{(N+1){\overline{p}}(x)-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) \right\} =\frac{mp_i^-}{{\overline{p}}^{-}} \left( \frac{(N+1){\overline{p}}^{-}-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) =\alpha _i. \end{aligned}$$

By (15) we have

$$\begin{aligned} 1<m<\frac{(N+\sigma +2){\overline{p}}^{-}}{(N+\sigma +2){\overline{p}}^{-}-N(\sigma +1)} <\frac{N}{{\overline{p}}^{-}}+1. \end{aligned}$$

(28)

According to (14) we get

$$\begin{aligned} \frac{\alpha _i}{p_i^-}=\frac{{\overline{\alpha }}}{{\overline{p}}^-}=\theta \in (0,1). \end{aligned}$$

Hölder’s inequality and (27) imply that, for all $i=1,\ldots ,N$

$$\begin{aligned} \begin{aligned}&y_{ni}= \int _0^T\int _{\Omega }|D_iu_n|^{\alpha _i}\,dx\,dt= \int _0^T \int _{\Omega }\frac{|D_iu_n|^{\alpha _i}}{(1+|u_n|)^{(\delta +\sigma )\theta }} (1+|u_n|)^{(\delta +\sigma )\theta }\,dx\,dt \\ {}&\le \left( C+C\left( \int _{Q_T} \Big (1+|u_n|\Big )^{(1-\delta )m'}\,dx\,dt\right) ^{\frac{1}{m'}}\right) ^{\theta }\left( \int _{Q_T} \Big (1+|u_n|\Big )^{(\delta +\sigma )\frac{\theta }{1-\theta }} \,dx\,dt\right) ^{1-\theta }. \end{aligned} \end{aligned}$$

(29)

Let $\delta =\frac{{\overline{p}}^-(1-m)(N+2)+mN(\sigma +1)-N\sigma }{{\overline{p}}^-(1-m)+N}$, then we have $(1-\delta )m'=\frac{(\delta +\sigma )\theta }{1-\theta }= \frac{N+2-\delta }{N}{\overline{\alpha }}$, and by (28)-(14) we deduce that $\delta \in (0,1)$. Putting $d=\frac{N+2-\delta }{N}{\overline{\alpha }}$, we obtain

$$\begin{aligned} d=\frac{m\Big ((N+1){\overline{p}}^--N(\sigma +1)\Big )}{{\overline{p}}^-(1-m)+N}. \end{aligned}$$

(30)

From (29), we deduce that

$$\begin{aligned} \begin{aligned}&y_{ni}^{\frac{{\overline{\alpha }}}{N\alpha _i}}\le C\left( 1+\int _{Q_T} \Big (1+|u_n|\Big )^{d}\,dx\,dt\right) ^{(1-\frac{\theta }{m}) \frac{{\overline{\alpha }}}{N\alpha _i}}, \end{aligned} \end{aligned}$$

hence

$$\begin{aligned} \begin{aligned}&\prod _{i=1}^Ny_{ni}^{\frac{{\overline{\alpha }}}{N\alpha _i}}\le C^N\left( 1+\int _{Q_T} \Big (1+|u_n|\Big )^{d}\,dx\,dt\right) ^{(1-\frac{\theta }{m})}. \end{aligned} \end{aligned}$$

(31)

By (15) and (19), we have

$$\begin{aligned} 2-\delta -d=\frac{N(2+\sigma )-(N+m){\overline{p}}^-}{{\overline{p}}^-(1-m)+N}<0, \end{aligned}$$

and

$$\begin{aligned} d-{{\overline{\alpha }}}^\star =\frac{m\left( (N+1){\overline{p}}^--N(\sigma +1)\right) \left( N(2+\sigma )-(N+m){\overline{p}}^-\right) }{({\overline{p}}^-(1-m)+N)(N(N+2+\sigma ) -m(N+1){\overline{p}}^-)}<0. \end{aligned}$$

Hence $2-\delta<d<{{\overline{\alpha }}}^\star$. Using the interpolation inequality, we get

$$\begin{aligned} \Vert u_n(\cdot ,t)\Vert _{L^{d}(\Omega )}\le \Vert u_n(\cdot ,t)\Vert _{L^{2-\delta }(\Omega )}^{1-\tau } \Vert u_n(\cdot ,t)\Vert _{L^{{{\overline{\alpha }}}^*}(\Omega )}^{\tau }, \quad \tau =\frac{(2-\delta -d){{\overline{\alpha }}}^\star }{(2-\delta -{{\overline{\alpha }}}^\star )d}. \end{aligned}$$

(32)

By virtue of (30) and (32), we obtain

$$\begin{aligned} \tau =\frac{N}{N+2-\delta },\text { and } d\tau ={\overline{\alpha }}. \end{aligned}$$

Using (27) and (32), the result is

$$\begin{aligned} \begin{aligned}&\int _0^{T}\Vert u_n\Vert ^{d}_{L^{d}(\Omega )}\,dt\le \Vert u_n\Vert ^{(1-\tau )d}_{{L^\infty }(0,T;L^{2-\delta }(\Omega ))} \int _0^{T}\Vert u_n\Vert ^{d\tau }_{L^{{{\overline{\alpha }}}^{\star }}(\Omega )} \,dt \\ {}&\le C\left( 1+\int _{Q_T} \left( 1+|u_n|\right) ^{d}\,dx\,dt\right) ^{\frac{(1-\tau )d}{(2-\delta )m'}} \int _0^{T}\Vert u_n\Vert ^{{\overline{\alpha }}}_{L^{{{\overline{\alpha }}}^{\star }}(\Omega )} \,dt \\ {}&=C\left( 1+\int _{Q_T} \left( 1+|u_n|\right) ^{d}\,dx\,dt\right) ^{\frac{{\overline{\alpha }}}{Nm'}} \int _0^{T}\Vert u_n\Vert ^{{\overline{\alpha }}}_{L^{{{\overline{\alpha }}}^{\star }}(\Omega )} \,dt. \end{aligned} \end{aligned}$$

(33)

From Lemma 2, we have

$$\begin{aligned} \int _0^{T}\Vert u_n\Vert ^{{\overline{\alpha }}}_{L^{{{\overline{\alpha }}}^{\star }}(\Omega )}\,dt \le C\int _0^{T} \prod _{i=1}^N\left( \int _{\Omega }|D_iu_n|^{\alpha _i}\,dx\right) ^\frac{{\overline{\alpha }}}{N\alpha _i}\,dt. \end{aligned}$$

$\sum _{i=1}^N\frac{{\overline{\alpha }}}{N\alpha _i}=1$, and the Hölder’s inequality, yield

$$\begin{aligned} \int _0^{T}\Vert u_n\Vert ^{{\overline{\alpha }}}_{L^{{{\overline{\alpha }}}^{\star }}(\Omega )}\,dt \le C\prod _{i=1}^N\left( \int _{Q_T}|D_iu_n|^{\alpha _i}\,dx\,dt\right) ^\frac{{\overline{\alpha }}}{N\alpha _i}. \end{aligned}$$

(34)

In view of (31), (33), and (34), we deduce

$$\begin{aligned} \begin{aligned} \int _{Q_T}|u_n|^{d}\,dx\,dt\le & {} C\left( 1+\int _{Q_T} |u_n|^{d}\,dx\,dt\right) ^{1+\frac{{\overline{\alpha }}}{Nm'}-\frac{\theta }{m}} \\ {}= & {} C\left( 1+\int _{Q_T} |u_n|^{d}\,dx\,dt\right) ^{1+\frac{{\overline{\alpha }}}{N} -\frac{{\overline{\alpha }}}{Nm}-\frac{{\overline{\alpha }}}{m{\overline{p}}^-}}. \end{aligned} \end{aligned}$$

(35)

By (28) we have

$$\begin{aligned} 1+\frac{{\overline{\alpha }}}{N}-\frac{{\overline{\alpha }}}{Nm}- \frac{{\overline{\alpha }}}{m{\overline{p}}^-}<1. \end{aligned}$$

Therefore, (35) implies that the sequence $(u_n)$ is bounded on $L^d(Q_T)$. Which then yields, by (29), a bound on the norm of $(D_iu_n)$ in $L^{\alpha _i}$, also in $L^{q_i^{+}}$. The result of Lemma 7 follows from $q_i(\cdot )\le q_i^+$, Remark 1, and (34).

Now let us consider a continuous variable exponent $q_i(\cdot )$ on ${\overline{\Omega }}$ satisfying (18) such that

$$\begin{aligned} q_i^{+}\ge \frac{mp_i^-}{{\overline{p}}^{-}} \left( \frac{(N+1){\overline{p}}^{-}-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) . \end{aligned}$$

By the continuity of $q_i(\cdot )$ and $p_i(\cdot )$ on ${\overline{\Omega }}$, there exists a constant $\delta >0$ such that for all $x\in \Omega$

$$\begin{aligned} \max _{z\in {\overline{Q(x,\delta )\cap \Omega }}}q_i(z)< & {} \min _{z\in {\overline{Q(x,\delta )\cap \Omega }}} \left\{ \frac{mp_i(z)}{{\overline{p}}(z)} \left( \frac{(N+1){\overline{p}}(z)-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) \right\} \end{aligned}$$

where $Q(x,\delta )$ is a cube with center x and diameter $\delta$. Observe that ${\overline{\Omega }}$ is compact and, therefore, we can cover it with a finite number of cubes $(Q'_{j})_{j=1,...,k}$ with edges parallel to the coordinate axes. We denote by $q_{ij}^{+}$ (resp. $p_{ij}^{-}$ ) the local maximum of $q_i(\cdot )$ on $\overline{(Q'_j\cap \Omega )}$ (resp. the local minimum of $p_i(\cdot )$ on $\overline{(Q'_j\cap \Omega )}$ ), such that

$$\begin{aligned} q_{ij}^{+}< & {} \frac{mp_{ij}^-}{{\overline{p}}_j^{-}} \left( \frac{(N+1){\overline{p}}_j^{-}-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) =\alpha _{ij},\quad \text{ for } \text{ all }\quad j=1,...,k. \end{aligned}$$

Observing that (7) and Lemma imply that $(u_n)$ is bounded in $L^{s_+(\cdot )}(\Omega )$. So from (17) and (12), it is easy to check that, instead of the global estimate (34), we find

$$\begin{aligned} \int _0^{T}\Vert u_n\Vert ^{{\overline{\alpha }}_j}_{L^{{{\overline{\alpha }}}^{\star }_j}(Q'_j\cap \Omega )}\,dt \le C\prod _{i=1}^N\left( 1+y_{nij}\right) ^\frac{{\overline{\alpha }}_j}{N\alpha _{ij}}, \end{aligned}$$

(36)

where $y_{nij}=\int _{(0,T)\times (Q'_j\cap \Omega )}|D_iu_n|^{\alpha _{ij}}\,dx\,dt$, $\frac{1}{{\overline{\alpha }}_j}=\frac{1}{N}\sum _{i=1}^N\frac{1}{\alpha _{ij}}$. According to (31), we obtain

$$\begin{aligned} \begin{aligned}&\prod _{i=1}^N\left( 1+y_{nij}\right) ^{\frac{{\overline{\alpha }}}{N\alpha _{ij}}}\le C^N\left( 1+\int _{(0,T)\times (Q'_j\cap \Omega )} \Big (1+|u_n|\Big )^{d_j}\,dx\,dt\right) ^{(1-\frac{\theta _j}{m})}, \end{aligned} \end{aligned}$$

(37)

where $\frac{\alpha _{ij}}{p^-_{ij}}=\frac{{\overline{\alpha }}_j}{{\overline{p}}^-_j}=\theta _j$, $d_j=\frac{N+2-\delta _j}{N}{\overline{\alpha }}_j$, $\delta _j=\frac{{\overline{p}}^-_j(1-m)(N+2)+mN(\sigma +1)-N\sigma }{{\overline{p}}^-_j(1-m)+N}$. Arguing locally as in (35), we obtain

$$\begin{aligned} \begin{aligned} \int _{(0,T)\times (Q'_j\cap \Omega )}|u_n|^{d_j}\,dx\,dt\le & {} C\left( 1+\int _{(0,T)\times (Q'_j\cap \Omega )} |u_n|^{d_j}\,dx\,dt\right) ^{1+\frac{{\overline{\alpha }}_j}{N} -\frac{{\overline{\alpha }}_j}{Nm}-\frac{{\overline{\alpha }}_j}{m{\overline{p}}^-_j}}, \end{aligned} \end{aligned}$$

(38)

where $1+\frac{{\overline{\alpha }}_j}{N}-\frac{{\overline{\alpha }}_j}{Nm}- \frac{{\overline{\alpha }}_j}{m{\overline{p}}^-_j}<1$. Combining (36), (37), and (38), we obtain

$$\begin{aligned} \Vert u_n\Vert _{L^{{\overline{\alpha }}_j}(0,T,L^{{\overline{\alpha }}^*_j}( (Q'_j\cap \Omega )))}\le C\quad \text{ and }\quad \Vert D_iu_n\Vert _{L^{\alpha _{ij}}((0,T)\times (Q'_j\cap \Omega ))}\le C. \end{aligned}$$

Knowing that $q_i(x)\le q_{ij}^+\le \alpha _{i,j}$ and ${{\overline{q}}}^*(x)\le {{\overline{q}}_j^+}^*\le {{\overline{\alpha }}_j}^*$ for all $x\in (Q'_j\cap \Omega )$, and all $j=1,\ldots ,k$, we conclude that $(D_iu_n)$ is bounded in $L^{q_{i}(\cdot )}((0,T)\times \Omega )$. Consequently, by (36), $(u_n)$ remains in a bounded set of ${L^{{\overline{q}}^-}}(0,T;L^{{{\overline{q}}}^*(\cdot )}(\Omega ))$. This finishes the proof of the Lemma 7. $\square$

Now we consider the following family of functions $(\phi _k)_{k>0}$:

• $\phi _k$ is a twice differentiable function, $\phi ^{'}_{k}$, $\phi ^{''}_{k}$ are bounded on $\mathbb {R}$.

• $\phi _k(\sigma )=\sigma$ if $|\sigma |\le k$, and $\phi '_k(\sigma )=0$ if $|\sigma |\ge k+(1/k)$, $0<\phi '_k<1$ on the set $(k,k+(1/k))\,\cup \,(-(k+(1/k)),-k)$.

The construction of this family $(\phi _k)_{k>0}$ can be made explicitly (See [6]).

Lemma 8

[10] There exists a constant $C_k$ dependent of k such that

$$\begin{aligned} \int _{Q_T}|D_i\phi _k(u_n)|^{p_i(x)}\,dx\,dt\le C_k,\quad i=1,\ldots ,N. \end{aligned}$$

Next we show that $(\partial _tu_n)$ is in a bounded set of $L^{r}(0,T;W^{-1,r}(\Omega ))+L^1(Q_T)$ for some $r>1$.

Lemma 9

Let

$$\begin{aligned} 1<r<\min _i\min _{x\in {\overline{\Omega }}}\left\{ \frac{m(N+1)p_i(x)}{(N+1-(1+\sigma )(m-1)) (p_i(x)-1){\overline{p}}(x)} \left( {\overline{p}}(x)-\frac{N(\sigma +1)}{N+1}\right) \right\} . \end{aligned}$$

(39)

The sequence $(\partial _tu_n)$ remains in a bounded set of $L^{r}(0,T;W^{-1,r}(\Omega ))+L^1(Q_T)$.

Proof

It is similar to the proof of Lemma 2.11 of [6]. The existence of $r>1$ is by virtue of the upper bound in the assumption (16). Knowing that $(f_n-F(\cdot ,\cdot ,u_n))$ is in a bounded set of $L^1(Q_T)$, we have to show that

$$\begin{aligned} w_n=\sum ^{N}_{i=1}D_i\big (b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\big ) \end{aligned}$$

belongs to a bounded set of $L^{r}(0,T;W^{-1,r}(\Omega ))$. In fact, setting for $t\in (0,T)$, $w_n(t)=w_n$. By (39), (3) and (5), we get

$$\begin{aligned} \Vert w_n\Vert _{W^{-1,r}(\Omega )}= & {} \sup _{\varphi \in W^{1,r'}_0(\Omega ),\; \Vert \varphi \Vert _{W^{1,r'}_0(\Omega )}\le 1} \left|\int _{\Omega }\sum _{i=1}^N\left( b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\right) D_i\varphi \,\;dx \right|\\\le & {} C_1\sup _{\; \Vert \varphi \Vert _{W^{1,r'}_0(\Omega )}\le 1}\sum _{i=1}^N \int _{\Omega }\left( g+\sum _{j=1}^N|D_j u_n|^{p_j(\cdot )}\right) ^ {1-\frac{1}{p_i(\cdot )}} |D_i\varphi |\,\,dx.\\ \end{aligned}$$

By the Hölder inequality, we get

$$\begin{aligned}&\Vert w_n\Vert _{W^{-1,r}(\Omega )} \\ {}\le & {} C_1\sup _{\Vert \varphi \Vert _{W^{1,r'}_0(\Omega )}\le 1}\sum _{i=1}^N \left( \int _\Omega G_i(t,x)dxdt\right) ^{\frac{1}{r}} \sum _{i=1}^N\left\| D_i\varphi \right\| _{L^{r'}(\Omega )} \end{aligned}$$

where

$$\begin{aligned} G_i(t,x)=\left( g+\sum _{j=1}^N|D_j u_n|^{p_j(\cdot )}\right) ^{(1-\frac{1}{p_i(\cdot )})r}(t,x),\text { for all }i=1,\cdots ,N. \end{aligned}$$

Thus

$$\begin{aligned}&\int _{0}^{T}\Vert w_n\Vert ^{r}_{W^{-1,r}(\Omega )}\,dt \le C\sum _{i=1}^N \int _{0}^{T}\int _{\Omega }G_i(t,x) \,dx\,dt. \end{aligned}$$

Thanks to (39) we have

$$\begin{aligned} \left( 1-\frac{1}{p_i(\cdot )}\right) r< \frac{m(N+1)}{N+1-(1+\sigma )(m-1)}\left( 1-\frac{N(\sigma +1)}{{\overline{p}}(x)(N+1)}\right) , i=1,\dots ,N. \end{aligned}$$

There exist $\theta$ such that for all $i=1,\dots ,N$

$$\begin{aligned} \left( 1-\frac{1}{p_i(\cdot )}\right) r<\theta < \frac{m(N+1)}{N+1-(1+\sigma )(m-1)}\left( 1-\frac{N(\sigma +1)}{{\overline{p}}(\cdot )(N+1)}\right) , \end{aligned}$$

from the upper bound in (14) we obtain that

$$\begin{aligned} \frac{m(N+1)}{N+1-(1+\sigma )(m-1)}\left( 1-\frac{N(\sigma +1)}{{\overline{p}}(\cdot )(N+1)}\right) <1. \end{aligned}$$

Therefore, $\theta \in (0,1)$ and

$$\begin{aligned} 1\le \theta p_{i}(\cdot )<\frac{mp_i(\cdot )}{{\overline{p}}(\cdot )} \left( \frac{(N+1){\overline{p}}(\cdot )-N(\sigma +1)}{N+1-(1+\sigma )(m-1)}\right) ,\;\left( 1-\frac{1}{p_i(\cdot )}\right) \frac{r}{\theta }<1. \end{aligned}$$

(40)

Writing $G_i=G_i^\frac{\theta }{\theta }$, by the Hölder inequality, we deduce

$$\begin{aligned}&\int _{0}^{T}\Vert w_n\Vert ^{r}_{W^{-1,r}_(\Omega )}\,dt \le C_5\sum _{i=1}^N \left( \int _{0}^{T}\int _{\Omega }\Big (g^\theta +\sum _{j=1}^N|D_j u_n|^{\theta p_j(\cdot )}\Big )\,dx\,dt\right) ^ {(1-\frac{1}{p_i(\cdot )})\frac{r}{\theta }} \\ {}\le & {} C_5\sum _{i=1}^N \left( \int _{0}^{T}\int _{\Omega }\left( g^\theta +\sum _{j=1}^N|D_j u_n|^{\theta p_j(\cdot )}\right) \,dx\,dt\right) ^ {(1-\frac{1}{p_i^+})\frac{r}{\theta }}+C_5N. \end{aligned}$$

By (9), Lemma 7, and (40) we get

$$\begin{aligned} \displaystyle \int _{0}^{T} \int _{\Omega }\sum _{j=1}^N|D_j u_n|^{\theta p_j(\cdot )}\,dx\,dt\le \sum _{j=1}^N\max \Big \{ \Vert D_ju_n\Vert _{L^{\theta p_j(\cdot )}(Q_T)}^{\theta p_j^-} ,\Vert D_ju_n\Vert _{L^{\theta p_j(\cdot )}(Q_T)}^{\theta p_j^+} \Big \}\le C. \end{aligned}$$

Since $g\in L^1(Q_T)$, we find

$$\begin{aligned} \int _{0}^{T}\Vert w_n\Vert ^{r}_{W^{-1,r}(\Omega )}\,dt \le C_6. \end{aligned}$$

This complete the proof of Lemma 9.$\square$

Lemma 10

Let $p_i$, $s_i$, $\sigma$, m $i=1,\ldots ,N$ are restricted as in Theorem 4. Then, there exists a constant $C>0$ independent of n, such that

$$\begin{aligned} \int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{1-(m(x)-1)s_+(x)+\sigma (x)}}\,dx\,dt+ \int _{0}^T\int _{\Omega }|u_n|^{m(x)s_+(x)}\,dx\,dt\le C. \end{aligned}$$

(41)

Proof

As in elliptic case [9], taking

$$\begin{aligned} \varphi (u_n)=\left( (1+|u_n|)^{(m(x)-1)s_+(x)}-1\right) {\text {sign}}(u_n), \end{aligned}$$

as a test function in (25), by (2), (3), (5), (14), and the fact that for a.e. $(t,x)\in Q_T$

$$\begin{aligned} D_i\varphi (u_n)=(m(x)-1)(1+|u_n|)^{(m(x)-1)s_+(x)}{\text {sign}}(u_n) D_is_+(x)\ln (1+|u_n|) \\+\frac{(m(x)-1)s_+(x)D_iu_n}{(1+|u_n|)^{1-(m(x)-1)s_+(x)}}+D_im(x) (1+|u_n |)^{(m(x)-1)s_+(x)} {\text {sign}}(u_n)s_+(x)\ln (1+|u_n|) \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Omega }\,dx\int _0^{u_n(\tau ,x)}\varphi (r)\,dr+\alpha (m^--1) s_+^-\sum _{i=1}^N\int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{1-(m(x)-1)s_+(x)+\sigma (x)}}\,dx\,dt \\&+\sum _{i=1}^N\int _{0}^T\int _{\Omega }|u_n|^{s_+(x)} \left( (1+|u_n|)^{(m(x)-1)s_+(x)}-1\right) \,dx\,dt \\ {}&\le \int _{0}^T\int _{\Omega }|f_n|\left( (1+|u_n|)^{(m(x)-1)s_+(x)}-1\right) \,dx\,dt\\ {}&+C_7\sum _{i=1}^N\int _{0}^T\int _{\Omega } (1+|u_n|)^{(m(x)-1)s_+(x)}\ln (1+|u_n|).\left( g +\sum _{j=1}^N|D_ju_n|^{p_j(x)}\right) ^{1-\frac{1}{p_i(x)}}\,dx\,dt \\ {}&+\int _{\Omega }\,dx\int _0^{u_n(0,x)}\varphi (r)\,dr. \end{aligned} \end{aligned}$$

By dropping the positif term, the fact that $|u_n|^{s_+(\cdot )}\ge 2^{-s_+(\cdot )}(1+|u_n|)^{s_+(\cdot )}-1$, (9), and Young inequality, we have

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^N\int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{1-(m(x)-1)s_+(x)+\sigma (x)}}\,dx\,dt +\frac{1}{2}\sum _{i=1}^N\int _{0}^T\int _{\Omega }(1+|u_n|)^{m(x)s_+(x)} \,dx\,dt \\ {}&\le C_8+C_8\max \Big (\Vert f_n\Vert ^{m^+}_{L^{m(\cdot )}(Q_T)}, \Vert f_n\Vert ^{m^-}_{L^{m(\cdot )}(Q_T)}\Big ) \\ {}&+C_8\sum _{i=1}^N\int _{0}^T\int _{\Omega } (1+|u_n|)^{(m(x)-1)s_+(x)}\ln (1+|u_n|)\times \left( g +\sum _{j=1}^N|D_ju_n|^{p_j(x)}\right) ^{1-\frac{1}{p_i(x)}}\,dx\,dt. \end{aligned} \end{aligned}$$

(42)

We can estimate the last term in (42) by application of Young’s inequality

$$\begin{aligned} \begin{aligned}&(1+|u_n|)^{(m(x)-1)s_+(x)}\ln (1+|u_n|)\times \left( g +\sum _{j=1}^N|D_ju_n|^{p_j(x)}\right) ^{1-\frac{1}{p_i(x)}} \\ {}&=(1+|u_n|)^{\sigma (x)+1-\frac{(1-(m(x)-1)s_+(x)+\sigma (x))}{p_i(x)}} \ln (1+|u_n|) \\ {}&\times \left( g+\sum _{j=1}^N|D_ju_n|^{p_j(x)}\right) ^{1-\frac{1}{p_i(x)}} (1+|u_n|)^{-\frac{(1-(m(x)-1)s_+(x)+\sigma (x))(p_i(x)-1)}{p_i(x)}} \\ {}&\le C_9(1+|u_n|)^{\sigma (x)p_i(x)+p_i(x)-(1-(m(x)-1)s_+(x)+\sigma (x))} (\ln (1+|u_n|))^{p_i(x)}+\frac{1}{4NC_8}g\\ {}&+ \frac{1}{4NC_8}\sum _{i=1}^N\frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{1-(m(x)-1)s_+(x)+\sigma (x)}}. \end{aligned} \end{aligned}$$

(43)

By (42) and (43), we obtain

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^N\int _{0}^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{1-(m(x)-1)s_+(x)+\sigma (x)}}\,dx\,dt +\sum _{i=1}^N\int _{0}^T\int _{\Omega }(1+|u_n|)^{m(x)s_+(x)} \,dx\,dt \\ {}&\le C_{10}+C_{11}\int _0^T\int _\Omega (1+|u_n|)^{\sigma (x)p_i(x)+p_i(x)-(1-(m(x)-1)s_+(x)+\sigma (x))} (\ln (1+|u_n|))^{p_i(x)}dxdt \\ {}&=I. \end{aligned} \end{aligned}$$

(44)

We observe that

$$\begin{aligned} (\sigma (x)+1)(p_i(x)-1)-s_+(x)\le ((\sigma (x)+1)(p_i(x)-1)-s_+(x))^+=d_i<\frac{d_i}{2}<0, \end{aligned}$$

due to the hypotheses (20), so $(1+|u_n|)^{(\sigma (x)+1)(p_i(x)-1)-s_+(x)-\frac{d_i}{2}}(\ln (1+|u_n|))^{p_i(x)}$ is bounded for all $x\in {\overline{\Omega }}$. We get by Young’s inequality,

$$\begin{aligned} \begin{aligned}&I=C_{10}+C_{11}\int _0^T\int _\Omega (1+|u_n|)^{m(x)s_i(x)+\frac{d_i}{2}}(1+|u_n|)^{(\sigma (x)+1)(p_i(x)-1)-s_i(x)- \frac{d_i}{2}}(\ln (1+|u_n|))^{p_i(x)} \\ {}&\le C_{12}+\frac{1}{2}\int _0^T\int _\Omega (1+|u_n|)^{m(x)s_i(x)}dxdt. \end{aligned} \end{aligned}$$

(45)

Therefore, (44) and (45) yield (41).

$\square$

Lemma 11

Let $p_i$, $s_i$, $\sigma$, m $i=1,\ldots ,N$ are restricted as in Theorem 5. Then, the approximate solution $u_n$ is bounded in $\cap _{i=1}^NL^{p_i^-}(0,T,W_0^{1,p_i(\cdot )}(\Omega ))\cap L^{1+s_+(\cdot )+\sigma (\cdot )}(Q_T)$.

Proof

Using $\varphi (u_n)=\left( (1+|u_n|)^{1+\sigma (\cdot )}-1\right) \mathrm { sign }(u_n)$ as test function in (25) and dropping the positif term, by (2) and (3), we obtain for all $\varepsilon >0$

$$\begin{aligned} \begin{aligned}&\alpha \sum _{i=1}^N\int _{0}^T\int _{\Omega }|D_iu_n|^{p_i(x)}\,dx\,dt \\&+\sum _{i=1}^N\int _{0}^T\int _{\Omega }|u_n|^{s_+(x)} \left( (1+|u_n|)^{(1+\sigma (x))}-1\right) \,dx\,dt \\ {}&\le C_{13}(\varepsilon )\int _{0}^T\int _{\Omega }|f_n|^{m(x)}dxdt+ \varepsilon \int _{0}^T\int _{\Omega }(1+|u_n|)^{(1+\sigma (x))m'(x)}dxdt \,dx\,dt\\ {}&+C_{14}\sum _{i=1}^N\int _{0}^T\int _{\Omega } (1+|u_n|)^{(1+\sigma (x))}\ln (1+|u_n|).\left( g +\sum _{j=1}^N|D_ju_n|^{p_j(x)}\right) ^{1-\frac{1}{p_i(x)}}\,dx\,dt \\ {}&+\int _{\Omega }(1+|u_n(0,x)|)^{2+\sigma (x)}\,dx+C_{15}. \end{aligned} \end{aligned}$$

Since (23) we have $(1+\sigma )m'\le 1+s_++\sigma$ and $2+\sigma \le (m-1)s_++1$. It follows from the Young inequality that

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^N\int _{0}^T\int _{\Omega }|D_iu_n|^{p_i(x)}\,dx\,dt+\int _{0}^T\int _{\Omega } |u_n|^{1+\sigma (x)+s_+(x)}\,dx\,dt \\ {}&\le C_{16}\sum _{i=1}^N\int _{0}^T\int _{\Omega } (1+|u_n|)^{(1+\sigma (x))p_i(x)}\ln (1+|u_n|)^{p_i(x)}\,dx\,dt+C_{17}. \end{aligned} \end{aligned}$$

(46)

Let us write

$$\begin{aligned} (\sigma (\cdot )+1)p_i(\cdot )=(\sigma (\cdot )+1)(p_i(\cdot )-1)-s_ +(\cdot )-\frac{\nu _i}{2}+\sigma (\cdot )+1+s_+(\cdot )+\frac{\nu _i}{2}, \end{aligned}$$

by (20), we get

$$\begin{aligned} \nu _i=\min _{x\in {\overline{\Omega }}}\{(\sigma +1)(p_i(x)-1)-s_+(x)\}<0. \end{aligned}$$

Arguing as in (45) and using (46), we obtain

$$\begin{aligned} \sum _{i=1}^N\int _{0}^T\int _{\Omega }|D_iu_n|^{p_i(x)}\,dx\,dt+\int _{0}^T\int _{\Omega } |u_n|^{1+\sigma (x)+s_+(x)}\,dx\,dt\le C_{18}. \end{aligned}$$

This concludes the proof of the lemma.$\square$

Lemma 12

Let $p_i(\cdot )$, $\sigma (\cdot )$, $s_i(\cdot )$, $m(\cdot )$ $i=1,...,N$ are restricted as in Theorem 4. Then, every solution $u_n$ of (25) satisfies the estimate

$$\begin{aligned} \Vert D_iu_n\Vert _{L^{q_i(\cdot )}(Q_T)}\le & {} C, \end{aligned}$$

where the $q_i(\cdot )$ defined as in (22).

Proof

Observe that (22) implies that $q_i(\cdot )<p_i(\cdot )$ and

$$\begin{aligned} \frac{(1+s_+(\cdot )+\sigma (\cdot ))q_i(\cdot )}{p_i(\cdot )}<m(\cdot )s_+(\cdot ). \end{aligned}$$

Then, by Young’s inequality, we have

$$\begin{aligned}&\int _0^T\int _{\Omega }|D_iu_n|^{q_i(x)}\,dx\,dt\\&= \int _0^T\int _{\Omega }\frac{|D_iu_n|^{q_i(x)}}{(1+|u_n|)^{\frac{(1-(m(x)-1)s_+(x)+\sigma (x))q_i(x)}{p_i(x)}}} (1+|u_n|)^{\frac{(1-(m(x)-1)s_+(x)+\sigma (x))q_i(x)}{p_i(x)}}\,dx\,dt, \\&\le \int _0^T\int _{\Omega }\Big (\frac{q_i(x)}{p_i(x)}\Big ) \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{(1-(m(x)-1)s_+(x)+\sigma (x))}} \,dx\,dt\\&+ \int _0^T\int _{\Omega }\Big (1-\frac{q_i(x)}{p_i(x)}\Big ) (1+|u_n|)^{\frac{(1-(m(x)-1)s_+(x)+\sigma (x))q_i(x)}{p_i(x)-q_i(x)}}\,dx\,dt. \end{aligned}$$

From (22), we deduce

$$\begin{aligned} \begin{aligned}&\int _0^T\int _{\Omega }|D_iu_n|^{q_i(x)}\,dx\,dt\\&\le C\int _0^T\int _{\Omega } \frac{|D_iu_n|^{p_i(x)}}{(1+|u_n|)^{(1-(m(x)-1)s_+(x)+\sigma (x))}} \,dx\,dt+C\int _0^T\int _{\Omega } (1+|u_n|)^{m(x)s_+(x)}\,dx\,dt. \end{aligned} \end{aligned}$$

(47)

Consequently, (47) and (41) imply the desert result. $\square$

4.3 Passage to the limit and proof of Theorem 3

By Lemma 7, the sequence $(u_n)$ remains in a bounded set of $\cap _{i=1}^NL^{q_i^-}(0,T;W_0^{1,q_i^-}(\Omega ))$ where the $q_i(\cdot )$ defined as in (18) and from Lemma 9, the sequence $(\partial _tu_n)$ remains in a bounded set of the space

$$\begin{aligned} L^1(0,T;(W^{1,{r}'}(\Omega ))')+L^1(Q_T)\hookrightarrow L^1(0,T;W^{-1,s}(\Omega ))+L^1(Q_T) \end{aligned}$$

for all $s<\min \{N/(N-1),r\}$. Therefore, $(\partial _tu_n)$ is bounded in $L^1(0,T;W^{-1,s}(\Omega ))+L^1(Q_T)$.

Now, we can use Corollary 4 in [12], we obtain that

$$\begin{aligned} u_n \quad \text{ is } \text{ relatively } \text{ compact } \text{ in } \quad L^1(Q_T). \end{aligned}$$

This implies that we can extract a subsequence (denote again by $(u_n)$) such that

$$\begin{aligned} u_n\rightarrow u\quad \quad \text{ a.e } \text{ on } Q_T. \end{aligned}$$

(48)

Lemma 13

([8]) Let $a_i$ be a function satisfying (2)-(4) and let F satisfy (6)-(7). Then

$$\begin{aligned} F(t,x,u_n)\rightarrow F(t,x,u) \quad \text{ strongly } \text{ in } \quad L^1(0,T;L^1(\Omega )). \end{aligned}$$

Now, using Lemma 8 and adapting the approach of [10], there exists a subsequence (still denoted $u_n$) such that

$$\begin{aligned} Du_n\rightarrow Du\quad \text{ a.e } \text{ on } Q_T. \end{aligned}$$

(49)

From (48), (49), Lemma 7, and assumption (3), we get

$$\begin{aligned} b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\rightarrow b_i(t,x,u)a_i(t,x,Du)\quad \text{ strongly } \text{ in } L^{\kappa _i(.)}(Q_T), \end{aligned}$$

(50)

for all continuous function $\kappa _i$ on $Q_T$ such that

$$\begin{aligned} 1<\kappa _i(\cdot )<\frac{mp_i(\cdot )}{(p_i(\cdot )-1){\overline{p}}(\cdot )} \left( \frac{(N+1){\overline{p}}(\cdot )-N(1+\sigma )}{N+1-(1+\sigma )(m-1)}\right) . \end{aligned}$$

This is possible because since we have the upper bound in (16). Using (48), Lemma (13), and (50), we can easily pass to the limit in (24). This proves Theorem (3).

4.4 Proof of Theorem 4

In order to prove this Theorem, we modify the proof of Theorem 3. It’s sufficient to replace only (50) with the following

$$\begin{aligned} b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\rightarrow b_i(t,x,u)a_i(t,x,Du)\quad \text{ strongly } \text{ in } L^{\tau _i(.)}(Q_T), \end{aligned}$$

(51)

for all continuous function $\tau _i$ on $Q_T$ such that

$$\begin{aligned} 1<\tau _i(\cdot )<\frac{m(\cdot ) p_i(\cdot )s_+(\cdot )}{(1+s_+(\cdot ) +\sigma (\cdot ))(p_i(\cdot )-1)}. \end{aligned}$$

This is possible because we have (20). Thus by (51) and Lemma 13, we can deduce that the limit function u is a weak solution of (1) possessing the regularity stated in (22). This proves Theorem 4.

4.5 Proof of Theorem 5

In the same way of the proof of Theorem 4 we have by (3) and Lemma 11 that

$$\begin{aligned} b_i(t,x,T_n(u_{n}))a_i(t,x,Du_{n})\rightharpoonup b_i(t,x,u)a_i(t,x,Du)\quad \text{ weakly } \text{ in } L^{p'_i(.)}(Q_T), \end{aligned}$$

therefore, we can easily passe to the limit in (24). So the theorem is proved.