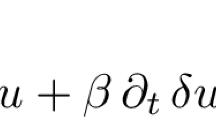On the longtime behavior of a viscous Cahn–Hilliard system with convection and dynamic boundary conditions

Abstract

In this paper, we study the longtime asymptotic behavior of a phase separation process occurring in a three-dimensional domain containing a fluid flow of given velocity. This process is modeled by a viscous convective Cahn–Hilliard system, which consists of two nonlinearly coupled second-order partial differential equations for the unknown quantities, the chemical potential and an order parameter representing the scaled density of one of the phases. In contrast to other contributions, in which zero Neumann boundary conditions were assumed for both the chemical potential and the order parameter, we consider the case of dynamic boundary conditions, which model the situation when another phase transition takes place on the boundary. The phase transition processes in the bulk and on the boundary are driven by free energy functionals that may be nondifferentiable and have derivatives only in the sense of (possibly set-valued) subdifferentials. For the resulting initial-boundary value system of Cahn–Hilliard type, general well-posedness results have been established in a recent contribution by the same authors. In the present paper, we investigate the asymptotic behavior of the solutions as times approaches infinity. More precisely, we study the $\omega$-limit (in a suitable topology) of every solution trajectory. Under the assumptions that the viscosity coefficients are strictly positive and that at least one of the underlying free energies is differentiable, we prove that the $\omega$-limit is meaningful and that all of its elements are solutions to the corresponding stationary system, where the component representing the chemical potential is a constant.

1 Introduction

The recent paper [16] addresses an initial-boundary value problem for the Cahn–Hilliard system with convection

$$\begin{aligned} \partial _{t}\rho + \nabla \rho \cdot u - \Delta \mu = 0 \quad {\text{and}}\quad \tau _\Omega \partial _{t}\rho - \Delta \rho + f'(\rho ) = \mu \qquad \text{in }Q_T:=\Omega \times (0,T), \end{aligned}$$

(1)

in the unknowns $\rho$, the order parameter, and $\mu$, the chemical potential. In the above equations, $\tau _\Omega$ is a nonnegative constant, $f'$ is the derivative of a double-well potential f, and u is a given velocity field.

Typical and significant examples of f are the so-called classical regular potential, the logarithmic double-well potential, and the double obstacle potential, which are given by

$$\begin{aligned} f_{reg}(r) := \frac{1}{4} \, (r^2-1)^2, \quad r \in {\mathbb {R}},\end{aligned}$$

(2)

$$\begin{aligned} f_{log}(r) := ( (1+r)\ln (1+r)+(1-r)\ln (1-r)) - c_1 r^2, \quad r \in (-1,1),\end{aligned}$$

(3)

$$\begin{aligned} f_{2obs}(r) := c_2 {(1 - r^2)}\quad {\text{if } |r|\le 1}\qquad \text{and}\qquad f_{2obs}(r) := +\infty \quad {\text{if } |r|>1}, \end{aligned}$$

(4)

where the constants in (3) and (4) satisfy $c_1>1$ and $c_2>0$, so that $f_{log}$ and $f_{2obs}$ are nonconvex. In cases like (4), one has to split f into a nondifferentiable convex part (the indicator function of $[-1,1]$ in the present example) and a smooth perturbation. Accordingly, one has to replace the derivative of the convex part by the subdifferential and interpret the second identity in (1) as a differential inclusion.

As far as the conditions on the boundary $\Gamma :=\partial \Omega$ are concerned, instead of the classical homogeneous Neumann boundary conditions, the dynamic boundary condition for both $\mu$ and $\rho$ are considered, namely,

$$\begin{aligned}&\partial _{t}\rho _\Gamma + \partial _{n}\mu - \Delta _\Gamma \mu _\Gamma = 0 \quad \text{and} \\ &\qquad \tau _\Gamma \partial _{t}\rho _\Gamma + \partial _{n}\rho - \Delta _\Gamma \rho _\Gamma + f_\Gamma '(\rho _\Gamma ) = \mu _\Gamma \quad \text{on } \Sigma _{T}:=\Gamma \times (0,T), \end{aligned}$$

(5)

where ${\mu _\Gamma =\mu _{|\Sigma _T}}$, ${\rho _\Gamma =\rho _{|\Sigma _T}}$, are the traces of $\mu$ and $\rho$, respectively, $\partial _{n}$ and $\Delta _\Gamma$ denote the outward normal derivative and the Laplace–Beltrami operator on $\Gamma$, $\tau _\Gamma$ is a nonnegative constant, and $f_\Gamma '$ is the derivative of another potential $f_\Gamma$.

The equations in (1) aim to describe a class of evolution phenomena with phase separation and fluid convection, in which the convection is represented by the term $\nabla \rho \cdot u$ for a known velocity vector u. Regarding this system of partial differential equations, some boundary conditions are usually prescribed and the standard approach leads to the no-flux conditions

$$\begin{aligned} \partial _{n}\mu = 0, \quad \partial _{n}\rho = 0 \qquad \text{on }\Sigma _T, \end{aligned}$$

for both $\mu$ and $\rho$. On the contrary, as already announced, here we are interested to handle the dynamic boundary conditions (5), which set a Cahn–Hilliard type system also on the boundary. The two potentials $f= \hat{\beta }+\hat{\pi }$ in the bulk and $f_\Gamma = \hat{\beta }_\Gamma + \hat{\pi }_\Gamma$ on the boundary are both the sum of a convex and lower semicontinuous part and a (possibly concave) perturbation; they are not completely independent but related by a suitable growth condition. Within the framework given by (1) and (5), initial conditions should be prescribed for $\rho$ both in the bulk and on the boundary.

All in all, the resulting initial and boundary value problem reads

$$\begin{aligned} \partial _{t}\rho + \nabla \rho \cdot u - \Delta \mu = 0 \quad \text{in } Q_T, \end{aligned}$$

(6)

$$\begin{aligned} \tau _\Omega \partial _{t}\rho - \Delta \rho + \beta (\rho ) + \pi (\rho ) \ni \mu \quad \text{in } Q_T, \end{aligned}$$

(7)

$$\begin{aligned} \rho _\Gamma = \rho _{|_{\Sigma _T}}, \quad \mu _\Gamma = \mu _{|_{\Sigma _T}} \quad {\text{and}}\quad \partial _{t}\rho _\Gamma + \partial _{n}\mu - \Delta _\Gamma \mu _\Gamma = 0 \qquad \text{on } \Sigma _T, \end{aligned}$$

(8)

$$\begin{aligned} \tau _\Gamma \partial _{t}\rho _\Gamma + \partial _{n}\rho - \Delta _\Gamma \rho _\Gamma + \beta _\Gamma (\rho _\Gamma ) + \pi _\Gamma (\rho _\Gamma ) \ni \mu _\Gamma \quad \text{on } \Sigma _T, \end{aligned}$$

(9)

$$\begin{aligned} \rho (0) = \rho _0\quad \text{in } \Omega \qquad \text{and}\qquad \rho _\Gamma (0) = {\rho _0}_{|\Gamma }\quad \text{on } \Gamma . \end{aligned}$$

(10)

The paper [16] is devoted to the study of the initial-boundary value problem (6)–(10). Under suitable assumptions and compatibility conditions on the potentials, well-posedness and regularity results are proved.

The aim of the present paper is investigating the longtime behavior. More precisely, we study the $\omega$-limit (in a suitable topology) of every trajectory $(\rho ,\rho _\Gamma )$. Under the additional assumptions that the viscosity coefficients $\tau _\Omega$ and $\tau _\Gamma$ are strictly positive and that at least one of the potentials f and $f_\Gamma$ is differentiable, we prove that the $\omega$-limit is meaningful and that every element $(\rho ^\omega ,\rho _\Gamma ^\omega )$ of it is a stationary solution $(\rho ^s,\rho _\Gamma ^s)$ of the system for $(\rho ,\rho _\Gamma )$ with some constant value $\mu ^s$ of the chemical potential.

Let us now review some related literature. About Cahn–Hilliard problems, we quote the pioneering contributions [1, 4, 20, 21, 35] and observe that for this class of evolution processes it turns out that the phases do not diffuse, but they separately concentrate and form the so-called spinodal decomposition. A discussion on the modeling aspects of phase separation, spinodal decomposition and mobility of atoms between cells can be found in [7, 12, 22, 31, 36]). Up to our knowledge, in the case of a pure Cahn–Hilliard system, that is, with $\tau _\Omega =\tau _\Gamma =0$, and without convective term ($u=0$), the problem (6)–(10) has been introduced by Gal [24] and formulated by Goldstein, Miranville and Schimperna [29]. It has been studied from various viewpoints in other contributions (see [6,7,8, 25, 29, 30]). In the case of general potentials, existence, uniqueness and regularity of the weak solution have been shown in [11] (see also [23] for an optimal control problem) by using an abstract approach. In the problem considered by Gal [24] the Laplace–Beltrami term was missing in the third condition in (8) (thus, the boundary condition was of Wentzell type); on the other hand, the presence of the term $- \Delta _\Gamma \mu _\Gamma$ actually enhances the dissipation mechanism in (6)–(10) and is helpful in order to recover a better regularity for the solution. However, it is worth to point out that in [16] the presence of the convective term $\nabla \rho \cdot u$ gives rise to further complications in the analysis.

Some class of Cahn–Hilliard systems, possibly including dynamic boundary conditions, have collected an increasing interest in recent years: we can quote [9, 32, 34, 37, 38, 40] among other contributions. In case of no convective term in (6), and assuming the homogeneous boundary condition $\partial _{n}\mu =0$ and the condition (9) with $\tau _\Gamma >0$ and $\mu _\Gamma$ as a given datum, the problem has been first addressed in [26]: the well-posedness and the large time behavior of solutions have been studied for regular potentials f and $f_\Gamma$, as well as for various singular potentials like the ones in (3) and (4). One can see [26, 27]: in these two papers, the authors were able to overcome the difficulties due to singularities using a set of assumptions for f and $f_\Gamma$ that gives the role of the dominating potential to f and entails some technical difficulties. The subsequent papers [13,14,15] follow a different approach, which was firstly considered in [5] and [19] to investigate the Allen–Cahn equation with dynamic boundary conditions. This approach consists in letting $f_\Gamma$ be the leading potential with respect to f: by this, the analysis turns out to be simpler. In particular, [13] contains many results about existence, uniqueness and regularity of solutions for general potentials that include (2)–(3), and are valid for both the viscous and pure cases, i.e., by assuming just $\tau _\Omega \ge 0$. The paper [10] deals with the well-posedness of the same system, but in which also an additional mass constraint on the boundary is imposed. The recent contribution [33] deals with the physical derivation of some Cahn–Hilliard systems in the bulk and on the boundary, arriving at the study of a model in which the two chemical potentials are completely independent. Finally, let us point out that the optimal control problems for (6)–(10) with the velocity as the control is thoroughly discussed in [17, 18].

The present paper is organized as follows. In the next section, we list our assumptions and notations, recall the properties already known and state our result on the longtime behavior. The last section is devoted to the corresponding proof.

2 Statement of the problem and results

In this section, we state precise assumptions and notations and present our results. First of all, the set $\Omega \subset {\mathbb {R}}^3$ is assumed to be bounded, connected and smooth. As in the introduction, $\nu$ is the outward unit normal vector field on $\Gamma :=\partial \Omega$, and $\partial _{n}$ and $\Delta _\Gamma$ stand for the corresponding normal derivative and the Laplace–Beltrami operator, respectively. Furthermore, we denote by $\nabla _\Gamma$ the surface gradient and write $|\Omega |$ and $|\Gamma |$ for the volume of $\Omega$ and the area of $\Gamma$, respectively. Moreover, we widely use the notations

$$\begin{aligned} Q_t := \Omega \times (0,T) \quad {\text{and}}\quad \Sigma _t := \Gamma \times (0,T) \qquad \text{for } 0<t\le +\infty . \end{aligned}$$

(11)

Next, if X is a Banach space, then $\Vert \,\cdot \,\Vert _X$ denotes both its norm and the norm of $X^3$, and the symbols $X^*$ and $\langle \,\cdot \,,\,\cdot \,\rangle _X$ stand for the dual space of X and the duality pairing between $X^*$ and X. The only exception from the convention for the norms is given by the Lebesgue spaces $L^p$, for $1\le p\le \infty$, whose norms will be denoted by $\Vert \,\cdot \,\Vert _p$. Furthermore, we put

$$\begin{aligned}H := L^{2}(\Omega ), \quad V := H^{1}(\Omega )\quad {\text{and}}\quad W := H^{2}(\Omega ), \end{aligned}$$

(12)

$$\begin{aligned}&H_\Gamma := L^{2}(\Gamma ), \quad V_\Gamma := H^{1}(\Gamma )\quad {\text{and}}\quad W_\Gamma := H^{2}(\Gamma ), \end{aligned}$$

(13)

$$\begin{aligned}&{{\mathcal{H}}} := H \times H_\Gamma , \quad {{\mathcal {V}}} := \{(v,v_\Gamma ) \in V \times V_\Gamma : \ v_\Gamma = v_{|\Gamma } \} \\ &\quad {\text{and}}\quad {{\mathcal{W}}} := ( W \times W_\Gamma ) \cap {{\mathcal {V}}}. \end{aligned}$$

(14)

In the following, we work in the framework of the Hilbert triplet $({{\mathcal {V}}},{{\mathcal{H}}},{\mathcal {V}}^{*})$. Thus, we have

$$\begin{aligned} \langle (g,g_\Gamma ),(v,v_\Gamma ) \rangle _{{\mathcal {V}}}=\int _{\Omega }gv+\int _\Gamma g_\Gamma v_\Gamma \quad \text{for every } (g,g_\Gamma )\in {{\mathcal{H}}} \text{ and } (v,v_\Gamma )\in {{\mathcal {V}}}. \end{aligned}$$

Now, we list our assumptions. For the structure of our system, we postulate the following properties, which are slightly stronger than those requested in [16]:

$$\begin{aligned} \tau _\Omega \text{ and } \tau _\Gamma \text{ are strictly positive real numbers}. \end{aligned}$$

(15)

$$\begin{aligned} \hat{\beta },\, \hat{\beta }_\Gamma : {\mathbb {R}}\rightarrow [0,+\infty ] \quad \text{are convex}, \text{proper}, \text{and l.s.c.}, \text{with }\hat{\beta }(0) = \hat{\beta }_\Gamma (0) = 0. \end{aligned}$$

(16)

$$\begin{aligned} \hat{\pi },\, \hat{\pi }_\Gamma : {\mathbb {R}}\rightarrow {\mathbb {R}}\quad \text{are of class } C^2 \text{ with Lipschitz continuous first derivatives}. \end{aligned}$$

(17)

$$\begin{aligned} \text{The functions } f:=\hat{\beta }+\hat{\pi }\text{ and } f_\Gamma :=\hat{\beta }_\Gamma +\hat{\pi }_\Gamma \text{ are bounded from below}. \end{aligned}$$

(18)

Thus, in contrast to [16], the constants $\tau _\Omega$ and $\tau _\Gamma$ are strictly positive, here, and (18) holds in addition. However, we remark that this assumption is very reasonable and fulfilled by all of the potentials (2)–(4). We set, for convenience,

$$\begin{aligned} \beta := \partial \hat{\beta }, \quad \beta _\Gamma := \partial \hat{\beta }_\Gamma , \quad \pi := \hat{\pi }', \quad {\text{and}}\quad \pi _\Gamma := \hat{\pi }_\Gamma ', \end{aligned}$$

(19)

and assume that, with some positive constants C and $\eta$,

$$\begin{aligned} D(\beta _\Gamma ) \subseteq D(\beta ) \quad {\text{and}}\quad |\beta ^\circ (r)| \le \eta |\beta _\Gamma ^\circ (r)| + C \qquad \text{for every } r\in D(\beta _\Gamma ). \end{aligned}$$

(20)

In (20), the symbols $D(\beta )$ and $D(\beta _\Gamma )$ denote the domains of $\beta$ and $\beta _\Gamma$, respectively. More generally, we use the notation $D({\mathcal{G}})$ for every maximal monotone graph ${\mathcal{G}}$ in ${\mathbb {R}}\times {\mathbb {R}}$, as well as for the associated maximal monotone operators induced on $L^2$ spaces. Moreover, for $r\in D({\mathcal{G}})$, ${\mathcal{G}}^\circ (r)$ stands for the element of ${\mathcal{G}}(r)$ having minimum modulus.

Remark 2.1

Notice that, physically speaking, the compatibility condition (20) means that the thermodynamic force driving the phase separation on the surface is stronger than the one in the bulk.

For the data, we make the following assumptions:

$$\begin{aligned} u \in (L^{2}(0,+\infty;\,L^{3}(\Omega )))^3 \quad \text{with }\partial _{t}u \in (L^{2}(0,+\infty ;\,L^{3/2}(\Omega )))^3. \end{aligned}$$

(21)

$$\begin{aligned} \text{div}\, u = 0 \quad \text{in } Q_\infty \qquad \text{and}\qquad u \cdot \nu = 0 \quad \text{on } \Sigma _\infty . \end{aligned}$$

(22)

$$\begin{aligned} (\rho _0,{\rho _0}_{|\Gamma }) \in {{\mathcal{W}}}, \quad \beta ^\circ (\rho _0) \in H \quad {\text{and}}\quad \beta _\Gamma ^\circ ({\rho _0}_{|\Gamma }) \in H_\Gamma . \end{aligned}$$

(23)

$$\begin{aligned} m_0:= \frac{ \int _{\Omega }\rho _0+ \int _\Gamma {\rho _0}_{|\Gamma }}{ |\Omega | + |\Gamma | } \quad \text{belongs to the interior of }D(\beta _\Gamma ). \end{aligned}$$

(24)

Since we are assuming (15) and (21)–(24), the regularity level required for the notion of solution on a finite time interval is higher than the one in [16]. Namely, a solution on (0, T) is a triple of pairs $((\mu ,\mu _\Gamma ),(\rho ,\rho _\Gamma ),(\zeta ,\zeta _\Gamma ))$ that satisfies

$$\begin{aligned}(\mu ,\mu _\Gamma )\in L^{\infty }(0,T;\,{\mathcal{W}}), \end{aligned}$$

(25)

$$\begin{aligned}(\rho ,\rho _\Gamma )\in W^{1,\infty }(0,T;\,{{\mathcal{H}}}) \cap H^{1}(0,T;\,{\mathcal {V}})\cap L^{\infty }(0,T;\,{\mathcal{W}}),\end{aligned}$$

(26)

$$\begin{aligned}(\zeta ,\zeta _\Gamma )\in L^{\infty }(0,T;\,{{\mathcal{H}}}). \end{aligned}$$

(27)

However, we write $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ instead of $((\mu ,\mu _\Gamma ),(\rho ,\rho _\Gamma ),(\zeta ,\zeta _\Gamma ))$, in order to simplify the notation. As far as the problem under study is concerned, we still state it in a weak form as in [16], on account of the assumptions (22) on u. Namely, we require that

$$\begin{aligned}&\int _{\Omega }\partial _{t}\rho \, v + \int _\Gamma \partial _{t}\rho _\Gamma \, v_\Gamma - \int _{\Omega }\rho u \cdot \nabla v + \int _{\Omega }\nabla \mu \cdot \nabla v + \int _\Gamma \nabla _\Gamma \mu _\Gamma \cdot \nabla _\Gamma v_\Gamma = 0 \\ &\quad \text{a.e. in } (0,T)\ \text{and for every } (v,v_\Gamma )\in {{\mathcal {V}}}, \end{aligned}$$

(28)

$$\begin{aligned}&\tau _\Omega \int _{\Omega }\partial _{t}\rho \, v + \tau _\Gamma \int _\Gamma \partial _{t}\rho _\Gamma \, v_\Gamma + \int _{\Omega }\nabla \rho \cdot \nabla v + \int _\Gamma \nabla _\Gamma \rho _\Gamma \cdot \nabla _\Gamma v_\Gamma \\ &\quad + \int _{\Omega }( \zeta + \pi (\rho ) ) v + \int _\Gamma ( \zeta _\Gamma + \pi _\Gamma (\rho _\Gamma )) v_\Gamma = \int _{\Omega }\mu v + \int _\Gamma \mu _\Gamma v_\Gamma \\&\qquad \text{a.e. in }(0,T)\ \text{and for every } (v,v_\Gamma )\in {{\mathcal {V}}}, \end{aligned}$$

(29)

$$\begin{aligned}\zeta \in \beta (\rho ) \quad \text{a.e. in }Q_T\qquad \text{and}\qquad \zeta _\Gamma \in \beta _\Gamma (\rho _\Gamma ) \quad \text{a.e. on }\Sigma _{T}, \end{aligned}$$

(30)

$$\begin{aligned}\rho (0) = \rho _0\quad \text{a.e. in }\Omega . \end{aligned}$$

(31)

However, every solution also satisfies the boundary value problem presented in the introduction. The basic well-posedness and regularity results are given by [16, Thms. 2.3 and 2.6]. We collect them in the following

Theorem 2.2

Assume (15)–(20) for the structure and (21)–(24) for the data, and let $T\in (0,+\infty ).$ Then problem (28)–(31) has at least one solution $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ satisfying (25)–(27). Moreover, the solution is unique if at least one of the operators $\beta$ and $\beta _\Gamma$ is single-valued.

We obviously deduce the following consequence:

Corollary 2.3

In addition to (15)–(20), assume that at least one of the operators $\beta$ and $\beta _\Gamma$ is single-valued. Moreover, assume (21)–(24) for the data. Then there exists a unique 6-tuple $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ defined on $(0,+\infty )$ that fulfils (25)–(27) and solves (28)–(31) for every $T\in (0,+\infty ).$

At this point, given a solution $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$, our aim is investigating its longtime behavior, namely, the $\omega$-limit (which we simply term $\omega$ for brevity) of the component $(\rho ,\rho _\Gamma )$. We notice that the property (26) holds for every $T\in (0,+\infty )$, which implies that $(\rho ,\rho _\Gamma )$ belongs to $C^{0}([0,+\infty );\,{\mathcal {V}})$. Hence, the next definition is meaningful. We set

$$\begin{aligned}&\omega := \{(\rho ^\omega ,\rho _\Gamma ^\omega )=\lim _{n\rightarrow \infty }(\rho ,\rho _\Gamma )(t_n) \quad \text{in the weak topology of } {{\mathcal {V}}} \\ &\quad \text{for some sequence }\{t_n\nearrow +\infty \}\}, \end{aligned}$$

(32)

and look for the relationship between $\omega$ and the set of stationary solutions to the system obtained from (28)–(30) by ignoring the convective term. Indeed, assumption (21) implies that

$$\begin{aligned} u \in (H^{1}(0,+\infty;\,L^{3/2}(\Omega )))^3, \end{aligned}$$

(33)

whence u(t) tends to zero strongly in $L^{3/2}(\Omega )$ as t tends to infinity. It is immediately seen from (28) that the components $\mu$ and $\mu _\Gamma$ of every stationary solution are constant functions and that the constant values they assume are the same. Therefore, by a stationary solution we mean a quadruplet $(\rho ^s,\rho _\Gamma ^s,\zeta ^s,\zeta _\Gamma ^s)$ satisfying for some $\mu ^s\in {\mathbb {R}}$ the conditions

$$\begin{aligned}(\rho ^s,\rho _\Gamma ^s)\in {{\mathcal {V}}} \quad {\text{and}}\quad (\zeta ,\zeta _\Gamma ^s)\in {{\mathcal{H}}}, \end{aligned}$$

(34)

$$\begin{aligned}&\int _{\Omega }\nabla \rho ^s\cdot \nabla v + \int _\Gamma \nabla _\Gamma \rho _\Gamma ^s\cdot \nabla _\Gamma v_\Gamma + \int _{\Omega }( \zeta ^s+ \pi (\rho ^s) ) v + \int _\Gamma ( \zeta _\Gamma ^s+ \pi _\Gamma (\rho _\Gamma ^s) ) v_\Gamma \\ &\quad = \int _{\Omega }\mu ^sv + \int _\Gamma \mu ^sv_\Gamma \quad \text{for every } (v,v_\Gamma )\in {{\mathcal {V}}}, \end{aligned}$$

(35)

$$\begin{aligned} \zeta ^s\in \beta (\rho ^s) \quad \text{a.e. in }\Omega \qquad \text{and}\qquad \zeta _\Gamma ^s\in \beta _\Gamma (\rho _\Gamma ^s) \quad \text{a.e. on }\Gamma . \end{aligned}$$

(36)

It is not difficult to show that (34)–(35) imply that the pair $(\rho ^s,\rho _\Gamma ^s)$ belongs to ${{\mathcal{W}}}$ and satisfies the boundary value problem

$$\begin{aligned} &- \Delta \rho ^s+ \zeta ^s+ \pi (\rho ^s) = \mu ^s\quad \text{a.e. in }\Omega , \\ &\partial _{n}\rho ^s- \Delta _\Gamma \rho _\Gamma ^s+ \zeta _\Gamma ^s+ \pi _\Gamma (\rho _\Gamma ^s) = \mu ^s\quad \text{a.e. on }\Gamma . \end{aligned}$$

Here is our result:

Theorem 2.4

Let the assumptions of Corollary 2.3 be satisfied, and let $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ be the unique global solution on $(0,+\infty ).$ Then the $\omega$-limit (32) is nonempty. Moreover, for every $(\rho ^\omega ,\rho _\Gamma ^\omega )\in \omega ,$ there exist $\mu ^s\in {\mathbb {R}}$ and a solution $(\rho ^s,\rho _\Gamma ^s,\zeta ^s,\zeta _\Gamma ^s)$ to (34)–(36) such that $(\rho ^\omega ,\rho _\Gamma ^\omega )=(\rho ^s,\rho _\Gamma ^s).$

3 Auxiliary material

The proof of Theorem 2.4 will be performed in the last section. Our argument needs some tools which we collect in the present section. In particular, we use the generalized mean value, the related spaces and the operator ${\mathcal{N}}$ which we introduce now. However, we proceed very shortly and refer to [16, Sect. 2] for further details. We set

$$\begin{aligned} {{\mathrm{mean}}}\,g^* := \frac{ \langle g^*,(1,1) \rangle _{{{\mathcal {V}}}} }{ |\Omega | + |\Gamma | } \quad \text{for } g^*\in {\mathcal {V}}^{\,*}\end{aligned}$$

(37)

and observe that

$$\begin{aligned} {\mathrm{mean}}(v,v_\Gamma ) = \frac{ \int _{\Omega }v + \int _\Gamma v_\Gamma }{ |\Omega | + |\Gamma | } \quad \text{if } g^*=(v,v_\Gamma )\in {{\mathcal{H}}}. \end{aligned}$$

(38)

Notice that the constant $m_0$ appearing in our assumption (24) is nothing but the mean value ${\mathrm{mean}}(\rho _0,{\rho _0}_{|\Gamma })$, and that taking $(v,v_\Gamma )=(|\Omega |+|\Gamma |)^{-1}(1,1)$ in (28) yields the conservation property for the component $(\rho ,\rho _\Gamma )$ of the solution,

$$\begin{aligned} \partial _{t}\ {\mathrm{mean}}(\rho ,\rho _\Gamma )= 0, \quad {\mathrm{whence}} \quad {\mathrm{mean}} (\rho ,\rho _\Gamma )(t) = m_0\qquad \text{for every } t\in [0,T]. \end{aligned}$$

(39)

We also stress that the function

$$\begin{aligned} {{\mathcal {V}}} \ni (v,v_\Gamma ) \mapsto \left( \Vert \nabla v \Vert _{H}^2 + \Vert \nabla _\Gamma v_\Gamma \Vert _{H_\Gamma}^2 + |{\mathrm{mean}}(v,v_\Gamma )|^2 \right)^{1/2} \end{aligned}$$

(40)

yields a Hilbert norm on ${{\mathcal {V}}}$ which is equivalent to the natural one. Now, we set

$$\begin{aligned} {\mathcal {V}}_{*0}:= \{ g^*\in {\mathcal {V}}^{\,*}: \ {\mathrm{mean}}\, g^* = 0 \}, \quad {{\mathcal{H}}}_0:= {{\mathcal{H}}} \cap {\mathcal {V}}_{*0}, \quad {\text{and}}\quad {\mathcal {V}}_0:= {{\mathcal {V}}} \cap {\mathcal {V}}_{*0}, \end{aligned}$$

(41)

and notice that the function

$$\begin{aligned} {\mathcal {V}}_0\ni (v,v_\Gamma ) \mapsto \Vert (v,v_\Gamma ) \Vert _{{\mathcal {V}}_0} := ( \Vert \nabla v \Vert _{H}^2 + \Vert \nabla _\Gamma v_\Gamma \Vert _{H_\Gamma}^2 )^{1/2} \end{aligned}$$

(42)

is a Hilbert norm on ${\mathcal {V}}_0$ which is equivalent to the usual one. Next, we define the operator ${\mathcal{N}}:{\mathcal {V}}_{*0}\rightarrow {\mathcal {V}}_0$ (which will be applied to ${\mathcal {V}}_{*0}$-valued functions as well) as follows. For every element $g^*\in {\mathcal {V}}_{*0}$,

$$\begin{aligned}&{\mathcal{N}}\ g^*=({\mathcal{N}}_\Omega g^*,{\mathcal{N}}_\Gamma g^*)\text{ is the unique pair } (\xi,\xi_\Gamma) \in {\mathcal {V}}_0\text{ such that} \\ &\int _{\Omega }\nabla \xi \cdot \nabla v + \int _\Gamma \nabla _\Gamma \xi _\Gamma \cdot \nabla _\Gamma v_\Gamma = \langle g^*, (v,v_\Gamma ) \rangle _{{\mathcal {V}}} \quad \text{for every } (v,v_\Gamma )\in {{\mathcal {V}}}. \end{aligned}$$

(43)

It turns out that ${\mathcal{N}}$ is well defined, linear, symmetric, and bijective. Therefore, if we set

$$\begin{aligned} \Vert g \Vert ^*_* := \Vert {\mathcal{N}}g^* \Vert _{{\mathcal {V}}_0}, \quad \text{for } g^*\in {\mathcal {V}}_{*0}, \end{aligned}$$

(44)

then we obtain a Hilbert norm on ${\mathcal {V}}_{*0}$ (equivalent to the norm induced by the norm of ${\mathcal {V}}^{\,*}$). Furthermore, we notice that

$$\begin{aligned} \langle \partial _{t}g^*, {\mathcal{N}}g^* \rangle _{{{\mathcal {V}}}} = \frac{1}{2} \, \frac{d}{dt} \, \Vert g^* \Vert _*^2 \quad \text{a.e. in }(0,T), \qquad \text{for every } g^* \in H^{1}(0,T;\,{\mathcal {V}}_{*0}). \end{aligned}$$

(45)

Finally, it is easy to see that ${\mathcal{N}}g^*$ belongs to ${{\mathcal{W}}}$ whenever $g^*\in {{\mathcal{H}}}_0$, and that

$$\begin{aligned} \Vert {\mathcal{N}}g^* \Vert _{{\mathcal{W}}} \le C_\Omega \Vert g^* \Vert _{{{\mathcal{H}}}}\quad \text{for every } g^*\in {{\mathcal{H}}}_0, \end{aligned}$$

(46)

where $C_\Omega$ depends only on $\Omega$.

In performing our estimates, we will repeatedly use the Young inequality

$$\begin{aligned} a\,b \le \delta \,a^2 + \frac{1}{4\delta } \, b^2 \quad \text{for all } a,b\in {\mathbb {R}}\text{ and } \delta >0, \end{aligned}$$

(47)

as well as Hölder’s inequality and the Sobolev inequality

$$\begin{aligned} \Vert v \Vert _p \le C_\Omega \Vert v \Vert _V \quad \text{for every } p\in [1,6] \text{ and } v\in V, \end{aligned}$$

(48)

which is related to the continuous embedding $V\subset L^p(\Omega )$ for $p\in [1,6]$ (since $\Omega$ is three-dimensional, bounded and smooth). In particular, by also using the equivalent norm (40) on ${{\mathcal {V}}}$, we have that

$$\begin{aligned} \Vert v \Vert _6^2 \le C_\Omega \left( \Vert \nabla v \Vert _{H}^2 + \Vert \nabla _\Gamma v_\Gamma \Vert _{H_\Gamma}^2 + |{\mathrm{mean}}(v,v_\Gamma )|^2 \right) \end{aligned}$$

(49)

for every $(v,v_\Gamma )\in {{\mathcal {V}}}$. In both (48) and (49), the constant $C_\Omega$ depends only on $\Omega$. Furthermore, we will owe to a well-known fact from interpolation theory. By [3, Thm. 5.2.1, p. 109], we have that

$$\begin{aligned} ( L^{3}(\Omega ), L^{3/2}(\Omega ))_{1/2,2} = L^{2}(\Omega ) \end{aligned},$$

where the interpolation can be understood also in the sense of the trace method (see [3, Sect. 3.12] for the equivalence between various interpolation methods). It follows that there hold the continuous embedding and the related inequality

$$\begin{aligned}&H^{1}(0,+\infty ;\,L^{3/2}(\Omega )) \cap L^{2}(0,+\infty ;\,L^{3}(\Omega )) \subset L^{\infty }(0,+\infty ;\,L^{2}(\Omega )), \\& \Vert u \Vert _{L^{\infty }(0,+\infty ;\,L^{2}(\Omega ))} \le C_\Omega \, \left( \Vert u \Vert _{L^{2}(0,+\infty ;\,L^{3}(\Omega ))} + \Vert \partial _{t}u \Vert _{L^{2}(0,+\infty ;\,L^{3/2}(\Omega ))} \right) \\ &\quad \text{for every } v\in H^{1}(0,+\infty ;\,L^{3/2}(\Omega ))\cap L^{2}(0,+\infty ;\,L^{3}(\Omega )), \end{aligned}$$

(50)

where $C_\Omega$ depends only on $\Omega$.

Finally, as far as constants are concerned, we employ the following general rule: the small-case symbol c stands for different constants which depend only on $\Omega$, the structure of our system and the norms of the data involved in the assumptions (21)–(24). A notation like $c_\delta$ (in particular, with $\delta =T$) allows the constant to depend on the positive parameter $\delta$, in addition. Hence, the meaning of c and $c_\delta$ may change from line to line and even within the same chain of inequalities. On the contrary, we mark the constants that we want to refer to by using a different notation (e.g., a capital letter).

4 Longtime behavior

This section is devoted to the proof of Theorem 2.4. Thus, we fix any global solution $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ once and for all. Our arguments relies on some global a priori estimates and on the study of the behavior of such a solution on intervals of a fixed length T whose endpoints tend to infinity.

To keep the paper at a reasonable length, we often proceed formally. However, we notice that the estimates to be obtained in this way can be performed rigorously by acting on the solution to a proper regularized or discrete problem. Indeed, the solution found in [16] was constructed in this way: first, a regularized $\varepsilon$-problem was introduced by replacing the graphs $\beta$ and $\beta _\Gamma$ by their Yosida regularizations $\beta _\varepsilon$ and $\beta _{\Gamma \!,\,\varepsilon }$. However, the same argument would work if $\beta _\varepsilon$ and $\beta _{\Gamma \!,\,\varepsilon }$ were smooth approximation of $\beta$ and $\beta _\Gamma$ with analogous boundedness and convergence properties (like the $C^\infty$ approximations introduced in [28, Sect. 3]). In order to solve such an approximating problem, a Faedo–Galerkin scheme depending on a parameter $n\in {\mathbb {N}}$ can be used. Its solution is smooth according to the smoothness of the nonlinearities that appear in the $\varepsilon$-problem. Then, the solution to the original problem is constructed by first letting n tend to infinity and then letting $\varepsilon$ tend to zero. Thus, our procedure would be completely rigorous if it were performed on one of the above approximating solutions. Indeed, the estimates established in this way would be uniform with respect to the parameters involved. We now start proving such global estimates.

First global estimate We write the Eqs. (28) and (29) at the time s and test them by $(\mu ,\mu _\Gamma )(s)\in {{\mathcal {V}}}$ and $\partial _{t}(\rho ,\rho _\Gamma )(s)\in {{\mathcal {V}}}$, respectively. Then, we integrate with respect to s over (0, t) with an arbitrary $t>0$, sum up and rearrange. We obtain

$$\begin{aligned}&\int _{Q_t}\partial _{t}\rho \, \mu + \int _{\Sigma _{t}}\partial _{t}\rho _\Gamma \, \mu _\Gamma + \int _{Q_t}|\nabla \mu |^2 + \int _{\Sigma _{t}}|\nabla _\Gamma \mu _\Gamma |^2 + \tau _\Omega \int _{Q_t}|\partial _{t}\rho |^2 + \tau _\Gamma \int _{\Sigma _{t}}|\partial _{t}\rho _\Gamma |^2 \\ &\qquad +\, \frac{1}{2} \int _{\Omega }|\nabla \rho (t)|^2 + \frac{1}{2} \int _\Gamma |\nabla _\Gamma \rho _\Gamma (t)|^2 + \int _{\Omega }f(\rho (t)) + \int _\Gamma f_\Gamma (\rho _\Gamma (t)) \\ &\quad = \int _{Q_t}\rho u \cdot \nabla \mu + \int _{Q_t}\mu \partial _{t}\rho + \int _{\Sigma _{t}}\mu _\Gamma \partial _{t}\rho _\Gamma \\ &\qquad +\, \frac{1}{2} \int _{\Omega }|\nabla \rho _0|^2 + \frac{1}{2} \int _\Gamma |\nabla _\Gamma {\rho _0}_{|\Gamma }|^2 + \int _{\Omega }f(\rho _0) + \int _\Gamma f_\Gamma ({\rho _0}_{|\Gamma }). \end{aligned}$$

Four integrals obviously cancel out, the ones on the left-hand side containing f and $f_\Gamma$ are bounded from below by (18), and the terms on the right-hand side involving the initial values are finite by (23). We deal with the convective term using the Young and Hölder inequalities, the Sobolev type inequality (49), and the conservation property (39). We have

$$\begin{aligned}&\int _{Q_t}\rho u \cdot \nabla \mu \le \frac{1}{2} \int _{Q_t}|\nabla \mu |^2 + \frac{1}{2} \int _0^t \Vert u(s) \Vert _3^2 \, \Vert \rho (s) \Vert _6^2 \, ds \\ &\quad \le \frac{1}{2} \int _{Q_t}|\nabla \mu |^2 + c \int _0^t \Vert u(s) \Vert _3^2 \, ( {\Vert \nabla \rho (s)\Vert _{H}^2 + \Vert \nabla _\Gamma \rho _\Gamma (s)\Vert _{H_\Gamma }^2} + m_0^2 ) \, ds. \end{aligned}$$

Since the function $s\mapsto \Vert u(s) \Vert _3^2$ belongs to $L^1(0,+\infty )$ by (21), we can apply the Gronwall lemma on $(0,+\infty )$ and obtain that

$$\begin{aligned}\int _{Q_\infty }|\nabla \mu |^2 + \int _{\Sigma _\infty }|\nabla _\Gamma \mu _\Gamma |^2 + \int _{Q_\infty }|\partial _{t}\rho |^2 + \int _{\Sigma _\infty }|\partial _{t}\rho _\Gamma |^2 < + \infty , \end{aligned}$$

(51)

$$\begin{aligned}f(\rho ) \in L^{\infty }(0,+\infty ;\,L^{1}(\Omega ))\quad {\text{and}}\quad f_\Gamma (\rho _\Gamma ) \in L^{\infty }(0,+\infty ;\,L^{1}(\Gamma )), \end{aligned}$$

(52)

as well as $(\nabla \rho ,\nabla _\Gamma \rho _\Gamma )\in (L^{\infty }(0,+\infty ;\,{\mathcal{H}}))^3$. From this, by accounting for the conservation property (39) once more, we conclude that

$$\begin{aligned} (\rho ,\rho _\Gamma )\in L^{\infty }(0,+\infty ;\,{\mathcal {V}}). \end{aligned}$$

(53)

Consequence By using the quadratic growth of $\hat{\pi }$ and $\hat{\pi }_\Gamma$ implied by the Lipschitz continuity of their derivatives, and combining with (52) with (53), we deduce that

$$\begin{aligned} \hat{\beta }(\rho ) \in L^{\infty }(0,+\infty ;\,L^{1}(\Omega ))\quad {\text{and}}\quad \hat{\beta }_\Gamma (\rho _\Gamma ) \in L^{\infty }(0,+\infty ;\,L^{1}(\Gamma )). \end{aligned}$$

(54)

Second global estimate We formally differentiate the Eqs. (28) and (29) with respect to time, where we argue as if $\beta$ and $\beta _\Gamma$ were smooth functions and write $\beta (\rho )$ and $\beta _\Gamma (\rho _\Gamma )$ instead of $\zeta$ and $\zeta _\Gamma$ (see (30)). We obtain that

$$\begin{aligned}&\int _{\Omega }\partial _{t}^2\rho \, v + \int _\Gamma \partial _{t}^2\rho _\Gamma \, v_\Gamma + \int _{\Omega }\nabla \partial _{t}\mu \cdot \nabla v + \int _\Gamma \nabla _\Gamma \partial _{t}\mu _\Gamma \cdot \nabla _\Gamma v_\Gamma \\ &\quad = \int _{\Omega }( \partial _{t}\rho \, u + \rho \partial _{t}u ) \cdot \nabla v \end{aligned}$$

(55)

$$\begin{aligned}&\tau _\Omega \int _{\Omega }\partial _{t}^2\rho \, v + \tau _\Gamma \int _\Gamma \partial _{t}^2\rho _\Gamma \, v_\Gamma + \int _{\Omega }\nabla \partial _{t}\rho \cdot \nabla v + \int _\Gamma \nabla _\Gamma \partial _{t}\rho _\Gamma \cdot \nabla _\Gamma v_\Gamma \\ &\qquad +\, \int _{\Omega }\beta '(\rho ) \partial _{t}\rho \, v + \int _\Gamma \beta _\Gamma '(\rho _\Gamma ) \partial _{t}\rho _\Gamma \, v_\Gamma \\ &\quad = \int _{\Omega }\partial _{t}\mu \, v + \int _\Gamma \partial _{t}\mu _\Gamma \, v_\Gamma - \int _{\Omega }\pi '(\rho ) \partial _{t}\rho \, v - \int _\Gamma \pi _\Gamma '(\rho _\Gamma ) \partial _{t}\rho _\Gamma \, v_\Gamma \end{aligned}$$

(56)

a.e. in $(0,+\infty )$ and for every $(v,v_\Gamma )\in {{\mathcal {V}}}$. By recalling that $\partial _{t}(\rho ,\rho _\Gamma )$ is ${\mathcal {V}}_0$-valued by (39), so that ${\mathcal{N}}\partial _{t}(\rho ,\rho _\Gamma )$ is well defined, we write the above equations at the time s and test them by ${\mathcal{N}}\partial _{t}(\rho ,\rho _\Gamma )(s)$ and $\partial _{t}(\rho ,\rho _\Gamma )(s)$, respectively. Then, we integrate with respect to s over (0, t) with an arbitrary $t>0$ and sum up. We have

$$\begin{aligned}&\int _0^t \langle \partial _{t}^2(\rho ,\rho _\Gamma )(s), {\mathcal{N}}\partial _{t}(\rho ,\rho _\Gamma )(s) \rangle _{{\mathcal {V}}} \, ds \\ &\qquad +\, \int _{Q_t}\nabla \partial _{t}\mu \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )) + \int _{\Sigma _{t}}\nabla _\Gamma \partial _{t}\mu _\Gamma \cdot \nabla _\Gamma {\mathcal{N}}_\Gamma (\partial _{t}(\rho ,\rho _\Gamma )) \\&\qquad +\, \frac{\tau _\Omega }{2} \int _{\Omega }|\partial _{t}\rho (t)|^2 + \frac{\tau _\Gamma }{2} \int _\Gamma |\partial _{t}\rho _\Gamma (t)|^2 + \int _{Q_t}|\nabla \partial _{t}\rho |^2 + \int _{\Sigma _{t}}|\nabla _\Gamma \partial _{t}\rho _\Gamma |^2 \\ &\qquad +\, \int _{Q_t}\beta '(\rho ) |\partial _{t}\rho |^2 + \int _{\Sigma _{t}}\beta _\Gamma '(\rho _\Gamma ) |\partial _{t}\rho _\Gamma |^2 \\&\quad = \int _{Q_t}( \partial _{t}\rho \, u + \rho \partial _{t}u ) \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma ))\, +\frac{\tau _\Omega }{2} \int _{\Omega }|\partial _{t}\rho (0)|^2 + \frac{\tau _\Gamma }{2} \int _\Gamma |\partial _{t}\rho _\Gamma (0)|^2 \\ &\qquad +\, \int _{Q_t}\partial _{t}\mu \, \partial _{t}\rho + \int _{\Sigma _{t}}\partial _{t}\mu _\Gamma \, \partial _{t}{\rho _\Gamma } - \int _{Q_t}\pi '(\rho ) |\partial _{t}\rho |^2 - \int _{\Sigma _{t}}\pi _\Gamma '(\rho _\Gamma ) |\partial _{t}\rho _\Gamma |^2. \end{aligned}$$

The integrals containing $\partial _{t}\mu$ and $\partial _{t}\mu _\Gamma$ cancel out by the definition (43) of ${\mathcal{N}}$ (with the choices $g^*=\partial _{t}(\rho ,\rho _\Gamma )(s)$ and $(v,v_\Gamma )=\partial _{t}(\mu ,\mu _\Gamma )(s)$), and the terms involving $\beta '$ and $\beta _\Gamma '$ are nonnegative. Moreover, the last two integrals on the right-hand side are bounded by (51) and the Lipschitz continuity of $\pi$ and $\pi _\Gamma$. Therefore, owing to (45) for the first term on the left-hand side, we deduce that

$$\begin{aligned}&\frac{1}{2} \, \Vert \partial _{t}(\rho ,\rho _\Gamma )(t) \Vert _*^2 + \frac{\tau _\Omega }{2} \int _{\Omega }|\partial _{t}\rho (t)|^2 + \frac{\tau _\Gamma }{2} \int _\Gamma |\partial _{t}\rho _\Gamma (t)|^2 + \int _{Q_t}|\nabla \partial _{t}\rho |^2 + \int _{\Sigma _{t}}|\nabla _\Gamma \partial _{t}\rho _\Gamma |^2 \\ &\quad \le \frac{1}{2} \, \Vert \partial _{t}(\rho ,\rho _\Gamma )(0) \Vert _*^2 + \frac{\tau _\Omega }{2} \int _{\Omega }|\partial _{t}\rho (0)|^2 + \frac{\tau _\Gamma }{2} \int _\Gamma |\partial _{t}\rho _\Gamma (0)|^2 \\ &\qquad +\, \int _{Q_t}\partial _{t}\rho \, u \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )) + \int _{Q_t}\rho \partial _{t}u \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )) + c. \end{aligned}$$

(57)

Thus, is suffices to obtain a bound for the ${{\mathcal{H}}}$-norm of $\partial _{t}(\rho ,\rho _\Gamma )(0)$ and to estimate the last two integrals. For the first aim, we write the Eqs. (28) and (29) at the time $t=0$, test them by $(\mu ,\mu _\Gamma )(0)$ and $\partial _{t}(\rho ,\rho _\Gamma )(0)$, respectively, and sum up. Then, we account for the regularity of $\rho _0$ ensured by (23) and integrate by parts the terms involving $\nabla \rho _0$ and $\nabla _\Gamma {\rho _0}_{|\Gamma }$. We obtain

$$\begin{aligned}&\int _{\Omega }\partial _{t}\rho (0) \, \mu (0) + \int _\Gamma \partial _{t}\rho _\Gamma (0) \, \mu _\Gamma (0) + \int _{\Omega }|\nabla \mu (0)|^2 + \int _\Gamma |\nabla _\Gamma \mu _\Gamma (0)|^2 \\ &\qquad +\, \tau _\Omega \int _{\Omega }|\partial _{t}\rho (0)|^2 + \tau _\Gamma \int _\Gamma |\partial _{t}\rho _\Gamma (0)|^2 - \int _{\Omega }\Delta \rho _0\, \partial _{t}\rho (0) - \int _\Gamma \Delta _\Gamma {\rho _0}_{|\Gamma }\, \partial _{t}\rho _\Gamma (0) \\ &\qquad +\, \int _{\Omega }(\beta + \pi )(\rho _0) \partial _{t}\rho (0) + \int _\Gamma (\beta _\Gamma + \pi _\Gamma )({\rho _0}_{|\Gamma }) \partial _{t}\rho _\Gamma (0) \\ &\quad = \int _{\Omega }\rho _0u(0) \cdot \nabla \mu (0) + \int _{\Omega }\mu (0) \partial _{t}\rho (0) + \int _\Gamma \mu _\Gamma (0) \partial _{t}\rho _\Gamma (0). \end{aligned}$$

Four integrals obviously cancel each other. Now, we rearrange and use the Young inequality and the Lipschitz continuity of $\pi$ and $\pi _\Gamma$. In view of the full (23), we infer that

$$\begin{aligned}&\int _{\Omega }|\nabla \mu (0)|^2 + \int _\Gamma |\nabla _\Gamma \mu _\Gamma (0)|^2 + \frac{\tau _\Omega }{2} \int _{\Omega }|\partial _{t}\rho (0)|^2 + \frac{\tau _\Gamma }{2} \int _\Gamma |\partial _{t}\rho _\Gamma (0)|^2 \\ &\quad \le c \left( \Vert (\rho _0,{\rho _0}_{|\Gamma }) \Vert _{{\mathcal{W}}}^2 + 1 + \Vert \beta (\rho _0) \Vert _H^2 + \Vert \beta _\Gamma ({\rho _0}_{|\Gamma }) \Vert _{H_\Gamma }^2 \right) + \int _{\Omega }\rho _0u(0) \cdot \nabla \mu (0) \\ &\quad \le c + \int _{\Omega }\rho _0u(0) \cdot \nabla \mu (0). \end{aligned}$$

In order to estimate the last integral, we use the Hölder and Young inequalities, the continuous embedding $W\subset L^{\infty }(\Omega )$, and the interpolation inequality (50), to conclude that

$$\begin{aligned}&\int _{\Omega }\rho _0u(0) \cdot \nabla \mu (0) \le \Vert \rho _0 \Vert _\infty \, { \Vert u(0) \Vert _2} \, \Vert \nabla \mu (0) \Vert _2 \\ &\quad \le \frac{1}{2} \int _{\Omega }|\nabla \mu (0)|^2 + c \, \Vert \rho _0 \Vert _W^2 \left( { \Vert u \Vert _{L^{2}(0,+\infty ;\,L^{3}(\Omega ))}^2 + \Vert \partial _{t}u \Vert _{L^{2}(0,+\infty ;\,L^{3/2}(\Omega ))}^2} \right) , \end{aligned}$$

and we observe that all of the last norms are finite by virtue of the assumptions (23) and (21) on $\rho _0$ and u. By combining this and the above inequality, we obtain the desired bound for the ${{\mathcal{H}}}$-norm of $\partial _{t}(\rho ,\rho _\Gamma )(0)$.

Finally, we estimate the last two integrals on the right-hand side of (57) by using the Hölder, Sobolev and Young inequalities (in particular (49)), the interpolation inequality (50), the conservation property (39), the regularity inequality (46) for ${\mathcal{N}}$, and the already established estimate (53). We have that

$$\begin{aligned}&\int _{Q_t}\partial _{t}\rho \, u \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )) \le \int _0^t \Vert \partial _{t}\rho (s) \Vert _4 \, \Vert u(s) \Vert _2 \, \Vert \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )(s)) \Vert _4 \, ds \\ &\quad \le c \, \Vert u \Vert _{L^{\infty }(0,+\infty ;\,H)} \int _0^t \Vert \partial _{t}\rho (s) \Vert _V \, \Vert {\mathcal{N}}(\partial _{t}(\rho ,\rho _\Gamma )(s)) \Vert _{{\mathcal{W}}} \, ds \\ &\quad \le \frac{1}{2} \, \left( \int _{Q_t}|\nabla \partial _{t}\rho |^2 + \int _{\Sigma _{t}}|\nabla _\Gamma \partial _{t}\rho _\Gamma |^2 \right) + c \int _0^t \Vert \partial _{t}(\rho ,\rho _\Gamma )(s) \Vert _{{{\mathcal{H}}}}^2 \, ds \\ &\quad \le \frac{1}{2} \, \left( \int _{Q_t}|\nabla \partial _{t}\rho |^2 + \int _{\Sigma _{t}}|\nabla _\Gamma \partial _{t}\rho _\Gamma |^2 \right) + c, \end{aligned}$$

as well as, with a similar argument,

$$\begin{aligned}&\int _{Q_t}\rho \partial _{t}u \cdot \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )) \le \int _0^t \Vert \rho (s) \Vert _6 \, \Vert \partial _{t}u(s) \Vert _{3/2} \, \Vert \nabla {\mathcal{N}}_\Omega (\partial _{t}(\rho ,\rho _\Gamma )(s)) \Vert _6 \, ds \\ &\quad \le c \, \Vert \rho \Vert _{L^{\infty }(0,+\infty ;\,V)} \, \Vert \partial _{t}u \Vert _{L^{2}(0,+\infty ;\,L^{3/2}(\Omega ))} \, \Vert \partial _{t}(\rho ,\rho _\Gamma ) \Vert _{L^{2}(0,+\infty ;\,{\mathcal{H}})} \le c . \end{aligned}$$

Coming back to (57) and taking these estimates into account, we conclude that

$$\begin{aligned} \partial _{t}(\rho ,\rho _\Gamma )\in L^{\infty }(0,+\infty ;\,{\mathcal{H}})\cap L^{2}(0,+\infty ;\,{\mathcal {V}}). \end{aligned}$$

(58)

Third global estimate Also in this step, we argue as if the graphs $\beta$ and $\beta _\Gamma$ were smooth functions (in particular, we write $\zeta =\beta (\rho )$ and $\zeta _\Gamma =\beta (\rho _\Gamma )$) and first notice that the inclusion $D(\beta _\Gamma )\subseteq D(\beta )$ (see (20)) and assumption (24) imply that

$$\begin{aligned} \beta (r) (r-m_0) \ge \delta _0 |\beta (r)| - C_0 \quad {\text{and}}\quad \beta _\Gamma (r) (r-m_0) \ge \delta _0 |\beta _\Gamma (r)| - C_0 \end{aligned}$$

(59)

for every r belonging to the respective domains, where $\delta _0$ and $C_0$ are some positive constants that depend only on $\beta$, $\beta _\Gamma$ and on the position of $m_0$ in the interior of $D(\beta _\Gamma )$ and of $D(\beta )$ (see, e.g., [26, p. 908]). Now, we recall the conservation property (39) and test (28) and (29) by ${\mathcal{N}}(\rho -m_0,\rho _\Gamma -m_0)$ and $(\rho -m_0,\rho _\Gamma -m_0)$, respectively. Then, we sum up without integrating with respect to time. We obtain that, almost everywhere in $(0,+\infty )$,

$$\begin{aligned}& \langle \partial _{t}(\rho ,\rho _\Gamma ), {\mathcal{N}}(\rho -m_0,\rho _\Gamma -m_0) \rangle _{{\mathcal {V}}} \\&\quad +\, \int _{\Omega }\nabla \mu \cdot \nabla {\mathcal{N}}_\Omega (\rho -m_0,\rho _\Gamma -m_0) + \int _\Gamma \nabla _\Gamma \mu _\Gamma \cdot \nabla _\Gamma {\mathcal{N}}_\Gamma (\rho -m_0,\rho _\Gamma -m_0) \\&\qquad +\, \tau _\Omega \int _{\Omega }\partial _{t}\rho \, (\rho -m_0) + \tau _\Gamma \int _\Gamma \partial _{t}\rho _\Gamma \, (\rho _\Gamma -m_0) + \int _{\Omega }|\nabla \rho |^2 + \int _\Gamma |\nabla _\Gamma \rho _\Gamma |^2 \\&\qquad +\, \int _{\Omega }\beta (\rho ) (\rho -m_0) + \int _\Gamma \beta _\Gamma (\rho _\Gamma ) (\rho _\Gamma -m_0) \\&\quad = \int _{\Omega }\rho u \cdot \nabla ({\mathcal{N}}_\Omega (\rho -\rho _0,\rho _\Gamma -{\rho _0}_{|\Gamma })) + \int _{\Omega }\mu (\rho -m_0) + \int _\Gamma \mu _\Gamma (\rho _\Gamma -m_0) \\&\qquad -\, \int _{\Omega }\pi (\rho ) (\rho -m_0) - \int _\Gamma \pi _\Gamma (\rho _\Gamma ) (\rho _\Gamma -m_0). \end{aligned}$$

All of the integrals involving $\mu$ and $\mu _\Gamma$ cancel out by (43). Now, we owe to (59), keep just the positive contributions on the left-hand side and move the other terms on the right-hand side. By also accounting for the Lipschitz continuity of $\pi$ and $\pi _\Gamma$, the Sobolev inequality related to the continuous embedding $V\subset L^{4}(\Omega )$, the interpolation inequality (50) on u, the regularity inequality (46) for ${\mathcal{N}}$, (53) and (58), we deduce that

$$\begin{aligned}&\int _{\Omega }|\nabla \rho |^2 + \int _\Gamma |\nabla _\Gamma \rho _\Gamma |^2 + \delta _0 \int _{\Omega }|\beta (\rho )| + \delta _0 \int _\Gamma |\beta _\Gamma (\rho _\Gamma )| \\&\quad \le \Vert \partial _{t}(\rho ,\rho _\Gamma ) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal {V}}_0^{\,*})} \, \Vert {\mathcal{N}}(\rho -m_0,\rho _\Gamma -m_0) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal {V}}_0)} \\&\qquad +\, c \, \Vert \partial _{t}(\rho ,\rho _\Gamma ) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{H}})} \, \Vert (\rho -m_0,\rho _\Gamma -m_0) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{H}})} \\&\qquad +\, c \, \Vert (\pi (\rho ),\pi _\Gamma (\rho _\Gamma )) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{H}})} \, \Vert (\rho -m_0,\rho _\Gamma -m_0) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{H}})} \\&\qquad +\, \Vert \rho \Vert _{L^{\infty }(0,+\infty ;\,L^{4}(\Omega ))} \, \Vert u \Vert _{L^{\infty }(0,+\infty ;\,L^{2}(\Omega ))} \, \Vert \nabla ({\mathcal{N}}_\Omega (\rho -\rho _0,\rho _\Gamma -{\rho _0}_{|\Gamma })) \Vert _{L^{\infty }(0,+\infty ;\,L^{4}(\Omega ))} \\&\quad \le c + c \, \Vert {\mathcal{N}}(\rho -\rho _0,\rho _\Gamma -{\rho _0}_{|\Gamma }) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{W}})}\\&\quad \le c + c \, \Vert (\rho -\rho _0,\rho _\Gamma -{\rho _0}_{|\Gamma }) \Vert _{L^{\infty }(0,+\infty ;\,{\mathcal{H}})} \le c . \end{aligned}$$

Since this holds a.e. in $(0,+\infty )$, we have (in particular) that

$$\begin{aligned} \zeta \in L^{\infty }(0,+\infty ;\,L^{1}(\Omega ))\quad {\text{and}}\quad \zeta _\Gamma \in L^{\infty }(0,+\infty ;\,L^{1}(\Gamma )). \end{aligned}$$

Now, we test (29) by (1, 1) and obtain a.e. in $(0,+\infty )$

$$\begin{aligned} (|\Omega |+|\Gamma |) {\mathrm{mean}}(\mu ,\mu _\Gamma )= \tau _\Omega \int _{\Omega }\partial _{t}\rho + \tau _\Gamma \int _\Gamma \partial _{t}\rho _\Gamma + \int _{\Omega }\zeta + \int _\Gamma \zeta _\Gamma + \int _{\Omega }\pi (\rho ) + \int _\Gamma \pi _\Gamma (\rho _\Gamma ). \end{aligned}$$

Thus, we infer that

$$\begin{aligned} {\mathrm{mean}}(\mu ,\mu _\Gamma )\in L^\infty (0,+\infty ). \end{aligned}$$

(60)

It was already clear from (53) that the $\omega$-limit $\omega$ is nonempty. Indeed, the continuous ${{\mathcal {V}}}$-valued function $(\rho ,\rho _\Gamma )$ is also bounded, so that there exists a sequence $t_n\nearrow +\infty$ such that the sequence $\{(\rho ,\rho _\Gamma )(t_n) \}$ is weakly convergent in ${{\mathcal {V}}}$. More precisely, any sequence of times that tends to infinity contains a subsequence of this type. Thus, it remains to prove the second part of the statement. Therefore, we fix an element $(\rho ^\omega ,\rho _\Gamma ^\omega )\in \omega$ and a corresponding sequence $\{t_n\}$ like in the definition (32). We also fix $T\in (0,+\infty )$ and set, for a.a. $t\in (0,T)$,

$$\begin{aligned}&\mu ^n(t) := \mu (t_n+t), \quad \rho ^n(t) := \rho (t_n+t), \quad \zeta ^n(t) := \zeta (t_n+t) \\&\mu _\Gamma ^n(t) := \mu _\Gamma (t_n+t), \quad \rho _\Gamma ^n(t) := \rho _\Gamma (t_n+t), \quad \zeta _\Gamma ^n(t) := \zeta _\Gamma (t_n+t) \\&u^n(t) := u(t_n+t) \end{aligned}$$

and notice that (21) and the interpolation inequality (50) applied to $u^n$ imply that

$$\begin{aligned} u^n\rightarrow 0 \quad \text{strongly in } L^{\infty }(0,T;\,L^{2}(\Omega )). \end{aligned}$$

(61)

Moreover, it is clear that the 6-tuple $(\mu ^n,\mu _\Gamma ^n,\rho ^n,\rho _\Gamma ^n,\zeta ^n,\zeta _\Gamma ^n)$ satisfies the regularity conditions (25)–(27) and the equations (28)–(30) with u replaced by $u^n$, as well as the initial condition $\rho ^n(0)=\rho (t_n)$. In particular, by construction, we have that

$$\begin{aligned} (\rho ^n,\rho _\Gamma ^n)(0) \rightarrow (\rho ^\omega ,\rho _\Gamma ^\omega )\quad \text{weakly in } {{\mathcal {V}}}. \end{aligned}$$

(62)

Furthermore, the global estimates already performed on $(\mu ,\mu _\Gamma ,\rho ,\rho _\Gamma ,\zeta ,\zeta _\Gamma )$ immediately imply some estimates on $(\mu ^n,\mu _\Gamma ^n,\rho ^n,\rho _\Gamma ^n,\zeta ^n,\zeta _\Gamma ^n)$ that are uniform with respect to n. Here is a list. From (53) and (58), we infer that

$$\begin{aligned} \Vert (\rho ^n,\rho _\Gamma ^n) \Vert _{H^{1}(0,T;\,{\mathcal{H}})\cap L^{\infty }(0,T;\,{\mathcal {V}})} \le c. \end{aligned}$$

(63)

By (51), we also deduce that

$$\begin{aligned}(\nabla \mu ^n,\nabla _\Gamma \mu _\Gamma ^n) \rightarrow 0 \quad \text{strongly in } (L^{2}(0,T;\,{\mathcal{H}}))^3 \end{aligned}$$

(64)

$$\begin{aligned}(\partial _{t}\rho ^n,\partial _{t}\rho _\Gamma ^n) \rightarrow 0 \quad \text{strongly in } L^{2}(0,T;\,{\mathcal{H}}). \end{aligned}$$

(65)

On the other hand, (60) yields a uniform estimate on the mean value ${\mathrm{mean}}(\mu ^n,\mu _\Gamma ^n)$. By combining this with (64), we conclude that

$$\begin{aligned} \Vert (\mu ^n,\mu _\Gamma ^n) \Vert _{L^{2}(0,T;\,{\mathcal {V}})} \le c_T. \end{aligned}$$

(66)

In the next steps, we perform further estimates that ensure some additional convergence properties for $(\mu ^n,\mu _\Gamma ^n,\rho ^n,\rho _\Gamma ^n,\zeta ^n,\zeta _\Gamma ^n)$ on the interval (0, T).

First auxiliary estimate Once again, we treat $\beta$ and $\beta _\Gamma$ as single-valued functions and write $\beta (\rho ^n)$ and $\beta _\Gamma (\rho ^n)$ in place of $\zeta ^n$ and $\zeta _\Gamma ^n$, respectively. We test (29), written for $(\mu ^n,\mu _\Gamma ^n,\rho ^n,\rho _\Gamma ^n,\zeta ^n,\zeta _\Gamma ^n)$ at the time s, by $(\beta (\rho ^n),\beta (\rho _\Gamma ^n))(s)\in {{\mathcal {V}}}$ and integrate over (0, t) with any $t\in (0,T)$. We have

$$\begin{aligned}&\frac{\tau _\Omega }{2} \int _{\Omega }\hat{\beta }(\rho ^n(t)) + \frac{\tau _\Gamma }{2} \int _\Gamma \hat{\beta }_\Gamma (\rho _\Gamma ^n(t)) + \int _{Q_t}\beta '(\rho ^n) |\nabla \rho ^n|^2 + \int _{\Sigma _{t}}\beta '(\rho ^n) |\nabla _\Gamma \rho _\Gamma ^n|^2 \\&\qquad +\, \int _{Q_t}|\beta (\rho ^n)|^2 + \int _{\Sigma _{t}}\beta _\Gamma (\rho _\Gamma ^n) \, \beta (\rho _\Gamma ^n) \\&\quad = \int _{Q_t}\bigl ( \mu ^n- \pi (\rho ^n) \bigr ) \, \beta (\rho ^n) + \int _{\Sigma _{t}}( \mu _\Gamma ^n- \pi _\Gamma (\rho _\Gamma ^n)) \, \beta (\rho _\Gamma ^n) \\&\qquad +\, \frac{\tau _\Omega }{2} \int _{\Omega }\hat{\beta }(\rho (t_n)) + \frac{\tau _\Gamma }{2} \int _\Gamma \hat{\beta }_\Gamma (\rho _\Gamma (t_n)). \end{aligned}$$

(67)

All of the integrals on the left-hand side are nonnegative but the last one, which we treat in the following way: we notice that (20), and the fact that $\beta$ and $\beta _\Gamma$ have the same sign by (16), imply that $\beta (r)\beta _\Gamma (r)\ge (2\eta )^{-1}\beta ^2(r)-c$ for all r. It follows that

$$\begin{aligned} \int _{\Sigma _{t}}\beta _\Gamma (\rho _\Gamma ^n) \, \beta (\rho _\Gamma ^n) \ge \frac{1}{2\eta } \int _{\Sigma _{t}}|\beta (\rho _\Gamma ^n)|^2 - c_T. \end{aligned}$$

Let us come to the right-hand side. The first integral can obviously be dealt with using the Young inequality. We treat the second one this way:

$$\begin{aligned}&{\int _{\Sigma _{t}}( \mu _\Gamma ^n- \pi _\Gamma (\rho _\Gamma ^n)) \, \beta (\rho _\Gamma ^n)} \\&\quad \le \frac{1}{4\eta } \int _{\Sigma _{t}}|\beta (\rho _\Gamma ^n)|^2 + c \int _{\Sigma _{t}}|\mu _\Gamma ^n|^2 {{}+ c \int _{\Sigma _{t}}(1 +|\rho _\Gamma ^n|^2)} \le \frac{1}{4\eta } \int _{\Sigma _{t}}|\beta (\rho _\Gamma ^n)|^2 + c, \end{aligned}$$

thanks to (66). Finally, the last two terms of (67) are bounded by (54). By combining all these inequalities, we derive that

$$\begin{aligned} \Vert \zeta ^n \Vert _{{L^{2}(0,T;\,H)}} \le c_T, \end{aligned}$$

(68)

as well as an estimate for $\Vert \beta (\rho _\Gamma ^n) \Vert _{L^{2}(0,T;\,H_\Gamma )}$ as a by-product.

Second auxiliary estimate We apply [16, Lem. 3.1] a.e. in $(0,+\infty )$ to (29), written for $(\mu ^n,\mu _\Gamma ^n,\rho ^n,\rho _\Gamma ^n,\zeta ^n,\zeta _\Gamma ^n)$ in the form

$$\begin{aligned}&\int _{\Omega }\nabla \rho ^n\cdot \nabla v + \int _\Gamma \nabla _\Gamma \rho _\Gamma ^n\cdot \nabla _\Gamma v_\Gamma + \int _\Gamma \beta _\Gamma (\rho _\Gamma ^n) v_\Gamma \\&\quad = \int _{\Omega }\mu ^nv + \int _\Gamma \mu _\Gamma ^nv_\Gamma - \tau _\Omega \int _{\Omega }\partial _{t}\rho ^n\, v - \tau _\Gamma \int _\Gamma \partial _{t}\rho _\Gamma ^n\, v_\Gamma \\&\qquad -\, \int _{\Omega }( \zeta ^n+ \pi (\rho ^n)) v - \int _\Gamma \pi _\Gamma (\rho _\Gamma ^n) v_\Gamma . \end{aligned}$$

We obtain, in particular, that

$$\begin{aligned} \Vert \beta _\Gamma (\rho _\Gamma ^n(t)) \Vert {_{H_\Gamma }} \le c \, \bigl ( \Vert (\mu ^n,\mu _\Gamma ^n)(t) \Vert _{{{\mathcal{H}}}} + { \Vert \partial _{t}(\rho ^n,\rho _\Gamma ^n)(t) \Vert _{{{\mathcal{H}}}}} + \Vert (\zeta ^n+\pi (\rho ^n))(t) \Vert _H \bigr ) \end{aligned}$$

for a.a. $t\in (0,+\infty )$, where c depends only on $\Omega$. By accounting for (63), (66) and (68), we conclude that

$$\begin{aligned} \Vert \zeta _\Gamma ^n \Vert _{L^{2}(0,T;\,H_\Gamma )} \le c_T. \end{aligned}$$

(69)

Limits We collect the estimates (63), (66), (68) and (69) and use standard weak and weak star compactness results. For a subsequence, still labeled by n, we have

$$\begin{aligned} (\rho ^n,\rho _\Gamma ^n)\rightarrow (\rho ^\infty ,\rho _\Gamma ^\infty )\quad \text{weakly star in } H^{1}(0,T;\,{{\mathcal{H}}})\cap L^{\infty }(0,T;\,{\mathcal {V}}), \end{aligned}$$

(70)

$$\begin{aligned} (\mu ^n,\mu _\Gamma ^n)\rightarrow (\mu ^\infty ,\mu _\Gamma ^\infty )\quad \text{weakly in } L^{2}(0,T;\,{\mathcal {V}}), \end{aligned}$$

(71)

$$\begin{aligned} (\zeta ^n,\zeta _\Gamma ^n)\rightarrow (\zeta ^\infty ,\zeta _\Gamma ^\infty )\quad \text{weakly in }L^{2}(0,T;\,{{\mathcal{H}}}). \end{aligned}$$

(72)

We now prove that $(\mu ^\infty ,\mu _\Gamma ^\infty ,\rho ^\infty ,\rho _\Gamma ^\infty ,\zeta ^\infty ,\zeta _\Gamma ^\infty )$ satisfies the integrated version of (28)–(29), where we read $u=0$, with time-dependent test functions $(v,v_\Gamma )\in L^{2}(0,T;\,{\mathcal {V}})$, and that (30) holds true as well. First of all, we notice that $\rho ^n$ converges to $\rho ^\infty$ weakly star in $L^{\infty }(0,T;\,L^{6}(\Omega ))$, by (70) and the continuous embedding $V\subset L^{6}(\Omega )$. Owing to (33), we see that $u^n$ tends to zero strongly in ${(}L^{\infty }(0,T;\,L^{3/2}(\Omega )){)^3}$ and deduce that $\rho ^nu^n$ converges to zero weakly star in ${(}L^{\infty }(0,T;\,L^{6/5}(\Omega )){)^3}$. Next, from (70) we derive the strong convergence

$$\begin{aligned} (\rho ^n,\rho _\Gamma ^n)\rightarrow (\rho ^\infty ,\rho _\Gamma ^\infty )\quad \text{strongly in } C^{0}([0,T];\,{\mathcal{H}}), \end{aligned}$$

(73)

which follows from the compact embedding ${{\mathcal {V}}}\subset {{\mathcal{H}}}$ and from applying, e.g., [39, Sect. 8, Cor. 4]. Then, $(\pi (\rho ^n),\pi _\Gamma (\rho _\Gamma ^n))$ converges to $(\pi (\rho ^\infty ),\pi _\Gamma (\rho _\Gamma ^\infty ))$ strongly in the same space, by Lipschitz continuity. This concludes the proofs that (28) and (29) hold for the limiting 6-tuple in an integrated form, which is equivalent to the pointwise formulation. In order to derive (30), i.e., $\zeta ^\infty \in \beta (\rho ^\infty )$ and $\zeta _\Gamma ^\infty \in \beta _\Gamma (\rho _\Gamma ^\infty )$, we combine the weak convergence (72) with the strong convergence (73) and apply, e.g., [2, Lemma 2.3, p. 38].

5 Conclusion

It remains to prove that the above limit leads to a stationary solution with the properties specified in the statement. To this end, we first derive that $(\rho ^\infty ,\rho _\Gamma ^\infty )$ belongs to $L^{2}(0,T;\,{\mathcal{W}})$ and solves the boundary value problem

$$\begin{aligned}&- \Delta \rho ^\infty + \zeta ^\infty + \pi (\rho ^\infty ) = \mu ^\infty \quad \text{a.e. in }Q_T, \end{aligned}$$

(74)

$$\begin{aligned}&\partial _{n}\rho ^\infty - \Delta _\Gamma \rho _\Gamma ^\infty + \zeta _\Gamma ^\infty + \pi _\Gamma (\rho _\Gamma ^\infty ) = \mu _\Gamma ^\infty \quad \text{a.e. on }\Sigma _{T}. \end{aligned}$$

(75)

From (65) and (70), we see that $\partial _{t}(\rho ^\infty ,\rho _\Gamma ^\infty )$ vanishes identically. Thus, we are dealing with a time-dependent elliptic problem in a variational form and can use the following well-known estimates from trace theory and from the theory of elliptic equations. For any v and $v_\Gamma$ that make the right-hand sides meaningful, we have that

$$\begin{aligned}& \Vert \partial _{n}v \Vert _{H^{-1/2}(\Gamma )} \le C_\Omega \left( \Vert v \Vert _{H^{1}(\Omega )} + \Vert \Delta v \Vert _{L^{2}(\Omega )} \right) , \end{aligned}$$

(76)

$$\begin{aligned}& \Vert \partial _{n}v \Vert _{L^{2}(\Gamma )} \le C_\Omega \left( \Vert v \Vert _{H^{3/2}(\Omega )} + \Vert \Delta v \Vert _{L^{2}(\Omega )} \right) , \end{aligned}$$

(77)

$$\begin{aligned}& \Vert v \Vert _{H^{2}(\Omega )} \le C_\Omega \left( \Vert v_{|\Gamma } \Vert _{H^{3/2}(\Gamma )} + \Vert \Delta v \Vert _{L^{2}(\Omega )} \right) , \end{aligned}$$

(78)

$$\begin{aligned}& \Vert v_\Gamma \Vert _{H^{2}(\Gamma )} \le C_\Omega \left( \Vert v_\Gamma \Vert _{H^{1}(\Gamma )} + \Vert \Delta _\Gamma v_\Gamma \Vert _{L^{2}(\Gamma )} \right) , \end{aligned}$$

(79)

$$\begin{aligned}& \Vert v_\Gamma \Vert _{H^{3/2}(\Gamma )} \le C_\Omega \left( \Vert v_\Gamma \Vert _{H^{1}(\Gamma )} + \Vert \Delta _\Gamma v_\Gamma \Vert _{H^{-1/2}(\Gamma )} \right) , \end{aligned}$$

(80)

where the positive constant $C_\Omega$ depends only on $\Omega$. By taking test functions (v, 0) with $v\in {H^1_0(\Omega )}$, we derive that (74) holds in the sense of distributions on $Q_T$. This implies that $\Delta \rho ^\infty \in L^{2}(0,T;\,H)$, so that $\partial _{n}\rho ^\infty$ is a well-defined element of $L^{2}(0,T;\,H^{-1/2}(\Gamma ))$ (see (76)) satisfying the integration–by–parts formula in a generalized sense. Coming back to (29) written for our limiting solution and arbitrary test functions $(v,v_\Gamma )\in {{\mathcal {V}}}$, we deduce that (75) holds in a generalized sense. From this, we infer that $\Delta _\Gamma \rho _\Gamma ^\infty \in L^{2}(0,T;\,H^{-1/2}(\Gamma ))$, so that $\rho _\Gamma ^\infty \in L^{2}(0,T;\,H^{3/2}(\Gamma ))$ (see (80)). It follows that $\rho ^\infty \in L^{2}(0,T;\,W)$ by (78). In particular, $\partial _{n}\rho ^\infty \in L^{2}(0,T;\,H_\Gamma )$ by (77) so that $\Delta _\Gamma \rho _\Gamma ^\infty \in L^{2}(0,T;\,H_\Gamma )$ and $\rho _\Gamma ^\infty \in L^{2}(0,T;\,W_\Gamma )$ by (79). Finally, as all of the ingredients are $L^2$ functions, it is also clear that equations (74)–(75) hold almost everywhere.

At this point, we are ready to conclude. Since $\partial _{t}(\rho ^\infty ,\rho _\Gamma ^\infty )$ vanishes and the same holds for $(\nabla \mu ^\infty ,\nabla _\Gamma \mu _\Gamma ^\infty )$ by (64), there exist $(\rho ^s,\rho _\Gamma ^s)\in {{\mathcal {V}}}$ and $\mu _\infty \in L^2(0,T)$ such that

$$\begin{aligned} (\rho ^\infty ,\rho _\Gamma ^\infty )(x,t) = (\rho ^s,\rho _\Gamma ^s)(x) \quad {\text{and}}\quad (\mu ^\infty ,\mu _\Gamma ^\infty )(x,t) = (\mu _\infty (t),\mu _\infty (t)) \qquad \text{for a.a. } (x,t)\in Q_T. \end{aligned}$$

We prove that $(\zeta ^\infty ,\zeta _\Gamma ^\infty )$ is time independent as well and that $\mu _\infty$ is a constant, by accounting for our assumptions on the graphs $\beta$ and $\beta _\Gamma$: at least one of them is single-valued. Assume first that $\beta$ is single-valued. Then $\zeta ^\infty =\beta (\rho ^\infty )$ is time independent and attains the value $\zeta ^s:=\beta (\rho ^s)$ at any time. From (74), it follows that $\mu ^\infty$ is time independent as well, so that the function $\mu _\infty$ is a constant that we term $\mu ^s$. Thus, the right-hand side of (75) is the same constant $\mu ^s$. As this does not depend on time, the same holds for ${\zeta _\Gamma ^\infty }$. Hence, it attains some value $\zeta _\Gamma ^s\in H_\Gamma$ a.e. in $(0,T)$. Assume now that $\beta _\Gamma$ is single-valued. Then, we first use (75) to derive that $\zeta _\Gamma ^\infty =\beta _\Gamma (\rho _\Gamma ^\infty )$ and $\mu _\Gamma ^\infty$ are time independent. In particular, ${\mu ^\infty }$ takes some constant value $\mu ^s$, so that $\zeta ^\infty$ is time independent, by comparison in (74). As in both cases (36) holds as a consequence of (30) for the limiting solution, the quadruplet $(\rho ^s,\rho _\Gamma ^s,\zeta ^s,\zeta _\Gamma ^s)$ is a stationary solution corresponding to the value $\mu ^s$ of the chemical potential. Finally, we prove that $(\rho ^s,\rho _\Gamma ^s)$ coincides with the given $(\rho ^\omega ,\rho _\Gamma ^\omega )$. Indeed, (70) implies weak convergence also in $C^{0}([0,T];\,{\mathcal{H}})$, whence

$$\begin{aligned} (\rho ^n,\rho _\Gamma ^n)(0) \rightarrow (\rho ^\infty ,\rho _\Gamma ^\infty )(0) = (\rho ^s,\rho _\Gamma ^s)\quad \text{weakly in }{{\mathcal{H}}}. \end{aligned}$$

By comparison with (62), we conclude that $(\rho ^s,\rho _\Gamma ^s)=(\rho ^\omega ,\rho _\Gamma ^\omega )$, and the proof is complete.