1 Introduction

Hydrological modeling is an effective procedure for understanding the hydrological process in a watershed and at the same time, it constitutes a tool for monitoring, planning and management of water resources (Rahmana et al. 2020; Tuo et al. 2016; Wellen et al. 2015). Rainfall is the main input parameter in rainfall–runoff simulation models. However, in arid and semi-arid zones, and particularly in developing countries, rainfall data are lacking due to the unavailability of rain gauges stations (Kenabatho et al. 2017; Lekula et al. 2018). Therefore, approaches such as remote sensing through the use of satellite data are a way to fill gaps in the recorded rainfall data. When it comes to downloading rainfall estimate data from satellite, there are several internet sources. These include among others, TRMM sensor package, famine early warning systems network rain fall estimation (FEWS-Net RFE), climate prediction center (CPC) morphing technique (CMORPH) and precipitation estimates from remotely sensed information using artificial neural networks (PERSIANN) (Lekula et al. 2018). However, a major problem arises regarding the reliability of the simulated precipitation compared to the observed one. In this context, several studies have focused on evaluating the accuracy of satellite rainfall data. The results were found to oscillation between satisfactory and unacceptable, depending on the study case. This suggests that corrections should be made to improve the quality of these results (Kawo et al. 2021; Khairul et al. 2018; Ma et al. 2019).

In this study, the main objective is to simulate the runoff in a watershed located between two countries: Algeria and Morocco. It is useful to specify that recorded data from the single pluviometric station and the monthly outflows in the Algerian part are quite well known, while those of the Moroccan part are completely unknown. It should be noted that one single rainfall station is not sufficient for the hydrological modeling. Therefore, the estimation of rainfall from satellite constitutes a solution as the recorded data can cover the entire watershed. In this context, several studies have indicated that hydrological modeling using TRMM data to estimate flows has given satisfactory performance (Meng et al. 2014; Wang et al. 2020; Soo et al. 2020). This encouraging result prompted us to investigate the same choice. It is worth specifying that the discharge forecast was made using the Zygos model.

2 Materials and Methods

2.1 Study Area

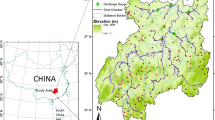
The watershed of Hammam Boughrara (Fig. 1), which has a semi-arid Mediterranean climate, is located between longitudes 1° 27′ W–2° 15′ W and latitudes 34° 19′ N–34° 59′ N in the northwestern of Algeria. It covers an area of 2921 km2, of which 57% is located in the Algerian territory and 43% in the Moroccan territory. With a capacity of 177 million m3, the Hammam Boughrara Dam was built in 1999 at the outlet of the watershed. This dam is fed by the confluence of three rivers, namely Wadi Mouilah, Wadi Mohguen and Wadi Tafna. Wadi Mouilah is the main tributary; it is 124 km long (Fig. 1). This Wadi is called Wadi Sly and Wadi Bounaim on the Moroccan side, and Wadi Mouilah in Algeria.

Fig. 1
figure 1

The study area map

Full size image

2.2 Data Used

In this study, the monthly observed data from the pluviometric station as well as the water inflows recorded at the Hammam Boughrara Dam were provided to us in Table 1. To complete the missing data, it was deemed necessary to use the monthly satellite values for TRMM 3B43V7 precipitation and GLDAS_NOAH025_M.V.2.1 for monthly evapotranspiration. All these data can be downloaded free of charge from the Giovanni website (https://giovanni.gsfc.nasa.gov/giovanni/). For this purpose, it is decided to consider nine satellite data points, spatially distributed to cover the entire watershed, as shown in Fig. 1.

Table 1 Data type and sources
Full size table

2.3 Bias Correction

The use of bias correction aims at optimizing as much as possible the consistency between the simulated precipitation and the observed precipitation. This action can have a positive impact in rainfall–runoff modeling. Note that in this work, consistency will be checked by making a comparison between the use of raw TRMM data and observed precipitation (Pobs). Several bias correction techniques, ranging from simple to complex, exist in the literature (Davis 1976; Ines and Hansen 2006; Kharin and Zwiers 2002; Schmidli et al. 2006). In the present study, two simple selected techniques are used. They are presented below.

2.3.1 Multiplicative Shift Technique (M)

This method (Ines and Hansen 2006) consists in applying a multiplicative factor to correct the satellite precipitation as follows:

$${\mathrm{TRMM}(M)}_{i}={\mathrm{TRMM}}_{i} \cdot M ,$$
(1)
$$\mathrm{with } \; M=\frac{\overline{\mathrm{Pobs}} }{\overline{\mathrm{TRMM}} } ,$$
(2)

where \(M\): multiplicative factor. i = 1:N, N: number of observations. \({\mathrm{TRMM}(M)}\): monthly TRMM corrected by multiplicative shift technique method. \(\overline{\mathrm{Pobs} }\) and \(\overline{\mathrm{TRMM} }\): monthly average of Pobs and TRMM.

2.3.2 Linear Regression (R)

The principle of this method (Kharin and Zwiers 2002) consists in studying the correlation between the TRMM with Pobs data. If the coherence between these two last types of data gives satisfactory results, then a correction should be made on the TRMM data using the linear regression line given by:

$${\mathrm{TRMM}(R)}_{ i}={a}_{0}+{\mathrm{TRMM}}_{i} \cdot {a}_{1},$$
(3)

where the coefficients \({a}_{0}\) and \({a}_{1}\) are:

$${a}_{1}=\frac{\mathrm{Cov}\left( {\mathrm{TRMM}}_{i},{\mathrm{Pobs}}_{i}\right)}{\mathrm{Var}\left({\mathrm{TRMM}}_{i}\right)} ,$$
(4)
$${a}_{0}=\overline{\mathrm{Pobs} }-{a}_{1} \cdot \overline{\mathrm{TRMM} } .$$
(5)

2.4 Hydrological Modeling

The Zygos model is a conceptual rainfall–runoff modeling tool which uses the reservoirs that schematically represent the soil and subsoil. This model is a simplified version of a semi-distributed simulation scheme that was developed at the National Technical University of Athens (NTUA) (Efstratiadis and Koutsoyiannis 2002; Rozos et al. 2004). It is similar to the Thornthwaite water balance model (Kozanis et al. 2010).The input and output parameters of the Zygos model are given in the following Table 2:

Table 2 Zygos model input and output parameters
Full size table

The Zygos model includes several parameters that allow defining the distribution of flows and the characteristics of each reservoir (Fig. 2). In addition, the Zygos model has a valve control system in open and closed mode, in order to truly represent the nature of the flows in each reservoir in the studied medium. These flows are the subsurface flow, the percolation, groundwater flow and the out flow catchment.

Fig. 2
figure 2

Schematic view of Zygos rainfall–runoff model (Kozanis et al. 2010) modified

Full size image

If the geological and hydrogeological environments are unknown, tests are carried out through the opening or closing of the functionalities of these flows in order to obtain the best optimization of the simulated runoff rate in comparison with the actual runoff rate. This option is done by iterating the eleven (11) variables of the calibration parameters (cp) until reaching the optimal value of NSE coefficient.

The model simulates the runoff as follows (Kozanis et al. 2010):

  • Runoff has four components

    $$\mathrm{Qc}=\mathrm{Qis}+\mathrm{Qss}+\mathrm{Qsub}+\mathrm{Qg },$$
    (6)

    where \(\mathrm{Qc}\): calculated runoff; \(\mathrm{Qis}\): runoff on impermeable surfaces; \(\mathrm{Qss}\): runoff on saturated surfaces; \(\mathrm{Qsub}\): subsurface flow; \(\mathrm{Qg}\): groundwater flow.

  • Surface hydrology processes

    Surface and subsurface flow simulations are performed using the following calculation steps:

    • \({\mathrm{Qis}}_{t}=k({P}_{t}-\mathrm{min}(\upvarepsilon {P}_{t},{E}_{{P}_{t}})),\)

    • \({S}_{\mathrm{int}}={S}_{t-1}+{P}_{t}-\mathrm{min}(\upvarepsilon {P}_{t},{E}_{{P}_{t}})-{\mathrm{Qsi}}_{t},\)

    • \({\mathrm{Qss}}_{t}=\mathrm{max}\left(0,{S}_{\mathrm{int}}-K\right),\)

    • \({S}_{\mathrm{int}}={S}_{\mathrm{int}}\left[1-\left(1-{e}^{-({E}_{{P}_{t}}-\mathrm{min}(\upvarepsilon {P}_{t},{E}_{{P}_{t}}))/K}\right)\right]-{\mathrm{Qss}}_{t},\)

    • \({\mathrm{Qsub}}_{t}=\mathrm{max}\left\{0,\uplambda \left({S}_{\mathrm{int}}-{H}_{1}\right)\right\},\)

    • \({S}_{\mathrm{int}}={S}_{\mathrm{int}}-{\mathrm{Qsub}}_{t},\)

    • \({\mathrm{Per}}_{t}=\mathrm{max}\left(0,\upmu {S}_{\mathrm{int}}\right),\)

    • \({S}_{\mathrm{int}}={S}_{\mathrm{int}}-{\mathrm{Per}}_{t},\) where \({P}_{t}\): monthly time series of precipitations; \({E}_{{P}_{t}}\): monthly time series of potential evapotranspiration; k \((\mathrm{cp})\): excess rain rate due to impermeable surfaces; \(\upvarepsilon (\mathrm{cp})\): rain rate available to have direct water evaporation from the soil; S: soil moisture storage; \({S}_{\mathrm{int}}(\mathrm{cp})\): initial soil moisture storage; K \((\mathrm{cp})\): maximum soil storage capacity; \(\uplambda (\mathrm{cp})\): discharge rate of the soil moisture tank, for production of the subsurface flow; \({H}_{1}(\mathrm{cp})\): soil moisture reservoir level for the production of subsurface flow; \({\mathrm{Per}}_{t}:\) percolation; \(\upmu \left(\mathrm{cp}\right):\) discharge rate of the soil moisture tank, for production of the percolation.

  • Groundwater hydrology processes

    Groundwater flow is performed using the following calculation steps:

    • \({R}_{\mathrm{int }}={R}_{t-1}+{\mathrm{Per}}_{t}-{\mathrm{Pum}}_{t},\)

    • \({\mathrm{Qg}}_{t}=\mathrm{max}\left\{0,\upxi \left({R}_{\mathrm{int}}-{H}_{2}\right)\right\},\)

    • \({R}_{\mathrm{int}}= {R}_{\mathrm{int}}-{\mathrm{Qg}}_{t},\)

    • \({Q}_{{\mathrm{out}}_{t}}={{\varphi }R}_{\mathrm{int}},\)

    • \({R}_{\mathrm{int}} = {R}_{\mathrm{int}}-{Q}_{{\mathrm{out}}_{t}},\) where R: groundwater storage; \({R}_{t-1} \left(\mathrm{cp}\right):\) Initial reserve of the groundwater; \({\mathrm{Pum}}_{t}\): volume of the water pumped from the aquifer; \(\upxi (\mathrm{cp})\): discharge rate of the groundwater tank, for production of the groundwater flow; \({H}_{2} (\mathrm{cp})\): groundwater reservoir level for production of groundwater flow; \({\varphi }(\mathrm{cp})\): discharge rate of the groundwater tank, for production of the outflow going outside the watershed; \({Q}_{{\mathrm{out}}_{t}}\): outflow going outside the watershed.

2.5 Operational Testing of Hydrological Simulation Models

The validation of the hydrological model is made with the split sample test (Klemes 1986). The principle consists of segmenting the sample into two different ways as follows:

  1. a.

    The first 70% of the sample is reserved for calibration and the remaining 30% for validation.

  2. b.

    The first 30% of the sample is reserved for validation and the remaining 70% for calibration.

The robust model is that gives satisfactory results in both cases.

2.6 Performance Test

To assess the efficiency of rainfall, it was deemed interesting to use the percent bias (PBIAS) and the determination coefficient (R2), while the NSE criterion was used to assess the rain flow. Statistical analysis was performed using statistical standard tools.

2.6.1 Percent Bias

It gives an indication of the error which exists between the observed data and the simulated ones. The optimal percent bias value is 0. Positive values indicate that the model has a bias that tends towards underestimation, while negative values indicate that the model has a bias that tends towards overestimation (Gupta et al. 1999). The percent bias is given by:

$$\mathrm{PBIAS}=\frac{\sum_{i=1}^{N}\left({\mathrm{Pobs}}_{i}-{\mathrm{TRMM}}_{i}\right)}{\sum_{i=1}^{N}{\mathrm{Pobs}}_{i}}\times 100\mathrm{\%}.$$
(7)

The PBIAS performance ranges are shown in the following (Moriasi et al. 2007): unsatisfactory |PBIAS| ≥ 25%; satisfactory 15% ≤ |PBIAS| < 25%; good 10% ≤ |PBIAS| < 15%; very good |PBIAS| < 10%.

2.6.2 Coefficient of Determination

Pearson’s linear coefficient of determination is used to assess the fit quality of the linear regression. Recall that the coefficient of determination is the proportion of variability obtained by the mathematical model compared to the total variability observed (Legates and McCabe 1999).

It is calculated by the following formula:

$$R^{2} = \frac{{\sum\nolimits_{{i = 1}}^{N} {\left( {{\text{Pobs}}_{i} - \overline{{{\text{Pobs}}}} } \right) \cdot \left( {{\text{TRMM}}_{i} - \overline{{{\text{TRMM}}}} } \right)} }}{{\sum\nolimits_{{i = 1}}^{N} {\left( {{\text{Pobs}}_{i} - \overline{{{\text{Pobs}}}} } \right)^{2} \cdot \sum\nolimits_{{i = 1}}^{N} {\left( {{\text{TRMM}}_{i} - \overline{{{\text{TRMM}}}} } \right)^{2} } } }}.$$
(8)

It should be indicated that R2 varies between 0 and 1. Values close to 1 indicate that there is a strong correlation between observed and simulated data. Generally values superior to 0.5 are considered acceptable (Santhi et al. 2001; Van Liew et al. 2003).

2.7 Nash–Sutcliffe Efficiency

The NSE criterion (Nash and Sutcliffe 1970) gives an indication of error between the observed data and the simulated data. It varies from − ∞ to 1; the optimal value is 1. Usually, the values superior to 0.5 are considered acceptable.

The NSE coefficient is estimated by:

$$\mathrm{NSE}=1-\frac{\sum_{i=1}^{N}{\left({\mathrm{Qobs}}_{i}-{\mathrm{Qsim}}_{i}\right)}^{2}}{\sum_{i=1}^{N}{\left({\mathrm{Qobs}}_{i}-\overline{\mathrm{Qobs} }\right)}^{2}},$$
(9)

where \({\mathrm{Qobs}}_{i}\): monthly observed runoff; \({\mathrm{Qsim}}_{i}\): monthly simulated runoff; \(\overline{\mathrm{Qobs} }\): average of observed runoff.

3 Results and Discussion

3.1 Precipitation Assessment Before Bias Correction

In our case, as there is only one observation station, the quality of the simulated precipitation is evaluated by comparing the data of two stations that have the same geo-referencing, i.e., the Pobs and TRMM1 (Fig. 1). First, the comparison is made on the basis of the annual monthly average to get a good graphical visualization.

As is clearly depicted in Fig. 3, TRMM1s are generally overestimated comparing to Pobs. Similar results have already been found in Casse et al. (2015), Li et al. (2018) and Zubieta et al. (2015).

Fig. 3
figure 3

Comparison of monthly average precipitation per year (Pobs and TRMM1) (2000–2019)

Full size image

Second, the linear regression graph (Fig. 4) indicates that there is a good adequacy between Pobs and TRMM1, with a correlation coefficient R2 equal to 0.722.

Fig. 4
figure 4

Linear regression between Pobs and TRMM1 data (period 2000–2019)

Full size image

Finally, according to PBIAS ranges in paragraph 2.6.1, it is shown that the PBIAS performance of TRMM1 is − 46.24%, which means that the result obtained is not satisfactory.

One concludes from the results shown above that, despite the good correlation between Pobs and TRMM1, the PBIAS performance is considered unacceptable. These results are in good agreement with those reported in a previous study which is conducted by Meng et al (2014). This means that it is necessary to apply the bias correction in order to increase the PBIAS coefficient and to achieve acceptable results.

3.2 Results After the Bias Correction of the Raw TRMMs

3.2.1 Multiplicative Shift Technique (M)

One calculates the multiplicative factor M from the monthly series of Pobs and TRMM1, which gives the following result:

$$M=\frac{\overline{\mathrm{Pobs}} }{\overline{\mathrm{TRMM}1} }=\frac{24.245}{31.772}=0.763,$$
$${\mathrm{TRMM}1(M)}_{i}={\mathrm{TRMM}1}_{i } \cdot 0.763.$$

This method can be applied in hydrological modeling. It is assumed that all the coefficients of the other stations have values close to the multiplicative coefficient of the station TRMM1.

The arithmetic average of the monthly precipitations of all the satellite stations, (Fig. 1) is given by:

$${\overline{\mathrm{TRMM}} }_{i}=\frac{\sum_{k=1}^{S}{\mathrm{TRMM}}_{i}\left(k\right)}{S},$$
(10)

where k = 1:S, S: satellite stations number.

Afterwards, the coefficient M = \(0.763\) is multiplied by \({\overline{\mathrm{TRMM}} }_{i}\); this then gives:

$${\overline{\mathrm{TRMM }(M)}}_{i}={\overline{\mathrm{TRMM}} }_{i} \cdot 0.763.$$
(11)

3.2.2 Linear Regression (R)

The bias correction using the linear regression method is carried out by correlating all the TRMMs with the Pobs station (Table 3).

Table 3 Correlation coefficient between TRMMs and Pobs data, the constants of the linear regression
Full size table

It can be observed that the coefficient R2 is satisfactory for all the TRMMs data provided by the stations in the watershed, which allows a reconstruction of all the TRMMs series using the results obtained from the linear regression line for each station (Table 3). For use in hydrological modeling, the monthly arithmetic mean of the corrected TRMM rainfall data by the linear regression method (\({\overline{\mathrm{TRMM }(R)}}_{i}\)) in the watershed is calculated using the formula (10).

3.3 Evaluation of TRMM1s After Bias Correction

The comparison is made on the basis of the annual monthly average. Figure 5 indicates clearly that there is great improvement in terms of approximation of TRMM1 corrected and Pobs curves.

Fig. 5
figure 5

The average monthly precipitation comparison during the year of Pobs, raw TRMM1, TRMM1(R) and TRMM1(M)

Full size image

One can easily observe that the TRMM1(R) curve more closely approximates the observed precipitation (Pobs) curve, which is confirmed by the calculated PBIAS (Table 4).

Table 4 Performance PBIAS of raw and corrected TRMM1s
Full size table

On the other hand, the results reported in the table indicate that the PBIAS performance exhibited a significant improvement in the TRMM1(R) which passed from − 46.24 to − 0.62; this corresponds to a shift from unsatisfactory to very good.

3.4 Hydrological Modeling

As the evaluation of the simulated precipitation after correction by the use of TRMM(R) gave a very good PBIAS performance, it would be more logical to choose it only for hydrological modeling. Note that in this work, various precipitation data are used as inputs to the model and a comparison is then made between the resulting calculated runoff. The results of the simulation performance are given in the following Table 5:

Table 5 NSE values for the different precipitation data used
Full size table

The table above clearly shows that the NSE is low for Pobs, which is quite normal since a single rainfall station cannot represent an entire watershed that covers an area of 2900 km2.

On the other hand, it was also noticed that, for the raw \({\overline{\mathrm{TRMM}} }_{{i}}\) data, the results found are not very satisfactory for the validation period from 2000 to 2005, because the NSE is equal to 0.341.

However, it is worth noting that some studies have shown that using monthly raw TRMMs proved to be quite successful in forecasting rainfall (Abdelmoneim et al. 2020; Le et al. 2018; Wang et al. 2020). This would certainly depend on the quality of the input data of the model used, the geographic location and the performance of the model used.

According to the ranges in paragraph 2.6.1, the TRMMs corrected performance is very satisfactory. The simulated results found are quite logical because the bias correction has significantly improved the quality of the simulated precipitation, which contributed to increase the reliability of the hydrological model. This is quite common in the field of rainfall–runoff modeling since the reliability of the input data has a great impact on the output parameters of the model (Liu et al. 2017; Meng et al. 2014).

It was deemed necessary to show the simulated results for the calibration period (between 2006 and 2019) as well as for the validation period from 2000 to 2005 for the purpose of illustrating (Fig. 6) the case where the modeling with \({\overline{\mathrm{TRMM }(R)}}_{i}\) presents a better NSE performance than with \({\overline{\mathrm{TRMM }(M)}}_{i}\).

Fig. 6
figure 6

Monthly observed and simulated runoff using \({\mathrm{TRMM}(R)}_{i}\)

Full size image

4 Conclusions

As the ground precipitation data are not adequately available in this study area, it was essential to choose TRMM data to capture rainfall data covering the entire Hammam Boughrara watershed in northwestern Algeria. The application of raw TRMMs for the simulation of discharges gave unsatisfactory results, so it was imperative to use a model that allows correcting the difference between the simulated and observed precipitation.

In this study, two simple bias correction methods were used: the multiplicative method and the linear regression method. It should be noted that these two methods require the availability of precipitation data from at least one monitoring station in the study area. The results of this correction made it possible to considerably improve the PBIAS performance of the TRMMs from unsatisfactory to very good. This had a positive impact on hydrological modeling with very good performance results of the simulated runoff by the meteorological inputs. This study confirms that the TRMMs based on precipitation measured on the ground surface proved their effectiveness in the simulation of flows. They are certainly a good alternative in the field of hydrometeorology.