1 Introduction

Since the final quarter of twentieth century, unprecedented human activities and fossil energy use led to environment and atmospheric pollution due to anthropogenic greenhouse gas (GHG) emissions. The consequent impacts are in the forms of global warming and climate change with increase in GHG emissions among which carbon dioxide plays the most important role (IPCC 2007, 2014). The most likely changes in physical climate variables or climate forcing agents are identified based on current knowledge following the IPCC AR5 uncertainty guidance ().

Maass et al. (1962) assumed implicitly that hydro-meteorological time series (temperature, precipitation, and streamflow) are stationary, i.e., without trend component. With the climate change implications, the stationarity hypothesis is dead, and now non-stationarity approaches, especially in terms of trends, became as the preliminary research topics. Science journal has published an article that argues the concept of stationarity, which means that natural systems fluctuate within an unchanging envelope of variability (Milly et al. 2008). The climate change and variability have led to temporal change in arithmetic average and variance of hydro-meteorological records. Another disturbance of the stationarity is due to water infrastructure constructions, drainage works, and channel modifications in addition to land-use and land-cover (LULC) alterations (IPCC 2007; Koutsoyiannis 2003; Koutsoyiannis and Montanari 2007; Sonali and Kumar 2013). Serinaldi et al. (2018) stated that the non-stationary structure of a time series has various statistical parameters different from the original data distribution in the sub-series, and hence, the stationarity assumption is shaken for direct use in various disciplines, especially those related to hydro-meteorology works. Any solution based on stationarity assumption leads to biased results with huge risks (Forsee and Ahmad 2011; Qaiser et al. 2011).

Fatichi et al. (2013) stated that as a result of climate change, trend identification, detection and evaluation became important subjects in different disciplines including meteorology, hydrology and climatology. For this purpose, the classical Mann–Kendall (MK) trend test has been employed frequently (Mann 1945; Kendall 1975) with Sen (1968) trend slope calculation. Many researchers have applied the MK methodology on a given hydro-meteoro-climatological time series records (Hirsch et al. 1982; Hirsh and Slack 1984; Cailas et al. 1986; Hipel et al. 1988; Demaree and Nicolis 1990; Yu et al. 1993; Gan 1998; Taylor and Loftis 1989; Lins and Slack 1999; Douglas et al. 2000; Hamilton et al. 2001; Kalra et al. 2008; Mohorji et al. 2017). Furthermore, for monotonic trend detection the most widely used technique is the non-parametric MK test (Hamed and Rao 1998).

Although the visual appreciation of trend component in a given hydro-climatologic time series is possible since the start of hydro-meteorological records in the second part of the eighteenth century, development of analytical methodologies came into existence in the first half of the nineteenth century (Mann 1945).

Another non-parametric model is suggested by Pettitt (1979) in detecting the abrupt change location and trend presence in the mean of a given time series (Mallakpour and Villarini, 2016). Chandler and Scott (2011), Serinaldi et al. (2018) and Şen (2019) stated that they often lead to the erroneous trend and abrupt change detections due to the serial autocorrelation effect in the hydro-meteorological records. Hence, prior to the application of these methodologies, it is necessary to convert available time series to serially independent version to get reliable results. For this purpose, pre-whitening (von Storch 1995) and more effective over-whitening (Şen 2016) procedures are suggested, but many papers concerned with the trend methodological applications do not take into consideration the relevance of serial independence assumption (Burn and Elnur 2002). Even though some researchers have dealt with the removal of the serial autocorrelation from a given series still there is less care for this consideration among the researchers (Yue and Wang 2004).

Wayne and Gray (1995) considered the problem of upward trend behavior determination in the global temperature anomaly series by means of a unit-root test method. Another serial-correlation-robust trend test is suggested by Alexandresson and Moberg (1997) that controls for the possibility of spurious evidence due to strong serial correlation, which is valid whether the errors are stationary or have a unit-root (strong serial correlation). Another attractive point in this test is that it does not require serial correlation parameter estimations. According to the work by Thomas and Timothy (2002), strong serial correlation (or a unit-root) in global temperature data could generate theoretically spurious evidence of a significant positive trend. Coggin (2012) used the concept of unit-root trend analysis in the climatology literature for testing trends in the HadCRUT3 global and hemispheric data.

There are already suitable parametric statistical techniques for trend analysis; specifically, regression quantile plots can be used for this purpose (Koenker 2004). Nalley et al. (2013) tried to detect trends in the mean surface air temperature over southern parts of Ontario and Québec, Canada, for the period of 1967–2006 using the discrete wavelet transform technique. They showed that the positive trends for the annual data are thought to be mostly attributable to warming during winter and summer seasons, which are manifested in the form of multi-year to decadal events (mostly between 8 and 16 years).

It is the main purpose of this review article to provide general conceptual ideas about the trend analyses methodologies, so that the researchers can select the most suitable one for their time series data. In addition, brief and illuminating information are presented about the current trend analyses procedures with their pros and cons with application guidances. The basic restrictive assumptions, their possible validation explanations, and improvements are presented on rational, logical and practical bases. Innovative and the most recent trend techniques are presented after the explanation of the classical trend methodologies. To support for serial correlation assumption restriction in the classical methodologies, pre- and over-whitening procedures are also explained with examples. Finally, a general set of suggestions are provided for future research possibilities.

2 Need for Trend Research

There are a good deal of discussion and curiosity about the natural event occurrences during the last century (Bradley 1968). These discussions have included comparisons among uncertainty in earth, atmospheric, hydro-meteorological and physics sciences, which led inevitably to the question of determinism and indeterminism in nature (Leopold and Langbein 1963; Krauskopf 1968; Mann 1970).

At the very core of scientific theories lies the notion of “cause” and “effect” relationship in an absolute certainty in analytical scientific studies. One of the modern philosophies of science, Popper (1957) stated that “to give a causal explanation of a certain specific event means deducing a statement describing this event from two kinds of premises: from some universal laws and from some singular or specific statements, which one may call the specific initial conditions”. According to him, there must be a very special kind of connection among the premises and the conclusions of a causal explanation and it must be logically deductive. In this manner, the conclusion follows necessarily from the premises. Prior to any mathematical formulation, the premises and the conclusion consist of verbal (linguistic) logical and rational statements. It is necessary to justify deductive argument at every step by citing a logical rule that is concerned with the relationships among statements. On the other hand, the concept of “law” lies at the heart of deductive explanation, and at the certainty of our knowledge about specific events.

The positive autocorrelation increases trend detection probability when there is no trend, and vice versa (Yue et al. 2002a; Yue and Pilon 2004). Although few studies have addressed this issue, autocorrelation in the data is either ignored or eliminated by pre-whitening procedure (von Storch 1995; Önöz and Bayazıt 2011).

Especially due to extreme event, global warming, climate change, land-use and environmental impacts embed systematic variation components into hydro-meteorological records such as trends, which need to be identified by a convenient method. Whoever wants to apply trend analysis, then the following points must be taken into consideration.

  1. (i)

    The first thing is to draw available time series and have a visual inspection for possibility of any trend. For instance, in Fig. 1, the reader can appreciate visually whether there is a linear (monotonic) trend or not. The original data for this figure are given in the Appendix.

  2. (ii)

    Consider the basic assumptions of each trend analysis methodology and decide on the best method. The most dominant assumptions in any parametric trend analysis are serial independence and normal (Gaussian) PDF.

  3. (iii)

    Unfortunately, in the literature, classical trend analyses are used without care of especially the assumptions in the second step, because most of the researchers use ready software without caring the basics of the methodology used.

  4. (iv)

    The longer is the time interval, the smaller is the serial correlation coefficient, and hence, practically the more suitable the application of classical trend methodologies. However, it must not be forgotten that even in annual time series, there may be significant serial coefficient, which restricts the use of the classical trend methodologies such as the regression and Mann–Kendall (MK) trend identification test.

Fig. 1
figure 1

Visual appreciation of a trend possibility

Full size image

In general, monotonic linear trends play significant role up to 30 years, for longer durations even visual inspection provides the first impression for trend possibility. In the case of innovative trend analysis (ITA) application, one can numerically identify the linearity or non-linearity (Şen 2017a, b). For this method, the most common parameters are the arithmetic average and variance in hydro-meteorological records series for trend identification. However, for the application of the classical trend analysis in addition to these parameters, there are specific test parameters as explained in the following different sections for each method.

In the statistically based methodologies such as the well-known MK trend test, at least 30 data records are necessary, but in the ITA, this can be even down to 10 samples.

2.1 Meteorology and Trends

Trend analyses in meteorological works have increased in an unprecedented manner during the last 4 decades especially as a result of climate change, which had impacts on the temperature, precipitation, wind speed, snow, evapotranspiration and other variables. For instance, anthropogenic climate change has the potential for slightly increasing the intensity of tropical cyclones through warming in the sea surface temperatures (Pielke and Landsea 1998). Emanuel (2005) has shown a striking association between sea surface temperatures and destructiveness by tropical cyclones in the Atlantic and western North Pacific basins.

2.2 Climatology and Trends

IPCC (2014) climate change report indicated a change in the global temperature, and climate due to the anthropogenic GHG concentration in the troposphere. This report mentions about temperature rising of 0.74 °C since about 1900 with an expected tendency to continue over this century. The consequences of such changes appear in major short-term meteorology and long-term climatology variables including temperature, precipitation, relative humidity, evapotranspiration and solar radiation in addition to the hydrological cycle variations by time at different locations all over the world. Bates et al. (2008) pointed out that over the last century, precipitation has increased primarily over land in high northern latitudes but decreased from 10° S to 30° N since the 1970s and globally the area of land classified as very dry has more than doubled since the 1970s due to climate change that impacts water resources systems at large.

2.3 Hydrology and Trends

Changes in precipitation and evapotranspiration cause increase in the frequency and severity of floods and droughts in the hydrological context. Hydrological regime changes do not take place equally throughout the years and places. Temperature increases in winter lead to early snowmelt, and consequent shift in the runoff discharge. In summer, there are decreases in the runoff amounts. Each one of these events implies increasing or decreasing trends depending on the environmental circumstances at different locations. Detailed up to date information is provided by Almazroui et al. (2018) about the impact of climate change, and trends on the engineering water structures.

3 Trend Definition

Trend search question varies enormously according to earth, environmental and atmospheric scientist’s objectives, but the solution algorithms may include the same or at least similar procedures. Some of the common questions that may be asked by various research groups are explained by Johnston (1989).

Any regular record along time axis at successively equal time intervals is referred to as time series, which, in general, may be composed of at least two components, namely, “deterministic” and “stochastic” parts. In particular, the former has sub-elements as trend, periodicity and sudden shift (jump), whereas the latter is composed of uncertainty. All these features are shown in Fig. 2.

Fig. 2
figure 2

Deterministic and uncertainty parts of a time series

Full size image

3.1 Trend Classification

Conceptually trends can be categorized into a set of classes depending on their mathematical shapes. The most commonly encountered one is the monotonic trends that extend over the whole record duration as a straight line (Fig. 3a). In some cases, the time series may have successive ups and downs over some sub-time duration along the record length, which is then referred to as the partial trend components that may either follow each other with end contacts or without (see Fig. 3b).

Fig. 3
figure 3

Trend types a monotonic and b partial

Full size image

Another classification depends on the trend slope as no trend, significant and insignificant trends that are decided based on different trend test methodologies as will be explained later in this paper. Furthermore, linear or non-linear trend classifications are also important in practical applications.

The main purpose of this review is to identify trends within an uncertainty world, and therefore, for the main topic Fig. 4 illustrates trend possibilities related to each statistical parameter.

Fig. 4
figure 4

Parametric trend types

Full size image

3.2 Probability and Statistical Features of Trends

Comparison of early and late time portions of a given time series record may have one of the four alternatives as in Fig. 5, where there are two PDFs schematized by the normal PDF, one for the past and the other for the present climate representations. After the visual inspection, one can state that there are changes climatically in each one of these graphs.

Fig. 5
figure 5

Trends, a increase in arithmetic average, b decrease in arithmetic average, c increase in standard deviation, d decrease in standard deviation, and e increase in the arithmetic mean and standard deviation

Full size image

In Fig. 5a, b, there is a shift in the recent PDF toward the right (left) and significant difference between the PDFs implies increasing (decreasing) trend embedment in the time series. In the same figure, the statistical parameters are also shown as \(\mu_{R}\), \(\sigma_{R}\), \(\mu_{P}\) and \(\sigma_{P}\). In Fig. 4c, d, shifts are available, but with different PDF kurtosis values, which implies that there are changes in the standard deviation, which is referred to as the climate variability.

Figure 4e implies change not in the position of the PDF, but in its variability, where extreme cold (hot) weather conditions increase in their frequency. It implies that the climate impact takes place simultaneously as changes in the arithmetic average and standard deviation (variability) such that the arithmetic average and the standard deviation of the past climate are less than the present climate statistical parameters.

4 Classical Trend Methodologies

In the literature, there are parametric methods for trend detection as linear regression approaches, rank-based non-parametric procedures and their mixtures. Parametric methodology includes a set of assumptions as normal (Gaussian) PDF of a given time series or residuals, and non-parametric tests require serially independent time series, which are rarely available in hydro-meteoro-climatological records. In many published papers in various journals, these basic requirements are not considered, and the data are treated for trend analysis by subjective assumptions that the data have normal (Gaussian) PDF, and serially independent. The MK trend test is frequently used for significant trend identification by numerous researchers (Gan 1998; Hamed and Rao 1998; Douglas et al. 2000; Burn and Hag Elnur 2002; Yue and Wang 2004; Yue et al. 2002a, b, c; Luo et al. 2008; Karpouzos et al. 2008). The presence of serial correlation in a time series affects the validity of the MK test (Yue et al. 2002a, b, c).

4.1 Moving Average

This is not trend identification methodology but provides less fluctuation in a time series by filtering it at a certain time window length through successive arithmetic average calculations, and hence by reducing the effect of randomness more visible temporal pattern emerges. The width of averaging window may be adjusted by researcher as 5 years (months), 10 years (month), etc. This filtering method provides a general idea about possible non-linear trends in a given time series by calculations of successive averages. It helps to smooth time series by filtering out the “noise” from random short-term fluctuations. In practical applications, it is recommended that at the maximum 7–8 times duration windows should be employed for smoothing and comparison among them.

Let a given time series as X1, X2, ..., Xn, where n is the number of data. For moving average application, it is necessary first to decide about the moving window length, m. There will be n−m moving average values, Mj (j = 1, 2,..., n−m), according to the following formulation:

$$ M_{j} = \frac{1}{m}\mathop \sum \limits_{j}^{j + m} X_{j} (j < n {-} m) . $$
(1)

For the sake of further discussions and explanations in the subsequent sections, the classical trend graph for the world mean annual temperature anomalies is adopted from the literature and given in Fig. 6 (IPCC 2014). This graph shows the record of global average temperature anomalies compiled by Global Climate Unit (GCU) at University of East Anglia in UK. The “zero” temperature on this graph corresponds to the mean temperature anomaly as suggested by the Intergovernmental Panel on Climate Change (IPCC, http://ete.cet.edu/gcc/?/globaltemp_teacherpage/#sthash.TSf1u4mD.dpuf). In this graph combination of the global land and marine surface tempereture is shown from 1850 to 2020 with third warmest record in 2019 anamoly as + 0.74 °C. It is obvious that there is temperature increasing trend after 1970 almost in a linear form. The moving average procedure may help to visualize various trend components along the record length.

Fig. 6
figure 6

Global air temperature change (http://www.cru.uea.ac.uk/)

Full size image

4.2 Regression Trend Identification

The regression monotonic line is among the parametric procedures for trend testing and the slope is computed by the least-squares estimate. Figure 7 summarizes what are the requirements for the regression methodology application.

Fig. 7
figure 7

Linear regression trend test chart

Full size image

In practical studies, this method is applied by assuming subjectively that the time series have independent serial structure with normal (Gaussian) PDFs without taking care of the basic assumption checks objectively by the statistical methodological applications. Furthermore, in the practical applications, the following set of restrictive assumptions is overlooked frequently.

  1. 1.

    The summation of differences (residuals) between the measurements and trend values must be equal to zero,

  2. 2.

    The square sum of the residuals must be the minimum according to the least squares’ technique,

  3. 3.

    The residuals must have zero serial correlation, i.e., they must have an independent structure,

  4. 4.

    The residuals must be distributed according to the normal (Gaussian) PDF,

  5. 5.

    The residuals must have homoscedasticity, i.e., constant variance,

  6. 6.

    The sample length must be preferably not less than 30.

Besides, this method is very sensitive to outliers. Prior to its application, the data should be transformed to a normal PDF. The independence can be checked by Anderson (1942) test and to get rid of the dependence, the data can be pre-whitened or over-whitened (see Sect. 7).

In any given hydro-meteorology time series, the search for a linear trend can be achieved by consideration of Fig. 1, where the trend appears visually. Objective trend analysis requires mathematical straight line basic expression, which can be presented as follows.

$$ v = a + bt, $$
(2)

where v represents hydro-meteorological variable as on the vertical axis of Fig. 1 and t is the time (hour, day, week, month, and year). Herein, a and b are the constant values of intercept and trend slope, respectively. Although there are statistical procedures in statistics textbooks, herein practically simple procedure is explained.

  1. 1.

    Take the averages of both sides in the basic expression (Eq. 2), which leads to the following equality.

    $$ \overline{v} = a + b\overline{t}. $$
    (3)
  2. 2.

    Multiply both sides of the basic expression by the independent variable on the right-hand side, which is t and then take the arithmetic average of both sides, which leads to

    $$ \overline{vt} = a\overline{t} + b\overline{{t^{2} }} . $$
    (4)
  3. 3.

    The solution of the two unknowns (a and b) by combination of Eqs. (3) and (4) leads to the numerical values of a and b.

  4. 4.

    For calculation, one can depend on excel sheet by consideration of each column as in Table 1.

    Table 1 Regression trend search calculation
    Full size table

The substitution of the last row (arithmetic averages) into Eqs. (3) and (4) provides a basis for the numerical solution of two unknowns (a and b). The necessary full table numerical calculations are given in the Appendix for 100 data. The trend component slope value is obtained as 0.022 and Fig. 8 shows the trend.

Fig. 8
figure 8

Regression trend line

Full size image

4.3 Mann–Kendall Method

Non-parametric procedures have significantly higher power than parametric procedures in cases of substantial departures from normal (Gaussian) PDF and the large sample sizes (Helsel and Hirsch 1992). The null hypothesis for this test is that the data are independent and randomly ordered, i.e., there is no trend or serial correlation structure among the observations (Fig. 9).

Fig. 9
figure 9

Mann–Kendal trend test chart

Full size image

This non-parametric trend test is initiated by Mann (1945) with later improvement with Kendall (1975) contribution. Hirsch et al. (1982) and Hirsh and Slack (1984) provided the MK trend identification test version for seasonal time series, which takes into consideration Kendall’s tau to provide the necessary association. The MK sign statistic, S, is defined as:

$$ S = \mathop \sum \limits_{i = 1}^{n - 1} \mathop \sum \limits_{j = i + 1}^{n} {\text{sign}}\left( {X_{j} - X_{i} } \right), $$
(5)

where

$$ {\text{sign}} = \left\{ {\begin{array}{*{20}l} { + 1 \quad{\text{if}}\, \left( {X_{j} - X_{i} } \right) > 0} \\ { 0\quad {\text{if}} \,\left( {X_{j} - X_{i} } \right) > 0} \\ { - 1\quad {\text{if}} \,\left( {X_{j} - X_{i} } \right) < 0} \\ \end{array} } \right.. $$
(6)

S confirms normal (Gaussian) PDF with zero arithmetic average and variance as follows:

$$ V\left( S \right) = \frac{1}{18}\left[ {n\left( {n - 1} \right)\left( {2n + 5} \right) - \mathop \sum \limits_{k = 1}^{m} t_{k} \left( {t_{k} - 1} \right)\left( {2t_{k} + 5} \right)} \right]. $$
(7)

Herein, k is the number of tied sets and tk is the size of kth group. The standardization of sign statistics, S, according to the following expression provides the test statistic, Z:

$$ Z = \left\{ {\begin{array}{*{20}l} {\frac{S - 1}{{\sqrt {V\left( S \right)} }}, \quad{\text{ if}}\, S > 0} \\ { 0 \quad{\text{if}}\, S = 0 } \\ {\frac{S + 1}{{\sqrt {V\left( S \right)} }}, \quad{\text{ if}}\, S < 0} \\ \end{array} } \right.. $$
(8)

The value of Z accords by the standard normal (Gaussian) PDF with zero mean and unit variance. It can be used to estimate whether linear regression line slope is different from zero. Prior to its application, the assumption of independence requires that either the time between measurements be sufficiently large so that there is no correlation or there is no serial correlation within the short (hour, day, and month) time intervals. Many researchers assume subjectively that hydro-meteorological records abide by the normal (Gaussian) PDF and serial correlation coefficient is equal to zero, i.e., time series is independent.

A simple example for the MK trend identification test parameters identification is given by usage of Eqs. (5)–(8) in the Appendix, where there are 100 data values. The parameters are obtained through software written by the authors in Matlab language. The parameters S and Z are calculated from Eqs. (5) and (8) leading to the numerical values as 1064 and 0.0094, respectively. The slope value is found as 0.0236 after application of Eqs. (9) and (10), which are presented in the following Sect. 4.4. It is obvious that the data have visually increasing trend, which has been confirmed by MK trend test and presented in Fig. 10.

Fig. 10
figure 10

MK trend component identifications

Full size image

4.4 Sen Trend Slope

This method is an alternative to the parametric least-squares regression line slope. To alleviate the restrictive assumptions in the regression analysis, Sen (1968) proposed a non-parametric slope calculation as the median of all possible slopes between each pair of successive time series values. Sen’s slope is fairly resistant to outliers, with a breakdown point of 0.29 (Wilcox 2001, p.208). Since the method is outlined first by Theil (1950) and later expanded by Sen (1968), it is sometimes called the Thiel–Sen estimator. Instead of the least squares-weighted mean to estimate the slope, Sen suggested the use of a median. The Sen Slope formulation is given as:

$$ S_{ij} = \frac{{ X_{j} - X_{i} }}{j - i}. $$
(9)

The calculations are for 1 \(\le i < j \le n\). The final slope value is given as the median of all the Sij slopes as:

$$ S = {\text{median}}\left( {S_{ij} } \right). $$
(10)

4.5 Spearman’s Rho Trend Test

This is a non-parametric distribution-free statistic, which is useful for the trend significance test (Spearman 1904). It is less widespread than the commonly applicable MK trend test and regression approach. These tests are equivalent for the case of serially independent and normally distributed time series. Daniel (1990) has provided further explanations and improvements in the application of the Spearman’s Rho approach.

The Spearman’s rank correlation coefficient helps to discover the strength of a relation between two sets of data. This is a rapid and simple test for trend search depending on the possibility of significant correlation between two time series. For its application, first, the data are ranked in ascending order and the Spearman’s Rho test value is calculated as:

$$ r_{s} = 1 - 6\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {R\left( {X_{i} } \right) - R\left( {Y_{i} } \right)} \right]^{2} }}{{n\left( {n^{2} - 1} \right)}}, $$
(11)

where R(Xi) and R(Yi) are the ranks of data values at ith position in time series Xi and Yi each with n number of data. The statistical test parameter of rs can be calculated according to the following z value:

$$ z = r_{s} \sqrt {n - 1} . $$
(12)

If z value is less than the standard normal PDF significance level \(\alpha\) value, \(z_{\alpha }\), then the data values do not vary significantly by time and this means that there is not a meaningful trend. For the application of the Spearman’s Rho trend test, the given time series can be divided into two parts, which are considered as two different time series. Figure 11 indicates various stages in the application of the non-parametric Spearman’s Rho trend test.

Fig. 11
figure 11

Spearman trend test chart

Full size image

Daniel (1990) compared MK and Spearman’s Rho tests and found that usually very little basis exists for preference one over the other. He also noted that MK statistic approaches normal PDF more rapidly that the Spearman case.

5 Innovative Trend Methodologies

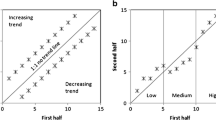
Innovative trend analysis (ITA) is another non-parametric trend search and identification methodology. Its original fundamentals are given by Şen (2012, 2014) based on the consideration of two non-overlapping halves of a given time series. The past and the present climates are conceptualized by the first and the second halves of the series.

The ITA template is presented in Fig. 12, where there are two triangular (upper and lower) parts (Şen 2017a, b). There is no assumption for the application of this trend methodology.

Fig. 12
figure 12

Innovative templates for trend slope

Full size image

This template helps to find whether a given series has trend or not. For this purpose, the arithmetic averages (\(\overline{X}_{1}\) and \(\overline{X}_{2}\)) of the two half series are calculated and their position in the template indicates trend possibility. For instance, if \(\overline{X}_{1}\) > \(\overline{X}_{2}\) (\(\overline{X}_{1}\) < \(\overline{X}_{2}\)), then there is an increasing (decreasing) trend with positive (negative) slope value. In case of \(\overline{X}_{1}\) = \(\overline{X}_{2}\), there is no trend because the point falls on the 1:1 line (point C in Fig. 12). The points A, B and C indicate the existence of increasing, decreasing and no trend cases, respectively.

The graphs in Fig. 5a, b can be represented by the same ITA template provided that the arithmetic averages of the past and present halves are considered on the corresponding axes. On the other hand, the standard deviations (\(\overline{S}_{1}\) and \(\overline{S}_{2}\)) of the two half series take the positions of point A for \(\overline{S}_{1}\) < \(\overline{S}_{2}\), point B for \(\overline{S}_{1}\) > \(\overline{S}_{2}\) and point C for \(\overline{S}_{1}\) = \(\overline{S}_{2}\).

The corresponding innovative template for the PDF graph in Fig. 4e must have two sets of points, one for the arithmetic averages and the other for the standard deviations. According to the previous explanations, one can then decide about possible increasing and decreasing trend component for the arithmetic averages and the standard deviations.

5.1 ITA Templates

This section provides information on how to combine the classical graphs with the ITA templates so that not only quantitative calculations, but also qualitative interpretations can be achieved rather easily. Since the upper triangular area is for increasing trend, it can be combined suitably with the arithmetic average classical graph in Fig. 5a.

In case of significant difference between the first and the second halves’ arithmetic averages (\(\overline{X}_{1}\) and \(\overline{X}_{2}\)), then a trend exists within the time series considered. The practical measure of significance can be calculated by the relative error percentage, α defined as (Şen 2017a, b):

$$ \alpha = 100\frac{{\overline{X}_{2} - \overline{X}_{1} }}{{\max \left( {\overline{X}_{1} , \overline{X}_{2} } \right)}}. $$
(13)

If the percentage error is less than ± 10 or preferably less than ± 5, then there is no significant difference between the arithmetic averages, and hence, no trend.

Each one of the two-PDF graphs reveals the fact that the difference between the two arithmetic averages takes place during a certain time period. Since the time difference between the arithmetic averages is equal to the half data number, the arithmetic average trend slope, Sa, can be calculated as (Şen 2017a, b):

$$ S_{a} = \frac{{\left( {\overline{X}_{2} - \overline{X}_{1} } \right)}}{n/2}, $$
(14)

where n is the number of data. ITA is the simplest trend identification application in practical works. However, to avoid the extreme value effects instead of the arithmetic averages the median values can also be used.

The same arguments are valid for the standard deviations and the standard deviation change slope, Ss can be defined like Eq. (14) as:

$$ S_{s} = \frac{{\left( {\overline{S}_{2} - \overline{S}_{1} } \right)}}{n/2}. $$
(15)

For the data in the Appendix, the application of the ITA template and its consequent trend analysis is given in Figs. 13 and 14, respectively.

Fig. 13
figure 13

Innovative trend analysis templates

Full size image
Fig. 14
figure 14

ITA monotonic trend components

Full size image

According to Eq. (14), the slope of the trend line is 0.0265, and hence, the ITA monotonic straight line is shown in Fig. 14.

5.2 Innovative Trend Significance Test

Applicability of an ITA statistical significance analysis is given by Şen (2017a, b) based on the sorted sub-samples from the same time series without assumption. The suggested methodology is valid even for time series with serial correlation structure. The necessary statistical equations are derived and then supported by linear trend slope test procedure, which is convenient for the construction of confidence intervals by taking into consideration the difference between two population means. For this purpose, the null hypothesis, H0, implies that there is not a significant trend if the calculated slope value, S, remains below a critical value, Scr. Otherwise, an alternative hypothesis, Ha, is valid when S > Scr. To develop an innovative significance test, it is necessary to derive the PDF of null hypothesis case. The slope parameter Eq. (14) shows that the stochastic property of Sa is a function of the first and second half time series arithmetic average values. Since \(\overline{X}_{1}\) and \(\overline{X}_{2}\) are sample variables, the slope value can be obtained by taking the expectation of both sides in Eq. (14):

$$ E\left( {S_{a} } \right) = \frac{{\left[ {E\left( {\overline{X}_{2} } \right) - E\left( {\overline{X}_{1} } \right)} \right]}}{n/2}. $$
(16)

After all what have been explained in the previous sections, in the case of no trend, the centroid point falls on the 1:1 line, which implies that E(\(\overline{X}_{1}\)) = E(\(\overline{X}_{2}\)), and therefore, E(Sa) = 0.

On the other hand, the variance of the slope can be calculated as V(\(S_{a} ) = E\left( {S_{a}^{2} } \right) - E^{2} \left( {S_{a} } \right)\), but in case of null hypothesis \(V\left( {S_{a} } \right) = E\left( {S_{a}^{2} } \right), \) which is equal to the second-order moment of the slope variable. This can be obtained by taking the expectation of both sides in Eq. (15) after the square operator resulting in:

$$ E(S_{a}^{2} ) = \frac{{\left[ {E\left( {\overline{X}_{2}^{2} } \right) - 2E\left( {\overline{X}_{2} \overline{X}_{1} } \right) + E\left( {\overline{X}_{1}^{2} } \right)} \right]}}{{n^{2} /4}}. $$
(17)

Due to null hypothesis \(E\left( {\overline{X}_{2}^{2} } \right) = E\left( {\overline{X}_{1}^{2} } \right)\), it is possible to obtain the following expression:

$$ E(S_{a}^{2} ) = \frac{{\left[ {E\left( {\overline{X}_{2}^{2} } \right) - E\left( {\overline{X}_{2} \overline{X}_{1} } \right)} \right]}}{{n^{2} /8}}. $$
(18)

The correlation coefficient between the two mean values is given according to the autocorrelation definition in any textbook on stochastic processes as follows (Cox and Miller 1965):

$$ \rho_{{\overline{X}_{1} \overline{X}_{2} = \frac{{E\left( {\overline{X}_{2} \overline{X}_{1} } \right) - E\left( {\overline{X}_{2} } \right)E\left( {\overline{X}_{1} } \right)}}{{S_{{\overline{X}_{1} }} S_{{\overline{X}_{2} }} }}}} . $$
(19)

Substitution of the numerator of this expression into Eq. (15) and consideration stochastically that \(S_{{\overline{X}_{2} }} = S_{{\overline{X}_{2} }} = S/\sqrt n\), Eq. (19) takes its final form as follows:

$$ E(S_{a}^{2} ) = \frac{{\left( {1 - \rho_{{\overline{X}_{2} \overline{X}_{1} }} } \right)}}{{n^{2} /8}}\frac{{S_{a}^{2} }}{n}. $$
(20)

In this last expression, \(\rho_{{\overline{X}_{2} \overline{X}_{1} }} \) implies cross-correlation coefficient between the ascending two halves’ arithmetic averages. The standard deviation of the sampling slope value can be obtained from Eq. (20) as:

$$ \sqrt {E\left( {S_{a}^{2} } \right)} = \frac{2\sqrt 2 }{{n\sqrt n }}S\sqrt {1 - \rho_{{\overline{X}_{2} \overline{X}_{1} }} } . $$
(21)

Furthermore, the third-order moment of the slope variable is also equal to zero and the same is valid for all odd order moments. This is the reason why the PDF of the slope, Sa, abides with the normal (Gaussian) PDF with zero mean and the standard deviation given in Eq. (21).

The ITA is applied to the long annual temperature records of Southeastern New Jersey (Şen 2017a, b). The simple statistical quantities of the record are presented in Table 2.

Table 2 Descriptive features of actual data
Full size table

If at α percent significance level, the confidence limits of a standard normal PDF with zero mean and standard deviation is \(\alpha_{{\text{cr }}}\) then the confidence limits (CL) of the trend slope can be written according to the following expression:

$$ {\text{CL}}_{{\left( {1 - \alpha } \right)}} = \pm \alpha_{{{\text{cr}}}} \sqrt {E\left( {S_{a}^{2} } \right)} . $$
(22)

All the necessary calculations and additional information with the operations in the last column are presented in Table 3.

Table 3 Innovative trend test results
Full size table

One of the important points in this table is high cross-correlation values in row 6 due to the ordered sequence in each half series. Slope value, Sa, falls outside the lower and upper confidence limits, and therefore, in row 11 the alternative hypotheses, Ha, is adopted and it indicates the existence of trends (Yes) as decisions (row 12). In the last row, the type of trend is stated depending on the slope sign in row 3.

6 Partial Trend Analysis

In the application of the previous techniques, the trends cover the whole record duration without consideration of possible distinctions between “low”, “medium” and “high” time series values.

The same ITA template can be visualized as 9-square sub-areas in accordance with three classifications as “low”, “medium” and “high” on both axis and these template sub-area couples are “low”–“low”, “low”–“medium”, “low”–“high”, “medium”–“low”, “medium”–“medium”, “medium”–“high”, “high”–“low”, “high”–“medium”, and “high”–“high” (see Fig. 15). This figure provides a set of possible partial that may occur in a given time series data.

Fig. 15
figure 15

Different partial trends in the innovative trend template domain

Full size image

The red circle on each line indicates the arithmetic average point (centroid) of the two halves. It also provides qualitative trend interpretation possibilities some of which are summarized as follows (Şen 2017a, b):

  1. 1.

    Extensive straight line (B or C) parallel to the 1:1 (45°) line implies a monotonic (increasing or decreasing) trend; line A indicates no trend case. Other shorter straight lines (D, E, I or L), parallel to the 1:1 (45°) line, are for partial trends that cover different classifications (”low”, “medium” or “high”). If the centroid point in the figure falls on the 1:1 (45°) straight line, then the hydro-climatological time series does not have any monotonic trend on the average.

  2. 2.

    Non-parallel (F, G, H, J, K, or M) to 1:1 (45°) straight line implies standard deviation change with time (homoscedasticity in the statistical sense). These straight lines indicate trends in the standard deviation.

  3. 3.

    Straight lines F and G have trends in the standard deviation, but not in the arithmetic mean.

  4. 4.

    Furthermore, H (K) and J (M) imply increasing (decreasing) standard deviation trend.

Three cases present no trend (A), increasing trend (B) and decreasing trend (C) time series like the conceptual cases in Fig. 12. Since, they are all parallel to the 1:1 (45°) straight line, they do not include trend in the standard deviation. The slope, Sa, of the possible trend can be calculated by Eq. (14).

7 Pre- and Over-whitening Procedures

Prior to the application of the classical trend methodologies such as MK and regression line, it is necessary to render the original time series serial correlation practically to zero. To assess the influence of the dependent serial correlation structure on trend identification, various authors have performed Monte Carlo simulation studies (Hamed and Rao 1998; Yue et al. 2002a, b, c; Matalas and Sankarasubramanian 2003). Pre-whitening (PW) procedure was suggested to reduce the serial correlation effect on MK trend analysis. As mentioned earlier, the presence of serial dependence in a given time series can complicate the trend identification. For instance, a positive serial correlation coefficient leads to false-positive outcomes in the use of the MK test (von Storch and Navarra 1995).

7.1 Pre-whitening Trend Procedure

To match the theoretical background of the MK test to actual records, serial correlation elimination is suggested from the original series through the pre-whitening (PW) treatment, which offsets the serial correlation structure. After the application of PW procedure to some flows in the United States, Douglas et al. (2000) indicated that trend is less than prior to PW implementation. PW has been applied to temperature and streamflow trend analyses prior to MK test trend identification without any proof of its ability to fulfill independence structure (Zhang et al. 2011; Hamilton et al. 2001; Burn and Hag Elnur 2002). Yue et al. (2002a, b, c) have shown that PW procedure is successful only in the case of first-order AutoRegressive, AR(1) process with an increasing absolute trend and positive serial correlation coefficient only. Yue and Wang (2002) have extended similar PW treatment through extensive Monte Carlo simulation studies and they have concluded that trend existence in a time series depends on the sample size, serial correlation magnitude and trend slope amount. In cases of large sample sizes combined with sufficiently high trend slopes, the serial correlation does not influence the MK test results significantly. Negative correlation removal by PW treatment in the AR (1) process inflates the trend.

The authors such as von Storch and Navarra (1995), Zhang et al. (2011), Burn and Hag Elnur (2002), and Blain (2012) among many others have proposed or used PW approaches to remove the effect of serial correlations on the trend test. As indicated in the significant study of Yue et al. (2002a, b, c), the removal of a positive autocorrelation component by PW, a given dataset may result in an erroneous reduction of the significance of an existing trend. The PW method has been proven to be harmful for trend test, because it damages the trend component itself, although the serial correlation coefficient can be removed to a significant extend (Hamed, 2009). About the PW procedure, Yue et al. (2002a, b, c) have proposed a trend-free PW to remove the serial correlation coefficient. This procedure suggests that the removal of trend is necessary prior to the conversion of the time series into independently structured form, and hence, the damage on the trend is reduced significantly, but still there are problems although this approach provides better application opportunity for MK trend test application (Rivard and Vigneault 2009; Rivard et al. 2009). The failure of trend-free PW procedure has been documented by Wang et al. (2015) and Serinaldi et al. (2018) with suggestion of another version of the trend-free PW methodology. Another problem with the PW process is that the calculation of the serial correlation coefficient from the original time series requires that the data should abide with the normal (Gaussian) PDF, which is not the case in many hydro-meteorological records.

7.2 Over-whitening Trend Procedure

Şen (2016) presented an OW procedure by which the original hydro-meteorological time series is added with a completely random (white noise) time series with zero mean and convenient standard deviation to render the original time series into a serially independent counterpart with the same trend component.

Based on the first-order autocorrelation coefficient, ρ, of the AR(1) process, the kth-order dependency coefficient, ρk, of OW process is given by Şen (2016) in terms of \(\beta\) and \(\gamma\), which are the trend slope and OW standard deviation, respectively. Yue et al. (2002b) argued that the removal of the trend as a first step may allow for more accurate estimate of the population’s lag-one autocorrelation coefficient, and subsequently better estimation of trend. To apply these arguments in an analytical manner, it is assumed that β = 0, and hence, the trend is removed, which leads to the autocorrelation coefficient as:

$$ \rho_{k} = \frac{{\rho^{k} }}{{1 + \gamma^{2} }} = \alpha \rho^{k} , $$
(23)

where 0 < α < 1, and it is referred to as the dependence reduction factor. This expression implies that the autocorrelation structure of any given time series with lag-one autocorrelation, \(\rho_{1}\) can be reduced to the first-order over-whitened serial correlation coefficient, ρo, as:

$$ \rho_{0} = \alpha \rho_{1} . $$
(24)

The relationship between ρo and ρ through α is given in Fig. 16 depending on ρ1. One can reduce it down to as small as possible by selecting a convenient α dependence reduction factor. It is not possible to obtain absolutely independent process unless the time series itself has completely independent structure, i.e., ρ1 = 0. This point agrees with the statement by Yue and Wang (2002) and Bayazıt and Önöz (2007) that by PW the dependence structure can be reduced such that the serial correlation coefficients becomes close to zero. The same statement is valid also for OW procedure.

Fig. 16
figure 16

OW chart

Full size image

This figure together with Eq. (21) indicate that it is not possible to make the autocorrelation structure of the time series purely independent even after OW, because for such a case α should be equal to zero, which is not possible practically. Yue and Wang (2002) stated that “…pre-whitening is not suitable for eliminating the effect of serial correlation coefficient on the MK test when trend exists in a time series”, because “…pre-whitening will remove a portion (equal to the lag-one autocorrelation coefficient) of trend, and hence, reduces the probability of rejecting the null hypothesis when it is false”. The OW procedure will not be affected from such shortcomings.

Bayazıt and Önöz (2007) stated that “…the trend (upward or downward) always has a positive contribution to serial correlation”. The standard deviation of over-whitening component is given as (Şen 2016):

$$ \gamma = \sqrt {\frac{1}{\alpha } - 1} . $$
(25)

Since α is always positive, γ will be positive. In practical applications, convenient α value should be chosen from the chart in Fig. 13 or calculated from Eq. (24) as:

$$ \alpha = \frac{{\rho_{0} }}{{\rho_{1} }}, $$
(26)

where ρo is desired OW first-order correlation coefficient that should be chosen so as to make the OW time series have almost independent correlation structure. The necessary steps for OW process application are given by Şen (2016).

8 Variability Detection by ITA

This section provides objective ITA methodology for the detection of the variability trend. For this purpose, the variability fundamentals are explained on the statistical foundations and simple formulations are developed for practical applications. The validity of the new formulations has been confirmed by Şen (2014) through extensive simulation techniques.

Climate change variability reflections appear in the hydrological records, and in the future any successful project design, operation, management and maintenance of water resources will depend on objective trend and variability features of the records, their detection and interpretation. Different researchers have touched on these significant points (Hannaford and Marsh 2006; Gupta 2007; Lorenzo-Lacruz et al. 2012; Larsen et al. 2013; Haktanır and Citakoglu 2014). The impact of climate change on different elements of the hydrological cycle has been investigated by many researchers in different disciplines (Bao et al. 2012; Douglas and Fairbank 2011; Ehsanzadeh et al. 2011; Garbrecht et al. 2004; Wagesho et al. 2012). Han et al. (2014) have performed simultaneously a comprehensive analysis of trends in precipitation and streamflow records at the Xiangxi River Watershed through multiple classical tests to detect the trends and their magnitudes. Trend variability features may result from various effects and lead to different consequences.

8.1 Methodology

In any fundamental textbook on climate, the climate change is explained based on simple PDF shift similar to Fig. 5 as in Fig. 17.

Fig. 17
figure 17

Variation without trend

Full size image

By considering the arithmetic mean and the standard deviation relative positions between two PDFs like Fig. 17, one can again distinguish three cases (A, B and C). In general, the standard deviations may be different from each other as \(\sigma - \Delta \sigma \ne \sigma \ne \sigma + \Delta \sigma\).

It is possible that the time series may not have the first-order stationarity, which implies that there is variation in the variance (standard deviation) by time. This is tantamount to saying that the time series does not have homoscedasticity property, i.e., variance constancy. There are variations without any trend existence on the arithmetic average level and two time series are comparable based on the standard deviation. The change in the standard deviation per time duration is the definition of the variation measure. Hence, like Eq. (15), one can deduce simply that the variation slope can be expressed as:

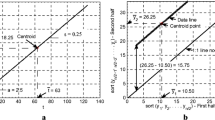
$$ S_{\sigma }^{ \pm } \, = \,\frac{(\sigma \, + \,\Delta \sigma )\, - \,\mu }{{\Delta t}}\, = \, \pm \,\,\frac{\Delta \sigma }{{\Delta t}}. $$
(27)

For the estimation of the simulation variability, first preselected set of simulation variability values are plotted against the same values so as to get a reference line of 1:1 (45°) line. Figure 18 indicates the validity of Eq. (15).

Fig. 18
figure 18

Validity confirmation of Eq. (15)

Full size image

It is obvious from this figure that the simulation line is slightly below the reference line and at the maximum difference is 0.11, which corresponds to 100 × 0.11/3.0 = 3.36% relative error and this is well below the acceptable level of ± 5%. In practice, trend and variation cases may take place simultaneously as shown in Fig. 19.

Fig. 19
figure 19

Trend with a uniform (homogeneous) variation and b non-uniform variation

Full size image

9 Crossing Trend Analysis Methodology

This approach is applicable whether the time series has dependent or independent structure. Any trend from the centroid of the given time series should have the maximum number of crossings (total number of up-crossings or down-crossings). A new trend analysis has already been suggested by Şen (2018) as the “crossing trend” procedure, which depends on the maximum number of crossings within a given hydro-climatological time series.

9.1 Rational Concept

To illustrate the crossing property, a hypothetical time series and its truncations at different trend levels are given with the number of crossing points in Fig. 20.

Fig. 20
figure 20

Time series and trend crossing numbers

Full size image

In this figure, a series of increasing and decreasing trends are given and among them the one with the maximum crossing number is the most representative trend line. In this manner, the trend identification depends neither on the PDF nor on the serial dependence structure of the hydro-climatologic variable. One can also calculate the surplus and deficit quantaties on the basis of the trend line, if necessary. In Fig. 21, various quantaties along the truncation level are shown. In this figure, SL (DL) implies surplus (deficit) lengths and there are 5 (4) of them.

Fig. 21
figure 21

Truncation (trend) level features

Full size image

9.2 Theoratical Background

In any hydro-climatologic record series crossing points at a truncation level provide not only information on wet and dry spell features, but also about the internal structure of the series (Şen 1977). For instance, the more is the crossing points at the median truncation level, the less is the serial dependence. In an independent series at the median level, practically the number of up-crossings expectation is equal to the down-crossing expectation number, which are equal to n/2. In Fig. 21, up-crossings and down-crossings are indicated with arrows. Theoretically, in an infinite independent series, irrespective of the PDF, the number of crossings abide by the Poisson process PDF (Feller 1967). In finite sample lengths, the expectation and the variance of the number of up-crossings, Nu, have been derived by Şen (1991) as,

$$ E\left( {N_{{\text{u}}} } \right) = np\left( {1 - p} \right), $$
(28)

and

$$ V\left( {N_{{\text{u}}} } \right) = E\left( {N_{{\text{u}}} } \right)\left( {1 - 3p + 3p^{2} } \right), $$
(29)

respectively. Herein, p is the probability of surplus over the median truncation level. The average number of up-crossings increases with the sample length, n, but decreases as the truncation level increases.

Under the light of the aforementioned information, it is possible to benefit from a normal (Gaussian) PDF for the significance test of innovative crossing trend either using Eqs. (28) and (29) or with their standardization as (Şen 2018):

$$ m_{S} = \frac{{E\left( {N_{{\text{u}}} } \right)}}{{n\left( {n - 1} \right)}}, $$
(30)

and

$$ s_{S} = \frac{{V\left( {N_{{\text{u}}} } \right)}}{{E\left( {N_{{\text{u}}} } \right)\left( {1 - 3p + 3p^{2} } \right)}}, $$
(31)

respectively. In Fig. 22, crossing trend identification result is given for İstanbul Göztepe meteorology station on the Asian continental side.

Fig. 21
figure 22

Innovative crossing trend components, İstanbul/Göztepe

Full size image

Visual inspection of this graph provides reflections that the innovative crossing trend analysis well identifies the trend component. For the sake of comparison trend calculated on the basis of Sen’s slope is also given on the same graphs, which expose negligiably small difference, which are due to the basic assumptions. As for in the Sen’s method coupled with the MK trend analysis, the record time series should have independent structure. Hence, the smaller the dependence structure of a time series the closer are the results from the innovative cross test slope and Sen’s slope approaches.

However, for quantitative analyses, Table 4 is prepared, where both MK trend test and the innovative crossing trend analysis quantaties are presented. In this table, LL and UL are for the lower and upper significance levels. It is to be noticed that the confidence limits in the trend test case remain the same without depending on the sample size. In the table, trend tests are probed for two levels, 90% and 95%.

Table 4 MK and innovative crossing trend statistical characteristics
Full size table

10 New Directions in Trend Identifications

All the trend identification methodologies that are explained in this paper are based on holistically or partially monotonic increments or decrements along the time durations in a given time series. Almost all of them are in the form of linear mathematical expressions with the slope and intercept values. As for the linear trend methodologies, the literature is at a stagnant level. The trend time durations are pre-determined by the researcher as for the non-overlapping halves or fixed time durations, for instance, one-third, one-fourth, one-fifth and so on time durations. The following points can be considered for future trend analysis and research activities.

  1. 1.

    The non-linear possibility of trends, say, exponentially increasing or decreasing trend possibilities must be searched.

  2. 2.

    Rather than fixed trend time durations pre-determined by the researcher, natural turning points must be identified with trend line fixations in each one in a subsequent manner.

  3. 3.

    Apart from the parametric methodologies, similar to PDFs in Fig. 3, one can compare the PDFs of two equal halves, or among different PDFs within fixed trend time durations.

  4. 4.

    Possible trends in the serial correlation coefficient have not been searched so far in the literature. It is possible that similar to the arithmetic average and standard deviation differences, there may be significant differences between the serial correlation coefficients along two or more fixed time durations of a given time series.

  5. 5.

    Similar researches may be conducted for the skewness and kurtosis parameters for better trend implications and interpretations.

  6. 6.

    Extrapolation of trends to future assumes that time series will keep changing in the future the way they have been changing in the past, which may not be valid deterministically, and therefore, future extension possibilities should be concerned with great care.

  7. 7.

    Adaptive trend analysis methodologies can be developed so that after each time series data and longtime duration, the trend may reach the classical trend line. In this manner, one can assess the trend evolution, and accordingly, may reach to useful information for a group of time series values and make future extensions accordingly.

  8. 8.

    Rather than crisp trend analysis, one can develop fuzzy trend identification possibilities, and hence, verbal quantitative interpretations can be obtained, which provide useful basic information for future trend extension possibilities. Fuzzy clustering-based trend analysis approaches help to get rid of restrictive assumptions.

  9. 9.

    Existing trend analyses are based on equally spaced time durations (daily, monthly, and annual, decadal). It is necessary to develop trend methodologies for non-equal time duration time series such as the floods, earthquakes and alike phenomena.

  10. 10.

    In addition to common sense imagination, description and idea production stages are necessary for effective trend modeling.

11 Conclusions

Trend analysis methodologies are gaining increasing importance in the hydrology, climatology and meteorology literature due to the global warming and climate change and variability implications as a result of anthropogenic effects that alter especially atmospheric environment. There are various parametric and non-parametric trend analyses methodologies in the literature, but they are rather inconsistently distributed in different scientific and grey literature arena. This revision paper provides the fundamentals of each trend methodology with their restrictive assumptions, critical evaluation and gives a concise and collective source for anyone who is interested to work with trend isolations from a given time series data.

If the author does not know or do not have any information of the restrictive assumptions about trend analysis, then one can apply innovative trend analysis (ITA), which does not have any assumption.