Volume of Fluid Method: A Brief Review

Abstract

Understanding and predicting multiphase flows is of great relevance due to the ubiquitous nature of such flows in both nature and in many industrial applications. Rapid development of high speed computers and problem-specific algorithms in the last 2 decades has enabled the study of multiphase flows through numerical simulations. In this paper, we give a brief overview of different methods used in direct numerical simulations of two-phase flows. In particular, we focus on the volume of fluid (VOF) method used for locating and advecting the interface. VOF method is a mesh based interface capturing method in which a scalar function called void fraction field (which is the ratio of tracked fluid to the cell volume) is advected in order to track the interface position. A geometric VOF algorithm is detailed in this work. which strikes a balance between accuracy, ease of implementation and volume conservation on a structured grid. Another challenge in two-phase flow simulations is the inclusion of surface tension forces accurately. Here, we give a brief overview of Eulerian surface tension models and detail an approach balancing computational cost, curvature estimation and imposed timestep restriction. Finally, we discuss the most recent advances in VOF methods and outline the various numerical challenges we expect to encounter.

1 Introduction

Figure 1:

Modeling approaches for numerical simulation of two-phase flows¹ and popular methods used in each approach. Interface capturing methods are represented as ellipses and those with colored background use a diffused interface approach while white background implies a sharp interface method.

Multiphase flows are ubiquitous in nature and in many industrial processes. Examples include but are not limited to bubbly flows^2,3, spray atomization⁴, breaking waves^5,6, ink-jet printing⁷ and rain formation⁸. Due to rapid development in high-performance computing and problem-specific algorithms, at present one can computationally study realistic two-phase flows⁹. Figure 1 gives an overview of different modeling approaches in numerical simulation of two-phase flows and popular methods in use in each approach.

Over the past 3 decades, several approaches have been developed for the numerical simulation of multiphase flows. Methods such as smooth particle hydrodynamics, two-fluid formulation, and one-fluid formulation are based on solving Navier–Stokes equations while lattice Boltzmann methods is based on solving mesoscopic kinetic equations on a lattice¹⁰. In two-fluid formulation in order to computationally simulate two-phase flows, we partition the domain into individual subdomains filled with distinct fluids. By solving Navier–Stokes equations in each subdomain and coupling the solutions at the interface using interface jump conditions, one can simulate the entire domain. The interface jump conditions are obtained using mass and momentum conservation principles. This approach was found to be extremely limiting for realistic flow simulations involving large deformations and topology changes⁹. A detailed review of two-fluid model is given by Ishii and Hibiki¹¹. Lattice Boltzmann method¹² and smoothed particle hydrodynamics^13,14 are promising and rapidly advancing modeling approaches for two-phase flow simulations.

Numerical methods for tracking interfaces in one-fluid approach can be broadly classified into interface tracking and interface capturing methods. The most popular methods in interface tracking approach are Front tracking^15,16 and Marker and Cell (MAC) methods. A detailed review of MAC method is given by Mangiavacchi et al.¹⁷. Popular interface capturing methods include volume of fluid (VOF), level-set approach, conservative level-set (CLS), phase field methods and constrained interpolation profile (CIP). An excellent review of these methods is given by Zaleski et al.¹⁸. A recent review of the state-of-the-art in one-fluid interface capturing methods is given by Dodd et al.¹. A recent review of level-set methods is given by Osher et al.¹⁹. In this article, we discuss in detail various implementation aspects of only one class of interface capturing method, namely volume of fluid (VOF) method.

This review is organized as follows. Section 2 gives a brief overview on one-fluid formulation and discuss volume of fluid method in general. Section 3 gives a brief outline of the development of VOF methods over the years and explains in detail a few important landmarks. Section 4 explains in detail the first step in VOF method, i.e., initialization of void fraction. Subsequently, Sects. 5 and 6 detail the critical steps in VOF, i.e., reconstruction of the interface and advection of void fraction, respectively. Section 7 gives a brief introduction into the numerical approximation of surface tension forces in one-fluid approach. Finally, Sect. 8 gives a brief overview of recent advances in VOF method and outlines the challenges that need to be addressed in the near future.

2 One-Fluid Formulation

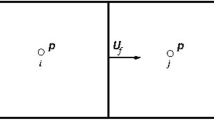
Consider a two-phase, incompressible fluid flow with a sharp (immiscible) interface between the fluid phases as shown in Fig. 2. Instead of solving the governing equations for each phase separately, one can use one set of governing equations for the whole domain with phase properties abruptly changing across the interface. Instead of using the jump conditions at the interface to conserve mass and momentum, a singular forcing term (Dirac-$\delta$ function) is added to the governing equations so as to capture the “extra” forces at the interface boundary. Thus, the use of single set of governing equations to describe the complete two-phase flow domain is called “one-fluid” formulation.

Figure 2:

Schematic showing a two-phase fluid flow domain with phases $\Omega _1$ and $\Omega _2$ separated by a sharp interface $\partial \Omega$.

Using one-fluid formulation, the modified Navier–Stokes equation governing the motion of the two fluids separated by an interface can be written as¹⁸:

$$\begin{aligned}{} & {} \rho (\phi ) \left( \frac{\partial {{\textbf {u}}}}{\partial {t}} + \varvec{\nabla \cdot }({\textbf {u}}{\textbf {u}}) \right) = -\nabla {p}\nonumber \\{} & {} + \varvec{\nabla \cdot }\left[ \mu (\phi ) \left( \nabla {{\textbf {u}}} + \nabla {{\textbf {u}}}^{T} \right) \right] +\rho (\phi ){\textbf {g}} + {\textbf {f}}^{\sigma }_{v} \end{aligned}$$

(1)

where $\phi$ represents an indicator function which is an implicit representation of the interface, $\rho (\phi )$ and $\mu (\phi )$ are the density and viscosity functions, respectively, which gives us the fluid density and viscosity at any point in the domain based on the indicator function. The capillary forces which act only at the interface are made volumetric using smoothed surface Dirac delta function, and are denoted by ${\textbf {f}}^{\sigma }_{v}$. The formulation of volumetric capillary forces and its numerical approximation will be discussed in detail in a subsequent section. Other interfacial forces such as electrohydrodynamic forces in leaky dielectric fluids in the presence of electric field are also generally included in ${\textbf {f}}^{\sigma }_{v}$.

Here, the interface position determines the value of the indicator function that we have used in the one-fluid formulation. Figure 3 represents the various ways in which we can numerically represent an interface between two fluids in one-dimensional flow. Here, the exact interface is represented by the Heaviside step function in the $i^{th}$ grid cell. This function represents the separation of the domain with fluid 1 on one side and fluid 2 on the other. The various ways in which we can numerically represent this well-defined interface are shown in the schematic.

Figure 3:

Interface representation using an indicator function I(x), a Heaviside step function H(x), a void fraction field C(x) and a level-set function $\phi (x)$.

The void fraction function is defined as the ratio of the amount of fluid 1 inside each grid cell to the total volume of the grid cell. The void fraction function has a value zero in cells that are completely filled with fluid 2 and one in cells that are completely filled with fluid 1. For every cell which contains an interface, the void fraction value lies in between zero and one. Thus, one can use an indicator function (denoted by I(x)) to numerically represent the interface. The interface can also be represented implicitly as the zero level set of a level-set function (denoted by dash–dot line), where level-set function is taken as a signed distance function which has a positive value in one fluid and negative in the other.

If we use void fraction field to represent the interface, we get a strongly discontinuous distribution of void fraction values in cells across the interface as shown in Fig. 4. since we have the underlying velocity field which advects each fluid phase, one can solve Eq. 2 to get an updated void fraction field and thus track the interface implicitly:

$$\begin{aligned} \frac{\partial {C}}{\partial {t}} + {\textbf {u}}\cdot \nabla {C} = 0 \end{aligned}$$

(2)

If we use higher order advection schemes to solve Eq. 2, we will incur too much dispersion error, due to strong discontinuity of the void fraction field across the interface thus making the void fraction field unphysical. In order to avoid this, if we choose a higher order non-oscillatory scheme to advect the interface, we observe diffusion of void fraction field across multiple cells around the interface thus losing the ability of the method to maintain a sharp interface. Thus, one needs specific algorithms and schemes to accurately advect Eq. 2 without losing the sharp nature of the interface. Based on how one advects the void fraction field and solve Eq. 2, VOF methods can be broadly classified into algebraic VOF and geometric VOF methods.

In algebraic VOF method, as the name implies, the fluxing of void fraction field through the cell faces is performed through algebraic approximation of the indicator function. Based on the flux calculation, these methods are classified as compressive schemes and THINC (tangent of hyperbola for interface capturing) schemes. Compressive schemes use the interface normal (orientation with respect to cell face) to determine the void fraction flux scheme. Examples of compressive schemes include but are not limited to high-resolution interface capturing scheme (HRIC)²⁰, compressive interface capturing scheme for arbitrary meshes (CICSAM)²¹, switching technique for advection and capturing of surfaces (STACS)²², high-resolution artificial compressive formulation (HiRAC) and modified-CICSAM (M-CICSAM)²³. Conventional algebraic VOF methods are generally not as accurate as geometric VOF methods and are subjected to stricter cell CFL number stability criteria. Recent progress in courant independent algebraic VOF schemes^24,25,26,27 looks very promising due to simplicity of implementation and computational cost. THINC schemes²⁸ are a class of algebraic VOF methods in which the fluxes through the cell faces are computed after approximating the indicator function with a hyperbolic tangent profile. THINC-based schemes have demonstrated comparable accuracy to certain geometric VOF methods without the computational cost^29,30 and has been validated for standard test cases including shear flows and vortex flows³¹. Rigorous testing and validation of THINC-based methods in realistic large-scale simulations are necessary to affirm these claims. Developing accurate algebraic VOF schemes is of great relevance due to the simplicity of implementation and computational cost and the authors feel significant progress will be made in the near future in this area.

Another way of solving Eq. 2 is to reconstruct the interface exactly from the underlying void fraction field and perform geometric flux calculation in order to update the void fraction field. This approach is often referred to as geometric VOF and in this review we will describe this interface tracking method in detail.

Figure 4:

Schematic showing a highly discontinuous void fraction field with fluid 1 cells having $C=1$ and fluid 2 having $C=0$ and interfacial cells with $0<C<1$.

Geometric advection based VOF methods have become the standard method for the numerical simulation of multiphase flows. Due to rapid development in computing power and problem-specific algorithms, even complex multiphase flows with highly disparate time and length scales can be simulated^32,33. For example, Fig. 5 shows the breakup of a liquid drop under a cross-flow, where the bag formation and subsequent atomization of droplet particles is captured numerically. Gerris³⁴, an open source multiphase solver which employs geometric VOF to capture the interface, was used to simulate the above.

Figure 5:

Numerical simulation of the disintegrating droplet under a cross-flow for Weber number, $We = 80$ at different times³⁵.

In this review, we describe the geometric VOF algorithm in detail. All the equations and examples are demonstrated for two-dimensional square grid cells. Relevant references are provided for the extension of the algorithm to three-dimensional and axisymmetric coordinate systems.

3 Volume of Fluid Method: Historical Perspective

Noh and Woodward (1976)³⁶ were first to attempt advection of void fraction using a reconstructed interface. In this method, called simple line interface construction (SLIC), the void fraction is advected by time splitting, where C is advected in each direction sequentially. During advection in the x direction a mixed cell is divided by vertical lines separating full and empty parts, based on the void fraction values of the neighboring cells. Thus, each mixed cell would have fluid occupation numbers. Now, one can reconstruct interface geometry (a vertical line) according to 3 base cases, considering left, center, and right fluid occupation numbers. Once interface is determined, Eq. 2 is solved in x-direction by time integration of fluxes. We repeat the process for y-direction using horizontal lines for interface reconstruction.

Hirt and Nichols (1981)³⁷ modified this method (coining the term volume of fluid) where reconstructed interface is parallel to the coordinate axis but same orientation is used for advection in each direction. The orientation of the interface (whether it is horizontal or vertical) was determined by finding normal to the interface (using gradient of the void fraction field in the neighboring cells) and determining whether interface is aligned more towards horizontal or vertical coordinate axis. Tests by Rudman et al.³⁸ showed that neither of these methods are particularly accurate and resulted in islands of phase 1 generated numerically called “floatsam” or “jetsam”. Even for simple flows, these islands of fluid 1 which are numerically generated can make the flow completely unphysical (Fig. 6).

Figure 6:

Reconstruction of the interface in VOF in two dimensions. a The original interface. b The original SLIC reconstruction. c Hirt and Nichols reconstruction. d The PLIC reconstruction.

Youngs (1982)³⁹ proposed the method of piecewise linear interface calculation(PLIC)¹ where the interface is represented as a line segment with arbitrary orientation. The orientation of the line segment is determined by the interface normal obtained by finding the gradient of the void fraction field. Once the interface is reconstructed, the void fraction is advected geometrically across the cell faces. Accuracy of PLIC-based methods depends on the computationally obtained interface normal and curvature accuracy.

More accurate methods for interface reconstruction like PROST (parabolic reconstruction of surface tension)⁴⁰, where interface is assumed to be a parabola and geometrical area preserving VOF method⁴¹, have been successfully used for interface reconstruction. Although more accurate, these methods have a significantly high computational cost compared to PLIC method. Hybrid methods have been proposed to combine the advantages of the VOF method with other interface tracking methods, such as coupled level-set volume of fluid method (CLSVOF)⁴² and phase field coupled with VOF⁴³. Among these hybrid methods, CLSVOF is the most widely adopted as it significantly improves the accuracy of the normal and curvature calculation⁴⁴. Although the accuracy of CLSVOF is higher than conventional VOF, the computational cost and bottlenecks in achieving parallel scalability are issues yet to be resolved. Considering the ease of implementation, computational cost and high degree of accuracy, the authors recommend using a PLIC-based VOF method⁴⁴ with geometric advection.

4 Initialization of Void Fraction

The first step in VOF method is the initialization of volume fraction in each grid cell in the computational domain. It is trivial to initialize the volume fraction field for grid cells which are lying completely inside either fluid 1 (where $C=1$) or completely inside fluid 2 (where $C=0$). For interfacial cells which contain the interface between fluid 1 and fluid 2, an accurate initialization of volume fraction is very important since initial loss of volume of a fluid can result in erroneous simulations as the flow progresses. For accurate determination of volume fraction in mixed cells, we need to compute the volume cut by the interface and the cell boundary.

Given an implicit equation of an interface, a direct method for initializing volume fraction in an interfacial cell is to distribute internal points and then volume fraction is the ratio of number of points inside the fluid 1 with total number of distributed points inside the cell. Monte Carlo methods based sampling techniques can be used to increase the accuracy of such methods⁴⁵. Another strategy is to recursively refine each grid cell locally and to use a linear line segment as an approximation of the interface in the most refined sub-cell⁴⁶. These methods while relatively easy to implement are computationally very expensive. The accuracy of these methods are directly proportional to the computational cost.

Table 1: Results for relative error in volume for a circle of radius 0.25 for different grid sizes.

A more robust method for determining the volume fraction field is by direct integration of the implicit equation of the interface. VOFI⁴⁷ is an open source library which initializes void fraction field upto machine accuracy given an implicit interface equation in square grid cells in Cartesian coordinate system using direct integration methods. For a given mixed cell, using the implicit interface equation, the local height function (see Fig. 14) is integrated with a variable number of nodes using double Gauss–Legendre quadrature rule. Table 1 shows the relative error in initialized volume fraction field between VOFI library and Gerris flow solver³⁴. We initialize a circle of radius $r=0.25$ in the center of a computational domain of size $1\times 1$. The area of the circle is given by $V_c = \pi r^2$. The accuracy of initialization can be determined by calculating the relative error in the volumes given by

$$\begin{aligned} E = \frac{\left| V - V_c \right| }{V_c} \end{aligned}$$

(3)

where V is the computed volume given by $V = \Sigma \Delta x \Delta y C$. Thus, it is quite clear that direct integration methods can initialize volume fraction fields up to machine accuracy. Ananthan and Tomar⁴⁸ proposed an algorithm using which one can extend this method to axisymmetric coordinate systems as well. An optimized version of VOFI library was recently released by Zaleski et al.⁴⁹.

5 Reconstruction

Given a volume fraction field in each grid cell in the computational domain, the first step in VOF method is the reconstruction of the PLIC-based line segment representing the interface in each mixed cell. Assume the equation of this line segment for a two-dimensional case given by

$$\begin{aligned} {\textbf {m}}.{\textbf {x}} = m_{x}x + m_{y}y = \alpha . \end{aligned}$$

(4)

Here, $m_x$ and $m_y$ are the components of the normal to the line and $\alpha$ is the line constant (Fig. 7).

Figure 7:

Reconstructed PLIC-based line segment representing the interface separating fluid 1 and fluid 2.

Since the void fraction within the cell does not provide any indication about the direction of the interface, the normals must be explicitly calculated. There exist many different methods to determine the normals, simplest approximation being the Youngs method³⁹. Here, the normal vector is given by the gradient of the volume fraction field:

$$\begin{aligned} {\textbf {m}} = -\nabla _{h}C. \end{aligned}$$

(5)

Green–Gauss gradient is used which employs a $3\times 3$ block of cells to determine the normal components at the central cell (i, j) (see Fig. 8a) as

$$\begin{aligned}{} & {} m^{x}_{i,j} = -\frac{1}{\Delta x}\nonumber \\{} & {} \quad (C_{i+1,j+1} + 2C_{i+1,j}+C_{i+1,j-1}\nonumber \\{} & {} \quad - C_{i-1,j+1} - 2C_{i-1,j} - C_{i-1,j-1}) \end{aligned}$$

(6)

$$\begin{aligned}{} & {} m^{y}_{i,j} = -\frac{1}{\Delta y}\nonumber \\{} & {} \quad (C_{i+1,j+1} + 2C_{i,j+1}+C_{i-1,j+1} \nonumber \\{} & {} \quad - C_{i+1,j-1} - 2C_{i,j-1} - C_{i-1,j-1}). \end{aligned}$$

(7)

This method is first-order accurate and can lead to drastic errors in estimation of normals. Scardovelli and Zaleski⁵⁰ introduced centered columns approach where in the same neighborhood block of cells, volume fractions can be added in a vertical/horizontal direction to determine a height/width function, respectively (see Fig. 14). Using this function, one can compute the interface normal with a centered scheme. Aulisa et al.⁵¹ introduced a method which combines Youngs method and centered columns approach, which is shown to perform accurately in both high and low resolutions. Due to low computational cost and high accuracy, this method, namely mixed Youngs centered (MYC), is widely adopted in several open source codes^34,52.

Figure 8:

Various methods in determining interface normal in PLIC-based reconstruction. a Youngs gradient method. b Least square minimization of area. c Moment of fluid method. d Spline interpolation method. Figure adapted from Comminal et al.⁵³.

Puckett et al.⁵⁴ proposed a least square VOF interface reconstruction algorithm (LVIRA) in which one minimizes the area between the extended interface into the nearby cells and the actual volume fractions in these cells (see Fig. 8b). Since the minimization requires solution of a non-linear problem, an iterative optimization algorithm is used in this method. Pilliod and Puckett⁵⁵ introduced a more efficient variation of this method called ELVIRA (Efficient LVIRA). Both LVIRA and ELVIRA are second-order accurate but computational cost is high compared to other methods especially for three-dimensional problems. Algorithm 1 discusses an efficient implementation⁵⁶ of ELVIRA algorithm of two-dimensional problems.

Algorithm 1

2D ELVIRA interface reconstruction algorithm⁵⁶

In moment of fluid interface reconstruction algorithm⁵⁷, one advects the center of mass of the liquid phase in each mixed cell. The algorithm consists of minimizing the distance $\delta$ between the center of mass of reconstructed interface and the advected center of mass, see Fig. 8c. Since a line can be determined by only two parameters (an intercept and a slope), the linear interface in a cell is actually over-determined by specifying the volume fraction and centroid; thus, an exact reconstruction of the linear interface can be computed⁵⁸. Another advantage of this method is that this algorithm does not have a dependency on the neighborhood volume fraction field. Recent studies^58,59,60 present moment of fluid method as a viable alternative for standard void fraction-based reconstruction algorithms. Alternatively, one can reconstruct the interface by spline interpolation of the slopes along the interface^61,62, see Fig. 8d. Using this algorithm, one can estimate the surface curvature more accurately which would be useful in modeling the surface tension forces.

Figure 9:

The standard case considered for interface reconstruction in which both $m_1, m_2 \ge 0$ and fluid 1 is occupying the bottom left corner of the cell.

Once the interface normal is obtained, the next step in PLIC interface reconstruction is the determination of the line constant $\alpha$. Given void fraction field and interface normals, one can enforce conservation of volume to determine the line constant geometrically. For two-dimensional square grid cell with unitary normal vector $|{\textbf {n}}|=1$, for the case $m_x,m_y \ge 0$, the volume/area enclosed by the PLIC interface is given by

$$\begin{aligned} V = \frac{\alpha ^2}{2 m_x m_y}, \end{aligned}$$

(8)

provided both the x and y intercepts of the PLIC line lie within the grid cell, that is,

$$\begin{aligned} \frac{\alpha }{ m_{x,y} } \le \Delta x. \end{aligned}$$

(9)

If this condition is not met (see Fig. 9), relevant triangular areas are subtracted from right hand side of Eq. 8 to obtain the enclosed volume. Since we know that enclosed volume is a function of the void fraction, one can analytically solve this equation to obtain a relationship between the void fraction, line constant and interface normal. Zaleski et al.⁶³ derived these relations for rectangular grids in Cartesian coordinates for a standard case ($m_x,m_y \ge 0$).

For a two-dimensional square grid cell, taking the positive normalized values of $m_{x}$ and $m_{y}$ and using the relation below, one can get the line constant $\alpha$. Let $m_{1} + m_{2} = 1,{(m_{1} \le m_{2})}$ and $A_{1} = m_{1}/{(2m_{2})}$, then,

$$\begin{aligned} \alpha&= \sqrt{2m_{1}m_{2}A} \qquad for: 0 \le A < A_{1} \end{aligned}$$

(10a)

$$\begin{aligned} \alpha&= m_{2}A + \frac{m_{1}}{2} \qquad for: A_{1} \le A \le \frac{1}{2}. \end{aligned}$$

(10b)

In practice since the normals can be negative, the geometry is mapped in to the standard case using linear transformations. Once the line constant is obtained, it is mapped back into the original configuration. Ananthan and Tomar⁴⁸ have extended this approach for axisymmetric coordinate system. Zaleski et al.⁶³ derived these relations for three-dimensional problems and Lehmann and Gekle⁶⁴ extended these relations to capture all the edge cases.

6 Advection of Void Fraction Field

Once the interface is reconstructed, the second recurring step in VOF method is the advection of void fraction. Given locally divergence-free velocity field at the cell faces of a computational grid cell of void fraction field (see Fig. 10), we advect the void fraction field geometrically using the advection equation:

Figure 10:

The control volume for a mixed cell where the void fraction values are stored in the cell center and velocities are stored in staggered positions in the cell faces.

$$\begin{aligned} \frac{\partial {C}}{\partial {t}} + {\textbf {u}}\cdot \nabla {C} = 0. \end{aligned}$$

(11)

Equation 11 can be written as

$$\begin{aligned} \frac{\partial {C}}{\partial {t}} + \nabla {\cdot ({\textbf {u}}C)} = C(\varvec{\nabla \cdot }{{\textbf {u}}}). \end{aligned}$$

(12)

Thus, one can time integrate Eq. 12 by finding the void fraction fluxes across the cell faces accurately. Based on the calculation of the fluxes of void fraction field, geometric advection methods can be classified into (a) unsplit methods⁶⁵ and (b) split methods⁵⁴. Split methods use operator splitting to advect the void fraction field in each spatial direction sequentially, while the unsplit methods advect in a single step.

Figure 11:

Unsplit advection methods with different flux polygon constructions. a Rider and Kothe⁶⁵ used staggered velocities to construct the trapezoid. b Lopez et al.⁶² introduced a method where velocities interpolated to cell vertices were used to construct the trapezoid. Figure adapted from Tryggvasson et al.¹⁸.

In unsplit method, the right hand side term in Eq. 12 goes to zero since the advection takes just a single step. Thus, in an unsplit method, the void fraction flux calculation across the cell faces involves calculation of volume/area of complex polyhedra/polygon cut by the interface. These calculations are computationally expensive and difficult to implement accurately, but the advantage being only a single advection and reconstruction step is required per timestep. Rider and Kothe⁶⁵ introduced one of the first unsplit algorithms in PLIC-based reconstruction. In this approach, face-centered velocities were used to construct trapezoids (see Fig. 11a), which were used to determine the fluxing volumes/areas. This leads to regions of overlap resulting in overshoots or undershoots and the void fraction field was not locally conserved. Lopez et al.⁶² introduced an unsplit method which uses cell vertex velocities to construct the advected polygon in two dimensions. This approach ensures no overlap between the fluxed volumes, see Fig. 11b. Owkes and Desjardins⁶⁶ extended this approach for three dimensions thus detailing a locally conservative and bounded unsplit algorithm. Interface reconstruction library is an open source code by Desjardins et al.⁶⁷ which can be used for accurate computation of the volume of complex polyhedra generated during unsplit advection.

In split method, we use operator splitting to advect the void fraction field in each spatial direction sequentially, thus the RHS term (called dilatation or divergence correction term) in Eq. 12 is needed since the velocity field is not divergence free in each direction independently. Split methods can be broadly divided into Eulerian and Lagrangian methods¹⁸. In Lagrangian methods the end points of the reconstructed interface are advected by the flow in each direction sequentially. Here, the local velocity maybe interpolated between the cell faces. A detailed overview of Lagrangian advection method is given by Tryggvasson et al.¹⁸. In Eulerian advection methods, the flux through each cell face is computed sequentially. We will be discussing Eulerian-based advection methods in detail here.

Given a volume fraction ($C_{i,j}^{n}$) and velocity field ($u_{i+1/2,j}^{n},v_{i,j+1/2}^{n}$) at the nth timestep, the discretized Eq. 12 is given by

$$\begin{aligned}&C_{i, j}^{n+1}= C_{i, j}^{n}+\frac{\Delta t}{\Delta x}\left( \delta V_{i-1 / 2, j}-\delta V_{i+1 / 2, j}\right) \\&+\frac{\Delta t}{\Delta y}\left( \delta V_{i, j-1 / 2}-\delta V_{i, j+1 / 2}\right) \\&+C_{i, j}^{n} \left( \frac{\Delta t}{\Delta x} \left( u_{i+1/2,j}^{n}-u_{i-1/2,j}^{n} \right) \right. \\&\left. + \frac{\Delta t}{\Delta y} \left( v_{i,j+1/2}^{n}-v_{i,j-1/2}^{n} \right) \right) \end{aligned}$$

(13)

where $\delta V_{i+1 / 2, j} = (uC)_{i+1/2,j}^{n}$ is the amount of volume fraction fluxed through the right cell face. Similarly, fluxes $\delta V_{i-1 / 2, j}, \delta V_{i, j+1/2}$ and $\delta V_{i, j-1/2}$ can be computed for other cell faces.

Using operator splitting, we can split the above equation as following:

$$\begin{aligned}{} & {} C_{i, j}^{*}= C_{i, j}^{n}+\frac{\Delta t}{\Delta x}\nonumber \\{} & {} \left( \delta V_{i-1 / 2, j}-\delta V_{i+1 / 2, j}\right) \nonumber \\{} & {} +C_{i, j}^{c}\left( \frac{\Delta t}{\Delta x} \left( u_{i+1/2,j}^{n} -u_{i-1/2,j}^{n} \right) \right) \end{aligned}$$

(14)

$$\begin{aligned}{} & {} C_{i, j}^{n+1}= C_{i, j}^{*}+ \frac{\Delta t}{\Delta y}\nonumber \\{} & {} \left( \delta V_{i, j-1 / 2}-\delta V_{i, j+1 / 2}\right) \nonumber \\{} & {} + C_{i, j}^{c}\left( \frac{\Delta t}{\Delta y} \left( v_{i,j+1/2}^{n} -v_{i,j-1/2}^{n} \right) \right) \end{aligned}$$

(15)

where $C_{i,j}^{*}$ is the intermediate value of the volume fraction. Here, $C_{i,j}^{c}$ is a function based on which we can get different operator splitting approaches. If $C_{i,j}^{c} = C_{i,j}^{*}$, then we get Puckett’s operator split approach⁵⁴. An implicit scheme is used in the first direction and an explicit scheme in the second direction to maintain the conservation of volume fraction⁵⁴. The order of sweep direction is alternated every timestep⁶⁸ (“Strang splitting”) to achieve second-order accuracy in time. If we use,

$$\begin{aligned} C_{i,j}^{c} = \left\{ \begin{array}{ll} 1 &{} C_{i,j}^{n} \ge 0.5\\ 0 &{} C_{i,j}^{n} < 0.5 \end{array} \right. \end{aligned}$$

(16)

where $C_{i,j}^{c}$ depends only on the previous timestep value of volume fraction, we get Weymouth and Yue’s operator split approach⁶⁹. This method is explicit in both the sweep directions.

For an operator split method to be strictly conservative, it has to fulfill (following Weymouth and Yue⁶⁹) a set of concurrent requirements:

• 1. The volume flux terms are conservative, and

• 2. the dilatation term sums to zero, and

• 3. no clipping or filling of a cell is needed to impose $0\le C \le 1$.

Using geometric advection for volume fluxing and a divergence-free velocity field, both Puckett’s and Weymouth and Yue’s methods satisfy the first two requirements. Puckett’s method does require clipping or filling of a cell to impose $0\le C \le 1$ and, therefore, is not strictly conservative. However, the mass conservation errors introduced in this method are small and thus it has been widely adopted previously. Weymouth and Yue⁶⁹ proved that, by imposing a grid Courant number restriction of,

$$\begin{aligned} \Delta t \sum _{d=1}^{N} |{ \frac{ u_d }{ \Delta x_d } }| < \frac{1}{2} \end{aligned}$$

(17)

one can satisfy the third requirement for the operator split approach to be conservative. Here, N is the number of sweep directions, and $u_d$ and $\Delta x_d$ are the maximum velocity and grid size in each of those directions. Thus, using Weymouth and Yue’s operator splitting approach, we can preserve the mass exactly when advecting the volume fraction field. Note that this method can be easily extended to three-dimensional calculations.

Figure 12:

The fluxed volume through the right face of the cell when $u_{i+1/2,j}$ is positive.

The volume flux through cell faces, $\delta V_{cell-face}$, is computed geometrically. Consider the schematic in Fig. 12, where the shaded region shows the volume of fluid-1 in the cell to be fluxed through the right face ($\delta V_{i+1/2,j}$). Considering the face velocity ($u_{i+1/2,j}$) to be positive, the flux can be computed as

$$ \delta V_{i+\frac{1}{2},j} = \frac{u_{i+1/2,j} V}{u_{i+1/2,j} \Delta t \Delta y} = \frac{V}{\Delta t \Delta y} $$

(18)

where V is the volume of fluid 1 fluxed through the right face (shown as the shaded region in Fig. 12). Since we have the equation of the PLIC line and the line of total fluxing (dashed line in Fig. 12), one can easily calculate the fluxed volume V through each face. Ananthan and Tomar⁴⁸ extended Weymouth and Yue’s approach for axisymmetric coordinate system.

Figure 13:

A few standard test cases for the validation of reconstruction and advection of void fraction.

Table 2 Results for relative error in change in volume for different test cases for $\Delta x = 0.25$ and $CFL = 0.25$

Figure 13 shows a few standard test cases for the validation of reconstruction and advection of the void fraction field. Void fraction field is initialized in a circle and subjected to underlying velocity fields and this velocity field is reversed after a certain number of timesteps for the same duration and final and initial geometries are then compared. Case (a) is a translating circle, case (b) is circle in a corner flow⁶⁹ and case (c) is circle in a vortex^65,70. Table 2 gives the relative change in volume for each of these cases for both Puckett’s method and Weymouth and Yue’s approach. Other standard test cases include Zalesak’s disk⁷¹ and three-dimensional deformation case proposed by Leveque⁷².

Note that geometric advection of void fraction conserves mass upto machine precision if the underlying discretized velocity field is divergence free. Ananthan and Tomar⁴⁸ found that as the divergence-free nature of the velocity deteriorates so does the accuracy of the geometric VOF. In practice, accuracy of the velocity field is determined by the error tolerance of the pressure Poisson equation. Thus, multiphase flow simulations require use of efficient and highly accurate pressure Poisson solvers⁷³.

7 Numerical Calculation of Surface Tension Forces

Consider one-fluid formulation of Navier–Stokes equation:

$$\begin{aligned}{} & {} \rho (\phi ) \left( \frac{\partial {{\textbf {u}}}}{\partial {t}} + \varvec{\nabla \cdot }({\textbf {u}}{\textbf {u}}) \right) = -\nabla {p}\nonumber \\{} & {} \quad + \varvec{\nabla \cdot }\left[ \mu (\phi ) \left( \nabla {{\textbf {u}}} + \nabla {{\textbf {u}}}^{T} \right) \right] \nonumber \\{} & {} \quad +\rho (\phi ){\textbf {g}} + {\textbf {f}}^{\sigma }. \end{aligned}$$

(19)

Here, ${\textbf {f}}^{\sigma }$ is the surface tension force per unit volume. Numerical approximation of the surface tension forces in two-phase flow simulations is an area which has seen considerable progress in the last 2 decades. An excellent review of these different methods is given by Popinet⁷⁴. Here, we will look into the numerical approximation of surface tension forces through volumetric formulation (body forces) since this approach ensures discrete balance of surface tension and pressure gradient terms⁷⁵.

In an elementary volume $\Omega$ intersected by the curve at two points A and B, the total surface tension force is given by $\int _\Omega {\textbf {f}}^{\sigma } = \oint _A^B \sigma d{\textbf {t}}$ where $\sigma$ is the surface tension and ${\textbf {t}}$ is the unit tangent vector. Using the first Frenet formula for parametric curves $d{\textbf {t}} = \kappa {\textbf {n}} ds$ where $\kappa$ is the curvature, ${\textbf {n}}$ is the unit normal and s the curvilinear coordinate, we get

$$\begin{aligned} \int _\Omega {\textbf {f}}^{\sigma } & = \oint _A^B \sigma \kappa {\textbf {n}} ds \\ & =\int _\Omega \sigma \kappa {\textbf {n}} \delta _s \end{aligned}$$

(20)

where $\delta _s$ is the surface Dirac $\delta$-function which is non-zero only at the interface¹⁸. For variable surface tension, tangential (Marangoni) stresses have to be included in this formulation. Afkhami et al.⁷⁶ extended this formulation for variable surface tension forces.

Based on the computation of curvature $\kappa$, the normal ${\textbf {n}}$ and the Dirac $\delta$-function, different numerical approximation for volumetric surface tension forces are obtained such as continuous surface force (CSF)⁷⁷, ghost-fluid method (GFM)⁷⁸ and smoothed Heaviside method⁷⁹. We discuss here the continuous surface force model of Brackbill et al.⁷⁷. The relation⁷⁴

$$\begin{aligned} \sigma \kappa {\textbf {n}} \delta _s = \sigma \kappa \nabla H({\textbf {x}} - {\textbf {x}}_{\textbf {s}}) \end{aligned}$$

(21)

where H is the Heaviside function and ${\textbf {x}}_{\textbf {s}}$ is the position of the interface gives a smoothed Dirac delta representation of the surface tension force. In CSF² model, we choose void fraction field, $H_{\epsilon } = C$ to represent the Heaviside function where $\epsilon = \Delta$, the grid size such that

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} H_{\epsilon } = H. \end{aligned}$$

(22)

Depending upon the choice of the numerical method, one can choose different approximations for the Heaviside function. The next step is to accurately estimate the interface curvature. One can use the relation ${\textbf {n}} = -\frac{\nabla C}{|\nabla C|}$ and $\kappa = -\nabla .{\textbf {n}}$. Even if we use a smoothed void fraction field $\tilde{C}$ as originally proposed by Brackbill et al., this approach does not result in a numerically consistent curvature estimation. A widely adopted and accurate method to estimate the curvature is to use the height function approach.

Figure 14:

Schematic showing the height function calculation for the case $|n_y| > |n_x|$ in the cell (i, j). Adapted from Afkhami et al.⁸⁰.

The height function approach is based on the simple idea that any interface can be described as a graph of a function defined in a local coordinate system. One can thus determine the derivatives of this function to estimate the curvature. Sussman⁸¹ introduced the height function approach for curvature calculation. Cummins et al.⁸² and Popinet⁸³ have analyzed and extended this approach for robust calculation of the curvature on a structured mesh. Estimation of the curvature using height function involves the following steps:

• 1. Determine the local coordinate orientation using the maximal component of the normal ${\textbf {n}}$.

• 2. Estimate the height function in this orientation by summing over the void fraction values.

• 3. Compute the curvature using central differencing.

In Fig. 14 for cell (i, j), we have $|n_y| > |n_x|$; thus, we use a $3\times 7$ stencil to compute the vertical height function $y = h(x)$. In order to compute the discrete height function, we use

$$\begin{aligned} h_i = \Delta x \sum _{k=-3}^{3} C_{i,j+k}. \end{aligned}$$

(23)

Thus, we can compute the curvature as

$$\begin{aligned} \kappa = - \frac{h_{xx}}{(1+h_x^2)^{3/2}} \end{aligned}$$

(24)

where the derivatives $h_x$ and $h_{xx}$ are computed using central differencing. Similarly, we can choose a $7\times 3$ stencil for the horizontal case. It is found that the height function approach is second-order accurate and fairly easy to implement in comparison to other methods of comparable accuracy. In order to reduce the computational expense and increase the accuracy of estimation of the curvature, one can adopt a variable stencil height function approach as described by Popinet⁸³ and Lopez et al.⁸⁴. Accuracy of curvature estimation using Height function approach deteriorates rapidly when the interface is not well resolved. Popinet⁷⁴ reported that when $\kappa \Delta x > 1/5$, it is extremely difficult to obtain consistent height functions. One has to use alternative techniques like parabolic reconstruction of interface (PROST)⁴⁰ in these scenarios. Desjardins et al.⁸⁵ introduced a mesh decoupled height function approach which is found to improve the curvature calculation for under-resolved interfaces thus alleviating this issue.

Figure 15:

The static drop test case in which a drop of diameter, $D=1$ is initialized into a domain of size $4\times 4$. The test parameters are Laplace number, $La= \frac{\rho _{liquid} D \sigma }{\mu _{liquid}^2} = 0.120$, the density and viscosity ratios are unity and $\frac{D}{\Delta x} = 30$.

Since volumetric formulation of surface tension forces are neither well balanced nor momentum conserving⁷⁴, we see spurious velocity currents generated at the interface. These numerically generated velocity currents can lead to artificial generation of kinetic energy and heat transfer^86,87. Dodd et al.⁸⁸ found that only if the root mean square velocity of the spurious currents is negligible in comparison to velocity fluctuations due to turbulence, one can resolve a turbulent flow fully. The standard benchmark test to access the accuracy of numerical implementation of surface tension forces is the static drop test case⁸⁹.

Figure 15 shows the static drop test case where we see spurious velocity currents in the long time limit. In this test case, the timescale required to reach equilibrium depends upon the oscillation timescale, $T_{\sigma } = \sqrt{\frac{\rho D^3}{\sigma }}$ and the viscous dissipation timescale $T_{\mu } = \frac{\rho D^2}{\mu }$. In order for the simulations to correspond to the equilibrium state, one needs to run the simulation longer than either of these timescales⁷⁴. As Magnini et al.⁹⁰ reported, it would be more insightful if one were to look at the time averaged norm of the spurious current than the spurious current magnitude at an instant. Detailed parameters and test case setup can be found in Lafaurie et al.⁹¹ and Popinet and Zaleski⁹². One can argue that if the current implementation of surface tension force limits the maximum magnitude of spurious current in the long time limit then it can be used accurately for simulation of multiphase flow. Other than the static drop test case one needs to look at the translated droplet test case⁸³. This test case is more relevant for practical applications and an interesting comparative study was presented in Abadie et al.⁹³. Other standard test cases include capillary oscillations of a drop/bubble in the limit of vanishing amplitude and viscosity both for planar and circular/spherical interfaces⁹⁴. Other more challenging variants can be found in Torres and Brackbill⁹⁵, Herrmann⁹⁶ and Fuster et al.³³. Another standard test case is that of the analytical solution of exponential damping of oscillatory modes of a capillary wave when viscosity is introduced. Prosperetti^97,98 derived closed-form solutions for this case and details for the test case are given in Popinet and Zaleski⁹².

8 Looking Ahead

Using VOF methods, many areas of practical interest other than two-phase flows have been extensively investigated including but not limited to heat transfer^99,100, thermocapillary motion^101,102, mass transfer^103,104, insoluble and soluble surfactants^105,106, electrohydrodynamics^107,108, boiling and evaporation^109,110,111, solidification and dendrite formation^112,113,114 and particle-laden flows¹¹⁵. In most of these cases, one needs to modify VOF or couple it with additional governing equations so as to capture the physics of the phenomenon under study. The authors anticipate significant advancements in these domains in the near future, both in terms of development of computational algorithms and in study of highly specialized areas using the VOF method.

Multiphase flows typically involve highly disparate time and length scales; thus, for numerical simulation of any realistic flow, one needs to use either unstructured grid or adaptive mesh refinement (AMR). Although VOF algorithm described here is for structured mesh, it is straight forward to adapt them for AMR grid structures. In both cell-based^34,83,116 and block-based¹¹⁷ AMR grids, geometric VOF methods have been implemented successfully. For unstructured grids, algebraic VOF is the preferred method due to inherent computational cost and difficulty of implementation of geometric VOF. In the last decade, we have seen open source tools and libraries like VOFTools^118,119 being used for geometric VOF in unstructured grids and we expect to see the community adopting these resources.

As in every other field of science and technology, machine learning (ML), Artificial intelligence (AI), and data science are rapidly adopted and used in fluid dynamics research also¹²⁰. In VOF methods, machine learning has been successfully used for the estimation of curvature^121,122,123, reconstruction of interface¹²⁴ and design of accurate schemes for advection of void fraction¹²⁵. Machine learning techniques are also being used for developing new robust predictive models for multiphase flows and reducing the overall computational effort and time¹²⁶. It is the firm belief of the authors that this is the beginning of a promising transformative paradigm and we are at its infancy.

In summary, in this review, we have given an overview of geometric VOF method and described in detail the methods and algorithms that maintain a balance between the ease of implementation, computational cost and accuracy of the solution. Using the framework of VOF method, one can tackle several interesting and relevant multiphase flow problems which in turn are expected to lead to creative extensions of these existing methods and development of entirely problem specific novel algorithms.