Co-movement of Cyclical Components Approach to Construct a Coincident Index of Business Cycles

Abstract

The accurate assessment of business conditions is a long-standing problem in macroeconomics. To construct a coincident index of growth cycles from a given set of indicators, we propose a new approach: the co-movement of cyclical components (triple-C) approach. For realizing the triple-C approach, we introduce a multi-objective optimization algorithm. We refer to the coincident index of growth cycles as the index of business cycles (IBC) of coincident economic indicators. The IBC based on the triple-C approach has the following properties: (1) its mean is globally stationary; (2) it is constructed as a common factor in the stationary parts of the selected economic indicators; and (3) its variations are as large as possible so that it contains a relatively large amount of information for business cycle analysis. We examine the performance of the constructed IBC by comparing it with a composite index based on data for coincident indicators in Japan.

1 Introduction

Following the seminal work of Burns and Mitchell (1946), the measurement of business cycles has been recognized as an important issue in macroeconomic studies. Furthermore, favorable or unfavorable business conditions are of great interest to many, because the assessment of business conditions has a significant influence on government economic policies. However, conventional indices may not accurately capture business cycles. Therefore, the question that arises is: what is a better way to produce useful and reliable indices? This is a long-standing problem and was a central question addressed by Stock and Watson (1989). In this paper, we present an alternative approach to constructing an index of business cycles (IBC) using coincident economic indicators. Specifically, we attempt to measure the growth cycles of the Japanese economy using the proposed approach. To the best of our knowledge, a monthly coincident index of growth cycles in Japan is a new development; hence, it may be of broad interest to macroeconomists and policy makers.

Conventionally, business conditions are assessed using summary measures for the state of macroeconomic activity in Japan and the United States (US). The composite index (CI) and diffusion index (DI) are representative summary measures. Although both have the advantage of manageability, they have faced criticism because they are not based on a structured statistical model. Given this, since the 1980s, many studies have been conducted on statistical methods for business cycle analysis. In Japan, business conditions are typically measured using the business cycle indices CI and DI, which are compiled by the Economic and Social Research Institute (ESRI) of the Japanese Cabinet Office. Since April 2008, the ESRI has placed greater emphasis on the CI than the DI in assessing business conditions in Japan. According to the Cabinet Office, the indicators for indices of business conditions are re-examined after each business cycle and changed if it is expected that the performance of the indices will improve. The DI and CI consist of three indices: a leading index, which is constructed based on 11 indicators, for predicting the prospective business conditions; a coincident index, which is based on 10 indicators, for assessing the present business conditions; and a lagging index, which is based on 9 indicators, for reconfirming the previous assessment of the business conditions. The DI represents the ratio of the number of indicators that increased in value during the most recent three-month period to the total number of applied indicators. Pioneering works in this area are by Stock and Watson (1989, 1991), who developed a statistical method to construct an IBC based on a state space model. Stock and Watson (1989, 1991) defined the business cycle as a co-movement of macroeconomic variables, and the Stock–Watson index is constructed by extracting the common factor hidden in multiple macroeconomic time series. Thus, their proposed model is commonly called the dynamic factor model, and it was first applied to analyze the US business cycle. Ohkusa (1992) and Fukuda and Onodera (2001) applied the Stock–Watson dynamic factor modeling approach to analyze Japanese business cycles.

The dynamic factor modeling approach has since been extended by Kanoh and Saito (1994), Mariano and Murasawa (2003, 2010), Watanabe (2003), and Urasawa (2014). Kanoh and Saito (1994) extended the dynamic factor model to include qualitative data from the Short-Term Economic Survey of Enterprises (abbreviated to Tankan), which is a statistical survey conducted by the Bank of Japan. Focusing on companies’ judgments about business conditions in Tankan, Kanoh and Saito (1994) considered that if such judgments reflect an overall assessment of actual business conditions, then a business index that statistically extracts the actual state of the economy from such judgments would be a more appropriate measure of the overall state of the economy than conventional indices. They concluded that the peaks and troughs projected by their proposed index have systematic relationships with the business cycles identified by experts from the Japanese government. Mariano and Murasawa (2003) indicated that the CI and Stock–Watson coincident indices have two shortcomings: first, they ignore information contained in quarterly indicators, such as quarterly real gross domestic product (GDP); and second, they lack economic interpretation. Therefore, Mariano and Murasawa (2003) extended the Stock–Watson coincident index by applying maximum likelihood (ML) factor analysis to a mixed-frequency series of quarterly real GDP and monthly coincident business cycle indicators. The resulting index is related to latent monthly real GDP. Furthermore, Mariano and Murasawa (2010) estimated Gaussian vector autoregression (VAR) and factor models for latent monthly real GDP and other coincident indicators using observable mixed-frequency series. For the ML estimation of a VAR model, the expectation-maximization algorithm helps to identify a good starting value for a quasi-Newton method. Mariano and Murasawa (2010) concluded that the smoothed estimate of latent monthly real GDP is a natural extension of the Stock–Watson coincident index. To obtain early estimates of Japan’s quarterly GDP growth in real time, Urasawa (2014) estimated a dynamic factor model using mixed-frequency data for GDP, industrial production, employment, private consumption, and exports. The results of a real-time forecasting exercise suggested that the model performs well.

Another prominent approach that differs from the dynamic factor modeling approach is the regime-switching modeling approach developed by Hamilton (1989). The dynamic factor modeling approach is associated with a CI-type index; however, the regime-switching modeling is associated with a DI-type index. Kim and Nelson (1998) developed a method that combined the above two approaches. Watanabe (2003) applied Kim and Nelson’s (1998) approach to the Japanese economy, and estimated a dynamic Markov switching factor model using macroeconomic data.

We note a data treatment problem regarding the Stock–Watson dynamic factor modeling approach and its extensions. Specifically, many earlier studies used differencing in time series data to obtain stationarity in cases where nonstationary data (e.g., the mean) was used for convenience. This results in a loss of significant information. In this paper, we propose an alternative approach to construct a coincident IBC via the decomposition of time series data into several possible components. In contrast to the Stock–Watson index, we consider an IBC that has the following properties: (1) it is globally stationary in the mean; (2) it is constructed using the co-movement of all the relevant coincident indicators; and (3) it has variations that are as large as possible so that it contains a relatively large amount of information for business cycle analysis.

In particular, we emphasize the importance of the measurement of growth cycles rather than classical cycles, and contribute to the field of estimation methods for a monthly coincident index of growth cycles in Japan. Major studies on issues of classical cycles and growth cycles include Harding and Pagan (2005) and Zarnowitz and Ozyildirim (2006). Harding and Pagan (2005) mentioned that many problems arise regarding a lack of clarity as to what cycle is being studied, and provided a classification scheme for cycle research. Zarnowitz and Ozyildirim (2006) indicated the importance of measuring growth cycles in business fluctuation; that is, growth cycles are more numerous than classical cycles because all recessions involve slowdowns, but not all slowdowns involve recessions. Our approach is also related to the unobserved component (UC) model of Morley et al. (2003) and multivariate UC model of Ma and Wohar (2013). Although the model used in our approach is different with the UC model in the formula, it is in fact a multivariate UC model so it belongs to the class of the UC models.

The remainder of this paper is organized as follows: In Sect. 2, we present a review of existing approaches. In Sect. 3, we explain the framework of our new approach for constructing a business cycle index. Then, we describe the parameter estimation procedure in Sect. 4. In Sect. 5, we present the results of the constructed IBC and compare the performance of the IBC based on the newly proposed approach with the CI for coincident indicators using Japanese economic data. In Sect. 6, we discuss our new approach. We present our conclusions in Sect. 7.

2 Review and Evaluation of Existing Approaches

2.1 A Review

2.1.1 Diffusion Index, Composite Index, and the MTV Model

No uniform set of official indicators is used to determine business conditions among developed countries. For example, the CI has a central role in measuring business cycles in the US, the United Kingdom, and Italy, whereas growth rates of GDP are emphasized in the measurement of business cycles in Canada.

The CI uses the same data as the DI. However, unlike the DI, which only expresses the direction of changes in indicators, the CI also indicates the degree of change. Therefore, the CI is considered to be useful in measuring the speed and magnitude of a business cycle. However, as indicated by Kanoh and Saito (1994), these indices are not derived from any sound statistical methods.

Kariya (1988, 1993) proposed a multivariate time series variance component model known as the MTV model. The basic concept of this model is that it uses principal component analysis (PCA) with time series data on macroeconomic variables. When we apply the MTV model to coincident indicators, a principal component of these indicators can be regarded as an IBC. Note that the MTV model may lead to different results depending on the component on which it focuses. Therefore, a definite conclusion cannot be obtained unless there is some objective criterion that justifies a focus on the obtained principal component.

2.1.2 Stock–Watson Approach

Stock and Watson (1989, 1991) proposed a more reliable index of business cycles that measures the state of the economy using a time series model. In this approach, the signal for business fluctuations is generally expressed by a co-movement of selected macroeconomic variables. Thus, Stock and Watson suggested decomposing macroeconomic variables into common factors and unique (idiosyncratic) factors. The common factor is considered to be derived using a single unobservable dynamic variable, which is called the state of the economy.

The Stock–Watson model contains a common factor that is expressed by an AR model, so it is called the dynamic factor model. The dynamic factor model can be expressed by a state space representation. Thus, the Kalman filter algorithm can be applied to estimate the parameters and the common factor. The estimate for the common factor is called the Stock–Watson index (SWI).

2.1.3 Classical Cycles and Growth Cycles

In empirical studies of business fluctuations, researchers need to clarify whether they are focusing on growth cycles or classical cycles (see Zarnowitz, 1991; Girardin, 2004, 2005; Harding & Pagan, 2005; Zarnowitz & Ozyildirim, 2006; Han et al., 2020). The difference between growth cycles and classical cycles is whether cycles are measured without trends. Specifically, cycles in a series excluding trends are called growth cycles, whereas those in a series including trends are called classical cycles. A growth cycle-type business index is preferable to highlight the economic wave. Additionally, as described in Girardin (2005), growth cycles provide lessons on when and how normal growth speeds up and slows down. However, to the best of our knowledge, an approach for estimating the monthly coincident index of growth cycles in Japan has not been established. We believe that our proposed method will be of broad interest to macroeconomists and policy makers.

2.2 Evaluating Existing Approaches

As mentioned in Fukuda (1994) and Komaki (2001), the approaches used to construct business cycle indices can be classified in terms of whether they consider trends and the cyclical components for an indicator as deterministic or stochastic. Specifically, DI, CI, and MTV modeling approaches are based on a deterministic perspective. By contrast, dynamic factor modeling is based on a stochastic perspective. An advantage shared by the DI and CI is their simplicity of construction. However, because they are not based on a clear statistical assumption, there can be difficulties in using them for prediction. The MTV modeling approach is based on a model involving PCA. However, generally, the data structure is not clearly defined.

Conversely, the Stock–Watson dynamic factor modeling approach is based on a state space model. Therefore, this approach is based on a set of statistical models that express the structure of the data. However, to satisfy the assumption of stationarity for the data used, many existing methods adopt an ad hoc approach to the treatment of data, such as the use of differences for the time series. Another problem with the Stock–Watson approach is the difficulty of determining whether to use differencing. Additionally, differencing a time series in first order is not a general approach to obtain stationarity because in a period of rapid economic growth, an economic variable may increase exponentially. Thus, to obtain stationarity, second differencing is considered first.

It is widely accepted that GDP is an inclusive measure of an economy’s performance and, therefore, that it can be used as a real business cycle index. However, using GDP in this manner poses a number of problems, largely because of a lack of statistical sufficiency and the conflict between the need for immediate reports and the fact that GDP statistics are published quarterly, not monthly, and there is a long lag prior to their publication. It should be noted that Mariano and Murasawa (2003, 2010) adopted GDP as an additional coincident indicator to construct a business cycle index. Although this is an excellent concept, the problem inherent in the Stock–Watson approach cannot be completely resolved because it remains based on dynamic factor modeling.

The interaction between economic growth and business cycles is always an issue in macroeconomics (see Kaihatsu et al., 2019). The difficulty with this issue is that there are no established definitions for these terms. They are also concerned with the concepts of trend and cycles for an indicator in statistical analysis. Recently, many approaches for trend-cycle decomposition have been proposed. For example, the Hodrick–Prescott filter (Hodrick & Prescott, 1997), Baxter–King approach (Baxter & King, 1999), UC modeling approach (Morley et al., 2003), and DECOMP program (see Kitagawa, 1981; Kitagawa & Gersch, 1984). In the present paper, we take the approach in the DECOMP program, that belongs to the UC modeling approach, as a base for proposing a new index of business cycles in Japan based on the concept of growth cycles.

3 Proposed Approach

3.1 Model Construction

Let $y_{it}$ denote a monthly time series, which is one of m coincident indicators with $i =1, 2, \ldots , m$. Generally, it is considered that each indicator (or its transformation) comprises nonstationary and stationary parts. Furthermore, the nonstationary part contains trend, seasonal, and cyclical components, which express a long-term tendency, a patterned variation that appears repeatedly every year, and a short-term variation caused by business cycles, respectively. In many cases, an irregular component is also taken into consideration. Kitagawa (2020, p. 204) and Kitagawa and Gersch (1984, p. 124) assumed that the cyclical component can be expressed by a stationary AR model, also called the AR component.

Let $z_{it} = g(y_{it})$ be a one-to-one transformation of the time series $y_{it}$ for the i-th indicator. Based on the above consideration, the model for $z_{it}$ can be written as a seasonal adjustment model (see Kitagawa, 2020, pp. 195–210). In many cases of business cycle analysis, the time series $z_{it}$ has been seasonally adjusted; hence, the model is written as follows:

$$\begin{aligned} z_{it} = \tau_{it} + a_{it} + \varepsilon_{it} \quad (i=1,2\ldots ,m), \end{aligned}$$

(1)

where $\tau _{it}$ and $a_{it}$ denote the trend and cyclical components, respectively, and $\varepsilon _{it}$ denotes the irregular component (also called observation noise). For statistical analysis, observation noise $\varepsilon _{it}$ is assumed to be a random variable distributed with $\varepsilon _{it} \sim \text{ N }(0,\sigma _{i}^{2})$. Note that the function $g(\cdot )$ is determined so that $z_{it} = g(y_{it})$ can be reasonably expressed in an additive multi-component form, as expressed in Eq. (1). As an example, a logarithmic function is frequently applied to $g(\cdot )$.

To obtain meaningful estimates for every component, we use several models for each component based on the assumptions as follows: As is typical for economic analysis, we assume that the trend component varies smoothly over time and that the cyclical component is stationary. Hence, we introduce a stochastic difference equation for the trend component. As mentioned in Sect. 2.1.2, in a period of rapid economic growth an economic variable may increase exponentially. It may be difficult to express the behavior of the trend using a first-order difference equation. Thus, we introduce a second-order equation as follows:

$$\begin{aligned} \Delta ^{2} \tau _{it} = \omega _{it} \quad (i=1,2,\ldots ,m), \end{aligned}$$

(2)

where $\Delta$ denotes the difference operator and $\omega _{it}$ denotes a random error distributed with $\omega _{it} \sim \text{ N }(0, \phi _{i}^{2})$. Furthermore, we use an AR model for $a_{it}$ as follows:

$$\begin{aligned} a_{it} = \sum _{j=1}^{q_{i}} \beta _{j}^{(i)} a_{i(t-j)} + \psi _{it} \quad (i=1,2,\ldots ,m), \end{aligned}$$

(3)

where $q_{i}$ is the model order, $\{\beta _{j}^{(i)}; j=1,2,\ldots ,q_{i}\}$ are the AR coefficients, and $\psi _{it}$ is Gaussian white noise distributed with $\psi _{it} \sim \text{ N }(0, \eta _{i}^{2})$.

The model in Eqs. (1)–(3) describes the structure to decompose the time series $z_{in}$ into two meaningful unobserved components, hence it is essentially a UC model. The model in Eq. (1) is an observation model for the time series $z_{it}$, and the models in Eqs. (2) and (3) can be considered as models for the trend $t_{it}$ and cyclical $a_{it}$ components, respectively. Clearly, Eqs. (1)–(3) take the form of a linear Gaussian model for the trend and cyclical components. For the case in which the model for each value of i is individually managed, Kitagawa (2020, p. 163) developed a ML method to estimate the parameters $\sigma _{i}^{2}$, $\phi _{i}^{2}$, $\eta _{i}^{2}$, and $\{\beta _{j}^{(i)}; j=1,2,\ldots ,q_{i}\}$ based on the Kalman filter algorithm.

As mentioned in Sect. 1, Stock and Watson (1989, 1991) defined the SWI as co-movements in a set of macroeconomic variables. Therefore, it is constructed by extracting a common factor that is hidden in multiple macroeconomic time series data. In contrast to the Stock–Watson approach, we consider that economic cycles can be organized using the basic classification of short and long-term cycles. Short-term cycles generally mean business cycles or business fluctuations. Thus, to simplify the analysis of business fluctuations, it is necessary to separate business cycles from other economic cycles in the longer term.

Therefore, based on the concept of growth cycles, we expect that an index for business fluctuations would have the following properties:

• 1. It is globally stationary in the mean.

• 2. It is as a co-movement of the stationary parts of the various economic indicators used.

• 3. It has variations that are as large as possible so that it contains a relatively large amount of information for business cycle analysis.

Thus, to construct an IBC using the co-movement of cyclical components in the time series for selected coincident indicators, we take the common factor of the cyclical components $\{a_{it}; i=1,2\ldots ,m\}$. Hence, we can consider a factor analysis model for $\{a_{it}; i=1,2\ldots ,m\}$. However, the estimation of such a comprehensive model is difficult; hence, we need some simplification for the estimation. This difficulty can be mitigated by applying the PCA method to the estimates for $\{a_{it}; i=1,2\ldots ,m\}$. The first principal component can be considered as an estimate of the common factor; thus, it can be used as the IBC.

To derive an index that is free from the scale of the data, we construct the IBC based on the results of normalized cyclical components; that is, we normalize the cyclical components as follows:

$$\begin{aligned} a_{it}^{*} = \frac{a_{it}}{\text{ SD }\{a_{it}\}} \quad (i=1,2,\ldots ,m), \end{aligned}$$

(4)

where $\text{ SD }\{a_{it}\}$ is the standard deviation of the time series $\{a_{it}\}$. Then, we construct the IBC using the first principal component of the normalized cyclical components $\{a_{it}^{*}; i=1,2,\ldots ,m\}$ as follows:

$$\begin{aligned} b_{t} = \sum _{i=1}^{m} w_{i} a_{it}^{*}, \end{aligned}$$

(5)

where $\{w_{i}; i=1,2,\ldots ,m\}$ denotes the principal component loadings for the first principal component, in which $\sum _{i=1}^{m} w_{i}^{2} = 1$.

Hereinafter, we refer to the index $b_{t}$ defined in Eq. (5) as the IBC, and call the method to construct the IBC the co-movement of cyclical components (triple-C) approach. In the following estimation procedure, we regard the cyclical component as a stationary AR process with mean zero so that the IBC is a stationary process with mean zero. Thus, the IBC coincides with the concept of growth cycles, and as with the CI, it can measure the speed and magnitude of business fluctuations. Moreover, we regard the zero level for the IBC as the midpoint between states of prosperity and depression.

3.2 Outline for Parameter Estimation

To estimate the parameters in the models in Eqs. (1)–(3), we introduce the following assumptions:

• 1. $\varepsilon _{it}$, $\omega _{it}$, and $\psi _{it}$ are independent of each other for all values of i and t.

• 2. $\varepsilon _{it_{1}}$ and $\varepsilon _{{\ell }t_{2}}$ are independent of each other when $i \ne \ell$ or $t_{1} \ne t_{2}$.

• 3. $\omega _{it_{1}}$ and $\omega _{{\ell }t_{2}}$ are independent of each other when $i \ne \ell$ or $t_{1} \ne t_{2}$.

• 4. $\psi _{it_{1}}$ and $\psi _{{\ell }t_{2}}$ are independent when $i = \ell$ for $t_{1} \ne t_{2}$, but may be dependent when $i \ne \ell$ for any values of $t_{1}$ and $t_{2}$.

• 5. The parameters $\sigma ^{2}_{i}$, $\phi ^{2}_{i}$, $\eta ^{2}_{i}$, and $\{\beta _{j}^{(i)}; j=1,2,\ldots , q_{i}\}$ are constant over time.

Under the above assumptions, except for $\tau _{it}$ and $a_{it}$, $q_{i}+3$ parameters exist for each indicator. When the values of these parameters are given, we can obtain the estimates for $\tau _{it}$ and $a_{it}$. Hereafter, for each value of i, we refer to $\tau _{it}$ and $a_{it}$ as latent variables, and $\sigma _{i}^{2}$, $\phi _{i}^{2}$, $\eta _{i}^{2}$, and $\{\beta _{j}^{(i)}; j=1,2,\ldots ,q_{i}\}$ as parameters.

The fourth assumption is based on the consideration that, among the cyclical components $a_{it}$ with $i=1,2,\ldots ,m$, there is a common factor to be estimated. Thus, in principle, $\tau _{it}$ and $a_{it}$ should be estimated simultaneously for all time points and all values of $i=1,2,\ldots ,m$; that is, let the sample size for the time series $y_{it}$ be N. Then it is necessary to estimate $\tau _{it}$ and $a_{it}$ for $t=1,2,\ldots ,N$ and $i=1,2,\ldots ,m$ simultaneously based on the estimates for the $\sum _{i}^{m}q_{i}+3m$ parameters. This is very difficult in practice.

To mitigate the estimation difficulties, we develop a new estimation technique that combines the ML method and PCA. A key quantity is the ratio of the variance of error in the cyclical component to that in the trend component; that is, for $i =1,2,\ldots ,m$, the proportion

$$\begin{aligned} \lambda _{i} = \frac{\phi _{i}^{2}}{\eta _{i}^{2}} \end{aligned}$$

(6)

is a key parameter for the present problem. By introducing this parameter, we can control the relative variations in the trend and cyclical components and, therefore, maintain the balance between the variances of errors.

As mentioned in the preceding subsection, our first objective in this study is to obtain the IBC in Eq. (5) with a relatively large variance, and our second is to fit the models to the data with a large goodness of fit. Thus, we propose a numeric optimization method for the parameter estimation as follows. We first estimate the ratio $\lambda _{i}$ by maximizing the variance of the IBC in Eq. (5) for given values of the other parameters. Then, we estimate the other parameters by maximizing the likelihood under the estimate of the parameter $\lambda _{i}$ in the early stage. Thus, this scheme of parameter estimation is essentially as a hierarchical optimization (HO) method (see Friesz, 1992). We introduce the algorithm for parameter estimation in Sect. 4.3 in detail.

Moreover, as we show in the following section, a set of initial values for the cyclical components $a_{in}$ is necessary for parameter estimation. As the initial values for $a_{it} \ (i=1,2,\ldots ,m)$, we use the differences between $z_{it}$ and its moving average with term $2L+1$:

$$\begin{aligned} {\widehat{a}}_{it}^{(0)} = z_{it} - \frac{1}{2L+1}\sum _{\ell =-L}^{L}z_{i(t+\ell )} \end{aligned}$$

(7)

for $t = L+1, L+2, \ldots , N-L$; otherwise, we use ${\widehat{a}}_{it}^{(0)} = 0$.

4 Estimation Method

4.1 Estimating the Trend and Cyclical Components

To simplify the estimation process, we tentatively assume that the parameters can be estimated individually for the model of each indicator with $i=1, 2, \ldots , m$. To express the model in a state space representation, we define the state vector based on related quantities in the trend and cyclical components as follows:

$$\begin{aligned} {\varvec{x}}_{it} = (\tau _{it}, \tau _{i(t-1)}, a_{it}, a_{i(t-1)}, \ldots , a_{i(t-q_{i}+1)})^{\texttt {T}}, \end{aligned}$$

and we use the following matrices:

$$\begin{aligned} {\varvec{F}}_{i} = \left[ \begin{array}{ccccccc} 2 &{} \quad -1 &{} \quad 0 &{}\quad \cdots &{}\quad \cdots &{} \quad \cdots &{}\quad 0 \\ 1 &{} \quad 0 &{} \quad 0 &{} \quad \cdots &{}\quad \cdots &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \beta _{1}^{(i)} &{}\quad \beta _{2}^{(i)} &{}\quad \cdots &{} \quad \cdots &{} \quad \beta _{q_{i}}^{(i)} \\ \vdots &{}\quad \vdots &{}\quad 1 &{} \quad 0 &{}\quad \cdots &{} \quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{} \quad 0 &{} \quad 1 &{}\quad \ddots &{} &{}\quad \vdots \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad \cdots &{} \quad 0 &{} \quad 1 &{}\quad 0 \\ \end{array} \right] , \ \ {\varvec{G}} = \left[ \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 0 \\ 0 &{}\quad 1 \\ 0 &{}\quad 0 \\ \vdots &{}\quad \vdots \\ \vdots &{}\quad \vdots \\ 0 &{} \quad 0 \\ \end{array} \right] , \ \ {\varvec{H}} = \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \\ \vdots \\ \vdots \\ 0 \end{array} \right] ^{\texttt {T}}. \end{aligned}$$

Moreover, to reduce the number of parameters that have to be estimated using numeric methods, we follow Kitagawa (2020, p. 165) and combine

$$\begin{aligned} {\widetilde{\varepsilon }}_{it} = \frac{\varepsilon _{it}}{\sigma _{i}}, \quad {\widetilde{\omega }}_{it} = \frac{\omega _{it}}{\sigma _{i}}, \quad {\widetilde{\psi }}_{it} = \frac{\psi _{it}}{\sigma _{i}}, \end{aligned}$$

with

$$\begin{aligned} {\widetilde{\phi }}^{2}_{i} = \frac{\phi ^{2}_{i}}{\sigma ^{2}_{i}}, \quad {\widetilde{\eta }}^{2}_{i} = \frac{\eta ^{2}_{i}}{\sigma ^{2}_{i}}. \end{aligned}$$

(8)

Then, the models in Eqs. (1)–(3) can be expressed by the following state space representation:

$$\begin{aligned} {\varvec{x}}_{it}\,=\, & {} {\varvec{F}}_{i} {\varvec{x}}_{i(t-1)} + {\varvec{G}} {\varvec{v}}_{it}, \end{aligned}$$

(9)

$$\begin{aligned} z_{it}\,=\, & {} {\varvec{H}} {\varvec{x}}_{it} + {\widetilde{\varepsilon }}_{it}, \end{aligned}$$

(10)

where ${\varvec{v}}_{it} = ({\widetilde{\omega }}_{it}, {\widetilde{\psi }}_{it})^{\texttt {T}}$. In the state space model comprising Eqs. (9) and (10), the latent variables $t_{it}$ and $a_{it}$ are included in the state vector ${\varvec{x}}_{it}$. Therefore, we can obtain their estimates from the estimate of ${\varvec{x}}_{it}$ under the assumption that the AR model order $q_{i}$ and the parameters ${\widetilde{\phi }}_{i}^{2}$, ${\widetilde{\eta }}_{i}^{2}$, and ${\varvec{\beta }}^{(i)} = (\beta _{1}^{(i)}, \beta _{2}^{(i)}, \ldots , \beta _{q_{i}}^{(i)})^{\texttt {T}}$ are given.

Let ${\varvec{x}}_{i0}$ denote the state at the initial time point and let $Z_{ik} = \{z_{i1}, z_{i2}, \ldots , z_{ik}\}$ denote a set of transformed observations for $z_{it}$ up to time point k. We assume that ${\varvec{x}}_{i0} \sim \text{ N }({\varvec{x}}_{i(0|0)}, {\varvec{C}}_{i(0|0)})$. It is well known that the density function $f({\varvec{x}}_{it}|Z_{ik})$ for the state ${\varvec{x}}_{it}$, conditional on $Z_{ik}$, is Gaussian and, therefore, it is only necessary to obtain the mean ${\varvec{x}}_{i(t|k)}$ and the covariance matrix ${\varvec{C}}_{i(t|k)}$ of ${\varvec{x}}_{it}$ with respect to $f({\varvec{x}}_{in}|Z_{ik})$.

When we provide the values of $q_{i}$, ${\widetilde{\phi }}_{i}^{2}$, ${\widetilde{\eta }}_{i}^{2}$, and ${\varvec{\beta }}^{(i)}$, the distribution $\text{ N }({\varvec{x}}_{i(0|0)}, {\varvec{C}}_{i(0|0)})$ for ${\varvec{x}}_{i0}$, and a set of observations for $z_{it}$ up to the time point N, we can obtain the estimates for the state ${\varvec{x}}_{it}$ using the well-known Kalman filter (for $t=1,2,\ldots ,N$) and fixed-interval smoothing (for $t=N-1, N-2, \ldots , 1$) recursively as follows (see Kitagawa, 2020, pp. 156–158):

[Kalman filter]

$$\begin{aligned} {\varvec{x}}_{i(t|t-1)}\,=\, & {} {\varvec{F}}_{i} {\varvec{x}}_{i(t-1|t-1)}, \\ {\varvec{C}}_{i(t|t-1)}\,=\, & {} {\varvec{F}}_{i} {\varvec{C}}_{i(t-1|t-1)} {\varvec{F}}_{i}^{\texttt {T}} + {\varvec{G}} {\varvec{Q}}_{i} {\varvec{G}}^{\texttt {T}}. \\ {\varvec{L}}_{it}\,=\, & {} {\varvec{C}}_{i(t|t-1)} {\varvec{H}}^{\texttt {T}} ({\varvec{H}} {\varvec{C}}_{i(t|t-1)} {\varvec{H}}^{\texttt {T}} + {\varvec{R}}_{i})^{-1}, \\ {\varvec{x}}_{i(t|t)}\,=\, & {} {\varvec{x}}_{i(t|t-1)} + {\varvec{L}}_{it} (z_{it} - {\varvec{H}} {\varvec{x}}_{i(t|t-1)}), \\ {\varvec{C}}_{i(t|t)}\,=\, & {} ({\varvec{I}} - {\varvec{L}}_{it} {\varvec{H}}) {\varvec{C}}_{i(t|t-1)}; \end{aligned}$$

[Fixed-interval smoothing]

$$\begin{aligned} {\varvec{P}}_{it}\,=\, & {} {\varvec{C}}_{i(t|t)} {\varvec{F}}_{i}^{\texttt {T}} {\varvec{C}}_{i(t+1|t)}^{-1}, \nonumber \\ {\varvec{x}}_{i(t|N)}\,=\, & {} {\varvec{x}}_{i(t|t)} + {\varvec{P}}_{it} ({\varvec{x}}_{i(t+1|N)} - {\varvec{x}}_{i(t+1|t)}), \nonumber \\ {\varvec{C}}_{i(t|N)}\,=\, & {} {\varvec{C}}_{i(t|t)} + {\varvec{P}}_{it} ({\varvec{C}}_{i(t+1|N)} - {\varvec{C}}_{i(t+1|t)}) {\varvec{P}}_{it}^{\texttt {T}}, \end{aligned}$$

where ${\varvec{R}}_{i} = \sigma _{i}^{2}$, ${\varvec{Q}}_{i} = \text{ diag }({\widetilde{\phi }}_{i}^{2}, {\widetilde{\eta }}_{i}^{2})$, and ${\varvec{I}}$ denotes an identity matrix.

Then, the smoother distribution of ${\varvec{x}}_{it}$ can be defined using ${\varvec{x}}_{i(t|N)}$, which is the mean vector, and ${\varvec{C}}_{i(t|N)}$, which is the covariance matrix. Subsequently, estimates for $\tau _{it}$ and $a_{it}$ can be obtained from ${\varvec{x}}_{i(t|N)}$ because the state space model described by Eqs. (9) and (10) incorporates $\tau _{it}$ and $a_{it}$ in the state vector ${\varvec{x}}_{it}$. Hereinafter, the estimates of $\tau _{it}$ and $a_{it}$ are denoted by ${\widehat{\tau }}_{it}$ and ${\widehat{a}}_{it}$, respectively.

4.2 Estimating the parameters

For $i=1,2, \ldots ,m$, Eqs. (6) and (8) lead to $\lambda _{i} = \frac{{\widetilde{\phi }}_{i}^{2}}{{\widetilde{\eta }}_{i}^{2}}$. Thus, ${\widetilde{\phi }}_{i}^{2}(\lambda _{i}) = \lambda _{i} {\widetilde{\eta }}_{i}^{2}$; that is, ${\widetilde{\phi }}_{i}^{2}$ corresponds to $\lambda _{i}$ one-to-one for the given value of ${\widetilde{\eta }}_{i}^{2}$. Therefore, we regard $\lambda _{i}$ as a parameter instead of ${\widetilde{\phi }}_{i}^{2}$. When the values of $q_{i}$, $\sigma _{i}^{2}$, and $\lambda _{i}$ together with the time series data $Z_{iN} = \{z_{i1}, z_{i2}, \ldots , z_{iN}\}$ are given, the likelihood function for the hyperparameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$, which is derived from the algorithm of the Kalman filter, is as follows:

$$\begin{aligned} f_{i}\big (Z_{iN} |{\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\big ) = \prod _{t=1}^{N} f_{it}\big (z_{it}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i(t-1)}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\big ), \end{aligned}$$

where $f_{it}(z_{it}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i(t-1)}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i}))$ is the conditional density function of $z_{it}$ given past history $Z_{i(t-1)} = \{\ldots , z_{i(t-2)}, z_{i(t-1)}\}$ and the parameters. We assume that $Z_{i0} = \{\ldots , z_{i(-1)}, z_{i0}\}$ is an empty set. Then,

$$\begin{aligned} f_{i1}\left( z_{i1}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i0}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\right) = f_{i1}\left( z_{i1}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\right) . \end{aligned}$$

By taking the logarithm of $f_{i}(Z_{iN} | {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i}))$, we obtain the log-likelihood as follows:

$$\begin{aligned} LL_{i}\left( {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}|\sigma _{i}^{2}, \lambda _{i}\right)= & {} \log f_{i}\left( Z_{iN} | {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\right) \nonumber \\= & {} \sum _{t=1}^{N}\log f_{it}\left( z_{it}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i(t-1)}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\right) . \end{aligned}$$

(11)

Following Kitagawa (2020, pp. 163–166), when the Kalman filter is achieved, the conditional density $f_{it}(z_{it}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i(t-1)}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i}))$ has a normal density given by

$$\begin{aligned} f_{it}\big (z_{it}| {\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}; Z_{i(t-1)}, \sigma _{i}^{2}, {\widetilde{\phi }}_{i}^{2}(\lambda _{i})\big ) = \frac{1}{\sqrt{2\pi \sigma _{i}^{2} w_{i(t|t-1)}}}\exp \Bigg \{ - \frac{(z_{it} - {\widehat{z}}_{i(t|t-1)})^{2}}{2 \sigma _{i}^{2} w_{i(t|t-1)}} \Bigg \}, \end{aligned}$$

(12)

where ${\widehat{z}}_{i(t|t-1)}$ is the one-step ahead prediction for $z_{it}$ and $w_{i(t|t-1)}$ is the variance of the predictive error. They are given respectively by

$$\begin{aligned} {\widehat{z}}_{i(t|t-1)} = {\varvec{H}} {\varvec{x}}_{i(t|t-1)}, \quad w_{i(t|t-1)} = {\varvec{H}} {\varvec{C}}_{i(t|t-1)} {\varvec{H}}^{\texttt {T}} + \sigma _{i}^{2}. \end{aligned}$$

Thus, under a given value of $\lambda _{i}$ together with $\sigma _{i}^{2} = 1$ which is a provisional setting for $\sigma _{i}^{2}$, we obtain the estimates of the parameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$ numerically using the ML method; that is, we estimate the parameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$ numerically by maximizing $LL_{i}({\widetilde{\eta }}_{i}^{2}, {\varvec{\beta }}^{(i)}|\sigma _{i}^{2}, \lambda _{i})$ in Eq. (11) together with Eq. (12). Furthermore, based on Kitagawa (2020, pp. 163–166), we obtain the estimate ${\widehat{\sigma }}_{i}^{2}$ for $\sigma _{i}^{2}$ analytically using

$$\begin{aligned} {\widehat{\sigma }}_{i}^{2} = \frac{1}{N} \sum _{t=1}^N \frac{(z_{it} - {\widehat{z}}_{i(t|t-1)})^{2}}{w_{i(t|t-1)}}. \end{aligned}$$

(13)

It is notable that we can increase the efficiency of estimating ${\varvec{\beta }}^{(i)}$ by applying the fast recursive estimation method proposed by Kyo and Noda (2011). Additionally, let $\widehat{{\widetilde{\tau }}}_{i}^{2}$ and ${\widehat{\lambda }}_{i}$ denote the estimates of ${\widetilde{\tau }}_{i}^{2}$ and $\lambda _{i}$, respectively. Then, from the above settings, the estimates for $\eta _{i}^{2}$ and $\tau _{i}^{2}$ are given by

$$\begin{aligned} {\widehat{\eta }}^{2}_{i} = {\widehat{\sigma }}_{i}^{2} \widehat{{\widetilde{\eta }}}_{i}^{2}, \quad {\widehat{\phi }}_{i}^{2} = {\widehat{\sigma }}_{i}^{2} \widehat{{\widetilde{\phi }}}_{i}^{2} = \frac{\widehat{{\widetilde{\phi }}}_{i}^{2} }{ \widehat{{\widetilde{\eta }}}_{i}^{2}} {\widehat{\sigma }}_{i}^{2} \widehat{{\widetilde{\eta }}}_{i}^{2} = {\widehat{\lambda }}_{i} {\widehat{\eta }}_{i}^{2}, \end{aligned}$$

(14)

respectively.

Clearly, the estimates for the parameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$ depend on the value of $\lambda _{i}$. Furthermore, from the Kalman filter algorithm, we can see that the estimates for the elements of the state vector constitute a set of functions of $\lambda _{i}$; that is, under a given value of $\lambda _{i}$, we can estimate the parameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$. Thus, as a function of $\lambda _{i}$, we can obtain the estimate for the cyclical component $a_{it}$ using the Kalman filter and fixed-interval smoothing. We assume that the estimates of the cyclical components for the other indicators (except that of the i-th) are given in advance. Hence, we normalize the estimates of the cyclical components using Eq. (4), and then apply PCA to the normalized estimates of the cyclical components. Then, we take the first principal component as $b_{t}$ defined in Eq. (5), which is called the IBC.

As mentioned in Sect. 3.1, as a measurement of business fluctuations, we expect that our IBC will have relatively large variations. Therefore, we obtain the estimate ${\widehat{\lambda }}_{i}$ of the parameter $\lambda _{i}$ by numerically maximizing the variance $\text{ Var }\{b_{t}\}$ of $b_{t}$, and simultaneously, we determine the order $q_{i}$ for the AR model. Note that we perform the above computation for parameter estimation iteratively because it has to be run for $i = 1, 2, \ldots , m$ recursively.

4.3 The Algorithm

To run the scheme for parameter estimation, the algorithm for the triple-C approach based on a numeric HO method is summarized as follows:

• 1. Assume $k = 0$, set an appropriate value for L, and then set the initial values:

  $$\begin{aligned} \{{\widehat{a}}_{it}^{(0)}; t=1, 2, \ldots ,N; i=1,2,\ldots ,m\} \end{aligned}$$

  for the cyclical components using Eq. (7), where N is the length of the time series data.

• 2. For $i=1,2,\ldots ,m$, perform the following steps.

• 3. Replace the value of k with $k + 1$.

  • (a) Estimate the parameters ${\widetilde{\eta }}_{i}^{2}$ and ${\varvec{\beta }}^{(i)}$ numerically by maximizing the log-likelihood in Eq. (11) together with Eq. (12) under the given value of $\lambda _{i}$.

  • (b) Compute the estimate of $\sigma _{i}^{2}$ using Eq. (13).

  • (c) Obtain the estimates $\{{\widehat{a}}_{it}^{(k)}; t=1,2,\ldots ,N\}$ for the cyclical component $a_{in}$ using the Kalman filter and a fixed-interval smoothing algorithm.

  • (d) Compute the normalized values $\{{\widehat{a}}_{it}^{*(k)}; t=1,2,\ldots ,N\}$ for $\{{\widehat{a}}_{it}^{(k)}$; $t=1,2,\ldots ,N\}$ using Eq. (4).

  • (e) Perform PCA for

    $$\begin{aligned} {\varvec{a}}_{t}^{*(i,k)} = \left\{ \begin{array}{ll} \big ({\widehat{a}}_{1t}^{*(k)}, {\widehat{a}}_{2t}^{*(k-1)}, \ldots {\widehat{a}}_{mt}^{*(k-1)}\big )^{\texttt {T}} &{}\quad \text{ if } \ \ i = 1, \\ \big ({\widehat{a}}_{1t}^{*(k)}, {\widehat{t}}_{2t}^{*(k)}, {\widehat{a}}_{3t}^{*(k-1)},\ldots {\widehat{a}}_{mt}^{*(k-1)}\big )^{\texttt {T}} &{}\quad \text{ if } \ \ i = 2, \\ \big ({\widehat{a}}_{1t}^{*(k)}, \ldots , {\widehat{a}}_{it}^{*(k)}, {\widehat{a}}_{(i+1)t}^{*(k-1)}, \ldots {\widehat{a}}_{mt}^{*(k-1)}\big )^{\texttt {T}} &{}\quad \text{ if } \ \ 2< i < m-1, \\ \big ({\widehat{a}}_{1t}^{*(k)}, \ldots , {\widehat{a}}_{(m-1)t}^{*(k)}, {\widehat{a}}_{mt}^{*(k-1)}\big )^{\texttt {T}} &{}\quad \text{ if } \ \ i= m-1, \\ \big ({\widehat{a}}_{1t}^{*(k)}, {\widehat{a}}_{2t}^{*(k)}, \ldots , {\widehat{a}}_{mt}^{*(k)}\big )^{\texttt {T}} &{}\quad \text{ if } \ \ i= m. \end{array} \right. \end{aligned}$$

    Consider $\{{\varvec{a}}_{t}^{*(i,k)}; t=1,2,\ldots ,N\}$ as a set of m-variate time series data, and then obtain

    $$\begin{aligned} b_{t}^{(i,k)} = {\varvec{w}}^{\texttt {T}} {\varvec{a}}_{t}^{*(i,k)} \end{aligned}$$

    as the first principal component of ${\varvec{a}}_{t}^{*(i,k)}$, where ${\varvec{w}} = (w_{1}, w_{2}, \ldots , w_{m})^{\texttt {T}}$ is the vector of principal component loadings and $\text{ Var }\{b_{t}^{(i,k)}\}$ is its variance.

  • (f) Estimate $\lambda _{i}$ and $q_{i}$ by numerically maximizing $\text{ Var }\{b_{t}^{(i,k)}\}$.

• 4. When the value of $\text{ Var }\{b_{t}^{(m,k)}\}$ almost converges to a fixed level, proceed to the next step; otherwise, return to step 2.

• 5. End the calculation and take the estimates corresponding to the values of $\lambda _{i}$ and $q_{i}$ as the final results.

• 6. Calculate the estimates for $\eta _{i}^{2}$ and $\phi _{i}^{2}$ using Eq. (14).

Note that we implemented this algorithm using a program that was written in R and it is used for real data analysis, as we illustrate in the next section.

5 IBC Results for Japan

5.1 Data Used for Analysis

In this paper, we focus on the analysis of business cycles in Japan using the proposed approach. We consider time series data for the coincident indicators, which are listed in Table 1, as the main materials, and use the coincident CI as an objective for comparing the performance with our IBC. We use GDP data as references.

The functions we use to transform the coincident indicators in the model in Eq. (6) are also shown in Table 1. To construct the additive multi-component form in Eq. (6) and equalize the error variance for each component over time, we use a logarithmic transformation as the function $g(\cdot )$ for most indicators, excluding C6 and C7, which contain some negative values; hence, the logarithmic transformation cannot be applied. We use the data for the indicators in the period January 1975 to December 2019. Figure 1 shows the transformed time series data for the indicators. Note that we obtained the original data for the indicators from the website of the ESRI, Cabinet Office, Government of Japan (https://www.esri.cao.go.jp/jp/stat/di/di.html).

Table 1 Outlines of the indicators

Fig. 1

Transformed time series data for the indicators

In Japan, monthly CI estimates are constructed from January 1985 and published on the same ESRI website as that for the indicators. Thus, as the objective for comparing the performance with our IBC, we can only use the estimated results for the CI in Japan in the period January 1985 to December 2019. Figure 2 shows the monthly time series of the coincident CI in Japan during this period.

Fig. 2

Time series data for the CI in Japan (January 1985 to December 2019)

We obtained quarterly time series data for GDP from another part of the website of the Cabinet Office, Government of Japan (https://www.esri.cao.go.jp/jp/sna/data/data_list/sokuhou/files/2001/qe011/gdemenuja.html). However, we could not obtain the entire set of time series data throughout the analyzed period. Thus, we obtained two sets of data as follows: one was the dataset for the period Q1, 1955 to Q4, 2000 (with the net asset value in 1990 of 10 hundred million Yen), and the other was the dataset for the period Q1, 1994 to Q4, 2019 (with the net asset value in 2005 of 10 hundred million Yen). The data for the time series of the logarithm of GDP are shown in Fig. 7a and b, respectively.

5.2 Constructing the Coincident IBC

To obtain the result of our IBC for the Japanese data, we apply our triple-C approach to the transformed data of 10 coincident indicators during the period January 1975 to June 2019 that are shown in Table 1 and Fig. 1.

As expressed in the algorithm in Sect. 4.3, the computation for parameter estimation is based on a set of initial values of the cyclical components using Eq. (7) in which the value of L is determined as $L = 12$. Then, the parameter estimation is computed by repetition. The result indicates that the variance of the IBC converges to a limited larger value (approximately 6.55) and it stabilizes from the sixth repetition.

For reference purposes, the main results for the hyperparameters in the models for the indicators are listed in Table 2, where i denotes the number of indicators. Note that we set the upper limit of the parameter $\lambda _{i}$ to $1.00 \times 10^5$.

Table 2 Main results for hyperparameter estimation

Figure 3 shows the estimated trend components for each transformed indicator. We can see that the behavior of each trend is distinct and, therefore, it may be difficult to extract a common factor from the estimated trend components.

Fig. 3

Estimated trend components (January 1975 to December 2019)

Figure 4 shows the estimated cyclical components for each transformed indicator. We can see that the estimates for the cyclical components vary with irregular cycles; however, most of the estimated cyclical components drop suddenly around 2009, caused by Lehman Brothers. The correlation matrix for the estimated cyclical components is provided in Table 3 (note that because the matrix is symmetric, only the elements below the diagonal are shown). This table illustrates that there is a very high positive correlation between pairs among the estimated cyclical components. Thus, it is possible to extract a common factor using the first principal component composed of the estimated cyclical components with a very high contribution rate.

Fig. 4

Estimated cyclical components (January 1975 to December 2019)

Table 3 Correlation matrix for the estimated cyclical components

Thus, to construct the IBC, we use PCA based on the correlation matrix shown in Table 3. The largest eigenvalue for the correlation matrix is 6.550, and the corresponding eigenvector is

$$\begin{aligned} {\varvec{w}} = (0.382, 0.361, 0.323, 0.268, 0.347, 0.164, 0.304, 0.352, 0.316, 0.290)^{\texttt {T}}. \end{aligned}$$

From these results, we can see that the contribution rate for the first principal component is $65.50\%$ because the sum of the variances for each of the normalized cyclical components is 10. Moreover, the eigenvector ${\varvec{w}}$ is equivalent to the vector of the principal component loadings for the IBC. An element in the vector of the principal component loadings expresses how the IBC depends on the corresponding indicator. For example, $w_{1} = 0.382$ is the maximum element and $w_{2}= 0.361$ is the second maximum element in the vector of principal component loadings. Hence, we can say that the index of industrial production (C1) has the largest effect on the IBC, the index of producers’ shipments (C2) has the second-largest effect, and so on.

Based on the normalized estimates for the cyclical components and the vector of principal component loadings ${\varvec{w}}$, we compute the estimate of the IBC, say $b_{t}$, using Eq. (5). Figure 5 shows the time series for the estimate of the IBC during the period January 1975 to December 2019. We can observe that the IBC varies around zero, and then drops suddenly in the first half of 2009 after the collapse of Lehman Brothers.

Fig. 5

Time series for estimate of the IBC

5.3 Comparing the Performance of our IBC with the Coincident CI

To verify the performance of our IBC, we compare it with the coincident CI. However, they cannot be directly compared because our IBC expresses growth cycles and the CI is concerned with classical cycles, although it looks almost stationary in the mean from Fig. 2. To retain the original cycles in the time series of the CI and remove the trend (if it has a trend) simultaneously, we consider a regression model for the time series $CI_{t}$ of the CI as

$$\begin{aligned} CI_{t} = a + bt + r_{t} \quad (n=1,2,\ldots ). \end{aligned}$$

We simply estimate the parameters a and b using a least squares method, and then regard ${\widehat{r}}_{t} = CI_{t} - {\widehat{a}} - {\widehat{b}}t$ as the detrended CI (abbreviated to DCI). Then, we can compare our IBC with the DCI. Note that the estimates of the parameters are ${\widehat{a}} = 84.25$ and ${\widehat{b}} = 0.0407$, respectively, and the time series of the DCI is shown in Fig. 6a. Moreover, to illustrate how the IBC correlates with the DCI, we create a scatter diagram of the IBC versus the DCI (see Fig. 6b) during the period January 1985 to December 2019, which corresponds to the data span of the CI. Note that the correlation coefficient between these two indices is 0.9257. This implies that there is a very high positive correlation between the IBC and DCI.

Fig. 6

a Time series of the DIC, and b scatter diagram of the IBC versus the DCI

An important issue is how well does the IBC express the state of business fluctuations? It is difficult to examine the performance of the IBC because we have no objective standard that expresses the level of business fluctuations. However, as mentioned in Sect. 2.2, it is widely accepted that GDP is an inclusive measure of economic performance; hence, Mariano and Murasawa (2010) used real GDP to measure business cycles. Thus, we use real GDP as an expediential reference for business cycles.

We use a seasonal adjustment model as follows:

$$\begin{aligned} \log (y_{t}) = \tau _{t} + s_{t} + a_{t} + \varepsilon _{t}, \quad \varepsilon _{t} \sim \text{ N }(0,\sigma ^{2}), \end{aligned}$$

where $y_{t}$ denotes the quarterly time series data for real GDP; $\tau _{t}$, $s_{t}$, and $a_{t}$ denote the trend, seasonal, and cyclical components, respectively; and $\varepsilon _{t}$ denotes the irregular component. We apply the models in Eqs. (2) and (3) for the trend and cyclical components. For the seasonal component, we use the seasonal model as follows:

$$\begin{aligned} s_{t} = - s_{t-1} - s_{t-2} - s_{t-3} + v_{t}, \quad v_{t} \sim \text{ N }(0,\xi ^{2}), \end{aligned}$$

where $\xi ^{2}$ denotes the unknown variance. Then, the logarithm of real GDP (log-GDP) can be decomposed into the trend, seasonal, and cyclical components together with the irregular component. A detailed explanation of the modeling and parameter estimation can be found in Kitagawa (2020, p. 204). Note that we applied the above modeling method to the time series data of log-GDP during the period Q1, 1955 to Q4, 2000 and that during the period Q1, 1994 to Q4, 2019 separately. The results for the decomposition of log-GDP shown in Fig. 7c, e, and g are the results for period Q1, 1955 to Q4, 2000, those shown in Fig. 7d, f, and h are the results for the period Q1, 1994 to Q4, 2019.

Fig. 7

Data and results for the decomposition of log-GDP

We consider the cyclical component of log-GDP (abbreviated to CLGDP) as a referential indicator of growth cycles. Thus, we can measure the performance of the IBC using its correlation with the CLGDP. We compare the performance of the IBC and CI by comparing the correlation coefficients of the IBC and DCI with the CLGDP for the data during each period. We perform comparative analysis in the following two overlapping periods, which are determined by the common data spans for the used data: the first period is 1985–2000, and the second period is 1994–2019. Note that for the correspondence to the quarterly GDP data, we take the sum of each three-month period as the value of each quarter for the IBC and DCI.

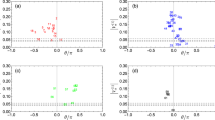
Figure 8a and b show scatter diagrams of the CLGDP with the DCI and IBC during the period Q1, 1985 to Q4, 2000, and Fig. 8c and d show similar scatter diagrams during the period Q1, 1994 to Q4, 2019.

Fig. 8

Scatter diagrams of the CLGDP with the DCI and IBC

Incidentally, in the period Q1, 1985 to Q4, 2000, the correlation coefficients of the CLGDP with the DCI and IBC are 0.7034 and 0.8038, respectively, whereas in the period Q1, 1994 to Q4, 2019, they are 0.4962 and 0.8023, respectively. Thus, the IBC has a higher correlation with the log-GDP than the coincident CI, which implies that the IBC outperforms the coincident CI.

It should be noted that the method for detrending the log-GDP is different from that for detrending the coincident CI, so it is somewhat inconsistent; But it is difficult to develop a consistent method because the structures for these time series are very different. However, it still can be used as a set of references.

6 Discussion

Although the analyzed results in Sect. 5 imply that the triple-C approach has very high performance, there are several issues that need to be discussed.

6.1 Hierarchical Optimization (HO)

To obtain a large variance of the IBC, we used a numeric HO method in the application of the triple-C approach. Using this method, we can estimate the cyclical components for the used indicators simultaneously, and thus construct a systematic method for obtaining the IBC. However, this method needs repetition of computation; hence, the computational costs may increase.

Alternatively, a natural approach for parameter estimation exists: the use of the ML method; that is, we can estimate all hyperparameters by directly maximizing the log-likelihood in Eq. (11) for each indicator separately. Although the ML method is more efficient for computation, it may reduce the performance of the constructed IBC.

We compare our HO method with the ML method numerically because a theoretical comparison may be very difficult. First, the averages of the correlation coefficients between every different pair of estimated cyclical components for the HO and ML methods are 0.5937 and 0.2841, which implies that the total correlation between the estimated cyclical components based on the ML method is low. Furthermore, the variance of the constructed IBC based on the ML method is 4.58, whereas that based on the HO method is 6.55 (as was shown previously); that is, the HO method can lead to an IBC with large variance. Finally, in the period Q1, 1985 to Q4, 2000, the correlation coefficients of the CLGDP with the IBCs based on the ML and HO methods are 0.7040 and 0.8038, whereas in the period Q1, 1994 to Q4, 2019, they are 0.7169 and 0.8023, respectively. Thus, the IBC based on the HO method has a higher correlation with the CLGDP than that based on the ML method. The above results demonstrate the high performance of the IBC using the HO method.

As typical examples, Fig. 9 shows the estimated trend and cyclical components using the ML method for the indicators C4 and C5. By comparison with the results using the MO method (as was shown in Figs. 3 and 4), we can see the following. In the ML method, only the goodness of fit is considered as the purpose function; hence, a part of the cyclical variation remains in the estimated trend. Thus, the variances of the estimated cyclical components are small, which leads to a small variance for the constructed IBC; hence, its expressive power becomes low.

Fig. 9

Estimated trend and cyclical components for C4 and C5

6.2 Differencing Order in the Trend Model

In Sect. 2.2, we justified the use of second differencing for the trend model. However, it is only a guess, not an inference. This issue can be confirmed from the perspective of goodness of fit for the models. To compare the goodness of fit for the trend models with first differencing and second differencing, we compute the maximum log-likelihood (MLL) for each model of the indicators.

Table 4 shows the values of the MLL of the model for each indicator with differencing orders $k = 1$ and $k = 2$. From this table, we can see that the goodness of fit, which is expressed by the MLL, for the model with $k=2$ is larger than that for the model with $k=1$, except for the model for C6. This justifies the use of second differencing in the trend model empirically.

Table 4 MLL values of the model for each indicator with various differencing orders

6.3 Comparison with Existing Methods

Another important issue is that comparing our approach or the constructed IBC with other existing methods or other indices can be considered as follows: (1) compare the triple-C approach with the Stock–Watson dynamic factor modeling approach; (2) compare the triple-C approach with the multivariate UC modeling method; and (3) compare the performance of the constructed IBC with other indices, for example, SWI and NBI (see, http://www.nikkei.com/biz/report/nkidx/). These are the subjects of current work and the details will be presented elsewhere.

7 Conclusions

In this paper, we proposed an alternative approach, which we refer to as the triple-C approach, to develop an IBC of coincident economic indicators, and constructed a coincident index of growth cycles, called the IBC, in Japan using the proposed approach.

We can summarize the framework of the triple-C approach as follows: (1) we used the same time series data as the CI and DI compiled by the ESRI; (2) we decomposed seasonally adjusted data into trend, cyclical, and irregular components; and (3) we constructed the IBC based on the first principal component of the normalized estimates for the cyclical components.

We examined whether the constructed coincident IBC performed better than that of the CI. The correlation coefficients of the cyclical component of real GDP with the CI and IBC for the data during the period Q1, 1985 to Q4, 2000 were 0.7034 and 0.8038, and those for the data during the period Q1, 1994 to Q4, 2019 were 0.4962 and 0.8023, respectively. This indicates that the IBC performed better than the CI.

Additionally, if we use the model in Eq. (5) instead of that in Eq. (6) and add a prior model for the seasonal component, we can process the time series data in advance without the need for seasonal adjustment. Thus, our triple-C approach can be widely applied as a more general method.