1 Introduction

Throughout the paper, we let \({\mathcal {H}}\) be a real Hilbert space and \({\mathcal {K}}\) be a non-empty subset of \({\mathcal {H}}\) which is closed and convex.

Recall that in a fixed point problem one needs to find a point \({\mathfrak {z}}\in {\mathcal {K}}\) in such a way that

$$\begin{aligned} S{\mathfrak {z}}={\mathfrak {z}}, \end{aligned}$$
(1.1)

where \(S:{\mathcal {K}}\rightarrow {\mathcal {H}}\) be a mapping. We indicate the solution set of problem (1.1) by \(\Lambda = \{{\mathfrak {z}}\in {\mathcal {K}}:S{\mathfrak {z}}={\mathfrak {z}}\}.\) Many researchers have studied problem (1.1) and have established various iterative methods to tackle it; see for example [5, 9, 11]. In 2000, Moudafi [25] considered problem (1.1) and proposed well known viscosity approximation method for finding a solution of problem (1.1) as follows: Take \(u_0\in {\mathcal {H}},\) and formulate an iterative sequence \(\{u_n\}\) as follows:

$$\begin{aligned} u_{n+1} = \psi _n\phi (u_n)+(1-\psi _n)Su_n,\quad n\ge 0, \end{aligned}$$
(1.2)

where \(\phi :{\mathcal {H}}\rightarrow {\mathcal {H}}\) is a contraction map and sequence \(\{\psi _n\}\in (0,\,1).\) He demonstrated that the sequence formulated by (1.2) converges strongly to a unique solution \({\mathfrak {z}}\in {\mathcal {K}}.\)

On the other hand, a problem in which one needs to find an element \({\mathfrak {z}}\in {\mathcal {K}}\) in such a way that

$$\begin{aligned} g({\mathfrak {z}},v)\ge 0,\quad \forall \,v\in {\mathcal {K}}, \end{aligned}$$
(1.3)

where \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) be a real valued nonlinear bi-function with \(g({\mathfrak {z}},{\mathfrak {z}})=0\) for all \({\mathfrak {z}}\in {\mathcal {K}}.\) The problem (1.3), was first suggested by Fan [15] and further established by Blum and Oettli [2]. Problem (1.3) is now known as equilibrium problem. The solution set of problem (1.3) is represented by \(\Gamma = \{{\mathfrak {z}}\in {\mathcal {K}}: g({\mathfrak {z}},v)\ge 0,\,\forall \,v\in {\mathcal {K}}\}.\) Many problems such as medical imaging problems, transportation problems, and financial engineering problems can be converted to find solution of problem (1.3), see, for example [14, 21, 28, 29] and the references therein.

In recent years, many iterative algorithms for solving the problem (1.3) have been developed, including the proximal point algorithm (TPPA) [12, 13], the normal S-iteration algorithm [20] the subgradient algorithm (TSA) [3], the extragradient algorithm (TEA) [17], subgradient extragradient algorithm [10, 19] and the gap function algorithm (TGFA) [24]. The explicit extragradient algorithm (TEEA) for solving problem (1.3) for pseudomonotone bi-functions satisfying Lipschitz-type condition (LTC) in real Hilbert space was introduced by Hieu et al. [30] in 2019 which is defined as following. Choose \(u_0\in {\mathcal {K}}\) and \(\tau _0>0,\,\eta \in (0,\,1),\) compute the sequences \(\{w_n\}\) and \(\{u_{n+1}\}\) by

$$\begin{aligned} w_n&= \mathrm{arg\,\min _{v\in {\mathcal {K}}}}\,\big \{g(u_n,v)+\dfrac{1}{2\tau _n}\Vert u_n-v\Vert ^2\big \},\nonumber \\ u_{n+1}&= \mathrm{arg\,\min _{v\in {\mathcal {K}}}}\,\big \{g(w_n,v)+\dfrac{1}{2\tau _n}\Vert u_n-v\Vert ^2\big \}, \end{aligned}$$
(1.4)

where the step size \(\tau _n\) is given as

$$\begin{aligned} \tau _{n+1} = \textrm{min}\Bigg \{\tau _n,\,\dfrac{\eta (\Vert u_n-w_n\Vert ^2+\Vert u_{n+1}-w_n\Vert ^2)}{2\,\textrm{max}\big \{0,g(u_n,u_{n+1})-g(u_n,w_n)-g(w_n,u_{n+1})\big \}}\Bigg \}. \end{aligned}$$

They proved the sequence \(\{u_n\}\) generated by (1.4) converges weakly to some point \({\mathfrak {z}}\in \Gamma .\)

In this paper, we consider a problem of approximating a common solution of equilibrium problem for pseudomonotone bi-function satisfying Lipschitz-type condition (LTC) and fixed point problem for \(\psi -\)strongly quasi-nonexpansive mappings in real Hilbert space. i.e., Find \({\mathfrak {z}}\in {\mathcal {K}}\) such that

$$\begin{aligned} {\mathfrak {z}}\in \Omega := \Gamma \cap \ \Lambda . \end{aligned}$$
(1.5)

Inspired and motivated by the work in [25] and Hieu et al. [30], the main goal of this paper is to present a viscosity-type extragradient algorithm which is a combination of extragradient method and viscosity approximation method with a new step size rule for solving problem (1.5) and discuss its convergence analysis. The fundamental advantage of the suggested approach is that it does not require the use of a linesearch procedure or the knowledge of Lipschitz-type constants in advance, which is a significant advantage. In this sense, the findings of this study generalise and extend certain previously published findings.

The following is how this paper is organised: In Sect. 2, we review some of the fundamental definitions and auxiliary results that were used throughout the paper. Our suggested algorithm and its convergence are presented in Sect. 3, and some consequences of our primary findings are discussed in Sect. 4. Moreover, we give a numerical example to support and justify our proposed algorithm in the last section.

2 Preliminaries

Let the inner product and induced norm equipped in Hilbert space \({\mathcal {H}}\) are denoted by \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert ,\) respectively. These convergences are represented by \(\rightharpoonup \) and \(\rightarrow \) symbols, respectively, when the sequence \(\{u_n\} \subset {\mathcal {H}}\) converges weakly and strongly. We start with some definitions about the monotonicity of bi-function \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}:\)

Definition 2.1

[2, 16, 26] The bi-function g is said to be

  1. (i)

    \(\gamma -\)strongly monotone on \({\mathcal {K}}\) if there exists \(\gamma >0\) such that

    $$\begin{aligned} g(u,v) + g(v,u) \le -\gamma \Vert u-v\Vert ^2,\quad \forall \,u,v\in {\mathcal {K}}; \end{aligned}$$
  2. (ii)

    monotone if

    $$\begin{aligned} g(u,v) + g(v,u) \le 0, \quad \forall \, u,v\in {\mathcal {K}}; \end{aligned}$$
  3. (iii)

    \(\gamma -\)strongly pseudomonotone on \({\mathcal {K}}\) if there exists \(\gamma >0\) such that

    $$\begin{aligned} g(u,v)\ge 0 \implies g(v,u)\le -\gamma \Vert u-v\Vert ^2,\quad \forall \,u,v\in {\mathcal {K}}; \end{aligned}$$
  4. (iv)

    pseudomonotone if

    $$\begin{aligned} g(u,v) \ge 0 \implies g(v,u) \le 0,\quad \forall \,u,v\in {\mathcal {K}}; \end{aligned}$$
  5. (v)

    satisfying the Lipschitz-type condition (LTC) on \({\mathcal {K}}\) if there exists two positive real numbers \(\lambda _1,\lambda _2\) such that

    $$\begin{aligned} g(u,w) \le g(u,v)+g(v,w)+\lambda _1\Vert u-v\Vert ^2+\lambda _2\Vert v-w\Vert ^2,\quad \forall \,u,v,w\in {\mathcal {K}}. \end{aligned}$$

Definition 2.2

[18] The metric projection \(P_{{\mathcal {K}}}(u)\) of u onto a closed, convex subset \({\mathcal {K}}\) of \({\mathcal {H}}\) is defined as follows:

$$\begin{aligned} P_{{\mathcal {K}}}(u) = \mathrm{arg~\min _{v\in {\mathcal {K}}}}\,\big \{\Vert v-u\Vert \big \}. \end{aligned}$$

Lemma 2.1

[22] Let \(P_{{\mathcal {K}}}(u):{\mathcal {H}}\rightarrow {\mathcal {K}}\) be the metric projection from \({\mathcal {H}}\) onto \({\mathcal {K}}.\) Then

  1. (i)

    \(\Vert u-P_{{\mathcal {K}}}(v)\Vert ^2+\Vert P_{{\mathcal {K}}}(v)-v\Vert ^2\le \Vert u-v\Vert ^2, \quad \forall u\in {\mathcal {K}},\,v\in {\mathcal {H}},\)

  2. (ii)

    \(w=P_{{\mathcal {K}}}(u) \iff \langle u-w,v-w\rangle \le 0,\quad \forall \,v\in {\mathcal {K}}.\)

Lemma 2.2

[18] Suppose that \(S:{\mathcal {H}}\rightarrow {\mathcal {H}}\) is a nonlinear mapping. Then \(I-S\) is said to be demiclosed at zero if for any \(\{u_n\}\in {\mathcal {H}},\) the following holds:

$$\begin{aligned} u_n\rightharpoonup {\mathfrak {z}}~~\textrm{and}~~(I-S)u_n\rightarrow 0\implies {\mathfrak {z}}\in \Lambda . \end{aligned}$$

Definition 2.3

Let \(S:{\mathcal {H}}\rightarrow {\mathcal {H}}\) be a mapping with \(\Lambda \ne \text{\O }.\) Then \(S:{\mathcal {H}}\rightarrow {\mathcal {H}}\) is said to be

  1. (i)

    firmly nonexpansive if

    $$\begin{aligned} \Vert Su-Sv\Vert ^2\le \langle Su-Sv,u-v\rangle ,\quad \forall \,u,v\in {\mathcal {H}}, \end{aligned}$$

    or comparatively

    $$\begin{aligned} \Vert Su-Sv\Vert ^2\le \Vert u-v\Vert ^2-\Vert (I-S)u-(I-S)v\Vert ^2,\quad \forall \,u,v\in {\mathcal {H}}, \end{aligned}$$
  2. (ii)

    directed if

    $$\begin{aligned} \langle w-Su,u-Su\rangle \le 0,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$

    or comparatively

    $$\begin{aligned} \Vert Su-w\Vert ^2\le \Vert u-w\Vert ^2-\Vert u-Su\Vert ^2,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$
  3. (iii)

    \(\psi -\)strongly quasi-nonexpansive with \(\psi >0\) if

    $$\begin{aligned} \Vert Su-w\Vert ^2\le \Vert u-w\Vert ^2-\psi \Vert u-Su\Vert ^2,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$

    or comparatively

    $$\begin{aligned} \langle Su-u,u-w\rangle \le \dfrac{-1-\psi }{2}\Vert u-Su\Vert ^2,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$
  4. (iv)

    quasi-nonexpansive

    $$\begin{aligned} \Vert Su-w\Vert \le \Vert u-w\Vert ,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$
  5. (v)

    \(\beta -\)demicontractive with \(\beta \in [0,\,1)\)

    $$\begin{aligned} \Vert Su-w\Vert ^2\le \Vert u-w\Vert ^2+\beta \Vert u-Su\Vert ^2,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}, \end{aligned}$$

    or comparatively

    $$\begin{aligned} \langle u-w,Su-u\rangle \le \dfrac{\beta -1}{2}\Vert u-Su\Vert ^2,\quad \forall \,w\in \Lambda ,\,u\in {\mathcal {H}}. \end{aligned}$$
    (2.1)

Recall that the proximal mapping \(\textrm{prox}_{\tau g_1}\) is defined by

$$\begin{aligned} \textrm{prox}_{\tau g_1}(u) = \mathrm{arg~min}\big \{ g_1(v)+\dfrac{1}{2\tau }\Vert u-v\Vert ^2:v\in {\mathcal {K}}\big \}, \end{aligned}$$

where \(g_1:{\mathcal {K}}\rightarrow {\mathbb {R}}\) with a parameter \(\tau >0\) is a proper, convex and lower semicontinuous function .

One can observe the following property of the proximal mapping \(\textrm{prox}_{\tau g_1}\):

Lemma 2.3

[1] For all \(u\in {\mathcal {H}},\,v\in {\mathcal {K}}\) and \(\tau >0,\) the following implication holds:

$$\begin{aligned} \tau \big \{g_1(v)-g_1(\textrm{prox}_{\tau g_1}(u))\big \}\ge \langle u-\textrm{prox}_{\tau g_1}(u),\,v-\textrm{prox}_{\tau g_1}(u)\rangle . \end{aligned}$$

Remark 2.1

If \(u = \textrm{prox}_{\tau g_1}(u)\) then

$$\begin{aligned} u\in \mathrm{arg~min}\big \{g_1(v):v\in {\mathcal {K}}\big \}:=\big \{u\in {\mathcal {K}}:g_1(u) = \mathrm{\min _{v\in {\mathcal {K}}}}\,g_1(v)\big \}. \end{aligned}$$

Lemma 2.4

[23] Let a sequence \(\{b_n\}\subset {\mathbb {R}}\) such that there exists a subsequence \(\{n_i\}\) of \(\{n\}\) such that \(b_{n_i}\le b_{n_{i+1}}\) for all \(i \in {\mathbb {N}}\). Then there exists an increasing sequence \(\{m_l\}\subset {\mathbb {N}}\) such that \(m_l\rightarrow \infty \) and the following properties are satisfied by all sufficiently large numbers \(l\in {\mathbb {N}}:\)

$$\begin{aligned} b_{m_l}\le {b_{m_{l}+1}} ~\mathrm{and~} b_l\le {b_{m_{l}+1}}. \end{aligned}$$

In fact, \(m_l:= \textrm{max}\{j\le l:b_j\le b_{j+1}\}.\)

Lemma 2.5

[27, 31] Let \(\{b_n\}\) be a sequence of non negative real numbers such that

$$\begin{aligned} b_{n+1}\le (1-\psi _n)b_n+\psi _n\delta _n,\quad \forall \,n\ge 0, \end{aligned}$$

where \(\psi _n\in (0,\,1)\) and \(\delta _n\subset {\mathbb {R}}\) satisfies the following conditions:

  1. (i)

    \(\sum _{n=0}^{\infty }\psi _n=\infty ;\)

  2. (ii)

    \(\lim \limits _{n\rightarrow \infty }\textrm{sup}\delta _n\le 0.\) Then \(\lim \limits _{n\rightarrow \infty }b_n=0.\)

Lemma 2.6

[1] For every \(u,v\in {\mathcal {H}}\) and \(\psi \in {\mathbb {R}},\) the following relations are true:

  1. (i)

    \(\Vert \psi u+(1-\psi )v\Vert ^2 = \psi \Vert u\Vert ^2+(1-\psi )\Vert v\Vert ^2-\psi (1-\psi )\Vert u-v\Vert ^2,\)

  2. (ii)

    \(\Vert u+v\Vert ^2\le \Vert u\Vert ^2+2\langle v,u+v\rangle .\)

Assumption 2.1

[30] Let a bi-function \(g : {\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) satisfies the following conditions:

  1. G1:

    g is pseudomontone on a feasible set \({\mathcal {K}}\) and for all \(u\in {\mathcal {K}},\,g(u; u) = 0;\)

  2. G2:

    g satisfy the Lipschitz-type condition (LTC) on \({\mathcal {H}}\) with positive constants \(\lambda _1\) and \(\lambda _2\);

  3. G3:

    \(\lim \limits _{n\rightarrow \infty }\textrm{sup}\,g(u_n,v)\le g({\mathfrak {z}},v)\) for every \(v\in {\mathcal {K}}\) and \(\{u_n\}\subset {\mathcal {K}}\) satisfy \(u_n\rightharpoonup {\mathfrak {z}};\)

  4. G4:

    g(u, \(\cdot\)) is convex and subdifferentiable on \({\mathcal {K}}\) for every \(u\in {\mathcal {K}}\).

3 Main result

In this section, we provide our main algorithm and discuss its convergence analysis under some mild assumptions. Let \(S:{\mathcal {K}}\rightarrow {\mathcal {H}}\) be a \(\psi -\)strongly quasi-nonexpansive operator such that \(I-S\) is demiclosed at zero. Suppose that \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) be a bi-function satisfying Assumptions 2.1 and \(\phi :{\mathcal {H}}\rightarrow {\mathcal {H}}\) be a contraction mapping with constant \(\xi \in [0,\,1).\) The following is the main algorithm that has been presented:

Algorithm 1

(A Viscosity-type Extragradient Algorithm)

Initialization: Choose \(u_0\in {\mathcal {K}}\) and \({\tau }_0>0,\,\eta \in (0,1).\) Let sequence \(\{\psi _n\}\in (0,\,1)\) satisfies the following conditions:

$$ \lim \limits _{n\rightarrow \infty }\psi _n=0\quad \textrm{and}\quad \sum _{n=0}^{\infty }\psi _n=\infty . $$
(3.1)

Iterative steps: Given \(u_n\) and \(\tau _n\) are known for \(n\ge 0.\)

Step 1: Compute

$$\begin{aligned} w_n = \mathrm{arg\,\min _{v\in {\mathcal {K}}}}\,\{g(u_n,v)+\dfrac{1}{2\tau _n}\Vert u_n-v\Vert ^2\}. \end{aligned}$$

If \(u_n=w_n;\) STOP. Otherwise go to step 2.

Step 2: Compute

$$\begin{aligned} v_n&= \mathrm{arg\,\min _{v\in {\mathcal {K}}}}\,\{g(w_n,v)+\dfrac{1}{2\tau _n}\Vert u_n-v\Vert ^2\}\quad \textrm{and}\\ u_{n+1}&= \psi _n\phi (u_n) + (1-\psi _n)Sv_n. \end{aligned}$$

and set

$$\begin{aligned} \tau _{n+1}=\textrm{min}\Bigg \{\tau _n,\,\dfrac{\eta (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2)}{2\,\textrm{max}\big \{0,g(u_n,v_n)-g(u_n,w_n)-g(w_n,v_n)\big \}}\Bigg \}. \end{aligned}$$
(3.2)

Set \(n := n + 1\) and return back to Iterative steps.

Remark 3.1

Under the Assumption 2.1 (G2), there exist positive constants \( \lambda _1~ \& ~\lambda _2\) such that

$$\begin{aligned} g(u_n,v_n) - g(u_n,w_n) - g(w_n,v_n)&\le \lambda _1\Vert u_n-w_n\Vert ^2+\lambda _2\Vert v_n-w_n\Vert ^2\\&\le \textrm{max}\{\lambda _1,\lambda _2\}(\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2). \end{aligned}$$

Thus, from the definition of the sequence \(\{\tau _n\},\) this sequence is bounded from below by \(\Big \{\tau _0,\,\dfrac{\eta }{2\textrm{max}\{\lambda _1,\lambda _2\}}\Big \}.\) Moreover, the sequence \(\{\tau _n\}\) is non-increasing monotone. Thus, there exists \(\tau \in {\mathbb {R}}\) such that \(\lim \limits _{n\rightarrow \infty }\tau _n=\tau .\) In fact, from (3.2), if \(g(u_n,v_n)-g(u_n,w_n)-g(w_n,v_n)\le 0\) than \(\tau _{n+1}:=\tau _n.\)

Consequently, we have the following outcomes:

Theorem 3.1

Let a bi-function \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) satisfying the Assumptions 2.1. Thus, for each \({\mathfrak {z}}\in \Omega :=\Gamma \cap \Lambda \ne \text{\O },\) we have

$$\begin{aligned} \Vert v_n-{\mathfrak {z}}\Vert ^2\le \Vert u_n-{\mathfrak {z}}\Vert ^2-\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2-\Vert v_n-w_n\Vert ^2\big ). \end{aligned}$$
(3.3)

Proof

In view of Lemma 2.3 and the definition of sequence \(\{v_n\}\) that

$$\begin{aligned} \langle u_n-v_n,v_n-v\rangle \ge \tau _n g(w_n,v_n)-\tau _n g(w_n,v),\quad \forall \,v\in {\mathcal {K}}. \end{aligned}$$
(3.4)

From the equation (3.2), we obtain

$$\begin{aligned} g(u_n,v_n)-g(u_n,w_n)-g(w_n,v_n)\le \dfrac{\eta \big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )}{2\tau _{n+1}}, \end{aligned}$$

which after multiplying both sides by \(\tau _n>0,\) implies that

$$\begin{aligned} \tau _n g(w_n,v_n)\ge \tau _n\big (g(u_n,v_n)-g(u_n,w_n)\big )-\dfrac{\eta \tau _n\big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )}{2\tau _{n+1}}, \end{aligned}$$
(3.5)

combining relations (3.4) and (3.5), we obtain

$$\begin{aligned} \langle u_n-v_n,v_n-v\rangle&\ge \tau _n\big \{g(u_n,v_n)-g(u_n,w_n)\big \}\nonumber \\&\quad -\dfrac{\eta \tau _n}{2\tau _{n+1}}\big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )-\tau _n g(w_n,v). \end{aligned}$$
(3.6)

Similarly, from Lemma 2.3 and the definition of the sequence \(\{w_n\},\) we also obtain

$$\begin{aligned} \tau _n\big (g(u_n,v_n)-g(u_n,w_n)\big )\ge \langle w_n-u_n,w_n-v_n\rangle . \end{aligned}$$
(3.7)

From the relations (3.6) and (3.7), we obtain

$$\begin{aligned} \langle u_n-v_n,v_n-v\rangle&\ge \langle w_n-u_n,w_n-v_n\rangle \nonumber \\&\quad -\dfrac{\eta \tau _n}{2\tau _{n+1}}\big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )-\tau _n g(w_n,v). \end{aligned}$$
(3.8)

Thus, by multiplying both sides of relation (3.8) by 2, we obtain

$$\begin{aligned} 2\langle u_n-v_n,v_n-v\rangle&\ge 2\langle w_n-u_n,w_n-v_n\rangle \nonumber \\&\quad -\dfrac{\eta \tau _n}{\tau _{n+1}}\big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )-2\tau _n g(w_n,v). \end{aligned}$$
(3.9)

We have the following equalities:

$$\begin{aligned} 2\langle u_n-v_n,v_n-v\rangle&= \Vert u_n-v\Vert ^2-\Vert v_n-u_n\Vert ^2-\Vert v_n-v\Vert ^2;\end{aligned}$$
(3.10)
$$\begin{aligned} 2\langle w_n-u_n,w_n-v_n\rangle&= \Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2-\Vert u_n-v_n\Vert ^2. \end{aligned}$$
(3.11)

Combining the relations (3.9), (3.10) and (3.11), we obtain

$$\begin{aligned} \Vert v_n-v\Vert ^2&\le \Vert u_n-v\Vert ^2-\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2\big )\nonumber \\&\quad -2\tau _n g(w_n,v),\quad \forall \,v\in {\mathcal {K}},\,\forall \,n\ge 0. \end{aligned}$$
(3.12)

For each \({\mathfrak {z}}\in \Gamma ,\) we have that \(g({\mathfrak {z}},w_n)\ge 0\) and by Assumptions 2.1 (G1) that \(g(w_n,{\mathfrak {z}})\le 0.\) Then using \(v={\mathfrak {z}}\in {\mathcal {K}}\) in relation (3.12), we obtain

$$\begin{aligned} \Vert v_n-{\mathfrak {z}}\Vert ^2&\le \Vert u_n-{\mathfrak {z}}\Vert ^2-\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2-\Vert v_n-w_n\Vert ^2\big ),\quad \forall \,{\mathfrak {z}}\in {\mathcal {K}},\,\forall \,n\ge 0. \end{aligned}$$

\(\square \)

Theorem 3.2

Let a bi-function \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) satisfying Assumptions 2.1. Thus, for each \({\mathfrak {z}}\in \Omega :=\Gamma \cap \Lambda \ne \text{\O },\) the sequence \(\{u_n\}\) generated by Algorithm 1 is bounded.

Proof

It is given that \({\mathfrak {z}}\in \Omega .\) Since \(\lim \limits _{n\rightarrow \infty }\tau _n = \tau >0,\)

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg ) = 1-\eta >0. \end{aligned}$$

Thus, there exists \(n_0\ge 1\) such that

$$\begin{aligned} 1-\dfrac{\eta \tau _n}{\tau _{n+1}}>0,\quad \forall \,n\ge n_0. \end{aligned}$$
(3.13)

From the Theorem 3.1 and relation (3.13), we obtain

$$\begin{aligned} \Vert v_n-{\mathfrak {z}}\Vert ^2\le \Vert u_n-{\mathfrak {z}}\Vert ^2. \end{aligned}$$
(3.14)

From the definition of \(\{u_{n+1}\}\) and due to the fact that \(\phi \) is a contraction with \(\xi \in [0,\,1),\) we have

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert&= \Vert \psi _n \phi (u_n) + (1-\psi _n)Sv_n-{\mathfrak {z}}\Vert \nonumber \\&= \Vert \psi _n(\phi (u_n)-{\mathfrak {z}}) + (1-\psi _n)(Sv_n-{\mathfrak {z}})\Vert \nonumber \\&\le \psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert + (1-\psi _n)\Vert Sv_n-{\mathfrak {z}}\Vert \nonumber \\&\le \psi _n\Vert \phi (u_n)-\phi ({\mathfrak {z}})\Vert + \psi _n\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert + (1-\psi _n)\Vert v_n-{\mathfrak {z}}\Vert \nonumber \\&\le \psi _n\xi \Vert u_n-{\mathfrak {z}}\Vert + \psi _n\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert + (1-\psi _n)\Vert v_n-{\mathfrak {z}}\Vert . \end{aligned}$$
(3.15)

Combining relations (3.1), (3.13) and (3.15), we obtain

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert&\le \psi _n\xi \Vert u_n-{\mathfrak {z}}\Vert + \psi _n\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert + (1-\psi _n)\Vert u_n-{\mathfrak {z}}\Vert \\&=(1-\psi _n+\psi _n\xi )\Vert u_n-{\mathfrak {z}}\Vert + \psi _n(1-\xi )\dfrac{\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert }{1-\xi }\\&\le \textrm{max}\bigg \{\Vert u_n-{\mathfrak {z}}\Vert ,\dfrac{\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert }{1-\xi }\bigg \}, \end{aligned}$$

continuing in the same way, we obtain

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert&\le \textrm{max}\bigg \{\Vert u_0-{\mathfrak {z}}\Vert ,\dfrac{\Vert \phi ({\mathfrak {z}})-{\mathfrak {z}}\Vert }{1-\xi }\bigg \}. \end{aligned}$$

Thus, we conclude that the sequence \(\{u_n\}\) is bounded. \(\square \)

Theorem 3.3

Let a bi-function \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) satisfying Assumptions  2.1. Thus, for each \({\mathfrak {z}}\in \Omega :=\Gamma \cap \Lambda \ne \text{\O },\) the sequence \(\{u_n\}\) generated by Algorithm 1 converges strongly to \({\mathfrak {z}},\) where \({\mathfrak {z}} = P_{\Omega }\phi ({\mathfrak {z}}).\)

Proof

By using Lemma 2.1 (ii), we have

$$\begin{aligned} \langle \phi ({\mathfrak {z}})-{\mathfrak {z}},v-{\mathfrak {z}}\rangle \le 0,\quad \forall \,v\in \Gamma . \end{aligned}$$
(3.16)

By Lemma 2.6 (i) and Theorem 3.1, we obtain

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert ^2&= \Vert \psi _n \phi (u_n) + (1-\psi _n)Sv_n-{\mathfrak {z}}\Vert ^2\nonumber \\&= \Vert \psi _n(\phi (u_n)-{\mathfrak {z}}) + (1-\psi _n)(Sv_n-{\mathfrak {z}})\Vert ^2\nonumber \\&=\psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert ^2 + (1-\psi _n)\Vert Sv_n-{\mathfrak {z}}\Vert ^2 - \psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2\nonumber \\&\le \psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert ^2 + (1-\psi _n)\Vert v_n-{\mathfrak {z}}\Vert ^2 - \psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2\nonumber \\&\le \psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert ^2 + (1-\psi _n)\bigg [\Vert u_n-{\mathfrak {z}}\Vert ^2-\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2\nonumber \\&\quad +\Vert v_n-w_n\Vert ^2\big )\bigg ] -\psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2\nonumber \\&\le \psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert ^2 +(1-\psi _n)\Vert u_n-{\mathfrak {z}}\Vert ^2 -(1-\psi _n)\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2\nonumber \\&\quad +\Vert v_n-w_n\Vert ^2\big ) -\psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2. \end{aligned}$$
(3.17)

The rest of the proof shall be divided into two cases:

Case I: Assume that there is a fixed number \(N_1\in {\mathbb {N}}\) such that

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert \le \Vert u_n-{\mathfrak {z}}\Vert ,\quad \forall \,n\ge N_1. \end{aligned}$$
(3.18)

Thus, above relation implies that \(\lim \limits _{n\rightarrow \infty }\Vert u_n-{\mathfrak {z}}\Vert \) exists and let \(\lim \limits _{n\rightarrow \infty }\Vert u_n-{\mathfrak {z}}\Vert =l.\) From (3.17), we obtain

$$\begin{aligned}&(1-\psi _n)\bigg (1-\dfrac{\eta \tau _n}{\tau _{n+1}}\bigg )\big (\Vert u_n-w_n\Vert ^2-\Vert v_n-w_n\Vert ^2\big )\\&\quad \le \psi _n\Vert \phi (u_n)-{\mathfrak {z}}\Vert ^2 +\Vert u_n-{\mathfrak {z}}\Vert ^2-\Vert u_{n+1}-{\mathfrak {z}}\Vert ^2-\psi _n\Vert u_n-{\mathfrak {z}}\Vert ^2-\psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2. \end{aligned}$$

Since \(\lim \limits _{n\rightarrow \infty }\Vert u_n-{\mathfrak {z}}\Vert =l\) and \(\lim \limits _{n\rightarrow \infty }\psi _n = 0,\) then from (3.13) and the above relation we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert u_n-w_n\Vert = \lim \limits _{n\rightarrow \infty }\Vert v_n-w_n\Vert =0. \end{aligned}$$
(3.19)

It follows from the above relation that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert u_n-v_n\Vert \le \lim \limits _{n\rightarrow \infty }\Vert u_n-w_n\Vert +\lim \limits _{n\rightarrow \infty }\Vert w_n-v_n\Vert = 0. \end{aligned}$$
(3.20)

We can also obtain

$$\begin{aligned} \Vert u_{n+1}-v_n\Vert ^2&= \psi _n\Vert \phi (u_n)-v_n\Vert ^2 + (1-\psi _n)\Vert Sv_n-v_n\Vert ^2 \nonumber \\&\quad - \psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2. \end{aligned}$$
(3.21)

and

$$\begin{aligned}&\Vert u_{n+1}-{\mathfrak {z}}\Vert ^2-\Vert v_n-{\mathfrak {z}}\Vert ^2-\Vert u_{n+1}-v_n\Vert ^2\nonumber \\&=2\langle u_{n+1}-v_n,v_n-{\mathfrak {z}}\rangle \nonumber \\&=2\psi _n\langle \phi (u_n)-v_n,v_n-{\mathfrak {z}}\rangle +2(1-\psi _n)\langle Sv_n-v_n,v_n-{\mathfrak {z}}\rangle \nonumber \\&\le 2\psi _n\langle \phi (u_n)-v_n,v_n-{\mathfrak {z}}\rangle -(1+\psi )(1-\psi _n)\Vert v_n-Sv_n\Vert ^2. \end{aligned}$$
(3.22)

From relations (3.21) and (3.22), we obtain

$$\begin{aligned} \Vert u_{n+1}-{\mathfrak {z}}\Vert ^2-\Vert v_n-{\mathfrak {z}}\Vert ^2&\le \psi _n\Vert \phi (u_n)-v_n\Vert ^2-\psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2\\&\quad +2\psi _n\langle \phi (u_n)-v_n,v_n-{\mathfrak {z}}\rangle -\psi (1-\psi _n)\Vert v_n-Sv_n\Vert ^2. \end{aligned}$$

Therefore

$$\begin{aligned} \psi (1-\psi _n)\Vert v_n-Sv_n\Vert ^2&\le \psi _n\Vert \phi (u_n)-v_n\Vert ^2-\psi _n(1-\psi _n)\Vert \phi (u_n)-Sv_n\Vert ^2\\&\quad +2\psi _n\langle \phi (u_n)-v_n,v_n-{\mathfrak {z}}\rangle -\Vert u_{n+1}-{\mathfrak {z}}\Vert ^2+\Vert v_n-{\mathfrak {z}}\Vert ^2. \end{aligned}$$

Using relation (3.18) and the fact that \(\lim \limits _{n\rightarrow \infty }\Vert u_n-{\mathfrak {z}}\Vert \) exists, we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert Sv_n-v_n\Vert =0. \end{aligned}$$
(3.23)

Next, we show that \(\lim \limits _{n\rightarrow \infty }\Vert u_{n+1}-u_n\Vert =0.\) Consider

$$\begin{aligned} \Vert u_{n+1}-u_n\Vert&= \Vert u_{n+1}-Sv_n+Sv_n-v_n+v_n-u_n\Vert \\&\le \Vert u_{n+1}-Sv_n\Vert +\Vert Sv_n-v_n\Vert +\Vert v_n-u_n\Vert \\&\le \psi _n\Vert \phi (u_n)-Sv_n\Vert +\Vert Sv_n-v_n\Vert +\Vert v_n-u_n\Vert . \end{aligned}$$

By using relations (3.1), (3.20) and (3.23), we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert u_{n+1}-u_n\Vert =0. \end{aligned}$$
(3.24)

Since, the sequences \(\{u_n\}, \{w_n\}\) and \(\{v_n\}\) are bounded. Then there exists a subsequence \(\{u_{n_k}\}\) of \(\{u_n\}\) such that \(\{u_{n_k}\}\rightharpoonup \hat{{\mathfrak {z}}}\in {\mathcal {H}}.\) Thus, by relation (3.23) and Lemma 2.2, we can conclude that \(\hat{{\mathfrak {z}}}\in Fix(T).\) Next, we need to show that \(\hat{{\mathfrak {z}}}\in \Gamma .\) Since \(\Vert u_n-w_n\Vert \rightarrow 0,\) we also have that \(\{w_{n_k}\}\rightharpoonup \hat{{\mathfrak {z}}}.\) Passing to the limit in relation (3.3) as \(k\rightarrow \infty \) and using Assumptions 2.1 (G3), the relation (3.19) and the fact that \(\lim \limits _{n\rightarrow \infty }\tau _n=\tau >0,\) we obtain

$$\begin{aligned} g(\hat{{\mathfrak {z}}},v)&\ge \lim \limits _{k\rightarrow \infty }\,\textrm{sup}\,g(w_{n_k},v)\nonumber \\&\ge \dfrac{1}{2\tau _n}\lim \limits _{k\rightarrow \infty }\,\textrm{sup}\,\big (\Vert v_n-v\Vert ^2-\Vert u_n-v\Vert ^2\big ),\quad \forall \,v\in {\mathcal {K}}. \end{aligned}$$
(3.25)

On the other hand, by the triangle inequality, we have

$$\begin{aligned} \bigg |\Vert v_n-v\Vert ^2-\Vert u_n-v\Vert ^2\bigg |\le \Vert v_n-u_n\Vert \big (\Vert v_n-u_n\Vert +\Vert u_n-v\Vert \big ). \end{aligned}$$

Thus, from the boundedness of the sequence \(\{u_n\}\) and the relation (3.20), we get for each \(v\in {\mathcal {K}}\)

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\bigg |\Vert v_n-v\Vert ^2-\Vert u_n-v\Vert ^2\bigg |=0. \end{aligned}$$
(3.26)

Combining the relations (3.25) and (3.26), we get \(g(\hat{{\mathfrak {z}}},v)\ge 0\) for all \(v\in {\mathcal {K}}\) so \(\hat{{\mathfrak {z}}}\in \Gamma .\) Therefore \(\hat{{\mathfrak {z}}}\in \Omega :=\Gamma \cap \Lambda .\) Next, we consider

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_n-{\mathfrak {z}}\rangle&= \lim \limits _{k\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n_k}-{\mathfrak {z}} \rangle \nonumber \\&= \langle \phi ({\mathfrak {z}})-{\mathfrak {z}},\hat{{\mathfrak {z}}}-{\mathfrak {z}} \rangle \le 0. \end{aligned}$$
(3.27)

We have \(\lim \limits _{n\rightarrow \infty }\Vert u_{n+1}-u_n\Vert =0.\) We can deduce that

$$\begin{aligned}&\lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad \le \lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-u_n\rangle \nonumber \\&\qquad + \lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n}-{\mathfrak {z}}\rangle \nonumber \\&\quad \le 0. \end{aligned}$$
(3.28)

From Lemma 2.6 (ii) and relation (3.3), we have

$$\begin{aligned}&\Vert u_{n+1}-{\mathfrak {z}}\Vert ^2\nonumber \\&\quad = \Vert \psi _n \phi (u_n)+(1-\psi _n)Sv_n-{\mathfrak {z}}\Vert ^2\nonumber \\&\quad = \Vert \psi _n(\phi (u_n)-{\mathfrak {z}})+(1-\psi _n)(Sv_n-{\mathfrak {z}})\Vert ^2\nonumber \\&\quad \le (1-\psi _n)^2\Vert Sv_n-{\mathfrak {z}}\Vert ^2 + 2\psi _n\langle \phi (u_n)-{\mathfrak {z}},(1-\psi _n)(Sv_n-{\mathfrak {z}}) + \psi _n(\phi (u_n)-{\mathfrak {z}})\rangle \nonumber \\&\quad =(1-\psi _n)^2\Vert v_n-{\mathfrak {z}}\Vert ^2+2\psi _n\langle \phi (u_n)-\phi ({\mathfrak {z}})+\phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad =(1-\psi _n)^2\Vert v_n-{\mathfrak {z}}\Vert ^2 + 2\psi _n\langle \phi (u_n)-\phi ({\mathfrak {z}}),u_{n+1}-{\mathfrak {z}}\rangle +2\psi _n\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad \le (1-\psi _n)^2\Vert v_n-{\mathfrak {z}}\Vert ^2 + 2\psi _n\xi \langle u_n-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle +2\psi _n\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad \le (1+{\psi _n}^2-2\psi _n)\Vert u_n-{\mathfrak {z}}\Vert ^2 + 2\psi _n\xi \Vert u_n-{\mathfrak {z}}\Vert ^2+2\psi _n\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad = (1-2\psi _n)\Vert u_n-{\mathfrak {z}}\Vert ^2 +{\psi _n}^2\Vert u_n-{\mathfrak {z}}\Vert ^2+ 2\psi _n\xi \Vert u_n-{\mathfrak {z}}\Vert ^2+2\psi _n\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle \nonumber \\&\quad =\big [1-2\psi _n(1-\xi )\big ]\Vert u_n-{\mathfrak {z}}\Vert ^2+2\psi _n(1-\xi )\bigg [\dfrac{\psi _n\Vert u_n-{\mathfrak {z}}\Vert ^2}{2(1-\xi )}+\dfrac{\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle }{1-\xi }\bigg ]. \end{aligned}$$
(3.29)

It follows from relations (3.28) and (3.29), that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\bigg [\dfrac{\psi _n\Vert u_n-{\mathfrak {z}}\Vert ^2}{2(1-\xi )}+\dfrac{\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{n+1}-{\mathfrak {z}}\rangle }{1-\xi }\bigg ]\le 0. \end{aligned}$$
(3.30)

Choose \(n\ge N_2\in {\mathbb {N}}\,(N_2\ge N_1)\) large enough such that \(2\psi _n(1-\xi )<1.\) By using relations (3.29) and (3.30) and applying Lemma 2.5, we conclude that \(\lim \limits _{n\rightarrow \infty }u_n\rightarrow {\mathfrak {z}}.\)

Case II: Assume that there is a subsequence \(\{n_i\}\) of \(\{n\}\) such that

$$\begin{aligned} \Vert u_{n_i}-{\mathfrak {z}}\Vert \le \Vert u_{n_{i+1}}-{\mathfrak {z}}\Vert ,\quad \forall \,i\in {\mathbb {N}}. \end{aligned}$$

Thus, by Lemma 2.4, there is a sequence \(\{m_k\}\subset {\mathbb {N}}\) as \(\lim \limits _{k\rightarrow \infty }m_k=\infty \) such that

$$\begin{aligned} \Vert u_{m_k}-{\mathfrak {z}}\Vert \le \Vert u_{{m_k}+1} -{\mathfrak {z}}\Vert \quad \textrm{and}\quad \Vert u_k-{\mathfrak {z}}\Vert \le \Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ,\quad \forall \,k\in {\mathbb {N}}. \end{aligned}$$
(3.31)

Similar to Case I, the relation (3.17) provides that

$$\begin{aligned}&(1-\psi _{m_k})\bigg (1-\dfrac{\eta \tau _{m_k}}{\tau _{{m_k}+1}}\bigg )\bigg (\Vert u_{m_k}-w_{m_k}\Vert ^2+\Vert v_{m_k}-w_{m_k}\Vert ^2\bigg ) \end{aligned}$$
(3.32)
$$\begin{aligned}&\quad \le \psi _{m_k}\Vert \phi (u_{m_k})-{\mathfrak {z}}\Vert ^2 + \Vert u_{m_k}-{\mathfrak {z}}\Vert ^2-\Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ^2-\psi _{m_k}\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2\nonumber \\&\qquad -\psi _{m_k}(1-\psi _{m_k})\Vert \phi (u_{m_k})-Sv_{m_k}\Vert ^2. \end{aligned}$$
(3.33)

By the relations (3.1), (3.13) and (3.31), we obtain

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert u_{m_k}-w_{m_k}\Vert =\lim \limits _{k\rightarrow \infty }\Vert v_{m_k}-w_{m_k}\Vert =0. \end{aligned}$$
(3.34)

Also, we can obtain as similar to Case I

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert Sv_{m_k}-v_{m_k}\Vert =0 \end{aligned}$$
(3.35)

and

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert u_{{m_k}+1}-u_{m_k}\Vert =0. \end{aligned}$$
(3.36)

We have to use the same justification as in Case I, such that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\,\textrm{sup}\,\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{{m_k}+1}-{\mathfrak {z}}\rangle \le 0. \end{aligned}$$
(3.37)

By using relations (3.29) and (3.31), we obtain

$$\begin{aligned} \Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ^2&\le \big [1-2\psi _{m_k}(1-\xi )\big ]\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2\nonumber \\&\quad +2\psi _{m_k}(1-\xi )\bigg [\dfrac{\psi _{m_k}\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2}{2(1-\xi )} + \dfrac{\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{{m_k}+1}-{\mathfrak {z}}\rangle }{1-\xi }\bigg ]\nonumber \\&\le \big [1-2\psi _{m_k}(1-\xi )\big ]\Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ^2\nonumber \\&\quad +2\psi _{m_k}(1-\xi )\bigg [\dfrac{\psi _{m_k}\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2}{2(1-\xi )} + \dfrac{\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{{m_k}+1}-{\mathfrak {z}}\rangle }{1-\xi }\bigg ]. \end{aligned}$$
(3.38)

It follows that

$$\begin{aligned} \Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ^2\le \dfrac{\psi _{m_k}\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2}{2(1-\xi )} + \dfrac{\langle \phi ({\mathfrak {z}})-{\mathfrak {z}},u_{{m_k}+1}-{\mathfrak {z}}\rangle }{1-\xi }. \end{aligned}$$
(3.39)

By the relations (3.1) and (3.31), relations (3.37) and (3.39) implies that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert u_{{m_k}+1}-{\mathfrak {z}}\Vert ^2 = 0. \end{aligned}$$

Thus, the above relation implies that

$$\begin{aligned} \lim \limits _{k\rightarrow \infty }\Vert u_k-{\mathfrak {z}}\Vert ^2\le \lim \limits _{k\rightarrow \infty }\Vert u_{m_k}-{\mathfrak {z}}\Vert ^2\le 0. \end{aligned}$$
(3.40)

Consequently, the sequence \(\{u_n\}\) converges strongly to \({\mathfrak {z}}\in \Omega :=\Gamma \cap \Lambda .\) \(\square \)

4 Applications

Application to pseudomonotone equilibrium problems:

Set \(S = I\) in Algorithm 1, then we have the following strong convergence algorithm for pseudomonotone equilibrium problem:

Corollary 4.1

Assume that \(g:{\mathcal {K}}\times {\mathcal {K}}\rightarrow {\mathbb {R}}\) is satisfying Assumption 2.1. Let the sequence \(\{u_n\},\{w_n\}\) and \(\{v_n\}\) be generated in the following manner: Choose \(u_0\in {\mathcal {K}},\) and \(\tau _0>0,\,\eta \in (0,\,1).\) Compute

$$\begin{aligned} w_n&= \textrm{prox}_{\tau _n g(u_n)}(u_n),\\ v_n&= \textrm{prox}_{\tau _n g(w_n)}(u_n),\\ u_{n+1}&= \psi _n \phi (u_n) + (1-\psi _n)v_n, \end{aligned}$$

and set

$$\begin{aligned} \tau _{n+1} = \textrm{min}\Bigg \{\tau _n,\dfrac{\eta (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2)}{2\,\textrm{max}\big \{0,g(u_n,v_n)-g(u_n,w_n)-g(w_n,v_n)\big \}}\Bigg \}. \end{aligned}$$

Then the sequences \(\{u_n\},\{w_n\}\) and \(\{v_n\}\) converge strongly to the solution \({\mathfrak {z}}\) of \(\Gamma .\)

Application to pseudomonotone variational inequality problems:

Recall that in the problem of classical variational inequality, one needs to find a point \({\mathfrak {z}}\in {\mathcal {K}}\) such that

$$\begin{aligned} \langle {\mathcal {A}}({\mathfrak {z}}),v-{\mathfrak {z}} \rangle \ge 0,\quad \forall \,v\in {\mathcal {K}}, \end{aligned}$$

where \({\mathcal {A}}:{\mathcal {H}}\rightarrow {\mathcal {H}}\) is an operator. We denote the solution set of classical variational inequality by the symbol \(VI({\mathcal {A}},{\mathcal {K}}).\) Set the bi-function \(g(u,v) := \langle {\mathcal {A}}(u),v-u\rangle \) for all \(u,v\in {\mathcal {K}}\) in Algorithm 1, we have

$$\begin{aligned} w_n&= \textrm{arg}\min _{v\in {\mathcal {K}}}\,\{g(u_n,v)+\frac{1}{2\tau _n}\Vert u_n-v\Vert ^2\}\\&= \textrm{arg}\min _{v\in {\mathcal {K}}}\,\{\langle {\mathcal {A}}(u_n),v-u_n\rangle +\frac{1}{2\tau _n}\Vert u_n-v\Vert ^2\}\\&= \textrm{arg}\min _{v\in {\mathcal {K}}}\,\{\langle {\mathcal {A}}(u_n),v-u_n\rangle +\frac{1}{2\tau _n}\Vert u_n-v\Vert ^2\}+\frac{\tau _n^2}{2}\Vert {\mathcal {A}}(u_n)\Vert ^2-\frac{\tau _n^2}{2}\Vert {\mathcal {A}}(u_n)\Vert ^2\\&= \textrm{arg}\min _{v\in {\mathcal {K}}}\{\frac{1}{2\tau _n}\Vert v-(u_n-\tau _n{\mathcal {A}}(u_n))\Vert ^2\}-\frac{\tau _n}{2}\Vert {\mathcal {A}}(u_n)\Vert ^2\\&= P_{{\mathcal {K}}}(u_n-\tau _n{\mathcal {A}}(u_n)). \end{aligned}$$

Similarly,

$$\begin{aligned} v_n =P_{{\mathcal {K}}}(u_n-\tau _n{\mathcal {A}}(v_n)). \end{aligned}$$

Assumption 4.1

Assume that \({\mathcal {A}}\) is satisfying the following assumptions:

\({\mathcal {A}}_1\)::

\({\mathcal {A}}\) is pseudomonotone on \({\mathcal {K}},\) that is, for all \(u,v\in {\mathcal {K}},\)

$$\begin{aligned} \langle {\mathcal {A}}(u),v-u\rangle \ge 0 \implies \langle {\mathcal {A}}(v), u-v \rangle \le 0. \end{aligned}$$

and \(VI({\mathcal {A}},{\mathcal {K}})\) is non-empty.

\({\mathcal {A}}_2:\):

\({\mathcal {A}}\) is Lipschitz continuous on \({\mathcal {K}}\) with \(L>0,\) that is, for all \(u,v\in {\mathcal {K}},\)

$$\begin{aligned} \Vert {\mathcal {A}}(u)-{\mathcal {A}}(v)\Vert \le L\Vert u-v\Vert . \end{aligned}$$
\({\mathcal {A}}_3:\):

\(\lim \limits _{n\rightarrow \infty }\,\textrm{sup}\,\langle {\mathcal {A}}(u_n),v-u_n\rangle \le \langle {\mathcal {A}}({\mathfrak {z}}),v-{\mathfrak {z}}\rangle \) for every \(v\in {\mathcal {K}}\) and \(\{u_n\}\subset {\mathcal {K}}\) satisfying \(u_n\rightharpoonup {\mathfrak {z}}.\)

Many researchers have studied variational inequality problem [8] and have established various iterative methods to tackle it; see for example [4, 6, 7, 32]. We have the following strong convergence theorem about the pseudomonotone variational inequality problem [8]:

Corollary 4.2

Assume that \({\mathcal {A}}:{\mathcal {K}}\rightarrow {\mathcal {H}}\) is satisfying Assumptions 4.1. Let the sequences \(\{u_n\},\{w_n\}\) and \(\{v_n\}\) be generated in the following manner: Choose \(u_0\in {\mathcal {H}}\) and \(\tau _0>0,\,\eta \in (0,\,1).\) Compute

$$\begin{aligned} w_n&= P_{{\mathcal {K}}}\big (u_n-\tau _n {\mathcal {A}}(u_n)\big ),\\ v_n&= P_{{\mathcal {K}}}\big (u_n-\tau _n {\mathcal {A}}(w_n)\big ),\\ u_{n+1}&= \psi _n \phi (u_n) + (1-\psi _n)v_n, \end{aligned}$$

and set

$$\begin{aligned} \tau _{n+1} = \textrm{min}\Bigg \{\tau _n,\dfrac{\eta (\Vert u_n-w_n\Vert ^2+\Vert v_n-w_n\Vert ^2)}{2\,\textrm{max}\big \{0,\langle {\mathcal {A}}(u_n),v_n-w_n\rangle - \langle {\mathcal {A}}(w_n), v_n-w_n \rangle \big \}}\Bigg \}. \end{aligned}$$

Then the sequences \(\{u_n\}.\{w_n\}\) and \(\{v_n\}\) strongly converge to the solution \({\mathfrak {z}}\) of \(VI({\mathcal {A}},{\mathcal {K}}).\)

5 Numerical illustrations

In this section, we provide a numerical example to support and justify our proposed algorithm. All codes are written in Matlab (2021a).

Example 5.1

Suppose that \({\mathcal {H}} = {\mathbb {R}}\) with the inner product \(\langle u,v\rangle := u\cdot v,\quad \forall \,u,v\in {\mathcal {H}}.\) and the induced norm \(\Vert u\Vert := |u|, \quad \forall \,u\in {\mathcal {H}}.\) Let \({\mathcal {K}} := \{u\in {\mathcal {H}}:|u|\le 1\}\) be the unit ball and defined an operator \({\mathcal {A}}:{\mathcal {K}}\rightarrow {\mathcal {H}}\) by

$$\begin{aligned} {\mathcal {A}}(u) := (u + |u|)/2. \end{aligned}$$

Clearly, \({\mathcal {A}}\) is \(1-\)Lipschitz continuous and pseudomonotone operator on \({\mathcal {K}}.\) We consider a contraction mapping \(g(u) = u/2\) for all \(u\in {\mathcal {H}}\) with \(\xi =1/2.\) The solution set of variational inequality problem (VI) is given by \(VI({\mathcal {A}},{\mathcal {K}}) = \{0\}\ne \text{\O }.\) Moreover, with respect to corollary 4.2, we take \(\psi _n = \dfrac{1}{1+n},\,\eta = 0.33,\,u_0 = 0.3.\)

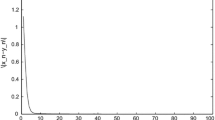
Numerical results of the sequence \(\{u_n\}\) generated by Corollary 4.2 for initial value \(u_0=0.3\) and different choices of step size \(\tau _0.\)

Numerical results for initial value \(u_0=0.3.\)

Number of iterations

\(\tau _0 = 0.1\)

\(\tau _0 = 0.2\)

\(\tau _0 = 0.5\)

1

0.300000

0.300000

0.300000

15

0.026389

0.009698

0.002684

30

0.004712

0.000538

0.000033

45

0.000955

0.000033

0.000000

69

0.000082

0.000000

0.000000

75

0.000045

0.000000

0.000000

90

0.000010

0.000000

0.000000

121

0.000000

0.000000

0.000000

Remark 5.1

In view of the above graphical representation (Fig. 1) of the sequence \(\{u_n\}\) , we see that the proposed algorithm work better when the value of the step size \(\tau _0\) is larger.

Fig. 1
figure 1

Graphical representation of the sequence \(\{u_n\}\) for initial value \(u_0 = 0.3\) and different choices of step size \(\tau _0.\)

Full size image