Synchronization of a nine-dimensional stochastic time-delayed hyperchaotic system

Abstract

Time delay and randomness are the two essential aspects of nonlinear systems, which precariously affect the control and synchronization of nonlinear systems. This paper considers the synchronization of a new nine-dimensional stochastic hyperchaotic system with time delay. This work advances a feedback control method to synchronize stochastic time-delay hyperchaotic systems based on the Lyapunov stability theory and linear matrix inequalities (LMIs) approach. Sufficient conditions are derived to guarantee the global asymptotical stability in the error system’s mean square; consequently, the drive system synchronizes with the response system.

1 Introduction

1.1 Background and motivation

The concept of a dynamical system is a mathematical formulation for any fixed law that depicts the time response of a point’s position. The hypothesis of the dynamical system manages the long-term subjective conduct. It concentrates the idea of the movement of a framework that is regularly mechanical or general physical phenomena, such as electronic circuits, planetary circles, financial aspects, and somewhere else. Most dynamical systems exhibit chaotic behavior due to nonlinearity, sensitivity to initial conditions, and non-periodicity. A chaotic system refers to the random irregular motion in a deterministic model. The behavior of chaotic systems is characterized by uncertainty, non-repeatable and unpredictable. Chaos is an intrinsic property of nonlinear dynamic systems and exhibits bifurcation under specific parameters; for more details, see [5, 19, 20]. In 1963, when designing a three-dimensional model for atmospheric convection, Lorenz [14] accidentally discovered the first chaotic system. Rössler [21] discovered a three-dimensional chaotic system with more simple algebra than the Lorenz system in 1976. There are also many well-known three-dimensional chaotic systems, such as Sprott systems [22], Chen system [4], Lü–Chen system [11] and so on. With the wide application of chaos theory in recent years, people have conducted extensive research on chaos theory and achieved many new results.

In 1990, Pecora and Carroll [18] first discovered chaos synchronization in electronic circuits, which increased chaos synchronization control research widely used in many fields, such as communication encryption, engineering optimization, and statistical prediction. Synchronization is coupling the motion of a drive and response system to standard behavior. Synchronization of the chaotic systems, hyperchaotic systems, and the unified chaotic systems have been reported in many papers, see [3, 16].

In control systems, the time delay due to sensor and actuator dynamics, signal transmission, and digital computations is an essential factor influencing stability and control performance. Time delay estimation in a control system is a challenging problem. It is even more complicated when the system dynamics are nonlinear and unknown. Time delays are regularly encountered in various industrial systems that must be controlled, because states of the system depend on the present time and a time in the past and frequently used in various fields such as communication, electronics, hydraulic and nonlinearity, sensitivity to initial conditions, and non-periodicity for theoretical and practical significance see [8, 12, 13].

In the meantime, stochastic modeling has arisen to strike an essential position in many branches of science and engineering. Also, in practice, noise perpetually inevitably exists in various practical systems since it is very difficult to reach an exact mathematical model of an object or process due to gradually changing parameters and environmental noise refer [15, 23]. In the stochastic framework, synchronization analysis for nonlinear chaotic time-delay stochastic systems has realized important research interests. However, to the best of the authors’ knowledge, the problem of synchronization for the stochastic systems with time delay and nonlinear disturbances has not been fully investigated, which remains challenging. The above facts motivate the present study.

1.2 Literature review

Abadneh [1] presented a new 4-D chaotic system and produced two equilibrium points at the origin. The fundamental characteristics of the system has been investigated by using equilibrium points, stability, and bifurcation diagram. Furthermore, an optimal controller has been established to make the system trajectories to the zero equilibrium. Vaidyanathan et al. [25] studied a new three-dimensional chaotic system with two nonlinearities. The quadratic and quartic nonlinearity have been examined in particular when building the new chaotic model. Authors estimated the feedback control laws using adaptive control theory to achieve global synchronization of identical chaotic systems with unknown parameters. In order to improve the further complexity of chaotic system, Huang et al. [9] introduced a new four-dimensional chaotic system based on Sprott B chaotic system. The use of a new sliding mode controller to construct a fractional-order chaotic system that rapidly enters a predefined motion state and maintains stability was proposed in [24]. In [27] Yu et al. investigated the circuit implementation of seven-dimensional hyperchaotic system with five nonlinear terms. Fan et al. [7] analyzed the stabilization problem of a class of double-wing chaotic system and also implemented the circuit for the proposed work. The presented work in [10] realized the four-dimensional chaotic system with multiscroll attractor via passive control approach. The authors in [17] investigated the PID type terminal sliding mode control method for machine and grid side converter modified controllers to reinforce the nonlinear relationship between the state-variable and control input BTB-converter. This control method reduces the reaction time of the BTB converter controllers and enhances their robustness to parameter uncertainty and external disturbances. Recently, Alattas et al. [2] investigated the nonsingular integral-type controllers to synchronize the N-dimensional hyperchaotic systems. This method proposed for a broad spectrum of hyper-chaotic systems allows for faster convergence while avoiding chattering and unstable fluctuations. The authors of [26] discussed an adaptive terminal sliding mode control for synchronizing chaotic systems based on a new sliding manifold with fast reaching conditions and highlighted its application to medical image encryption techniques.

1.3 Contribution

Through the above discussions, we find that most of the chaotic systems studied in the existing literature are deterministic and do not consider the influence of stochastic factors and time delay on the system. In addition, when introducing the stochastic factor, it is natural to consider the expected value of the solution of the system, which is crucial to prove the synchronization of the system and will bring analytical difficulties. The main contributions of this paper are summarized as follows

• 1. High-dimensional hyperchaotic systems have more complex dynamic behaviors, better randomness, and unpredictability to the best of the authors’ knowledge. The high-dimensional hyperchaotic system is used in secure communication, image encryption, text encryption, and voice encryption for larger keyspace and higher security. Due to the facts, a novel nine-dimensional hyperchaotic system is developed by introducing new system parameters with eleven nonlinear terms. The nonlinearity could increase the essence of the unpredictability of the future from the past.

• 2. Different from the existing literature, this paper addresses the globally asymptotic synchronization in the mean square sense of the proposed nine-dimensional hyperchaotic system with stochastic and time delay via LMIs framework.

• 3. Based on the state feedback controller and time delay, a suitable new Lyapunov functional is constructed by superimposing the triple and quadruple integral terms to show the delay information and attain the faster feasibility.

• 4. The derived sufficient conditions guarantee the globally asymptotic synchronization in terms of solvable LMIs by employing the Lyapunov stability theory.

1.4 Paper organization

The rest of this paper is summarized as follows: Sect. 2 presents the model description and problem formulation of a nine-dimension stochastic time-delayed hyperchaotic system. In Sect. 3, some sufficient conditions are demonstrated for the proposed hyperchaotic system via the LMI approach. Also, numerical simulation is given in Sect. 3.1 to show the effectiveness of this paper. Finally, Sect. 4 states the conclusion and future direction of the proposed work followed the conclusion section.

2 Model description and problem formulation

Yu et al. [27] proposed a 7-D hyperchaotic system given as follows:

$$\begin{aligned} \frac{dx_1}{dt}=\, & {} a(x_2(t)-x_1(t))+x_4(t)-x_5(t)-x_7(t)\nonumber \\ \frac{dx_2}{dt}= \,& {} cx_1(t)-x_2(t)-x_1(t)x_3(t)-x_6(t)\nonumber \\ \frac{dx_3}{dt}=\, & {} -bx_3(t)+x_1(t)x_2(t)\nonumber \\ \frac{dx_4}{dt}= \,& {} dx_4(t)-x_2(t)x_3(t)\nonumber \\ \frac{dx_5}{dt}=\,& {} ex_7(t)+x_2(t)x_3(t)\nonumber \\ \frac{dx_6}{dt}= \,& {} fx_1(t)+x_2(t)x_3(t)\nonumber \\ \frac{dx_7}{dt}=\, & {} rx_1(t), \end{aligned}$$

(1)

where $x_1(t),x_2(t),\dots ,x_7(t)$ refer state vectors of (1), (a, b, c, d, e, f, r) denote system parameters. For $a=10$, $b=8/3$, $c=28$, $d=-1$, $e=8$, $f=1$, and $r=5$, system (1) exhibits hyperchaotic behavior. Based on this work, we include six non-linear terms and two state vectors to the above system (1). The novel 9-D hyperchaotic system is given as follows:

$$\begin{aligned} \frac{dx_1}{dt}=\, & {} a(x_2(t)-x_1(t))+x_4(t)-(x_5(t)+x_7(t)+x_8(t))+x_9(t)\nonumber \\ \frac{dx_2}{dt}=\, & {} cx_1(t)-x_2(t)-x_1(t)x_3(t)-x_6(t)\nonumber \\ \frac{dx_3}{dt}=\, & {} -bx_3(t)+x_1(t)x_2(t)\nonumber \\ \frac{dx_4}{dt}=\, & {} dx_4(t)-x_2(t)x_3(t)\nonumber \\ \frac{dx_5}{dt}= \,& {} ex_7(t)+x_2(t)x_3(t)+x_1(t)x_3(t)-x_1(t)x_2(t)\nonumber \\ \frac{dx_6}{dt}=\, & {} fx_1(t)+x_2(t)x_3(t)\nonumber \\ \frac{dx_7}{dt}= \,& {} r_1x_1(t)+x_1(t)x_3(t)\nonumber \\ \frac{dx_8}{dt}=\, & {} r_2 x_2(t)+x_2(t)x_3(t)+x_1(t)x_3(t)-x_1(t)x_2(t)\nonumber \\ \frac{dx_9}{dt}=\, & {} r_3 x_1(t), \end{aligned}$$

(2)

where $x(t)=[x_1(t),x_2(t),\dots ,x_9(t)]^T\in \mathbb {R}^9$ refer to the state vectors of (2), a, b, c, d, e, f, $r_1$, $r_2$, and $r_3$ denote system parameters. For $a=100$, $b=8/3$, $c=28$, $d=-10$, $e=80$, $f=100$, and $(r_1,r_2,r_3)=(5,15,30)$, system (2) exhibits hyperchaotic behavior. The following Figs. 1, 2, 3 and 4 depict the chaotic attractor for system (2). Figure 5 denotes the time response of the state vectors $x_1(t),x_2(t),\dots , x_9(t)$ for system (2). Figure 6 clearly depicts that the system (2) has three positive Lyapunov exponents and six negative Lyapunov exponents. The fractal dimension is also a typical characteristic of chaos and is calculated by utilizing Lyapunov exponents in the following Kaplan–Yorke dimension formula [6]. $\varLambda =\mu +\sum \nolimits _{i=1}^\mu \frac{\lambda _i}{|\lambda _{\mu +1}|},$ where each $\lambda _i$ denote Lyapunov exponent, $\mu$ refers to the first $\mu$ Lyapunov exponent is non-negative.

In this manuscript, by observing the values of nine Lyapunov exponents, one can determine the value of $\mu$ is 3. Now the Kaplan–Yorke dimension can be expressed as follows:

$$\begin{aligned} \varLambda =3+\frac{(0.0232+0.0134+0.0161)}{|0.0796|}\approx 3.6621. \end{aligned}$$

In view of Kaplan–Yorke dimension, the value of fractal dimension takes the fractional value. Hence, system (2) rush into hyperchaotic in nature.

Fig. 1

Chaotic attractors for the system (2): $x_1(t)-x_2(t)$, $x_1(t)-x_3(t)$, $x_1(t)-x_4(t)$, $x_1(t)-x_5(t)$, $x_1(t)-x_6(t)$, $x_1(t)-x_7(t)$, $x_1(t)-x_8(t)$, $x_1(t)-x_9(t)$, $x_2(t)-x_3(t)$

Fig. 2

Chaotic attractors for the system (2): $x_2(t)-x_4(t)$, $x_2(t)-x_5(t)$, $x_2(t)-x_6(t)$, $x_2(t)-x_7(t)$, $x_2(t)-x_8(t)$, $x_2(t)-x_9(t)$, $x_3(t)-x_4(t)$, $x_3(t)-x_5(t)$, $x_3(t)-x_6(t)$

Fig. 3

Chaotic attractors for the system (2): $x_3(t)-x_7(t)$, $x_3(t)-x_8(t)$, $x_3(t)-x_9(t)$, $x_4(t)-x_5(t)$, $x_4(t)-x_6(t)$, $x_4(t)-x_7(t)$, $x_4(t)-x_8(t)$, $x_4(t)-x_9(t)$, $x_5(t)-x_6(t)$

Fig. 4

Chaotic attractors for the system (2): $x_5(t)-x_7(t)$, $x_5(t)-x_8(t)$, $x_5(t)-x_9(t)$, $x_6(t)-x_7(t)$, $x_6(t)-x_8(t)$, $x_6(t)-x_9(t)$, $x_7(t)-x_8(t)$, $x_7(t)-x_9(t)$, $x_8(t)-x_9(t)$

Fig. 5

Time response for the nine-dimensional hyperchaotic system (2)

Fig. 6

Trajectory for Lyapunov exponent of the proposed nine-dimensional hyperchaotic system (2)

The equation of stability for system (2) is given as follows:

$$\begin{aligned}&a(x_2(t)-x_1(t))+x_4(t) -(x_5(t)+x_7(t)+x_8(t))+x_9(t)=0\nonumber \\&cx_1(t)-x_2(t)-x_1(t)x_3(t)-x_6(t)=0\nonumber \\&-bx_3(t)+x_1(t)x_2(t)=0\nonumber \\&dx_4(t)-x_2(t)x_3(t)=0\nonumber \\&ex_7(t)+x_2(t)x_3(t)+x_1(t)x_3(t)-x_1(t)x_2(t)=0\nonumber \\&fx_1(t)+x_2(t)x_3(t)=0\nonumber \\&r_1x_1(t)+x_1(t)x_3(t)=0\nonumber \\&r_2 x_2(t)+x_2(t)x_3(t)+x_1(t)x_3(t)-x_1(t)x_2(t)=0\nonumber \\&r_3 x_1(t)=0 \end{aligned}$$

(3)

Solving the above equations described in (3), one can have the equilibrium point $\mathscr {O}(0, x^*,0,0,ax^*,-x^*,0,0,0)$, $x^*\in \mathbb {R}^9$ which is independent of the system parameters except a. The Jacobian matrix at $\mathscr {O}$ is given by

$$\begin{aligned} \mathscr {J}=\begin{bmatrix} -a&{}a&{}0&{}1&{}-1&{}0&{}-1&{}-1&{}1\\ c&{}-1&{}0&{}0&{}0&{}-1&{}0&{}0&{}0\\ x^*&{}0&{}-b&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}-x^*&{}d&{}0&{}0&{}0&{}0&{}0\\ -x^*&{}0&{}x^*&{}0&{}0&{}0&{}e&{}0&{}0\\ f&{}0&{}x^*&{}0&{}0&{}0&{}0&{}0&{}0\\ r_1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -x^*&{}r_2&{}x^*&{}0&{}0&{}0&{}0&{}0&{}0\\ r_3&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{bmatrix}. \end{aligned}$$

For the proposed system parameters, the characteristic polynomial of $|\mathscr {J}-\lambda I|$ is $-\frac{1}{3}\lambda ^3(9(x^*)^2\lambda ^3+369(x^*)^2\lambda ^2+3015 (x^*)^2\lambda -450(x^*)^2-6x^*\lambda ^4-82x^*\lambda ^3-236 x^*\lambda ^2-160 x^*\lambda +3\lambda ^6+341\lambda ^5-4257 \lambda ^4-63085\lambda ^3+188910\lambda ^2+821800 \lambda -88000).$ When $x^*=0$, the characteristic equation can be rewritten as:

$$\begin{aligned} -\lambda ^9- & {} \frac{341}{3}\lambda ^8+1419\lambda ^7+\frac{63085}{3} \lambda ^6-62970\lambda ^5-\frac{821800}{3} \lambda ^4+\frac{88000}{3}\lambda ^3=0. \end{aligned}$$

(4)

Solving the above Eq. (4), one can obtain the following nine eigenvalues:

$$\begin{aligned}&\lambda _1=17.871,\ \lambda _2=4.753,\ \lambda _3=0.105,\\&\lambda _4=0,\ \lambda _5=0,\ \lambda _6=0,\\&\lambda _7=-8/3,\ \lambda _8=-10,\ \lambda _9=-123.730. \end{aligned}$$

From the above eigenvalues, one can conclude that Eq. (4) has three positive and three negative eigenvalues. The remaining three eigenvalues are zero. Hence, it can be shown as $\mathscr {O}$ is an unstable saddle point when $x^*=0$. Assume that $\varPsi$ is the domain in the smooth surface $\mathbb {R}^9$ and $\mathscr {V}(t)$ is the volume of $\varPsi (t)$.

$$\begin{aligned} \frac{d\mathscr {V}(t)}{dt}=\int \limits _{\varPsi (t)} (\nabla \cdot \mathscr {V})dx_1dx_2dx_3dx_4dx_5dx_6dx_7dx_8dx_9. \end{aligned}$$

(5)

From Eq. (5), one can calculate the dissipation of hyperchaotic system.

$$\begin{aligned} \nabla \cdot \mathscr {V}= & {} \frac{\partial \dot{x_1}}{\partial x_1} +\frac{\partial \dot{x_2}}{\partial x_2}+\frac{\partial \dot{x_3}}{\partial x_3}+\frac{\partial \dot{x_4}}{\partial x_4}+ \frac{\partial \dot{x_5}}{\partial x_5}+\frac{\partial \dot{x_6}}{\partial x_6}+\frac{\partial \dot{x_7}}{\partial x_7} +\frac{\partial \dot{x_8}}{\partial x_8}+\frac{\partial \dot{x_9}}{\partial x_9}\nonumber \\= & {} -a-1-b+d=\delta . \end{aligned}$$

(6)

We have, $a=100$, $b=8/3$, and $d=-10$ which implies that $\delta =-\frac{341}{3}<0$. Substitute (6) into (5), one can have

$$\begin{aligned} \frac{d\mathscr {V}(t)}{dt}=-\frac{341}{3} \mathscr {V}(t), \end{aligned}$$

(7)

where $\mathscr {V}(t)$ is the 9-D hyperchaotic system. Solving (7), $\mathscr {V}(t)=e^{-\frac{341}{3}}\mathscr {V}(0),$ if $\nabla \cdot \mathscr {V}<0$ then system (2) is dissipative. Hence, system (2) satisfies the principle of hyperchaotic state. For our convenience, system (2) can be rewritten as:

$$\begin{aligned} \dot{x}(t)=Ax(t)+\hat{f}(t,x(t)), \end{aligned}$$

(8)

where $x(t)=(x_1(t),x_2(t),\dots ,x_9(t))^T$ is the state variable, $A\in \mathbb {R}^{9\times 9}$ is the linear parameter matrix, and $\hat{f}(t,x(t))$ is the non-linear term. Since every real-time dynamical model will be affected by the environmental noise. In nature, the deterministic model (8) may affect by the external noise that could be captured by incorporating the model into stochastic differential systems involving Brownian motion. Hence, studying the hyperchaotic system involving Brownian motion for real-time phenomena is necessary. In this proposed work, the following stochastic delay differential equation is considered to analyze the synchronization of the hyperchaotic system. Let $\tau >0$ be the delay term. Let $C([-\tau ,0];\mathbb {R}^n)$ be the family of continuous functions $\phi$ from $[-\tau ,0]$ to $\mathbb {R}^n$. Let $L^2_{F_0}([-\tau ,0];\mathbb {R}^n)$ be the family of all $F_0$-measurable $C([-\tau ,0];\mathbb {R}^n)$-valued random variables $\chi =\{\chi (\theta )|-\tau \le \theta \le 0\}$ such that $\sup \limits _{\theta \in [-\tau ,0]}E|\chi (\theta )|^2<\infty$.

$$\begin{aligned} dx(t)= & {} [Ax(t)+Bx(t-\tau )+\hat{f}(t,x(t),x(t-\tau ))]dt+\hat{g}(t,x(t), x(t-\tau ))dW(t),\nonumber \\ x_0= & {} \chi ,\ \chi \in L^2_{F_0}([-\tau ,0];\mathbb {R}^n),\ -\tau \le t\le 0, \end{aligned}$$

(9)

where x(t) is the state of the system, $A,B\in \mathbb {R}^{9\times 9}$ are the linear parameter matrices, $W(t)=(w_1(t),w_2(t),\dots ,w_9(t))^T$ is the 9-D Brownian motion defined on the complete probability space $(\varOmega , \mathscr {F},\mathbb {P})$ which satisfies $E[dW(t)]=0,$ $E[dW^2(t)]=dt$. $\hat{f}(t,\cdot ,\cdot )$ and $\hat{g}(t,\cdot ,\cdot )$ are Lipschitz functions satisfy respectively $\hat{f}(t,0,0)=0$ and $\hat{g}(t,0,0)=0$. To illustrate the concept of synchronization, we consider system (9) as a drive system. The response system is defined by

$$\begin{aligned} dy(t) &= [Ay(t)+By(t-\tau )+\hat{f}(t,y(t),y(t-\tau ))+u(t)]dt+\hat{g}(t,y(t), y(t-\tau ))dW(t),\nonumber \\ y_0 &= \chi ,\ \chi \in L^2_{F_0}([-\tau ,0];\mathbb {R}^n),\ -\tau \le t\le 0, \end{aligned}$$

(10)

where $y(t)=(y_1(t),y_2(t),\dots ,y_9(t))^T$ is the state variable of response system, $A,B\in \mathbb {R}^{9\times 9}$ are the linear parameter matrices, $\hat{f}(t,y(t),y(t-\tau ))$ and $\hat{g}(t,y(t),y(t-\tau ))$ are two non-linear functions and u(t) is the control input. $\tau$ is the delay term. Define the synchronization error vector of the drive and response system as $e(t)=y(t)-x(t)$, where $e(t)=(e_1(t),e_2(t),\dots ,e_9(t))^T$. One can obtain the following error dynamics of proposed hyperchaotic system:

$$\begin{aligned} de(t)= [Ae(t)+Be(t-\tau )+f(t,e(t),e(t-\tau ))+u(t)]dt+g(t,e(t),e(t-\tau ))dW(t), \end{aligned}$$

(11)

where $f(t,e(t),e(t-\tau ))=\hat{f}(t,y(t),y(t-\tau ))-\hat{f}(t,x(t),x(t-\tau ))$, and $g(t,e(t),e(t-\tau ))=\hat{g}(t,y(t),y(t-\tau ))-\hat{g}(t,x(t),x(t-\tau ))$ represent nonlinear functions. For simplicity, Eq. (11) can be rewritten as

$$\begin{aligned} de(t)=\tilde{f}(t) dt+\tilde{g}(t) dW(t), \end{aligned}$$

(12)

where $\tilde{f}(t)=Ae(t)+Be(t-\tau )+f(t,e(t),e(t-\tau ))+u(t)$ is the drift term and $\tilde{g}(t)=g(t,e(t),e(t-\tau ))$ is the diffusion term. In this work, we endorse the state feedback controller as $u(t)=-Ke(t),$ where $K\in \mathbb {R}^{n\times n}$ is the control gain to be designed.

Fig. 7

Time response for the error dynamics (11)

Figure 7 clearly depicts the unsynchronized response for the drive and response systems (9) and (10) respectively.

To facilitate the following discussions, we restate the following definitions and assumptions.

Definition 1

[28] The error system (11) is said to be globally asymptotically stable in mean square if for any given initial condition such that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }E\Vert e(t)\Vert ^2\rightarrow 0, \end{aligned}$$

(13)

where $E(\cdot )$ is the mathematical expectation.

Assumption 1

If there exist positive constant $\mu$ and positive definite matrix $Q>0$ such that $f(t,e(t),e(t-\tau ))$ satisfies the following quadratic inequality:

$$\begin{aligned} f^T(t,e(t),e(t-\tau ))Qf(t,e(t),e(t-\tau ))\le \mu ^2 e^T(t)Qe(t). \end{aligned}$$

(14)

Assumption 2

There exist positive constants $\alpha _1$, $\alpha _2$ and positive definite matrix $Q>0$ such that

$$\begin{aligned} Trace(\tilde{g}^T(t)Q\tilde{g}(t))\le \alpha _1 e^T(t)Qe(t)+\alpha _2 e^T(t-\tau )Qe(t-\tau ). \end{aligned}$$

(15)

3 Main results

This section presents an LMI approach to solve the global asymptotic synchronization in the mean square for nine-dimensional hyperchaotic systems using a feedback controller. The following theorem shows a synchronization scheme to ensure that the controlled response system (10) can precisely track the drive system (9), which is formulated by employing the feasibility of an LMI.

Theorem 1

By considering the Assumptions (1) and (2), the error system (11) is globally asymptotically stable in mean square, for a given positive scalar $\tau$, any scalar $\mu >0$, there exist positive definite diagonal matrix $P=diag(p_1,p_2,\dots ,p_n)>0$, positive definite matrices $R_i=(r_{jk})_{n\times n}>0,\ i=1,2,\dots , 13$, and control gain matrix $K=diag(k_1,k_2,\dots ,k_n)$ such that

$$\begin{aligned} \varPhi =\begin{bmatrix} [\varOmega _{1}]_{9\times 9} &{} [\varOmega _{2}]_{9\times 1} &{} [\varOmega _{3}]_{9\times 9} \\ *&{} \varUpsilon &{} [\varOmega _{4}]_{1\times 9}\\ *&{}*&{} [\varOmega _{5}]_{9\times 9} \end{bmatrix}<0, \end{aligned}$$

(16)

where

$$\begin{aligned} \varOmega _1&=\begin{bmatrix} \varPsi _{1} &{} \varPsi _{2} &{} \varPsi _{3}&{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} \varPsi _{4} &{} 0&{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} \varPsi _{5}&{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} \varPsi _{6}&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} *&{} \varPsi _{7}&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} *&{} *&{} \varPsi _{8} &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} *&{} *&{} * &{} \varPsi _{9} &{} 0&{} 0\\ * &{} * &{} * &{} *&{} *&{} * &{} * &{} \varPsi _{10}&{} \varPsi _{11}\\ * &{} * &{} * &{} *&{} *&{} * &{} *&{} *&{} \varPsi _{12} \end{bmatrix}, \varOmega _2=\begin{bmatrix} 0&0&0&0&0&0&0&0&\frac{12 R_7}{\tau ^3} \end{bmatrix}^T,\\ \varUpsilon &= \frac{-36 R_7}{\tau ^4}-\frac{16 R_{10}}{\tau ^3}, \varOmega _3=[0]_{9\times 9},\ \varOmega _4=\begin{bmatrix} \frac{40 R_{10}}{\tau ^4}&0&0&0&0&0&0&0&0 \end{bmatrix},\\ \varOmega _5 &= \begin{bmatrix} \varPsi _{13} &{} 0 &{} 0&{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} \varPsi _{14} &{} \varPsi _{15}&{} 0&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} \varPsi _{16}&{} \varPsi _{17}&{} 0&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} \varPsi _{18}&{} \varPsi _{19}&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} *&{} \varPsi _{20}&{} 0 &{} 0 &{} 0&{} 0\\ * &{} * &{} * &{} *&{} *&{} \varPsi _{21} &{} \varPsi _{22} &{} 0&{} 0\\ * &{} * &{} * &{} *&{} *&{} * &{} \varPsi _{23} &{} \varPsi _{24}&{} 0\\ * &{} * &{} * &{} *&{} *&{} * &{} * &{} \varPsi _{25}&{} \varPsi _{26}\\ * &{} * &{} * &{} *&{} *&{} * &{} *&{} *&{} \varPsi _{27} \end{bmatrix}, \end{aligned}$$

with

$$\begin{aligned} \varPsi _{1}&= {} P(A-K)+(A-K)^T P+R_1+\tau R_4-\frac{\tau ^2}{2} R_7+\frac{\tau ^3}{6} R_{10}+P+\mu ^2 R_{13},\\ \varPsi _{2} &= PB,\ \varPsi _{3}=P, \varPsi _{4}=-R_1+P,\ \varPsi _{5}=-R_{13}, \varPsi _{6}= R_2+\tau R_5-\frac{\tau ^2}{2} R_8+\frac{\tau ^3}{6} R_{11},\\ \varPsi _{7}&= -R_2, \varPsi _{8}= R_3+\tau R_6-\frac{\tau ^2}{2} R_9+\frac{\tau ^3}{6} R_{12}, \varPsi _{9}= -R_3,\ \varPsi _{10}=-\frac{4}{\tau } R_4,\\ \varPsi _{11}&= \frac{6R_4}{\tau ^2},\ \varPsi _{12}=-\frac{12 R_4}{\tau ^3}-\frac{6R_7}{\tau ^2}, \varPsi _{13}=-\frac{160 R_{10}}{\tau ^5},\ \varPsi _{14}=-\frac{4 R_5}{\tau }, \varPsi _{15}= \frac{6 R_5}{\tau ^2},\\ \varPsi _{16}&= -\frac{12 R_5}{\tau ^3}-\frac{6 R_8}{\tau ^2}, \varPsi _{17}=\frac{12 R_8}{\tau ^3},\ \varPsi _{18}=-\frac{36 R_8}{\tau ^4}-\frac{16 R_{11}}{\tau ^3},\\ \varPsi _{19} &= \frac{40 R_{11}}{\tau ^4},\ \varPsi _{20}=-\frac{160 R_{11}}{\tau ^5},\\ \varPsi _{21} &= -\frac{4 R_6}{\tau }, \varPsi _{22}=\frac{6R_6}{\tau ^2},\ \varPsi _{23}= -\frac{12 R_6}{\tau ^3}-\frac{6R_9}{\tau ^2}, \varPsi _{24}=\frac{12 R_9}{\tau ^3},\\ \varPsi _{25} &= -\frac{36 R_9}{\tau ^4}-\frac{16 R_{12}}{\tau ^3}, \varPsi _{26}=\frac{40 R_{12}}{\tau ^4},\ \varPsi _{27}=-\frac{160 R_{12}}{\tau ^5}. \end{aligned}$$

Proof

Consider the Lyapunov–Krasovskii functional as follows:

$$\begin{aligned} \mathscr {K}(t)=\sum \limits _{i=1}^5 \mathscr {K}_i, \end{aligned}$$

(17)

where

$$\begin{aligned} \mathscr {K}_1 &= e^T(t)Pe(t).\\ \mathscr {K}_2= & {} \int \limits _{t-\tau }^t e^T(s)R_1e(s)ds+\int \limits _{t-\tau }^t \tilde{f}^T(s)R_2\tilde{f}(s)ds+\int \limits _{t-\tau }^t \tilde{g}^T(s)R_3\tilde{g}(s)ds.\\ \mathscr {K}_3= & {} \int \limits _{-\tau }^0\int \limits _{t+\theta }^t e^T(s)R_4 e(s)dsd\theta +\int \limits _{-\tau }^0\int \limits _{t+\theta }^t \tilde{f}^T(s)R_5 \tilde{f}(s)dsd\theta +\int \limits _{-\tau }^0\int \limits _{t+\theta }^t \tilde{g}^T(s)R_6 \tilde{g}(s)dsd\theta .\\ \mathscr {K}_4= & {} \int \limits _{-\tau }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t e^T(s)R_7 e(s)dsd\theta d \beta +\int \limits _{-\tau }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t \tilde{f}^T(s)R_8 \tilde{f}(s)dsd\theta d \beta \\&+\int \limits _{-\tau }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t \tilde{g}^T(s)R_9 \tilde{g}(s)dsd\theta d \beta .\\ \mathscr {K}_5= & {} \int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t e^T(s)R_{10} e(s)ds d\theta d \beta d \delta +\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t \tilde{f}^T(s)R_{11} \tilde{f}(s)ds d\theta d \beta d \delta \\&+\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{\beta }^0\int \limits _{t+\theta }^t \tilde{g}^T(s)R_{12} \tilde{g}(s)dsd\theta d \beta d\delta . \end{aligned}$$

Using Ito’s process, we have

$$\begin{aligned} d\mathscr {K}(t)=d\mathscr {K}_1+d\mathscr {K}_2 +d\mathscr {K}_3+d\mathscr {K}_4+d\mathscr {K}_5. \end{aligned}$$

(18)

By using Assumption (1), one can have the following inequality:

$$\begin{aligned} \mu ^2 e^T(t)R_{13} e(t)-f^T(t,e(t),e(t-\tau ))R_{13}f(t,e(t),e(t-\tau ))\ge 0. \end{aligned}$$

(19)

Using the above inequality (19) and Assumption (2) with $\alpha _1=\alpha _2=1$, we have

$$\begin{aligned} d\mathscr {K}_1\le & {} [2 e^T(t)P (A-K)e(t)+2e^T(t)PBe(t-\tau ) +2e^T(t)Pf(t,e(t),e(t-\tau ))\nonumber \\&+e^T(t)Pe(t)+e^T(t-\tau )Pe(t-\tau )+\mu ^2 e^T(t)R_{13} e(t)\nonumber \\&-f^T(t,e(t),e(t-\tau ))R_{13}f(t,e(t),e(t-\tau ))]dt +2e^T(t)P\tilde{g}(t) dW(t). \end{aligned}$$

(20)

$$\begin{aligned} d\mathscr {K}_2= & {} e^T(t)R_1 e(t)+\tilde{f}^T(t)R_2\tilde{f}(t)+\tilde{g}^T(t)R_3\tilde{g}(t) -[e^T(t-\tau )R_1 e(t-\tau )\nonumber \\&+\tilde{f}^T(t-\tau )R_2\tilde{f}(t-\tau )+\tilde{g}^T(t-\tau )R_3\tilde{g}(t-\tau )]. \end{aligned}$$

(21)

Using second version of Wirtinger’s inequality [23] for single integral, one can have the following inequality:

$$\begin{aligned} d\mathscr {K}_3\le & {} \tau (e^T(t)R_4 e(t)+\tilde{f}^T(t)R_5\tilde{f}(t)+\tilde{g}^T(t)R_6\tilde{g}(t)) -\frac{1}{\tau }\bigg (\int \limits _{t-\tau }^te(s) ds\bigg )^T 4R_4\bigg (\int \limits _{t-\tau }^te(s) ds\bigg )\nonumber \\&+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^te(s) ds\bigg )^T 3R_4 \bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta e(s) ds d \theta \bigg )+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta e(s) ds d \theta \bigg )^T 3R_4 \bigg (\int \limits _{t-\tau }^te(s) ds\bigg )\nonumber \\&-\frac{4}{\tau ^3}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta e(s) ds d \theta \bigg )^T 3R_4\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta e(s) ds d \theta \bigg )-\frac{1}{\tau }\bigg (\int \limits _{t-\tau }^t\tilde{f}(s) ds\bigg )^T 4R_5\bigg (\int \limits _{t-\tau }^t\tilde{f}(s) ds\bigg )\nonumber \\&+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^t\tilde{f}(s) ds\bigg )^T 3R_5 \bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{f}(s) ds d \theta \bigg )+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{f}(s) ds d \theta \bigg )^T 3R_5 \bigg (\int \limits _{t-\tau }^t\tilde{f}(s) ds\bigg )\nonumber \\&-\frac{4}{\tau ^3}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{f}(s) ds d \theta \bigg )^T 3R_5\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{f}(s) ds d \theta \bigg )-\frac{1}{\tau }\bigg (\int \limits _{t-\tau }^t\tilde{g}(s) ds\bigg )^T 4R_6\bigg (\int \limits _{t-\tau }^t\tilde{g}(s) ds\bigg )\nonumber \\&+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^t\tilde{g}(s) ds\bigg )^T 3R_6 \bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{g}(s) ds d \theta \bigg )+\frac{2}{\tau ^2}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{g}(s) ds d \theta \bigg )^T 3R_6 \bigg (\int \limits _{t-\tau }^t\tilde{g}(s) ds\bigg )\nonumber \\&-\frac{4}{\tau ^3}\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{g}(s) ds d \theta \bigg )^T 3R_6\bigg (\int \limits _{t-\tau }^t\int \limits _{t-\tau }^\theta \tilde{g}(s) ds d \theta \bigg ). \end{aligned}$$

(22)

Using second version of Wirtinger’s inequality [23] for double integral, one can obtain the following inequality:

$$\begin{aligned} d\mathscr {K}_4\le & {} \frac{-\tau ^2}{2} (e^T(t)R_7 e(t)+\tilde{f}^T(t)R_8\tilde{f}(t)+\tilde{g}^T(t)R_9\tilde{g}(t))- \frac{1}{\tau ^2}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^te(s) ds d \beta \bigg )^T\nonumber \\&\times 6R_7\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^te(s) ds d \beta \bigg )+\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^te(s) ds d \beta \bigg )^T 4R_7\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )\nonumber \\&+\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )^T 4R_7 \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^te(s) ds d \beta \bigg )-\frac{9}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 4R_7 \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )-\frac{1}{\tau ^2}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta \bigg )^T 6R_8\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta \bigg )\nonumber \\&+\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta \bigg )^T 4R_8\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )+\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 4R_8 \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta \bigg )-\frac{9}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )^T 4R_8 \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )\nonumber \\&-\frac{1}{\tau ^2}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta \bigg )^T 6R_9\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta \bigg ) +\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta \bigg )^T\nonumber \\&\times 4R_9\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )+\frac{3}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )^T 4R_9 \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta \bigg )\nonumber \\&-\frac{9}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )^T 4R_9 \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0 \int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg ).\nonumber \\ \end{aligned}$$

(23)

Using second version of Wirtinger’s inequality [23] for triple integral, one can obtain the following inequality:

$$\begin{aligned} d\mathscr {K}_5\le & {} \frac{\tau ^3}{6} (e^T(t)R_{10} e(t) +\tilde{f}^T(t)R_{11}\tilde{f}(t)+\tilde{g}^T(t)R_{12}\tilde{g}(t))-\frac{1}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 16R_{10}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 10R_{10}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta d \nu \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta d \nu \bigg )^T \nonumber \\&\times 10 R_{10} \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )-\frac{16}{\tau ^5}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta d \nu \bigg )^T\nonumber \\&\times 10R_{10}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta d \nu \bigg )-\frac{1}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 16R_{11}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 10R_{11}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta d \nu \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta d \nu \bigg )^T\nonumber \\&\times 10 R_{11} \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )-\frac{16}{\tau ^5}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta d \nu \bigg )^T\nonumber \\&\times 10 R_{11}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta d \nu \bigg )-\frac{1}{\tau ^3}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 16R_{12}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )^T\nonumber \\&\times 10R_{12}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta d \nu \bigg )+\frac{4}{\tau ^4}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta d \nu \bigg )^T\nonumber \\&\times 10 R_{12} \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )-\frac{16}{\tau ^5}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta d \nu \bigg )^T\nonumber \\&\times 10 R_{12}\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta d \nu \bigg ) \end{aligned}$$

(24)

Substituting Eqs.  (20)–(24) in Eq. (18), we have the following inequality that

$$\begin{aligned} d\mathscr {K}(t)\le \mathscr {L}\mathscr {K}(t) dt+2 e^T(t) P \tilde{g}(t) dW(t), \end{aligned}$$

(25)

where $\mathscr {L}\mathscr {K}(t)=\sum \nolimits _{i=1}^5 d\mathscr {K}_i,$ and each $d\mathscr {K}_i$ is defined in Eqs. (20)–(24). Taking mathematical expectation on both sides of Eq. (25), we have

$$\begin{aligned} E\bigg [\frac{d\mathscr {K}(t)}{dt}\bigg ]\le E[\zeta ^T(t) \varPhi \zeta (t)], \end{aligned}$$

(26)

where

$$\begin{aligned} \zeta (t)= & {} \bigg [e^T(t)\ e^T(t-\tau )\ f^T(t,e(t),e(t-\tau ))\ \tilde{f}(t)\ \tilde{g}^T(t) \ \tilde{f}^T(t-\tau )\ \tilde{g}^T(t-\tau ) \ \bigg (\int \limits _{t-\tau }^te(s) ds \bigg )^T\\&\bigg (\int \limits _{t-\tau }^t\tilde{f}(s) ds \bigg )^T\ \bigg (\int \limits _{t-\tau }^t\tilde{g}(s) ds \bigg )^T\ \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^te(s) ds d \beta \bigg )^T\ \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta \bigg )^T\ \bigg (\int \limits _{-\tau }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta \bigg )^T\\&\bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta \bigg )^T\ \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta \bigg )^T \ \bigg (\int \limits _{-\tau }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta \bigg )^T\\&\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^te(s) ds d \beta d \delta d \nu \bigg )^T \ \bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{f}(s) ds d \beta d \delta d \nu \bigg )^T\\&\bigg (\int \limits _{-\tau }^0\int \limits _{\nu }^0\int \limits _{\delta }^0\int \limits _{t+\beta }^t\tilde{g}(s) ds d \beta d \delta d \nu \bigg )^T \bigg ]^T. \end{aligned}$$

From Eq. (26), it is clear that LMI (16) holds, then system (11) is asymptotically stable. Also from Eq. (26) and Ito formula, it is obvious to see that

$$\begin{aligned} E\mathscr {K}(t)-E\mathscr {K}(t_0)=E\int \limits _{t_0}^t \mathscr {L}\mathscr {K}(s) ds. \end{aligned}$$

(27)

From the definition of Lyapunov functional (17), there exist positive constant $\lambda$ such that

$$\begin{aligned} \lambda E\Vert e(t)\Vert ^2\le & {} E\mathscr {K}(t)\le E\mathscr {K}(t_0)+E\int \limits _{t_0}^t \mathscr {L}\mathscr {K}(s) ds\nonumber \\\le & {} E\mathscr {K}(t_0)+\lambda _{\max }E\int \limits _{t_0}^t\Vert e(s)\Vert ^2 ds, \end{aligned}$$

(28)

where $\lambda _{\max }$ is the maximum eigenvalue of $\varPhi <0$. Hence, system (11) is globally asymptotically stable in mean square. This completes the proof. $\square$

Remark 1

Different from the existing literature, the second version of Wirtinger’s inequality in [23] is introduced in this paper to deal with (22)–(24). Also one can observe that by introducing some new Lyapunov functional with inclusion of triple and quadruple integral terms leading the reduction of conservativeness.

3.1 Numerical simulation

In this section, numerical example is provided to validate the effectiveness of the synchronization criteria. Consider the 9-D stochastic time-delayed hyperchaotic error system (11). Let

$$\begin{aligned} A= & {} \begin{bmatrix} -75 &{} 75 &{} 0 &{} 0.75 &{} -0.75 &{} 0 &{} -0.75 &{} -0.75 &{} 0.75\\ 21 &{} -0.75 &{} 0&{} 0&{} 0&{} -0.75 &{} 0&{} 0&{} 0\\ 0&{}0&{} -2&{} 0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}-7.5&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}60&{}0&{}0\\ 75&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 3.75&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}11.25&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 22.5&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{bmatrix},\quad \hbox { and }\\ B= & {} \begin{bmatrix} -25 &{} 25 &{} 0 &{} 0.25 &{} -0.25 &{} 0 &{} -0.25 &{} -0.25 &{} 0.25\\ 7 &{} -0.25 &{} 0&{} 0&{} 0&{} -0.25 &{} 0&{} 0&{} 0\\ 0&{}0&{} -0.6667&{} 0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}-2.5&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}20&{}0&{}0\\ 25&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 1.25&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}3.75&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 7.5&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{bmatrix} \end{aligned}$$

be the system parameters matrices. Let $\tau =0.2$ seconds and assume that the Lipschitz constant as $\mu =500$ with step size $h=0.001$. By using LMI toolbox, one can obtain feasible control gain matrix K is given as follows:

$$\begin{aligned} K= \begin{bmatrix} 160.3 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 176.1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 144.9 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 132.9 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 226.8 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 246.5 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 152.4 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 154.8 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 162.8 \end{bmatrix}. \end{aligned}$$

Fig. 8

Synchronized chaotic attractor for the states $(x_1(t),x_3(t))$ and $(y_1(t),y_3(t))$ with delay and stochastic term in system (11)

Fig. 9

Synchronized chaotic attractor for the states $(x_1(t),x_3(t))$ and $(y_1(t),y_3(t))$ without delay and stochastic term in system (11)

Fig. 10

Synchronized time response for drive system (9) and response system (10) without delay and stochastic term

Fig. 11

Synchronized time response for drive system (9) and response system (10) with delay and stochastic term

Fig. 12

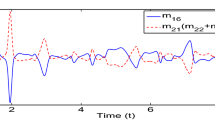
Comparative time response of system (11) including and excluding time delay and stochastic term

Fig. 13

Time response for error system (11) without delay and stochastic term

Fig. 14

Time response for error system (11) with delay and stochastic term

Figures 8 and 9 depict the synchronized phase portraits for the state variables $(x_1(t),x_3(t))$ and $(y_1(t),y_3(t))$. One can see that the chaotic attractors for the proposed system (8) are different when the dynamical system includes the Brownian motion and delay term. Furthermore, the same feedback control gain matrix K will synchronize the chaotic attractor of the drive and response system with and without stochastic and time-delayed nature. Figures 10 and 11 demonstrate the time responses of the drive and response system with and without stochastic terms, respectively. Also, Fig. 12 shows the time responses for the proposed hyperchaotic system and the stochastic time-delayed hyperchaotic system in comparison. Figure 13 depicts the time response for the error dynamics of the system (11) excluding the stochastic time delay. Figure 14 depicts the time response for the error dynamics of the proposed nine-dimensional stochastic time-delayed hyperchaotic system (11). Hence, one can easily verify that the rate of convergence for system (11) without delay and noise is highly faster than the (11).

Remark 2

The parameters (b, c, d, e, f) are chosen from the literature [27] for a fixed time scale. The system (2) exhibits hyperchaotic nature only by fixing the parameter values $r_1=5$, $r_2=15$, $r_3=30$ and $a\ge 30.2$. In this paper, one can assume the parameter value for a as 100 with initial condition $(10.1,10.3,10.5,10.7,10.9,-10.7,-10.5,-10.3,-10.1)$. For this fixed parameters, the control gain matrix K is estimated by using LMI toolbox. The aforementioned control gain matrix K will stabilize the error system (11) with and without stochastic disturbances included in the proposed framework.

Remark 3

The synchronization of drive and response systems is guaranteed if the stochastic disturbance is considered in both drive and the response systems. Figures 13 and 14 depict that the convergence rate of the error system (11) is less when excluding the stochastic term. Hence, one can conclude that the stabilization of the error system (11) without stochastic term yields less conservativeness than the system (11) with stochastic disturbance.

4 Conclusions

A new nine-dimensional hyperchaotic system has been designed and analyzes the behavior of the proposed method by Lyapunov exponent, fractal dimension, equilibrium stability, and dissipation. The proposed framework has nine equations with only one equilibrium point. A new LMIs criterion was employed to synchronize drive and response systems with stochastic and time delay via the Lyapunov stability theory and the Linear Matrix Inequality approach. A feedback controller guarantees the globally asymptotic stability of proposed error dynamics in the mean square sense. Furthermore, the numerical simulation demonstrates the effectiveness of the proposed nine-dimensional hyperchaotic system with and without stochastic and time delay.

5 Future direction

In the future, the proposed synchronization work will be extended into the fractional-order hyperchaotic neural network with non-instantaneous impulses. Also implementing the proposed work as a circuit model and study the synchronization to secure communication will be undertaken.