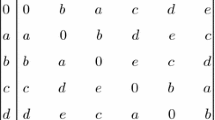1 Introduction and preliminaries

The concept of fuzzy set was introduced by Zadeh [7]. Recently, Andrzej Walendzik [6] defined BF-algebras. The notion of interval-valued fuzzy set was first introduced by Zadeh [8] as an extension of fuzzy sets. In [2], Liu and Meng constructed quotient BCI (BCK)-algebra via fuzzy ideals and [5] Ramesh with others applied the concept of quotient BF-algebra via interval-valued fuzzy ideals. In this paper we introduce the notion of quotient BF-algebra via interval-valued Intuitionistic fuzzy ideals and investigate some interesting properties.

By a BF-algebra we mean an algebra satisfying the axioms:

  1. 1.

    x * x = 0,

  2. 2.

    x * 0 = x,

  3. 3.

    0 * (x * y) = y * x, for all x, y ∊ X.

Throughout this paper, X is a BF-algebra.

Example 1.1

Let R be the set of real numbers and let A = (R, *, 0) be the algebra with the operation * defined by

$$ {\text{x}} * {\text{y}} = \left\{ {\begin{array}{*{20}l} {\text{x,}} \hfill & {{\text{if}}\,\,{\text{y}} = 0} \hfill \\ {\text{y,}} \hfill & {{\text{if}}\,\,{\text{x}} = 0} \hfill \\ { 0 ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

Definition 1.2

[1] The subset I of X is said to be an ideal of X, if (i) 0 ∊ I and (ii) x * y ∊ I and y ∊ I ⇒ x ∊ I.

We now review some fuzzy logic concepts. A fuzzy set in X is a function μ:X → [0, 1]. For fuzzy sets μ ∊ X and t ∊ [0, 1]. The sets U(μ; t) = {x ∊ X:μ(x) ≥ t} is called upper t-level cut of μ.

Definition 1.3

[3] A fuzzy set in a set S is a function μ from S into [0,1].

Definition 1.4

[4] The fuzzy set μ in X is called a fuzzy subalgebra of X, if μ(x * y) ≥ min{μ(x), μ(y)}, for all x, y ∊ X.

Definition 1.5

[3] A fuzzy set μ of X is called a fuzzy ideal of X if

  1. (F1).

    μ(0) ≥ μ(x)

  2. (F2).

    μ(x) ≥ min{μ(x * y), μ(y)} for all x, y ∊ X.

The fuzzy set μ in X is called a fuzzy sub algebra of X, if μ(x * y) ≥ min{μ(x), μ(y)}, for all x, y ∊ X.

An intuitionistic fuzzy set (shortly IFS) in a non-empty set X is an object having the form A = {(x, μA(x), λA(x)):x ∊ X}, where the function μA:X → [0, 1] and λA:X → [0, 1] denote the degree of membership (namely μA(x)) and the degree of non membership (namely λA(x)) of each element x ∊ X. For the sake of simplicity we use the symbol form A = (X, μA, λA) or A = (μA, λA).

By interval number D we mean an interval [a−, a+] where 0 ≤ a− ≤ a+ ≤ 1. The set of all closed subintervals of [0, 1] is denoted by D[0, 1]. For interval numbers D1 = [a −1 , b +1 ], D2 = [a −2 , b +2 ].

We define

  • $$ \begin{aligned} { \hbox{min} }\left( {{\text{D}}_{ 1} , {\text{D}}_{ 2} } \right) = {\text{D}}_{ 1} \cap {\text{D}}_{ 2} & = { \hbox{min} }\left( {\left[ {{\text{a}}_{ 1}^{ - } , {\text{b}}_{ 1}^{ + } } \right], \left[ {{\text{a}}_{ 2}^{ - } , {\text{b}}_{ 2}^{ + } } \right]} \right) \\ & = \left[ {{ \hbox{min} }\left\{ {{\text{a}}_{ 1}^{ - } , {\text{a}}_{ 2}^{ - } } \right\},{ \hbox{min} }\{ {\text{b}}_{ 1}^{ + } , {\text{b}}_{ 2}^{ + } \} } \right] \\ \end{aligned} $$
  • $$ \begin{aligned} { \hbox{max} }\left( {{\text{D}}_{ 1} , {\text{D}}_{ 2} } \right) = {\text{D}}_{ 1} \cup {\text{D}}_{ 2} & = { \hbox{max} }\left( {\left[ {{\text{a}}_{ 1}^{ - } , {\text{b}}_{ 1}^{ + } \left] {, } \right[{\text{a}}_{ 2}^{ - } , {\text{b}}_{ 2}^{ + } } \right]} \right) \\ & = \, \left[ {{ \hbox{max} }\left\{ {{\text{a}}_{ 1}^{ - } , {\text{a}}_{ 2}^{ - } } \right\},{ \hbox{max} }\{ {\text{b}}_{ 1}^{ + } , {\text{b}}_{ 2}^{ + } \} } \right] \\ \end{aligned} $$
    • $$ {\text{D}}_{ 1} + {\text{D}}_{ 2} = [ {\text{a}}_{ 1}^{ - } + {\text{a}}_{ 2}^{ - } - {\text{a}}_{ 1}^{ - } . {\text{a}}_{ 2}^{ - } , {\text{ b}}_{ 1}^{ + } + {\text{b}}_{ 2}^{ + } - {\text{b}}_{ 1}^{ + } . {\text{b}}_{ 2}^{ + } ] $$

    • And put

    • $$ {\text{D}}_{ 1} \le {\text{D}}_{ 2} \Leftrightarrow {\text{a}}_{ 1}^{ - } \le {\text{a}}_{ 2}^{ - } \,\,{\text{and}}\,\,{\text{b}}_{ 1}^{ + } \le {\text{b}}_{ 2}^{ + } $$
    • $$ {\text{D}}_{ 1} = {\text{D}}_{ 2} \Leftrightarrow {\text{a}}_{ 1}^{ - } = {\text{a}}_{ 2}^{ - } \,\,{\text{and}}\,\,{\text{b}}_{ 1}^{ + } = {\text{b}}_{ 2}^{ + } , $$
    • $$ {\text{D}}_{ 1} < {\text{D}}_{ 2} \Leftrightarrow {\text{D}}_{ 1} \le {\text{D}}_{ 2} \,\,{\text{and}}\,\,{\text{D}}_{ 1} \ne {\text{D}}_{ 2} $$
    • $$ {\text{mD}} = {\text{m[a}}_{ 1}^{ - } , {\text{ b}}_{ 1}^{ + } ]= [ {\text{ma}}_{ 1}^{ - } , {\text{ mb}}_{ 1}^{ + } ],\quad \,{\text{where}}\,0 \le {\text{m}} \le 1. $$

Let L be a given nonempty set. An interval-valued fuzzy set B on L is defined by B = {(x, [μ −B (x), μ +B (x)]:x ∊ L}, Where μ −B (x) and μ +B (x) are fuzzy sets of L such that μ −B (x) ≤ μ +B (x) for all x ∊ L. Let \( {\tilde{\upmu }}_{\text{B}} ({\text{x}}) = \left[ {\upmu_{\text{B}}^{ - } \left( {\text{x}} \right),\upmu_{\text{B}}^{ + } \left( {\text{x}} \right)} \right] \), then \( {\text{B}} = \{ (\text{x},{\tilde{\upmu }}_{\rm{B}} ({\text{x}})):{\text{x}} \in {\text{L}} \} \)where \( {\tilde{\upmu }}_{\text{B}} : {\text{L}} \to {\text{D[0, 1]}} \)

A mapping \( {\text{A}} = ({\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \): L → D[0, 1] × D[0, 1] is called an interval-valued intuitionistic fuzzy set (i–v IF set, in short) in L if 0 ≤ μ +A (x) + λ +A (x) ≤ 1 and 0 ≤ μ −A (x) + λ −A (x) ≤ 1 for all x ∊ L (that is, A+ = (X, μ +A , λ +A ) and A− = (X, μ −A , λ −A ) are intuitionistic fuzzy sets), where the mappings \( {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} = [\upmu_{\rm{A}}^{ - } ( {\text{x),}}\upmu_{\rm{A}}^{ + } ( {\text{x)]:L}} \to {\text{D[0, 1]}} \) and \( {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} = [\uplambda_{\rm{A}}^{ - } ( {\text{x),}}\uplambda_{\rm{A}}^{ + } ( {\text{x)]:L}} \to {\text{D[0, 1]}} \) denote the degree of membership (namely \( {\tilde{\upmu }}_{\rm{A}} ( {\text{x))}} \) and degree of non-membership (namely \( {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} \) of each element x ∊ L to A respectively.

Definition 1.6

An interval-valued intuitionistic fuzzy set \( {\text{A}} = ({\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \) is called an interval-valued intuitionistic fuzzy ideal (i–v intuitionistic fuzzy ideal) of BF-algebra X if satisfies the following inequalities

(I–v F1) \( {\tilde{\upmu }}_{\rm{A}} ( 0 )\ge {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} \) and \( {\tilde{\uplambda }}_{\rm{A}} ( 0 )\le {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} \)

(I–v F2) \( {\tilde{\upmu }}_{A} (x) \ge min\{ {\tilde{\upmu }}_{A} \left( {{\hbox{x}} * {\hbox{y}}} \right), {\tilde{\upmu }}_{A} (y)\} \)

(I–v F3) \({\tilde{\uplambda}}_{{\rm A}} ({{\rm x}}) \ge {{\rm max}}\{ {\tilde{\uplambda }}_{{\rm A}} \left( {{\rm x}} * {{\rm y}} \right) ,{\tilde{\uplambda }}_{{\rm A}} ( {\rm y}) \}\), for all x, y, z ∊ X.

Example 1.7

Consider a BF-algebra X = {0, a, b, c} with following table

figure a

Let Abe an interval-valued fuzzy set in X defined by \( {\tilde{\upmu }}_{\rm{A}} ( 0 )= {\tilde{\upmu }}_{\rm{A}} ( {\text{a)}} = \left[ { 0. 6 , { 0} . 7} \right] \)\( {\tilde{\upmu }}_{\rm{A}} ( {\text{b)}} = {\tilde{\upmu }}_{\rm{A}} ( {\text{c)}} = \left[ { 0. 2 , { 0} . 3} \right] \) and \( {\tilde{\uplambda }}_{\rm{A}} ( 0 )= {\tilde{\uplambda }}_{\rm{A}} ( {\text{a)}} = \left[ { 0. 2 , { 0} . 3} \right] \), \( {\tilde{\uplambda }}_{\rm{A}} ( {\text{b)}} = {\tilde{\uplambda }}_{\rm{A}} ( {\text{c)}} = \left[ { 0. 6 , { 0} . 7} \right] \) it is easy to verify that A is an i–v intuitionistic fuzzy ideal of X.

2 Quotient BF-algebras induced by interval-valued intuitionistic fuzzy ideals

Let \( {\text{A}} = ({\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \) be an i–v intuitionistic fuzzy ideals of X. For any x, y ∊ X, define relation \( \sim \) on X by \( x\sim y \) if and only if \( {\tilde{\upmu }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\upmu }}_{\rm{A}} ( 0 )\,\,{\text{and}}\,\,{\tilde{\upmu }}_{\rm{A}} ( {\text{y}} * {\text{x)}} = {\tilde{\upmu }}_{\rm{A}} ( 0 ) \)

$$ {\tilde{\uplambda }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\uplambda }}_{\rm{A}} ( 0 )\,\,{\text{and}}\,\,{\tilde{\uplambda }}_{\rm{A}} ( {\text{y}} * {\text{x)}} = {\tilde{\uplambda }}_{\rm{A}} ( 0 ) $$

Lemma 2.1

\( \sim \)is an equivalence relation of X.

Definition 2.2

A quotient BF-algebra is a BF-algebra that is the quotient of a BF-algebras X and one of its ideals I, denoted X/I. Let I be an ideal of X, then for all, y ∊ X and x * I, y * I ∊ X/I, we define (x * I) * (y * I) = (x * y) * I.

Theorem 2.3

Let I be an ideal of BF-algebra X. If\( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} , { }{\tilde{\uplambda }}_{\rm{A}} ) \)is an i–v intuitionistic fuzzy ideal of X, then the i–v intuitionistic fuzzy set\( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \)of X/I defined by\( {\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{a}} * {\text{I)}} = \mathop { \sup }\nolimits_{{{\text{x}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( {\text{a}} * {\text{x)}} \)and\( {\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{a}} * {\text{I)}} = \mathop { \inf }\nolimits_{{{\text{x}} \in {\text{I}}}} {\tilde{\uplambda }}_{\rm{A}} ( {\text{a}} * {\text{x)}} \)is an i–v intuitionistic fuzzy ideal of the quotient algebra X/I of X with respect to I.

Proof

Cleary, \( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \) is well-defined. It is easy to see that \( {\tilde{\upmu }}_{\rm{A}}^{ * } ( 0 )\ge {\tilde{\upmu }}_{\rm{A}} ( {\text{x}} * {\text{I)}} \) and \( {\tilde{\uplambda }}_{\rm{A}}^{ * } ( 0 )\le {\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{x}} * {\text{I)}} \) for all x * I ∊ X. Let x * I, y * I, z * I ∊ X/I, then

$$ \begin{aligned} {\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{x}} * {\text{I)}} &= \mathop { \sup }\limits_{{{\text{u}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( {\text{a}} * {\text{u)}} \\ & \mathop { = { \sup }}\limits_{{{\text{s}} * {\text{t}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( {\text{a}} * ({\text{s}} * {\text{t))}} \\ & \mathop { \ge { \sup }}\limits_{{{\text{s,t}} \in {\text{I}}}} { \hbox{min} }\left\{ {{\tilde{\upmu }}_{\rm{A}} ( ( {\text{x}} * {\text{y)}} * {\text{s),}}{\tilde{\upmu }}_{\rm{A}} ( {\text{y}} * {\text{t)}}} \right\} \\ & = { \hbox{min} }\left\{ {\mathop { \sup }\limits_{{{\text{s}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( ( {\text{x}} * {\text{y)}} * {\text{s), }}\mathop { \sup }\limits_{{{\text{t}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( {\text{y}} * {\text{t)}}} \right\} \\ & = { \hbox{max} }\left\{ {{\tilde{\upmu }}_{\rm{A}}^{ * } ( ( {\text{x}} * {\text{y)}} * {\text{I),}}{\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{y}} * {\text{I)}}} \right\} \\ & {\text{And}}\,\,{\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{x}} * {\text{I)}} = \mathop { \inf }\limits_{{{\text{u}} \in {\text{I}}}} {\tilde{\uplambda }}_{\rm{A}} ( {\text{a}} * {\text{u)}} \\ & \mathop { = { \inf }}\limits_{{{\text{s}} * {\text{t}} \in {\text{I}}}} {\tilde{\uplambda }}_{\rm{A}} ( {\text{a}} * ({\text{s}} * {\text{t))}} \\ & \mathop { \le \inf \, }\limits_{{{\text{s,t}} \in {\text{I}}}} { \hbox{max} }\left\{ {{\tilde{\uplambda }}_{\rm{A}} ( ( {\text{x}} * {\text{y)}} * {\text{s),}}{\tilde{\uplambda }}_{\rm{A}} ( {\text{y}} * {\text{t)}}} \right\} \\ & = { \hbox{max} }\left\{ {{\tilde{\uplambda }}_{\rm{A}}^{ * } ( ( {\text{x}} * {\text{y)}} * {\text{I),}}{\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{y}} * {\text{I)}}} \right\} \\ \end{aligned} $$

Hence \( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \) is a i–v intuitionistic fuzzy ideal of X/I.

Theorem 2.4

Let I be an ideal of a BF-algebras X. Then there is a one-to-one correspondence between the set of i–v intuitionistic fuzzy ideal\( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \)of X such that\( {\tilde{\upmu }}_{\rm{A}} \left( 0\right) = {\tilde{\upmu }}_{\rm{A}} \left( {\text{s}} \right) \)and\( {\tilde{\uplambda }}_{\rm{A}} \left( 0\right) = {\tilde{\uplambda }}_{\rm{A}} \left( {\text{s}} \right) \)for all s ∊ I and the set of all i–v intuitionistic fuzzy ideal\( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \)of\( {\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\text{I}}$}} \).

Proof

Let \( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \) be an i–v intuitionistic fuzzy ideal of X. Using Theorem 2.2, we prove that μ* defined by

$$ {\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{a}} * {\text{I)}} = \mathop { \sup }\limits_{{{\text{x}} \in {\text{I}}}} {\tilde{\upmu }}_{\rm{A}} ( {\text{a}} * {\text{x)}}\,\, {\text{and}}\,\,{\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{a}} * {\text{I)}} = \mathop { \inf }\limits_{{{\text{x}} \in {\text{I}}}} {\tilde{\uplambda }}_{\rm{A}} ( {\text{a}} * {\text{x)}} $$

is an i–v IF ideal of \( {\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\text{I}}$}} \). Since \( {\tilde{\upmu }}_{\rm{A}} \left( 0\right) = {\tilde{\upmu }}_{\rm{A}} \left( {\text{s}} \right) \) and \( {\tilde{\uplambda }}_{\rm{A}} \left( 0\right) = {\tilde{\uplambda }}_{\rm{A}} \left( {\text{s}} \right) \) for all s ∊ I, is straightforward verification, we have \( {\tilde{\upmu }}_{\rm{A}} \left( {{\text{a}} * {\text{s}}} \right) = {\tilde{\upmu }}_{\rm{A}} \left( {\text{a}} \right) \) for all s ∊ I, that is \( {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{a}} * {\text{I}}} \right) = {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {\text{a}} \right) \). And we have \( {\tilde{\uplambda }}_{\rm{A}} \left( {{\text{a}} * {\text{s}}} \right) = {\tilde{\uplambda }}_{\rm{A}} \left( {\text{a}} \right) \) for all s ∊ I, that is \( {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{a}} * {\text{I}}} \right) = {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {\text{a}} \right) \). Hence the correspondence \( {\tilde{\upmu }}_{\rm{A}} \to {\tilde{\upmu }}_{\rm{A}}^{ * } \), \( {\tilde{\uplambda }}_{\rm{A}} \to {\tilde{\uplambda }}_{\rm{A}}^{ * } \) are one-to-one. Let \( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \) be an i–v IF ideal of \( {\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\text{I}}$}} \) and define i–v IF set \( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \) in X by \( {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{a}} * {\text{I}}} \right) = {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {\text{a}} \right) \) and \( {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{a}} * {\text{I}}} \right) = {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {\text{a}} \right) \) for all a ∊ I. For x, y, z ∊ X, we have

$$ \begin{aligned} {\tilde{\upmu }}_{\rm{A}} \left( {\text{x}} \right) &= {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\text{I}}} \right) \\ & \ge { \hbox{min} }\left\{ {{\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\text{I}}} \right) ,{\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{y}} * {\text{I}}} \right)} \right\} \\ & = { \hbox{min} }\left\{ {{\tilde{\upmu }}_{\rm{A}} \left( {\text{x}} \right) ,{\tilde{\upmu }}_{\rm{A}} \left( {\text{y}} \right)} \right\} \\ & {\text{And}} \\ {\tilde{\uplambda }}_{\rm{A}} \left( {\text{x}} \right)& = {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\text{I}}} \right) \\ & \le { \hbox{max} }\left\{ {{\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\text{I}}} \right) ,{\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{y}} * {\text{I}}} \right)} \right\} \\ & = { \hbox{max} }\left\{ {{\tilde{\uplambda }}_{\rm{A}} \left( {\text{x}} \right) ,{\tilde{\uplambda }}_{\rm{A}} \left( {\text{y}} \right)} \right\} \\ \end{aligned} $$

Thus \( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} , { }{\tilde{\uplambda }}_{\rm{A}} ) \) is an i–v IF ideal of X. Note that \( {\tilde{\upmu }}_{\rm{A}} \left( {\text{z}} \right) = {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{z}} * {\text{I}}} \right) = {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {\text{I}} \right) \) and \( {\tilde{\uplambda }}_{\rm{A}} \left( {\text{z}} \right) = {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{z}} * {\text{I}}} \right) = {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {\text{I}} \right) \) for all z ∊ I, which shows that \( {\tilde{\upmu }}_{\rm{A}} \left( {\text{z}} \right) = {\tilde{\upmu }}_{\rm{A}} \left( 0\right) \) and \( {\tilde{\uplambda }}_{\rm{A}} \left( {\text{z}} \right) = {\tilde{\uplambda }}_{\rm{A}} \left( 0\right) \) for all z ∊ I. This ends the proof.

Theorem 2.5

Let\( {\text{A}} = ( {\text{X,}} \, {\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \)be an i–v intuitionistic fuzzy ideal of a BF-algebras X and let\( {\tilde{\upmu }}_{\rm{A}} ( 0 )= {\tilde{t}} \)and\( {\tilde{\uplambda }}_{\rm{A}} ( 0 )= {\tilde{s}} \). Then the i–v intuitionistic fuzzy sub set of\( {\text{A}}^{ * } = ( {\text{X,}} \, {\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \)of\( \left( {{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ; \, {\tilde{t}} )}$}} , { }{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ; \, {\tilde{s}} )}$}}} \right) \)defined by\( {\tilde{\upmu }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )} \right) = {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} \)and\( {\tilde{\uplambda }}_{\rm{A}}^{ * } \left( {{\text{x}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )} \right) = {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} \)for all x ∊ X is an i–v intuitionistic fuzzy Ideal of\( \left( {{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )}$}} , { }{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )}$}}} \right) \).

Proof

\( {\text{A}}^{ * } = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}}^{ * } , { }{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \) is well-defined because

$$ \begin{aligned} & {\text{x}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )= {\text{y}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )\quad \quad \forall {\text{x,y}} \in {\text{X}} \\ & \Rightarrow {\text{x}} * {\text{y}} \in {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )\\ & \Rightarrow {\tilde{\upmu }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\upmu }}_{\rm{A}} ( 0 )\\ & \Rightarrow {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} = {\tilde{\upmu }}_{\rm{A}} ( {\text{y)}} \\ & \Rightarrow {\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{x}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ( {\text{x);}}{\tilde{t}} ) )= {\tilde{\upmu }}_{\rm{A}}^{ * } ( {\text{y}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ( {\text{x);}}{\tilde{t}} ) )\\ & {\text{And}}\,\,{\text{x}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )= {\text{y}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )\quad \quad \forall {\text{x,y}} \in {\text{X}} \\ & \Rightarrow {\text{x}} * {\text{y}} \in {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )\\ & \Rightarrow {\tilde{\uplambda }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\uplambda }}_{\rm{A}} ( 0 )\\ & \Rightarrow {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} = {\tilde{\uplambda }}_{\rm{A}} ( {\text{y)}} \\ & \Rightarrow {\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{x}} * {{\bar{\rm L}(}}{\tilde{\uplambda }}_{\rm{A}} ( {\text{x);}}{\tilde{s}} ) )= {\tilde{\uplambda }}_{\rm{A}}^{ * } ( {\text{y}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ( {\text{x);}}{\tilde{s}} ) )\\ \end{aligned} $$

Nest we show that \( {\text{A}}^{ * } = ( {\text{X,}}{\tilde{\upmu }}_{\rm{A}}^{ * } ,{\tilde{\uplambda }}_{\rm{A}}^{ * } ) \)is an i–v intuitionistic fuzzy ideal of X. Clearly, \( {\tilde{\upmu }}_{\rm{A}}^{ * } (0) \ge {\tilde{\upmu }}_{\rm{A}}^{ * } ({\text{x}} * {\bar{U}}({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}}) \), \( {\tilde{{\uplambda }}}_{\rm{A}}^{ * } ( 0 )\le {\tilde{{\uplambda }}}_{\rm{A}}^{ * } ( {\text{x}} * {{\bar{\rm L}(\tilde{\uplambda }}}_{\rm{A}} ; {{\tilde{\rm s})}} \) for all x ∊ X. For x, y, z ∊ X,

$$ \begin{aligned} {\text{U}}^{ * } ( ( {\text{x)}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} ) ) &= {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} \ge { \hbox{min} }\left\{ {{\tilde{\upmu }}_{\rm{A}} ( {\text{x}} * {\text{y),}}{\tilde{\upmu }}_{\rm{A}} ( {\text{y)}}} \right\} \\ & = { \hbox{min} }\left\{ {{\text{U}}^{ * } ( {\text{x}} * {\text{y)}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} ) , {\text{U}}^{ * } ( {\text{y)}} * {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )} \right\} \\ & {\text{And}}\,\,{\text{L}}^{ * } ( ( {\text{x)}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} ) )= {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} \le { \hbox{max} }\left\{ {{\tilde{\uplambda }}_{\rm{A}} ( {\text{x}} * {\text{y),}}{\tilde{\uplambda }}_{\rm{A}} ( {\text{y)}}} \right\} \\ & = { \hbox{max} }\left\{ {{\text{L}}^{ * } ( {\text{x}} * {\text{y)}} * {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} ) , {\text{L}}^{ * } ( {\text{y)}} * {{\bar{\rm L}(}}{\tilde{\uplambda }}_{\rm{A}} ;{\tilde{s}} )} \right\} \\ \end{aligned} $$

This completes the proof.

Theorem 2.6

Let\( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} , { }{\tilde{\uplambda }}_{\rm{A}} ) \)be an i–v intuitionistic fuzzy ideal of a BF-algebras X and let\( \left( {{\tilde{f}},{\tilde{f}}^{\prime } } \right) \)be an i–v intuitionistic fuzzy ideal of\( {\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\text{I}}$}} \)such that\( {\tilde{f}} ( {\text{x}} * {\text{I)}} = {\tilde{f}} ( {\text{x)}} \), \( {\tilde{f}}^{\prime } ( {\text{x}} * {\text{I)}} = {\tilde{f}}^{\prime } ( {\text{x)}} \), then x ∊ I there exists an i–v intuitionistic fuzzy ideal\( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \)of X such that

  1. (i)

    \( {\bar{U}} ({\tilde{\upmu }}_{\rm{A}} ;\,{\tilde{t}} )= {\text{I}} \) , where \( {\tilde{\upmu }}_{\rm{A}} ( 0 )= {\tilde{t}} \) and \( {\tilde{f}} = {\tilde{\upmu }}_{\rm{A}}^{ * } \)

  2. (ii)

    \( {\bar{L}} ({\tilde{\uplambda }}_{\rm{A}} ;\,{\tilde{s}} )= {\text{I}} \) , where \( {\tilde{\uplambda }}_{\rm{A}} ( 0 )= {\tilde{s}} \) and \( {\tilde{f}}^{\prime } = {\tilde{{\uplambda }}}_{\rm{A}}^{ * } \)

Proof

Define an i–v intuitionistic fuzzy ideal \( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} , { }{\tilde{\uplambda }}_{\rm{A}} ) \) of X by \( {\tilde{{\upmu }}}_{\rm{A}} ( {\text{x)}} = {{\tilde{\rm f}(x}} * {\text{I)}} \) and \( {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} = {\tilde{f}}^{\prime } ( {\text{x}} * {\text{I)}} \) for all x ∊ X. It is easy to see that \( {\text{A}} = ( {\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \) is i–v intuitionistic fuzzy ideal of X such that \( {\text{U(}}{\tilde{\upmu }}_{\rm{A}} ;{\tilde{t}} )= {\text{I}} \) because

$$ \begin{aligned} & \Leftrightarrow {\tilde{\upmu }}_{\rm{A}} ( {\text{x)}} = {\tilde{t}} = {\tilde{\upmu }}_{\rm{A}} ( 0 )\,\,{\text{and}}\,\, \Leftrightarrow {\tilde{\uplambda }}_{\rm{A}} ( {\text{x)}} = {\tilde{s}} = {\tilde{\uplambda }}_{\rm{A}} ( 0 )\\ & \Leftrightarrow {\tilde{f}} ( {\text{x}} * {\text{I)}} = {\tilde{f}} ( {\text{I)}} \Leftrightarrow {\tilde{f}}^{\prime } ( {\text{x}} * {\text{I)}} = {\tilde{f}}^{\prime } ( {\text{I)}} \\ & \Leftrightarrow {\text{x}} \in {\text{I}} \Leftrightarrow {\text{x}} \in {\text{I}} \\ \end{aligned} $$

We conclude that \( {\tilde{{\upmu }}}_{\rm{A}}^{ * } = {\tilde{{\rm f}}} \) and \( {\tilde{{\uplambda }}}_{\rm{A}}^{ * } = {\tilde{{\rm f}}}^{\prime } \) because

$$ \begin{aligned} & {\tilde{{\upmu }}}_{\rm{A}}^{ * } ( {\text{x}} * {\text{I)}} = {\tilde{{\upmu }}}_{\rm{A}}^{ * } ( {\text{x}} * {{\bar{\rm U}(\tilde{\upmu }}}_{\rm{A}} ; {{\tilde{\rm t}))}} = {\tilde{{\upmu }}}_{\rm{A}} ( {\text{x)}} = {{\tilde{\rm f}(x}} * {\text{I)}} \\ & {\text{And}} \\ & {\tilde{{\uplambda }}}_{\rm{A}}^{ * } ( {\text{x}} * {\text{I)}} = {\tilde{{\uplambda }}}_{\rm{A}}^{ * } \left( {{\text{x}} * {{\bar{\rm U}(\tilde{\uplambda }}}_{\rm{A}} ; {{\tilde{\rm s})}}} \right) = {\tilde{{\uplambda }}}_{\rm{A}} ( {\text{x)}} = {\tilde{{\rm f}}}^{\prime } ( {\text{x}} * {\text{I)}} \\ \end{aligned} $$

This ends the proof.

Theorem 2.7

(i–v intuitionistic fuzzy correspondence theorem) Let f: X1 → X2be a homomorphism of BF-algebras X1onto X2. Then the following hold:If\( {\text{A}} = ( {\text{X,}}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} ) \)is an i–v intuitionistic fuzzy ideal of X1, then\( {\text{f(A)}} = ( {\text{f(}}{\tilde{\upmu }}_{\rm{A}} ) , {\text{ f(}}{\tilde{\uplambda }}_{\rm{A}} ) ) \)is an i–v intuitionistic fuzzy ideal of X2, If\( {\text{B}} = ( {\text{X, }}{\tilde{\upmu }}_{\text{B}} ,{\tilde{\uplambda }}_{\text{B}} ) \)is an i–v intuitionistic fuzzy ideal of X2, then\( {\text{f}}^{ 1} ( {\text{B)}} = ( {\text{f}}^{ - 1} ({\tilde{\upmu }}_{\text{B}} ) , {\text{ f}}^{ - 1} ({\tilde{\uplambda }}_{\text{B}} ) ) \)is an i–v intuitionistic fuzzy ideal of X1.

Proof

Straightforward.

Let \( {\text{A}} = \left( {{\text{X, }}{\tilde{\upmu }}_{\rm{A}} ,{\tilde{\uplambda }}_{\rm{A}} } \right) \) be an i–v intuitionistic fuzzy ideal of a BF-algebra X. For any x, y ∈ X, define a binary relation ~ on X by x ~ y if and only if \( {\tilde{\upmu }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\upmu }}_{\rm{A}} ( 0 ) \) and \( {\tilde{\uplambda }}_{\rm{A}} ( {\text{x}} * {\text{y)}} = {\tilde{\uplambda }}_{\rm{A}} ( 0 ) \). Then ~ is a congruence relation of X. We denote \( ({\tilde{\upmu }}_{\rm{A}} [ {\text{x],}}{\tilde{\uplambda }}_{\rm{A}} [ {\text{x])}} \) the equivalence class containing x, and \( \left( {{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{\upmu }}_{{\text{A}}} }$}},{\raise0.5ex\hbox{$\scriptstyle {\text{X}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{\uplambda }}_{{\text{A}}} }$}}} \right)= \{ {\tilde{\upmu }}_{{\text{A}}} [{\text{x}}],{\tilde{\uplambda }}_{{\text{A}}} [{\text{x}}]/{\text{x}} \in {\rm X }\}\) the set of all equivalence classes of X. Then \( \left( {{\raise0.5ex\hbox{$\scriptstyle \varsigma $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}} ,{\raise0.5ex\hbox{$\scriptstyle \varsigma $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}}} \right) \) is a BF-algebra under the following operation: \( {\tilde{{\upmu }}}_{\rm{A}} [ {\text{x]}} * {\tilde{{\upmu }}}_{\rm{A}} [ {\text{y]}} = {\tilde{{\upmu }}}_{\rm{A}} [ {\text{x}} * {\text{y]}}\,\tilde{\uplambda }_{\rm{A}} [ {\text{x]}} * \tilde{\uplambda }_{\rm{A}} [ {\text{y]}} = \tilde{\uplambda }_{\rm{A}} [ {\text{x}} * {\text{y]}}\quad \forall {\text{x}}, {\text{y}} \in {\text{X}} \).

Theorem 2.8

(First i–v intuitionistic fuzzy isomorphism theorem) Let f: X1 → X2be an epimorphism of BF-algebras and let\( {\text{A}} = ( {{\hbox{X}}, {\tilde{\upmu }}}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ) \)be an i–v intuitionistic fuzzy ideal of X2. Then\( \left( {{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} )}$}} ,{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} )}$}}} \right) \cong \left( {{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}} ,{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}}} \right) \)or\( {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}} \)and\( {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}} \)

Proof

Define mapping \( {{\uptheta }}_{ 1} :{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} )}$}} \to {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}} \) by \( {{\uptheta }}_{ 1} ( {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) [ {\text{x])}} = {\tilde{{\upmu }}}_{\rm{A}} [ {\text{f(x)]}} \). θ1 is well defined since \( {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) [ {\text{x]}} = {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) [ {\text{y]}} \)

$$ \begin{aligned} & \Rightarrow {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) ( {\text{x}} * {\text{y)}} = {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) ( 0 )\\ & \Rightarrow {\tilde{{\upmu }}}_{\rm{A}} ( {\text{f(x)}} * {\text{f(y))}} = {\tilde{{\upmu }}}_{\rm{A}} ( {\text{f(0))}} \\ & \Rightarrow {\tilde{{\upmu }}}_{\rm{A}} ( {\text{f(x)}} * {\text{f(y))}} = {\tilde{{\upmu }}}_{\rm{A}} ( 0 )\\ & {\text{i}}.{\text{e}}.,\,{\tilde{{\upmu }}}_{\rm{A}} [ {\text{f(x)]}} = {\tilde{{\upmu }}}_{\rm{A}} [ {\text{f(y)]}} \\ \end{aligned} $$

θ1 is one to one because

$$ \begin{aligned} & {\tilde{{\upmu }}}_{\rm{A}} [ {\text{f(x)]}} = {\tilde{{\upmu }}}_{\rm{A}} [ {\text{f(y)]}} \\ & \Rightarrow {\tilde{{\uplambda }}}_{\rm{A}} ( {\text{f(x)}} * {\text{f(y))}} = {\tilde{{\uplambda }}}_{\rm{A}} ( 0 )\\ & \Rightarrow {\tilde{{\upmu }}}_{\rm{A}} ( {\text{f(x)}} * {\text{f(y))}} = {\tilde{{\upmu }}}_{\rm{A}} ( {\text{f(0))}} \\ & \Rightarrow {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) ( {\text{x}} * {\text{y)}} = {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) ( 0 )\\ & \Rightarrow {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) [ {\text{x]}} = {\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} ) [ {\text{y]}} \\ \end{aligned} $$

Since f is an onto θ1 is an onto. Finally, θ1 a homomorphism because

$$ \begin{aligned} \uptheta_{ 1} \left( {{\text{f}}^{ - 1} \left( {{\tilde{\upmu }}_{\rm{A}} } \right) [ {\text{x}}]} \right) *\left( {{\text{f}}^{ - 1} \left( {{\tilde{\upmu }}_{\rm{A}} } \right) [ {\text{y}}]} \right) &=\uptheta_{ 1} \left( {\text{f}}^{ - 1} \left( {{\tilde{\upmu }}_{\rm{A}} } \right) [{ \text{x}} * { \text{y}}] \right) \\ & = { \tilde{\upmu }}_{\rm{A}} [ {\text{f}}({\hbox{x}}* {\text{y}} )]\\ & = { \tilde{\upmu }}_{\rm{A}} [{{ \text{f}}({ \text{x}})} * { \text{f}}({\text{y}})] \\ & = { \tilde{\upmu }}_{\rm{A}} [ { \text{f(x) }}] * {\tilde{\upmu }}_{\rm{A}} [ {\text{f(y)}}] \\ & =\uptheta_{ 1} ( {\text{f}}^{ - 1} ({\tilde{\upmu }}_{\rm{A}} ) [ { \text{x}}]) *\uptheta_{ 1} ( { \text{f}}^{ - 1} ({\tilde{\upmu }}_{ \rm{A}} ) [ {\text{y}}]) \end{aligned} $$

Hence \( {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}}. \,\) Define mapping \( \, {{\uptheta }}_{ 2} :{\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} )}$}} \to {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}} \) by \( {{\uptheta }}_{ 2} ( {\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} ) [ {\text{x])}} = {\tilde{{\uplambda }}}_{\rm{A}} [ {\text{f(x)]}} . \) Similarly, we can prove that

$$ {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}}. $$

Hence \( \, {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\upmu }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\upmu }}}_{\rm{A}} }$}} \) and \( {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 1} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\text{f}}^{ - 1} ( {\tilde{{\uplambda }}}_{\rm{A}} )}$}} \cong {\raise0.5ex\hbox{$\scriptstyle {{\text{X}}_{ 2} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {{\tilde{{\uplambda }}}_{\rm{A}} }$}}. \,\) We state the following i–v intuitionistic fuzzy isomorphism Theorems without proofs.

Theorem 2.9

(Second i–v intuitionistic fuzzy isomorphism theorem) Let\( {\text{A}} = ( {\text{X}}, {\tilde{\upmu }}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ) \)be an i–v intuitionistic fuzzy subalgebra of BF-algebra and let\( {\text{B}} = ( {\text{X}}, {\tilde{\upmu }}_{\text{B}} , {\tilde{{\uplambda }}}_{\text{B}} ) \)be an i–v intuitionistic fuzzy ideal of BF-algebra. Then

  1. (i)

    \( {\text{B}} = ( {\text{X}}, \tilde{\upmu }_{\text{B}} , {\tilde{{\uplambda }}}_{\text{B}} ) \) is an i–v intuitionistic fuzzy ideal of, \( {\text{A}} * {\text{B}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\rm{A}} * {\tilde{{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\rm{A}} * {\tilde{{\uplambda }}}_{\text{B}} ) \)

  2. (ii)

    \( {\text{A}} \cap {\text{B}} = ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} ) \) is an i-v intuitionistic fuzzy ideal of \( {\text{A}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ), \)

  3. (iii)

    \( \left( {\frac{{{\tilde{{\upmu }}}_{\rm{A}} * {\tilde{{\upmu }}}_{\text{B}} }}{{{\tilde{{\upmu }}}_{\text{B}} }} , { }\frac{{{\tilde{{\uplambda }}}_{\rm{A}} * {\tilde{{\uplambda }}}_{\text{B}} }}{{{\tilde{{\uplambda }}}_{\text{B}} }}} \right) \cong \left( {\frac{{{\tilde{{\upmu }}}_{\rm{A}} }}{{{\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} }} , { }\frac{{{\tilde{{\uplambda }}}_{\rm{A}} }}{{{\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} }}} \right) \).

Theorem 2.10

(Third i–v intuitionistic fuzzy isomorphism theorem) Let X1be a BF-algebra having i–v intuitionistic fuzzy ideals\( {\text{A}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ) \)and\( {\text{B}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\text{B}} ) \)with\( {\text{A}} \le {\text{B}} = ( {\tilde{{\upmu }}}_{\rm{A}} \le {\tilde{{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\rm{A}} \le {\tilde{{\uplambda }}}_{\text{B}} ) \). Then

  1. (i)

    \( \left( {\frac{{{\tilde{{\upmu }}}_{\text{B}} \, }}{{{\tilde{{\upmu }}}_{\rm{A}} \, }} , { }\frac{{{\tilde{{\uplambda }}}_{\text{B}} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}} \right) \)is i–v intuitionistic fuzzy ideal of\( \left( {\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\upmu }}}_{\rm{A}} }} , { }\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}} \right) \),

  2. (ii)

    \( \left( {{\raise0.7ex\hbox{${\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\upmu }}}_{\rm{A}} }}}$} \!\mathord{\left/ {\vphantom {{\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\upmu }}}_{\rm{A}} }}} {\frac{{{\tilde{{\upmu }}}_{\text{B}} \, }}{{{\tilde{{\upmu }}}_{\rm{A}} \, }}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\frac{{{\tilde{{\upmu }}}_{\text{B}} \, }}{{{\tilde{{\upmu }}}_{\rm{A}} \, }}}$}} , { }{\raise0.7ex\hbox{${\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}}$} \!\mathord{\left/ {\vphantom {{\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}} {\frac{{{\tilde{{\uplambda }}}_{\text{B}} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\frac{{{\tilde{{\uplambda }}}_{\text{B}} }}{{{\tilde{{\uplambda }}}_{\rm{A}} }}}$}}} \right) \cong \left( {\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\upmu }}}_{\text{B}} }} , { }\frac{{{\text{X}}_{ 1} }}{{{\tilde{{\uplambda }}}_{\text{B}} }}} \right) \)

Lemma 2.11

(i–v intuitionistic fuzzy Zassenhaus lemma) Let\( {\text{A}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ) \)and\( {\text{B}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\text{B}} ) \)be i–v intuitionistic fuzzy subalgebras of a BF-algebra (X, *, 0) and let\( {\text{A}}_{ 1} = ( {\text{X}}, {{\tilde{\upmu }}}_{{{\text{A}}_{ 1} }} , {\tilde{{\uplambda }}}_{{{\text{A}}_{ 1} }} ) \)and\( {\text{B}}_{ 2} = ( {\text{X}}, {{\tilde{\upmu }}}_{{{\text{B}}_{ 2} }} , {\tilde{{\uplambda }}}_{{{\text{B}}_{ 2} }} ) \)be i–v intuitionistic fuzzy ideals of\( {\text{A}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\rm{A}} , {\tilde{{\uplambda }}}_{\rm{A}} ) \)and\( {\text{B}} = ( {\text{X}}, {{\tilde{\upmu }}}_{\text{B}} , {\tilde{{\uplambda }}}_{\text{B}} ) \)respectively. Then

  1. (a).

    \( ( {\tilde{{\upmu }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} ) , {\tilde{{\uplambda }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} ) ) \)is an i–v intuitionistic fuzzy ideal of\( ( {\tilde{{\upmu }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} ) , {\tilde{{\uplambda }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} ) ) \),

  2. (b).

    \( ( {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} \cap {\tilde{{\upmu }}}_{\rm{A}} ) , {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} \cap {\tilde{{\uplambda }}}_{\text{B}} ) ) \) is an i–v intuitionistic fuzzy ideal of \( ( {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} ) , {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} ) ) \)

  3. (c).

    \( \left( {\frac{{{\tilde{{\upmu }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} )}}{{{\tilde{{\upmu }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} )}} , { }\frac{{{\tilde{{\uplambda }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} )}}{{{\tilde{{\uplambda }}}_{{{\text{A}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} )}}} \right) \cong \left( {\frac{{{\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\upmu }}}_{\rm{A}} \cap {\tilde{{\upmu }}}_{\text{B}} )}}{{{\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\upmu }}}_{{{\text{B}}_{ 1} }} \cap {\tilde{{\upmu }}}_{\rm{A}} )}} , { }\frac{{{\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{\rm{A}} \cap {\tilde{{\uplambda }}}_{\text{B}} )}}{{{\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} * ( {\tilde{{\uplambda }}}_{{{\text{B}}_{ 1} }} \cap {\tilde{{\uplambda }}}_{\text{B}} )}}} \right) \).

3 Conclusion

To investigate the structure of an algebraic system, we see that the interval-valued fuzzy ideals with special properties always play a central role. The purpose of this paper is to initiated the concept of On Quotient BF-algebras via interval-valued intuitionistic fuzzy ideals. It is our hope that this work would other foundations for further study of the theory of BF-algebras. In our future study of fuzzy structure of BCH/BF/BF1-algebra, may be the following topics should be considered: (i) to find Quotient BF/BF1-algebras via interval-valued intuitionistic fuzzy positive implicative ideals, (ii) Quotient BF/BF1-algebras via interval-valued intuitionistic fuzzy commutative ideals, H-ideals, a-ideals and p-ideals.