On interval valued intuitionistic fuzzy $\beta$-subalgebras

Abstract

This paper deals the notion of interval valued instuitionistic fuzzy subalgebras of $\beta$-algebra and investigate some of the related results.

1 Introduction

Zadeh [15, 16] invented fuzzy set in 1965 and also made an extension of a fuzzy set in 1975 by an interval valued fuzzy set (ie. a fuzzy set with an interval valued membership function). Attanasov [2, 3] introduced the concept of intuitionistic fuzzy set in 1986, in which not only the membership value is considered but also it includes non-membership values and the interval valued intuitionstic fuzzy sets in 1989 as a generalization of an ordinary fuzzy sets.

In 1996, Imai et al. [6, 7] proposed two classes of algebras originated from the classical and non-classical propositional logic. These algebras are known as BCK-algebras and BCI-algebras. It is known that the notion of BCI-algebra is a generalization of BCK-algebras, in the sense that the class of BCK-algebras is a proper subclass of the class of BCI-algebras. In 2002 Neggers et al. [9] established the notion of B-algebras which is another generalization of BCK-algebras and also they implemented the notion of $\beta$-algebra [8]. In 2012 Jun et al. [13] discussed some related topics on $\beta$-subalgebras.

In [4], Biswas defined Interval valued fuzzy subgroups (ie.i-v fuzzy subgroups) and investigated some elementary properties. The fuzzy BCI-subalgebras with interval valued membership functions were initiated by Houng et al. [10]. Later in 2000 Jun [14] dealt the notion of interval valued fuzzy subalgebras/ideals in BCK-algebras. Then in 2012, Tapan Senapati et al. [12] introduced the notion of interval valued fuzzy intuitionstic fuzzy BG-subalgebras.

Recently in 2013, Ansari et al. [1] discussed fuzzy $\beta$-subalgebras of $\beta$-algebras and Sujatha et al. [11] studied the notion of intuitionistic fuzzy $\beta$-subalgebras. Applying these ideas Hemavathi et al. [5] proposed interval valued fuzzy $\beta$-subalgebras of a $\beta$-algebra. With all these Motivation this paper intend to extend the notion of interval valued intuitionstic fuzzy $\beta$-subalgebra of a $\beta$-algebra.

2 Preliminaries

This section recalls some basic definitions and results that are needed in the sequel.

Definition 2.1

A fuzzy set in X is defined as a function $\mu :X\rightarrow [0,1]$. For each element x in X, $\mu (x)$ is called the membership value of $x\in X$ and X is a universal set.

Definition 2.2

An interval valued fuzzy set (briefly i-v fuzzy set) A defined on X is given by

$$\begin{aligned} A=\left\{ \left( x,\left[ \mu ^{L}_{A}(x) ,\mu ^{U}_{A}(x)\right] \right) \right\} \,\,\forall \,x \in X \hbox { (briefly denoted by } A=[\mu ^{L}_{A} ,\mu ^{U}_{A}]), \end{aligned}$$

where $\mu ^{L}_{A}$ and $\mu ^{U}_{A}$ are two fuzzy sets in X such that $\mu ^{L}_{A}(x) \le \mu ^{U}_{A}(x)\,\,\forall \,x\in X$.

Let $\overline{\mu }_{A}(x)=[\mu ^{L}_{A}(x) ,\mu ^{U}_{A}(x)]\,\,\forall \,x\in X$ and let D[0, 1] denotes the family of all closed sub intervals of [0, 1]. If $\mu ^{L}_{A}(x)=\mu ^{U}_{A}(x)=c$, say, where $0\le c\le 1$, then $\overline{\mu }_{A}(x)=[c,c]$ which also assume, for the sake of convenience, to belong to D[0, 1]. Thus $\overline{\mu }_{A}(x)\in D[0,1]~~\forall ~x \in X$, and therefore the i-v fuzzy set A is given by

$$\begin{aligned} A=\lbrace (x,\overline{\mu }_{A}(x))\rbrace \quad \forall ~x\in X,\quad \hbox { where }\overline{\mu }_{A}:X\rightarrow D[0,1]. \end{aligned}$$

Now the term refined mimimum(briefly rmin) of two elements in D[0, 1] and the symbols “$\ge$” , “$\le$” and “$=$” in case of two elements in D[0, 1] are defined as follows:

Consider two elements $D_{1}:=[a_{1},b_{1}]$ and $D_{2}:=[a_{2},b_{2}]\in D[0,1]$.

Then

$$\begin{aligned} rmin(D_{1},D_{2})= & {} [min\lbrace a_{1},a_{2}\rbrace ,min\lbrace {b}_{1},b_{2}\rbrace ];\\ D_{1}\ge & {} D_{2}\hbox { if and only if }a_{1}\ge a_{2},~b_{1}\ge b_{2}; \end{aligned}$$

Similarly $D_{1}\le D_{2}$ and $D_{1}=D_{2}$.

Definition 2.3

[8] A $\beta$-algebra is a non-empty set X with a constant 0 and two binary operations $+$ and − satisfying the following axioms:

• (i) $x-0 = x$

• (ii) $(0-x)+x=0$

• (iii) $(x-y)-z=x-(z+y)~~\forall ~ x,y,z \in X$

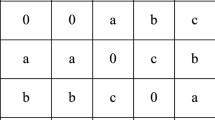
Example 2.4

Let $X=\lbrace 0,a,b,c \rbrace$ be a set with constant 0 and binary operations $+$ and − are defined on X by the following cayley’s table

$$\begin{aligned} \begin{array}{|c|c|c|c|c|} \hline + &{} 0 &{} a &{} b &{} c \\ \hline 0 &{} 0 &{} a &{} b &{} c \\ \hline a &{} a &{} b &{} c &{} 0 \\ \hline b &{} b &{} c &{} 0 &{} a \\ \hline c &{} c &{} 0 &{} a &{} b \\ \hline \end{array} \begin{array}{|c|c|c|c|c|} \hline - &{} 0 &{} a &{} b &{} c \\ \hline 0 &{} 0 &{} c &{} b &{} a \\ \hline a &{} a &{} 0 &{} c&{} b \\ \hline b &{} b &{} a &{} 0 &{} c \\ \hline c &{} c &{} b &{} a &{} 0 \\ \hline \end{array} \end{aligned}$$

Then $(X,+,-,0)$ is a $\beta$-algebra.

Definition 2.5

[13] A non empty subset A of a $\beta$-algebra $(X,+,-,0)$ is called a $\beta$-sub algebra of X, if   $(i)~x+y \in A$ and $(ii)~x-y \in A ~~~~\forall ~~ x,y \in A$

Example 2.6

In the above example of the $\beta$-algebra , the subset $A=\lbrace 0,b\rbrace$ is a $\beta$-sub algebra of X.

Definition 2.7

[1] Let $\mu$ be a fuzzy set in a $\beta$-algebra X. Then $\mu$ is called a fuzzy $\beta$-sub algebra of X if   $\forall ~ x,y \in X$

• (i) $\mu (x+y)\ge min \lbrace \mu (x),\mu (y)\rbrace$ and

• (ii) $\mu (x-y)\ge min \lbrace \mu (x),\mu (y)\rbrace$

Definition 2.8

[2] An Intuitionistic fuzzy set (IFS) in a nonempty set X is defined by

$$\begin{aligned} A= \lbrace \langle x,\mu _{A}(x),\nu _{A}(x) \rangle / x\in X \rbrace \end{aligned}$$

where $\mu _{A}:X\rightarrow [0,1]$ is a membership function of A and $\nu _{A}:X\rightarrow [0,1]$ is a non membership function of A satisfying $0\le \mu _{A}(x)+\nu _{A}(x)\le 1 ~~ \forall ~x\in X$.

Definition 2.9

[11] Let $(X,+,-,0)$ be a $\beta$-algebra. Then the intuitionistic fuzzy set $A=\lbrace \langle x,\mu _{A}(x),\nu _{A}(x) \rangle / x\in X \rbrace$ is called an intuitionistic fuzzy (IF) $\beta$-subalgebra of X, if   $\forall ~ x \in X$

• (i) $\mu _{A}(x+y)\ge min\lbrace \mu _{A}(x),\mu _{A}(y)\rbrace$  and  $\nu _{A}(x+y)\le max\lbrace \nu _{A}(x),\nu _{A}(y)\rbrace$

• (ii) $\mu _{A}(x-y)\ge min\lbrace \mu _{A}(x),\mu _{A}(y)\rbrace$  and  $\nu _{A}(x-y)\le max\lbrace \nu _{A}(x),\nu _{A}(y)\rbrace$

Definition 2.10

[5] Let $\overline{\mu }_{A}$ be an i-v fuzzy subset in X. Then $\overline{\mu }_{A}$ is said to be interval valued fuzzy(i-v fuzzy) $\beta$-sub algebra of X if   $~~\forall ~ x,y \in X$

• (i) $\overline{\mu }_{A}(x+y)\ge rmin \lbrace \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\rbrace$ and

• (ii) $\overline{\mu }_{A}(x-y)\ge rmin \lbrace \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\rbrace$

Definition 2.11

[3] An Interval valued intuitionisic fuzzy set (i-v IFS) A over X is an object having the form $A=\lbrace \langle x, \overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle / x \in X\rbrace$ where $\overline{\mu }_{A}:X\rightarrow D[0,1]$ and $\overline{\nu }_{A}:X\rightarrow D[0,1]$, where D[0, 1] is the set of all sub intervals of [0, 1].

The intervals $\overline{\mu }_{A}(x)$ and $\overline{\nu }_{A}(x)$ denote the intervals of the degree of membership and degree of non-membership of the element x to the set A, where $\overline{\mu }_{A}(x)=[\mu _{A}^{L}(x),\mu _{A}^{U}(x)]$ and $\overline{\nu }_{A}(x)=[\nu _{A}^{L}(x),\nu _{A}^{U}(x)]~~ \forall ~x \in ~X$, with the condition $0\le \mu _{A}^{L}(x)+\nu _{A}^{L}(x)\le 1$ and $0\le \mu _{A}^{U}(x)+\nu _{A}^{U}(x)\le 1$.

Also note that $\overline{\overline{\mu }}_{A}(x)=[1-\mu _{A}^{U}(x),1-\mu _{A}^{L}(x)]$ and $\overline{\overline{\nu }}_{A}(x)=[1-\nu _{A}^{U}(x),1-\nu _{A}^{L}(x)]$, where $[\overline{\overline{\mu }}_{A}(x),\overline{\overline{\nu }}_{A}(x)]$ represents the complement of x in A.

Definition 2.12

Consider two elements $D_{1}$,$D_{1} \in D[0,1]$. If $D_{1}=[a_{1},b_{1}]$ and $D_{2}=[a_{2},b_{2}]$, then $rmax(D_{1},D_{2})=[max(a_{1},a_{2}),max(b_{1},b_{2})]$ which is denoted by $D_{1}\bigvee ^{r} D_{2}$ and $rmin(D_{1},D_{2})=[min(a_{1},a_{2}),min(b_{1},b_{2})]$ which is denoted by $D_{1}\bigwedge ^{r} D_{2}$.

Thus if $D_{i}=[a_{i},b_{i}]\in D[0,1]$ for i $=$ 1,2,3.... Let us define

$$\begin{aligned} rsup_{i}(D_{i})= & {} [sup_{i}(a_{i}),sup_{i}(b_{i})],\\ i.e. \quad \bigvee _{i}^{r}D_{i}= & {} \left[ \bigvee _{i}a_{i},\bigvee _{i}b_{i}\right] \end{aligned}$$

similarly

$$\begin{aligned} rinf_{i}(D_{i})= & {} [inf_{i}(a_{i}),inf_{i}(b_{i})]\\ \hbox {i.e} \quad \bigwedge _{i}^{r}D_{i}= & {} \left[ \bigwedge _{i}a_{i},\bigwedge _{i}b_{i}\right] . \end{aligned}$$

Now $D_{1}\ge D_{2}$ iff $a_{1}\ge a_{2}$ and $b_{1}\ge b_{2}$.

Similarly the relations $D_{1}\le D_{2}$ and $D_{1}=D_{2}$ are defined.

3 Interval valued intuitionistic fuzzy $\beta$-subalgebra

This section deals the notion of Interval valued intuitionistic fuzzy $\beta$-subalgebra of a $\beta$-algebra and prove some related results. Also, in the rest of the paper, X is a $\beta$-algebra unless, otherwise specified.

Definition 3.1

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : ~x\in ~X\rbrace$ be an Interval valued intuitionstic fuzzy set in X. Then the set A is an Interval valued intuitionstic fuzzy $\beta$-subalgebra (i-v IF $\beta$-subalgebra)over the binary operations $+$ and −, if $\forall ~ x,y \in X$ it satisfies the following conditions.

• (i) $\overline{\mu }_{A}(x+y)\ge rmin \lbrace \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\rbrace \quad \mathrm{and}\quad \overline{\mu }_{A}(x-y)\ge rmin \lbrace \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\rbrace$

• (ii) $\overline{\nu }_{A}(x+y)\le rmax \lbrace \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\rbrace \quad \mathrm{and}\quad \overline{\nu }_{A}(x-y)\le rmax \lbrace \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\rbrace$

Example 3.2

Consider the $\beta$-algebra X defined in the Example 2.4. Define an i-v IF subset on X as follows.

$$\begin{aligned} \overline{\mu }_{A}(x)= \left\{ \begin{array}{l} {[}0.3,0.5{]}:\quad x=0\\ {[}0.2,0.4{]}:\quad x=b\\ {[}0.1,0.3{]}:\quad x=a,c\\ \end{array}\right. \quad \overline{\nu }_{A}(x)= \left\{ \begin{array}{l} {[0.2,0.3]}: \quad x=0\\ {[0.3,0.5]}: \quad x=b\\ {[0.4,0.6]}:\quad x=a,c\\ \end{array}\right. \end{aligned}$$

Then $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : ~x\in ~X\rbrace$ is an i-v IF $\beta$-sub algebra of X

Definition 3.3

Let $(X,+,-,0)$ and $(Y,+,-,0)$ be two $\beta$-algebras. A mapping $f:X\rightarrow Y$ is said to be a $\beta$-homomorphism, if

• (i) $f(x+y)=f(x)+f(y)$

• (ii) $f(x-y)=f(x)-f(y) ~~\forall ~ x,y \in X$

Definition 3.4

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle \rbrace$ and $B=\lbrace \langle x,\overline{\mu }_{B}(x),\overline{\nu }_{B}(x)\rangle \rbrace$ be two i-v IF set on X, then the intersection of A and B denoted by $A\cap B$ is defined by

$$\begin{aligned} A\cap B= & {} \left\{ \left\langle x,\overline{\mu }_{A\cap B}(x),\overline{\nu }_{A\cap B}(x)\right\rangle \right\} \\= & {} \left\{ \left\langle x,\left[ min(\mu _{A}^{L}(x),\mu _{B}^{L}(x)), min(\mu _{A}^{U}(x),\mu _{B}^{U}(x))\right] ,\right. \right. \\&\left. \left. \left[ max(\nu _{A}^{L}(x),\nu _{B}^{L}(x)),max(\nu _{A}^{U}(x),\nu _{B}^{U}(x))\right] \right\rangle :x\in X\right\} . \end{aligned}$$

Theorem 3.5

An i-v IF set $A=[[\mu _{A}^{L},\mu _{A}^{U}],[\nu _{A}^{L},\nu _{A}^{U}]]$ in X is an i-v IF $\beta$-subalgebra of X if and only if $\mu _{A}^{L} , \mu _{A}^{U}$ are fuzzy $\beta$-subalgebras and $\nu _{A}^{L}$ , $\nu _{A}^{U}$ are anti fuzzy $\beta$-subalgebras of X.

Proof

Let $\mu _{A}^{L}$ and $\mu _{A}^{U}$ be fuzzy $\beta$-subalgebras of X and let $\nu _{A}^{L}$ and $\nu _{A}^{U}$ be anti fuzzy $\beta$-subalgebras of X $~~ \forall x,y\in X$. Then

$$\begin{aligned} \mu _{A}^{L}(x+y)\ge min\left\{ \mu _{A}^{L}(x),\mu _{A}^{L}(y)\right\} \quad \hbox { and }\quad \nu _{A}^{L}(x+y)\le max\left\{ \nu _{A}^{L}(x),\nu _{A}^{L}(y)\right\} \\ \mu _{A}^{U}(x+y)\ge min\left\{ \mu _{A}^{U}(x),\mu _{A}^{U}(y)\right\} \quad \hbox { and }\quad \nu _{A}^{U}(x+y)\le max\left\{ \nu _{A}^{U}(x),\nu _{A}^{U}(y)\right\} \end{aligned}$$

Now

$$\begin{aligned} \overline{\mu }_{A}(x+y)&=[\mu _{A}^{L}(x+y),\mu _{A}^{U}(x+y)]\\&\ge [min\left\{ \mu _{A}^{L}(x),\mu _{A}^{L}(y)\right\} ,min\lbrace \mu _{A}^{U}(x),\mu _{A}^{U}(y)\rbrace ]\\&=rmin\left\{ [\mu _{A}^{L}(x),\mu _{A}^{U}(x)],[\mu _{A}^{L}(y),\mu _{A}^{U}(y)]\right\} \\&=rmin\left\{ [\overline{\mu }_{A}(x),\overline{\mu }_{A}(y)]\right\} \end{aligned}$$

Also,

$$\begin{aligned} \overline{\nu }_{A}(x+y)&=[\nu _{A}^{L}(x+y),\nu _{A}^{U}(x+y)]\\&\le [max\left\{ \nu _{A}^{L}(x),\nu _{A}^{L}(y)\right\} ,max\left\{ \nu _{A}^{U}(x),\nu _{A}^{U}(y)\right\} ]\\&=rmax\left\{ [\nu _{A}^{L}(x),\nu _{A}^{U}(x)],[\mu _{A}^{L}(y),\nu _{A}^{U}(y)]\right\} \\&=rmax\left\{ \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\right\} \end{aligned}$$

Similarly,

$$\begin{aligned} \overline{\mu }_{A}(x-y)\ge rmin\left\{ \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\right\} \quad \text {and} \quad \overline{\nu }_{A}(x-y)\le rmax\left\{ \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\right\} \end{aligned}$$

Hence A is an i-v IF $\beta$-subalgebra of X.

Conversly,

Assume that A is an i-v IF $\beta$-subalgebra of X. Then for any $x,y\in X$, Now

$$\begin{aligned}{}[\mu _{A}^{L}(x+y),\mu _{A}^{U}(x+y)]&=\overline{\mu }_{A}(x+y)\\&\ge rmin\left\{ \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\right\} \\&=rmin\left\{ \left[ \mu _{A}^{L}(x),\mu _{A}^{U}(x)\right] ,\left[ \mu _{A}^{L}(y),\mu _{A}^{U}(y)\right] \right\} \\&=\left[ min\left\{ \mu _{A}^{L}(x),\mu _{A}^{L}(y)\right\} ,min\left\{ \mu _{A}^{U}(x),\mu _{A}^{U}(y)\right\} \right] \end{aligned}$$

Thus

$$\begin{aligned} \mu _{A}^{L}(x+y)\ge min\lbrace \mu _{A}^{L}(x),\mu _{A}^{L}(y)\rbrace \quad \text {and}\quad \mu _{A}^{U}(x+y)\ge min\lbrace \mu _{A}^{U}(x),\mu _{A}^{U}(y)\rbrace \end{aligned}$$

Similarly,

$$\begin{aligned} \mu _{A}^{L}(x-y)\ge min\lbrace \mu _{A}^{L}(x),\mu _{A}^{L}(y)\rbrace \quad \text {and}\quad \mu _{A}^{U}(x-y)\ge min\lbrace \mu _{A}^{U}(x),\mu _{A}^{U}(y)\rbrace . \end{aligned}$$

Also

$$\begin{aligned}{}[\nu _{A}^{L}(x+y),\nu _{A}^{U}(x+y)]&=\overline{\nu }_{A}(x+y)\\&\le rmax\left\{ \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\right\} \\&=rmax\left\{ \left[ \nu _{A}^{L}(x),\nu _{A}^{U}(x)],[\nu _{A}^{L}(y),\nu _{A}^{U}(y)\right] \right\} \\&=\left[ max\left\{ \nu _{A}^{L}(x),\nu _{A}^{L}(y)\right\} ,max\left\{ \nu _{A}^{U}(x),\nu _{A}^{U}(y)\right\} \right] \end{aligned}$$

Thus

$$\begin{aligned} \nu _{A}^{L}(x+y)\le max\left\{ \nu _{A}^{L}(x),\nu _{A}^{L}(y)\right\} \quad \text {and}\quad \nu _{A}^{U}(x+y)\le max\left\{ \nu _{A}^{U}(x),\nu _{A}^{U}(y)\right\} \end{aligned}$$

Similarly,

$$\begin{aligned} \nu _{A}^{L}(x-y)\le max\left\{ \nu _{A}^{L}(x),\nu _{A}^{L}(y)\right\} \quad \text {and}\quad \nu _{A}^{U}(x-y)\le max\lbrace \nu _{A}^{U}(x),\nu _{A}^{U}(y)\rbrace \end{aligned}$$

Hence $\mu _{A}^{L}, \mu _{A}^{U}$ are fuzzy $\beta$-subalgebras and $\nu _{A}^{L},\nu _{A}^{U}$ are anti fuzzy $\beta$-subalgebras of X. $\square$

Theorem 3.6

Let $A_{1}$ and $A_{2}$ be two i-v IF $\beta$-subalgebras of X. Then $A_{1}\cap A_{2}$ is an i-v IF $\beta$-subalgebra of X.

Proof

Let $A_{1}$ and $A_{2}$ be two i-v IF $\beta$-subalgebras of X.

Now,

$$\begin{aligned} \overline{\mu }_{A_{1}\cap A_{2}}(x+y)&=\left[ \mu _{A_{1}\cap A_{2}}^{L}(x+y),\mu _{A_{1}\cap A_{2}}^{U}(x+y)\right] \\&=\left[ min(\mu _{A_{1}}^{L}(x+y),\mu _{A_{2}}^{L}(x+y)),min(\mu _{A_{1}}^{U}(x+y),\mu _{A_{2}}^{U}(x+y))\right] \\&\ge \left[ min(\mu _{(A_{1}\cap A_{2})}^{L}(x),(\mu _{(A_{1}\cap A_{2})}^{L}(y)),min(\mu _{(A_{1}\cap A_{2})}^{U}(x),(\mu _{(A_{1}\cap A_{2})}^{U}(y))\right] \\&=rmin\left\{ \overline{\mu }_{A_{1}\cap A_{2}}(x),\overline{\mu }_{A_{1}\cap A_{2}}(y)\right\} \\ \end{aligned}$$

Similarly, $\overline{\mu }_{A_{1}\cap A_{2}}(x-y)\ge rmin \lbrace \overline{\mu }_{A_{1}\cap A_{2}}(x),\overline{\mu }_{A_{1}\cap A_{2}}(y)\rbrace$.     

Also,

$$\begin{aligned} \overline{\nu }_{A_{1}\cap A_{2}}(x+y)&=\left[ \nu _{A_{1}\cap A_{2}}^{L}(x+y),\nu _{A_{1}\cap A_{2}}^{U}(x+y)\right] \\&=\left[ max(\nu _{A_{1}}^{L}(x+y),\nu _{A_{2}}^{L}(x+y)),max(\mu _{A_{1}}^{U}(x+y),\mu _{A_{2}}^{U}(x+y))\right] \\&\le \left[ max(\nu _{(A_{1}\cap A_{2})}^{L}(x),(\nu _{(A_{1}\cap A_{2})}^{L}(y)),max(\nu _{(A_{1}\cap A_{2})}^{U}(x),(\nu _{(A_{1}\cap A_{2})}^{U}(y))\right] \\&=rmax\left\{ \overline{\nu }_{A_{1}\cap A_{2}}(x),\overline{\nu }_{A_{1}\cap A_{2}}(y)\right\} \end{aligned}$$

Similarly , $\overline{\nu }_{A_{1}\cap A_{2}}(x-y)\le rmax \lbrace \overline{\nu }_{A_{1}\cap A_{2}}(x),\overline{\nu }_{A_{1}\cap A_{2}}(y)\rbrace$. $\square$

Lemma 3.7

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF $\beta$-subalgebra of X. Then

• 1. $\overline{\mu }_{A}(x)\le \overline{\mu }_{A}(0)$ and $\overline{\nu }_{A}(x)\ge \overline{\nu }_{A}(0)~~\forall ~x\in X$

• 2. $\overline{\mu }_{A}(x)\le \overline{\mu }_{A}(x^{*})\le \overline{\mu }_{A}(0)$ and $\overline{\nu }_{A}(x)\ge \overline{\nu }_{A}(x^{*})\ge \overline{\nu }_{A}(0)~~\forall ~ x\in X$ where $x^{*} = 0-x$

Proof

• 1. For any $x\in X$,

  $$\begin{aligned} \overline{\mu }_{A}(x)&=\left[ \mu ^{L}_{A}(x),\mu ^{U}_{A}(x)\right] \\&\le \left[ \mu ^{L}_{A}(0),\mu ^{U}_{A}(0)\right] \\ {}&= \overline{\mu }_{A}(0) \end{aligned}$$

  and

  $$\begin{aligned} \overline{\nu }_{A}(x)&=\left[ \nu ^{L}_{A}(x),\nu ^{U}_{A}(x)\right] \\&\ge \left[ \nu ^{L}_{A}(0),\nu ^{U}_{A}(0)\right] \\&= \overline{\nu }_{A}(0) \end{aligned}$$

• 2. Also for any $x\in X$,

  $$\begin{aligned} \overline{\mu }_{A}(x)&=\left[ \mu ^{L}_{A}(x),\mu ^{U}_{A}(x)\right] \\&\le \left[ \mu ^{L}_{A}(x^*),\mu ^{U}_{A}(x^*)\right] \\&=\overline{\mu }_{A}(x^*) \end{aligned}$$

  Hence $\overline{\mu }_{A}(x)\le \overline{\mu }_{A}(x^*)\le \overline{\mu }_{A}(0)$ For every $x\in X$,

  $$\begin{aligned} \overline{\nu }_{A}(x)&=\left[ \nu ^{L}_{A}(x),\nu ^{U}_{A}(x)\right] \\&\ge \left[ \nu ^{L}_{A}(x^*),\nu ^{U}_{A}(x^*)\right] \\&=\overline{\nu }_{A}(x^*) \end{aligned}$$

  Hence $\overline{\nu }_{A}(x)\ge \overline{\nu }_{A}(x^*)\ge \overline{\nu }_{A}(0)$

$\square$

Theorem 3.8

Let A be an i-v IF $\beta$-algebra of X there exists a sequence $\lbrace x_{n}\rbrace$ in X such that $\lim \nolimits _{n\rightarrow \infty }\overline{\mu }_{A}(x_{n})=[1,1]$ and $\lim \nolimits _{n\rightarrow \infty }\overline{\nu }_{A}(x_{n})=[0,0]$ then $\overline{\mu }_{A}(0)=[1,1]$ and $\overline{\nu }_{A}(0)=[0,0]$

Proof

Since $\overline{\mu }_{A}(0)\ge \overline{\mu }_{A}(x)~~ \forall ~ x \in X$, Therefore $\overline{\mu }_{A}(0)\ge \overline{\mu }_{A}(x_{n})$ for every positive integer n.

Note that, $[1,1]\ge \overline{\mu }_{A}(0)\ge \ \lim _{n\rightarrow \infty }\overline{\mu }_{A}(x_{n})=[1,1]$

Hence  $\overline{\mu }_{A}(0)=[1,1]$

Since $\overline{\nu }_{A}(0)\le \overline{\nu }_{A}(x)~~\forall ~ x \in X$, we have $\overline{\nu }_{A}(0)\le \overline{\nu }_{A}(x_{n})$ for every positive integer n.

Now, $[0,0]\le \overline{\nu }_{A}(0)\le \ \lim _{n\rightarrow \infty }\overline{\nu }_{A}(x_{n})=[0,0]$

Hence  $\overline{\nu }_{A}(0)=[0,0]$ $\square$

Theorem 3.9

If $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X, then the sets $X_{\overline{\mu }_{A}}$=$\lbrace$ x $\in$ X / $\overline{\mu }_{A}(x)=\overline{\mu }_{A}(0)\rbrace$ and $X_{\overline{\nu }_{A}}$=$\lbrace$ x $\in$ X / $\overline{\nu }_{A}(x)=\overline{\nu }_{A}(0)\rbrace$ are $\beta$-subalgebra of X.

Proof

Let x,y $\in X_{\overline{\mu }_{A}}$.

Then   $\overline{\mu }_{A}(x)=\overline{\mu }_{A}(0)$, $\overline{\mu }_{A}(y)=\overline{\mu }_{A}(0)$

Now

$$\begin{aligned} \overline{\mu }_{A}(x+y)&\ge rmin\left\{ \overline{\mu }_{A}(x),\overline{\mu }_{A}(y)\right\} \\&=rmin\left\{ \overline{\mu }_{A}(0),\overline{\mu }_{A}(0)\right\} \\&=\overline{\mu }_{A}(0) \end{aligned}$$

Similarly, $\overline{\mu }_{A}(x-y)\ge \overline{\mu }_{A}(0)$

Hence  $x+y , x-y \in X_{\overline{\mu }_{A}}$

$\therefore ~~~~~X_{\overline{\mu }_{A}}$ is a $~~\beta$-subalgebra of X.

Let x,y $\in X_{\overline{\nu }_{A}}$. Then $\overline{\nu }_{A}(x)=\overline{\nu }_{A}(0)$, $\overline{\nu }_{A}(y)=\overline{\nu }_{A}(0)$

Now

$$\begin{aligned} \overline{\nu }_{A}(x+y)&\le rmax\lbrace \overline{\nu }_{A}(x),\overline{\nu }_{A}(y)\rbrace \\&=rmax\lbrace \overline{\nu }_{A}(0),\overline{\nu }_{A}(0)\rbrace \\&=\overline{\nu }_{A}(0) \end{aligned}$$

Similarly, $\overline{\nu }_{A}(x-y)\le \overline{\nu }_{A}(0)$

Hence  $x+y , x-y \in X_{\overline{\nu }_{A}}$

$\therefore ~~~~~X_{\overline{\nu }_{A}}$ is a $~~\beta$-subalgebra of X. $\square$

Theorem 3.10

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X. Then

$A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X if and only if $\square A=(x,\overline{\nu }_{A}^c,\overline{\nu }_{A})$ is an i-v IF $\beta$-subalgebra of X.

Proof

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X.

To prove $\square A$ is i-v IF $\beta$-subalgebra, it is enough to prove

$$\begin{aligned} \overline{\nu }_{A}^c(x+y)\ge rmin\lbrace \overline{\nu }_{A}^c(x),\overline{\nu }_{A}^c(y)\rbrace \end{aligned}$$

For,

$$\begin{aligned} (\overline{\nu }_{A})(x+y)\le & {} rmax\lbrace (\overline{\nu }_{A})(x),(\overline{\nu }_{A})(y)\rbrace \\ \Leftrightarrow [1,1]-(\overline{\nu }_{A})(x+y)\le & {} [1,1]-rmax \lbrace (\overline{\nu }_{A})(x),(\overline{\nu }_{A})(y)\rbrace \\ \Leftrightarrow \overline{\nu }_{A}^c(x+y)\ge & {} rmin\lbrace ([1,1]- \overline{\nu }_{A}(x)),([1,1]-\overline{\nu }_{A}(y))\rbrace \\ \Leftrightarrow \overline{\nu }_{A}^c(x+y)\ge & {} rmin\lbrace \overline{\nu }_{A}^c(x),\overline{\nu }_{A}^c(y)\rbrace \end{aligned}$$

Using the above theorem let us have the following. $\square$

Corollary 3.11

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X. Then

$A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X if and only if $\square A=(x,\overline{\nu }_{A}^c,\overline{\nu }_{A})$ is an i-v IF $\beta$-subalgebra of X $\Leftrightarrow$ $\square A^{L}=(x,(\nu _{A}^{L})^c,\nu _{A}^{L})$ and $\square A^{U}=(x,(\nu _{A}^{U})^c,\nu _{A}^{U})$ are IF $\beta$-subalgebra of X.

Theorem 3.12

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X. Then

$A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X if and only if $\lozenge A=(x,\overline{\mu }_{A},(\overline{\mu }_{A})^c)$ is an i-v IF $\beta$-subalgebra of X $\Leftrightarrow$ $\lozenge A^{L}=(x,\mu _{A}^{L},(\mu _{A}^{L})^c)$ and $\lozenge A^{U}=(x,\mu _{A}^{U},(\mu _{A}^{U})^c)$ are IF $\beta$-subalgebra of X.

Proof

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X.

To prove $\lozenge A$ is i-v IF $\beta$-subalgebra, it is enough to prove

$$\begin{aligned} \overline{\mu }_{A}^c(x+y)\le rmax\lbrace \overline{\mu }_{A}^c(x),\overline{\mu }_{A}^c(y)\rbrace \end{aligned}$$

For,

$$\begin{aligned} (\overline{\mu }_{A})(x+y)\ge & {} rmin\lbrace (\overline{\mu }_{A})(x),(\overline{\mu }_{A})(y)\rbrace \\ \Leftrightarrow [1,1]-(\overline{\mu }_{A})(x+y)\ge & {} [1,1]-rmin \lbrace (\overline{\mu }_{A})(x),(\overline{\mu }_{A})(y)\rbrace \\ \Leftrightarrow \overline{\mu }_{A}^c(x+y)\le & {} rmax\lbrace ([1,1]- \overline{\mu }_{A}(x)),([1,1]-\overline{\mu }_{A}(y))\rbrace \\ \Leftrightarrow \overline{\mu }_{A}^c(x+y)\le & {} rmax\lbrace \overline{\mu }_{A}^c(x),\overline{\mu }_{A}^c(y)\rbrace \end{aligned}$$

Using the above theorem let us have the following. $\square$

Corollary 3.13

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ be an i-v IF set of X. Then

$A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle : x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X if and only if $\lozenge A=(x,\overline{\mu }_{A},(\overline{\mu }_{A})^c)$ is an i-v IF $\beta$-subalgebra of X $\Leftrightarrow$ $\lozenge A^{L}=(x,\mu _{A}^{L},(\mu _{A}^{L})^c)$ and $\lozenge A^{U}=(x,\mu _{A}^{U},(\mu _{A}^{U})^c)$ are IF $\beta$-subalgebra of X.

Definition 3.14

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle :~x \in ~X\rbrace$ be an i-v IF set in Xand f be a mapping from a set X into a set Y,  then the image of A under f, f(A) is defined as $f(A)=\lbrace \langle x,f_{rsup}(\overline{\mu }_{A}),f_{rinf}(\overline{\nu }_{A})\rangle :~x\in ~Y\rbrace$, where

$$\begin{aligned} f_{rsup}(\overline{\mu }_{A})(y)= & {} \left\{ \begin{array}{ll} rsup_{x\in ~f^{-1}(y)}~\overline{\mu }_{A}(x),&{}\quad \text {if }f^{-1}(y)\ne \emptyset \\ {[0,0]},&{}\quad \text {otherwise} \end{array} \right. \\ f_{rinf}(\overline{\nu }_{A})(y)= & {} \left\{ \begin{array}{ll} rinf_{x\in ~f^{-1}(y)}~\overline{\nu }_{A}(x),&{}\quad \text {if}f^{-1}(y)\ne \emptyset \\ {[1,1]},&{}\quad \text {otherwise} \end{array}\right. \end{aligned}$$

Definition 3.15

An i-v IF set A in any set X is said to have the $rsup-rinf$ property if for subset T of X there exist $t_{0}\in T$ such that $\overline{\mu }_{A}(t_{0})=\mathop {rsup }\nolimits _{t_{0}\in T}$ and $\mathop {rinf }\nolimits _{t_{0}\in T}$ respectively.

Theorem 3.16

Let $f:X\rightarrow Y$ be a homomorphism of a $\beta$-algebra X into a $\beta$-algebra Y. If $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle :x\in X\rbrace$ is an i-v IF $\beta$-subalgebra of X, then the image $f(A)=\lbrace \langle x, f_{rsup}(\overline{\mu }_{A}),f_{rinf}(\overline{\nu }_{A})\rangle :x\in X\rbrace$ of A under f is an i-v IF $\beta$-subalgebra of Y.

Proof

Let $A=\lbrace \langle x, \overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle :x\in X\rbrace$ be an i-v IF $\beta$-subalgebras of X and let $y_{1},y_{2}\in Y$.

We know that

$$\begin{aligned} \lbrace x_{1}+x_{2}:x_{1}\in f^{-1}(y_{1}) ,x_{2}\in f^{-1}(y_{2})\rbrace \subseteq \lbrace x\in X:x\in f^{-1}(y_{1}+y_{2})\rbrace . \end{aligned}$$

Now,

$$\begin{aligned} f_{rsup}\left\{ \overline{\mu }_{A}(y_{1}+y_{2})\right\}&=rsup\left\{ \overline{\mu }_{A}(x)/x \in f^{-1}(y_{1}+y_{2})\right\} \\&\ge rsup\left\{ \overline{\mu }_{A}(x_{1}+x_{2})/ x_{1}\in f^{-1}(y_{1}),x_{2}\in f^{-1}(y_{2}) \right\} \\&\ge rsup \left\{ rmin \left\{ \overline{\mu }_{A}(x_{1}),\overline{\mu }_{A}(x_{2})\right\} ,x_{1}\in f^{-1}(y_{1}),x_{2}\in f^{-1}(y_{2})\right\} \\&=rmin \left\{ rsup\left\{ \overline{\mu }_{A}(x_{1})/x_{1}\in f^{-1}(y_{1})\right\} ,rsup\left\{ \overline{\mu }_{A}(x_{2})/x_{2}\in f^{-1}(y_{2})\right\} \right\} \\&=rmin\left\{ f_{rsup}(\overline{\mu }_{A}(y_{1})),f_{rsup}(\overline{\mu }_{A}(y_{2}))\right\} \end{aligned}$$

Similarly, $f_{rsup}\lbrace \overline{\mu }_{A}(y_{1}-y_{2})\rbrace \ge rmin\lbrace f_{rsup}(\overline{\mu }_{A}(y_{1})),f_{rsup}(\overline{\mu }_{A}(y_{2}))\rbrace$

$$\begin{aligned} f_{rinf}\left\{ \overline{\nu }_{A}(y_{1}+y_{2})\right\}&=rinf \left\{ \overline{\nu }_{A}(x)/x \in f^{-1}(y_{1}+y_{2})\right\} \\&\le rinf\left\{ \overline{\nu }_{A}(x_{1}+x_{2})/ x_{1}\in f^{-1}(y_{1}),x_{2}\in f^{-1}(y_{2}) \right\} \\&\le rinf \left\{ rmax \left\{ \overline{\nu }_{A}(x_{1}),\overline{\nu }_{A}(x_{2})\right\} ,x_{1}\in f^{-1}(y_{1}),x_{2}\in f^{-1}(y_{2})\right\} \\&=rmax \left\{ rinf\left\{ \overline{\nu }_{A}(x_{1})/x_{1}\in f^{-1}(y_{1})\right\} ,rinf\left\{ \overline{\nu }_{A}(x_{2})/x_{2}\in f^{-1}(y_{2})\right\} \right\} \\&=rmax\left\{ f_{rinf}(\overline{\nu }_{A}(y_{1})),f_{rinf}(\overline{\nu }_{A}(y_{2}))\right\} \end{aligned}$$

Similarly, $f_{rinf}\lbrace \overline{\nu }_{A}(y_{1}-y_{2})\rbrace \le rmax\lbrace f_{rinf}(\overline{\nu }_{A}(y_{1})),f_{rinf}(\overline{\nu }_{A}(y_{2}))\rbrace$ $\square$

Theorem 3.17

Let $f:X\rightarrow Y$ be a homomorphism of a $\beta$-algebras. If $B=\lbrace \langle x,\overline{\mu }_{A},\overline{\nu }_{A}\rangle :x\in Y\rbrace$ is an i-v IF $\beta$-subalgebra of Y, then the inverse image $f^{-1}(B)=\lbrace \langle x,f^{-1}(\mu _{B}),f^{-1}(\nu _{B})\rangle :x\in X\rbrace$ of B under f is an i-v IF $\beta$-subalgebra of X.

Proof

Assume that $B=\lbrace \langle x,\overline{\mu }_{A},\overline{\nu }_{A}\rangle :x\in Y\rbrace$ is an i-v IF $\beta$-subalgebra of Y and let $x,y\in X$.

Then

$$\begin{aligned} f^{-1}(\overline{\mu }_{B})(x+y)&=\overline{\mu }_{B}(f(x+y))\\&=\overline{\mu }_{B}(f(x)+f(y))\\&\ge rmin\lbrace \overline{\mu }_{B}(f(x)),\overline{\mu }_{B}(f(y))\rbrace \\&=rmin\lbrace f^{-1}(\overline{\mu }_{B})(x),f^{-1}(\overline{\mu }_{B})(y)\rbrace \end{aligned}$$

and

$$\begin{aligned} f^{-1}(\overline{\nu }_{B})(x+y)&=\overline{\nu }_{B}(f(x+y))\\&=\overline{\nu }_{B}(f(x)+f(y))\\&\le rmax\lbrace \overline{\nu }_{B}(f(x)),\overline{\nu }_{B}(f(y))\rbrace \\&=rmax\lbrace f^{-1}(\overline{\nu }_{B})(x),f^{-1}(\overline{\nu }_{B})(y)\rbrace \end{aligned}$$

Similarly,

$$\begin{aligned} f^{-1}(\overline{\mu }_{B})(x-y)\ge & {} rmin\lbrace f^{-1}(\overline{\mu }_{B})(x),f^{-1}(\overline{\mu }_{B})(y)\rbrace \hbox { and }\\ f^{-1}(\overline{\nu }_{B})(x-y)\le & {} rmax\lbrace f^{-1}(\overline{\nu }_{B})(x),f^{-1}(\overline{\nu }_{B})(y)\rbrace \\ \therefore \,\,f^{-1}(B)= & {} \lbrace \langle x,f^{-1}(\mu _{B}),f^{-1}(\nu _{B})\rangle :x\in X\rbrace \hbox { is an i-v IF } \beta \mathrm{-}\hbox {subalgebra of }X. \end{aligned}$$

$\square$

Theorem 3.18

Let $(X,+,-,0)$ and $(Y,+,-,0)$ be two $\beta$-algebras. Let $f:X\rightarrow Y$ be an endomorphism. If A is an i-v IF $\beta$-subalgebra of X, define

$f(A)=\left\{ \langle x,\overline{\mu }_{f}(x)=\overline{\mu }(f(x)),\overline{\nu }_{f}(x)=\overline{\nu }(f(x))\rangle \vert x\in X\right\}$. Then f(A) is an i-v IF $\beta$-subalgebra of Y .

Proof

Let $x,y\in X$. Now,

$$\begin{aligned} \overline{\mu }_{f}(x+y)= & {} \overline{\mu }(f(x+y))\\= & {} \overline{\mu }(f(x)+f(y))\\\ge & {} rmin\lbrace \overline{\mu }(f(x)),\overline{\mu }(f(y))\rbrace \\= & {} rmin \lbrace \overline{\mu }_{f}(x),\overline{\mu }_{f}(y)\rbrace \end{aligned}$$

Similarly, $\overline{\mu }_{f}(x-y)\ge rmin \lbrace \overline{\mu }_{f}(x),\overline{\mu }_{f}(y)\rbrace$

Further,

$$\begin{aligned} \overline{\nu }_{f}(x+y)= & {} \overline{\nu }(f(x+y))\\= & {} \overline{\nu }(f(x)+f(y))\\\le & {} rmax\lbrace \overline{\nu }(f(x)),\overline{\nu }(f(y))\rbrace \\= & {} rmax \lbrace \overline{\nu }_{f}(x),\overline{\nu }_{f}(y)\rbrace \end{aligned}$$

Similarly, $\overline{\nu }_{f}(x-y)\le rmax \lbrace \overline{\nu }_{f}(x),\overline{\nu }_{f}(y)\rbrace$

Hence f(A) is an i-v IF $\beta$-subalgebra of Y. $\square$

4 Product of interval valued intuitionstic fuzzy $\beta$-subalgebra

This section, introduces the notion of product on Interval valued intuitionistic fuzzy $\beta$-subalgebras of $\beta$-algebras and prove some elegant results.

Definition 4.1

Let $(X,+,-,0)$ and $(Y,+,-,0)$ be two sets.

Let $A=\lbrace \langle x,\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rangle :x\in X\rbrace$ and $B=\lbrace \langle y,\overline{\mu }_{B}(y),\overline{\nu }_{B}(y)\rangle :y \in Y\rbrace$

be i-v IF subsets in X and Y respectively. The Cartesian product of A and B denoted by $A \times B$ is defined to be the set

$A\times B=\lbrace \langle (x,y),\overline{\mu }_{A \times B}(x,y),\overline{\nu }_{A \times B}(x,y) \rangle :(x,y)\in X \times Y \rbrace$

where $\overline{\mu }_{A\times B}:X\times Y\rightarrow D[0,1]$ is given by $\overline{\mu }_{A\times B}(x,y)\ge rmin\lbrace \overline{\mu }_A(x),\overline{\mu }_B(y)\rbrace$ and $\overline{\mu }_{A\times B}:X\times Y\rightarrow D[0,1]$ is given by $\overline{\nu }_{A\times B}(x,y)\le rmax\lbrace \overline{\nu }_A(x),\overline{\nu }_B(y)\rbrace$.

Theorem 4.2

Let $A=\lbrace x\in X:\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rbrace$ and $B=\lbrace y \in Y:\overline{\mu }_{B}(y),\overline{\nu }_{B}(y)\rbrace$ be any two i-v IF $\beta$-subalgebras of X and Y respectively. Then ${A\times B}$ is also an i-v IF $\beta$-subalgebra of $X \times Y$.

Proof

Let $A=\lbrace x\in X:\overline{\mu }_{A}(x),\overline{\nu }_{A}(x)\rbrace$ and $B=\lbrace y \in Y:\overline{\mu }_{B}(y),\overline{\nu }_{B}(y)\rbrace$ be any two i-v IF $\beta$-subalgebras of X and Y. Take $(a,b)\in X \times Y$, where $a=(x_{1},y_{1})$ and $b= (x_{2},y_{2})$.

$$\begin{aligned} \overline{\mu }_{A\times B}(a+b)&=\overline{\mu }_{A\times B}((x_{1},y_{1})+(x_{2},y_{2}))\\&=[\mu _{A\times B}^{L}((x_{1},y_{1})+(x_{2},y_{2})),\mu _{A\times B}^{U}((x_{1},y_{1})+(x_{2},y_{2}))]\\&\ge [min \lbrace \mu _{A\times B}^{L}(x_{1},y_{1}),\mu _{A\times B}^{L}(x_{2},y_{2})\rbrace , min \lbrace \mu _{A\times B}^{U}(x_{1},y_{1}),\mu _{A\times B}^{U}(x_{2},y_{2})\rbrace \\&=rmin\lbrace [\mu _{A\times B}^{L}(x_{1},y_{1}), \mu _{A\times B}^{U}(x_{1},y_{1})],[\mu _{A\times B}^{L}(x_{2},y_{2}),\mu _{A\times B}^{U}(x_{2},y_{2})\rbrace \\&=rmin\lbrace \overline{\mu }_{A\times B}(x_{1},y_{1}),\overline{\mu }_{A\times B}(x_{2},y_{2})]\rbrace \\&=rmin\lbrace \overline{\mu }_{A\times B}(a),\overline{\mu }_{A\times B}(b)\rbrace \end{aligned}$$

Similarly, $\overline{\mu }_{A\times B}(a-b)\ge rmin\lbrace \overline{\mu }_{A\times B}(a),\overline{\mu }_{A\times B}(b)\rbrace$

Further,

$$\begin{aligned} \overline{\nu }_{A\times B}(a+b)&=\overline{\nu }_{A\times B}((x_{1},y_{1})+(x_{2},y_{2}))\\&=[\nu _{A\times B}^{L}((x_{1},y_{1})+(x_{2},y_{2})),\nu _{A\times B}^{U}((x_{1},y_{1})+(x_{2},y_{2}))]\\&\le [max \lbrace \nu _{A\times B}^{L}(x_{1},y_{1}),\nu _{A\times B}^{L}(x_{2},y_{2})\rbrace , max \lbrace \nu _{A\times B}^{U}(x_{1},y_{1}),\nu _{A\times B}^{U}(x_{2},y_{2})\rbrace ]\\&=rmax\lbrace [\nu _{A\times B}^{L}(x_{1},y_{1}), \nu _{A\times B}^{U}(x_{1},y_{1})],[\nu _{A\times B}^{L}(x_{2},y_{2}),\nu _{A\times B}^{U}(x_{2},y_{2})]\rbrace \\&=rmax\lbrace \overline{\nu }_{A\times B}(x_{1},y_{1}),\overline{\nu }_{A\times B}(x_{2},y_{2})\rbrace \\&=rmax\lbrace \overline{\nu }_{A\times B}(a),\overline{\nu }_{A\times B}(b)\rbrace \end{aligned}$$

Similarly, $\overline{\nu }_{A\times B}(a-b)\le rmax\lbrace \overline{\nu }_{A\times B}(a),\overline{\nu }_{A\times B}(b)\rbrace$ $\square$

Theorem 4.3

If $A \times B$ is an i-v IF $\beta$-subalgebra of $X\times Y$, then either A is an i-v IF $\beta$-subalgebra of X or B is an i-v IF $\beta$-subalgebra of Y.

Proof

Let $A\times B$ is an i-v IF $\beta$-subalgebra of $X\times Y$

Take $(x_{1},y_{1})$ and $(x_{2},y_{2})\in X \times Y$.

Then, $\overline{\mu }_{A\times B}\lbrace (x_{1},y_{1})+(x_{2},y_{2})\rbrace \ge rmin \lbrace \overline{\mu }_{A\times B}(x_{1},y_{1}),\overline{\mu }_{A\times B}(x_{2},y_{2})\rbrace$, put $x_{1}=x_{2}=0\; \mathrm{we\,\, get}~~ \overline{\mu }_{A\times B}\lbrace (0,y_{1}),(0,y_{2})\rbrace \ge rmin \lbrace \overline{\mu }_{A\times B}(0,y_{1}),\overline{\mu }_{A\times B}(0,y_{2})\rbrace$

Now $\overline{\mu }_{A\times B}\lbrace (0+0),(y_{1}+y_{2})\rbrace \ge rmin \lbrace \overline{\mu }_{A\times B}(0,y_{1}),\overline{\mu }_{A\times B}(0,y_{2})\rbrace$

So,    $\overline{\mu }_{B}(y_{1}+y_{2})\ge rmin\lbrace \overline{\mu }_{B}(y_{1}),\overline{\mu }_{B}(y_{2})\rbrace$

Similarly,   $\overline{\mu }_{B}(y_{1}-y_{2})\ge rmin\lbrace \overline{\mu }_{B}(y_{1}),\overline{\mu }_{B}(y_{2})\rbrace$ and

$\overline{\nu }_{A\times B}\lbrace (x_{1},y_{1})+(x_{2},y_{2})\rbrace \ge rmax \lbrace \overline{\nu }_{A\times B}(x_{1},y_{1}),\overline{\nu }_{A\times B}(x_{2},y_{2})\rbrace ,$ put $x_{1}=x_{2}=0\; \mathrm{we\,\, get}~~ \overline{\nu }_{A\times B}\lbrace (0,y_{1}),(0,y_{2})\rbrace \ge rmax \lbrace \overline{\nu }_{A\times B}(0,y_{1}),\overline{\nu }_{A\times B}(0,y_{2})\rbrace$

Then   $\overline{\nu }_{A\times B}\lbrace (0+0),(y_{1}+y_{2})\rbrace \ge rmax \lbrace \overline{\nu }_{A\times B}(0,y_{1}),\overline{\nu }_{A\times B}(0,y_{2})\rbrace .$ $\therefore ~~ \overline{\nu }_{B}(y_{1}+y_{2})\le rmax\lbrace \overline{\nu }_{B}(y_{1}),\overline{\nu }_{B}(y_{2})\rbrace$

Similarly,   $\overline{\nu }_{B}(y_{1}-y_{2})\le rmax\lbrace \overline{\nu }_{B}(y_{1}),\overline{\nu }_{B}(y_{2})\rbrace$

Hence B is an i-v IF $\beta$-subalgebra of Y. $\square$

Definition 4.4

Let $A_{i}\,=\,\lbrace x \in X_{i}: \overline{\mu }_{A_{i}}(x),\overline{\nu }_{A_{i}}(x)\rbrace$ be an i-v IF $\beta$-subalgebra of $X_{i}$, i $=$ 1,2,...n. Then $\prod \nolimits _{i=1}^n A_{i}$ is called direct product of finite i-v IF $\beta$-subalgebra of $\prod \nolimits _{i=1}^n X_{i}$ if

• (a)

  • (i) $\prod \nolimits _{i=1}^n \overline{\mu }_{A_{i}}(x_{i}+y_{i})\ge rmin\left\{ \prod \nolimits _{i=1}^n\overline{\mu }_{A_{i}}(x_{i}),\prod \nolimits _{i=1}^n\overline{\mu }_{A_{i}}(y_{i})\right\}$

  • (ii) $\prod \nolimits _{i=1}^n \overline{\mu }_{A_{i}}(x_{i}-y_{i})\ge rmin\left\{ \prod \nolimits _{i=1}^n\overline{\mu }_{A_{i}}(x_{i}),\prod \nolimits _{i=1}^n\overline{\mu }_{A_{i}}(y_{i})\right\}$

• (b)

  • (i) $\prod \nolimits _{i=1}^n \overline{\nu }_{A_{i}}(x_{i}+y_{i})\le rmax\left\{ \prod \nolimits _{i=1}^n\overline{\nu }_{A_{i}}(x_{i}),\prod \nolimits _{i=1}^n\overline{\nu }_{A_{i}}(y_{i})\right\}$

  • (ii) $\prod \nolimits _{n=1}^n \overline{\nu }_{A_{i}}(x_{i}-y_{i})\le rmax\left\{ \prod \nolimits _{i=1}^n\overline{\nu }_{A_{i}}(x_{i}),\prod \nolimits _{i=1}^n\overline{\nu }_{A_{i}}(y_{i})\right\}$

Theorem 4.5

Let $A_{i}=\lbrace x \in X_{i}/ \overline{\mu }_{A_{i}}(x),\overline{\nu }_{A_{i}}(x)\rbrace$ be an i-v IF $\beta$-sub algebra of $X_{i}$ respectively, for i=1,2...n. Then $\prod \nolimits _{i=1}^n A_{i}$ is an i-v IF $\beta$-sub algebra of $\prod \nolimits _{i=1}^n X_{i}$

Proof

Let $A_{i}=\lbrace x \in X_{i}/ \overline{\mu }_{A_{i}}(x),\overline{\nu }_{A_{i}}(x)\rbrace$ be an i-v IF $\beta$-sub algebra of $X_{i}$.

Let $(x_{1},\ldots \,x_{n})$ and $(y_{1},\ldots \,y_{n})\in \prod \nolimits _{i=1}^n X_{i}$

Take $a=(x_{1},\ldots \,x_{n})$ and $b=(y_{1},\ldots \,y_{n})$

Then

$$\begin{aligned} \mathrm{(i)}\quad \prod \limits _{i=1}^n \overline{\mu }_{A_{i}} (a+b)&\ge rmin \lbrace \overline{\mu }_{A_{1}}(a+b)\ldots \overline{\mu }_{A_{n}}(a+b)\rbrace \\&=rmin \lbrace rmin \lbrace \overline{\mu }_{A_{1}}(a),\overline{\mu }_{A_{1}}(b)\rbrace \ldots \,rmin\lbrace \overline{\mu }_{A_{n}}(a),\overline{\mu }_{A_{n}}(b)\rbrace \rbrace \\&=rmin \lbrace rmin \lbrace \overline{\mu }_{A_{1}}(a),\ldots \,\overline{\mu }_{A_{n}}(a)\rbrace ,rmin\lbrace \overline{\mu }_{A_{1}}(b),\ldots \,\overline{\mu }_{A_{n}}(b)\rbrace \rbrace \\&=rmin \left\{ \prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(a),\prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(b)\right\} \end{aligned}$$

Similarly,

$$\begin{aligned} \prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(a-b)&\ge rmin \lbrace \prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(a),\prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(b)\rbrace \\ \mathrm{(ii)}\quad \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(a+b)&\le rmax \lbrace \overline{\nu }_{A_{1}}(a+b)\ldots \overline{\nu }_{A_{n}}(a+b)\rbrace \\&=rmax \lbrace rmax \lbrace \overline{\nu }_{A_{1}}(a),\overline{\nu }_{A_{1}}(b)\rbrace \ldots \,rmax\lbrace \overline{\nu }_{A_{n}}(a),\overline{\nu }_{A_{n}}(b)\rbrace \rbrace \\&=rmax \lbrace rmax \lbrace \overline{\nu }_{A_{1}}(a),\ldots \,\overline{\nu }_{A_{n}}(a)\rbrace ,rmax\lbrace \overline{\nu }_{A_{1}}(b),\ldots \,\overline{\nu }_{A_{n}}(b)\rbrace \rbrace \\&=rmax \left\{ \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(a),\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(b)\right\} \end{aligned}$$

Similarly,

$$\begin{aligned} \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(a-b)\le rmax \left\{ \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(a),\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(b)\right\} \end{aligned}$$

Hence $\prod \nolimits _{i=1}^n A_{i}$ is an i-v IF $\beta$-sub algebra of $\prod \nolimits _{i=1}^n X_{i}$ $\square$

Theorem 4.6

Let $A_{i}=(\overline{\mu }_{A_{i}},\overline{\nu }_{A_{i}})$ be an i-v IF $\beta$-subalgebras of $\prod \nolimits _{i=1}^n X_{i}$,for $i=1,2,\ldots ,n$ respectively. Then the sets $\prod \nolimits _{i=1}^n \overline{\mu }_{A_{i}}$ and $\prod \nolimits _{i=1}^n (\overline{\nu }_{A_{i}})^{c}$ are i-v fuzzy $\beta$-subalgebras of $\prod \nolimits _{i=1}^n X_{i}$

Proof

Since $A_{i}=(\overline{\mu }_{A_{i}},\overline{\nu }_{A_{i}})$ be an i-v IF $\beta$-subalgebras of $\prod \nolimits _{i=1}^n X_{i}$, for $i=1,2,\ldots ,n$ respectively.

Now, let for any $(x_{1},\ldots ,x_{n})$ and $(y_{1},\ldots ,y_{n}) \in \prod \nolimits _{i=1}^n X_{i}$

Then

$$\begin{aligned} \prod \limits _{i=1}^n \overline{\mu }_{A_{i}}((x_{1},\ldots ,x_{n}) + (y_{1},\ldots ,y_{n}))\ge rmin\left\{ \prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(x_{1},\ldots ,x_{n}),\prod \limits _{i=1}^n \overline{\mu }_{A_{i}}(y_{1},\ldots ,y_{n})\right\} \end{aligned}$$

and

$$\begin{aligned}&\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}((x_{1},\ldots ,x_{n}) + (y_{1},\ldots ,y_{n}))\\&\quad \le rmax\left\{ \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(x_{1},\ldots ,x_{n}),\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(y_{1},\ldots ,y_{n})\right\} \\&[1,1]-\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}((x_{1},\ldots ,x_{n}) + (y_{1},\ldots ,y_{n}))\\&\quad \ge [1,1]- rmax\left\{ \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(x_{1},\ldots ,x_{n}),\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}(y_{1},\ldots ,y_{n})\right\} \\&\quad = rmin \left\{ [1,1]-\prod \limits _{i=1}^n\overline{\nu }_{A_{i}}(x_{1},\ldots ,x_{n}),[1,1]-\prod \limits _{i=1}^n\overline{\nu }_{A_{i}}(y_{1},\ldots ,y_{n})\right\} \\&\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}^{c}(x_{1},\ldots ,x_{n}) + (y_{1},\ldots ,y_{n}) \\&\quad \ge rmin \left\{ \prod \limits _{i=1}^n \overline{\nu }_{A_{i}}^{c}(x_{1},\ldots ,x_{n}),\prod \limits _{i=1}^n \overline{\nu }_{A_{i}}^{c}(y_{1},\ldots ,y_{n})\right\} \end{aligned}$$

Hence $\prod \nolimits _{i=1}^n \overline{\mu }_{A_{i}}$ and $\prod \nolimits _{i=1}^n \overline{\nu }_{A_{i}}^{c}$ are i-v fuzzy $\beta$-subalgebras of $\prod \nolimits _{i=1}^n X_{i}$. $\square$