Introduction

Purifying wastewater from the contaminants is very essential to safeguard public health and wastewater treatment plants are needed to purify the water from contaminants.

The contaminants commonly occurring in the wastewater that are hazardous to human health include nitrate compounds, nitrite compounds, ammonium compounds, and biodegradable substances. The main aim of wastewater treatment plants is to reduce the concentration of these substances before discharge into the surroundings. While there can be a process to minimize biodegradable residue within the wastewater treatment itself, it is important to develop strategies to minimize this as much as possible. Wastewater treatment plants have to deal with continuous and unpredictable changes in the composition of the incoming untreated impure water. This paper demonstrates the use of a rigorous multiobjective optimal control strategy to ensure that the wastewater treatment plant is operated in a manner such that the amounts of all the problem-causing contaminants in the effluent water are minimized. This multiobjective optimal control strategy does not involve the use of arbitrary weight functions or additional constraints and the state-of-the-art global optimization solver BARON is used.

Background

The nonlinearity of the wastewater treatment process has led to a lot of modeling work, (Martin 2000; Meijer 2001; Singh et al. 2002; Hulsbeek, et al. 2002) and more recently by (Daughton 2018; Chen et al. 2019; Barceló 2020; Bijlsma et al. 2021; Adhikari and Halden 2022) The need to obtain optimal parameters in order to ensure the efficient operation of the process was investigated by Olsson et al. (2005) and Santin et al. (2016). The irregular variation of the influent along with the complex biochemical processes cause the optimization and control of the process to be challenging. Since the influent composition and the amount of contaminants changes irregularly, it is necessary to use a dynamic optimization to be able to ensure an effective continuous operation of the process. Amand et al. (2013) investigated in detail the effect of controlling the aeration in the wastewater treatment process. The use of advanced control strategies on the wastewater treatment plant process was also studied by (O’Brien et al; 2011; Amand et al. 2013; and Santin et al. 2016). The wastewater treatment is an aerobic process and since aeration demands a considerable amount of energy (McCarty et al. 2011; Daverey et al. 2019) the process must be operated in an effective manner. Real-time optimization and model predictive control of waste water treatment plants were studied by Vega et al. (2014); Santin et al. (2016); Piotrowski et al. 2008; Brdys et al. 2008; Tatjewski 2008 and Darby et al. 2011).

Two of the common process configurations for biological wastewater treatment process are the continuous-flow activated sludge process and the sequencing batch reactor process (Henze et al., 2008). Sun et al. compared the nitrogen and ammonia removal from waste water for both these processes and reported almost complete ammonia removal in both processes but observed higher total nitrogen removal in the continuous-flow activated sludge process than in the sequencing batch reactor process A complete ammonia removal in the sequencing batch reactor process was confirmed in a number of experimental studies (Yalmaz and Öztürk 2001; Andreottola et al. 2001). A comparison of the two processes for the treatment of industrial wastewater was performed by Papadimitriou et al. (2009), who found a higher removal of contaminants by the sequencing batch reactor process. Dionisi et al. 2016, and Dionisi 2017 developed a strategy to calculate the periodic steady state of sequencing batch reactors for biological wastewater treatment.

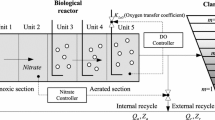
The reduced BSM1 (benchmark simulation model 1) is commonly used for the waste water treatment process (Julien et al. 1999; Gómez-Quintero and Spérandio 2004; Steffens et al. 1997; Zhao et al. 1994; Silvana et al. 2017). Details of this model can be found in all these articles. This model considers the anoxic and aerobic zones in the wastewater treatment plant. The process details of these zones are given in Silvana et al. 2017.

The values of the parameters, constants and the names of the variables for the equations in this model are shown in Tables 1, 2 and 3. The equations that constitute the model are

$$\rho_{11} = \mu_H \left( {\frac{{S_{s1} }}{{K_s + S_{s1} }}} \right)\left( {\frac{{S_{O1} }}{{K_{OH} + S_{O1} }}} \right)X_{BH}$$
(1)
$$\rho_{12} = \mu_H \left( {\frac{{S_{s2} }}{{K_s + S_{s2} }}} \right)\left( {\frac{{S_{O2} }}{{K_{OH} + S_{O2} }}} \right)X_{BH}$$
(2)
$$\rho_{21} = \mu_H \left( {\frac{{S_{s1} }}{{K_s + S_{s1} }}} \right)\left( {\frac{{K_{OH} }}{{K_{OH} + S_{O1} }}} \right)\left( {\frac{{S_{NO1} }}{{K_{OH} + S_{NO1} }}} \right)\eta_g X_{BH}$$
(3)
$$\rho_{22} = \mu_H \left( {\frac{{S_{s2} }}{{K_s + S_{s2} }}} \right)\left( {\frac{{K_{OH} }}{{K_{OH} + S_{O2} }}} \right)\left( {\frac{{S_{NO2} }}{{K_{OH} + S_{NO2} }}} \right)\eta_g X_{BH}$$
(4)
$$\rho_{31} = \mu_A \left( {\frac{{S_{O1} }}{{K_{OA} + S_{O1} }}} \right)\left( {\frac{{S_{NH1} }}{{K_{NH} + S_{NH1} }}} \right)X_{BA}$$
(5)
$$\rho_{32} = \mu_A \left( {\frac{{S_{O2} }}{{K_{OA} + S_{O2} }}} \right)\left( {\frac{{S_{NH2} }}{{K_{NH} + S_{NH2} }}} \right)X_{BA}$$
(6)
$$\begin{aligned} \frac{{dS_{NH1} }}{dt} & = \frac{1}{V_1 }[Q_{{\text{in}}} S_{NHin} + Q_a S_{NH2} - (Q_{{\text{in}}} + Q_a )S_{NH1} ] \\ & - i_{Xb} \rho_{11} - i_{Xb} \rho_{21} - \left( {i_{Xb} + \frac{1}{Y_A }} \right)\rho_{31} \\ \end{aligned}$$
(7)
$$\begin{aligned} \frac{{dS_{NH2} }}{dt} & = \frac{1}{V_2 }[(Q_{{\text{in}}} + Q_a )S_{NH1} - (Q_{in} + Q_a )S_{NH2} ] \\ & - i_{Xb} \rho_{12} - \left( {i_{Xb} + \frac{1}{Y_A }} \right)\rho_{32} \\ \end{aligned}$$
(8)
$$\begin{aligned} \frac{{dS_{NO1} }}{dt} & = \frac{1}{V_1 }[Q_a S_{NO2} - (Q_{{\text{in}}} + Q_a )S_{NO1} ] \\ & - \left( {\frac{1 - Y_H }{{2.86Y_H }}} \right)\rho_{21} + \frac{1}{Y_A }\rho_{31} \\ \end{aligned}$$
(9)
$$\begin{aligned} \frac{{dS_{NO2} }}{dt} & = \frac{1}{V_2 }[(Q_{{\text{in}}} + Q_a )S_{NO1} - (Q_{{\text{in}}} + Q_a )S_{NO2} ] \\ & - \left( {\frac{1 - Y_H }{{2.86Y_H }}} \right)\rho_{22} + \frac{1}{Y_A }\rho_{32} \\ \end{aligned}$$
(10)
$$\begin{aligned} \frac{{dS_{ss1} }}{dt} & = \frac{1}{V_1 }[Q_{{\text{in}}} S_{s\sin } + Q_a S_{ss2} - (Q_{in} + Q_a )S_{ss1} ] \\ & - \left( {\frac{1}{Y_H }} \right)\rho_{11} - \left( {\frac{1}{Y_H }} \right)\rho_{21} \\ \end{aligned}$$
(11)
$$\begin{aligned} \frac{{dS_{ss2} }}{dt} & = \frac{1}{V_2 }[(Q_{{\text{in}}} + Q_a )S_{ss1} - (Q_{in} + Q_a )S_{ss2} ] \\ & - \left( {\frac{1}{Y_H }} \right)\rho_{12} - \left( {\frac{1}{Y_H }} \right)\rho_{22} \\ \end{aligned}$$
(12)
$$\begin{aligned} \frac{{dS_{O1} }}{dt} & = \frac{1}{V_1 }[Q_a S_{O2} - (Q_{{\text{in}}} + Q_a )S_{O1} ] \\ & - \left( {\frac{1 - Y_H }{{Y_H }}} \right)\rho_{11} + \left( {\frac{4.57}{{Y_A }} + 1} \right)\rho_{31} \\ \end{aligned}$$
(13)
$$\begin{aligned} \frac{{dS_{O2} }}{dt} & = \frac{1}{V_2 }\left[ {(Q_{{\text{in}}} + Q_a )S_{O1} - (Q_{{\text{in}}} + Q_a )S_{O2} } \right] - \left( {\frac{1 - Y_H }{{Y_H }}} \right)\rho_{12} \\ & + \left( {\frac{4.57 - Y_A }{{Y_A }}} \right)\rho_{32} + KLa(S_{O,{\text{sat}}} - S_{O2} ) \\ \end{aligned}$$
(14)
Table 1 Parameter values
Full size table
Table 2 Process values that are treated as constant
Full size table
Table 3 Time dependent variables
Full size table

Optimal Control

In the multiobjective nonlinear optimal control (MOOC) strategy (Flores Tlacuahuaz et al. 2012; Sridhar 2019) used in this work the single objective optimal control problem is first solved for each of the objective functions. For a multiobjective optimal control problem

$$\begin{gathered} \min \Phi (x,u) = (\phi_{1} ,\;\phi_{2} ,\phi_{3} ,\phi_{4} ,\;\phi_{5} ....\phi_{n} ) \hfill \\ {\text{subject}}\;{\text{to}}\;\;\frac{dx}{{dt}} = {\rm K}(x,u) \hfill \\ h(x,u) \le 0 \hfill \\ x^{L} \le x \le x^{U} \hfill \\ u^{L} \le u \le u^{U} , \hfill \\ \end{gathered}$$
(15)

the single objective optimization problems are solved independently minimizing each \(\phi_{i}\) (i = 1, 2, 3…n) individually. This will lead to minimized values.

\(\phi_{i}^{*}\)(i = 1, 2, 3,..n). Then the problem that will be solved is

$$\begin{gathered} \min \;\sqrt {\left\{ \sum\limits_{i = 1}^{n} {(\phi_{i} } - \phi_{i}^{*} )^{2} \right\} } \hfill \\ {\text{subject}}\;{\text{to}}\;\;\frac{dx}{{dt}} = {\rm K}(x,u) \hfill \\ h(x,u) \le 0 \hfill \\ x^{L} \le x \le x^{U} \hfill \\ u^{L} \le u \le u^{U} \hfill \\ \end{gathered}$$
(16)

The optimization program, Pyomo (Hart et al. 2017), where the differential equations are automatically converted to a Nonlinear Program (NLP) using the orthogonal collocation method (Biegler 2007) is used for performing the dynamic optimization calculations. The Lagrange-Radau quadrature with three collocation points and ten finite elements are chosen. The resulting nonlinear optimization problem was solved using the solver BARON 19.3 (Tawarmalani and Sahinidis 2005), accessed through the Pyomo-GAMS27.2 (Bussieck and Meeraus 2004) interface. BARON implements a Branch-and-reduce strategy and provides a guaranteed global optimal solution. This procedure does not involve the use of weighting functions nor does it impose additional parameters or additional constraints on the problem unlike the weighted function or the epsilon correction method. (Miettinen 1999).

Results and Discussion

Three single objective and one multiobjective optimal control problems were solved. First, the biodegradable substrate was minimized (objective value = 1.4958E-5), subject to Eqs. 1 to 14 The second optimal control problem involves the minimization of ammonium concentration in the effluent (objective value = 13.1765), while the third optimal control problem deals with the minimization of the nitrite and nitrate compounds (objective value = 23.3579). In the multiobjective optimal control problem the function minimized is \(\sqrt {(\sum {S_{S2} - } 1.4958E - 5)^{2} + (\sum {S_{NH2} - } 13.1765)^{2} + (\sum {S_{NO2} - } 23.3579)^{2} }\). The multiobjective optimal control objective function value obtained is 0.5927. Table 4 shows the values of the objective functions.

Table 4 Values of Objective functions
Full size table

Figure 1a–f shows the concentration profiles when the concentration of the biodegradable substance was minimized Fig. 2a–f shows the profiles when the concentration of the ammonium compounds was minimized while Fig. 3a–f is obtained when the nitrite/nitrate compositions are minimized. Figure 4a–f shows the profiles when the multiobjective optimal control was performed. Figure 5a shows the Pareto curve that gives the variation of \(S_{S2}\) with \(S_{O2}\).

Fig. 1
figure 1

a Minimizing Ss2 (Ss1 vs t), b Minimizing Ss2(Ss2 vs t), c Minimizing Ss2 (Snh1 vs t), d Minimizing Ss2(Snh2 vs t), e Minimizing Ss2(Sno1 vs t), f Minimizing Ss2(Sno2 vs t), g Minimizing Ss2(So1 vs t), h Minimizing Ss2(So2 vs t)

Full size image
Fig. 2
figure 2

a Minimizing Snh2(Ss1 vs t), b Minimizing Snh2(Ss2 vs t), c Minimizing Snh2(Snh1 vs t), d Minimizing Snh2(Snh2 vs t), e Minimizing Snh2(Sno1 vs t), f Minimizing Snh2(Sno2vs t), g Minimizing Snh2(So1 vs t), h Minimizing Snh2(So2 vs t)

Full size image
Fig. 3
figure 3

a Minimizing Sno2(Ss1 vs t), b Minimizing Sno2(Ss2 vs t), c Minimizing Sno2(Snh1 vs t), d Minimizing Sno2(Snh2 vs t), e Minimizing Sno2(Sno1 vs t), f Minimizing Sno2(Sno2 vs t), g Minimizing Sno2(So1 vs t), h Minimizing Sno2(So2 vs t)

Full size image
Fig. 4
figure 4

a Multiobjective Optimal Control(Ss1 vs t), b Multiobjective Optimal Control(Ss2 vs t), c Multiobjective Optimal Control(Snh1 vs t), d-a Multiobjective Optimal Control(Snh2 vs t, t = 5), d-b Multiobjective Optimal Control (Snh2 vs t) with total time increase, e Multiobjective Optimal Control(Sno1 vs t), f Multiobjective Optimal Control(Sno2 vs t), g Multiobjective Optimal Control(So1 vs t), h Multiobjective Optimal Control(So2 vs t)

Full size image
Fig. 5
figure 5

Pareto Curve generated by multiobjective optimal control (Snh2 vs So1)

Full size image

Two following important issues can be observed from these results:

  1. 1.

    The multiobjective optimal control yields qualitatively similar results in the cases of \(S_{s2}\) (Figs. 1b and 4b) and \(S_{NO2}\) (Figs. 3f and 4f) while in the case of \(S_{NH2}\) (Figs. 2d and 4d–a) the multiobjective optimal control profile seems to be qualitatively different from the single optimal control where only \(S_{NH2}\) was minimized. However, this could be remedied by increasing the total operation time from 5 to 8 h when the multiobjective optimal control was performed (Figs. 2d and 4d–b). This demonstrates that increasing the time will cause the multiobjective optimal control to be as effective as the single objective optimal control while controlling all the variables.

  2. 2.

    The Pareto curve 5a shows a spike. This indicates that the wastewater treatment problem is highly nonlinear and local optimal strategies may not be as effective as global optimization strategies in obtaining the most beneficial solution.

The objective of this work was to minimize Nitrite/Nitrate, ammonium, and biodegradable organic contaminants. It was seen that in the case of the Nitrite/Nitrate and the biodegradable contaminants the multiobjective and single objective profiles were qualitatively similar, but this was not true in the case of the ammonium compounds. However, increasing the time of the operation for the multiobjective optimal control caused the profiles for the ammonium contaminant to be qualitatively similar. This implies that by increasing the time of the operation the multiobjective optimal control could be made as effective as the single objective optimal control operation with the added advantage of being able to control all the variables. This is very beneficial to industry workers who can effectively purify the wastewater as much as possible before it is discharged into the environment.

Conclusions

Single and multiobjective optimal control using BARON which is a state of the art global optimization solver of the Wastewater treatment process is performed. The main aim of this optimal control was to minimize the Nitrite/Nitrate, ammonium and biodegradable organic contaminants. It is shown that by increasing the time of the operation the multiobjective optimal control could be made as effective as the single objective optimal control operation with the added advantage of being able to control all the variables. This provides an effective strategy for industries to obtain a more beneficial and to minimize the contaminants and ensure that the wastewater discharged into the surroundings is not harmful to the environment.