Probing nucleon effective mass splitting with light particle emission

Abstract

The main objective of this study was to investigate the impact of effective mass splitting on heavy-ion-collision observables. We first analyzed correlations between different nuclear matter parameters obtained from 119 effective Skyrme interaction sets. The values of the correlation coefficients illustrate that the magnitude of effective mass splitting is crucial for tight constraints on the symmetry energy via heavy-ion collisions. The $^{86}$Kr + $^{208}$Pb system at beam energies ranging from 25 to 200A MeV was simulated within the framework of the improved quantum molecular dynamics model (ImQMD-Sky). Our calculations show that the slopes of the spectra of $\ln$[Y(n)/Y(p)] and $\ln$[Y(t)/Y($^3$He)], which are the logarithms of the neutron to proton and triton to helium-3 yield ratios, are directly related to effective mass splitting and can be used to probe the effective mass splitting.

1 Introduction

The nucleon effective mass $m_\text {N}^*$ is used to describe the motion of nucleons in a momentum-dependent potential, which is equivalent to the motion of a quasi-nucleon of mass $m_\text {N}^*$ in a momentum-independent potential [1,2,3,4]. Isospin splitting of the nucleon effective mass indicates that the neutron effective mass is not equal to the proton effective mass, that is, $m_\text {n}^*\ne m_\text {p}^*$, in isospin asymmetric nuclear matter. Both the effective mass and effective mass splitting are important quantities in the isospin asymmetric nuclear equation of state and serve as important microscopic inputs for the study of the thermal properties of protoneutron stars, such as thermal conductivity [5, 6], specific heat [7], and neutrino reaction rates [8,9,10,11,12]. Furthermore, effective mass splitting is important for improving symmetry energy constraints [13].

Much effort has been made to constrain effective mass splitting using heavy-ion collisions (HICs) [13,14,15,16,17,18], nucleon–nucleus optical potentials [19,20,21], and giant monopole resonance [22,23,24,25]. An interesting finding is that the effective mass splitting obtained using the nucleon–nucleus optical potential analysis favors $m_\text {n}^*>m_\text {p}^*$ [19], whereas the HIC data support $m_\text {n}^*<m_\text {p}^*$ [13,14,15, 17, 26]. A possible reason for this discrepancy is that the different probes reflect values of the effective mass splitting at different densities and momentum regions. Further understanding of the constraints of effective mass splitting by HICs requires new probes for neutron-rich HICs and comparison with experimental observables in the future.

Currently, the new generation rare isotope facilities or planned facilities, such as the Heavy Ion Research Facility in Lanzhou (HIRFL/Lanzhou) [27], Facility for Rare Isotope Beams at Michigan State University (FRIB/MSU) [28], Radioactive Isotope Beam Factory (RIBF/RIKEN) [29], Rare isotope Accelerator complex for ON-line experiment (RAON/Korea) [30], and Beijing Isotope Separation On-line (BISOL/Beijing) [31], can produce rare isotope beams from tens to hundreds MeV per nucleon for studying the dynamical evolution of neutron-rich nuclear systems. Some important neutron-rich HIC experiments [32,33,34,35,36] have been performed to extract information on the density dependence of symmetry energy and effective mass splitting by comparing the data with transport model simulations [34, 37].

Recently, an experiment on the $^{86}$Kr + $^{208}$Pb system was performed using the Compact Spectrometer for Heavy IoN Experiment (CSHINE) [38,39,40,41], which was installed at the final focal plane of the Radioactive Ion Beam Line in Lanzhou (RIBLL-I/HIRFL) [42, 43]. Both yield and kinetic variables of the $A = 3$ isobars, that is, t and $^3$He, were measured. This provides an opportunity to constrain the symmetry energy [44] at subsaturation densities and further verify the capability of the transport models. In addition, constraining effective mass splitting using the facilities in Lanzhou requires calculations to extend the beam energy of $\sim$100A–200A MeV, as this energy region has been found to be the optimal beam energy in previous calculations [13, 45].

In this study, we first analyze the correlations between different nuclear matter parameters to illustrate the significance of the investigation of effective mass splitting. We then investigate the impacts of effective mass splitting on the HIC observables, such as neutron to proton yield ratios, triton to helium-3 yield ratios, of the $^{86}$Kr + $^{208}$Pb system at beam energies ranging from 25A to 200A MeV using ImQMD-Sky model.

2 Theoretical model

In the ImQMD-Sky model, each nucleon is represented by a Gaussian wave packet given by

$$\begin{aligned} \phi _{k_{i0}}({\varvec{r}}_i)=\frac{1}{(2\pi \sigma _r^2)^{3/4}} \exp \left[ -\frac{({\varvec{r}}_i-{\varvec{r}}_{i0})^2}{4\sigma _r^2}+\textrm{i}({\varvec{r}}_i-{\varvec{r}}_{i0})\cdot {\varvec{k}}_{i0}\right] , \end{aligned}$$

(1)

where $\sigma _r$ and ${\varvec{r}}_{i0}$ denote the width and centroid of the wave packet, respectively; ${\varvec{k}}_{i0}$ is the momentum of the nucleon; and the subscript $k_{i0}$ corresponds to the state of the ith nucleon. For an N-body system, the system wavefunction is assumed to be a direct product of N coherent states:

$$\begin{aligned} \Psi ({\varvec{r}}_1, \ldots ,{\varvec{r}}_N)=\phi _{k_1}({\varvec{r}}_1)\phi _{k_2}({\varvec{r}}_2) \ldots \phi _{k_N}({\varvec{r}}_N). \end{aligned}$$

(2)

By using the Wigner transformation, the phase-space density distribution of the system can be obtained as

$$\begin{aligned} \begin{aligned} f_N&({\varvec{r}}_1, \ldots ,{\varvec{r}}_N; {\varvec{p}}_1, \ldots ,{\varvec{p}}_N) \\&= \Pi _{i} \frac{1}{(\pi \hbar )^{3}}\exp \left[ -\frac{({\varvec{r}}_i-{\varvec{r}}_{i0})^2}{2\sigma _r^2}-\frac{({\varvec{p}}_i-{{\varvec{p}}_{i0}})^2}{2\sigma _p^2}\right] ,\end{aligned} \end{aligned}$$

(3)

where $\sigma _r\sigma _p=\hbar /2$ and ${\varvec{r}}_i$ and ${\varvec{p}}_i$ denote the position and momentum of the ith nucleon, respectively. The Hamiltonian of the nucleonic part is calculated as follows:

$$\begin{aligned} \begin{aligned} H&= \langle \Psi |{\hat{T}}+{\hat{U}}|\Psi \rangle \\&\equiv \sum _{i}\int \frac{\hat{{\varvec{p}}}_i^2}{2m}f_i({\varvec{r}},{\varvec{p}})\text {d}^3r\text {d}^3p \\&\quad + \sum _{i< j}\int {\hat{v}}^{ij}_{sky} f_i({\varvec{r}},{\varvec{p}})f_j({\varvec{r}}',{\varvec{p}}')\text {d}^3 r\text {d}^3p\text {d}^3 r'\text {d}^3p'\\&= \sum _{i}\left( \frac{p_{i0}^2}{2m}+C(\sigma _r)\right) +\int u_\text {sky} \text {d}^3 r. \end{aligned} \end{aligned}$$

(4)

Where $C(\sigma _r)=\frac{1}{2m}\frac{3\hbar ^2}{4\sigma _r^2}$ denotes the contribution of the wave packet width to the kinetic energy term and $u_\text {sky}$ is the potential energy density in coordinate space.

For the nucleonic potential, the Skyrme-type nucleonic potential energy density without the spin-orbit term is used:

$$\begin{aligned} u_{\text {sky}}=u_{\text {loc}}+u_{\text {md}}. \end{aligned}$$

(5)

The local potential energy density is

$$\begin{aligned} \begin{aligned} u_\text {loc}&= \frac{\alpha }{2}\frac{\rho ^2}{\rho _0} +\frac{\beta }{\eta +1}\frac{\rho ^{\eta +1}}{\rho _0^\eta }+\frac{g_\text {sur}}{2\rho _0 }(\nabla \rho )^2 \\&\quad +\frac{g_\text {sur,iso}}{\rho _0}[\nabla (\rho _\text {n}-\rho _\text {p})]^2 \\&\quad +A_{\text {sym}}\frac{\rho ^2}{\rho _0}\delta ^2+B_{\text {sym}}\frac{\rho ^{\eta +1}}{\rho _0^\eta }\delta ^2, \end{aligned} \end{aligned}$$

(6)

where $\rho =\rho _\text {n}+\rho _\text {p}$ is the nucleon density, $\delta =(\rho _\text {n}-\rho _\text {p})/\rho$ is the isospin asymmetry, $\alpha$ is a parameter related to the two-body term, $\beta$ and $\eta$ are related to the three-body term, $g_\text {sur}$ and $g_\text {sur,iso}$ are related to the surface terms, and $A_\text {sym}$ and $B_\text {sym}$ are the coefficients of the symmetry potential that originate from the two- and three-body interaction terms [46]. Their values can be obtained from the standard Skyrme interactions.

The nonlocal potential energy density or momentum-dependent interaction term, that is, $u_\text {md}$, is also considered as a Skyrme-type momentum-dependent energy density functional. It is obtained based on its interaction form $\delta ({\varvec{r}}_1-{\varvec{r}}_2 ) ({\varvec{p}}_1-{\varvec{p}}_2 )^2$ [47], that is,

$$\begin{aligned} \begin{aligned} u_\text {md}&= C_0\sum _{ij}\int \text {d}^3p\text {d}^3p' f_i({\varvec{r}},{\varvec{p}})f_j({\varvec{r}},{\varvec{p}}')({\varvec{p}}-{\varvec{p}}')^2 \\&\quad + D_0\sum _{ij\in n}\int \text {d}^3 p \text {d}^3 p'f_i({\varvec{r}},{\varvec{p}}) f_j({\varvec{r}},{\varvec{p}}')({\varvec{p}}-{\varvec{p}}')^2 \\&\quad + D_0\sum _{ij\in p}\int \text {d}^3p \text {d}^3p' f_i({\varvec{r}},{\varvec{p}})f_j({\varvec{r}},{\varvec{p}}')({\varvec{p}}-{\varvec{p}}')^2, \end{aligned} \end{aligned}$$

(7)

where $C_0$ and $D_0$ are parameters related to momentum-dependent interactions. These are related to the standard Skyrme interaction as follows:

$$\begin{aligned} \begin{aligned} C_0&= \frac{1}{16\hbar ^2}\left[ t_1(2+x_1)+t_2(2+x_2) \right] \\ D_0&= \frac{1}{16\hbar ^2}\left[ t_2(2x_2+1)-t_1(2x_1+1) \right] . \end{aligned} \end{aligned}$$

(8)

Further details can be found in Ref. [48]. The parameters in Eqs. (6) and (7) are obtained from the standard Skyrme interaction parameters as in Refs. [49, 50]. The Coulomb term was treated using the standard method in quantum molecular dynamics type models.

Initialization was performed in the same manner as in Ref. [46]. The centroids of the wave packets for neutrons and protons were sampled within the empirical radii of neutrons and protons [46]. After the positions of all nucleons are finally prepared, the density distribution is known. The momenta of nucleons were sampled using a local density approach.

It should be noted that the effects of the width of the wave packet on the momentum sampling in the initialization are considered in this work. Usually, $C(\sigma _r)$ is omitted in the quantum molecular dynamics type models for the study of intermediate-high energy HICs because it has no effect on the equation of motion, and its correction to the initial momentum is relatively small. However, this effect cannot be neglected, particularly when studying low-energy reactions. This is because $C(\sigma _r)$ in the kinetic energy term reaches $\sim$25% of the Fermi energy at a normal density, $\sim$35 MeV. For example, $C(\sigma _r)$ is 8.97 MeV when the width of the wave packet takes a typical value, that is, $\sigma _r$ = 1.32 fm. For the expected momentum values of the nucleons sampled in the calculations, the width of the wave packet has no direct effect because $\langle \phi _i|{\varvec{p}}|\phi _i\rangle ={\varvec{p}}_{i0}$. To satisfy the requirements for reasonably describing the binding energy of the initial nuclei with Gaussian wave packets [51,52,53], the sampled ${\varvec{p}}_{i0}$ should be reduced to a smaller value than that obtained without considering the width of the wave packet.

3 Results and discussion

To understand the importance of effective mass splitting on symmetry energy constraints, we first analyzed the correlations between different nuclear matter parameters. Subsequently, the influence of effective mass splitting on the HIC observables is presented and discussed.

3.1 Nuclear matter parameters and their correlations

For the Skyrme effective interaction used in this work, the corresponding isospin asymmetric equation of state for cold nuclear matter is

$$\begin{aligned} \begin{aligned} E/A&= \frac{3\hbar ^2}{10m}\left( \frac{3\pi ^2}{2}\rho \right) ^{2/3} \\&\quad +\frac{\alpha }{2}\frac{\rho }{\rho _{0}}+\frac{\beta }{\eta +1}\frac{\rho ^{\eta }}{\rho ^{\eta }_{0}}+g_{\rho \tau }\frac{\rho ^{5/3}}{\rho _{0}^{5/3}} + S(\rho )\delta ^2, \end{aligned} \end{aligned}$$

(9)

where the density dependence of the symmetry energy $S(\rho )$ is

$$\begin{aligned} \begin{aligned} S(\rho )&= \frac{\hbar ^2}{6m}\left( \frac{3\pi ^2\rho }{2}\right) ^{2/3}+A_{\text {sym}}\frac{\rho }{\rho _{0}} \\&\quad + B_{\text {sym}}\left( \frac{\rho }{\rho _{0}}\right) ^{\eta }+C_{\text {sym}}(m_s^*,m_v^*)\left( \frac{\rho }{\rho _{0}}\right) ^{5/3}. \end{aligned} \end{aligned}$$

(10)

The terms $g_{\rho \tau }$ in Eqs.  (9) and $C_\text {sym}$ in Eq. (10) originate from the energy density functional of the Skyrme-type momentum-dependent interaction, and its relationship to the standard Skyrme interaction can be found in Ref. [54]. The pressure in the nuclear fluid is calculated as follows:

$$\begin{aligned} P=\rho ^2\frac{\partial E/A(\rho ,\delta )}{\partial \rho }. \end{aligned}$$

(11)

The saturation density $\rho _0$ for symmetric nuclear matter is obtained using

$$\begin{aligned} P=\rho _0^2\left( \frac{\textrm{d}}{\textrm{d}\rho }\frac{E}{A}(\rho ,\delta =0)\right) |_{\rho =\rho _0}=0. \end{aligned}$$

(12)

Correspondingly, the nuclear matter parameters at the saturation density were obtained. For example, the binding energy $E_0$ and the incompressibility $K_0$ are

$$\begin{aligned} E_0= & {} E/A(\rho _0), \end{aligned}$$

(13)

$$\begin{aligned} K_0= & {} 9\rho _0^2\frac{\partial ^2 E/A}{\partial \rho ^2}|_{\rho _0}. \end{aligned}$$

(14)

The symmetry energy coefficient $S_0$ and slope of the symmetry energy L are

$$\begin{aligned} S_0= & {} S(\rho _0),\end{aligned}$$

(15)

$$\begin{aligned} L= & {} 3\rho _0\frac{\partial S(\rho )}{\partial \rho }|_{\rho _0}. \end{aligned}$$

(16)

The effective mass of neutron and proton is obtained from the neutron and proton potentials, respectively, as follows:

$$\begin{aligned} \frac{m}{m_q^*} = 1+\frac{m}{p}\frac{\partial V_q}{\partial p}, \quad q={\text { n,p}}, \end{aligned}$$

(17)

where $V_q$ is the single-particle potential for a neutron or proton and the form of $V_q$ can be found in Appendix A. For the Skyrme interaction, the neutron and proton effective masses are

$$\begin{aligned} \frac{m}{m_q^*}=1+4mC_0\rho +4mD_0\rho _q. \end{aligned}$$

(18)

The isoscalar effective mass $m_s^*$ can be obtained at $\rho _q=\rho /2$ from Eq. (18), and the isovector effective mass $m_v^*$ can be obtained at $\rho _q=0$, which represents the neutron (proton) effective mass in pure proton (neutron) matter, as in Refs. [22, 55]. They are

$$\begin{aligned} \frac{m}{m_s^*}= & {} 1+4m\left( C_0+\frac{D_0}{2}\right) \rho ,\end{aligned}$$

(19)

$$\begin{aligned} \frac{m}{m_v^*}= & {} 1+4mC_0\rho . \end{aligned}$$

(20)

By using $m_s^*$ and $m_v^*$, the effective mass splitting $\Delta m_\text {np}^*=(m_\text {n}^*-m_\text {p}^*)/m$ can be expressed as

$$\begin{aligned} \Delta m_\text {np}^*=\frac{m_\text {n}^*-m_\text {p}^*}{m}=2\frac{m_s^*}{m}\sum _{n=1}^\infty \left( \frac{m_s^*-m_v^*}{m_v^*}\right) ^{2n-1}\delta ^{2n-1}, \end{aligned}$$

(21)

as in Ref. [22]. As described in Eq. (21), the exact value of $\Delta m_\text {np}^*=(m_\text {n}^*-m_\text {p}^*)/m$ depends on the expansion and the isospin asymmetry of the system, $\delta$. To avoid dependence on the expansion and $\delta$, we define the quantity

$$\begin{aligned} f_I=\frac{1}{2\delta } \left( \frac{m}{m_\text {n}^*}-\frac{m}{m_\text {p}^*} \right) = \frac{m}{m_s^*}-\frac{m}{m_v^*} \end{aligned}$$

(22)

to describe the isospin effective mass splitting, which has the opposite sign to $\Delta m_\text {np}^*$.

Because the aforementioned nuclear matter parameters are obtained from the same energy density functional, one can expect correlations between them. For example, as expressed in Eq. (10), $S(\rho )$ depends on the two-body, three-body, and momentum-dependent interaction terms. These three terms are correlated with $E_0$, $K_0$, and $m_s^*$ [55] and $S_0$, L, and $m_v^*$ [50]. The correlation strength depends on the effective set of Skyrme interaction parameters used [55].

To describe the correlation between different nuclear matter parameters with less bias, one can calculate the linear correlation coefficient $C_{AB}$ between the nuclear matter parameters A and B from the published parameter sets, which satisfy the current knowledge of the nuclear matter parameters [50]:

$$\begin{aligned} \begin{aligned} 200 \text { MeV} \leqslant K_0&\leqslant 280 \text { MeV}, \\ 25 \text { MeV} \leqslant S_0&\leqslant 35 \text { MeV}, \\ 30 \text { MeV} \leqslant L&\leqslant 120 \text { MeV}, \\ 0.6 \leqslant m_s^*/&m \leqslant 1.0, \\ -0.5 \leqslant f_I&\leqslant 0.4. \end{aligned} \end{aligned}$$

(23)

The quantities A or B = $\{\rho _0, E_0, K_0, S_0, L, m_s^*, m_v^*\}$ and the correlation coefficient $C_{AB}$ are calculated as follows:

$$\begin{aligned} \begin{aligned} C_{AB}&= \frac{ \text {cov} ( A, B ) }{ \sigma ( A ) \sigma ( B ) }, \\ \text {cov} ( A, B )&= \frac{1}{N-1} \sum _i ( A_i - \langle A \rangle ) ( B_i - \langle B \rangle ), \\ \sigma ( X )&= \sqrt{ \frac{1}{N-1} \sum _i ( X_i - \langle X \rangle )^2 }, \quad X = A, B \\ \langle X \rangle&= \frac{1}{N} \sum _i X_i, \quad i = 1,\dots , N, \end{aligned} \end{aligned}$$

(24)

where $\text {cov} ( A, B )$ is the covariance between A and B, $\sigma (X)$ is the standard deviation of X, and $\langle X \rangle$ denotes the average values obtained from $N=119$ standard Skyrme parameter sets, selected according to the criteria in Eq. (23).

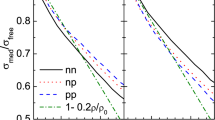
The values of these parameters are listed in Table 1, and the correlation coefficients $C_{AB}$ are shown in Fig. 1. A positive value of $C_{AB}$ reflects a positive linear correlation, whereas a negative value indicates a negative linear correlation. Correlations exist between the different nuclear matter parameters. Specifically, the correlations between $S_0 \text { and } \rho _0$, $L \text { and } S_0$, $m_v^* \text { and } m_s^*$, $K_0 \text { and } \rho _0$, and $S_0 \text { and } E_0$ are stronger than those of the other nuclear matter parameter pairs. The ‘strange’ correlation between $\rho _0$ and $S_0$ can be understood as follows: $\rho _0$ can be determined using Eq. (12), which is related to the parameters $\alpha$, $\beta$, $\eta$, and $g_{\rho \tau }$, or to the nuclear matter parameters, as presented in Eq. (5) of Ref. [50]. These correlations indicate that obtaining tight constraints on the density dependence of the symmetry energy using HICs requires knowing information not only on $S_0$ and L but also on $m_s^*$ and $m_v^*$ (or the effective mass splitting).

Fig. 1

(Color online) Correlation coefficients between the different nuclear matter parameter pairs

Table 1 Nuclear matter parameters calculated from 119 Skyrme interaction sets

3.2 Symmetry potential

Based on Eq. (17), effective mass splitting is related to the symmetry potential, which plays an important role in HICs. The symmetry potential $V_\text {sym}$ is also called the Lane potential, which equals the difference between the neutron and proton potentials:

$$\begin{aligned} \begin{aligned} V_\text {Lane} (\rho ,p)&= \frac{ V_{\text {n}} - V_{\text {p} }}{ 2 \delta } \\&= 2 A_{\text {sym}} \frac{\rho }{ \rho _0 } + 2 B_{\text {sym}} \left(\frac{\rho }{\rho _0}\right)^\eta \\&\quad + \hbar ^2 D_0\left(\frac{3\pi ^2}{2}\rho \right)^{2/3}\rho + D_0 \rho p^2\\&= V_\textrm{sym}^\textrm{loc}+2 D_0 m \rho E_k, \end{aligned} \end{aligned}$$

(25)

where $V_\textrm{sym}^\textrm{loc}=2 A_{\text {sym}} \frac{\rho }{\rho _0 } + 2 B_{\text {sym}} (\frac{\rho }{\rho _0})^\eta + \hbar ^2 D_0(\frac{3\pi ^2}{2}\rho )^{2/3}\rho$ and $E_k=p^2/2\,m$.

To quantitatively understand the momentum and density dependence of $V_\text {Lane}$ on HIC observables, we investigate $V_\text {Lane}(\rho ,p)$ for two typical Skyrme interaction parameter sets: SkM* and SLy4. These two Skyrme interaction parameter sets were selected for the following reasons: first, the incompressibility ($K_0$), symmetry energy coefficient ($S_0$), and isoscalar effective mass ($m_s^*$) should be within reasonable and commonly accepted ranges; that is, $K_0=230\pm 20$ MeV, $S_0=32\pm 2$ MeV, and $m^*_s/m=0.7\pm 0.1$. Second, the parameter sets have different signs of effective mass splitting: $\Delta m^*_\text {np}=(m_\text {n}^*-m_\text {p}^*)/m>0$ or $<0$. The SLy4 set [55] has $\Delta m^*_\text {np}<0$ (or $f_I>0$) in neutron-rich matter, and the slope of the symmetry energy L is 46 MeV. The set SkM* has $\Delta m^*_\text {np}>0$ (or $f_I<0$) and $L = 46$ MeV. For convenience, the values of the nuclear matter parameters in SkM* and SLy4 are listed in Table 2.

Table 2 Nuclear matter parameters of SLy4 and SkM*

Fig. 2

(Color online) Lane potential $V_\text {Lane}$ as functions of kinetic energy $E_\text {k}$ at densities of $\rho = 0.3 \rho _0,~0.8 \rho _0 \text {, and } 1.2 \rho _0$

In Fig. 2, we present $V_\text {Lane}$ as a function of kinetic energy for cold nuclear matter with isospin asymmetry $\delta =0.2$ at different densities. $V_\text {Lane}$ increased (decreased) as the kinetic energy increased for $\delta m^*_\text {np}<0$ ($\delta m^*_\text {np}>0$). They influence the neutron to proton yield ratio Y(n)/Y(p) as a function of the kinetic energy in HICs according to the following relationship:

$$\begin{aligned} \begin{aligned} \frac{{Y(\text {n})}}{{Y(\text {p})}}&\propto \exp \left( \frac{ \mu _\text {n} - \mu _\text {p}}{ T }\right) \\&= \exp \left[ \frac{ 2\left( V_\textrm{sym}^\textrm{loc} +2D_0m\rho E_\text {k} \right) \delta }{ T } \right] , \end{aligned} \end{aligned}$$

(26)

where T is the temperature of the emitting source and $\mu _\text {n}$ and $\mu _\text {p}$ are the chemical potentials of neutrons and protons, respectively. The above relationship can be obtained using statistical and dynamic models [56,57,58,59,60,61]. Therefore, one can expect that the larger the Lane potential, the larger the neutron to proton yield ratios. Similar effects on the triton to $^3$He yield ratios are also expected [62]:

$$\begin{aligned} \begin{aligned} \frac{\text {Y(t)}}{ \text {Y}(^3\text {He}) }&\propto \exp \left( \frac{ \mu _{\text {t}} - \mu _{ ^3\text {He} } }{ T }\right) \approx \exp \left( \frac{ \mu _\text {n} - \mu _\text {p}}{ T }\right) \\&= \exp \left[ \frac{ 2 \left( V_{\text {sym}}^{\text {loc}}+2D_0m\rho E_k \right) \delta }{ T } \right] . \end{aligned} \end{aligned}$$

(27)

In addition, one can expect that the slopes of the Y(n)/Y(p) ratios with respect to $E_k$ will differ from the effective mass splitting according to Eq. (26) and a similar behavior is also expected for Y(t)/Y($^3$He).

3.3 Y(n)/Y(p) and Y(t)/Y($^3$He)

To observe the effects of effective mass splitting on HIC observables such as Y(n)/Y(p) and Y(t)/Y($^3$He), we performed a simulation of the $^{86}$Kr + $^{208}$Pb system at beam energies from $E_{\text {beam}} = 25A$ to 200A MeV. In the calculations, the impact parameter $b = 1$ fm and the number of events were 100,000. The dynamic evolution time is stopped at 400 fm/c.

Fig. 3

(Color online) Yield ratios of Y(n)/Y(p) and Y(t)/Y($^3$He) as functions of the normalized nucleon center-of-mass energy $E_\text {k}/E_\text {beam}$ at beam energies of $E_{\text {beam}}$ = 25A, 100A, and 200A MeV

The left panels of Fig. 3 show the Y(n)/Y(p) ratios as functions of the normalized nucleon center-of-mass energy $E_\text {k}/E_\text {beam}$. The errors of Y(n)/Y(p) are statistical uncertainties obtained using the error propagation formula from the errors of Y(n) and Y(p). By using $E_\text {k}/E_\text {beam}$, the shapes of Y(n)/Y(p) as a function of the kinetic energy can be compared and understood on a similar scale for different beam energies. The red lines correspond to the results obtained with SLy4 ($m_\text {n}^*<m_\text {p}^*$) and the blue lines correspond to SkM* ($m_\text {n}^*>m_\text {p}^*$). Our calculations show that the Y(n)/Y(p) ratios obtained with both SLy4 and SkM* decrease as the nucleon kinetic energy increases, owing to Coulomb effects. Furthermore, the Y(n)/Y(p) ratios obtained using SLy4 ($m_\text {n}^*<m_\text {p}^*$) are larger than those obtained using SkM* ($m_\text {n}^*>m_\text {p}^*$). At a beam energy of 200A MeV, a flatter Y(n)/Y(p) dependence on the nucleon kinetic energy was observed for SLy4. This is because SLy4 has stronger Lane potentials at high kinetic energies and enhanced neutron emission at high nucleon energies.

Specifically, the difference in Y(n)/Y(p) between SLy4 ($m_\text {n}^*<m_\text {p}^*$) and SkM*($m_\text {n}^*>m_\text {p}^*$) maintains a constant value with the nucleon kinetic energy at 25A MeV and increases with the nucleon kinetic energy at a beam energy of $> 100A$ MeV. This can be understood from the Lane potentials shown in Fig. 2. At 25A MeV, the system is less compressed and excited than that at 100A or 200A MeV, and most of the emitted nucleons originate from the low-density region. The corresponding symmetry potentials for SLy4 and SkM* varied weakly as a function of kinetic energy (see Fig. 2a). Therefore, one can expect that the difference in Y(n)/Y(p) between SLy4 ($m_\text {n}^*<m_\text {p}^*$) and SkM* ($m_\text {n}^*>m_\text {p}^*$) is small and changes weakly as the kinetic energy increases. At a beam energy of $>100A$ MeV, the system can be compressed to higher densities, where the magnitude of the splitting increases with the kinetic energy, as shown in Fig. 2b, c.

The right panels of Fig. 3 show the Y(t)/Y($^3$He) ratios as functions of the normalized nucleon center-of-mass energy, that is, $E_\text {k}/E_\text {beam}$. Similar to Y(n)/Y(p), the Y(t)/Y($^3$He) ratios are also sensitive to effective mass splitting. This can also be explained using Eq. (27). At a beam energy of 200A MeV, the sensitivity of the Y(t)/Y($^3$He) ratios to the kinetic energy becomes weak, which may be due to cluster effects and stronger nonequilibrium effects than those at lower beam energies.

Furthermore, Fig. 3 also shows that the Y(n)/Y(p) ratio decreases exponentially with respect to $E_\text {k}/E_\text {beam}$ in the range $0.3 \leqslant E_\text {k}/E_\text {beam} \leqslant 1.0$. For t/$^3$He ratios, a similar behavior can be observed in $0.2 \leqslant E_\text {k}/E_\text {beam} \leqslant 0.5$ since the kinetic energy per nucleon for the emitted tritons or $^3$He is approximately one-half of the beam energy. According to Eqs. (26) and (27), the exponentially decreasing behavior indicates that the emitted nucleons are in equilibrium in momentum space and can be described by the slopes of $\ln$[Y(n)/Y(p)] or $\ln$[Y(t)/Y($^3$He)], and the slopes of $\ln$[Y(n)/Y(p)] and $\ln$[Y(t)/Y($^3$He)] are directly related to $D_0$ as follows:

$$\begin{aligned} \begin{aligned} S_{\text {n/p}}&= \frac{\partial \ln [{Y(\text {n})/Y(\text {p})} ]}{\partial E_\text {k}}=4D_0 m\delta \rho /T, \\ S_{{\text {t/}^3\text {He}}}&= \frac{\partial \ln [{Y(\text {t})/Y(^3 \text {He)} ]}}{\partial E_\text {k}}=4D_0 m\delta \rho /T. \end{aligned} \end{aligned}$$

(28)

In the following analysis, we perform the linear fit of $\ln [Y(\text {n})/Y(\text {p})]$ and $\ln [Y(\text {t})/Y(^3\text {He})]$:

$$\begin{aligned} \ln \left[ \frac{ {Y(\text {n})} }{ {Y(\text {p})} } \right] = S_{\text {n/p}} \frac{E_\text {k}}{E_\text {beam}} + b_0^\text {n/p} \end{aligned}$$

(29)

in the range of $0.3 \leqslant E_\text {k}/E_\text {beam} \leqslant 1.0$ and

$$\begin{aligned} \ln \left[ \frac{Y(\text {t}) }{Y(^3\text {He}) } \right] = S_{\text {t}/^3 \text {He} } \frac{E_k}{E_\text {beam}} + b_0^\text {t}/^3\text {He} \end{aligned}$$

(30)

in the range of $0.2 \leqslant E_\text {k}/E_\text {beam}\leqslant 0.5$ to obtain the slopes of $S_\text {n/p}$ ($S_{ \text {t}/ ^3 \text {He}}$) and the intercepts of $b_0^\text {n/p}$ ($b^{\text {t}/^3\text {He}}_0$). To describe the goodness of linear fit of $\ln (Y(\text {n})/Y(\text {p}))$ and $\ln (Y(\text {t})/Y(^3\text {He}))$, we present the coefficients of determination, $R^2$ [63] in Table 3.

Table 3 Coefficients of determination, $R^2$, for the linear fit of ln(Y(n)/Y(p)) and ln(Y(t)/Y($^3$He))

Fig. 4

(Color online) $S_X$ and $b_0^{X}$ as functions of $E_\text {beam}$ for SLy4 and SkM*. Upper panels are X = n/p and bottom panels are X = t/$^3$He

Figure 4 presents $S_\text {n/p}$ ($S_{ \text {t/} ^3 \text {He}}$) and $b_0^\text {n/p}$ ($b_0^{t/^3\text {He}}$) as functions of the beam energy to determine the optimal energy for probing effective mass splitting. Panel (a) shows $S_\text {n/p}$ and panel (c) shows $S_{ \text {t/} ^3 \text {He}}$. Our calculations show that the values of $S_\text {n/p}$ ($S_{ \text {t/} ^3 \text {He}}$) obtained with SLy4 are higher than those obtained with SkM* except for the beam energy of 25A MeV. Specifically, the impact of effective mass splitting on $S_\text {n/p}$ becomes evident at a beam energy of 200A MeV. For $S_{ \text {t/} ^3 \text {He}}$, the impact of effective mass splitting is greatest at a beam energy of $\sim 100A$ MeV under the influence of the cluster formation mechanism. For the $b_0^\text {n/p}$, the calculations show that it weakly depends on the effective mass splitting, except for the value of $b_0^\text {n/p}$ at beam energies $E_\text {beam}=200A$ MeV. At this beam energy, the value of $b_0^\text {n/p}$ obtained using SkM* is larger than that obtained using SLy4. For $b_0^{t/^3\text {He}}$, the value obtained using SkM* was lower than that obtained using SLy4 at a beam energy of 25A MeV. At $E_\text {beam}> 100A$ MeV, the values of $b_0^{t/^3\text {He}}$ obtained with SkM* were greater than those obtained with SLy4.

4 Summary and outlook

In summary, we compiled 119 Skyrme interaction sets and their corresponding nuclear matter parameters to understand the correlations between different nuclear matter parameters. By analyzing the linear correlation coefficient, the strength of the correlation between different nuclear matter parameters was quantitatively obtained. Furthermore, the correlations between different nuclear parameters indicates that obtaining tight constraints on the symmetry energy requires knowing not only the values of the symmetry energy coefficient $S_0$ and the slope of the symmetry energy L but the isoscalar effective mass $m_s^*$ and the isovector effective mass $m_v^*$ or the effective mass splitting, given that $K_0$ and $E_0$ are well constrained.

To understand the impact of effective mass splitting on HIC observables, we simulated the $^{86}$Kr + $^{208}$Pb system at beam energies ranging from 25 to 200 MeV per nucleon. Two observables were analyzed: the emitted neutron to proton yield ratio and the triton to $^3$He yield ratio. Our results show that the energy spectra of Y(n)/Y(p) and Y(t)/Y($^3$He) can be used to distinguish the effective mass splitting, which is consistent with previous studies in Refs. [13, 45]. Furthermore, we constructed the characteristic variables, namely the slope and intercept of $\ln$[Y(n)/Y(p)] and $\ln$[Y(t)/Y($^3$He)], respectively, which can be directly related to the effective mass splitting. The greatest effects were observed at 200A MeV for (Y(n)/Y(p)), whereas the greatest effects were observed at 100A MeV for (Y(t)/Y($^3$He)). This difference can be attributed to the cluster formation mechanism.

Appendix 1: Single-particle potential

For the Skyrme interaction, the single-particle potential in uniform nuclear matter can be written as the summation of the local and nonlocal (momentum-dependent) parts as follows:

$$\begin{aligned} V_q=V_q^\textrm{loc}+V_{q}^\textrm{md}. \end{aligned}$$

(A.1)

Based on the definition of the single-particle potential, $V_q$ should be obtained from the derivatives of the net energy E of the system with respect to the number of particles. For the local part, $V_q^\text {loc}$ is

$$\begin{aligned} \begin{aligned} V^\textrm{loc}_q (\rho , \delta )&= \frac{ \partial u_\textrm{loc }( \rho , \delta ) }{ \partial \rho _q } \\&= \alpha \frac{\rho }{ \rho _0 } + \beta \frac{ \rho ^\eta }{ \rho _0^\eta } + (\eta - 1) B_\textrm{sym} \frac{\rho ^\eta }{\rho _0^\eta }\delta ^2\\&\quad \pm 2 \left( A_\textrm{sym} \frac{\rho }{\rho _0}+ B_\textrm{sym} \left( \frac{\rho }{\rho _0} \right) ^{\eta } \right) \delta , \end{aligned} \end{aligned}$$

(A.2)

where ‘$+$’ is for neutrons and ‘−’ for protons. The nonlocal part of the single-particle potential depends not only on the position but also on the momentum, which can be obtained by taking the functional derivative of the energy density with respect to the phase-space distribution function of protons or neutrons $f_q(r,p)$:

$$\begin{aligned} \begin{aligned} V^\textrm{md}_q(\rho ,\delta ,p)&= \frac{\delta u_\textrm{md}}{\delta f_q} \\&= 2(C_0\rho +D_0\rho _q)p^2+ 2\hbar ^2C_0\tau +2\hbar ^2D_0\tau _q, \end{aligned} \end{aligned}$$

(A.3)

where $\tau$ is the kinetic energy density and is the summation of the kinetic energy densities of neutrons and protons (i.e.,$\tau =\tau _\text{n}+\tau _\text{p}$) and $\tau _q=\frac{3}{5}k_{q,F}^2\rho _q$, with $k_{q,F}=(3\pi ^2\rho _q)^{1/3}$.