1 Introduction

Stroke is a major cause of serious disability. The biomechanical function and neurophysiological characteristics of the external hand muscles responsible for individual finger coordination may change, lead to decreased finger independence and changes in muscle interaction (passive coupling between muscle structure and neural control) (Alexanderson and Beskow 2016, Alexanderson et al. 2017). In China, more than 2.5 million people suffer from stroke every year. More than half of them need help to carry out their daily activities due to hand disabilities. Intensive training is desired for hand disability treatment. Most stroke patients will back home after they leave the hospital for long-term rehabilitation training with family members and professional medical staff. Comparing the motion characteristics of the hands at different ages and different states can help us understand the impact of human hands in these situations better and conduct an effective assessment. If patients can use portable equipment at home for recovery assessment, it will greatly reduce the time and energy of patients and therapists, and reduce the cost of rehabilitation (Aristidou 2016).

Common techniques used in hand motion capture include: data glove (Aristidou and Lasenby 2009; Buchholz and Armstrong 1992; Chen et al. 2016), additional force (Cole et al. 2010; da Silva et al. 2011), surface electromyography (SEMG), and image based vision system (Denavit and Hartenberg 1955; Dong et al. 2015; Erol et al. 2007, Fang et al. 2017a). Image-based systems usually use optical motion capture systems or computer image recognition. However, the equipment is large in scale and un-portable. Data gloves based on various sensors are more mature, including commercial products such as cyberGlove and 5DT Data glove. But these devices are usually expensive and costly. In 2011, da Silva et al. (Fang et al. 2017b; da Silva et al. 2011) proposed a wearable induction glove based on fiber Bragg grating (FBG) sensor for monitoring hand posture, but there is a problem in real-time analysis of fiber sensor data, and fibers are easy to worn or damage during large movements. In 2014, Kortier et al. (Aristidou and Lasenby 2009; Kortier et al. 2014) proposed a new 3D measurement system with multiple miniature inertial sensors (PowerGlove) to understand hand function and quantify the symptoms of hand movement in clinical practice.

An equipment for patients at home for recovery assessment should not be costly, besides, its lightness is also an important factor. Too complicated equipment is not easy to carry and not suitable for daily use, too heavy equipment will affect the accurate acquisition of hand movements and may cause secondary damage to the limb in the healing process. The availability of micro electro mechanical system (MEMS) technology enables inertial sensors to be integrated into a single chip. It reduces the volume of the inertial sensor and greatly reduces the power, which can thus be used for dynamic motion analysis (Guanglong and Zhang 2014). Inertial and magnetic measurement unit (IMMU) has proven to be an accurate approach in estimating body segment orientations without external actuators or cameras (Hoyet et al. 2012). It is non-obtrusive, comparably cost-effective and easy to set up. Here, we will use the MPU9250 which deploys System in Package technology and combines 9-axes inertial and magnetic sensors in a very small package. This results in the design and development of low-cost, low-power and light-weight IMMU. This again enables powering of multiple IMMUs by a micro control unit (MCU), which reduces the total weight of the system. Moreover, small IMMU can be fastened to the glove easily, making it much easier to use.

The IMMU based data gloves are composed of micro accelerometers and microgyroscopes, magnetometers and microprocessors to improve the measurement accuracy, basing on it, many data gloves have been developed. However, due to the complexity of hand movement, they arranged each joint with a micro inertial sensor to restore the hand motion (Aristidou and Lasenby 2009; Jarrasse et al. 2013; Van Den Noort et al. 2018; Kortier et al. 2014), as shown in Fig. 1a–c. This method of deploying sensors will not only lead to a huge amount of computation, but also more complex wiring that may affect the normal movement of the hand. In order to make a light and portable data glove for patients using at home, the number of the sensors need to be reduced and the sensor layout strategy must be optimized. In the optical motion capture, in order to restore the physical and hand motion simultaneously, some studies have proposed methods trying to reduce the number of markers (Lambrecht and Kirsch 2014; Latash et al. 2006; Lathuiliere and Herve 2000; Li et al. 2011; Maycock and Botsch 2015; Phillips et al. 2006; Pisharady and Saerbeck 2015; Rijpkema and Girard 1991), which inspired us to propose an optimized sensor layout strategy.

Fig. 1
figure 1

a Aristidou and Lasenby (2009), Jarrasse et al. (2013), b Van Den Noort et al. (2018) and c Kortier et al. (2014) are existing complex sensor layout methods; d Li et al. (2011) the method to reduce the markers in optical motion capture system

Full size image

In this paper, the forward and inverse kinematics models of human hand are constructed, basing on the inverse kinematics, an optimized sensor layout strategy of the IMMU-based data glove is proposed. In order to obtain reliable hand transportation and simplify the device at the same time, the number of sensors is reduced and the data of multiple sensors are fused based on Kalman filtering. This optimized sensor layout strategy that reduces the number of sensors not only reduces the cost of data gloves, but also successfully captures hand movements while reducing the burden of the data glove. In addition, the results of different placement strategies are brought into our hand kinematics model to compare the accuracy of hand movements. The results show that the data glove based on optimized sensor layout strategy is within acceptable range compared with the data glove based on traditional sensor layout strategy. The developed data glove is expected to provide hand capability assessment for stroke patients in residential environment.

2 Methods

2.1 Hand modelling

Hand movement is determined by its anatomical structure. Human hand is composed of bones and soft tissues such as ligaments and muscles. As shown in Fig. 2, the structure of human hand is complex. The wrist is composed of 8 bones arranged in almost 2 rows. The thumb sticks out from the large angle of the wrist, including 1 metacarpal and 2 phalanx; index finger, middle finger, ring finger and little finger each include 1 metacarpal and 3 phalanx (referred to as root bone, interphalangeal bone, finger end bone) (Samadani et al. 2012). The joint is divided into palm joint and finger joint. The joints of the thumb are interphalangeal joint (IP), metacarpophalangeal joint (MCP), and trapeziometacarpal joint (TMC); the remaining four-finger joints include: metacarpophalangeal joint (MCP), proximal interphalangeal joint (PIP), and distal interphalangeal joint (DIP). Some studies indicated that the model of the ring finger and the little finger should add another joint, carpometacarpal joint (CMC) (Schröder et al. 2015). This section describes the finger models and their corresponding forward kinematics and inverse kinematics in the Denavit–Hartenberg (D–H) coordinate system (Schroeder et al. 2014).

Fig. 2
figure 2

Complete human hand joint model. a The model that will be used in this article; b The model which the ring finger and the little finger add carpometacarpal joint (CMC)

Full size image

2.1.1 Forward kinematics

The forward kinematic solution of each finger will be assigned using homogeneous matrices and is used to determine the position and orientation of fingertips relative to the base coordinate system located in the center of wrist (Stoppa et al. 2015). The model equation is calculated by D–H parameter. The derivation of forward kinematics is as follows.

Let

\( \theta_{{{\text{i}},{\text{j}}}} \)::

joint angle of the finger

\( \text{d}_{\text{i, j}} \)::

joint distance of the finger

\( \ell_{{{\text{i}},{\text{j}}}} \)::

 link length of the each joint

\( \alpha_{{{\text{i}},{\text{j}}}} \)::

 link twist angle

where i and j indices represents, respectively, the corresponding finger and joint (Table 1).

Table 1 D–H parameters for the thumb
Full size table
  1. 1.

    Thumb finger

The model of the thumb finger can be seen in Fig. 3a, based on which we can get D–H parameters:

Fig. 3
figure 3

Finger models a thumb finger; b index finger, middle finger, ring finger and little finger

Full size image

The forward kinematic for the thumb finger is defined

$$ {{\text{P}}}_{{\text{T}}} = {}_{0}^{{\text{w}}} {{\text{T}}}_{{\text{T}}} \left( {\ell_{{{{\text{T}}},{{\text{w}}}}} } \right){}_{1}^{0} {{\text{T}}}_{{\text{T}}} \left( {\theta_{{{{\text{T}}},{{\text{TMC}}}}} } \right){}_{2}^{1} {{\text{T}}}_{{\text{T}}} \left( {\theta_{{{{\text{T}}},{{\text{MCP}}}}} } \right){}_{3}^{2} {{\text{T}}}_{{\text{T}}} \left( {\theta_{{{{\text{T}}},{{\text{IP}}}}} } \right){}_{4}^{3} {{\text{T}}}_{{\text{T}}} \left( {\theta_{{{{\text{T}}},{{\text{D}}}}} } \right), $$
(1)
$$ {}_{\text{k}}^{{{\text{k}} - 1}} {\text{T}}_{\text{T}} \left( {\theta_{{{\text{i}},{\text{j}}}} } \right) = \left[ {\begin{array}{*{20}c} {\cos (\theta_{{{\text{i}},{\text{j}}}} )} & { - \sin (\theta_{{{\text{i}},{\text{j}}}} )} & 0 & {{\text{d}}_{{{\text{i}},{\text{j}}}} } \\ {\cos ({{\alpha }}_{{{\text{i}},{\text{j}}}} )\sin \left( {\theta_{{{\text{i}},{\text{j}}}} } \right)} & {\cos ({{\alpha }}_{{{\text{i}},{\text{j}}}} )\cos \left( {\theta_{{{\text{i}},{\text{j}}}} } \right)} & { - \sin (\alpha_{{{\text{i}},{\text{j}}}} )} & { - \ell_{{{\text{i}},{\text{j}}}} \sin (\alpha_{{{\text{i}},{\text{j}}}} )} \\ {\sin ({{\alpha }}_{{{\text{i}},{\text{j}}}} )\sin \left( {\theta_{{{\text{i}},{\text{j}}}} } \right)} & {\sin ({{\alpha }}_{{{\text{i}},{\text{j}}}} )\cos \left( {\theta_{{{\text{i}},{\text{j}}}} } \right)} & {\cos (\alpha_{{{\text{i}},{\text{j}}}} )} & {\ell_{{{\text{i}},{\text{j}}}} \cos (\alpha_{{{\text{i}},{\text{j}}}} )} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]. $$
(2)

When k = 0, k−1 = w representing the center of the wrist.

So, each of the matrices \( {\text{T}}_{\text{T}} \) are given by:

$$ {}_{0}^{\text{w}} {\hbox{T}}_{\text{T}} \left( {\ell_{{{\text{T}},{\text{w}}}} } \right) = \left[ {\begin{array}{*{20}l} 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad {\ell_{{{\text{T}},{\text{w}}}} } \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right], $$
(3)
$$ {}_{\text{s}}^{{{\text{s}} - 1}} {\text{T}}_{\text{T}} \left( {\theta_{{{\text{T}},{\text{j}}}} } \right) = \left[ {\begin{array}{*{20}c} {\cos (\theta_{{{\text{T}},{\text{j}}}} )} & { - \sin (\theta_{{{\text{T}},{\text{j}}}} )} & 0 & 0 \\ {\cos (\alpha_{{{\text{T}},{\text{v}}}} )\sin \left( {\theta_{{{\text{T}},{\text{j}}}} } \right)} & {\cos (\alpha_{{{\text{T}},{\text{v}}}} )\cos \left( {\theta_{{{\text{T}},{\text{j}}}} } \right)} & { - \sin (\alpha_{{{\text{T}},{\text{v}}}} )} & { - \ell_{{{\text{T}},{\text{v}}}} \sin (\alpha_{{{\text{T}},{\text{v}}}} )} \\ {\sin (\alpha_{{{\text{T}},{\text{v}}}} )\sin \left( {\theta_{{{\text{T}},{\text{j}}}} } \right)} & {\sin (\alpha_{{{\text{T}},{\text{v}}}} )\cos \left( {\theta_{{{\text{T}},{\text{j}}}} } \right)} & {\cos (\alpha_{{{\text{T}},{\text{v}}}} )} & {\ell_{{{\text{T}},{\text{v}}}} \cos (\alpha_{{{\text{T}},{\text{j}}}} )} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], $$
(4)

where s = 1, 2, v = MCP and j = TMC, MCP, in this order,

$$ {}_{3}^{2} {\text{T}}_{\text{T}} \left( {\theta_{{{\text{T}},{\text{IP}}}} } \right) = \left[ {\begin{array}{*{20}c} {\cos (\theta_{{{\text{T}},{\text{IP}}}} )} & { - \sin (\theta_{{{\text{T}},{\text{IP}}}} )} &\quad 0 &\quad {{\text{d}}_{{{\text{T}},{\text{P}}}} } \\ {\sin (\theta_{{{\text{T}},{\text{IP}}}} )} &\quad {\cos (\theta_{{{\text{T}},{\text{IP}}}} )} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right], $$
(5)
$$ {}_{4}^{3} {\text{T}}_{\text{T}} \left( {\theta_{{{\text{T}},{\text{D}}}} } \right) = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 &\quad {{\text{d}}_{{{\text{T}},{\text{D}}}} } \\ 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right]. $$
(6)
  1. 2.

    Other fingers

As shown in Fig. 2b, the D–H parameters for other fingers can be obtained just like the thumb finger (Table 2).

Table 2 D–H parameters for the other fingers
Full size table

The forward kinematic for the other fingers is defined

$$ P_{\beta } = {}_{0}^{w} T_{\beta } \left( {\ell_{\beta ,w} } \right){}_{1}^{0} T_{\beta } \left( {\theta_{\beta ,MCP} } \right){}_{2}^{1} T_{\beta } \left( {\theta_{\beta ,PIP} } \right){}_{3}^{2} T_{\beta } \left( {\theta_{\beta ,DIP} } \right){}_{4}^{3} T_{\beta } \left( {\theta_{\beta ,D} } \right), $$
(7)

where β = I, M, R, L (index, middle, ring, little), \( {\text{T}}_{{{\beta }}} \) are the matrices like that showed in Eq. (8), given by:

$$ {}_{0}^{{\text{w}}} {{\text{T}}}_{{{\beta }}} \left( {\ell_{{{{\beta }},{{\text{w}}}}} } \right) = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad {\ell_{{{{\beta }},{{\text{w}}}}} } \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right], $$
(8)
$$ T_{T} \left( {\theta_{\beta ,MCP} } \right) = \left[ {\begin{array}{*{20}c} {\cos (\theta_{\beta ,MCP} )} & { - \sin (\theta_{\beta ,MCP} )} & 0 & {d_{i,j} } \\ {\cos \left( {\alpha_{\beta ,MCP} } \right)\sin \left( {\theta_{\beta ,MCP} } \right)} & {\cos \left( {\alpha_{\beta ,MCP} } \right)\cos \left( {\theta_{\beta ,MCP} } \right)} & { - \sin \left( {\alpha_{\beta ,MCP} } \right)} & { - \ell_{\beta ,MCP} \sin \left( {\alpha_{\beta ,MCP} } \right)} \\ {\sin \left( {\alpha_{\beta ,MCP} } \right)\sin \left( {\theta_{\beta ,MCP} } \right)} & {\sin \left( {\alpha_{\beta ,MCP} } \right)\cos \left( {\theta_{\beta ,MCP} } \right)} & {\cos \left( {\alpha_{\beta ,MCP} } \right)} & {\ell_{\beta ,MCP} \cos \left( {\alpha_{\beta ,MCP} } \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], $$
(9)
$$ {}_{s}^{s - 1} T_{\beta } \left( {\theta_{\beta ,j} } \right) = \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{\beta ,j} } \right)} &\quad { - \sin (\theta_{\beta ,j} )} &\quad 0 &\quad {d_{\beta ,v} } \\ {\sin (\theta_{\beta ,j} )} &\quad {\cos (\theta_{\beta ,j} )} &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right], $$
(10)

where s = 2, 3, j = PIP, DIP and v = P, M,

$$ {}_{4}^{3} T_{\beta } \left( {\theta_{\beta ,D} } \right) = \left[ {\begin{array}{*{20}l} 1 &\quad 0 &\quad 0 &\quad {d_{\beta ,D} } \\ 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 1 \\ \end{array} } \right] . $$
(11)

2.1.2 Inverse kinematics

Inverse kinematics (IK) is a method to calculate postures by estimating each individual degree of freedom to satisfy a given task; it plays an important role in computer animation and simulation of personage simulation (Unzueta et al. 2008). The demand for accurate biomechanical modeling and body size based on anthropometric data makes the IK method a popular method for fast and reliable solutions. Inverse kinematics can determine joint configuration in the case of a given pose or end position. There are two main methods in IK: analysis-based and differential-based (Wang et al. 2016). The analysis IK is obtained by finding the closed form solution for the inverse of the forward kinematic function, and is applicable only to the specific structure studied. The differential IK uses the Jacobian determinant to map the Descartes velocity along the point of the motion chain to the speed of the chain along the chain, and it has universal applicability (Unzueta et al. 2008; Wang et al. 2010).The differential IK of the simplified index finger shown in Fig. 4 as an example is discussed in this paper, which is also applicable to other fingers according to the characteristics of differential IK.

Fig. 4
figure 4

Simplified index finger model

Full size image

The Jacobian matrix is a partial derivative matrix of the determined joint position (\( \gamma_{i} \)) relative to the joint angle of the structure (\( \theta_{i} \)):

$$ J = \frac{{\partial \gamma_{i} }}{{\partial \theta_{i} }}. $$
(12)

The link position of the finger \( \gamma_{\text{i}} \) can be represented by a matrix containing fingers position coordinates and orientations:

$$ \gamma_{i} = \left[ {\begin{array}{*{20}c} x & y & \emptyset \\ \end{array} } \right]^{T} . $$
(13)

According to Eqs. 12 and 13, The Jacobian matrix is given as:

$$ J = \left[ {\begin{array}{*{20}c} {\frac{\partial x}{{\partial \theta_{MCP} }}} &\quad {\frac{\partial x}{{\partial \theta_{PIP} }}} &\quad {\frac{\partial x}{{\partial \theta_{DIP} }}} \\ {\frac{\partial y}{{\partial \theta_{MCP} }}} &\quad {\frac{\partial y}{{\partial \theta_{PIP} }}} &\quad {\frac{\partial y}{{\partial \theta_{DIP} }}} \\ {\frac{\partial \emptyset }{{\partial \theta_{MCP} }}} &\quad {\frac{\partial \emptyset }{{\partial \theta_{PIP} }}} &\quad {\frac{\partial \emptyset }{{\partial \theta_{DIP} }}} \\ \end{array} } \right], $$
(14)

where,

$$ x = \ell_{1} \cos \theta_{MCP} + \ell_{2} \cos \left( {\theta_{MCP} + \theta_{PIP} } \right) + \ell_{3} \cos (\theta_{MCP} + \theta_{PIP} + \theta_{DIP} ) = \ell_{1} C_{1} + \ell_{2} C_{12} + \ell_{3} C_{123} , $$
(15)
$$ y = \ell_{1} \sin \theta_{MCP} + \ell_{2} \sin (\theta_{MCP} + \theta_{PIP} ) + \ell_{3} \sin (\theta_{MCP} + \theta_{PIP} + \theta_{DIP} ) = \ell_{1} S_{1} + \ell_{2} S_{12} + \ell_{3} S_{123} , $$
(16)

where \( \ell_{1} , \ell_{2} , \ell_{3} \) are defined in Fig. 3, indicating the link length between MCP and PIP, PIP and DIP, DIP and fingertip, respectively.

$$ \emptyset = \theta_{PIP} + \theta_{MCP} + \theta_{DIP} $$
(17)

Hence,

$$ \frac{\partial x}{{\partial \theta_{MCP} }} = - \ell_{1} S_{1} - \ell_{2} S_{12} - \ell_{3} S_{123} , $$
(18)
$$ \frac{\partial x}{{\partial \theta_{PIP} }} = - \ell_{2} S_{12} - \ell_{3} S_{123} , $$
(19)
$$ \frac{\partial x}{{\partial \theta_{DIP} }} = - \ell_{3} S_{123} , $$
(20)
$$ \frac{\partial y}{{\partial \theta_{MCP} }} = - \ell_{1} C_{1} - \ell_{2} C_{12} - \ell_{3} C_{123} , $$
(21)
$$ \frac{\partial y}{{\partial \theta_{PIP} }} = - \ell_{2} C_{12} - \ell_{3} C_{123} , $$
(22)
$$ \frac{\partial y}{{\partial \theta_{DIP} }} = - \ell_{3} C_{123} , $$
(23)
$$ \frac{\partial \emptyset }{{\partial \theta_{MCP} }} = 1,\frac{\partial \emptyset }{{\partial \theta_{PIP} }} = 1,\frac{\partial \emptyset }{{\partial \theta_{DIP} }} = 1. $$
(24)

By substituting of Eqs. (18–24) into Eq. 14, the Jacobian matrix becomes:

$$ J = \left[ {\begin{array}{*{20}c} { - \ell_{1} S_{1} - \ell_{2} S_{12} - \ell_{3} S_{123} } & { - \ell_{2} S_{12} - \ell_{3} S_{123} } & { - \ell_{3} S_{123} } \\ { - \ell_{1} C_{1} - \ell_{2} C_{12} - \ell_{3} C_{123} } & { - \ell_{2} C_{12} - \ell_{3} C_{123} } & { - \ell_{3} C_{123} } \\ 1 & 1 & 1 \\ \end{array} } \right]. $$
(25)

2.2 Data glove with optimized sensor layout

2.2.1 Sensor layout strategy

As shown in Fig. 1d, in animation production, due to the complexity of the anatomical structure of the hand and the subsequent difficulties in capturing all its subtle movements, actions in animation are usually omitted or created manually by the animator. When using motion capture system to capture the whole body motion of an actor, due to the complexity of the hand and the small size of the marker used (for example, the size of the projection surface of the 6 mm marker is less than five times of the 14 mm marker), there will be a large number of occlusion and marking errors in the manual post-processing process, which significantly increases the workload of the animator. Researchers found that finger movements using inverse kinematics reconstruction from a simplified set of 8 markers per hand were thought to be very similar to the corresponding movements using a full set of 20 markers. The data obtained from reduced markers can be calculated by IK to reconstruct the completed hand movement, which inspires us to use the same strategy of reducing the number of sensors on IMMU-based data gloves.

A hand sensor placement strategy based on inverse kinematics is proposed allowing for the reconstruction of hand motion from a limited number of sensors. The reduced sensor layout can be determined by using a priori knowledge. The researchers performed principal component analysis (PCA) through the hand movement database to find that 3–6 hand joint subspaces were sufficient to restore 90% of the hand movements (Phillips et al. 2006).

A set of eigenvectors and eigenvalues can be obtained by performing PCA on the hand movement posture database, which can be used to construct a \( 26 \times \left( {6 + l} \right) \) matrix of principal components M. Given the PCA matrix M, the full parameter vector \( \theta \in R^{26} \) can be computed from the reduced subspace parameters \( \alpha \in R^{6 + l} \) as

$$ \theta = M\alpha + \mu , $$
(26)

where \( \mu \in {\text{R}}^{26} \) is the mean of the database postures.

In this way, we can represent the forward kinematics of the effect points \( \gamma_{i} \) according to the subspace parameters:

$$ \gamma = \gamma \left( \alpha \right) = \gamma \left( {\theta \left( \alpha \right)} \right), $$
(27)

Based on this representation, the IK problem can also be represented by subspace parameters:

$$ J_{s} = \frac{\partial \gamma }{\partial \alpha } = \frac{\partial \gamma }{\partial \theta } \cdot \frac{\partial \theta }{\partial \alpha } = J \cdot M. $$
(28)

The IK of subspace constraints enables us to restore the complete hand model from a limited number of points, but the selection of the sensor location is not arbitrary, two different layout methods (Fig. 5) were compared.

Fig. 5
figure 5

Comparison of the layouts of the sensors on the hand: a traditional full sensor set (with 12 sensors) covering all joints of the hand; b The optimized sensor layout strategy with fewer sensors (6 sensors)

Full size image

No sensors were placed in PIP joints because it is almost impossible to move the PIP joints without moving the DIP joint, and vice versa (Wheatland and Zordan 2013). The joint angle-dependent relationship between PIP and DIP joints can be expressed as (Xu et al. 2012):

$$ \theta_{DIP} = \frac{2}{3}\theta_{PIP} . $$
(29)

2.2.2 Attitude solution

There are many methods for calculating and representing the attitude information of the carrier in space motion, such as the Euler angle method, the direction cosine method and the quaternion method (Xue et al. 2018; Yoshimoto et al. 2015). The quaternion method has only four unknown numbers, so the amount of calculation is smaller, and there is no influence on the angle constraint without solution. By updating the number of four elements, the attitude information of the carrier can be reacted in real time, which is very suitable for the attitude calculation of the low dynamic performance carrier.

The quaternion can take advantage of the nature of the hyper complex number to completely rotate the reaction vector, and can be expressed as

$$ q = q_{0} + q_{1} i + q_{2} j + q_{3} k, $$
(30)

where i, j, k are mutually orthogonal unit vectors, \( {\text{q}}_{0} \), \( {\text{q}}_{1} \), \( {\text{q}}_{2} \), \( {\text{q}}_{3} \) are real numbers. Let \( {\text{C}}_{\text{b}}^{\text{n}} \) be the attitude transformation matrix of the sensor’s own coordinate system and the navigation reference coordinate system, using the calculation property of the quaternion, we can get the attitude transformation matrix:

$$ C_{b}^{n} = \left( {\begin{array}{*{20}c} {q_{0}^{2} + q_{1}^{2} - q_{2}^{2} - q_{3}^{2} } & {2\left( {q_{1} q_{2} - q_{0} q_{3} } \right)} & {2\left( {q_{1} q_{3} + q_{0} q_{2} } \right)} \\ {2\left( {q_{1} q_{2} + q_{0} q_{3} } \right)} & {q_{0}^{2} - q_{1}^{2} + q_{2}^{2} - q_{3}^{2} } & {2\left( {q_{2} q_{3} - q_{0} q_{1} } \right)} \\ {2\left( {q_{1} q_{3} - q_{0} q_{2} } \right)} & {2\left( {q_{2} q_{3} + q_{0} q_{1} } \right)} & {q_{0}^{2} - q_{1}^{2} - q_{2}^{2} + q_{3}^{2} } \\ \end{array} } \right). $$
(31)

The quaternion update equation over time is:

$$ \dot{q} = \frac{1}{2}q \cdot \omega_{nb}^{b} , $$
(32)

where \( \omega_{\text{nb}}^{\text{b}} = \left( {\begin{array}{*{20}c} 0 & { - \omega_{x} } & { - \omega_{y} } & { - \omega_{z} } \\ {\omega_{x} } & 0 & {\omega_{z} } & { - \omega_{y} } \\ {\omega_{y} } & { - \omega_{z} } & 0 & {\omega_{x} } \\ {\omega_{z} } & {\omega_{y} } & { - \omega_{x} } & 0 \\ \end{array} } \right), \) the amount of ingredients is as follows:

$$ \begin{aligned} \dot{q}_{0} = - 0.5\left( {q_{1} \omega_{x} + q_{2} \omega_{y} + q_{3} \omega_{z} } \right), \hfill \\ \dot{q}_{1} = 0.5\left( {q_{0} \omega_{x} - q_{3} \omega_{y} + q_{2} \omega_{z} } \right), \hfill \\ \dot{q}_{2} = 0.5\left( {q_{3} \omega_{x} + q_{0} \omega_{y} - q_{1} \omega_{z} } \right), \hfill \\ \dot{q}_{3} = - 0.5\left( {q_{2} \omega_{x} - q_{1} \omega_{y} - q_{0} \omega_{z} } \right), \hfill \\ \end{aligned} $$
(33)

where \( \omega_{\text{x}} \), \( \omega_{\text{y}} \), \( \omega_{\text{z}} \) are the angular velocity of the three axes of the sensor coordinate system.

In order to obtain more accurate measurement of the hand motion, the data from different sensors in different locations needs to be integrated. Here Kalman filtering method is used for signal processing and filtering (Zheng et al. 2016). This recursive algorithm realizes that the previous observation information is concentrated in the estimated value, and does not need to record all the historical information. It is an efficient autoregressive processing algorithm, which can handle multidimensional and non-stationary random processes.

Let \( {\hat{\text{x}}}_{{{\text{k}}|{\text{k}}}} \) be the state estimation at time k, \( {\text{P}}_{{{\text{k}}|{\text{k}}}} \) be the error correlation matrix, in the prediction phase

$$ \hat{x}_{k|k - 1} = F_{k} \hat{x}_{k - 1|k - 1} + B_{k} u_{k} , $$
(34)
$$ P_{k|k - 1} = F_{k} P_{k - 1|k - 1} F_{k}^{T} + Q_{k} . $$
(35)

In the update phase:

Measuring margin:

$$ \tilde{y}_{k} = z_{k} - H_{k} \hat{x}_{k|k - 1} . $$
(36)

The covariance of the measure margin:

$$ S_{k} = H_{k} P_{k|k - 1} H_{k}^{T} + R_{k} . $$
(37)

Optimal Kalman gain:

$$ K_{k} = P_{k|k - 1} H_{k}^{T} S_{k}^{ - 1} , $$
(38)
$$ \hat{x}_{k|k} = \hat{x}_{k|k - 1} + K_{k} \tilde{y}_{k} , $$
(39)
$$ P_{k|k} = \left( {{\text{I}} - K_{k} H_{k} } \right)P_{k|k - 1} . $$
(40)

Kalman filter is mainly used in linear systems, the vast majority of the systems are nonlinear in practice. There are nonlinear factors in differential equations of micro inertial measurement system. In addition, not all observation models are linear. Therefore, in order to adapt to the nonlinear realistic environment, an extended version of Kalman filter is designed, in which the state transition and observation model is replaced by a differentiable function:

$$ x_{k} = f\left( {x_{k - 1} ,u_{k} ,w_{k} } \right), $$
(41)
$$ z_{k} = h\left( {x_{k} ,v_{k} } \right). $$
(42)

Calculating the partial derivative matrix gives:

$$ {\text{F}}_{\text{k}} = \frac{{\partial {\text{f}}}}{{\partial {\text{x}}}}|_{{{\hat{\text{x}}}_{{{\text{k}} - 1|{\text{k}} - 1,}} {\text{u}}_{\text{k}} }} ,\;{\text{H}}_{\text{k}} = \frac{{\partial {\text{h}}}}{{\partial {\text{x}}}}|_{{{\hat{\text{x}}}_{{{\text{k}}|{\text{k}} - 1}} }} . $$
(43)

Therefore, the extended Kalman filter equation is:

The prediction phase:

$$ \hat{x}_{k|k - 1} = f\left( {x_{k - 1} ,u_{k} ,0} \right), $$
(44)
$$ P_{k|k - 1} = F_{k} P_{k - 1|k - 1} F_{k}^{T} + Q_{k} . $$
(45)

The update phase:

$$ \begin{aligned} \tilde{y}_{k} = z_{k} - h\left( {\hat{x}_{k|k - 1} ,0} \right), \hfill \\ S_{k} = H_{k} P_{k|k - 1} H_{k}^{T} + R_{k} , \hfill \\ K_{k} = P_{k|k - 1} H_{k}^{T} S_{k}^{ - 1} , \hfill \\ \hat{x}_{k|k} = \hat{x}_{k|k - 1} + K_{k} \tilde{y}_{k} , \hfill \\ P_{k|k - 1} = F_{k} P_{k - 1|k - 1} F_{k}^{T} + Q_{k} . \hfill \\ \end{aligned} $$
(46)

To denoise the collected data, the angle value and acceleration value of the sensor output was filtered, the data before and after filtering was compared. it shows that our extended Kalman filtering method can filter out the noise and error generated by IMMU in data acquisition and transmission. The results of comparison are shown in Fig. 6. Acceleration and Euler angle keep the trend of original data after Kalman filter, but filter out unreasonable mutation and noise, and reduce the error effect. There are many choices of observing object and state object in Kalman filtering algorithm. In the calculation of inertial navigation attitude, Euler angle is selected as observing object and quaternion is state object. The attitude angle is calculated by output value of gyroscope sensor, acceleration sensor and magnetic sensor respectively. Then the optimal attitude information can be obtained by filtering and fusing the data with Kalman filtering algorithm.

Fig. 6
figure 6

Comparison of output angle and acceleration of IMMUs before and after filtering: a acceleration before filtering; b acceleration after filtering; c Euler angle before filtering; d Euler angle after filtering

Full size image

3 Experiments and results discussion

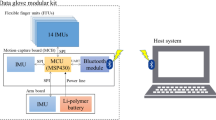
Several experiments were carried out to illustrate the superior performance of the data glove. In order to ensure the normal and stable operation of the system and reduce the interference caused by the production process and the use environment, the sensors including gyroscopes, magnetometers and accelerometers were calibrated before being used. In order to adjust the position of the sensors flexibly, IMMUs were attached to a right-hand glove using velcro according to the position of the red dot in Fig. 5. The developed data glove based on IMMU is shown in Fig. 7. Figure 7a is a conventional full sensor set. Figure 7b is the glove based on our optimized sensor placement strategy with fewer sensors. It is obvious that the decrease of the number of sensors greatly reduces the burden of the data glove on the hand, and can reduce its effect on the motion of hand. In addition, the reduction in the number of sensors will directly reduce the cost of data gloves. An MCU was used to obtain data from multiple IMMUs, and then sent the obtained data to the computer for processing by MATLAB.

Fig. 7
figure 7

The developed data gloves: a traditional full sensor set; b Our optimized sensor layout strategy with reduced sensor set

Full size image

From the Euler angle and acceleration obtained by the sensor, the angles of the joints can be calculated according to the inverse kinematics. The angles of the joints calculated when the hand remains still are shown in Table 3.

Table 3 The calculated joint angles at the given moment
Full size table

To verify the ability of the data glove to decode the hand gesture, more experiments were performed. During the experiment, the subjects were asked to do make some gestures common in daily life. The subjects sat near the edge of the table and put their right arm on the table in a comfortable position. They were instructed to make two common gestures, the gesture of the number one and the gesture of fist clench. At the beginning of each experiment, the subjects extended their right hand into a natural full extension. Hearing the “go” command (in Chinese), the subjects began to complete gestures at a fixed speed. The IMMUs obtained data every 0.02 s and then sent to MCU. After the experiment, the data collected by MCU were sent to the computer, processed by MATLAB, and the calculated joint angle was sent to the visual hand model. As shown in Fig. 8, the restoration accuracy can be evaluated by comparing the real motion with the model posture. Based on the optimized sensor layout method, the hand motion can be accurately reconstructed with the reduced number of sensors.

Fig. 8
figure 8

Comparison of real hand motions and models: only extend the index finger with a data glove with fewer sensors and b with full sensor set; and make a fist with c data glove with fewer sensors and d with full sensor set

Full size image

The same experiment was repeated 50 times. Comparing the real hand with the reconstructed gestures in the model, the recognition rate of the optimized sensor layout method is nearly 85% compared with 90% of the 12 sensor methods.

At the same time, another experiment was carried out to compared the continuous joint angles calculated by the two methods. Firstly, the subjects were asked to wear the data gloves with full sensor set, extended their right hand into a natural full extension, and then began to complete the gesture of clenching fist at a fixed speed, the acquired data was processed with MATLAB as shown in the red curve in Fig. 9. Secondly, the subjects were asked to wear the data gloves with fewer sensors, and then began to complete the gesture of clenching fist at a fixed speed under the same conditions. The acquired data was processed with MATLAB as shown in the blue curve in Fig. 9. As shown in Fig. 9, the trend of the joint angles during the whole movement calculated by the two methods are almost the same. Large errors in some joints (such as T_MCP, I_PIP, I_MCP) have been noticed. We speculate that these errors may be caused by the following reasons: (1) The data calculated by the two methods were obtained from two experiments, we cannot guarantee that the actions in the experiments are exactly the same. In the follow-up study, we should add more convincing methods to obtain joint angles for verification, such as using the data obtained by motion capture system as a standard, compare the data obtained by two different sensor combinations with the standard, and then compare their differences after calculating. (2) When several specific joints with larger errors are in motion, the position of IMMUs may be offset because they are not firmly fixed on the glove. (3) For the thumb, because the thumb joint is more complex, and we adopt the simplified model to calculate, the data may have larger errors.

Fig. 9
figure 9figure 9

Comparison of angles (radian) calculated by the two methods in two similar moves

Full size image

Compared with the full sensor set, the mean and standard deviation (SD) of error of the angles of the joints calculated by our method are shown in Table 4, the error is within 15%.

Table 4 The mean and standard deviation (SD) of error
Full size table

4 Conclusion

To reduce the effect of the data glove on the hand and make a low-cost data glove suitable for using at home, a sensor layout method is proposed in this paper based on the inverse kinematics so that the hand motion can be captured with fewer sensors. The hand motion is reconstructed by using space constraints. For the data collected from the hand sensor network, the extended Kalman filtering methods are used to solve the data fusion. An experimental evaluation was carried out and reconstructed several hand motions under the two sensor configurations. Experimental results showed that our hand sensor layout method can reconstructed hand motion accurately and completely. Compared with the traditional gloves with full sensor set, the error generated by the new set was acceptable. In the future, real-time processing algorithm will be investigated to enable online motion capture. Also, an objective and universal method will be studied to evaluate the degree of hand motion reconstruction. Data glove calibration methods were also studied to improve the accuracy of reconstruction by determining the joint bone length of the individual through several sets of movements. The captured hand data will be used in a rehabilitation system which can help the impaired hand perform training using the data of another healthy hand.