1 Introduction

Observed data are often generated by random processes that induce dependence. Common examples of such data are time series, spatial data, longitudinal data, and functional data. Often, we may only have one realization from such a process over the domain of interest. This can make it challenging to consider realistic dependence structure in statistical models. Arguably, the most common tool for studying dependence structure is the covariance (or correlation) between any pairs of observations or hypothetical observations in the domain. In practice, this requires construction and computation with a covariance or correlation matrix, which can be challenging computationally when the number of observations or inference locations becomes large. An alternate way of analyzing such a random process is by representing it as a series expansion of some deterministic basis functions with associated random coefficients. In practice, a finite number of such basis functions are used to expand the process and the random coefficients are then estimated. This is sometimes referred to as “random field discretization” and it reduces the computational burden since the process is expressed as a low dimensional (reduced rank) series (Wikle 2010). Importantly, this expansion implies a covariance function.

There are many examples of random field discretization methods. The most common examples are spectral expansions (e.g.,  Shinozuka and Deodatis 1991; Grigoriu 1993). In addition, polynomial based expansion methods (typically called “polynomial chaos”) are also quite common in the uncertainty quantification literature (see Li and Der Kiureghian 1993); Zhang and Ellingwood 1994); Xiu 2009) for a review of these methods). Another popular approach of direct relevance to this manuscript is the expansion method proposed by Karhunen (Karhunen 1946) and Loève (Lóeve 1955), which is now widely known as the Karhunen-Loève expansion (KLE).

As we show here, the KLE is analogous to the diagonalization of a given matrix and hence, has close ties with many commonly known statistical techniques such as principal component analysis (PCA) (Hotelling 1933), singular value decomposition (Golub and Van Loan 1996), empirical eigenfunction decomposition (Sirovich 1987), factor analysis (Mulaik 2009), proper orthogonal decomposition (Lumley 1967), and empirical orthogonal function (EOF) decomposition for spatio-temporal data (Cressie and Wikle 2011). One important aspect of the KLE is its bi-orthogonality; i.e., the use of orthogonal basis functions for the expansion and associated uncorrelated random coefficients. As discussed herein, the KLE is the optimal procedure among all reduced-rank expansion methods in the sense of reducing global mean square error.

The literature concerned with the KLE is vast and it is beyond the scope of this manuscript to provide a comprehensive review. Fortunately, many review articles are available that provide historical developments of the KLE and its application in various field. For example, the KLE is tied closely to matrix factorization and one can find a review of matrix decomposition methods in Stewart Gilbert (1993). Additional details of the history of the KLE are provided in Van Trees (2004). Application of the KLE in statistics can be divided into a few distinct categories. For example, KLE methods are used to simulate random fields as described in Zheng and Dai (2017) and Gutiérrez et al. (1992). In addition, there is a very large literature on using KLE approaches in numerical solution to various types of problems. Many of these approaches are closely related to Galerkin and finite element methods as used in the computational solution of partial differential equations. Some examples can be found in Boente and Fraiman (2000); Phoon et al. (2004, 2002); Hu and Zhang (2015); Spanos et al. (2007); Ghanem and Spanos (2003), and Spanos and  Ghanem (1989). Furthermore, Huang et al. (2001) studied the convergence of the KLE when used as a numerical solution approach. In the area of data analysis and applications, KLE methods have been used extensively to analyze spatio-temporal data in the geophysical sciences and statistical analysis of such data. Overviews can be found in Jolliffe and Cadima (2016); Cressie and Wikle (2011); Wikle et al. (2019), and examples of applications include Obled and Creutin (1986); Monahan et al. (2009); Hannachi et al. (2007); Fontanella and Ippoliti (2012); Bradley et al. (2017); Wikle et al. (2019); Hu (2013), and Dong et al. (2006). The KLE has also been applied to the study of the Gaussian Processes (GPs) ( Levy 2008; Jin 2014; Greengard and O’Neil 2021) and non-Gaussian processes (Poirion 2016; Dai et al. 2019; Li et al. 2007; Li and Zhang 2013). Further application areas of the KLE are in pattern recognition (Zhao et al. 2020; Barat and  Roy 1998; Yamashita et al. 1998; Kirby and Sirovich 1990), machine learning (Yeung et al. 2021; Rasmussen 2003), functional data analysis (Ramsay and Silverman 2002; Castrillon-Candas et al. 2021; Jacques and Preda 2014, 2014; Zapata et al. 2019), and discretization of random fields (Betz et al. 2014; Rahman 2018; Huang et al. 2014; Li et al. 2008) (among many others).

It is apparent that the KLE has become a common approach for modeling dependent processes across many disciplines. That said, by far the majority of these studies have only considered a univariate KLE. Much less attention has been devoted to the multivariate KLE and thus, our primary goal in this manuscript is to revisit the multivariate KLE and describe its utility when modeling in statistics, primarily in the context of spatial and spatio-temporal statistics. As we will show, the multivariate KLE can be cast similar to the univariate version when one considers them from an underlying reproducing kernel Hilbert space (RKHS) perspective. Thus, we also provide an overview of the univariate approach and show through simulation and an optimal spatial data aggregation example that these methods can be effective even when one does not know the underlying dependence structure corresponding to the data generating process.

The remainder of the manuscript is structured as follows. For background, we first present a brief overview of RKHS theory and its connection to the KLE in Sect. 2. This is followed by the multivariate version of the RKHS and KLE in Sect. 3. We then show how the KLE can be used in statistical modeling through simulation and application in Sect. 4, from both the univariate and multivariate perspectives. We provide a brief conclusion in Sect. 5.

2 Univariate Karhunen-Loève Expansion

To set the stage for discussion of the multivariate KLE, we first present theoretical motivation for the univariate KLE, which is based on the theory of reproducing kernel Hilbert spaces and associated representation theorems.

2.1 Reproducing Kernel Hilbert Space (RKHS)

The analysis of a stochastic process involves the study of functional data. That is, we consider the observed data to be a realization from an unknown function with the indexing variable being an argument that belongs to an infinite continuous set. The building blocks of such fields are functions that span the process over the entire domain of interest (e.g., a spatial domain). Thus, we shall begin the mathematical formulation of the KLE by studying a particular vector space formed by functions, namely the Hilbert space, which was first formulated in the beginning of the 20th century with David Hilbert and Erhard Schmidt’s study of integral equations. We define the Hilbert space in Definition 2.1. Note, Table 1 provides the notation used in this subsection.

Definition 2.1

(Hilbert Space) A Hilbert space \(\mathcal {H}\) is a vector space over its domain (e.g., \(\mathbb {R}\), \(\mathbb {R}^n\), \(\mathbb {C}\), etc.) equipped with a norm \(\Vert \cdot \Vert _{\mathcal {H}}\) such that the space is complete with respect to the norm.

Although this general definition of a Hilbert space may take any space as its argument, we shall specifically focus on spaces defined over \(\mathbb {R}\) (univariate) and \(\mathbb {R}^n\) (multivariate). We begin reviewing the univariate case and then extend it over \(\mathbb {R}^n\) in the multivariate case, noting that any extension to a general metric space is similar to the study over \(\mathbb {R}^n\).

The particular Hilbert space of interest in this manuscript is the one formed by all functions defined over a fixed domain and range set. In the remainder of this section we motivate the construction of such a Hilbert space, commonly known as a reproducing kernel Hilbert space (RKHS). More details about the RKHS can be found in Aronszajn (1950); Wahba (1990); Kailath (1971), and Wang (2008), among others.

Table 1 Notation and definitions for RKHS and KLE
Full size table

We first briefly review the univariate RKHS and KLE. In that context, assume that \(\mathcal {Y}\subseteq \mathbb {R}\), although the domain set can be from an arbitrary subspace of \(\mathbb {R}^d\). For example, a spatio-temporal univariate random variable \(X_{s_1, s_2, t}\) is a 1-dimensional stochastic process, but the domain set is 3-dimensional with, for example, latitude, longitude, and time serving as the three input arguments. Formally, the univariate RKHS is defined as:

Definition 2.2

(Univariate Reproducing Kernel Hilbert Space) A Hilbert space \(\mathcal {H}\) of functions f from \(\mathcal {D}\) to \(\mathcal {Y}\) is called a RKHS if there exists a function \(\mathcal {K}_{\mathcal {H}}: \mathcal {D}\times \mathcal {D}\rightarrow \mathcal {Y}\) such that the following holds:

  1. i

    For all \(t \in \mathcal {D}\), the function \(\mathcal {K}(., t)\) is an element from the Hilbert space \(\mathcal {H}\).

  2. ii

    For all \(t \in \mathcal {D}\) and for every function \(\phi \in \mathcal {H}\), the following relation is satisfied

    $$\begin{aligned} \langle \phi , \mathcal {K}(., t) \rangle _{\mathcal {H}} = \phi (t) \end{aligned}$$

The second property given in (ii) above is called the “reproducing property” of the Hilbert space and hence, the function \(\mathcal {K}_{\mathcal {H}}\) associated with the space \(\mathcal {H}\) is called a reproducing kernel associated with the space \(\mathcal {H}\).

To study the properties of a RKHS, we first consider its associated reproducing kernel. Consider the following lemmas (for proofs, see Appendix A):

Lemma 2.1

The reproducing kernel \(\mathcal {K}\) (or \(\mathcal {K}_{\mathcal {H}}\)) associated with \(\mathcal {H}\) is symmetric in its argument.

Lemma 2.2

The reproducing kernel \(\mathcal {K}_{\mathcal {H}}\) of a Hilbert space \(\mathcal {H}\) is unique.

We now drop the suffix from a reproducing kernel \(\mathcal {K}_{\mathcal {H}}\) and simply denote it as \(\mathcal {K}\). A reproducing kernel also has another very important property that will be utilized throughout the manuscript.

Lemma 2.3

A reproducing kernel is always positive semi-definite in the sense of E. H. Moore. That is, given any set of scalars \(\{c_i\}_{i=1}^{n}\) and any set of elements \(\{ u_i\}_{i=1}^{n}\) from \(\mathcal {D}\) for \(i=1, \ldots , n\), \(\sum _{i=1}^n \sum _{j=1}^n c_i c_j \mathcal {K}(u_i, u_j) \ge 0\) for any n.

The above properties of symmetry and positive semi-definiteness are used to characterize kernels, which are functions of two arguments. Kernels are used extensively in many areas of statistics (non-parametric statistics, Gaussian processes, basis function expansions, etc.). Note, the terms “kernel” and “reproducing kernel” can be used interchangeably since every reproducing kernel satisfies both symmetry and positive semi-definiteness, which are the conditions that kernels must satisfy.

Now, associated with every such kernel \(\mathcal {K}\) over a domain \(\mathcal {D}\), there exists a Hilbert space \(\mathcal {H}\) of functions from \(\mathcal {D}\rightarrow \mathcal {Y}\) such that \(\mathcal {K}\) reproduces the Hilbert Space \(\mathcal {H}\). This is known as Moore-Aronszajn Theorem (Aronszajn 1950) and is stated as follows:

Theorem 2.1

(Moore-Aronszajn Theorem) Let \(\mathcal {K}: \mathcal {D}\rightarrow \mathcal {Y}\) be a kernel. For every \(t \in \mathcal {D}\), define the function \(\mathcal {K}_t\): \(\mathcal {K}_t(x) = \mathcal {K}(t, x)\). Then there exists an unique RKHS \(\mathcal {H}_{\mathcal {K}}\) such that \(\mathcal {K}\) reproduces \(\mathcal {H}_{\mathcal {K}}\). The space is given as:

$$\begin{aligned} \mathcal {H}_{\mathcal {K}} = Closure \Big \{ \sum _i c_i \mathcal {K}_{t_i} \Big \}, {\qquad c_i \in \mathcal {Y}}. \end{aligned}$$

The Moore-Aronszajn Theorem completes the connection between kernels and the associated RKHS in both directions – i.e., associated with every kernel there exists a RKHS and vice versa. The RKHS spanned by a kernel is formally called the “native space” associated with the kernel (Schaback 1998).

2.1.1 Examples of Kernels

There are an infinite number of kernels that can be used. In practice, some specific ones have proven useful. We present a few examples here for illustration (for more, see Small and McLeish 2011).

Example 2.1

Let \(\{e_1, \ldots , e_n\}\) be an orthonormal basis of \(\mathcal {H}\) and define:

$$\begin{aligned} \mathcal {K}(x, y) = \sum _{i=1}^n e_i(x) e_j(y). \end{aligned}$$

Then, for any x,

$$\begin{aligned} \mathcal {K}_y(\cdot ) = \mathcal {K}(\cdot , y) = \sum _{i=1}^n e_j(y) e_i(\cdot ) \end{aligned}$$

belongs to \(\mathcal {H}\). Now, take any function \(\psi\) from \(\mathcal {H}\) where

$$\begin{aligned} \psi (\cdot ) = \sum _{i=1}^n \lambda _i e_i(\cdot ). \end{aligned}$$

Then, we get the following

$$\begin{aligned} \langle \psi , \mathcal {K}_y)\rangle _{\mathcal {H}}&= \Big \langle \sum _{i=1}^n \lambda _i e_i, \sum _{j=1}^n e_j(y) e_i\Big \rangle _{\mathcal {H}} \\&= \sum _{i=1}^n \sum _{j=1}^n \lambda _i e_j(y) \langle e_j, e_i\rangle _{\mathcal {H}} \\&= \sum _{i=1}^n \lambda _i e_i(y) = \psi (y) . \end{aligned}$$

Example 2.2

Let \(\mathcal {D}= \mathbb {R}^+\). The function \(\mathcal {K}(x,y) = min(x,y)\) is a kernel. To show this, we note that

$$\begin{aligned} \mathcal {K}(x,y) = \int _{\mathbb {R}^+} \int _{\mathbb {R}^+} \mathbf {1}_{[0,x]}(t) \mathbf {1}_{[0,y]}(t) dt , \end{aligned}$$

which means there exists a map \(\phi (x) = \mathbf {1}_{[0,x]}(t)\) such that \(\mathcal {K}(x,y) = \langle \phi (x), \phi (y)\rangle _{\mathcal {H}}\) and hence, it is a kernel.

Example 2.3

Let \(\mathcal {L}_2\) denote the set of second order functions from \(\mathcal {D}\rightarrow \mathbb {R}\). Then, \(\mathcal {L}_2\) is a Hilbert space with inner product

$$\begin{aligned} \langle f,g\rangle _{\mathcal {L}_2} = \int \int fg d\mathbb {P}. \end{aligned}$$

Example 2.4

Let \((\Omega , \mathcal {A}, \mathbb {P})\) be a probability space and let \(\mathcal {H}\) be a Hilbert space with inner product \(\langle .,.\rangle _{\mathcal {H}}\). Let \(\mathcal {L}_2(\Omega , \mathcal {A}, \mathbb {P})\) be the set of random variables X with values in \(\mathcal {H}\). Then, \(\mathcal {L}_2(\Omega , \mathcal {A}, \mathbb {P})\) is a Hilbert space with inner product given by

$$\begin{aligned} \langle f,g\rangle _{\mathcal {L}^2} = \mathbb {E}_{\mathbb {P}} (\langle X, Y\rangle _{\mathcal {H}}). \end{aligned}$$

2.2 Representation Theorems

We now shift our focus to representation theorems that facilitate the Karhunen-Loève representation. Representation of any Hilbert space corresponds to finding a set of vectors in another space such that the inner product of the “representation vector” remains the same as the original inner product in the range space. We seek to represent a stochastic process as an infinite series through the Mercer representation theorem, which in turn leads to the Karhunen-Loéve representation. First, we formally define representation.

Definition 2.3

(Representation) We consider a stochastic process \(X_t, t \in \mathcal {D}\) with the associated kernel being the covariance function \(\varvec{C}(s,t) = Cov(x_s, x_t)\). A family of vectors \(\{\phi (t) : \mathcal {D}\rightarrow \mathcal {Y}\}\) is called a representation of \(X_t\) if for all \(s, t \in \mathcal {D}\), we have \(\langle \phi (s), \phi (t)\rangle = \varvec{C}(s,t).\)

Next, we discuss the Mercer representation of a second order stochastic process \(X_t: t \in \mathcal {D}\) with covariance function R (De Vito et al. 2013; Carmeli et al. 2006). The assumptions are the same as before, but we make some additional assumptions concerning the existence of two quantities, \(\nu\) and \(L_{\nu }\), as defined by

$$\begin{aligned}&\nu (A) = \int _A \frac{1}{1 + \Vert \varvec{C}(x,x)\Vert _{\mathcal {Y}}} d \mu (x) \text {; A } \in \mathcal {D}, \nonumber \\&(L_{\nu } f) (\cdot ) = \int _A \varvec{C}(\cdot , t) f(t) d\nu (t) {; \forall f \in \mathcal {H}}. \end{aligned}$$
(1)

If the measure \(\nu\) is a bounded, positive measure, the integral \(\int \varvec{C}(x,x) d \nu (x) < \infty\). When this is satisfied, we get the Mercer representation theorem (Theorem 2.2).

Theorem 2.2

(Mercer Representation Theorem) Assume that the conditions in (1) hold. Then there exists a countable set I and corresponding countable sequence of eigenfunctions \(\{\phi _i: \mathcal {D}\rightarrow \mathcal {Y}, i \in I\}\), orthonormal with respect to \(\langle \cdot ,\cdot \rangle _{\varvec{C}}\), along with corresponding non-increasing non-negative eigenvalues \(\{\lambda _i\}_{i \in I}\) such that

  1. i

    \(\varvec{C}(u,v) = \sum _{i \in I} \lambda _i \phi _i(u) \phi _i(v)\)

  2. ii

    For all \(i \in I\), \(\int _{\mathcal {D}} \varvec{C}(u,v) \phi _i(v) dv = \lambda _i \phi _i(u)\).

The second equation is known as Fredholm Integral Equation (Freiberger and Grenander 1965; Holmstrom 1977; Davenport et al. 1958). The proof of Mercer’s theorem is beyond the scope of this manuscript (see Riesz and Nagy 1955 for the proof). Given Mercer’s theorem, we note the following important lemma.

Lemma 2.4

Below are the consequences of the Mercer’s theorem.

  1. i

    The family \(\{\phi _i\}_{i \in I}\) is an orthogonal basis of \(L_{\nu }\)

  2. ii

    \(\int \phi _i(s) \phi _j(s) ds = \delta _{ij}\)

  3. iii

    The family \(\{\sqrt{\lambda _i} \phi _i\}_{i \in I}\) is orthonormal in \(\mathcal {H}_{\varvec{C}}\).

2.2.1 Karhunen-Loève Representation Theorem

Mercer’s theorem and the associated lemma lead directly to the Karhunen-Loéve (KL) representation of a stochastic process. Without loss of generality, assume we have mean zero univariate random variables from a stochastic process. Recall, we seek a KLE that represents such a process through a series with orthogonal basis functions and uncorrelated random coefficients. The formal KL representation theorem is stated in Theorem 2.3.

Theorem 2.3

(Karhuen-Loéve Representation Theorem) Let \(\{X_t,t \in \mathcal {D}\}\) be a zero mean second order stochastic process with continuous covariance function \(\varvec{C}(s,t)\). Then, there exists a sequence of mean zero, uncorrelated random variables \(\{\alpha _i: i \in I\}\), with corresponding non-increasing non-negative eigenvalues \(\lambda _i: i \in I\) with \(\sum _{i \in I} \lambda _i^2 < \infty\) and orthonormal eigenfunctions \(\phi _i: i\in I\) such that the following holds:

$$\begin{aligned} \int \varvec{C}(u, v) \phi _i(v) dv&= \lambda _i \phi _i(u) \\ \varvec{C}(u,v)&= \sum _{i \in I} \lambda _i \phi _i(u) \phi _i(v) \\ \alpha _i&= \int \phi _i(t) X_t dt \\ X_t&= \sum _{i \in I} \alpha _i \phi _i(t). \end{aligned}$$

Additionally, if \(X_t\) is a Gaussian process, \(\alpha _i \sim \mathbb {N}(0, \lambda _i)\).

To recap, the KLE is a direct consequence of the Mercer representation theorem. Since Mercer’s theorem finds an orthonormal basis to represent a positive semi-definite matrix, the basis is a representation of a covariance kernel in an infinite series. Because this representation deals with a linear transformation, one can find the associated eigenvalue-eigenvector pairs corresponding to the linear operator. Thus, one obtains an orthonormal basis function representation of the process where the basis expansion coefficients are uncorrelated. This in turn shows the bi-orthogonal property of the KLE.

Without loss of generality, let the index set I be \(\{1,2, \ldots \}\). Then, the convergence of the KLE is in mean square, i.e., \(\mathbb {E}[X_t - \sum _{i=1}^K \alpha _i \phi _i(t)]^2 \rightarrow 0\) as K increases. This is very useful in practice since it is impossible to work directly with an infinite sum of representative features. Hence, in practice, one truncates the summation. Fixing the number of terms, the following theorem provides the rationale as to why the KLE is the best representation in terms of squared-error loss.

Theorem 2.4

Consider the following representation of a stochastic process \(X_t\)

$$\begin{aligned} X_p(t) = \sum _{i=1}^{p} \alpha _i \phi _i(t), \end{aligned}$$

where \(\phi _i(t)\)s are mutually orthonormal. Define the error of this truncated representation as \(e_p(t) = X(t) - X_p(t)\). Then among all such expansions, the KLE minimises the integrated mean squared error. That is, \(\int _t \mathbb {E}[e_p^2(t)] dt\) is minimized when the expansion is the KLE. In this case, we have

$$\begin{aligned} e_p(t) = \sum _{i=p+1}^{\infty } \alpha _i \phi _i(t). \end{aligned}$$

As with principal component analysis, one may decide to choose p terms that explain a pre-specified amount of the variation (e.g., 90% or 95%) using the first few eigenvalues, or consider scree plots, etc. (see Wikle et al. 2019 for examples in spatio-temporal statistics). This also provides the link between the KLE and many statistical techniques close to PCA (e.g., EOFs as mentioned in Sect. 1).

2.3 Implementation of the KLE

For numerical computation, the main idea behind the KLE is to use the Fredholm integral equation. For example, assume that we are given a \(n \times n\) covariance matrix \(\varvec{\varvec{C}}\), for which we need to find the KL decomposition numerically. For any such matrix, the eigenfunctions and eigenvalues can be obtained by performing an eigendecomposition using any numerical integration method (e.g., Riemann integration, Gaussian quadrature, trapezoid integration, etc.); i.e., by solving \(\varvec{\varvec{C}} \varvec{W} \Psi = \Lambda \Psi\), where \(\Psi\) is the collection of eigenvectors and \(\Lambda\) is the diagonal matrix of eigenvectors. The weight matrix \(\varvec{W}\) can vary depending on the integral method, e.g., \(\varvec{W} = \frac{1}{n}\varvec{I}\) for Riemann integral, or \(\varvec{W} =\) \(\hbox {diag}(\frac{1}{2(n-1)}, \frac{1}{n-1}, \ldots , \frac{1}{n-1}, \frac{1}{2(n-1)})\) for Trapezoid integral etc.

A more common approach in this setting is to consider an expansion method using any choice of basis functions and then project them linearly onto the KL eigenfunctions. This is useful when one has many data points and cannot take the eigendecomposition of a large covariance matrix. The initially chosen basis functions are called “generating basis functions (GBF)” and they can be chosen from any family of basis functions, e.g., the Fourier basis, Legendre polynomials, Haar basis, radial basis, bisquare basis, spline basis, etc.

Consider a one-dimensional index set (e.g., time). Denote the j-th GBF at time t as \(\theta _j(t)\) and the i-th KL eigenfunction as \(\psi _j(t)\). In matrix form, the GBF matrix is written by \(\varvec{\Theta } = ((\theta _{ij})) = \theta _j(i)\). Then the linear expansion of GBFs is accomplished by assuming \(\varvec{\Psi } = \varvec{\Theta F}\), where the matrix \(\varvec{F}\) contains the expansion coefficients. The Fredholm equation is then used to solve for the unknown coefficients in \(\varvec{F}\), which then are plugged in the above equation to get \(\varvec{\Psi }\). The detailed computation for the above method of solving \(\varvec{F}\) is explained in Appendix B. It should be noted that when one uses K many GBFs, the expansion method only needs the eigendecomposition of a \(K \times K\) positive definite matrix, which is more computationally feasible than doing the same to a \(n \times n\) covariance matrix for large n. Hence, this expansion method using GBFs is usually chosen for practical purposes, and will be of our main interest in this manuscript.

We now discuss the case where we assume that the true covariance model is not known and instead we are given one or more realizations from a stochastic process that has an unknown covariance function. When more than one realization is present (for example, in the cases of functional data), an empirical covariance matrix can be computed from the data, which is then used to get the KL decomposition of the unknown covariance matrix. A more common scenario (specifically with spatial or spatio-temporal data) is the presence of a single realization, where an empirical covariance matrix can not be computed without further model assumptions. Even in this case, the KLE can be used, implicitly providing a parameterization that allows for estimation in a manner that corresponds to Mercer’s theorem. We discuss one algorithm to implement the KLE in this context as presented in Bradley et al. (2017) and Bradley et al. (2021) for the case of one realization, where the covariance kernel is estimated under a Bayesian framework, and thereby posterior estimates of the KLE are obtained from this estimated covariance. We call this the ‘Obled-Creutin’ (OC) basis model following a similar early development in Obled and Creutin (1986).

2.4 Obled-Creutin Basis Model

Assume that \(\varvec{Y} = (Y_1, \ldots , Y_n)\) are observations following an unknown covariance matrix \(\varvec{C}\) with kernel \(\varvec{C}(s,t)\) and we want to find the KLE of \(\varvec{C}\) based on \(\varvec{Y}\). This is modeled as:

$$\begin{aligned} \varvec{Y} = \varvec{\Psi } \varvec{\eta } + \varvec{\epsilon } , \end{aligned}$$
(2)

where \(\varvec{\Psi }\) contains the KL eigenfunctions and \(\varvec{\epsilon }\) are truncation and measurement errors. Like before, starts with a set of GBFs \(\theta _j(t)\) and then linearly projects them to get the KL eigenfunctions as \(\varvec{\Psi } = \varvec{\Theta F}\). However, without the knowledge of the covariance kernel \(\varvec{C}(s,t)\), we cannot estimate the coefficients \(\varvec{F}\) and hence the KL eigenfunctions \(\varvec{\Psi }\) can not be computed from \(\varvec{\Theta }\). So, the algorithm is modified as below. First, define \(\varvec{W}\) as the matrix with (i, j)th element as \(W_{ij} = \int _t \theta _i(t) \theta _j (t) dt\). For the KL eigenfunctions to satisfy the Fredholm equation, we need the following condition to hold

$$\begin{aligned} \varvec{F^T W F} = \varvec{I} . \end{aligned}$$
(3)

Assuming that \(\varvec{W}\) is positive definite and let \(\varvec{Q}\) be the Cholesky decomposition of \(\varvec{W}^{-1}\). Then, \(\varvec{F} = \textit{\textbf{Q G}}\) satisfies Condition (3), where \(\varvec{G}\) is any orthonormal matrix of proper size. Hence, given \(\varvec{G}\), and a solution of the KL eigenfunction can be obtained as \(\varvec{\Psi } = \varvec{\Theta Q G }\). Plugging this into the Model 2, one gets

$$\begin{aligned} \varvec{Y}&= \varvec{\Theta Q G} \varvec{\eta } + \varvec{\epsilon } = \varvec{\Phi } \varvec{\nu } + \varvec{\epsilon }. \end{aligned}$$

where \(\varvec{\Phi } = \varvec{\Theta Q}\) and \(\varvec{\nu }\) = \(\varvec{G\eta }\). Note that \(\varvec{\Phi }\) is an orthonormal basis function and is computed in an unsupervised manner with only the knowledge of the GBFs, but \(\varvec{\nu }\) needs to be estimated here. If \(\lambda _1 \ge \lambda _2 \ge \cdots\) are the eigenvalues of the unknown covariance matrix \(\varvec{C}\), \(\hbox {Cov}(\varvec{\eta }) = \Lambda = \hbox {diag}(\lambda _1 , \lambda _2, \ldots )\) and hence \(\hbox {Cov}(\varvec{\nu }) = \varvec{G \Lambda G}^T\), where \(\varvec{\epsilon }\) corresponds to the measurement and truncation error. Now, to perform Bayesian inference, we can specify the following prior distributions:

$$\begin{aligned}&\varvec{Y} = \varvec{\Phi } \varvec{\nu } + \varvec{\epsilon } \nonumber \\&\varvec{\epsilon } \sim \mathcal {N}_n(0, \tau ^2\varvec{I}) \nonumber \\&\varvec{\nu } \sim \mathcal {N}_K(0, \varvec{\Sigma }) \nonumber \\&\varvec{\Sigma } = \frac{1}{\sigma ^2} \big [\varvec{R}^{-1} \mathcal {A}^{(+)}{\varvec{Q}'(\varvec{I}-\varvec{A})\varvec{Q}} \varvec{R}^{-T} \big ]^{-1} = \frac{1}{\sigma ^2} \varvec{M}^{-1} \nonumber \\&\sigma ^2 \sim IG(a_{\sigma }, b_{\sigma }) \nonumber \\&\sigma ^2 \sim IG(a_{\tau }, b_{\tau }). \end{aligned}$$
(4)

This prior for \(\varvec{\Sigma }\) has been used in Bradley et al. (2017) and Bradley et al. (2015) and is called a the Moran’s I (MI) prior due to it’s similarity with Moran’s I statistic in spatial statistics. Here \(\varvec{A}\) is the adjacency matrix of the locations, \((\varvec{Q}, \varvec{R})\) are the QR decomposition of the basis matrix \(\varvec{\Phi }\) and \(\mathcal {A}^{(+)}(\cdot )\) is the best positive definite approximation of a matrix. With model and prior distributions, we can perform MCMC estimation, generating Gibbs samples of the posteriors. Details of the Gibbs sampler for this model ar given in Appendix C. The posterior estimates of \(\varvec{\Sigma }\) are then used to get the eigendecomposition as \(\widehat{\varvec{\Sigma }} = \widehat{\varvec{G}} \widehat{\varvec{\Lambda }} \widehat{\varvec{G}}^T\), which is used to get the KL eigenfunctions as \(\widehat{\varvec{\Psi }} = \varvec{\Phi } \widehat{\varvec{G}}\) and eigenvectors as diagonal elements of \(\widehat{\varvec{\Lambda }}\).

Note that in general one does not need to build the full Bayesian structure as given above to obtain the KLE of the unknown process if one has regularly space observations and enough replicates to estimate the required \(n \times n\) covariance matrix. Then, the symmetric decomposition of the estimated covariance matrix can give the appropriate KL eigenfunctions. However, as originally demonstrated in Obled and Creutin (1986), in cases where one has irregularly spaced observations (say, in a spatial case), and seeks to have eigenfunctions corresponding to any location, then the KLE approach presented here is optimal, as it takes into account the “area of influence” of a particular data point through the integration of the GBFs.

3 Multivariate Karhunen-Loéve Expansion

Increasingly there is a need to model multivariate dependent processes. The multivariate case is more complicated than the univariate setting because one needs to account for the dependence structure between the random variables as well as the different indexing points. Although the multivariate KLE (MKLE) is analogous to the univariate case presented in Sect. 2, it is more complicated in the sense that there is no unique MKLE.

Before presenting the mathematical details, we shall first discuss the scenario at hand. The response variable in this section will be treated as a multivariate random variable, \(\varvec{X}_t\), indexed by t from an arbitrary continuous index set \(\mathcal {D}\). We assume \(\varvec{X}_t = (X_{t1}, \ldots , X_{tK})'\). Additional assumptions are the same as in Sect. 2; that is, \(t \in \mathcal {D}\in \mathbb {R}^m\) and \(\mathcal {H}\) is the Hilbert space of functions from \(\mathcal {D}\) to \(\mathcal {Y}\), where \(\mathcal {Y}\) is now a subset of \(\mathbb {R}^K\) for some \(K > 1\) with a (multivariate) norm \(\Vert \cdot \Vert _{\mathcal {H}}\) and inner product \(\langle \cdot ,\cdot \rangle _{\mathcal {H}}\). In the remainder of this section we briefly discuss multivariate (reproducing) kernels, the multivariate extension of Mercer’s theorem, and the associated multivariate Karhunen-Lóeve representation theorem (for details, see Carmeli et al. 2006; Berlinet and Thomas-Agnan 2004; Chiou et al. 2014).

3.1 Multivariate RKHS

In this subsection we describe the multivariate RKHS. First, we define a multivariate reproducing kernel.

Definition 3.1

(Multivariate (Reproducing) Kernel) A multivariate kernel is a function \(\mathcal {K}\) from \(\mathcal {D}\times \mathcal {D}\) to \(\mathcal {Y}\) such that the following holds.

  1. i

    \(\mathcal {K}\) is symmetric, i.e., \(\mathcal {K}(u, v) = \mathcal {K}(v, u)^T\).

  2. ii

    \(\mathcal {K}\) is positive definite in the sense of E.H. Moore; i.e., for any collection of vectors \(\{c_i\}_{i=1}^n\) and any set of elements \(\{u_i\}_{i=1}^n\) from \(\mathcal {D}\), the following holds:

    $$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^n c_i^T \mathcal {K}(u_i, u_j)c_j&= \sum _{i=1}^n \sum _{j=1}^n c_i^T \langle \mathcal {K}(u_i), \mathcal {K}(u_j)\rangle _{\mathcal {H}} c_j \\&= \Big \langle \sum _{i=1}^n c_i^T \mathcal {K}(u_i), \sum _{j=1}^n c_j^T \mathcal {K}(u_j)\Big \rangle _{\mathcal {H}} \ge 0. \end{aligned}$$

Thus, multivariate kernels are analogous to the univariate kernels discussed in Sect. 2, with the extension that they are now matrices rather than scalars. As in the univariate case, any multivariate kernel \(\mathcal {K}\) has an associated native Hilbert space \(\mathcal {H}_{\mathcal {K}}\). This native space can be constructed as

$$\begin{aligned} \mathcal {H}_{\mathcal {K}} = Closure \Big \{ \sum _i c_i \mathcal {K}_{t_i} \Big \} {\qquad c_i \in \mathcal {Y}}, \end{aligned}$$

where \(\mathcal {K}_{t}\) are similarly defined. Interested readers can also see De Vito et al. (2013); Carmeli et al. (2006), which discuss extensively the properties of such kernels.

Multivariate kernels still hold the reproducing property, i.e., for any \(\phi\) from the Hilbert space \(\mathcal {H}\) associated with the kernel \(\mathcal {K}\), \(\langle \varvec{\phi }, \mathcal {K}_t\rangle = \varvec{\phi }(t)\) is still satisfied. We can define \(\mathcal {K}_t^j\) as the j-th coordinate of the function \(\mathcal {K}_t(\cdot )\), which simplifies notation:

$$\begin{aligned}&\mathcal {K}_t^j \in \mathcal {H}{j=1, \ldots , N}\\&\varvec{\phi }(t) = (\langle \varvec{\phi }, \mathcal {K}_t^1\rangle _{\mathcal {H}}, \ldots , \langle \varvec{\phi }, \mathcal {K}_t^N\rangle _{\mathcal {H}}). \\ \end{aligned}$$

3.2 Multivariate Representation Theorems

Similar to the univariate case, Mercer’s theorem allows the multivariate kernel to be represented as an infinite series

Theorem 3.1

(Multivariate Mercer Theorem) Assume a kernel \(\mathcal {K}: \mathcal {D}\times \mathcal {D}\rightarrow \mathcal {Y}\subseteq \mathbb {R}^N\), \(\mathcal {H}_{\mathcal {K}}\) is separable, and \(\int _{\mathcal {D}} \mathcal {K}(t,t) dt < \infty\). Then, there exists a countable sequence of continuous orthonormal eigenfunctions \(\{\varvec{\phi }_i: \mathcal {D}\rightarrow \mathcal {Y}: i \in I\}\) and a sequence of non-negative decreasing eigenvalues \(\{\lambda _i: i \in I\}\) with \(\sum _{i \in I} \lambda _i^2 < \infty\) such that

$$\begin{aligned}&\lambda _i \varvec{\phi }_i(u) = \int _{\mathcal {D}} \mathcal {K}(u,v) \varvec{\phi }_i(v) dv\\&\mathcal {K}(u, v) = \sum _{i \in I} \lambda _i \varvec{\phi }_i(u) \varvec{\phi }_i^T (u).\\ \end{aligned}$$

Following from the Mercer representation theorem, the multivariate Karhunen-Loève representation theorem for the multivariate stochastic process \(\varvec{X}_t\) is given in Theorem 3.2.

Theorem 3.2

(Multivariate KL Representation Theorem) Assume \(\varvec{X}: \mathcal {D}\rightarrow \mathcal {Y}\) denotes a mean-zero square integrable stochastic process with covariance matrix \(\varvec{C}(t,s) = Cov(\varvec{X}_t, \varvec{X}_s)\). Then, there exists a countable sequence of random variables \(\{\alpha _i: i \in I\}\) and associated eigenvectors \(\{\lambda _i: i \in I\}\) and orthonormal eigenfunctions \(\{\varvec{\phi }_i: \mathcal {D}\rightarrow \mathcal {Y}: i \in I\}\), such that

$$\begin{aligned} \lambda _i \varvec{\phi }_i(u)&= \int _{\mathcal {D}} \mathcal {K}(u,v) \varvec{\phi }_i(v) dv\\ C(u, v)&= \sum _{i \in I} \lambda _i \varvec{\phi }_i(u) \varvec{\phi }_i^T (u)\\ \alpha _k&= \int _{\mathcal {D}} \varvec{\phi }_i(u)^T \varvec{X}(u) du\\ \varvec{X}_t&= \sum _{i \in I} \alpha _i \varvec{\phi }_i(t), \end{aligned}$$

and if \(\varvec{X}_t\) is Gaussian Process, \(\alpha _i \sim \mathcal {N}(0, \lambda _k).\)

Again, this is the direct consequence of the multivariate Mercer theorem.

3.3 Relation between Multivariate and Univariate KLEs

Consider the MKLE as in Sect. 3.2 of the form \(\varvec{X}_t = \sum _i \alpha _i \varvec{\phi }_i(t)\), where the multivariate eigenfunctions are vector valued (N-dimensional) functions. An immediate question is how is the multivariate KLE related to the univariate KLEs of each of the corresponding processes. This can be found in Proposition 5 from Happ and Greven (2018), which is stated in the theorem below. Here, we denote the full covariance matrix of \(\varvec{X}\) is denoted as the block matrix:

$$\begin{aligned} \varvec{C}= \begin{bmatrix} \varvec{C}_{11} &{} \ldots &{} \varvec{C}_{1N}\\ \vdots &{} \vdots &{} \vdots \\ \varvec{C}_{N1} &{} \ldots &{} \varvec{C}_{NN} \end{bmatrix}, \end{aligned}$$

where the elements of j, k-th blocks are \(\varvec{C}^{jk}_{st} = \varvec{C}^{jk}(s,t)\) = \(Cov(X^{(j)}_{s}, X^{(k)}_{t})\). Let the eigenvalues and eigenvectors of \(\varvec{C}\) be \(\{\lambda _1 \ge \lambda _2 \ge \ldots \}\) and \(\{\varvec{\phi }_1, \varvec{\phi }_2, \ldots \}\), and let the j-th element of \(\varvec{\phi }_i\) be denoted as \(\big [\varvec{\phi }_i\big ]_j\). The j-th univariate process with covariance matrix \(\varvec{C}_{jj}\) has the KLE \(\varvec{X}^{(j)}_t = \sum _i \alpha ^{(j)}_i \psi ^{(j)}_i(t)\), with eigenvalues \(\lambda ^{(j)}_1 \ge \lambda ^{(j)}_2 \ge \ldots\) and eigenfunctions \(\{\psi ^{(j)}_1, \psi ^{(j)}_2, \ldots \}\). Then, we have the following theorem to link the multivariate KLE to the univariate KLEs.

Theorem 3.3

(Relation between Multivariate KLE and process specific Univariate KLEs) The multivariate vector \(\varvec{X}_t = (X_{t}^{(1)}, \ldots , \varvec{X}_{t}^{(N)}): t \in \mathcal {D}\) has a KL expansion as \(\varvec{X}_t = \sum _i \alpha _i \varvec{\phi }_i(t)\) if and only if each of the univariate processes \(X_{t}^{(1)}, \ldots , X_{t}^{(N)} : t \in \mathcal {D}\) has an univariate KL expansion. Then the following two conditions hols.

  1. 1.

    Given the multivariate KLE, the eigenvalues of the covariance kernel corresponding to the j-th univariate process correspond to the eigenvalues of the matrix \(\varvec{\varvec{R}}^{(j)}\) with the (m, l)-th element as

    $$\begin{aligned} \varvec{R}^{(j)}_{ml} = \sqrt{\lambda _m \,\lambda _l} \, \langle \big [\varvec{\phi }_m\big ]_j \big [\varvec{\phi }_l\big ]_j\rangle . \end{aligned}$$

    Consider the k-th orthonormal eigenvector of \(\varvec{\varvec{R}}^{(j)}\) as \(\varvec{u}_k^{(j)}\) and denote the l-th entry as \(u_{kl}^{(j)}\). Then, the eigenfunctions of \(\varvec{C}_{jj}\) are given by

    $$\begin{aligned} \psi ^{(j)}_k(t) = \frac{1}{\sqrt{\lambda _k^{(j)}}} \sum _l \sqrt{\lambda _l} u_{kl}^{(j)}\big [\varvec{\phi }_k\big ]_j(t). \end{aligned}$$
  2. 2.

    Given the univariate KLEs of each individual process, the eigenvalues of the large covariance matrix \(\varvec{C}\) correspond to the positive eigenvalues of the block matrix \(\varvec{\mathcal {K}}\) with blocks \(\varvec{\mathcal {K}}^{(jk)}\), where the (m, l)-th element of \(\varvec{\mathcal {K}}^{(jk)}\) is \(\varvec{\mathcal {K}}^{(jk)}_{ml} = \hbox {Cov}\big (\alpha _m^{(j)}, \alpha _l^{(k)} \big )\). The j-th element of the k-th multivariate eigenfunction of \(\varvec{C}\) is constructed as

    $$\begin{aligned} \big [\varvec{\phi }_k\big ]_j(t) = \sum _i \varvec{v}_{ki}^{(j)} \psi ^{(j)}_k(t), \end{aligned}$$

    where \(\varvec{v}_{ki}^{(j)}\) denotes the i-th element of the j-th block of an orthonormal eigenvector \(\varvec{v}_k\) of \(\varvec{\mathcal {K}}\) associated with eigenvalue \(\lambda _k\).

Theorem 3.3 shows that one does not need to directly deal with the full covariance matrix and instead can work with the process specific KLEs for each of the univariate process. We discuss this alternative approach for constructing the MKLE starting from the univariate processes in the next section.

3.4 Alternative MKLE Construction

We note that it is more difficult to work with the multivariate KL representation for developing expansions as compared to univariate expansions because of the matrix-valued formulation. Hence, it is often of interest to consider whether a reasonable multivariate expansion can be obtained from the individual univariate KLEs. As with any multivariate process, there are multiple ways to achieve such an expansion. We next summarize two such approaches as presented in Cho et al. (2013).

3.4.1 Multiple Uncorrelated KLEs (muKL)

Perhaps the simplest approach is to treat the K-dimensional multivariate process as K observations from one univariate stochastic process by tweaking the indexing variables. To demonstrate this in simple terms, assume that we have a K-variate random stochastic process \(\varvec{X}_t = (X_{t}^{(1)}, \ldots , X_{t}^{(K)})\) and assume that we observe n many such vector observations, namely \(\varvec{X}_{1}, \ldots , \varvec{X}_{n}\), observed at some index points \(t_1, \ldots , t_n \in \mathcal {D}\). The covariance structure is given by a block matrix \(\varvec{C}\) with the (j, k)-th block \(\varvec{C}^{(jk)}\) with elements \(\varvec{C}^{(jk)}_{st} = \varvec{C}^{(jk)}(s,t) = \hbox {Cov}(\varvec{X}_{s}^{(j)}, \varvec{X}_{t}^{(k)})\). The goal here is to create an assembled (i.e., augmented or stacked) univariate process from the vectorized data, such that

$$\begin{aligned} {\widetilde{\varvec{X}}}_t= & {} \varvec{X}_{t}^{(1)}\hbox {if}\,\,t \le n, \\= & {} \varvec{X}_{(t - n)}^{(2)}\hbox {if}\,\,n< t \le 2n, \\\vdots&&\\= & {} \varvec{X}_{(t - (K-1)n)}^{(K)}\,\,\,\,\hbox {if}\,\, (K-1)n < t \le Kn. \end{aligned}$$

The assembled process is still a stochastic process, with a new covariance matrix of size \(Kn \times Kn\) with elements

$$\begin{aligned} \widetilde{\varvec{C}}(s, t)&= \hbox {Cov}({\widetilde{\varvec{X}}}_s, {\widetilde{\varvec{X}}}_t) \\&= \hbox {Cov}(\varvec{X}_{(s - (i-1)n)}^{(i)}, \varvec{X}_{(t - (j-1)n)}^{(j)}) \\&= \varvec{C}^{(ij)}(s - (i-1)n, t - (j-1)n), \end{aligned}$$

where \((i-1)\,n< s \le in, (j-1)\,n < t \le jn t\).

The above representation is simple and easily connected to the univariate setup from Sect. 2. The covariance matrix of the assembled process \({\widetilde{\varvec{X}}}\), \(\varvec{\widetilde{C}}\), is still the same as the original “unassembled” process, but is indexed using different sets of parameters when compared to the original process. The vector process is now expanded using this assembled covariance matrix \(\varvec{\widetilde{C}}\), which is assumed to have an eigen-decomposition with eigenvalues \(\lambda _1 \ge \lambda _2 \ge \cdots\) and eigenfunctions \(\{\phi _1, \phi _2, \ldots \}\). Hence, using the univariate formulations, \({\widetilde{\varvec{X}}}\) has a KLE as

$$\begin{aligned} {\widetilde{\varvec{X}}}_t = \sum _{i=1}^{\infty } \alpha _i \phi _i(t), \text { where } \alpha _i = \int _{\mathcal {D}} {\widetilde{\varvec{X}}}_t \phi _i(t) dt . \end{aligned}$$

Note that in our vector representation all the observations from the first variable are grouped together, followed by those for the second variable, and so on. Following the same ordering, we can now back-calculate to determine the KLE of any particular variable \(X_j\) as follows. First, define \(\psi ^i_j(t) = \phi _j(t + (i-1)n)\) where \((i-1)n < t \le in\). Then, define the vector \(\varvec{\psi }_j(t) = (\psi ^{(1)}_j(t), \ldots , \psi ^{(N)}_j(t))'\). Now, the multivariate process has the following expansion

$$\begin{aligned} \varvec{X}_t = \sum _{j=1}^{\infty } \alpha _j \varvec{\psi }_j(t). \end{aligned}$$

Importantly, the random coefficients (\(\alpha _i\)s) are shared among different variables in this expansion and hence, induces dependence. This suggests that this approach is best used when the individual processes are somewhat alike. Importantly, one must be careful because the covariance matrix constructed from a collection of small matrices is not guaranteed to be positive definite, even though individual blocks represent valid covariance matrices Cho et al. (2013).

3.5 Multiple Correlated KLEs (mcKL)

An alternative approach to implement the multivariate KLE is given here. This is a more generally applicable scenario where one has an arbitrary set of correlated stochastic processes. We use the same notation for the available data and covariance matrices as discussed previously. In this approach, one uses the KLE of each individual variable separately first then computes the matrix of correlation coefficients that give the joint covariance matrix (\(\varvec{\varvec{C}}\) from above).

Mathematically, consider the j-th process \(\varvec{X}_j\) to have a KLE as

$$\begin{aligned} X_{t}^{(j)} = \varvec{X}_j(t) = \sum _{m=1}^{\infty } \alpha _{m}^{(j)} \phi _{m}^{(j)}(t). \end{aligned}$$

For each j, this can be derived from univariate KLE of \(\varvec{C}_{jj}\). For a fixed j, the coefficients \(\alpha _{m}^{(j)}\) are uncorrelated for different m and the variances of \(\alpha _{m}^{(j)}\) is given by the m-th eigenvalue of \(\varvec{C}_{jj}\). From these univariate KLEs, the next step is to get the full covariance matrix by estimating the terms of the cross covariance functions between the variables. For that, we define

$$\begin{aligned} \mathcal {K}_{ij}^{ml} = \hbox {Cov}\big [\alpha _{m}^{(i)}, \alpha _{l}^{(j)}\big ] = \mathbb {E} \big [\alpha _{m}^{(i)}, \alpha _{l}^{(j)} \big ]. \end{aligned}$$

Then, the cross-covariances are obtained as the following weighted linear combination of the univariate eigenfunctions

$$\begin{aligned} \hbox {Cov}[{\varvec{X}}_{si}, {\varvec{X}}_{tj}]&= \hbox {Cov}\left[ \sum _{m=1}^{\infty } \alpha _{m}^{(i)} \phi _{m}^{(i)}(t), \sum _{l=1}^{\infty } \alpha _{l}^{(j)} \phi _{l}^{(j)}(t) \right] \\&= \sum _{m=1}^{\infty } \sum _{l=1}^{\infty } \phi _{m}^{(i)}(s) \phi _{l}^{(j)}(t) Cov [\alpha _{m}^{(i)}, \alpha _{l}^{(j)}] \\&= \sum _{m=1}^{\infty } \sum _{l=1}^{\infty } \mathcal {K}_{ij}^{ml} \phi _{m}^{(i)}(s) \phi _{l}^{(j)}(t). \end{aligned}$$

Hence, to get a multivariate KLE, the remaining task here is to solve for \(\mathcal {K}_{ij}^{ml}\). One can show that this can be solved using the following relationship

$$\begin{aligned} \mathcal {K}_{ij}^{ml} = \int _{\mathcal {D}} \int _{\mathcal {D}} C_{ij}(s, t) \phi _{m}^{(i)}(s) \phi _{l}^{(j)}(t) \,ds \,dt. \end{aligned}$$
(5)

Let \(\varvec{\mathcal {K}}_{ij}\) be the matrix with (m, l)-th element \(\mathcal {K}_{ij}^{ml}\) and define \(\varvec{\mathcal {K}}\) to be the block matrix with the (i, j)-th block \(\varvec{\mathcal {K}}_{ij}\), where the diagonal blocks \(\varvec{\mathcal {K}}_{ii}\)s are defined to be an identity matrix. Also collect all the variable-wise expansion coefficients into a large vector as in \(\mathrm {A} = \big (\alpha _{11}, \alpha _{21}, \ldots , \alpha _{1K}, \alpha _{2K}, \ldots \big )'\). To get the multivariate KLE, consider a Cholesky decomposition of \(\varvec{\mathcal {K}} = \varvec{R} \varvec{R}^T\) and then define \(\widetilde{\mathrm {A}} = \varvec{R}^{-1} \mathrm {A}\). So, \(\widetilde{\mathrm {A}}\) are uncorrelated because \(\mathbb {E}\big [\widetilde{\mathrm {A}} \widetilde{\mathrm {A}}^T\big ] = \varvec{R}^{-1} \mathbb {E}\big [\mathrm {A}\mathrm {A}^T \big ] \varvec{R}^{-T} = \varvec{R}^{-1} \varvec{\mathcal {K}} \varvec{R}^{-T} = \mathbf {I}\). Similarly the univariate eigenfunctions \(\phi _m^{(i)}(\cdot )\) can be collected in a vector to define a multivariate eigenfunction \(\Phi _m^{(i)}(\cdot )\) and then they can be made orthonormal by a similar transformation as in \({\widetilde{\Phi }}(\cdot ) = \Phi (\cdot ) \varvec{R}\). Thus, we obtain the orthonormal eigenfunctions and uncorrelated coefficients that gives the MKLE from the univariate KLEs of each process.

Construction of the MKLE from the univariate KLEs is the most interesting feature due to it’s practical implementation and simplicity of the expansion. The truncated univariate expansion of each process is easy to obtain and a simple cartesian product of the eigenfunctions is all that is needed to construct the multivariate expansion. Discussions and theorems supporting this approach can be found in Steinwart and Christmann (2008); Flaxman et al. (2017); De Vito et al. (2013). Specifically, the Proposition 3.5 from De Vito et al. (2013) provides the necessary intuition that when we deal with a bivariate process, the m-th bivariate eigenfunction can be obtained by multiplying the m-th univariate eigenfunctions from the individual univariate KLEs. Hence, when one knows the univariate expansions, the dependence structure of the off-diagonal elements can be easily derived. For example, if one starts with two random variables, each with a Gaussian covariance kernel : \(\mathcal {K}_1(x,y) = \exp ({-{(x-y)^2}/{2r_1^2}})\) and \(\mathcal {K}_2(x,y) = \exp ({-{(x-y)^2}/{2r_2^2}})\), one can set the following eigenexpansion of the j-th variable as

$$\begin{aligned}&\psi _i^{(j)}(t) = \frac{t^i}{\sqrt{i!} r_j^i} \exp (-{x^2}/{2r_j^2}), \end{aligned}$$

since the following is satisfied:

$$\begin{aligned} \sum _i \psi _i^{(j)}(x) \psi _i^{(j)}(y)&= \sum _i \frac{x^i}{\sqrt{i!} r_j^i} \exp ({-{x^2}/{2r_j^2}}) \frac{y^i}{\sqrt{i!} r_j^i} \exp (-{y^2}/{2r_j^2})\\&= \sum _i \frac{(xy)^i}{i! r_j^{2i}} \exp (-{(x^2 + y^2)}/{2r^2}) \\&= \exp (-{(x-y)^2}/{2r_j^2}) = \mathcal {K}_j(x,y). \end{aligned}$$

The off-diagonal elements of the full covariance matrix can now be given by

$$\begin{aligned} \mathcal {K}_{1,2}(x,y) = \sum _i \psi _i^{(1)}(x) \psi _i^{(2)}(y) = \exp \Big ( -\frac{1}{2}({x}/{\sigma _1} - {y}/{\sigma _2})^2 \Big ). \end{aligned}$$

Note that the off-diagonal elements are not Gaussian kernels.

As another example, a univariate Brownian bridge kernel between [0, 1] is given by

$$\begin{aligned} \mathcal {K}(x,y) = \min (xy) - xy, \end{aligned}$$

and has a KLE with the following eigenfunctions and eigenvalues:

$$\begin{aligned}&e_i(x) = \sqrt{2} sin(i\pi x) \\&\lambda _i = \frac{1}{\pi ^2 i^2} \\&\mathcal {K}(x,y) = \sum _i \frac{\sqrt{2}}{\pi ^2 i^2} sin(i\pi x). \end{aligned}$$

Given two such correlated variables, both individually following the same kernel, the off-diagonals of the covariance matrix of the bivariate process can then be constructed from the expansion

$$\begin{aligned} \mathcal {K}_{1,2}(x,y) = \sum _i \frac{2}{\pi ^4 i^4} \sin (i\pi x) \sin (i\pi y). \end{aligned}$$

3.6 Implementation of the MKLE from GBFs

The implementation of the MKLE is similar to the univariate case. The muKL method essentially transforms the multivariate problem into an univariate problem and hence the analysis is analogous to starting with univariate GBFs to get an univariate KLE of the vectorized process and then re-indexing the eigenfunctions. That said, the mcKL approach is truly multivariate and is of our interest for this discussion. Noting again that mcKL requires individual KLEs from each stochastic process, one needs to start with a set of GBFs for each individual random variable and perform analogous operations as in the univariate case to get the individual KLEs. After that, the computation of the multivariate KLE is done by estimating the \(\varvec{\mathcal {K}}\) matrix in (5) from Sect. 3.5. The mathematical details are given in Appendix D.

Alternatively, one may also start with multivariate GBFs to get multivariate KLEs. For a K-variate random process, one starts with any multivariate basis function \(\varvec{\phi }_k: \mathcal {D}\rightarrow \mathbb {R}^K\) for \(k=1, \ldots , M\). Letting \(\Phi (t)\) be the \(T \times M\) matrix with the k-th column as \(\varvec{\phi }_k\), the KL eigenfunctions are constructed as

$$\begin{aligned} \varvec{\psi }_i(\cdot ) = \sum _{j=1} f_{ij}\varvec{\phi }_j(\cdot ). \end{aligned}$$

Similar to the univariate case, one must satisfy the condition \(\varvec{F}^T \varvec{W} \varvec{F} = \varvec{I}\) where the i, j-th element of \(\varvec{W}\) is \(W_{ij} = \int \phi _i(t)^T \phi _j(t) \,dt\). Hence, if \(\varvec{Q}\) is a Cholesky decomposition of \(\varvec{W}^{-1}\) and if \(\varvec{G}\) is some orthonormal matrix, we get \(\varvec{F} = \varvec{Q G}\) and thus the KL eigenfunctions are given by \(\varvec{\Psi } = \varvec{QG\Phi }\). Although this is more in line with the univariate GBF expansion, we note that it can be problematic to choose multivariate GBFs from individual processes. Also, this involves much larger matrix operations compared to the univariate KLEs.

We conclude this section by re-emphasizing that when the true (or any target) covariance matrix \(\varvec{\mathcal {K}}\) is known, the coefficient matrix \(\varvec{F}\) can be exactly solved. However, the analogous MKLE case where the multivariate covariance matrix is unknown is still unsolved and is the subject of on-going research.

4 Simulations and Applications

To illustrate the KLE we provide a simple univariate construction example with simulated data in Sect. 4.1. This is followed in Sect. 4.2 by an important application that uses the univeraite KLE as part of a criterion to determine the optimal regionalization of spatial data. This is then followed in Sects. 4.3 and 4.4 with simulated examples illustrating the MKLE. Finally, Sect. 4.5 presents a data example considering multivariate spatio-temporal data (maximum and minimum temperature for weather stations over the USA from 1990 to 1993).

4.1 Univariate: Expansion of a Univariate Exponential Covariance Kernel

In this example, we demonstrate the univariate KLE construction approach using GBFs. The covariance matrix chosen here is based on the covariance function of the form \(\varvec{C}(s,t) = \exp \{{-\frac{\Vert s-t\Vert }{\lambda }}\}\). We choose \(\lambda =1\) and \(n=200\) locations in 1-d space to evaluate the covariance matrix, which gives us a \(200 \times 200\) covariance matrix. The evaluation locations are chosen on a regular grid \(t=\{t_1, \ldots , t_n\} = \{-1, -1+\delta , -1+2\delta , \ldots , 1-2\delta , 1-\delta ,1\}\), where \(\delta = \frac{2}{(n-1)}= \frac{2}{199}\). As explained in Sect. 2, our goal is to construct the KL eigenfunctions \(\psi _j(\cdot )\), which will be obtained as a linear projection of some chosen family of GBFs. Here, we use Legendre polynomial basis functions for GBFs (see Appendix B for details of Legendre polynomials and the computation of the KL eigenfunctions).

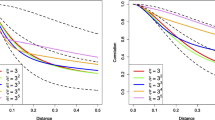
Following the methodology described in Sect. 2.3, the first two eigenfunctions from the KLE and the reconstructed autocovariance functions are given in Figs.  1 and 2, respectively. We have used different numbers of GBFs for illustration, but find little difference between the KLE eigenvalues and eigenfunctions for the different values (e.g., see Fig. 1 for a plot of the first two eigenfunctions based on the 10 basis function representation). In addition, the reconstructed autocovariance plots in Fig. 2 show that 10 or more basis functions do a reasonable job of representing the true correlation structure.

Fig. 1
figure 1

The first two eigenfunctions \(\psi _1(\cdot )\) and \(\psi _2(\cdot )\) obtained from the univariate KL representations of an exponential covariance function using 10 generating basis functions

Full size image
Fig. 2
figure 2

Reconstructed autocovariance function for the exponential covariance function as a function of univariate lag differences. The true autocorrelation function is given by the red line, and the univariate KL expansions with 5, 10 and 15 basis functions are shown by the blue, golden and green lines, respectively

Full size image

4.2 CAGE: Criterion for Spatial Aggregation Error

Spatial change of support is a long-standing problem in geography and spatial statistics in which one seeks to do spatial inference at different spatial scales without inducing effects from aggregation (the so-called “ecological fallacy”). Bradley et al. (2017) showed how the KLE could be used to mitigate this through a criterion for spatial aggregation error (CAGE). We repeat the essence of this approach here to illustrate the value of the univariate KLE in generating optimal regionalizations for spatial statistical inference.

Consider a spatial stochastic process \(\mathcal {Y}\) that has been observed across several regions at a particular spatial scale. For example, one might consider the unemployment rate for counties across different states in the United States, yet we might wonder how we could aggregate the county level estimates at different geographies than those given by the state boundaries. The CAGE procedure assumes there exists some point (or very small spatial) level process \(\mathrm {Z}\) (denoted \(\mathrm {Z}_{\varvec{s}}(\cdot )\)) and an associated larger-scale areal level process (denoted \(\mathrm {Z}_{ {A}}(\cdot )\)). Consider the stochastic process \(\mathrm {Z}_{\varvec{s}}(\cdot )\) to have a covariance function \(\hbox {Cov}(\mathrm {Z}_{\varvec{s}}(t), \mathrm {Z}_{\varvec{s}}(u)) = \varvec{C}(t, u)\) and note the KLE of this covariance function is given by

$$\begin{aligned} \varvec{C}(t, u)= & {} \sum _{j = 1}^{\infty } \phi _{\varvec{s}, j}(t) \phi _{\varvec{s}, j}(u) \lambda _j \\ \mathrm {Z}_{\varvec{s}}(t)= & {} \sum _{j = 1}^{\infty } \phi _{\varvec{s}, j}(t) \alpha _j, \end{aligned}$$

where \(\hbox {var}(\alpha _j) = \lambda _j\) and \(\alpha _j = \int _{\mathcal {D}} \phi _{\varvec{s}, j}(t) \mathrm {Z}_{\varvec{s}}(t)\, dt\). Then, the areal random variable is obtained from

$$\begin{aligned} \mathrm {Z}_{ {A}}(U) = \int _{t \in U} \mathrm {Z}_{\varvec{s}}(t) \, dt . \end{aligned}$$

The KLE of the areal level process can then be obtained from the point level KLE as

$$\begin{aligned} \phi _{ {A}, j}(U)= & {} \int _{t \in U} \phi _{\varvec{s}, j}(t) \, dt \\ \mathrm {Z}_{ {A}}(U)= & {} \sum _{j = 1}^{\infty } \phi _{ {A}, j}(U) \alpha _j \\ \hbox {Cov}(\mathrm {Z}_{ {A}}(U), \mathrm {Z}_{ {A}}(V))= & {} \sum _{j = 1}^{\infty } \phi _{ {A}, j}(U) \phi _{ {A}, j}(V) \lambda _j. \end{aligned}$$

The proof of this result can be found in Bradley et al. (2017). This representation in turn helps one to provide an optimal discretization of the point level process that can be used to construct an optimal areal level process from the point level data. The CAGE statistic provided in Bradley et al. (2017) can be used for this purpose and is given by:

$$\begin{aligned} CAGE(U) = \frac{1}{|U|} \int _{t \in U} \Big [ \sum _{j = 1}^{\infty } \lambda _j [\phi _{\varvec{s}, j}(t) - \phi _{ {A}, j}(U)]^2 \Big ]\, dt. \end{aligned}$$
(6)

The CAGE statistic can be implemented in the rcage (Bradley et al. 2021) R package. Here, we apply it to an ocean color dataset (Leeds et al. 2014; Wikle et al. 2013) over the coastal Gulf of Alaska. The dataset contains SeaWiFS ocean color satellite observations – ocean color is a proxy for phytoplankton at the near surface of the ocean. We then use ROMS ocean model output to predict the ocean color because the SeaWiFS data have areas of missing data due to cloud cover. Specifically, we use the ROMS ocean model output variables chlorophyll, sea surface temperature, and sea surface height as covariates to predict the response, SeaWiFs satellite ocean color, using the model given in (4). W consider data for May 12, 2000, which contains 4718 observations. The approach we consider is described in Sect. 2.4, with a slight change given the existence of the covariates. Specifically, we consider

$$\begin{aligned} \varvec{Y}= & {} \varvec{\mu } + \varvec{\Phi } \varvec{\nu } + \varvec{\epsilon } \\ \varvec{\mu }= & {} \mu \varvec{1} \\ \mu\sim & {} \mathcal {N} (0, \sigma ^2_{\mu }) \\ \varvec{\epsilon }\vert \tau ^2\sim & {} \mathcal {N}_n(0, \tau ^2\varvec{I}) \\ \varvec{\nu }\vert \sigma ^2\sim & {} \mathcal {N}_K(0, \varvec{\Sigma }) \\ \varvec{\Sigma }= & {} \sigma ^2 \big [\varvec{R}^{-1} \mathcal {A}^{(+)}{\varvec{Q}'(\varvec{I}-\varvec{A})\varvec{Q}} \varvec{R}^{-T} \big ]^{-1} = \sigma ^2 \varvec{M}^{-1} \\ \sigma ^2\sim & {} IG(a_{\sigma }, b_{\sigma }) \\ \tau ^2\sim & {} IG(a_{\tau }, b_{\tau }). \end{aligned}$$

We use bisquare basis functions as the GBFs here, which are defined as

$$\begin{aligned} \theta _i^{(j)}(t)&= \Big (1 - \frac{(t - \varvec{c}_j)^2}{\omega ^2} \Big )^2 \text { if }\Vert t - \varvec{c}_j\Vert \le \omega \\&= 0 \,\qquad \qquad \qquad \quad \text { otherwise}, \end{aligned}$$

where \(\omega\) is chosen as 1.5 times the minimum distance among the locations. The knots are carefully chosen following the space-filling “coverage designs” using a swapping algorithm (Johnson et al. 1990). As shown in the model description, the “MI prior” is the choice for the prior for the unknown covariance matrix \(\varvec{\Sigma }\). In addition, \(\sigma ^2_{\mu }\) is chosen to be large, \(a_{\tau } =b_{\tau } =1\) and \(a_{\sigma }\) and \(b_{\sigma }\) are chosen based on the suggestions in Sect. 3.2 of Sørbye and Rue (2014). Posteriors are obtained using Gibbs sampling, and this is then used to estimate the CAGE Criterion (6).

Note that in the CAGE procedure, the clustering component is done in two stages. Consider that S many samples have been drawn from the posterior distribution. Then, based on each sample there is a “prediction” for each element of \(\varvec{Y}\), i.e., \({\varvec{Y}}_s \mid \cdot : s=1, \ldots , S\). Now, using any naive clustering algorithm, one obtains clusters for each Gibbs sample. Note that, in most applications, we recommend that one consider a clustering procedure that explicitly accounts for spatial location and can keep elements of the cluster to be spatially contiguous (e.g., in the rcage package one can select structural hierarchical clustering to accomplish this). The cluster centroids are used as the center of the areal units. Then in the second step, the CAGE criterion is calculated based on these areal units to determine the optimal number of clusters. For this example, we considered a range for the number of clusters from \(g_L = 200\) to \(g_U = 250\), where 217 clusters were retained as optimal. Figure 3 shows the optimal regionalizations that we obtained from this procedure. Note that this aggregation represents an order of magnitude reduction in the number of spatial units compared to the point level prediction. Thus, the KLE, which is fundamental to the CAGE methodology, has demonstrated value in providing dimension reduction for spatial data.

Fig. 3
figure 3

Regionalization of ocean color by the CAGE approach. The top left panel shows the prediction at the point level. The top right panel shows the prediction for the optimal areal units obtained from the CAGE approach. The bottom left panel shows the areal level prediction errors and the bottom right panel shows the evaluation of the CAGE criterion over the areal units

Full size image

4.3 Multivariate: Expansion of a Bivariate Exponential Covariance Function

In this example, we demonstrate the MKLE estimation procedure with a bivariate stochastic process \(\varvec{X}_t= (X_{t1}, X_{t2})\). The j-th processes is assumed to follow an exponential covariance function \(\varvec{C}_j\) given by

$$\begin{aligned} \hbox {Cov}(X_{sj}, X_{tj}) = \exp \left( {-\frac{\Vert X_{sj} - X_{tj}\Vert }{\lambda _j}}\right) , \end{aligned}$$

and the cross-covariance function \(\varvec{C}_{12}\) is specified as

$$\begin{aligned} \hbox {Cov}(X_{s1}, X_{t2}) = \exp \left( {-\frac{\Vert X_{s1} - X_{t2}\Vert }{\lambda _{12}}}\right) . \end{aligned}$$

This representation gives a valid covariance function if \(\lambda _1 \lambda _2 \le \lambda _{12}^2\). Hence, we consider \(\lambda _1 = 0.5\), \(\lambda _2 = 0.8\), \(\lambda _{12} = 0.6\).

For both processes, orthonormal Legendre polynomials are used as the GBFs. Figure 4 shows the first two eigenfunctions as constructed from the individual KLE of each of the two univariate process. Figure 5 shows the reconstructed autocovariance function for both the univariate processes and also for the cross-covariance. The true and the estimated autocovariance functions align with one another, which is expected from the KL theory.

Fig. 4
figure 4

KL eigenfunctions from two individual univariate processes where the KLE for each univariate process is first obtained using 10 Legendre polynomials as GBFs. The top row contains the first two eigenfunctions \(\big (\psi _1(\cdot )\) and \(\psi _2(\cdot )\big )\) from the first process and bottom row contains the same for the second process

Full size image
Fig. 5
figure 5

Left panel: the estimated autocovariance function based on the truncated KLE for process 1 compared to the truth; Middle panel: the estimated autocovariance function based on the truncated KLE for process 2 compared to the truth; Right panel: the estimated cross-covariance function from the MKLE approach compared to the truth

Full size image

4.4 Multivariate: Estimating KLE from Functional Data

Consider the full covariance matrix

$$\begin{aligned} \varvec{C}= \begin{bmatrix} \varvec{C}_{11} &{} \varvec{C}_{12} \\ \varvec{C}_{21} &{} \varvec{C}_{22} \end{bmatrix}, \end{aligned}$$

where \(\varvec{C}_{jj}\) is a covariance matrix based on exponential covariance functions

$$\begin{aligned} \varvec{C}_{jj}(s, t)= & {} \exp \left( {-\frac{\Vert X_{sj} - X_{tj}\Vert }{\lambda _j}}\right) \\ \varvec{C}_{12}(X_{s1}, X_{t2})= & {} \exp \left( {-\frac{\Vert X_{s1} - X_{t2}\Vert }{\lambda _{12}}}\right) . \end{aligned}$$

Consider the index points \(t_1, \ldots , t_T\) with \(\varvec{X}_1, \ldots , \varvec{X}_n (n = 1000)\) simulated from a multivariate Gaussian distribution with the covariance matrix \(\varvec{C}\) and mean \(\varvec{0}\), where \(\varvec{X}_i(t) = (\varvec{X}_{i1}(t), \varvec{X}_{i2}(t))\) with \(\varvec{X}_{ij}(t)\) being the i-th observation of the j-th variable at time t. We denote \(\varvec{X}= \big [ \varvec{X}_1; \varvec{X}_2 \big ]\), where \(\varvec{X}_j\) is a \(n \times K\) matrix, with each row as an observation and the k-th column of \(\varvec{X}_j\) being the evaluations of the j-th variable at the k-th time. Our goal is to get a KLE of the covariance matrix and thereby obtain the expansion of the cross-covariance matrix from individual KLEs. We first get the estimated covariance matrix

$$\begin{aligned} {\widehat{\varvec{C}}} = \begin{bmatrix} {\widehat{\varvec{C}}}_{11} &{} {\widehat{\varvec{C}}}_{12} \\ {\widehat{\varvec{C}}}_{21} &{} {\widehat{\varvec{C}}}_{22} \end{bmatrix}, \end{aligned}$$

where \({\widehat{\varvec{C}}}_{ij} = \frac{1}{N-1}\varvec{X}_i^T \varvec{X}_j\). From the simulated data, we will use the expansion of the estimated covariance matrix, \({\widehat{\varvec{C}}}\).

Now, we begin with the individual covariance matrices \(\varvec{C}_{11}\) and \(\varvec{C}_{22}\) and compute KLEs for each of them following the previously mentioned technique, i.e., start with K Legendre polynomial basis functions\(\varvec{\Theta }^{(j)}\) and then compute the KL eigenfunctions \(\varvec{\Psi }^{(j)}\) and eigenvalues \(\lambda _i^{(j)}\). Then the multivariate KLE can be found from \({\widehat{\varvec{C}}}_{12}\) and by orthonormalizing the process-specific random coefficients and eigenfunctions (see details in Appendix D).

The individual eigenfunctions from the two processes reconstructed by the individual KLEs are shown in Fig. 6. The eigenfunctions are similar to the ones in the univariate examples above. We then perform the multivariate KLE by estimating the \(\varvec{\mathcal {K}}\) matrix and reconstruct the full covariance matrix by estimating the off-diagonals. We compare the true versus the target versus the reconstructed covariances for the 3 different blocks (\(\varvec{C}_{11}, \varvec{C}_{22},\varvec{C}_{12})\) in Fig. 8. Here ‘true’ is the true covariance model, ‘target’ is the estimated covariance matrix from the data \(\varvec{X}\) (this is what we are attempting to reconstruct from the individual KLEs) and ‘estimated’ is the reconstructed covariance function from the KLEs.

With the functional data, one can compute the scores (i.e., expansion coefficients) for the data \(\varvec{X}\). Given the matrix \(\varvec{\Psi }\), the scores are computed via a linear model as in \(\varvec{X}= \Psi \varvec{\eta } + \varvec{\epsilon }\), where \(\varvec{\epsilon }\) is the prediction error. We plot the score variances corresponding to the eigenvalues in Fig. 7 and examine the \(95\%\) credible intervals in Table 2 to show that these are consistent with what is expected from the theory.

Fig. 6
figure 6

Univariate process eigenfunctions obtianed from the individual process specific KLEs where 10 Legendre polynomials are used for the expansion in each case. The top row contains the first two eigenfunctions \(\big (\psi _1(\cdot )\) and \(\psi _2(\cdot ) \big )\) from Process 1 and bottom row contains the same for Process 2

Full size image
Table 2 Summary of the scores (Coefficients of linear expansion using the KL eigenfunctions) : Individual scores are expected to have mean 0. The table presents the \(95\%\) credible intervals and the true and observed variances for these scores
Full size table
Fig. 7
figure 7

Score variances vs. eigenvalues for the simulated bivariate data. In this case, close agreement between the score variances and the eigenvalues is observed

Full size image
Fig. 8
figure 8

Left panel: the estimated autocovariance function based on the truncated KLE for Process 1 compared to the truth; Middle panel: the estimated autocovariance function based on the truncated KLE for Process 2 compared to the truth; Right panel: the estimated cross-covariance function from the MKLE approach compared to the truth

Full size image

4.5 Multivariate Data Application: Maximum and Minimum Temperatures Over Space and Time

We consider the KLE of a bivariate process that generates daily maximum and minimum temperature observations obtained from the US National Oceanic and Atmospheric Administration (NOAA) National Climatic Data Center. The spatial locations considered are 138 weather stations in USA (between \(32^{\circ } N-46^{\circ }N\) and \(80^{\circ }W-100^{\circ }W\)) and the observations are recorded daily between 1990 and 1993. The two variables of importance are denoted as Tmax (maximum daily temperature) and Tmin. For the purposes of demonstration, we consider the observations as replications over the spatial domain and the temporal process at each location is our bivariate stochastic process of interest. So, these data are treated as observations from a bivariate functional (temporal) process with spatial replicates and we demonstrate how an expansion of the bivariate autocorrelation function is obtained from the individual KL expansions of each variable.

As shown with the simulation example of an multivariate functional data in Sect. 4.4, we label the time indices as \(t_1, \ldots , t_T\). Removing all the missing observations, the full data with \(T=87\) days are treated as bivariate time series with \(n=1461\) spatial locations serving as replicates. As before, the data are denoted as \(\varvec{X}_1, \ldots , \varvec{X}_n\), where \(\varvec{X}_i(t) = (\varvec{X}_{i1}(t), \varvec{X}_{i2}(t))'\) with \(\varvec{X}_{ij}(t)\) being the i-th observation of the j-th variable at time t. Write \(\varvec{X}= \big [ \varvec{X}_1; \varvec{X}_2 \big ]\), where \(\varvec{X}_j\) is a \(n \times T\) matrix, with each row as an observation and the k-th column of \(\varvec{X}_j\) being the value of the j-th variable at the k-th time. Our goal is to get a KLE of the covariance matrix and thereby obtain the expansion of the cross-covariance matrix from individual KLEs.

As was the case for the multivariate functional data example, we estimate the covariance matrix

$$\begin{aligned} {\widehat{\varvec{C}}} = \begin{bmatrix} {\widehat{\varvec{C}}}_{11} &{} {\widehat{\varvec{C}}}_{12} \\ {\widehat{\varvec{C}}}_{21} &{} {\widehat{\varvec{C}}}_{22} \end{bmatrix}, \end{aligned}$$

where \({\widehat{\varvec{C}}}_{ij} = \frac{1}{N-1}\varvec{X}_i^T \varvec{X}_j\). We will use the expansion of \({\widehat{\varvec{C}}}\) matrix for the KLE. The individual covariance matrices \(\varvec{C}_{11}\) and \(\varvec{C}_{22}\) are first expanded using individual KLEs, i.e., using GBFs \(\varvec{\Theta }^{(j)}\) and then projecting them linearly to compute the KL eigenfunctions \(\varvec{\Psi }^{(j)}\) and eigenvalues \(\lambda _i^{(j)}\). As stated in Theorem 3.3, univariate KLEs for the two processes are used to compute the the bivariate KLE of the given bivariate process. This is done by estimating the terms of the \(\varvec{\mathcal {K}}\) using the estimated cross-covarince matrix \({\widehat{\varvec{C}}}_{12}\) and then by comupting \(\varvec{\mathcal {K}}\) matrix (see details in Appendix D). After computing \(\varvec{\mathcal {K}}\), the eigenvalues and eigenvectors of \(\varvec{\mathcal {K}}\) are computed to get the bivariate orthonormal eigenfunctions and eigenvalues.

Here we first show the estimated eigenfunctions from the two individual univariate stochastic processes in Fig. 9. The multivariate KLE is then used to compute the scores or the coefficients (i.e., the expansion coefficients \(\alpha\)s in the KLE \(\varvec{X}_t = \sum _i \alpha _i \varvec{\phi }_i(t)\)). Note that the k-th estimated coefficient from the variables in \(\varvec{X}_j\) are random variables with mean 0 and variance \(\lambda _k^{(j)}\). We show this in Table 3.

Fig. 9
figure 9

The first \(\big (\psi _1(\cdot ) \big )\) and second \(\big (\psi _2(\cdot ) \big )\) estimated eigenfunctions for Tmax and Tmin plotted against Time

Full size image
Table 3 Summary of coefficient scores associated with the estimated KLE eigenfunctions
Full size table

Finally, we show in Fig. 10 how the covariance reconstruction performs compared to the original data. Similarly, the cross-covariances are shown in Fig. 11. In both cases, ‘target’ is the estimated function that we are targeting to reconstruct, and ‘estimated’ is the estimated function from the KLEs.

Fig. 10
figure 10

Individual Process Autocovariances: The target autocovariance function vs the estimated autocovariance function from the KLE for the maximum and minimum temperature example

Full size image
Fig. 11
figure 11

Target and estimated autocovariance functions from the KLE for the maximum and minimum temperature example

Full size image

5 Conclusion

The univariate KLE is well-known in statistics and has many practical uses, including dimension reduction and determining optimal regionalizations in space. In addition, considering the increasing interest in recent years in data from multivariate correlated processes, the multivariate KLE is also a highly relevant topic, but has not seen a great deal of research or application in the statistics literature. The multivariate KLE is applicable over any general multivariate stochastic process with stationary or non-stationary covariance functions. Hence, it is very useful in applications because it allows one to account for dependence structure, both between different processes and within each process.

The multivariate KLE is more complex than the univariate KLE due to the matrix-valued structure of the kernels. But, the univariate KLE can be derived in terms of a RKHS. Similarly, the multivariate case is based on multivariate version of RKHS and corresponding matrix valued kernels. We discussed how one can utilize the univariate KLE of each process to get the multivariate expansion by estimating the terms of the cross covariance matrix. The same can also be done by re-indexing different processes and thereby converting it to a vectorized univariate process, but this latter method is only suitable for a multivariate process where individual processes are somewhat alike. The takeaway here is that there can be more than one way to approach the problem of multivariate KLE and this is a topic of interest for future study.

From the numerical perspective, the use of generalized basis functions (GBFs) has been described here. One can further focus on how the choice different basis functions affects the multivariate KLE. Other similar expansion methods (e.g., polynomial expansions, Fourier series, etc.) are applied as the methods described here. Other approaches to induce dependence between processes (e.g., copula models) could be considered here and are a subject of future research.