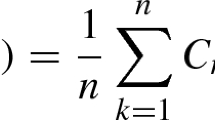1 Introduction

We first explain the motivation behind this work. Many probabilistic like Dunnage, Das, Sambadham, Nayak and Mahanty etc. have done many works on estimation of average number of real zeros of random polynomials where coefficients following Cauchy, normal and stable distributions in general. But no one has considered the case of semi-stable distribution which is the generalization of stable distribution. Shimizu (1968, 1969, 1970) have studied a lot on the domain of partial attraction of semi-stable distribution. On the basis of his findings, we have proceeded to the proof of our theorems. A distribution on \(R_{+}\) with Laplace - Stieltjes transform \(\phi (\tau )\) is said to be stable if for any \(\alpha \in (0, 1)\) there exists \(\lambda >0\) such that for all \(\tau \ge 0,~ \phi (\tau )\ne 0\) and \( \ln (\phi (\tau ))=\lambda \ln \phi (\alpha \tau )\). But, in case of semi-stable distribution the above relation holds for all \(\tau ,~ \phi (\tau )\) for some \(\alpha \in (0, 1)\) and \(\lambda >0\) . So, this can have better practical implementations than stable distribution. This motivates us for our work.

Dunnage (1966) has considered the trigonometric polynomial \(\sum \nolimits _{k=1}^{n}a_k\cos {k\theta }\) when \(a_k\)’s are independent and identically distributed normal random variables and proved that this polynomial has \(\dfrac{2}{\sqrt{3}}n+O(n^{11/3}(\log n)^{3/13})\) zeros in \([0, 2\pi ]\) except for a set of probability not exceeding \(\dfrac{1}{\log n}\). Later Das (1968) has given an estimation for expected number of real zeros of the polynomial \(\sum \nolimits _{k=1}^{n}b_k a_k\cos {k\theta }\) in \([0, 2\pi ]\) where \(a_k\)’s are independent and identically distributed normal random variables and \(b_k\)’s are constants. Assuming that \(b_k=k^\sigma (\sigma >-3/2)\), he proved that the average number of zeros is \(\left( \dfrac{2\sigma +1}{2\sigma +3}\right) ^{1/2} 2n+O(n)\) for \(\sigma \ge -1/2\) and of order \(n^{3/2}+\sigma \) in the remaining cases.

Sambandham (1976a, b) studied the same polynomial when \(a_k\)’s are dependent normal random variables and proved that the average number of zeros in \([0, 2\pi ]\) is \(\dfrac{2n}{\sqrt{3}}+O(n^{11/(13+\epsilon )})\), except for a set of probability almost \(\dfrac{1}{n^{2\epsilon }}\) where \(0<\epsilon <1/13\). Also Sambandham (1976b) studied for non-identically distributed case taking \(b_k=k^{\sigma }(\sigma \ge 0)\) and showed that the average number is \(2\left( \dfrac{2\sigma +1}{2\sigma +3}\right) ^{1/2}n+O(n^{11+13/\eta })\) except for a set of probability almost \(\dfrac{1}{n^{2\eta }}\) where \(0<\eta <1/13\). Nayak and Mohanty (1989) studied the polynomial when \(a_n\)’s are random variables following proper stable law with index \(\alpha \), where \(1<\alpha \le 2\). Mahanti (2004, 2009) studied the expected number of real zeros of \(\sum a_k \cos {k\theta }\) and \(\sum a_k\cosh {k\theta }\). Here we are going to study about the expected number of zeros of \(T_n(\theta )\) in \((0, 2\pi )\), where random variables are following semi-stable distribution with \(1\le \alpha \le 2\) which has not studied before and obtained a sharp estimation.

However, we for the first time estimated the average number of real zeros of a random trigonometric polynomial given by

$$\begin{aligned} T_n(\theta )=\sum _{k=1}^{n}\left( \frac{a_0}{n}+a_k b_k \sin {k\theta }\right) \end{aligned}$$
(1.1)

where \(a_{0}, ~a _{1},\ldots ,a_{n}\) be a sequence of mutually independent random variables following semi-stable distribution with characteristic function \(exp \left( - (C + \cos {\log |t|} )|t|^\alpha \right) \), \(1 \le \alpha \le 2\) and \(C>1\). Let \(b_{1}, ~ b_{2},\ldots ,b_{n}\) be positive constants and \(N_n(\beta , \gamma )\) be the number of real zeros of the random trigonometric polynomial \(T_n(\theta )\) in the interval \((\beta , \gamma )\) with multiple zeros counted only once and \(EN_n(\beta , \gamma )\) its expected value. Here we only consider the case when \(b_k=k^{\sigma -\frac{1}{\alpha }}\), \(\sigma =-\dfrac{2}{3\alpha }\). A characteristic function \(\phi (t)\) corresponding to distribution function F(x) is said to be semi-stable if for some constants \(b\ge d > 1\), \(\varphi (t)=\phi (d^{-1}t)\) for every t.

2 Main Results

Theorem 2.1

Let \(T_n(\theta )=\displaystyle \sum \nolimits _{k=1}\left( \dfrac{a_0}{n}+a_k b_k\sin {k\theta }\right) \) be a random trigonometric polynomial where \(a_k\)’s are random variables following semi-stable distribution with characteristic function

$$\begin{aligned} exp\left( -(C+\cos {\log |t|}) |t|^{\alpha }\right) ,~ 1\le \alpha \le 2, ~C>1. \end{aligned}$$

Let \(b_{1}, b_{2},\ldots ,b_{k}\) form a set of positive constants and \(P(a_{0}=0)=0\). Then the average number of real zeros \(EN[0, 2\pi ]\) of \(T_n(\theta )\) in \([0, 2\pi ]\) is asymptotically equal to \(2n+o(1)\), \(b_k=k^{\sigma -1/\alpha },~\sigma =-\dfrac{2}{3\alpha }\) except for a set of measure tending to zero as \(n\rightarrow \infty \).

Before proving our main result, we first partition the interval \([0, 2\pi ]\) into two types of intervals, namely

$$\begin{aligned}&Type~ (I): \left( \epsilon ,~ \frac{\pi }{k}-\epsilon \right) \displaystyle \bigcup _{k=2}^{n} \left( \frac{\pi }{k}+\epsilon , ~ \frac{\pi }{(k-1)}-\epsilon \right) \\&\quad \bigcup _{k=2}^{n}\left( \pi -\frac{\pi }{(k-1)}+\epsilon , ~ \pi -\frac{\pi }{k-1}-\epsilon \right) \\&\quad \displaystyle \bigcup _{k=2}^{n} \left( \pi -\frac{\pi }{k}+\epsilon , ~\pi +\frac{\pi }{k}-\epsilon \right) \displaystyle \bigcup _{k=2}^{n}\left( \pi +\frac{\pi }{k}+\epsilon ,~ \pi +\frac{\pi }{(k-1)}-\epsilon \right) \\&\quad \displaystyle \bigcup _{k=2}^{n} \left( 2\pi -\frac{\pi }{(k-1)}+\epsilon , ~ 2\pi -\frac{\pi }{k}-\epsilon \right) \displaystyle \bigcup _{k=2}^{n} \left( 2\pi -\frac{\pi }{k}+\epsilon ,~ 2\pi -\epsilon \right) =\lambda (say).\\&Type ~(II): \left[ 0,~ \epsilon \right] \displaystyle \bigcup _{k=1}^{n}\left[ \frac{\pi }{k}-\epsilon ,~ \frac{\pi }{k}+\epsilon \right] \displaystyle \bigcup _{k=1}^{n}\left[ \pi -\frac{\pi }{k}-\epsilon ,~ \pi -\frac{\pi }{k}+\epsilon \right] \\&\quad \displaystyle \bigcup _{k=1}^{n}\left[ \pi +\frac{\pi }{k}-\epsilon ,~ \pi +\frac{\pi }{k}+\epsilon \right] \displaystyle \bigcup _{k=1}^{n}\left[ \pi -\frac{\pi }{(k-1)}-\epsilon , ~ \pi +\frac{\pi }{(k-1)}+\epsilon \right] \\&\quad \displaystyle \bigcup _{k=1}^{n}\left[ 2\pi -\frac{\pi }{k}-\epsilon , ~ 2\pi -\frac{\pi }{k}+\epsilon \right] \displaystyle \bigcup _{k=1}^{n} \left[ 2\pi -\epsilon , ~ 2\pi \right] = \lambda ^{prime} (say). \end{aligned}$$

Let us take \(\epsilon =\dfrac{\pi }{2n}\) which is less than one half of the smallest interval. Also for this value of \(\epsilon \), all the intervals of type (I) and type (II) are well-defined and no two intervals of any type overlap. Let us denote \(M_n(\lambda )\) as average number of zeros in subintervals of type (I) and \(M_n^{Prime}(\lambda )\) as average number of zeros in subintervals of type (II). We denote \(M_n(\beta , \gamma )\) is the average number of zeros in the subinterval \((\beta , \gamma )\) of type (I). The next lemma will be useful to prove the main result.

Lemma 2.1

Let \(M_n(\beta , \gamma )\) be the average number of zeros in the subinterval \((\beta , \gamma )\) of type-I, i.e., of the partition of interval \([0, 2\pi ]\) such that \(\sec {\theta }\) is defined in each subinterval. Then

$$\begin{aligned} M_n\left( \beta , \gamma \right) =\frac{1}{\pi } \int _{\beta }^{\gamma } \left( \frac{4XZ-Y^2}{X^2}\right) ^{1/2} d\theta \end{aligned}$$

where \(X =\sum S_k^2\), \(Y =\sum S_kC_k\), \(Z =\sum C_k^2\), \(C_k=S_k k \cot k\theta -S_k\) and \( S_k^2= \left| b_k \sin {k\theta }\right| ^\alpha \).

Proof

According to Kac (1959), we have

$$\begin{aligned} M_n(\beta , \gamma )= \int _{\beta }^{\gamma }d\theta \int _{-\infty }^{\infty } |y| p(0, y) dy, \end{aligned}$$
(2.1)

where p(x, y) being probability density function of joint variables \((T_n(\theta ), T_n^{Prime}(\theta ))\) with

$$\begin{aligned} T_n(\theta )=\displaystyle \sum _{k=1}^{n} a_k b_k \sin k\theta = X \end{aligned}$$
(2.2)

and

$$\begin{aligned} T_n^{Prime}(\theta )=-\displaystyle \sum _{k=1}^{n} k b_k a_k \cos k\theta = Y. \end{aligned}$$
(2.3)

The joint characteristic function of X and Y is given by

$$\begin{aligned} G(z, w)= exp\left( -(C-1)\sum \left| b_k\sin k\theta z-kb_k\cos k\theta w\right| ^\alpha \right) . \end{aligned}$$

Since \(\sin {k\theta }\) is bounded in \((\beta , \gamma )\) of type-I. So we have, \(\dfrac{1}{n}+|b_k\sin {k\theta }|^{\alpha }\sim |b_k\sin {k\theta }|^{\alpha }\). Here \(a_k\)’s are random variables with characteristic function \(exp\left( -(C+\right. \)\(\left. \cos {\log |t|})|t|^{\alpha }\right) \), \(C>1\) and \(1\le \alpha \le 2\). By Fourier inversion formula, we have

$$\begin{aligned}&\int _{-\infty }^{\infty } |y| e^{-\epsilon |y| }p(0, y) dy = \frac{1}{\pi ^2} \int _{0}^{\infty } \frac{(\epsilon ^2-w^2)}{(\epsilon ^2+w^2)^2} \nonumber \\&\quad \times \,\int _{-\infty }^{\infty } exp\left( -(C-1)\sum \left| b_k\sin k\theta z-kb_k\cos k\theta w\right| ^\alpha \right) dw dz, \end{aligned}$$
(2.4)

where \(\int _{-\infty }^{\infty } |y| e^{-\epsilon |y|}e^{-iyw } dy =2 \dfrac{(\epsilon ^2-w^2)}{(\epsilon ^2+w^2)^2}\).

Let \(b_k \sin {k\theta }\), \(kb_k \cos {k\theta }\) to be arbitrary non-zero constants then the joint probability density function \(\overline{p}(x, y)\) corresponding to joint variable \(\left( \overline{X}, \overline{Y}\right) \) where \(X=T_n(\theta )=A\overline{X}\), \(Y=T_n^{\prime }(\theta )=B\overline{Y}\), (A, B being arbitrary constants) are zero as \((\overline{X}, \overline{Y})\) degenerates. Then the result corresponding to Eq. (2.4) will be

$$\begin{aligned} 0 = \frac{1}{\pi ^2} \int _{0}^{\infty } \frac{(\epsilon ^2-w^2)}{(\epsilon ^2+w^2)^2}dw \int _{-\infty }^{\infty } e^{ -(C-1) \left| Az-Bw\right| ^\alpha } dz. \end{aligned}$$
(2.5)

Then from (2.4) and (2.5), as \(\epsilon \rightarrow 0\) we have

$$\begin{aligned}&\int _{-\infty }^{\infty } |y| e^{-\epsilon |y| }p(0, y) dy = \frac{1}{\pi ^2} \nonumber \\&\quad \int _{0}^{\infty }\int _{-\infty }^{\infty } {e^{ -(C-1)\left| Az-Bw\right| ^{\alpha }} - [e^{ -(C-1)\sum \left| A_1z-B_1w\right| ^{\alpha }}]/w^2} dzdw. \end{aligned}$$
(2.6)

where \(A_1=b_k\sin {k\theta }\), \(B_1=kb_k\cos {k\theta }\). Putting \(z=uw\), w is fixed. Then we have

$$\begin{aligned} \int _{-\infty }^{\infty } |y| p(0, y) dy = \frac{1}{\pi ^2}\int _{-\infty }^{\infty }\log \left( \frac{\sum \left| A_1u-B_1\right| ^{\alpha }}{\left| Au-B\right| ^{\alpha }}\right) dwdu. \end{aligned}$$
(2.7)

Let us make a choice of A and B as \(|A|^{\alpha }=|B|^{\alpha } =\sum \limits _{k=1}^{n}|b_k\sin {k\theta }|^{\alpha }\). Set \(\phi _k(\theta )=\dfrac{\left| b_k\sin {k\theta }\right| ^{\alpha }}{\displaystyle \sum _{k=1}^{n}\left| b_k\sin {k\theta }\right| ^{\alpha }}\). Then

$$\begin{aligned} \int _{-\infty }^{\infty } |y|p(0, y) dy =\frac{1}{\pi ^2} I, \end{aligned}$$
(2.8)

where \(I=\int _{-\infty }^{\infty }\log \left( \frac{\sum \left| u-kcotk{\theta }\right| ^{\alpha }}{\left| u-1\right| ^{\alpha }}{\phi }_k(\theta )\right) du\).

Let

$$\begin{aligned} S_k^2=\left| b_k\sin {k\theta }\right| ^{\alpha }. \end{aligned}$$
(2.9)

Putting \(u-1=v\)

$$\begin{aligned} I= \int _{-\infty }^{\infty }\log \left( \frac{\sum (vS_k-C_k)^2}{\sum (vS_k)^2}\right) dv, \end{aligned}$$
(2.10)

where \(C_k=-S_k+S_{k}k\cot {k\theta }\). Putting \(t={\eta }^2\) and \(v{\eta }={\xi }\), we have

$$\begin{aligned} I= {\pi } \int _{-\infty }^{\infty }R_n({\xi }, {\theta })d{\xi }, \end{aligned}$$
(2.11)

where \(R_n({\xi }, {\theta })=\displaystyle \frac{1}{{\pi }^2}\int _{-\infty }^{\infty } \frac{e^{-X{\xi }^2}-e^{-X{\xi }^2+Y{\eta }{\xi }-Z{\eta }^2}}{{\eta }^2}d{\eta }\). Writing \(X=A/2\), \(Y=B\), \(Z=C/2\). Then

$$\begin{aligned} R_n({\xi }, {\theta })=\frac{1}{{\pi }}\int _{-\infty }^{\infty } \frac{e^{-1/2A{\xi }^2}-e^{-A{\xi }^2+B{\eta }{\xi }-1/2C{\eta }^2}}{{\eta }^2}d{\eta }. \end{aligned}$$
(2.12)

Das (1968) has evaluated this integral subject to the condition \(AC-B^2>0\). Then restricting ourselves to the case \(4XZ-Y^2>0\), following the result of Das (1968)

$$\begin{aligned} \int _{-\infty }^{\infty } |y|p(0, y) dy =\frac{1}{\pi } \frac{(4XZ-Y^2)^{1/2}}{X}. \end{aligned}$$
(2.13)

Therefore, from Eq. (2.1), we have

$$\begin{aligned} M_n\left( {\beta }, {\gamma }\right) =\frac{1}{{\pi }}\int _{{\beta }}^{{\gamma }} \frac{(4XZ-Y^2)^{1/2}}{X}d{\theta }. \end{aligned}$$
(2.14)

It is true for any subinterval \(({\beta }, {\gamma })\) of type-I.

$$\begin{aligned} X({\theta })= & {} \sum S_k^2=\sum \left| b_k\sin {k\theta }\right| ^{\alpha } \end{aligned}$$
(2.15)
$$\begin{aligned} Y({\theta })= & {} 2\sum S_k C_k=2\sum \left| b_k\sin {k\theta }\right| ^{\alpha }\left| k\cot {k\theta }-1\right| \end{aligned}$$
(2.16)
$$\begin{aligned} Z({\theta })= & {} S_k^2\left| k\cot {k\theta }-1\right| =\sum \left| b_k\sin {k\theta }\right| ^{\alpha }\left| k\cot {k\theta }-1\right| ^2. \end{aligned}$$
(2.17)

\(\square \)

Now let us estimate the expected number of zeros of \(T_n({\theta })\) in any subinterval of type-II. Following lemma is necessary for estimate \(M_n\left( \overline{\omega }-\epsilon , \overline{\omega }+\epsilon \right) \).

Lemma 2.2

\(\displaystyle P\left( n(\epsilon ) > 1+ \frac{2n({\alpha }n^3+1)\epsilon + \log {D_n}}{\log 2}\right) < \frac{{\mu }_{3}}{e^{\alpha n^4\epsilon }}\), for some constant \({\mu }\), where \(n(\epsilon )\) denote the number of zeros of \(T_n(\theta )\) in \(|z|\le \epsilon \).

Proof

By following Sambandham and Renganathan (1984) for the function \(T_n(\theta )\), we have

$$\begin{aligned} n(\epsilon )\le \frac{1}{2\pi \log 2} \int _{0}^{2\pi }\log {\left| \frac{T_n(2 \epsilon e^{i\theta })}{T_n(0)}\right| }d{\theta }, \end{aligned}$$
(2.18)

provided \(T_n(\theta )\ne 0\). We have \(T_n(0)=a_0\). This implies \(P(T_n(0)=0)=0\), \(a_0 \ne 0\). Also \(T_n(\theta )\) is a continuous probability distribution for every set \(\{a_{0},~ a_{1},\ldots ,a_{n}\}\). So Eq.(2.15) holds with probability one. If F(x) and \(\phi (t)\) denote respectively the distribution function and the characteristic function of the random variable \(a_k\), then by Gnedenko and Kolmogorov (1954).

$$\begin{aligned} P\left( \{|a_k|>n\}\right) =1-\{F(n)-F(-n)\}< \frac{\mu }{n^{\alpha }} \end{aligned}$$
(2.19)

for some constant \(\mu \). If \(max_{1\le k \le n}|a_k|=h_n\), then from (2.16) we have

$$\begin{aligned} P \left( h_n\le e^{\alpha n^4 \epsilon }\right) \ge 1-\frac{\mu }{e^{n^4 {\alpha }^2 \epsilon }}. \end{aligned}$$
(2.20)

Since \(\left| \sin {(2k\epsilon e^{i\theta })}\right| \le 2 e^{2k\epsilon }\),

$$\begin{aligned} P\left( \left| \frac{T_n(2 \epsilon e^{i\theta })}{T_n(0)}\right| \le \frac{2 e^{\alpha n^4 \epsilon +2n\epsilon D_n}+e^{\alpha n^4\epsilon }}{e^{-\alpha n^4 \epsilon }}\right) >1-\frac{\mu _2}{e^{\alpha n^4 \epsilon }}, \end{aligned}$$
(2.21)

where \(h_n=e^{\alpha n^4 \epsilon }\) and \(D_n=\sum |b_k|\). Then from Eqs. (2.15) and (2.18), we have

$$\begin{aligned} P\left( n(\epsilon )> \left( 1+ \frac{2n\epsilon (\alpha n^3+1)+\log D_n}{\log 2}\right) 2n^4 \alpha \epsilon \right) \le \frac{{\mu }^{\prime }n}{e^{\alpha n^4 \epsilon }}. \end{aligned}$$
(2.22)

\(\square \)

Proof of Theorem 2.1

As there are 4n disjoint interval in type-II like \([\overline{\omega }-\epsilon , \overline{\omega }+\epsilon ]\), \([0,~ \epsilon ]\), \([2\pi -\epsilon , ~ 2\pi ]\) and \(\displaystyle \epsilon =\frac{\pi }{2n}\), we have

$$\begin{aligned} P\left\{ M_n(\lambda )^{\prime }> 4n^2\alpha \pi + \frac{4n^2\alpha \pi \left( \alpha n \pi +\frac{\pi }{n^2}\right) +\log D_n}{\log {2}}\right\} <\frac{ {\mu }_2}{e^{\alpha n^4 \epsilon }}. \end{aligned}$$
(2.23)

So

$$\begin{aligned} M_n({\lambda }^{\prime })=O\left( \frac{4{\mu }^{\prime } n^4 \alpha \pi }{e^{\alpha n\pi /2}}\left( \frac{1}{n}+ \frac{\alpha \pi +\pi /n^2 +\frac{\log D_n}{n}}{\log {2}}\right) \right) \end{aligned}$$
(2.24)

which tends to zero as n tends to \(\infty \). So \(M_n({\lambda }^{\prime })=o(1)\) as n tends to \(\infty \). So when n become larger and larger \(M_n({\lambda }^{\prime })\) does not contribute substantially to \( M_n(0, 2\pi )\). From Eq. (2.12), (2.13) and (2.14) X, Y, Z are periodic function with period \(\pi \). Also in any subinterval of type-I the maximum value of \(|\csc {k\theta }|\) is \(<2n\). Let us take \(b_k=k^{\sigma -\frac{1}{\alpha }}(\sigma > 0)\), we have

$$\begin{aligned} X= & {} \sum _{k=1}^{n}\left| b_{k}\sin {k\theta } \right| ^{\alpha } =\frac{n^{{\alpha }{\sigma }+1}}{{\alpha }{\sigma }+1}\left( 1+O\left( \frac{1}{n}\right) \right) , \end{aligned}$$
(2.25)
$$\begin{aligned} Y= & {} 4 \frac{n^{{\alpha }{\sigma }+1}}{{\alpha }{\sigma }+1} \left[ 1+O\left( \frac{1}{n}\right) \right] , \end{aligned}$$
(2.26)
$$\begin{aligned} Z= & {} 2^{2-{\alpha }} \frac{n^{{\alpha }{\sigma }-{\alpha }+4}}{{\alpha }{\sigma } +2}\left[ 1+O\left( \frac{1}{n}\right) \right] , \end{aligned}$$
(2.27)
$$\begin{aligned} \left| \frac{4XZ-Y^2}{X^2}\right|= & {} 16\left( \frac{ \alpha \sigma + 1}{\alpha \sigma +2}\right) ^2 {n^2}. \end{aligned}$$
(2.28)

Therefore, we have

$$\begin{aligned} M_n(\lambda )= & {} \frac{1}{\pi }\int _{0}^{2\pi }\frac{(4XZ-Y^2)^{1/2}}{X}d\theta \\= & {} \frac{1}{\pi }\int _{0}^{2\pi }4\left( \frac{\alpha \sigma +1}{\alpha \sigma +2}\right) n d\theta \\= & {} 8\left( \frac{\alpha \sigma +1}{\alpha \sigma +2}\right) n =2n. \end{aligned}$$

where \(\sigma =-\dfrac{2}{3\alpha }\), \(1\le \alpha \le 2\). So, we have

$$\begin{aligned} EN_n[0, 2\pi ]\sim 2n+ o(1), ~ ~~~ 1\le \alpha \le {2}. \end{aligned}$$

\(\square \)