Long-term prediction of time series based on fuzzy time series and information granulation

Abstract

Time-series prediction involves forecasting future data by analyzing and modeling historical data. The prediction process involves analyzing and mining various features hidden in the data to predict future data. Compared with one-step forecasting, long-term forecasting is urgently needed, which contributes to capturing the overall picture of future trends and enables discovering prospective ranges and development patterns. This study presents a new long-term forecasting model named the TIG_FTS_SEL model, which is developed by integrating trend-based information granules (TIGs), fuzzy time series, and ensemble learning. First, a time series is converted into a series of equal-length trend-based information granules to capture the fluctuation range and trend information effectively. Then the trend-based information granules are fuzzified to form fuzzy time series, which contributes to realizing the long-term prediction at a high abstract level. Furthermore, different models are used to establish an ensemble long-term forecasting approach by introducing a selection strategy for individual models. The ensemble method performs the prediction tasks using part models with solid prediction performances while disregarding the remaining models. Finally, the developed model is verified by experiments on different time-series datasets. The results demonstrate the sound prediction performance and efficiency of the proposed model.

1 Introduction

Time-series prediction involves forecasting future data by analyzing and modeling historical data, which has been extensively used in various fields, including economics (Kumar et al. 2022), medicine (Fang et al. 2022), industry (Liu et al. 2020), and other fields (Granata and Di Nunno 2021; Huang et al. 2022). Time-series prediction can be performed using different models, the most common models include classical models and machine learning methods.

The classical models, such as exponential smoothing (Brown 1959), AR (Box et al. 1976), MA (Box et al. 1976), ARIMA (Box et al. 1976), are based on statistical principles and are widely used for time-series analysis and forecasting. Implementing these models is relatively straightforward and can yield precise forecasts for particular types of time-series data. Machine learning methods, including the support vector machine (SVM) model (Vapnik 1995) and the artificial neural network (ANN) model (McCulloch and Pitts 1943), offer more flexible ways of handling complex patterns and relationships. However, both traditional statistical models and machine learning methods face challenges in handling uncertain historical data and can provide interpretable semantic results, particularly in long-term prediction tasks.

Fuzzy logic is a mathematical framework for addressing data uncertainty by allowing partial membership in multiple categories. Song and Chissom (1993b) introduce the fuzzy time-series model through the application of fuzzy logic, which aids in extracting rules from uncertain historical data. The classical fuzzy time-series model consists of several key steps: dividing the discourse into intervals, defining the fuzzy sets, establishing fuzzy logic relationships, making inferences and defuzzifying the results.

Several advanced models for fuzzy time-series prediction incorporate the four fundamental steps of the fuzzy time-series framework. Chen (1996) introduces simple arithmetic operations to reduce computation overhead while implementing fuzzy time-series forecasting. Chen and Tanuwijaya (2011) propose a fuzzy time-series model that utilizes automatic clustering techniques to divide the universe of discourse into intervals of varying lengths. Iqbal et al. (2020) introduce an innovative method for fuzzy time-series prediction. This method combines fuzzy clustering and information granules and incorporates a weighted average approach to handle uncertainty in the data series. Intelligent optimization algorithms are used to obtain the optimal interval length, which improves the prediction accuracy of fuzzy time-series models (Chen and Chung 2006; Goyal and Bisht 2023; Chen et al. 2019; Chen and Phuong 2017; Zeng et al. 2019). Wang et al. (2013) present an advanced approach to enhance the prediction accuracy and interpretability of the model by utilizing fuzzy C-means clustering and information granules for determining unequal-length temporal intervals. Lu et al. (2015) construct information granules within the amplitude change space to divide intervals, considering the trend information and distribution of the time-series data.

Fuzzy logic relationships are extracted based on fuzzing discourse intervals to form the "If-Then" interpretable semantic rules. The fuzzy rule-based approach is a frequently used method for data modeling (Cheng et al. 2016; Askari and Montazerin 2015; Chen and Jian 2017; Gautam et al. 2018). The fuzzy rule model is usually combined with machine learning techniques to develop new uncertain data analysis methods. Huarng and Yu (2006) use back propagation neural networks to determine fuzzy relations, and then form a fuzzy time-series model. Subsequently, fuzzy relations are determined using a variety of artificial neural networks, which helps to improve model efficacy. These neural network models include feed-forward artificial neural network (FFANN) (Aladag et al. 2009), Pi-Sigma neural network (Bas et al. 2018), and generalized regression neural network (GRNN) (Panigrahi and Behera 2018). Panigrahi and Behera (2020) apply multiple methods, including long-short term memory (LSTM), support vector machines (SVM), and deep belief network (DBN) to determine fuzzy relations.

The majority of fuzzy time-series models primarily emphasize one-step forecasting, which strives to achieve higher accuracy at the numerical level. However, there is an increasing demand for long-term forecasts. The cumulative error may occur when the one-step prediction model directly attempts to make long-term predictions. Moreover, these models rely solely on a single model for determining fuzzy relations. It is widely acknowledged that prediction models invariably require parameters and data preprocessing, and different approaches can yield varying outcomes. Therefore, selecting a suitable model that can precisely forecast the results of most tasks is challenging. The combination of prediction models is rooted in the understanding that no single model can excel across all the data, but the fusion of multiple models has the potential power to yield an estimate closely aligned with the actual data. Thus, an ensemble approach that assigns weights to individual models is designed from different perspectives (Hao and Tian 2019; Song and Fu 2020; Kaushik et al. 2020), which can usually improve the prediction results compared to using a single model, particularly for weak learners. Several weighted determination methods are suggested to consider the different performance levels of various component models (Adhikari and Agrawal 2014; Maaliw et al. 2021). One of the weighting methods is based on an in-sample error weight scheme, where each weight is assigned inversely proportional to the corresponding in-sample error.

Zadeh (1979) introduces the concept of information granule, which is now considered a crucial foundation in granular computing. By granulating time-series data into information granules, the overall features of the time series within a specific period can be extracted to characterize the dynamic change process, rather than emphasizing precise values at a particular time point. The principle of justifiable granularity (Pedrycz and Vukovich 2001) is a guideline that should be adhered to when converting a numerical time series into a sequence of information granules, enabling the extraction of valuable information from the time series and facilitating the interpretability of the results. Most existing models focus mainly on amplitude information while neglecting the important trend information in time-series data, which is crucial for decision-making. For time series representation, the trend-based information granules (TIGs) developed by Guo et al. (2021) are more representative and informative, encompassing time-series amplitude and trend information. It offers a promising method for the long-term prediction of time series by treating abstract entities as a whole rather than numerical entities.

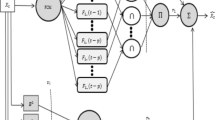
This study develops a new long-term forecasting model named TIG_FTS_SEL that combines TIGs, fuzzy time series, and ensemble learning. In the initial stage of the proposed approach, a given numerical time series is granulated into smaller units called granules. This allows for prediction at the granularity level, where each granule represents a fundamental unit that reflects time-series variation range and trend information. Then the fuzzy C-means clustering algorithm is applied to assign the semantic description for the time series features captured by the information granules. Next, fuzzy relations are determined, and predictions are implemented using a variety of techniques, encompassing back propagation neural network (BPNN), SVM, LSTM, DBN, GRNN, and the fuzzy logic group (FLRG). Finally, an ensemble scheme based on weighted linear combination techniques is employed to integrate the forecasts derived from the individual models. This scheme selects models exhibiting superior performance by defining a predetermined number of models. The study’s main contributions are outlined as follows:

• The proposed TIG_FTS_SEL model implements the prediction at the granularity level, which can reduce the cumulative error.

• The proposed TIG_FTS_SEL model adopts an ensemble approach to alleviate potential problems that may arise from relying solely on a single model, thus improving the prediction performance.

The organization of this study is as follows: an introduction to the theoretical foundations that underlie the construction of TIG and fuzzy time series is presented in Sect. 2. The entire process of the suggested long-term forecasting model is provided in Sect. 3. The experimental results of the proposed TIG_FTS_SEL model and other comparison models on seven datasets are exhibited in Sect. 4. The conclusions obtained are described in Sect. 5.

2 Trend-based information granulation and fuzzy time series

This section discusses the process of creating TIGs, as well as the concepts related to fuzzy time series.

2.1 Trend-based information granulation

Given a numerical time series $\left\{ x_1,x_2,\ldots ,x_n\right\}$, we granulate it by dividing it into q subsequences denoted by $S_1,S_2,\ldots ,S_q$, and set the corresponding time-domain windows to $T_1,T_2,\ldots ,T_q$. We illustrate the formation of TIGs with $S_i=\left\{ x_{i1},x_{i2},\ldots ,x_{in_i}\right\}$ as an example, where $n_i$ denotes the size of $S_i$. Using Cramer’s decomposition theorem as a guide, the sequence $S_i$ can be represented as follows (Guo et al. 2021):

$$\begin{aligned} x_{it}=k_{i}t+c_{i}+u_{it}, \qquad t=1, 2, \ldots , n_i \end{aligned}$$

(1)

where $c_i$ is a constant that denotes the intercept of $S_i$, and $k_i$ represents the slope of $S_i$, they can be estimated by applying the least squares estimation method. Then the interval information granule $\mathrm {\Omega }_{i}^{u}=[a_{i}^{u},b_{i}^{u}]$ is constructed on the residual error sequence $U_i=\left\{ u_{i1}, u_{i2}, \ldots , u_{in_i}\right\}$ using the principle of justifiable granularity. The construction process must fulfill two intuitive requirements (Pedrycz and Vukovich 2001), which are as follows:

1. Coverage: The interval information granule should contain as many data points as possible. The cardinality of $\mathrm {\Omega }_{i}^{u}$ is considered a measure of its coverage, that is, $\rm{card}\left\{ u_{it}|u_{it}\in \mathrm {\Omega }^{u}_{i}\right\}$. In this study, an increasing function $f_1$ of this cardinality is used, and it can be expressed by $f_1(u)=\frac{u}{N}$, where N is the length of $U_i$.

2. Specificity: The length of an interval should be as specific as possible. The function of the size of the interval, i.e., $m( \mathrm {\Omega }_{i}^{u})=\vert {b_{i}^{u}-a_{i}^{u}\vert }$, is used as an indicator of specificity. More generally, this study considers a decreasing function $f_2$ of the length of the interval, which can be represented by $f_2(u)=1-\frac{u}{range}$, where $range=\vert {\max \left( U_i\right) -\min \left( U_i\right) \vert }$.

The principle of justifiable granularity emphasizes the need for a broad scope of coverage while maintaining a high level of specificity. However, specificity tends to decrease as coverage increases. To achieve a balance between these two conflicting aspects, we can rely on an indicator that considers the product of coverage and specificity, i.e., $f=f_1\times f_2$. Using this indicator, the lower bound $a_{i}^{u}$ and upper bound $b_{i}^{u}$ of the information granule $\mathrm {\Omega }_{i}^{u}$ can be determined independently as follows:

$$\begin{aligned} a^{u}_{i,\rm{opt}}= & {} \max _{a^{u}_{i}\le \rm{rep}(U_{i})} V(a^{u}_{i}), \end{aligned}$$

(2)

$$\begin{aligned} b^{u}_{i,\rm{opt}}= & {} \max _{b^{u}_{i}\ge \rm{rep}(U_{i})} V(b^{u}_{i}), \end{aligned}$$

(3)

where:

$$\begin{aligned} \begin{aligned} V(a^{u}_{i})=f_1\left( {\rm{card}\left\{ u_{it}|u_{it}\in [a^{u}_{i},\rm{rep}(U_{i})]\right\} }\right) \times f_2\left( \vert \rm{rep}(U_{i})-a_{i}^{u} \vert \right) , \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} V(b^{u}_{i})=f_1\left( {\rm{card}\left\{ u_{it}|u_{it}\in [\rm{rep}(U_{i}),b_{i}^{u}]\right\} }\right) \times f_2\left( \vert b_{i}^{u}-\rm{rep}(U_{i}) \vert \right) , \end{aligned} \end{aligned}$$

(5)

where $\rm{rep}(U_i)$ takes the mean value of the residual error sequence $U_i$. Following this process, an interval information granule $\mathrm {\Omega }_{i}^{u}=[a_{i}^{u},b_{i}^{u}]$ is constructed for $U_i$. Then the TIG can be represented as $G_i=\left\{ \mathrm {\Omega }_{i},k_i\right\} =\left\{ c_i+\mathrm {\Omega }_{i}^{u},k_i\right\} =\left\{ [c_i+a_{i}^{u},c_i+b_{i}^{u}],k_i\right\} =\left\{ [a_i,b_i],k_i\right\}$.

2.2 Fuzzy time series

Let $U=\left\{ u_1,u_2,\ldots ,u_n\right\}$ be the universe of discourse. A fuzzy set A on U can be represented as $A=\left\{ \mu _A(u_1), \mu _A(u_2), \cdots , \mu _A(u_n) \right\}$, where $\mu _A$ is the membership function of the fuzzy set A, $\mu _A:U \rightarrow \left[ 0,1\right]$, $\mu _A(u_i)$ denotes the membership degree of $u_i$ belonging to the fuzzy set A, and $1 \le i \le n$.

Definition 1

(Song and Chissom 1993b) Let Y(t) be the universe of discourse and the fuzzy sets defined on it are $f_i(t)$ $\left( i=1,2,\ldots \right)$. If F(t) consists of $f_1(t), f_2(t), \ldots$, it is referred to as a fuzzy time series on Y(t).

Definition 2

(Song and Chissom 1993b) Let $F(t)=A_i$ and $F(t-1)=A_j$, where $A_i$ and $A_j$ are fuzzy sets. If F(t) can be determined by $F(t-1)$, the relationship is expressed by a fuzzy logical relationship $A_i \rightarrow A_j$.

Definition 3

(Song and Chissom 1993b) When F(t) is determined by $F(t-1),F(t-2),\ldots ,F(t-n)$, the relationship between them can be characterized as the n-th order fuzzy logical relationship $F(t-n),\ldots ,F(t-2),F(t-1) \rightarrow F(t)$.

Fig. 1

The framework of the proposed TIG_FTS_SEL model

3 The fuzzy time-series model for long-term prediction

This section introduces a fuzzy time-series prediction model that utilizes TIGs, fuzzy time series, and ensemble learning for long-term forecasting. First, a numerical time series is transformed into a sequence of equal-length TIGs, and trend feature datasets, including the intercept dataset, the fluctuation range dataset, and the slope dataset, are constructed. Next, each trend feature dataset is fuzzified using the fuzzy C-means clustering algorithm. Then various machine learning methods are applied to the training dataset to determine fuzzy relations and calculate the prediction error of each model to select several methods with solid performance. The predicted values obtained by the selected models are integrated to produce the final predicted results of the test dataset. The framework of the proposed approach is presented in Fig. 1. For a given time series $x=\left\{ x_1,x_2,\ldots ,x_n\right\}$, the forecasting procedure includes the following steps:

Step 1: Granulate time series and construct trend feature datasets

1) Granulate a given numerical time series.

As discussed in Sect. 2.1, a specific time series x is converted into a collection of TIGs by employing a fixed time window size T, and a granular time series $G=\left\{ G_1,G_2,\ldots ,G_q\right\}$ is formed, where $G_i=\left\{ [a_i,b_i],k_i\right\}$, and $q=n/T$.

2) Construct trend feature datasets.

Through the information granulation process, trend features are extracted from the original time series to construct trend feature datasets. Table 1 presents constructed trend feature datasets, including the intercept dataset, the fluctuation range dataset, and the slope dataset. The slope $k_i$, which is determined by Eq. (1), represents the changing trend of $G_i$. On the other hand, the intercept $a_i$ characterizes the start level of the changing trend of $G_i$. The fluctuation range can be calculated by $(b_i-a_i)$, indicating the fluctuation level of $G_i$.

Step 2: Fuzzify each trend feature dataset.

1) Clustering for each trend feature dataset.

Three trend feature datasets are clustered using the fuzzy C-means clustering algorithm, and clustering prototypes for each cluster are generated.

2) Divide the universe of discourse of each trend feature dataset into intervals of unequal length.

The clustering prototypes are sorted from smallest to largest for each trend feature dataset. Let $V_i$ and $V_{i+1}$ be two adjacent clustering prototypes, defining the lower bound $\rm{interval}\_L_{i}$ and upper bound $\rm{interval}\_U_{i}$ of the i-th interval as follows:

$$\begin{aligned} \rm{interval}\_U_{i}= & {} \frac{V_{i}+V_{i+1}}{2}, \end{aligned}$$

(6)

$$\begin{aligned} \rm{interval}\_L_{i+1}= & {} \rm{interval}\_U_{i}. \end{aligned}$$

(7)

Equations (6) and (7) are not applicable for determining the lower bound $\rm{interval}\_L_{1}$ of the first interval and the upper bound $\rm{interval}\_U_{c}$ of the last interval. Hence, these values are computed in the following form:

$$\begin{aligned} \rm{interval}\_L_{1}= & {} V_1-\left( \rm{interval}\_U_{1}-V_1\right) , \end{aligned}$$

(8)

$$\begin{aligned} \rm{interval}\_U_{c}= & {} V_c+\left( V_c-\rm{interval}\_L_{c}\right) , \end{aligned}$$

(9)

where c is the number of clusters. Following the abovementioned calculation procedure, the interval of unequal length is obtained. The midpoint $\rm{interval}\_M_{i}$ of the i-th interval is determined based on its lower bound $\rm{interval}\_L_{i}$ and upper bound $\rm{interval}\_U_{i}$:

$$\begin{aligned} \rm{interval}\_M_{i}=\frac{\rm{interval}\_L_{i}+\rm{interval}\_U_{i}}{2}. \end{aligned}$$

(10)

3) Define the fuzzy sets on the universe of discourse of each trend feature dataset.

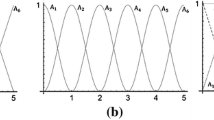
Linguistic terms can be defined on a set of obtained intervals $u_1,u_2,\ldots ,u_r$ and can be represented in the following form using fuzzy sets $A_i$:

$$\begin{aligned} A_i=f_{i1}/u_1+f_{i2}/u_2+\ldots +f_{ir}/u_r, \end{aligned}$$

(11)

where $f_{ij}\in \left[ 0,1\right]$ is the membership degree of the interval $u_j$ belonging to the fuzzy set $A_i$, which is defined as follows:

$$\begin{aligned} f_{ij} = {\left\{ \begin{array}{ll} 1 & j=i \\ 0.5 & j=i-1 \; or ; j=i+1 \\ 0 & \rm{otherwise}. \end{array}\right. } \end{aligned}$$

(12)

Thus, each interval is associated with all fuzzy sets at different membership degrees. In this way, fuzzy sets on the intercept dataset, the fluctuation range dataset, and the slope dataset can be defined, respectively.

Table 1 Trend feature datasets

4) Fuzzify the element of each trend feature dataset.

If an element belongs to the interval $u_i$, it is fuzzified into the fuzzy set $A_i$. At this point, the fuzzification of parameters is achieved.

Step 3: Extract fuzzy relations.

After fuzzification of the three trend feature datasets, it is necessary to determine fuzzy relations. In this study, fuzzy relations are determined using BPNN (Rumelhart et al. 1986), SVM (Vapnik 1995), LSTM (Hochreiter and Schmidhuber 1997), DBN (Hinton et al. 2006), GRNN (Specht et al. 1991), and FLRG (Song and Chissom 1993a), and the corresponding models are referred to as TIG_FTS_BPNN, TIG_FTS_SVM, TIG_FTS_LSTM, TIG_FTS_DBN, TIG_FTS_GRNN, and TIG_FTS_RULE, respectively. The index number i of the fuzzy set $A_i$ is taken as the input and output of the models. For instance, consider three observations of $\left[ A_5,A_4,A_1\right]$, where the input values of $\left[ A_5,A_4\right]$ are 5 and 4, and the target value of $A_1$ is 1. In this step, min–max normalization is performed on the fuzzified data to constrain its values within the range between zero and one. The normalized value of an element in the fuzzified data can be calculated by dividing the difference between the element and the minimum value of the fuzzified data by the difference between the maximum and minimum values of the fuzzified data.

Step 4: Select individual models and defuzzfied.

The trained models are selected based on their performance on the training set. The predicted index number is obtained by de-normalizing the model’s output, and it is subsequently rounded to the nearest integer. The midpoint of the interval that corresponds to the predicted index number is defined as the defuzzified prediction. When the index number exceeds the number of intervals, the midpoint of the final interval is employed as the defuzzified prediction. When the index number is less than one, the midpoint of the first interval is applied as the defuzzified prediction. The model’s defuzzified prediction provides predictions of the trend variations, which are used to estimate the prediction of the actual data. Assuming that the trend features of the $(N+1)$-th granule are predicted, this granule can be translated into specific predictions by:

$$\begin{aligned} \hat{y}_{N+1}\_L& = k_{N+1}^{*}\times t+a_{N+1}^{*}, \end{aligned}$$

(13)

$$\begin{aligned} \hat{y}_{N+1}\_U & = \hat{y}_{N+1}\_L+(b-a)_{N+1}^{*}, \end{aligned}$$

(14)

where $t\in \left[ 1,T\right]$, T represents the length of equal-length granulation, $a_{N+1}^{*}$ denotes the predicted beginning level of the $\left( N+1\right)$-th granule, $(b-a)_{N+1}^{*}$ indicates the predicted fluctuation range of the $\left( N+1\right)$-th granule, $k_{N+1}^{*}$ signifies the predicted changing trend of the $\left( N+1\right)$-th granule, $\hat{y}_{N+1}\_L$ represents the lower bound of the prediction and $\hat{y}_{N+1}\_U$ represents the upper bound of the prediction. To evaluate the prediction performance, the final prediction is calculated as follows:

$$\begin{aligned} \hat{y}_{N+1}=\left( \hat{y}_{N+1}\_L+\hat{y}_{N+1}\_U\right) /2. \end{aligned}$$

(15)

In this way, predictions on the training set can be obtained from individual model. To assess the efficacy of individual model on the training set, the root mean square error (RMSE) is utilized as an evaluation indicator. The models are then ranked according to their RMSE values, where lower values signify higher rankings. Based on these rankings, several models with high rankings are selected to make predictions on the test set.

Step 5: Ensemble predictions.

By combining the prediction results of several component models, the ensemble method improves the overall performance and mitigates the risk associated with model selection. A frequently employed ensemble technique based on a parallel strategy entails aggregating the prediction outcomes of multiple models that forecast time-series data. Let $y=[y_1,y_2,\ldots ,y_n]$ represent the test data, and $\hat{y}^{i}=[\hat{y}_1^i,\hat{y}_2^i,\ldots ,\hat{y}_n^i]$ denote the corresponding prediction outcome generated by the i-th model computed by Eqs. (13)–(15). The predictions of the models are linearly weighted as follows:

$$\begin{aligned} \hat{y}_{k}=w_1\hat{y}_k^1+w_2\hat{y}_k^2+\ldots +w_p\hat{y}_k^p=\sum _{u=1}^{p}w_u\hat{y}_k^u. \end{aligned}$$

(16)

Here, p represents the number of selected models, $\hat{y}_k^u$ is the predicted output of each model for the k-th test data, and $w_u$ represents the importance assigned to each model, which is calculated as follows:

$$\begin{aligned} w_i= & {} \frac{w_{i}'}{\sum _{u=1}^{p}w_{u}'}, \end{aligned}$$

(17)

$$\begin{aligned} w_{i}'= & {} \frac{1}{\rm{RMSE}(i)}, \end{aligned}$$

(18)

where $\rm{RMSE}(i)$ represents the prediction error of the i-th model on the training set. To guarantee that models with relatively minor errors on the training set acquire more weight and vice versa, weight is assigned in inverse proportion to the models’ errors. The proposed TIG_ FTS_SEL model’s predictions come true through the previously described process.

Step 6: Examine the performance of the TIG_FTS_SEL model.

We use the root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) to examine the performance of the proposed TIG_FTS_SEL model, and they are calculated as follows:

$$\begin{aligned} RMSE= & {} \sqrt{\frac{1}{L }\sum _{t=1}^{L }(\hat{y}-y_{t})^{2}}, \end{aligned}$$

(19)

$$\begin{aligned} MAPE= & {} \frac{1}{L }\sum _{t=1}^L \frac{|\hat{y}-y_{t} |}{y_{t}}\times 100, \end{aligned}$$

(20)

$$\begin{aligned} MAE= & {} \frac{1}{L }\sum _{t=1}^L |\hat{y}-y_{t} |, \end{aligned}$$

(21)

where L denotes the number of predicted data, and $\hat{y}$ and $y_{t}$ represent the predicted and actual values, respectively.

4 Experiments

In this section, the experiments are conducted to examine the performance of the proposed TIG_FTS_SEL model. The experiments are performed on different time-series datasets, including Mackey–Glass time series, Melbourne temperature time series (MT time series), Zuerich monthly sunspot numbers, the minimum daily temperature of Cowichan Lake Forestry of British Columbia (daily temperature time series), standard’s and Poor’s 500 (stock index time series), monthly mean total sunspot time series, and historical levels of Lake Erie time series. In addition, the proposed model is compared with two types of models: numerical time-series prediction models (AR (Box et al. 1976), MA (Box et al. 1976), ARIMA (Box et al. 1976), NARnet (Benmouiza and Cheknane 2013), linear SVR (Hsia and Lin 2020)) and granular time-series models (LFIGFIS (Yang et al. 2017), IFIGFIS (Yang et al. 2017), TFIGFIS (Yang et al. 2017), Dong and Pedrycz’s model (2008), Wang et al.’s model (2015), Feng et al.’s model (2021)). Furthermore, the proposed TIG_FTS_SEL model is compared with the individual component model and the traditional ensemble method based on the involved component models (TIG_FTS_EL). Based on empirical evidence, the performance of the ensemble model tends to reach a state of saturation after employing approximately four or five individual methods (Makridakis and Winkler 1983). This suggests that the prediction performance of the ensemble model remains relatively stable as the number of component models increases. In this work, we take four approaches from different component models and merge them, discarding the other approaches.

4.1 Experiment on Mackey–Glass time series

The following delay differential equation yields the Mackey–Glass time series, which is a classic description of chaotic systems:

$$\begin{aligned} \frac{Y(t)}{dt}=\frac{0.2Y(t-\tau )}{1+Y^{10}(t-\tau )}-0.1Y(t). \end{aligned}$$

(22)

Fig. 2

Mackey–Glass time series

Fig. 3

Comparison between actual and predicted values

Table 2 Trend feature datasets of the Mackey–Glass time series

Table 3 Linguistic values

Let $Y(t)=0$, $\tau =1.7$, and a chaotic time series with 1201 values is obtained, as shown in Fig. 2. For the purpose of comparison, the time window length T is set to 13, which converts the time series into 92 information granules and a granular time series $G=\left\{ G_1,G_2,\ldots ,G_{92}\right\}$ is obtained. The experimental test set consists of the final 3 information granules, whereas the first 89 information granules are used as the training set. Further, the trend feature datasets are constructed following the procedure described in Sect. 3, as shown in Table  2. Using the fuzzy C-means algorithm, the unequal-length interval of each trend feature dataset is obtained by Eqs. (6)–(9). Furthermore, the fuzzy sets $A_i$, $B_i$, and $C_i$ ($i=1,2,\ldots ,13$) for the intercept dataset, the fluctuation range dataset, and the slope datasets are defined using Eqs. (11) and (12). At the same time, linguistic terms are assigned to every defined fuzzy set to describe each trend feature dataset. The corresponding linguistic descriptions for trend feature datasets are presented in Table  3. In this study, fuzzy relations are determined using BPNN, SVM, LSTM, GRNN, DBN, and FLRG, where the input and output of the models are the index number of the fuzzy set. To ensure the fairness of the comparison experiment, all models are assigned the same lag value of 2, indicating that they have the same order. The fitting errors of the individual models on the training set are determined using the RMSE as an evaluation indicator. The models’ performances on this dataset are ranked according to the fitting error, as presented in Table 4. The top four models that are selected for combination include the TIG_FTS_GRNN, TIG_FTS_SVM, TIG_FTS_LSTM, and TIG_FTS_DBN models.

Each of the four selected models is utilized for predicting the test data, and their prediction results are combined using a linearly weighted ensemble approach. For the prediction by a single model, TIG_ FTS_ GRNN is selected as an example to illustrate the prediction of test data $x_{1159}$ $(1159=89\times 13+2)$. The TIG_FTS_GRNN model predicts the index numbers for each parameter of $G_{90}$ as 12, 6, and 8. The obtained defuzzification results are 1.2345, 0.0438, and 0.0050, representing the trend characteristics of $G_{90}$. The predictions of the lower and upper bounds of $x_{1159}$ are obtained as follows:

Table 4 Ranking results of different models

$$\begin{aligned} \hat{x}_{1159}\_L= & {} 0.0050\times 2+1.2345=1.2445,\\ \hat{x}_{1159}\_U= & {} \hat{x}_{1159}\_L+0.0438=1.2883. \end{aligned}$$

To evaluate the performance of the model, the final prediction of the TIG_ FTS_ GRNN model for $x_{1159}$ is calculated as follows:

$$\begin{aligned} \begin{aligned} \hat{x}_{1159}^1=&\left( \hat{x}_{1159}\_L+\hat{x}_{1159}\_U\right) /2\\ =&\left( 1.2445+1.2883\right) /2\\ =&1.2664. \end{aligned} \end{aligned}$$

Similarly, the predictions $\hat{x}_{1159}^2$, $\hat{x}_{1159}^3$, and $\hat{x}_{1159}^4$ of $x_{1159}$ are obtained using the TIG_FTS_SVM, TIG_ FTS_LSTM, and TIG_FTS_DBN models.

Finally, the weighted linear ensemble method is used to combine the four models, and weight is assigned to each model according to its performance on the training set, which is calculated as follows:

$$\begin{aligned} \begin{aligned} w=&\left[ w_1,w_2,w_3,w_4\right] \\ =&\left[ \frac{w'_1}{\sum _{i=1}^{4}w'_i}, \frac{w'_2}{\sum _{i=1}^{4}w'_i},\frac{w'_3}{\sum _{i=1}^{4}w'_i},\frac{w'_4}{\sum _{i=1}^{4}w'_i}\right] \\ =&\left[ 0.3034,0.2459,0.2335,0.2172\right] , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} w'=&\left[ w'_1,w'_2,w'_3,w'_4\right] \\ =&\left[ \frac{1}{0.0693},\frac{1}{0.0856},\frac{1}{0.0901},\frac{1}{0.0969}\right] \\ =&\left[ 14.4300,11.6822,11.0988,10.3199\right] . \end{aligned} \end{aligned}$$

The final prediction $\hat{x}_{1159}$ of $x_{1159}$ obtained by the ensemble method is calculated as follows:

$$\begin{aligned} \hat{y}_{1159}=w_1\hat{x}_{1159}^1+w_2\hat{x}_{1159}^2+w_3\hat{x}_{1159}^3+w_4\hat{x}_{1159}^4=1.2136. \end{aligned}$$

Table 5 RMSE, MAPE, and MAE comparisons for Mackey–Glass time series

Table 6 RMSE, MAPE, and MAE comparisons for MT time series

Table 7 RMSE, MAPE, and MAE comparisons for Zuerich monthly sunspot numbers time series

Predictions of the other test data can be obtained by conducting the aforementioned procedures. The comparison of the prediction results of the TIG_FTS_SEL model and the actual data is presented in Fig. 3, where it can be seen that the trend of the predicted values aligns with that of the actual data. In addition, the TIG_FTS_SEL model is compared with the traditional linear ensemble model involving all component models (TIG_FTS_EL), granular models, and numerical models, as well as component models, including TIG_FTS_BPNN, TIG_FTS_SVM, TIG_FTS_LSTM, TIG_FTS_GRNN, TIG_FTS_DBN, and TIG_FTS_RULE. The models’ performances are evaluated using RMSE, MAPE, and MAE. In Table 5, the prediction performances of the TIG_FTS_SEL model and comparison models on this dataset are presented. It is generally believed that the smaller the values of RMSE, MAPE, and MAE are, the better the performance of the prediction model is. Based on the results presented in Table 5, the TIG_FTS_SEL model exhibits the lowest RMSE, MAPE, and MAE values among all the models. This suggests that the TIG_FTS_SEL model outperforms the other models in terms of prediction effectiveness. In general, both the proposed selection-based ensemble model (TIG_FTS_SEL) and the traditional ensemble model based on the involved component models (TIG_FTS_EL) exhibit superior performance compared to the individual models. In addition, the proposed TIG_FTS_SEL model contributes to improving the prediction performance of the TIG_FTS_EL model. This can be explained by the fact that not all models yield accurate predictions for a specific time series. Thus, the ensemble long-term forecasting approach with a selection strategy might make the model perform better in making predictions.

4.2 Experiment on MT time series

The dataset utilized in this experiment comprises a temporal sequence of maximum daily temperatures in Melbourne, Australia, spanning from 1981 to 1990, including 3650 data points. In this experiment, the time-series data are divided into 40 time-domain windows, each of which contains 91 data points. The training set covers the previous 38 temporal windows for prediction purposes, while the last 2 are reserved for testing. The model order is fixed at two throughout the experiment. Table 6 shows the prediction errors in terms of RMSE, MAPE, and MAE obtained by the TIG_FTS_SEL model and comparative models on the test samples. As shown in Table 6, the TIG_FTS_SEL model outperforms all component models except for the component model TIG_FTS_DBN, which has a lower MAPE. Compared to the related numerical and granular models, the TIG_FTS_SEL model exhibits superior performance in terms of MAE and is second only to the LFIGFIS model in terms of RMSE and MAPE. Although the TIG_FTS_EL model demonstrates sound prediction performance in terms of MAPE, the TIG_FTS_SEL model outperforms it when evaluating the results using RMSE and MAE.

Table 8 RMSE comparisons for daily temperature time series

Table 9 MAPE comparisons for stock index time series

Table 10 RMSE comparisons for monthly mean total sunspot time series

Table 11 RMSE comparisons for historical levels of Lake Erie time series

4.3 Experiment on Zuerich monthly sunspot numbers time series

The Zurich monthly sunspot numbers time series covers 2820 data points spanning from 1749 to 1983. Setting the time-domain window size to a fixed length of 33 results in the generation of 84 information granules. The initial 79 information granules are utilized as the training set for predicting the subsequent 2 information granules. Table 7 presents the evaluation indicator values of the TIG_FTS_SEL model and the other comparison models. The table shows that the TIG_FTS_SEL model has the smallest evaluation indicator values, except when MAPE is used as an evaluation indicator. In that case, the TIG_FTS_SEL model is second to the traditional ensemble model based on all component models (TIG_FTS_EL) and the component model TIG_FTS_BPNN. This suggests that the TIG_FTS_SEL model has the highest prediction performance.

4.4 Experimental summary

Supplementary experiments are conducted on four distinct time-series datasets, including daily temperature time series (minimum daily temperature of Cowichan Lake Forestry of British Columbia recorded from April 1, 1979 to May 30, 1996), stock index time series (Standard’s and Poor’s 500 (S &P 500) time series from January 3, 1994 to October 23, 2006), monthly mean total sunspot time series (spanning from January 1749 to December 2019), and historical levels of Lake Erie time series (spanning from January 1860 to September 2016). The performances of the TIG_FTS_SEL model, along with those of the other comparative models, in predicting these datasets are shown in Tables 8, 9, 10 and 11. Regarding the RMSE and MAPE values on these datasets, both the proposed method and the conventional method within the ensemble framework exhibit superior performance compared to their corresponding component models. Also, the proposed TIG_FTS_SEL method, based on the ranking selection model, enhances the prediction performance of the traditional ensemble method (TIG_FTS_EL) that relies on all component models. In addition, compared to the existing granular models and numerical models, the proposed TIG_FTS_SEL model achieves sound evaluation indicator values.

5 Conclusion

This study proposes a long-term forecasting method named TIG_FTS_SEL, which is based on trend information granules, fuzzy time series, and ensemble learning. In the proposed method, the time series is initially granulated to extract the valuable information inherent in the original time series effectively, enabling prediction at the granular level and reducing accumulative errors. Then the trend features captured by information granules are used to construct the trend feature datasets, which are further fuzzified by applying the fuzzy C-means clustering algorithm to enable linguistic descriptions of these features. In addition, the proposed model uses different methods to determine fuzzy relations, and constructs an ensemble model for predictive purposes. Instead of merging all models, the ensemble model just incorporates those that outperform on the training set. Generally, this method exhibits superior performance on datasets compared to its component models and the ensemble method based on all component models, mitigating the potential drawbacks of relying on a single model. Through comparison experiments with other granular models and numerical models on seven available time-series datasets, the validity of the proposed model is confirmed.