Several hybrid aggregation operators for triangular intuitionistic fuzzy set and their application in multi-criteria decision making

Abstract

In this paper, on the basis of analyzing some existing limitations in the operational laws defined for triangular intuitionistic fuzzy numbers (TIFNs), we first proposed some improved operational laws for TIFNs. Then, based on new operational laws, we developed some aggregation operators for TIFNs, such as triangular intuitionistic fuzzy-weighted averaging operator, triangular intuitionistic fuzzy geometric operator, triangular intuitionistic fuzzy-ordered-weighted averaging operator, triangular intuitionistic fuzzy-ordered-weighted geometric operator, triangular intuitionistic fuzzy hybrid averaging operator, and triangular intuitionistic fuzzy hybrid geometric operators, and discussed some desirable properties of these operators. Furthermore, based on these aggregation operators, we developed a multi-criteria decision-making (MCDM) method in which the criteria values were represented by TIFNs. Finally, a numerical example was used to show the practicality and effectiveness of the proposed MCDM method by comparing the proposed method with the existing methods.

1 Introduction

With the arising complexities of decision-making environment, the decision makers felt difficulties to get a decision within appropriate time using imprecise, vague, and uncertain information (Liu and Li 2017a; Liu and Shi 2017; Liu and Tang 2016; Liu and Wang 2017; Liu et al. 2016; Chen and Hong 2014a, b; Qin 2017; Pedrycz and Chen 2015; Chen et al. 2014). Intuitionistic fuzzy sets (IFSs) proposed by Atanassov (1986) are one of the most admissible theories to handle the impreciseness, vagueness, and uncertainties (Garg 2016; Jiang et al. 2017; Xu and Yager 2006; Liu 2017; Liu and Chen 2017; Liu and Li 2017b; Liu et al. 2017; Xu 2007a, b; Xu and Gou 2017; Chen et al. 2016a, b, c; Chen and Chang 2015, 2016; Chen and Randyanto 2013). However, in some circumstances, it is difficult to give the preference of decision makers by a crisp number and it is suitable to manifest the preference of decision makers by TIFNs (Liu and Yuan 2007). The basic feature of TIFNs is that the values of its truth-membership and falsity-membership functions are triangular fuzzy numbers rather than exact numbers. Now, some research achievements for TIFNs have been done. Liang et al. (2014) introduced the TIFWG operator, TIFOWG operator, and the TIFHG operator for TIFNs and applied them to multiple-attribute group decision making (MAGDM) with TIFNs. Wang (2008a, b) introduced the fuzzy number intuitionistic fuzzy set (FNIFS) and proposed some aggregation operators for FNIFSs, such as FNIFOWA operator, FNIFHA operator, FNIFWG operator, FINIFOWG operator, and FNIFHG operator then applied them to MCDM problems with FNIFNs. Recently, Zhou and Chang (2014) proposed some Hamacher aggregation operators for FNIFNs and applied them to MCDM problems with FNIFNs. Wei et al. (2010) proposed some induced ordered weighted geometric (I-TIFOWG) operators for TIFNs to deal with MCDM problems. More and more MCDM methods (Qiu 2011; Wang 2012; Zhao et al. 2015) have been applied under triangular intuitionistic fuzzy (TIF) environment. However, these methods can only deal with decision-making problems with TIFNs and cannot handle trapezoidal intuitionistic fuzzy information. To solve these problems, Ye (2014) proposed the concepts of trapezoidal intuitionistic fuzzy sets (TrIFSs), trapezoidal intuitionistic fuzzy numbers (TrIFNs), and defined some operational laws, score and accuracy functions. Furthermore, they defined some prioritized aggregation operators for TrIFNs, such as TRIFPWA operators and prioritized weighted geometric (TrIFPWG) operator for TrIFNs, and developed an MCDM method based on these prioritized aggregation operators Liu and Su (2010). The proposed trapezoidal fuzzy linguistic sets and defined some aggregation operators applied them to MCDM problems. Moreover, Liu and Qin (2017) proposed Maclaurin symmetric mean (MSM) operators of linguistic intuitionistic fuzzy numbers, and Şahin and Liu (2017) proposed possibility induced aggregation operator for simplified neutrosophic sets and applied them MCDM. Ye (2015) introduced the concept of trapezoidal neutrosophic set and defined some aggregation operators and applied them to MCDM. Ye (2016) proposed projection and bidirectional projection measures for single-valued neutrosophic sets, and based on these, measures presented MCDM method to solve mechanical design scheme problem.

Practically, all the above studies are reasonable under the conditions that truth-membership or falsity-membership degrees are not equal to zero. However, suppose that there are two TIFNs $\tilde{a}_{1}$ and $\tilde{a}_{2}$, such that $T\left( {\tilde{a}_{1} } \right) = 0$ and $T\left( {\tilde{a}_{2} } \right) \ne 0$, or $F\left( {\tilde{a}_{1} } \right) = 0$ and $F\left( {\tilde{a}_{2} } \right) \ne 0$, then based on the aggregation operators defined for TIFNs or for FNIFNs, the overall aggregated value of either truth-membership or falsity-membership values is zero. In other words, there is no effect of other degrees on the overall aggregated values either truth membership or falsity membership. Moreover, it has been pointed out that the overall truth-membership degree (or falsity-membership degree) is independent of their relative falsity-membership degree (or truth-membership degree) in the aggregation process. Therefore, the aggregated results are unacceptable. Hence, there is a need to modify these existing operations by a proper considering the correlation between truth-membership degree and falsity-membership degree.

Thus, the objective of this article is to propose some modified operations for TIFNs. Then, based on these operational laws, we propose some aggregation operators, such as triangular intuitionistic fuzzy-weighted averaging (TIFWA) operator, triangular intuitionistic fuzzy-weighted geometric (TIFWG) operator, triangular intuitionistic fuzzy-ordered-weighted averaging (TIFOWA) operator, triangular intuitionistic fuzzy-ordered-weighted geometric (TIFOWG) operator, triangular intuitionistic fuzzy hybrid averaging (TIFHA) operator, and triangular intuitionistic fuzzy hybrid geometric (TIFHG) operator to overcome the limitations of the existing operators. Then, we apply them to MCDM problems under TIF information. Finally, a comparison has been made with the existing MCDM methods.

The rest of the article is arranged as follows. In Sect. 2, some basic definitions of TIFNs are given. In Sect. 3, we define some improved operational laws for TIFNs. In Sect. 4, based on these operations, some weighted averaging aggregation and weighted geometric operators are developed. In Sect. 5, some ordered weighted averaging aggregation, ordered weighted geometric operators, and hybrid aggregation operators for TIFNs are proposed. In Sect. 6, we develop an MADM method to handle MADM problem under TIF environment. In Sect. 7, a numerical example adapted from Herrera et al. (2000) is used to show the practicality and effectiveness of the proposed method, and comparison and discussion are done. At the end, the concluding remarks and future work are given.

2 Preliminaries

In this section, some basic definitions and operational laws of TIFSs are briefly reviewed.

2.1 Triangular intuitionistic fuzzy set and their operations

Definition 1 (Liu and Yuan 2007)

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U}$ be a non-empty universe of discourse set. Then, a triangular intuitionistic set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}$ in $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U}$ is defined and mathematically represented as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} = \left\{ {\left\langle {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ,\,T_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ),F_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )\,} \right\rangle |\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} \in \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{U} } \right\}$$

(1)

where $T_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )$ and $F_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )$ are two triangular fuzzy numbers $T_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{1} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )\,,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )} \right)$ and $F_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{1} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )\,,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} )} \right)$ satisfying the condition $0 \le \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }}^{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) \le 1$. For simplicity, let $T_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) = \left\langle {p,\,q,\,r} \right\rangle$ and $F_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M} }} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ) = \left\langle {t,\,u,\,v} \right\rangle$, then the TIFN is denoted by $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \left\langle {\left( {p,\,q,\,r} \right),\,\left( {t,\,u,\,v} \right)} \right\rangle .$

Definition 2 (Liu and Yuan 2007)

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \langle {( {p,\,q,\,r} ),\,( {t,\,u,\,v} )} \rangle ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \langle {( {p_{1} ,\,q_{1} ,\,r_{1} } ),\,( {t_{1} ,\,u_{1} ,\,v_{1} } )} \rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \langle {( {p_{2} ,\,q_{2} ,\,r_{2} } ),\,( {t_{2} ,\,u_{2} ,\,v_{2} } )} \rangle$ be any three TIFNs and $\chi \ge 0$. Then, some operational laws for TIFNs are defined as follows:

$$(1)\,\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} = \left\langle {\left( {p_{1} + p_{2} - p_{1} p_{2} ,\,q_{1} + q_{2} - q_{1} q_{2} ,\,r_{1} + r_{2} - r_{1} r_{2} } \right),\,\left( {t_{1} t_{2} ,\,u_{1} u_{2} ,\,v_{1} v_{2} } \right)} \right\rangle,$$

(2)

$$(2)\;\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {p_{1} p_{2} ,\,q_{1} q_{2} ,\,r_{1} r_{2} } \right),\,\left( {t_{1} + t_{2} - t_{1} t_{2} ,\,u_{1} + u_{2} - u_{1} u_{2} ,\,v_{1} + v_{2} - v_{1} v_{2} } \right)} \right\rangle,$$

(3)

$$(3)\,\,\,\,\,\,\,\,\;\chi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \langle {( {1 - ( {1 - p} )^{\chi } ,\,1 - ( {1 - q} )^{\chi } ,\,1 - ( {1 - r} )^{\chi } } ),\,( {t^{\chi } ,\,u^{\chi } ,\,v^{\chi } } )} \rangle,$$

(4)

$$(4)\,\,\,\,\,\,\,\,\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{\chi } = \left\langle {\left( {p^{\chi } ,\,q^{\chi } ,\,r^{\chi } } \right),\,\left( {1 - \left( {1 - t} \right)^{\chi } ,\,1 - \left( {1 - u} \right)^{\chi } ,\,1 - \left( {1 - v} \right)^{\chi } } \right)} \right\rangle .$$

(5)

The above-defined operational laws for TIFNs have some limitations which can be discussed in an example given below.

Example 1

Three groups of professors $P_{j} \;(j = 1,\,2,\,3)$ want to select a student for research project among three students $a_{i} \;(i = 1,\,2,\,3)$, and the selection and rejection rating of the three students from the three groups of professors is given by TIFN $L_{ij} (i,\,j = 1,\,2,\,3).$ Suppose $L_{11} = \langle {( {0.1,\,0.2,\,0.3} ),\,( {0.3,\,0.4,\,0.5} )} \rangle ,$ $\,L_{12} = \langle {( {0.3,\,0.4,\,0.5} ),\,( {0.1,\,0.1,\,0.2} )} \rangle$, and $L_{13} = \langle {( {0.4,\,0.5,\,0.6} ),\,( {0.0,\,0.0,\,0.0} )} \rangle$, and the corresponding importance degree of the groups of three professors is $\omega = ( {0.3,\,0.2,\,0.4} )^{T} ;$ then, by the operations defined in Definition 2, we get the overall triangular intuitionistic fuzzy information $L_{1} = \mathop \oplus \nolimits_{i = 1}^{3} \omega_{i} L_{1i} =$ $\left\langle {\left( {0.2178,\,0.3116,\,0.4072} \right),\,\left( {0.0,\,0.0,\,0.0,\,0.0} \right)} \right\rangle .$ That is to say that $F_{{L_{1j} }} (j = 1,\,2)$ have no effects on the overall result. This is an undesirable property. Obviously, these operations can handle a situation in which membership and non-membership functions are not equal to zero. In other words, if either of the membership or no-membership degree equals to zero, respectively, then there is no effect of the other membership or no-membership degrees on the overall aggregated result in the aggregation process.

Definition 3 (Wang 2012)

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \left\langle {\left( {p,\,q,\,r} \right),\,\left( {t,\,u,\,v} \right)} \right\rangle$ be a TIFN. Then, the score and accuracy functions defined by Wang (2012) are as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} ) = \frac{p + 2q + r}{4} - \frac{t + 2u + v}{4},$$

(6)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} ) = \frac{p + 2q + r}{4} + \frac{t + 2u + v}{4}.$$

(7)

Definition 4

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {p_{1} ,\,q_{1} ,\,r_{1} } \right),\,\left( {t_{1} ,\,u_{1} ,\,v_{1} } \right)} \right\rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {p_{2} ,\,q_{2} ,\,r_{2} } \right),\,\left( {t_{2} ,\,u_{2} ,\,v_{2} } \right)} \right\rangle$ be any two TIFNs. Then, the comparison rules for comparing TIFNs are defined as follows:

• 1. If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ) > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ),$ then $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} .$

• 2. If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ) > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ),$ then $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} .$

• 3. If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ),$ then $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} .$

3 Improved operational laws for TIFNs

In this section, we propose some improved operational laws for TIFNs.

Definition 5

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \left\langle {\left( {p,\,q,\,r} \right),\,\left( {t,\,u,\,v} \right)} \right\rangle ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {p_{1} ,\,q_{1} ,\,r_{1} } \right),\,\left( {t_{1} ,\,u_{1} ,\,v_{1} } \right)} \right\rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {p_{2} ,\,q_{2} ,\,r_{2} } \right),\,\left( {t_{2} ,\,u_{2} ,\,v_{2} } \right)} \right\rangle$ be any three TIFNs and $\psi \ge 0$. Then, new operational laws for TIFNs are defined as follows:

$$\begin{aligned} (1)\,\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} &= \left\langle {\left( {1 - \left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right),\,1 - \left( {1 - q_{1} } \right)\left( {1 - q_{2} } \right),1 - \left( {1 - r_{1} } \right)\left( {1 - r_{2} } \right)} \right),} \right. \\ &\left( {\left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right) - \left( {1 - \left( {p_{1} + t_{1} } \right)} \right)\left( {1 - \left( {p_{2} + t_{2} } \right)} \right),\left( {1 - q_{1} } \right)\left( {1 - q_{2} } \right) - \left( {1 - \left( {q_{1} + u_{1} } \right)} \right)\left( {1 - \left( {q_{2} + u_{2} } \right)} \right),} \right. \\ & \left. {\left. {\left( {1 - r_{1} } \right)\left( {1 - r_{2} } \right) - \left( {1 - \left( {r_{1} + v_{1} } \right)} \right)\left( {1 - \left( {r_{2} + v_{2} } \right)} \right)} \right)} \right\rangle, \\ \end{aligned}$$

(8)

$$\begin{aligned} (2)\,\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} &= \langle {( {( {1 - t_{1} } )( {1 - t_{2} } ) - ( {1 - ( {p_{1} + t_{1} } )} )( {1 - ( {p_{2} + t_{2} } )} ),} } \hfill \\ & ( {1 - u_{1} } )( {1 - u_{2} } ) - ( {1 - ( {q_{1} + u_{1} } )} )( {1 - ( {q_{2} + u_{2} } )} ), \hfill \\ & \ {( {1 - v_{1} } )( {1 - v_{2} } ) - ( {1 - ( {r_{1} + v_{1} } )} )( {1 - ( {r_{2} + v_{2} } )} )} ), \hfill \\ & {( {( {1 - ( {1 - t_{1} } )( {1 - t_{2} } )} ),\,( {1 - ( {1 - u_{1} } )( {1 - u_{2} } )} ),\,( {1 - ( {1 - v_{1} } )( {1 - v_{2} } )} )} )} \rangle \hfill ,\\ \end{aligned}$$

(9)

$$\begin{aligned} (3)\;\,\psi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} & = \langle {( {1 - ( {1 - p} )^{\psi } ,\,1 - ( {1 - q} )^{\psi } ,\,1 - ( {1 - r} )^{\psi } } )} , \\ & { ( {( {1 - p} )^{\psi } - ( {1 - ( {p + t} )} )^{\psi } ,\,( {1 - q} )^{\psi } - ( {1 - ( {q + u} )} )^{\psi } ,( {1 - r} )^{\psi } - ( {1 - ( {r + v} )} )^{\psi } } )} \rangle ,\\ \end{aligned}$$

(10)

$$\begin{aligned} (4)\,\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} ^{\psi } & = \langle {( {( {1 - t} )^{\psi } - ( {1 - ( {p + t} )} )^{\psi } ,\,( {1 - u} )^{\psi } - ( {1 - ( {q + u} )} )^{\psi } ,( {1 - v} )^{\psi } - ( {1 - ( {r + v} )} )^{\psi } } )} , \\ & {( {1 - ( {1 - t} )^{\psi } ,\,1 - ( {1 - u} )^{\psi } ,\,1 - ( {1 - v} )^{\psi } } )} \rangle . \\ \end{aligned}$$

(11)

Example 2

If we re-calculate Example 1 with this new operations of TIFNs in Definition 5, then we get the overall triangular intuitionistic information of the student $a_{1}$ as

$$L_{1}^{ \circ } = \mathop \oplus \limits_{i = 1}^{3} \omega_{i} L_{1i} = \left\langle {\left( {0.2178,\,0.3116,\,0.4072} \right),\,\left( {0.1106,\,0.1496,\,0.2253} \right)} \right\rangle .$$

This new operations are more effective and practical in some cases than the other operations defined in Definition 2.

Theorem 1

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \left\langle {\left( {p,\,q,\,r} \right),\,\left( {t,\,u,\,v} \right)} \right\rangle ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} = \left\langle {\left( {p_{1} ,\,q_{1} ,\,r_{1} } \right),\,\left( {t_{1} ,\,u_{1} ,\,v_{1} } \right)} \right\rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} = \left\langle {\left( {p_{2} ,\,q_{2} ,\,r_{2} } \right),\,\left( {t_{2} ,\,u_{2} ,\,v_{2} } \right)} \right\rangle$ be any three TIFNs and $\chi ,\,\chi_{1} ,\,\chi_{2} \ge 0$. Then

• 1. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ;$

• 2. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ;$

• 3. $\,\chi ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = \chi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \chi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ;$

• 4. $\,( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } )^{\chi } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1}^{\chi } \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2}^{\chi } ;$

• 5. $\,\,\chi_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} \oplus \chi_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \left( {\chi_{1} + \chi_{2} } \right)\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d};$

• 6. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{{\chi_{1} }} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{{\chi_{2} }} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{{\left( {\chi_{1} + \chi_{2} } \right)}} .$

4 Some aggregation operators for TIFNs

In this section, we defined some aggregation operator for TIFNs based on these improved operational laws.

4.1 TIF-weighted averaging and TIF-weighted geometric operator

In this section, we propose TIF-weighted averaging and TIF-weighted geometric operators to aggregate TIF information.

Definition 6

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. If the mapping

$${\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \omega_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \omega_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} \oplus \cdots \oplus \omega_{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} = \mathop \oplus \limits_{z = 1}^{m} \omega_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} \,,$$

(12)

then, TIFWA is called triangular intuitionistic fuzzy-weighted averaging (TIFWA) operator, where $\omega = ( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } )^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} (z = 1,\,2, \ldots ,\,m)$ with the condition that $\omega_{z} \in [ {0,\,1} ],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$ Especially, when the importance degree $\omega = ( {\tfrac{1}{m},\,\tfrac{1}{m}, \ldots ,\,\tfrac{1}{m}} )^{T}$, then the TIFWA operators becomes TIFA operator:

$${\text{TIFA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \frac{1}{m}( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} \oplus \ldots. \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} } ).$$

(13)

Theorem 2

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. Then

$$\begin{aligned}& TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{m} ) = \left\langle {\left( {1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{z} } \right)^{{\omega _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{z} } \right)^{{\omega _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{z} } \right)^{{\omega _{z} }} } \right),} \right. \\ & \quad \left( {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {p_{z} + t_{z} } \right)} \right)^{{\omega _{z} }} ,\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {q_{z} + u_{z} } \right)} \right)^{{\omega _{z} }} ,} \right. \\ & \quad \left. {\left. {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {r_{z} + v_{z} } \right)} \right)^{{\omega _{z} }} } \right)} \right\rangle , \end{aligned}$$

(14)

where $\omega = \left( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } \right)^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} (z = 1,\,2, \ldots ,\,m)$ with the condition that $\omega_{z} \in \left[ {0,\,1} \right],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

Proof

We prove Eq. (14) using mathematical induction on $m.$

• 1. When $m = 1,\,\;\omega_{1} = 1,$ we have

  $$\begin{aligned} {\text{TrIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ) & = \left\langle {\left( {1 - \left( {1 - p_{1} } \right)^{1} ,\,1 - \left( {1 - q_{1} } \right)^{1} ,\,1 - \left( {1 - r_{1} } \right)^{1} } \right)} \right.,\left( {\left( {1 - p_{1} } \right)^{1} - \left( {1 - \left( {p_{1} + t_{1} } \right)} \right)^{1} ,} \right. \\ & \quad \left. {\left. {\left( {1 - q_{1} } \right)^{1} - \left( {1 - \left( {q_{1} + u_{1} } \right)} \right)^{1} ,\left( {1 - r_{1} } \right)^{1} - \left( {1 - \left( {r_{1} + v_{1} } \right)} \right)^{1} } \right)} \right\rangle . \\ \end{aligned}$$

  Thus, Eq. (4) is true for $m = 1.$

• 2. For $m = 2,$, we have

  $$\begin{aligned} \omega_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} &= \left\langle {\left( {1 - \left( {1 - p_{1} } \right)^{{\omega_{1} }} ,1 - \left( {1 - q_{1} } \right)^{{\omega_{1} }} ,1 - \left( {1 - r_{1} } \right)^{{\omega_{1} }} } \right)} \right.,\left( {\left( {1 - p_{1} } \right)^{{\omega_{1} }} - \left( {1 - \left( {p_{1} + t_{1} } \right)} \right)^{{\omega_{1} }} ,} \right. \hfill \\ & \quad \left( {1 - q_{1} } \right)^{{\omega_{1} }} - \left( {1 - \left( {q_{1} + u_{1} } \right)} \right)^{{\omega_{1} }} ,\left( {1 - r_{1} } \right)^{{\omega_{1} }} \left. {\left. { - \left( {1 - \left( {r_{1} + v_{1} } \right)} \right)^{{\omega_{1} }} } \right)} \right\rangle \hfill, \\ \end{aligned}$$
  $$\begin{aligned} \omega_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} &= \left\langle {\left( {1 - \left( {1 - p_{2} } \right)^{{\omega_{2} }} ,1 - \left( {1 - q_{2} } \right)^{{\omega_{2} }} ,1 - \left( {1 - r_{2} } \right)^{{\omega_{2} }} } \right)} \right., \hfill \\ & \quad \left. {\left( {\left( {1 - p_{2} } \right)^{{\omega_{2} }} - \left( {1 - \left( {p_{2} + t_{2} } \right)} \right)^{{\omega_{2} }} ,\left( {1 - q_{2} } \right)^{{\omega_{2} }} - \left( {1 - \left( {q_{2} + u_{2} } \right)} \right)^{{\omega_{2} }} ,\left( {1 - r_{2} } \right)^{{\omega_{2} }} - \left( {1 - \left( {r_{2} + v_{2} } \right)} \right)^{{\omega_{2} }} } \right)} \right\rangle \hfill, \\ \end{aligned}$$
  $$\begin{gathered} {\text{TIFWA}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} } \right) = \left\langle {\left( \begin{gathered} 1 - \left( {1 - \left( {1 - \left( {1 - p_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot 1 - \left( {1 - \left( {1 - \left( {1 - p_{2} } \right)^{{\omega _{2} }} } \right)} \right),1 - \left( {1 - \left( {1 - \left( {1 - q_{1} } \right)^{{\omega _{1} }} } \right)} \right) \hfill \\ \cdot 1 - \left( {1 - \left( {1 - \left( {1 - q_{2} } \right)^{{\omega _{2} }} } \right)} \right),1 - \left( {1 - \left( {1 - \left( {1 - r_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot 1 - \left( {1 - \left( {1 - \left( {1 - r_{2} } \right)^{{\omega _{2} }} } \right)} \right) \hfill \\ \end{gathered} \right)} \right., \hfill \\ \left( {\left( {1 - \left( {1 - \left( {1 - p_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot \left( {1 - \left( {1 - \left( {1 - p_{2} } \right)^{{\omega _{2} }} } \right)} \right) - \left( {1 - \left( {1 - \left( {1 - p_{1} } \right)^{{\omega _{1} }} } \right)} \right) + \left( {\left( {1 - p_{1} } \right)^{{\omega _{1} }} - \left( {1 - \left( {p_{1} + t_{1} } \right)^{{\omega _{1} }} } \right)} \right)} \right. \hfill \\ \cdot \left( {1 - \left( {1 - \left( {1 - p_{2} } \right)^{{\omega _{2} }} } \right)} \right) + \left( {\left( {1 - p_{2} } \right)^{{\omega _{2} }} - \left( {1 - \left( {p_{2} + t_{2} } \right)^{{\omega _{2} }} } \right)} \right),\left( {1 - \left( {1 - \left( {1 - q_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot \left( {1 - \left( {1 - \left( {1 - q_{2} } \right)^{{\omega _{2} }} } \right)} \right) \hfill \\ - \left( {1 - \left( {1 - \left( {1 - q_{1} } \right)^{{\omega _{1} }} } \right)} \right) + \left( {\left( {1 - q_{1} } \right)^{{\omega _{1} }} - \left( {1 - \left( {q_{1} + u_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot \left( {1 - \left( {1 - \left( {1 - q_{2} } \right)^{{\omega _{2} }} } \right)} \right) + \left( {\left( {1 - q_{2} } \right)^{{\omega _{2} }} - \left( {1 - \left( {q_{2} + u_{2} } \right)^{{\omega _{2} }} } \right)} \right), \hfill \\ \left( {1 - \left( {1 - \left( {1 - r_{1} } \right)^{{\omega _{1} }} } \right)} \right) \cdot \left( {1 - \left( {1 - \left( {1 - r_{2} } \right)^{{\omega _{2} }} } \right)} \right) - \left( {1 - \left( {1 - \left( {1 - r_{1} } \right)^{{\omega _{1} }} } \right)} \right) + \left( {\left( {1 - r_{1} } \right)^{{\omega _{1} }} - \left( {1 - \left( {r_{1} + v_{1} } \right)^{{\omega _{1} }} } \right)} \right) \hfill \\ \left. {\left. { \cdot \left( {1 - \left( {1 - \left( {1 - r_{2} } \right)^{{\omega _{2} }} } \right)} \right) + \left( {\left( {1 - r_{2} } \right)^{{\omega _{2} }} - \left( {1 - \left( {r_{2} + v_{2} } \right)^{{\omega _{2} }} } \right)} \right)} \right)} \right\rangle \hfill \\ = \left\langle {\left( {1 - \left( {1 - p_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - p_{2} } \right)^{{\omega _{2} }} ,1 - \left( {1 - q_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - q_{2} } \right)^{{\omega _{2} }} ,1 - \left( {1 - r_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - r_{2} } \right)^{{\omega _{2} }} } \right)} \right., \hfill \\ \left( {\left( {1 - p_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - p_{2} } \right)^{{\omega _{2} }} - \left( {\left( {1 - \left( {p_{1} + t_{1} } \right)} \right)^{{\omega _{1} }} \cdot \left( {1 - \left( {p_{2} + t_{2} } \right)} \right)^{{\omega _{2} }} } \right)} \right., \hfill \\ \left( {1 - q_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - q_{2} } \right)^{{\omega _{2} }} - \left( {\left( {1 - \left( {q_{1} + u_{1} } \right)} \right)^{{\omega _{1} }} \cdot \left( {1 - \left( {q_{2} + u_{2} } \right)} \right)^{{\omega _{2} }} } \right), \hfill \\ \left. {\left. {\left( {1 - r_{1} } \right)^{{\omega _{1} }} \cdot \left( {1 - r_{2} } \right)^{{\omega _{2} }} - \left( {\left( {1 - \left( {r_{1} + v_{1} } \right)} \right)^{{\omega _{1} }} \cdot \left( {1 - \left( {r_{2} + v_{2} } \right)} \right)^{{\omega _{2} }} } \right)} \right)} \right\rangle . \hfill \\ \end{gathered}$$

  That is, Eq. (14) holds for $m = 2.$

• 3. Let us assume that Eq. (14) is true for $m = l$, that is

  $${\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{l} ) = \left\langle {\left( {1 - \mathop \prod \limits_{z = 1}^{l} \left( {1 - p_{z} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{l} \left( {1 - q_{z} } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{l} \left( {1 - r_{z} } \right)^{{\omega_{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{z = 1}^{l} \left( {1 - p_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{l} \left( {1 - \left( {p_{z} + t_{z} } \right)} \right)} \right.^{{\omega_{z} }} ,$$
  $$\left. {\left. {\mathop \prod \limits_{z = 1}^{l} \left( {1 - q_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{l} \left( {1 - \left( {q_{z} + u_{z} } \right)} \right)^{{\omega_{z} }} ,\mathop \prod \limits_{z = 1}^{l} \left( {1 - r_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{l} \left( {1 - \left( {r_{z} + v_{z} } \right)} \right)^{{\omega_{z} }} } \right)} \right\rangle .$$

• 4. Now, when $m = l + 1,$

  $$\begin{gathered} {\text{TIFWA}}( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} , \ldots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{l + 1}} } ) = \oplus _{{z = 1}}^{{l + 1}} \omega _{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{z} = {\text{TIFWA}} ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} , \ldots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{l} } ) + \omega _{{l + 1}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{l + 1}} \hfill \\ = \left\langle {\left( {1 - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - p_{z} } \right)^{{\omega _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - q_{z} } \right)^{{\omega _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - r_{z} } \right)^{{\omega _{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{{z = 1}}^{l} \left( {1 - p_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - \left( {p_{z} + t_{z} } \right)} \right)^{{\omega _{z} }} ,} \right. \hfill \\ \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - q_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - \left( {q_{z} + u_{z} } \right)} \right)^{{\omega _{z} }} ,\left. {\left. {\mathop \prod \limits_{{z = 1}}^{l} \left( {1 - r_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{l} \left( {1 - \left( {r_{z} + v_{z} } \right)} \right)^{{\omega _{z} }} } \right)} \right\rangle \hfill \\ + \left\langle {\left( {1 - \left( {1 - p_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} ,1 - \left( {1 - q_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} ,1 - \left( {1 - r_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} } \right),\left( {1 - \left( {1 - p_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} - \left( {1 - \left( {p_{{l + 1}} + t_{{l + 1}} } \right)} \right)} \right.^{{\omega _{{l + 1}} }} ,} \right. \hfill \\ \left. {\left. {1 - \left( {1 - q_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} - \left( {1 - \left( {q_{{l + 1}} + u_{{l + 1}} } \right)} \right)^{{\omega _{{l + 1}} }} ,1 - \left( {1 - r_{{l + 1}} } \right)^{{\omega _{{l + 1}} }} - \left( {1 - \left( {r_{{l + 1}} + v_{{l + 1}} } \right)} \right)^{{\omega _{{l + 1}} }} } \right)} \right\rangle \hfill \\ = \left\langle {\left( {1 - \mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - p_{z} } \right)^{{\omega _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - q_{z} } \right)^{{\omega _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - r_{z} } \right)^{{\omega _{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - p_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - \left( {p_{z} + t_{z} } \right)} \right)^{{\omega _{z} }} ,\mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - q_{z} } \right)^{{\omega _{z} }} - } \right. \hfill \\ \left. {\left. {\mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - \left( {q_{z} + u_{z} } \right)} \right)^{{\omega _{z} }} ,\mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - r_{z} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{{l + 1}} \left( {1 - \left( {r_{z} + v_{z} } \right)} \right)^{{\omega _{z} }} } \right)} \right\rangle . \hfill \\ \end{gathered}$$

  Hence, Eq. (14) is true for $m = l + 1.$ Therefore, Eq. (14) is true for all $m = z.$

Theorem 3

If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \left\langle {\left( {p_{z} ,\,q_{z} ,\,r_{z} } \right),\,\left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right\rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. Then, the aggregated result using TIFWA operator is also a TIFN, i.e., $TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \in TIFNs.$

Proof

Since $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \left\langle {\left( {p_{z} ,\,q_{z} ,\,r_{z} } \right),\,\left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right\rangle \in {\text{TIFNs}}\;(z = 1,\,2, \ldots ,\,m),\,\;$ so by Definition 1, we have

$$0 \le \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right),\,\left( {t_{z} ,\,u_{z} ,\,v_{z} } \right) \le 1\,\,{\text{and }}0 \le \mathop {\hbox{max} }\limits \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right) + \mathop {\hbox{max} }\limits \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right) \le 1.$$

Then

$$0 \le 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right)} \right)^{{\omega_{z} }} \le 1,0 \le \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right) + \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right)^{{\omega_{z} }} \le 1,$$

and

$$\begin{aligned} &\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right)} \right)^{{\omega_{z} }} } \right) + \left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right) + \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right)^{{\omega_{z} }} } \right) \\ &= 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z} ,\,q_{z} ,\,r_{z} } \right) + \left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right)^{{\omega_{z} }} \in \left[ {0,\,1} \right]. \\ \end{aligned}$$

${\text{Thus, TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} )\,{\text{is}}\;{\text{TIFNs}} .$Now, we discussed some desirable properties of TIFWA operators.

Theorem 4

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{z} = \left\langle {\left( {p_{z}^{ \circ } ,\,q_{z}^{ \circ } ,\,r_{z}^{ \circ } } \right),\,\left( {t_{z}^{ \circ } ,\,u_{z}^{ \circ } ,\,v_{z}^{ \circ } } \right)} \right\rangle$ be two families of TIFNs and $\omega = \left( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } \right)$ is the associated importance degree satisfying $\omega_{z} \in \left[ {0,\,1} \right]$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

• 1. $\left( {Idempotency} \right)$. If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} = \left\langle {\left( {p_{0} ,\,q_{0} ,\,r_{0} } \right),\,\left( {t_{0} ,\,u_{0} ,\,v_{0} } \right)} \right\rangle$ for all $z,$ then $TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} .$

• 2. $( {Boundedness} )$. Let

  $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ - } = {\langle {\hbox{max} ( {0,\,\hbox{min} (p_{z} + t_{z} ) - \hbox{max} (t_{z} ),\,\hbox{min} (q_{z} + u_{z} ) - \hbox{max} (u_{z} ),\,\hbox{min} (r_{z} + v_{z} ) - \hbox{max} (v_{z} )} )}} \rangle ,\langle {{( {\hbox{max} (t_{z} ),\,\hbox{max} (u_{z} ),\,\hbox{max} (v_{z} )} )} \rangle } .$$

  and

  $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ + } = \left\langle {\hbox{max} \left. {\left( {\hbox{max} (p_{z} + t_{z} ) - \hbox{min} (t_{z} ),\,\hbox{max} (q_{z} + u_{z} ) - \hbox{min} (u_{z} ),\,\hbox{max} (r_{z} + v_{z} ) - \hbox{min} (v_{z} )} \right)} \right\rangle ,} \right.\left. {\left\langle {\left( {\hbox{min} (t_{z} ),\,\hbox{min} (u_{z} ),\,\hbox{min} (v_{z} )} \right)} \right.} \right\rangle.$$

  Then, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ - } \le TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ + }.$

• 3. $\left( {Monotonicity} \right)$. When $p_{z} \le p_{z}^{ \circ } ,\,q_{z} \le q_{z}^{ \circ } ,\,r_{z} \le r_{z}^{ \circ } ,\,t_{z} \ge t_{z}^{ \circ } ,\,u_{z} \ge u_{z}^{ \circ } ,\,v_{z} \ge v_{z}^{ \circ } ,\,$ for all $z,$ then $TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le TIFWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{m} ).$

Proof

• 1. Since $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} = \left\langle {\left( {p_{0} ,\,q_{0} ,\,r_{0} } \right),\,\left( {t_{0} ,\,u_{0} ,\,v_{0} } \right)} \right\rangle \,\;(z = 1,\,2, \ldots ,\,m)$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$, then by Theorem 2, we have

  $$\begin{aligned} &{\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \left\langle {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{z}^{{}} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{z}^{{}} } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{z}^{{}} } \right)^{{\omega_{z} }} } \right),} \right. \\ & \left. {\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{z}^{{}} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{z}^{{}} + t_{z}^{{}} } \right)} \right)^{{\omega_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{z}^{{}} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{z}^{{}} + u_{z}^{{}} } \right)} \right)^{{\omega_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{z}^{{}} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{z}^{{}} + v_{z}^{{}} } \right)} \right)^{{\omega_{z} }} } \right)} \right\rangle ,\\ & = \left\langle {\left( {1 - \left( {1 - p_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} ,\,1 - \left( {1 - q_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} ,1 - \left( {1 - r_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} } \right),} \right. \\ & \left. {\left( {\left( {1 - p_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \left( {p_{0} + t_{0} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} ,\left( {1 - q_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \left( {q_{0} + u_{0} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} ,\left( {1 - r_{0} } \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \left( {r_{0} + v_{0} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} } \right)} \right\rangle ,\\ & = \left\langle {\left( {p_{0} ,\,q_{0} ,\,r_{0} } \right),\,\left( {t_{0} ,\,u_{0} ,\,v_{0} } \right)} \right\rangle = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} . \\ \end{aligned}$$

• 2. Since

  $$\begin{aligned} \mathop {\hbox{max} }\limits (t_{z} ) &= 1 - \left( {1 - \mathop {\hbox{max} }\limits (t_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} ,\mathop {\hbox{max} }\limits (u_{z} ) & = 1 - \left( {1 - \mathop {\hbox{max} }\limits (u_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} , \\ \mathop {\hbox{max} }\limits (v_{z} ) & = 1 - \left( {1 - \mathop {\hbox{max} }\limits (v_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }}. \\ \end{aligned}$$

  and

  $$\begin{aligned} 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} \ge & 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \mathop {\hbox{min} }\limits (t_{z} )} \right)^{{\omega_{z} }} = 1 - \left( {1 - \mathop {\hbox{min} }\limits (t_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} = \mathop {\hbox{min} }\limits (t_{z} ), \\ 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} \ge & 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \mathop {\hbox{min} }\limits (u_{z} )} \right)^{{\omega_{z} }} = 1 - \left( {1 - \mathop {\hbox{min} }\limits (u_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} = \mathop {\hbox{min} }\limits (u_{z} ), \\ 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} \ge & 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \mathop {\hbox{min} }\limits (v_{z} )} \right)^{{\omega_{z} }} = 1 - \left( {1 - \mathop {\hbox{min} }\limits (v_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} = \mathop {\hbox{min} }\limits (v_{z} ). \\ \end{aligned}$$

  thus

  $$\begin{aligned} \mathop {\hbox{max} }\limits (p_{z} + t_{z} ) - \mathop {\hbox{min} }\limits (t_{z} ) = & \left( {1 - \mathop {\hbox{min} }\limits \left( {t_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \mathop {\hbox{max} }\limits (p_{z} + t_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (p_{z} + t_{z} )} \right)^{{\omega_{z} }} \\ \ge & \left( {1 - \mathop {\hbox{max} }\limits \left( {t_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \left( {1 - \mathop {\hbox{min} }\limits (p_{z} + t_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }}=&\mathop {\hbox{min} }\limits (p_{z} + t_{z} ) - \mathop {\hbox{max} }\limits (t_{z} ), \\ \end{aligned}$$
  $$\begin{aligned} \mathop {\hbox{max} }\limits (q_{z} + u_{z} ) - \mathop {\hbox{min} }\limits (u_{z} ) = & \left( {1 - \mathop {\hbox{min} }\limits \left( {u_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \mathop {\hbox{max} }\limits (q_{z} + u_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (q_{z} + u_{z} } \right))^{{\omega_{z} }} \\ \ge & \left( {1 - \mathop {\hbox{max} }\limits \left( {u_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \mathop {\hbox{min} }\limits (q_{z} + u_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} = & \mathop {\hbox{min} }\limits (q_{z} + u_{z} ) - \mathop {\hbox{max} }\limits (u_{z} ), \\ \end{aligned}$$
  $$\begin{aligned} \mathop {\hbox{max} }\limits (r_{z} + v_{z} ) - \mathop {\hbox{min} }\limits (v_{z} ) = & \left( {1 - \mathop {\hbox{min} }\limits \left( {v_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \mathop {\hbox{max} }\limits (r_{z} + v_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} \ge \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (r_{z} + v_{z} } \right))^{{\omega_{z} }} \\\ge & \left( {1 - \mathop {\hbox{max} }\limits \left( {v_{z} } \right)} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} - \left( {1 - \mathop {\hbox{min} }\limits (r_{z} + v_{z} )} \right)^{{\sum \nolimits_{z = 1}^{m} \omega_{z} }} = & \mathop {\hbox{min} }\limits (r_{z} + v_{z} ) - \mathop {\hbox{max} }\limits (v_{z} ). \\ \end{aligned}$$

  Then, according to Theorem 3, we have

  $$\mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (p_{z} + t_{z} )} \right)^{{\omega_{z} }} \ge 0,\,\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (q_{z} + u_{z} )} \right)^{{\omega_{z} }} \ge 0,\mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (r_{z} + v_{z} )} \right)^{{\omega_{z} }} \ge 0.$$

  Therefore,

  $$\begin{aligned} & \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} { - }\mathop \prod \limits_{z = 1}^{m} \left( {1 - (p_{z} + t_{z} )} \right)^{{\omega_{z} }} ,\,\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (q_{z} + u_{z} )} \right)^{{\omega_{z} }} , & \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (r_{z} + v_{z} )} \right)^{{\omega_{z} }}\\\ge & \left\langle {\hbox{max} \left. {\left( {0,\,\hbox{min} (p_{z} + t_{z} ) \hbox{max} (t_{z} ),\,\hbox{min} (q_{z} + u_{z} ) - \hbox{max} (u_{z} ),\,\hbox{min} (r_{z} + v_{z} ) - \hbox{max} (v_{z} )} \right)} \right\rangle ,\left\langle {\left( {\hbox{max} (t_{z} ),\,\hbox{max} (u_{z} ),\,\hbox{max} (v_{z} )} \right)} \right.} \right\rangle . \\ \end{aligned}$$

  Hence, we can obtain that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ - } \le {\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ + } .$

• 3. Since $p_{z} \le p_{z}^{ \circ } ,\,q_{z} \le q_{z}^{ \circ } ,\,r_{z} \le r_{z}^{ \circ } ,$, we have $1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{z} } \right)^{{\omega_{z} }} \le 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{z}^{ \circ } } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{z} } \right)^{{\omega_{z} }} \le 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{z}^{ \circ } } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{z} } \right)^{{\omega_{z} }} \le 1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{z}^{ \circ } } \right)^{{\omega_{z} }} .$ Because $t_{z} \ge t_{z}^{ \circ } ,\,u_{z} \ge u_{z}^{ \circ } ,\,v_{z} \ge v_{z}^{ \circ } ,\,w_{z} \ge w_{z}^{ \circ } ,\,\;$ and $p_{z} + t_{z} \le p_{z}^{ \circ } + t_{z}^{ \circ } ,\,q_{z} + u_{z} \le q_{z}^{ \circ } + u_{z}^{ \circ } ,r_{z} + v_{z} \le r_{z}^{ \circ } + v_{z}^{ \circ } ,$ $\,\,s_{z} + w_{z} \le s_{z}^{ \circ } + w_{z}^{ \circ }$ $(z = 1,\,2, \ldots ,\,m)$, we have

  $$\begin{aligned} \;\mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (p_{z} + t_{z} )} \right) \le \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z}^{ \circ } } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (p_{z}^{ \circ } + t_{z}^{ \circ } )} \right),\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (q_{z} + u_{z} )} \right) \hfill \\ \, \le \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z}^{ \circ } } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (q_{z}^{ \circ } + u_{z}^{ \circ } )} \right),\,\mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (r_{z} + v_{z} )} \right) \le \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z}^{ \circ } } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - (r_{z}^{ \circ } + v_{z}^{ \circ } )} \right). \hfill \\ \end{aligned}$$

  Therefore, according to Definition 5, we have

  $${\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le {\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{2} \,,\ldots,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{m} \,).$$

Definition 7

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {\left( {p_{z} ,\,q_{z} ,\,r_{z} } \right),\,\left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. If the mapping

$${\text{TIFWG}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1}^{{\omega_{1} }} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2}^{{\omega_{2} }} \otimes \ldots. \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m}^{{\omega_{m} }} = \mathop \otimes \limits_{z = 1}^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z}^{{\omega_{z} }} ,$$

(15)

then, TIFWG is called triangular intuitionistic fuzzy-weighted geometric operator (TIFWG), where $\omega = ( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } )^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} (z = 1,\,2, \ldots ,\,m)$ with the condition that $\omega_{z} \in [ {0,\,1}],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$ Especially, when the importance degree $\omega =( {\tfrac{1}{m},\,\tfrac{1}{m}, \ldots ,\,\tfrac{1}{m}} )^{T}$, then the TIFWG operators becomes TIFG operator:

$${\text{TIFG}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} \oplus \cdots \oplus \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} } )^{{\tfrac{1}{m}}} .$$

(16)

Theorem 5

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2,\ldots,\,m)$ be a family of TIFNs. Then

$$\begin{aligned} TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) &= \left\langle {\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} } \right.\left( {1 - \left( {p_{z} + t_{z} } \right)} \right)^{{\varpi_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{z} + u_{z} } \right)} \right)^{{\varpi_{z} }} } \right., \hfill \\ &\left. {\mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{z} + v_{z} } \right)} \right)^{{\varpi_{z} }} } \right),\left. {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{z} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{z} } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{z} } \right)^{{\omega_{z} }} } \right)} \right\rangle , \hfill \\ \end{aligned}$$

(17)

where $\omega = \left( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } \right)^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} (z = 1,\,2, \ldots ,\,m)$ with the condition that $\omega_{z} \in \left[ {0,\,1} \right],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

Proof

The proof of Theorem (5) is the same as in Theorem (2).

Theorem 6

If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. Then, the aggregated result using TIFWG operator is also a TIFN, i.e., $TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \in TIFNs.$

Theorem 7

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \left\langle {\left( {p_{z} ,\,q_{z} ,\,r_{z} } \right),\,\left( {t_{z} ,\,u_{z} ,\,v_{z} } \right)} \right\rangle$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{z} = \left\langle {\left( {p_{z}^{ \circ } ,\,q_{z}^{ \circ } ,\,r_{z}^{ \circ } } \right),\,\left( {t_{z}^{ \circ } ,\,u_{z}^{ \circ } ,\,v_{z}^{ \circ } } \right)} \right\rangle$ be two families of TIFNs and $\omega = \left( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } \right)^{T}$ is the associated importance degree satisfying $\omega_{z} \in \left[ {0,\,1} \right]$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

• 1. $\left( {Idempotency} \right)$. If $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} = \left\langle {\left( {p_{0} ,\,q_{0} ,\,r_{0} } \right),\,\left( {t_{0} ,\,u_{0} ,\,v_{0} } \right)} \right\rangle$ for all $z,$ then $TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{0} .$

• 2. $\left( {Boundedness} \right)$. Let

  $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ - } = \left\langle {\hbox{max} \left( {0,\,\hbox{min} (p_{z} + t_{z} ) - \hbox{max} (t_{z} ),\,\hbox{min} (q_{z} + u_{z} ) - \hbox{max} (u_{z} ),\,\hbox{min} (r_{z} + v_{z} ) - \hbox{max} (v_{z} )} \right),\left( {\hbox{max} (t_{z} ),\,\hbox{max} (u_{z} ),\,\hbox{max} (v_{z} )} \right)} \right\rangle,$$

  and

  $$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}^{ + } = \left\langle {\hbox{max} \left( {\hbox{max} (p_{z} + t_{z} ) - \hbox{min} (t_{z} ),\,\hbox{max} (q_{z} + u_{z} ) - \hbox{min} (u_{z} ),\,\hbox{max} (r_{z} + v_{z} ) - \hbox{min} (v_{z} )} \right),\left( {\hbox{min} (t_{z} ),\,\hbox{min} (u_{z} ),\,\hbox{min} (v_{z} )} \right)} \right\rangle.$$

  Then, $d^{ - } \le TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le d^{ + }.$

• 3. $( {{{Monotonicity}}} )$ When $p_{z} \le p_{z}^{ \circ } ,\,q_{z} \le q_{z}^{ \circ } ,\,r_{z} \le r_{z}^{ \circ } ,\,t_{z} \ge t_{z}^{ \circ } ,\,u_{z} \ge u_{z}^{ \circ } ,\,v_{z} \ge v_{z}^{ \circ } ,\,$ for all $z,$ then $TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) \le TIFWG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{2} , \ldots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{m} \,).$

Proof

Same as Theorem 4.

5 Some hybrid aggregation operators for TIFNs

In this section, some ordered weighted averaging, ordered weighted geometric operators and hybrid weighted averaging, hybrid weighted geometric operators are developed.

Definition 8

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. If the mapping

$${\text{TIFOWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \omega_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)} \oplus \omega_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (2)} \oplus \cdots \oplus \omega_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (m)} = \mathop \oplus \limits_{z = 1}^{m} \omega_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}.$$

(18)

Then, TIFOWA is called triangular intuitionistic fuzzy-ordered-weighted averaging operator, where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}$ is the $z$th largest value of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{(z)} (z = 1,\,2, \ldots ,\,m),\,\omega = ( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } )^{T} ,$ is the importance degree of TIFOWA operator with $\omega_{z} \in [ {0,\,1}],$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$ In a special case, when $\omega = ( {\tfrac{1}{m},\,\tfrac{1}{m}, \ldots ,\,\tfrac{1}{m}} )^{T} ,$ then the TIFOWA operator reduce to TIFA operator.

Definition 9

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. If the mapping

$${\text{TIFOWG}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)}^{{\omega_{1} }} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (2)}^{{\omega_{2} }} \otimes \cdots \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (m)}^{{\omega_{m} }} = \mathop \otimes \limits_{z = 1}^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}^{{\omega_{z} }},$$

(19)

then TIFOWG is called triangular intuitionistic fuzzy-ordered-weighted geometric operator, where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}$ is the $z$ th largest value of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{(z)} (z = 1,\,2,\ldots,\,m),\,\omega = ( {\omega_{1} ,\,\omega_{2} ,\ldots,\,\omega_{m} } )^{T}$ is the importance degree of TIFOWG operator with $\omega_{z} \in [ {0,\,1} ],$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$ In a special case, when $\omega = ( {\tfrac{1}{m},\,\tfrac{1}{m}, \ldots ,\,\tfrac{1}{m}} )^{T} ,$ then the TIFOWG operator reduced to TIFA operator.

Theorem 8

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} }),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. Then

$$\begin{aligned} & TIFOWA(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \left\langle {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)} } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{\sigma (z)} } \right)^{{\omega_{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)} } \right)^{{\omega_{z} }} } \right. \hfill \\ & \quad -\mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{\sigma (z)} + t_{\sigma (z)} } \right)} \right)^{{\omega_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{\sigma (z)} + u_{\sigma (z)} } \right)} \right)^{{\omega_{z} }} ,\left. {\left. {\mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{\sigma (z)} + v_{\sigma (z)} } \right)} \right)^{{\omega_{z} }} } \right)} \right\rangle,\, \hfill \\ \end{aligned}$$

(20)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}$ is the $zth$ largest value of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{(z)} (z = 1,\,2, \ldots ,\,m),\,\omega = \left( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{z} } \right)^{T}$ is the importance degree of TIFOWG operator with $\omega_{z} \in [ {0,\,1} ],$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

Proof

The proof is similar to Theorem 2.

Theorem 9

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} })} \rangle (z = 1,\,2, \ldots ,\,m)$ be a family of TIFNs. Then

$$\begin{aligned} TIFWOG(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} ) = \left\langle {\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{\sigma (z)} + t_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} } \right.} \right.,\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{\sigma (z)} + u_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} \hfill, \\ \left. {\mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{\sigma (z)} + v_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} } \right),\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{\sigma (z)} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{\sigma (z)} } \right)\left. {^{{\omega_{z} }} ,\left. {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{\sigma (z)} } \right)^{{\omega_{z} }} } \right)} \right\rangle }. \right.\hfill \\ \end{aligned}$$

(21)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}$ is the $zth$ largest value of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{(z)} (z = 1,\,2, \ldots ,\,m),\,\omega = ( {\omega_{1} ,\,\omega_{2} , \ldots ,\,\omega_{m} } )^{T}$ is the importance degree of TIFOWG operator with $\omega_{z} \in [ {0,\,1} ],$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$

Proof

Same as Theorem 2.The TIFOWA and the TIFWG operators have the same properties than the TIFWA and TIFWG operators. However, TIFOWA and TIFOWG operators also satisfy the property of commutativity.

Theorem 10

Assume that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z}^{ \cdot } = \langle {( {p_{z}^{ \cdot } ,\,q_{z}^{ \cdot } ,\,r_{z}^{ \cdot } } ),\,( {t_{z}^{ \cdot } ,\,u_{z}^{ \cdot } ,\,v_{z}^{ \cdot } } )} \rangle (z = 1,\,2, \ldots ,\,m)$ is any permutation of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} } )} \rangle (z = 1,\,2, \ldots ,\,m),$ then

$$TIFOWA( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1}^{ \cdot } ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2}^{ \cdot } , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m}^{ \cdot } } ) = TIFOWA( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} } ).$$

(22)

Proof

Since

$$\begin{aligned} &{\text{TIFOWA}}( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1}^{ \cdot } ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2}^{ \cdot } , \ldots ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m}^{ \cdot } } ) = \left\langle {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)}^{ \cdot } } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)}^{ \cdot } } \right)} \right.} \right.^{{\omega_{z} }} ,\left. {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{\sigma (z)}^{ \cdot } } \right)^{{\omega_{z} }} } \right),\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)}^{ \cdot } } \right)^{{\omega_{z} }} } \right. \hfill \\ & \quad -\mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{\sigma (z)}^{ \cdot } + t_{\sigma (z)}^{ \cdot } } \right)} \right)^{{\varpi_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)}^{ \cdot } } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{\sigma (z)}^{ \cdot } + u_{\sigma (z)}^{ \cdot } } \right)} \right)^{{\varpi_{z} }} ,\left. {\left. {\mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{\sigma (z)}^{ \cdot } } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{\sigma (z)}^{ \cdot } + v_{\sigma (z)}^{ \cdot } } \right)} \right)^{{\varpi_{z} }} } \right)} \right\rangle \hfill \\ & \quad {\text{TIFOWA}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{m} } \right) = \left\langle {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)} } \right)^{{\omega_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)} } \right)^{{\omega_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - r_{\sigma (z)} } \right)^{{\omega_{z} }} } \right),} \right.\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - p_{\sigma (z)} } \right)^{{\omega_{z} }} } \right. \hfill \\ & \quad - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{\sigma (z)} + t_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - q_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{\sigma (z)} + u_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left. {\left. {\left( {1 - r_{\sigma (z)} } \right)^{{\omega_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{\sigma (z)} + v_{\sigma (z)} } \right)} \right)^{{\varpi_{z} }} } \right)} \right\rangle , \hfill \\ \end{aligned}$$

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z}^{ \cdot } = \left\langle {\left( {p_{z}^{ \cdot } ,\,q_{z}^{ \cdot } ,\,r_{z}^{ \cdot } } \right),\,\left( {t_{z}^{ \cdot } ,\,u_{z}^{ \cdot } ,\,v_{z}^{ \cdot } } \right)} \right\rangle (z = 1,\,2,\ldots,\,m)$ is any permutation of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = \langle {( {p_{z} ,\,q_{z} ,\,r_{z} } ),\,( {t_{z} ,\,u_{z} ,\,v_{z} })} \rangle (z = 1,\,2,\ldots,\,m),$ then $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)}^{ \cdot } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)}$

$${\text{TIFOWA}}( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1}^{ \cdot } ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2}^{ \cdot } ,...,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{m}^{ \cdot } } ) = {\text{TIFOWA}}( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} ,...,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{m} } ).$$

Since the TIFWA and TIFWG operators only consider the importance degree of TIFNs and cannot consider the importance degree of the position, the TIFOWA and TIFOWG operators only consider the importance degree of the position and cannot consider the importance degree of the TIFNs. To overcome this limitation, we proposed TIF hybrid aggregation operators.

Definition 10

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} = \langle {( {p_{\sigma (z)} ,\,q_{\sigma (z)} ,\,r_{\sigma (z)} } ),\,( {t_{\sigma (z)} ,\,u_{\sigma (z)} ,\,v_{\sigma (z)} } )} \rangle (z = 1,\,2,\ldots,\,m)$ be a family of TIFNs. Then, if the mapping

$${\text{TIFHA}}_{\omega ,\,\varpi } ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} } ) = \varpi_{1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)}^{ \cdot \cdot } \oplus \varpi_{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (2)}^{ \cdot \cdot } \oplus \ldots \oplus \varpi_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}^{ \cdot \cdot } = \mathop \oplus \limits_{z = 1}^{m} \varpi_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}^{ \cdot \cdot } ,$$

(23)

then ${\text{TIFHA}}_{\omega ,\,\varpi }$ is said to be triangular intuitionistic fuzzy hybrid averaging operator, where $\varpi = ( {\varpi_{1} ,\,\varpi_{2} ,\ldots,\,\varpi_{z} } )^{T}$ is the importance degree of the TIFHA operator with $\varpi_{z} \in [ {0,\,1}],\,\sum \nolimits_{z = 1}^{m} \varpi_{z} = 1.$ and is the $zth\;$ largest of the TIF values $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = m\omega_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} \;(z = 1,\,2,\ldots,\,m),$ $\;( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (2)} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} } )$ is any permutation of the weighted TIFNs $( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} })$ which satisfies $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z - 1)} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} \;(z = 1,\,2,\ldots,\,m),$ $\omega = ( {\omega_{1} ,\,\omega_{2} ,\ldots,\,\omega_{z} })^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} \;(z = 1,\,2,\ldots,\,m)$, such that $\omega_{z} \in [ {0,\,1} ],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1,$ and $m$ is the balancing coefficient.

Assume that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} = \langle {( {p_{\sigma (z)} ,\,q_{\sigma (z)} ,\,r_{\sigma (z)} } ),\,( {t_{\sigma (z)} ,\,u_{\sigma (z)} ,\,v_{\sigma (z)} } )} \rangle (z = 1,\,2,\ldots,\,m)$ be a family of TIFNs. Then, we have

$$\begin{gathered} {\text{TIFHA}}_{{\omega ,\,\varpi }} ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} ,....,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{z} } ) = \left\langle {\left( {1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} } \right. \hfill \\ - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {p_{{\sigma (z)}}^{{ \cdot \cdot }} + t_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)} \right)^{{\varpi _{z} }} ,\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {q_{{\sigma (z)}}^{{ \cdot \cdot }} + u_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)} \right)^{{\varpi _{z} }} ,\left. {\left. {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)^{{\varpi _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {r_{{\sigma (z)}}^{{ \cdot \cdot }} + v_{{\sigma (z)}}^{{ \cdot \cdot }} } \right)} \right)^{{\varpi _{z} }} } \right)} \right\rangle .\, \hfill \\ \end{gathered}$$

(24)

Definition 11

Let $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} = \langle {( {p_{\sigma (z)} ,\,q_{\sigma (z)} ,\,r_{\sigma (z)} } ),\,( {t_{\sigma (z)} ,\,u_{\sigma (z)} ,\,v_{\sigma (z)} } )} \rangle (z = 1,\,2,\ldots,\,m)$ be a family of TIFNs. Then, if the mapping

$${\text{TIFHG}}_{{\omega ,\,\varpi }} ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{2} ,....,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{z} } ) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{\sigma (1)}}^{{ \cdot \cdot \varpi _{1} }} \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{\sigma (2)}}^{{ \cdot \cdot \varpi _{2} }} \otimes ... \otimes \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{\sigma (z)}}^{{ \cdot \cdot \varpi _{z} }} = \mathop { \otimes \,}\limits_{{z = 1}}^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{\sigma (z)}}^{{ \cdot \cdot \varpi _{z} }} .$$

(25)

then ${\text{TIFHG}}_{\omega ,\,\varpi }$ is called triangular intuitionistic fuzzy hybrid geometric operator, where $\varpi = \left( {\varpi_{1} ,\,\varpi_{2} ,\ldots,\,\varpi_{z} } \right)^{T}$ is the importance degree of the TIFHG operator with $\varpi_{z} \in \left[ {0,\,1} \right],\,\sum \nolimits_{z = 1}^{m} \varpi_{z} = 1.$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)}^{ \cdot \cdot }$ is the $z - th\;$ largest of the TIF values $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} = m\omega_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} \;(z = 1,\,2,\ldots,\,m),\,\;( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (1)} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (2)} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} } )$ is any permutation of the weighted TIFNs $( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} } )$ which satisfies $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z - 1)} \ge \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} \;(z = 1,\,2,\ldots,\,m),$ $\omega = \left( {\omega_{1} ,\,\omega_{2} ,\ldots,\,\omega_{z} } \right)^{T}$ is the importance degree of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} \;(z = 1,\,2,\ldots,\,m),$ such that $\omega_{z} \in {0,\,1}],\,\sum \nolimits_{z = 1}^{m} \omega_{z} = 1$ and $m$ is the balancing coefficient.

Assume that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{\sigma (z)} = \langle {( {p_{\sigma (z)} ,\,q_{\sigma (z)} ,\,r_{\sigma (z)} } ),\,( {t_{\sigma (z)} ,\,u_{\sigma (z)} ,\,v_{\sigma (z)} } )} \rangle (z = 1,\,2,\ldots,\,m)$ be a family of TIFNs. Then, we have

$$\begin{aligned} {\text{TIFHG}}_{\omega ,\,\varpi } ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} ,\ldots.,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{z} } ) = \left\langle {\left( {\mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {p_{\sigma (z)}^{ \cdot \cdot } + t_{\sigma (z)}^{ \cdot \cdot } } \right)} \right)} \right.} \right.^{{\varpi_{z} }} ,\mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {q_{\sigma (z)}^{ \cdot \cdot } + u_{\sigma (z)}^{ \cdot \cdot } } \right)} \right)^{{\varpi_{z} }}, \hfill \\ \left. {\mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} - \mathop \prod \limits_{z = 1}^{m} \left( {1 - \left( {r_{\sigma (z)}^{ \cdot \cdot } + v_{\sigma (z)}^{ \cdot \cdot } } \right)} \right)^{{\varpi_{z} }} } \right),\left. {\left( {1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - t_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} ,\,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - u_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} ,1 - \mathop \prod \limits_{z = 1}^{m} \left( {1 - v_{\sigma (z)}^{ \cdot \cdot } } \right)^{{\varpi_{z} }} } \right)} \right\rangle \,. \hfill \\ \end{aligned}$$

(26)

The proof is similar to the above theorems.

6 The MCDM approach with TIFNs

For MCDM problem with TIF information, assume that there is a set of the alternatives $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} = \{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{2} ,...,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{n} } \}$, and there is a set of criteria $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} = \{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{1} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{2} ,\ldots,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{m} } \},$ with associated importance degree $\omega = \left( {\omega_{1} ,\,\omega_{2} ,\ldots,\,\omega_{m} } \right)^{T} ,$ satisfying $\omega_{z} \in \left[ {0,\,1} \right]$ and $\sum \nolimits_{z = 1}^{m} \omega_{z} = 1.$ The decision maker can give the criteria value $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{z} (z = 1,2, \ldots ,m)$ of alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{y} (y = 1,\,2,\ldots,\,n)$ by the form of TIFNs $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{yz} = \left\langle {\left( {p_{yz} ,\,q_{yz} ,\,r_{yz} } \right),\,\left( {t_{yz} ,\,u_{yz} ,\,v_{yz} } \right)} \right\rangle (y = 1,\,2,\ldots,\,n,\,z = 1,\,2,\ldots,\,m),$ where $\left( {p_{yz} ,\,q_{yz} ,\,r_{yz} } \right)$ indicates the degree of membership of the alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{y}$ with respect to the criteria $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{z} ,\,\left( {t_{yz} ,\,u_{z} ,\,v_{z} } \right)$ indicates the degree of non-membership of the alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{y}$ with respect to the criteria $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{z} \;(y = 1,\,2,\ldots,\,n,\,z = 1,\,2,\ldots,\,m).$ Assume that $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{D} = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{yz} )_{n \times m}$ is the decision matrix. Consequently, a ranking of alternatives is required.

In general, the decision steps of this MCDM problem are shown as follows.

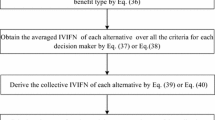
Step 1: Calculate the overall TIFN $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{y}$ $(y = 1,\,2,\ldots,\,n)$ for the alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{y} (y = 1,\,2,\ldots,\,n)$ which is shown by

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{y} &= \left\langle {\left( {p_{y} ,\,q_{y} ,\,r_{y} } \right),\,\left( {t_{y} ,\,u_{y} ,\,v_{y} } \right)} \right\rangle, \, \\ &= {\text{TIFWA}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{y1}} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{y2}} ,...,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{ym}} ) = \left\langle {\left( {1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{{yz}} } \right)^{{\omega _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{{yz}} } \right)^{{\omega _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{{yz}} } \right)^{{\omega _{z} }} } \right)} \right.,\left( {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - p_{{yz}} } \right)^{{\omega _{z} }} - } \right.\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {p_{{yz}} + t_{{yz}} } \right)} \right)^{{\omega _{z} }} ,\\ & \quad \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - q_{{yz}} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {q_{{yz}} + u_{{yz}} } \right)} \right)^{{\omega _{z} }} ,\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - r_{{yz}} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left. {\left. {\left( {1 - \left( {r_{{yz}} + v_{{yz}} } \right)} \right)^{{\omega _{z} }} } \right)} \right\rangle, \, \\ \end{aligned}$$

(27)

or

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{y} &= \left\langle {\left( {p_{y} ,\,q_{y} ,\,r_{y} } \right),\,\left( {t_{y} ,\,u_{y} ,\,v_{y} } \right)} \right\rangle a \\ &= {\text{TIFWG}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{y1}} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{y2}} ,...,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{{ym}} ) = \left\langle {\left( {\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - t_{{yz}} } \right)} \right.^{{\omega _{z} }} } \right. - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {p_{{yz}} + t_{{yz}} } \right)} \right)^{{\omega _{z} }} ,\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - u_{{yz}} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - \left( {q_{{yz}} + u_{{yz}} } \right)} \right)^{{\omega _{z} }} , \\ &\mathop \prod \limits_{{z = 1}}^{m} \left( {1 - v_{{yz}} } \right)^{{\omega _{z} }} - \mathop \prod \limits_{{z = 1}}^{m} \left. {\left( {1 - \left( {r_{{yz}} + v_{{yz}} } \right)} \right)^{{\omega _{z} }} } \right),\left. {\left( {1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - t_{{yz}} } \right)^{{\omega _{z} }} ,\,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - u_{{yz}} } \right)^{{\omega _{z} }} ,1 - \mathop \prod \limits_{{z = 1}}^{m} \left( {1 - v_{{yz}} } \right)^{{\omega _{z} }} } \right)} \right\rangle , \\ \end{aligned}$$

(28)

where $y = 1,\,2,\ldots,\,n$.

Step 2: Calculate the score and accuracy values of the final TIFNs $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{y} (y = 1,\,2,\ldots,\,n)$ by the following formulas:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} _{y} ) = \frac{{p_{y} + 2q_{y} + r_{y} }}{4} - \frac{{t_{y} + 2u_{y} + v_{y} }}{4},$$

(29)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}) = \frac{{p_{y} + 2q_{y} + r_{y} }}{4} + \frac{{t_{y} + 2u_{y} + v_{y} }}{4}.$$

(30)

Step 3: Rank all the alternatives and select the best one.

Use the comparison method defined in Definition 4 to rank the alternatives and select the best one(s). First, we can compare with score values of all alternatives, the bigger the score value for one alternative is, the better this alternative is. If the score values for some alternatives are equal, then we can compare with them by accuracy values of all alternatives. The bigger the accuracy value for one alternative is, the better this alternative is.

7 Illustrated example

The following example is adapted on the basis of the case used by Herrera et al. (2000).

Example 3

Let us assume that an investment company wants to invest a sum of money in the best option. There are four possible companies are taken into consideration, which are described as follows:

• 1. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1}$ is a car company.

• 2. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ is a food company.

• 3. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3}$ is a computer company.

• 4. $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4}$ is an arm company.

The investment company must take a decision according to the following four criteria:

• (a) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{1}$ is the risk analysis.

• (b) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{2}$ is the growth analysis.

• (c) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{3}$ is the social–political impact analysis.

• (d) $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}_{4}$ is the environmental impact.

The importance degree of the criteria is $\omega = (0.2,\,0.2,\,0.3,\,0.3)^{T}$, and the assessment values of each alternative given by the decision makers are in the form of TIFNs and are shown in Table 1.The goal of this decision problem is to select one best company for investing.

Table 1 Decision matrix of Example 3

7.1 Decision steps of the proposed method

Step 1: The overall evaluation value of each alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{y}$ $(y = 1,\,2,3,4)$ is obtained using Eq. (27) and is given as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0.325,\,0.426,\,0.528} \right),\,\left( {0. 1 2 6 ,0. 203 ,0. 3 1 3} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 5 8 4 ,0. 6 4 8 ,0. 7 5 1} \right),\,\left( {0.104,\,0.103,\,0.125} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0.372,\,0.452,\,0.553} \right),\,\left( {0.161,\,0.201,\,0.306} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 30 3 ,0. 40 3 ,0. 4 7 6} \right),\,\left( {0. 1 6 4 ,0. 1 9 3 ,0.309} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.215,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.549,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.240,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.182.$$

Step 3: By the comparison rules defined in Definition 4, we can get the ranking order of alternatives as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Therefore, the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

In a similar way, the following procedure can be done by TIFWG operator.

Step 1: The overall evaluation value of each alternative is obtained using Eq. (28) which is given as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 30,0.430 ,0. 5 4 0} \right),\,\left( {0. 1 2 1 ,0. 2 ,0. 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0.588,\,0.651,\,0.754} \right),\,\left( {0.1,\,0.1,\,0.121} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0.371,\,0.454,\,0.559} \right),\,\left( {0.161,\,0.2,\,0.3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 30 3 ,0. 40 3 ,0. 4 7 9} \right),\,\left( {0. 1 6 4 ,0. 1 9 3 ,0.300} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.227,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.556,\,\;\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.244\;,\,S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.186.$$

Step 3: By the comparison rules defined in Definition 4, we can get the ranking order of alternatives as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Therefore, the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

Obviously, the ranking results produced by the TIFWA operator and TIFWG operator are the same, i.e., the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

7.2 The validity of the proposed method compared with some existing methods

To show the validity of the proposed method in this paper, now, we calculate Example 3 using aggregation operators proposed by Wang (2008a, b), Zhou and Chang (2014) and Wang et al. (2015), and then compare with the ranking results.

(1) Compared with the method proposed by Wang (2008a, b)

The steps are shown as follows.

Step 1: The overall evaluation value of each alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{y}$ $(y = 1,\,2,3,4)$ is obtained using FNIFWA operator defined by Wang (2008a, b), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 2 5 ,0. 4 2 6 ,0. 5 2 8} \right),\,\left( {0. 1 1 5 ,0. 2 ,0. 300} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 5 8 4 ,0. 6 4 8 ,0. 7 5 1} \right),\,\left( {0. 1 ,0. 1 ,0. 1 1 5} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0.372,\,0.452,\,0.553} \right),\,\left( {0. 1 5 2 ,0. 2 ,0. 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 30 3 ,0. 40 3 ,0. 4 7 6} \right),\,\left( {0. 1 4 3 ,0. 1 7 6 ,0. 2 7 1} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.223,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.554,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.244,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.205.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Therefore, the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

Obviously, this ranking result is the same as one produced by the proposed method in this paper.

In a similar way, when we use the FNIFWG operator proposed by Wang (2008a, b) to solve this problem, we can get the following steps.

Step 1: The overall evaluation value of each alternative is obtained using FNIFWG operator, and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 30 7 ,0. 4 10,0. 5 1 2} \right),\,\left( {0. 1 2 1 ,0. 2 ,0. 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 5 5 9 ,0. 6 3 5 ,0. 7 3 5} \right),\,\left( {0.1,\,0.1,\,0.121} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 3 6 7 ,0. 4 4 7 ,0. 5 4 8} \right),\,\left( {0.161,\,0.2,\,0.3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 9 3 ,0. 3 9 5 ,0. 4 6 4} \right),\,\left( {0. 1 6 4 ,0. 1 9 3 ,0.300} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.205,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.536\;,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.237\;,\,S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.174.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4}.$$

Therefore, the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

This result is the same as the above all ranking results. Therefore, it can show the validity of the proposed method in this paper.

(2) Compared with the method proposed by Zhou and Chang (2014)

In the part, we can compare the proposed method with the method proposed by Wang (2008a, b), and the steps are shown as follows.

Step 1: The overall evaluation value of each alternative $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{y}$ $(y = 1,\,2,3,4)$ is obtained by the FNIFHWA operator defined by Zhou and Chang (2014), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 2 3 ,0. 4 2 4 ,0. 5 2 5} \right),\,\left( {0. 1 1 5 ,0. 2 ,0. 3} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 5 80,0. 6 4 6 ,0. 7 4 9} \right),\,\left( {0. 1 ,0. 1 ,0. 1 1 5} \right)} \right\rangle ;\,\;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 3 7 1 ,0. 4 5 1 ,0. 5 5 2} \right),\,\left( {0. 1 5 2 ,0. 2 ,0. 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 30 1 ,0. 40 2 ,0. 4 7 4} \right),\,\left( {0. 1 4 4 ,0. 1 7 8 ,0. 2 7 4} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.220,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.552,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.243,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.201.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4}.$$

Obviously, this ranking result is the same as ones produced by the proposed method in this paper and by Wang (2008a, b)’ method.

(3) Compared with the method proposed by Wang et al. (2015)

In a similar way, we can compare the proposed method with the method proposed by Wang et al. (2015), and the steps are shown as follows.

Step 1: The overall evaluation value of each alternative is obtained by the FNIFHWG operator, and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 30 9 ,0. 4 1 3 ,0. 5 1 5} \right),\,\left( {0. 1 2 0 ,0. 2 ,0. 3 0 0} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 5 6 3 ,0. 6 3 7 ,0. 7 3 8} \right),\,\left( {0.1,\,0.1,\,0.120} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 3 6 8 ,0. 4 4 8 ,0. 5 4 9} \right),\,\left( {0.160,\,0.2,\,0.3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 9 4 ,0. 3 9 6 ,0. 4 6 6} \right),\,\left( {0. 1 6 1 ,0. 1 9 1 ,0.295} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.207,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.539,\,\;\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.238\;,\,S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.178.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Obviously, this ranking result is the same as ones produced by the proposed method in this paper, by Wang (2008a, b)’ method and by Wang et al. (2015)’ method.

This show that our proposed method is valid based on these improved operational laws.

7.3 Comparison and discussion

Because all ranking results are all same compared with above three methods, it is difficult to show the advantage of the proposed method. In this part, we give some revised data from Example 3. Since the triangular intuitionistic fuzzy sets are a generalization of the IFSs and are a better mathematical tool to handle uncertain and inconsistent information then IFS.

For comparison, we take Example 3 with the TIF information values, as given in Table 2.

Table 2 Revised decision matrix

(1) Ranking by the method in Wang (2008a, b)

Now, the steps based on the FNIFWA operator defined by Wang (2008a, b) are shown as follows.

Step 1: The overall evaluation values obtained using FNIFWA defined by Wang (2008a, b), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 3 8 ,0. 4 2 4 ,0. 5 3 5} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 2 6 8 ,0. 3 8 4 ,0. 5 7 2} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 8 1 ,0. 3 8 1 ,0. 500} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 4 5 ,0. 3 2 6 ,0. 3 2 6} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.430,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.402,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.385\;,\,S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.305.$$

Step 3: Therefore, the ranking order according to their score values is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$

Then, the steps based on the FNIFWG operator defined by Wang (2008a, b) are shown as follows.

Step 1: The overall evaluation values is obtained using the FNIFWG operator defined Wang (2008a, b), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 2 4 9 ,0. 2 9 8 ,0. 4 2 1} \right),\,\left( {0. 20 5 ,0. 2 7 4 ,0. 3 6 4} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0.0,\,0.0,\,0.0} \right),\,\left( {0.0 8 1 ,0.0 8 1 ,0. 1 3 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 7 7 ,0. 3 7 8 ,0. 500} \right),\,\left( {0. 1 1 3 ,0. 1 6 4 ,0. 2 1 8} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0.0,\,0.0,\,0.0} \right),\,\left( {0. 10 3 ,0. 200,0. 2 7 9} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.038,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = - 0.094,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} }) = 0.219,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = - 0.195.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Obviously, this ranking result is different from the one produced by the FNIFWA operator defined by Wang (2008a, b).

(2) Ranking by the method in Zhou and Chang (2014)

We use the method in Zhou and Chang (2014) to solve this problem and the steps are shown as follows.

Step 1: The overall evaluation values obtained by the FNIFHWA defined by Zhou and Chang (2014), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 2 4 ,0. 40 6 ,0. 5 1 8} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 2 5 6 ,0. 3 6 7 ,0. 5 4 2} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 80,0. 3 8 1 ,0. 500} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 3 5 ,0. 3 1 1 ,0. 3 1 1} \right),\,\left( {0.0,\,0.0,\,0.0} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.413,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.383,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.385\;,\,S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.292.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Obviously, this ranking result is different from the ones produced by the method defined by Wang (2008a, b).

(3) Ranking by the method in Wang et al. (2015)

The steps are shown as follows.

Step 1: The overall evaluation values is obtained by the the FNIFHWG operator defined Wang et al. (2015), and we have

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 2 5 8 ,0. 3 1 3 ,0. 4 3 8} \right),\,\left( {0. 1 9 5 ,0. 2 60,0. 3 4 8} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0.0,\,0.0,\,0.0} \right),\,\left( {0. 1 ,0.0 80,0. 1 3 1} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 7 7 ,0. 3 7 8 ,0. 500} \right),\,\left( {0. 1 1 1 ,0. 1 6 1 ,0. 2 1 2} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0.0,\,0.0,\,0.0} \right),\,\left( {0. 10 1 ,0. 1 9 3 ,0. 2 6 7} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), to calculate the score and accuracy values of the overall evaluation values, we can obtain

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.065,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = - 0.093,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.222,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = - 0.188.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

This result is the same as one produced by the FNIFWG operator defined by Wang (2008a, b), and is different from the other ranking results.

(4) Ranking by the proposed method in this paper

Now, we use the proposed method in this paper to solve this problem, and steps are shown as follows.

Step 1: The overall evaluation value is obtained using Eq. (27) as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 3 3 8 ,0. 4 2 4 ,0. 5 3 5} \right),\,\left( {0. 1 6 6 ,0. 2 1 4 ,0. 2 8 9} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 2 6 8 ,0. 3 8 4 ,0. 5 7 2} \right),\,\left( {0.0 7 9 ,0.0 8 2 ,0. 1 4 5} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 8 1 ,0. 3 8 1 ,0. 500} \right),\,\left( {0. 1 1 7 ,0. 1 7 1 ,0. 2 2 9} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 4 5 ,0. 3 2 6 ,0. 3 2 6} \right),\,\left( {0.0 9 5 ,0. 1 9 8 ,0. 2 8 8} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), we get

$$S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.210,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.305,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.214,\,\;S( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.111.$$

Step 3: Therefore, the ranking order according to their score values is

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} .$$

Therefore, the best alternative is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2}$ and the worst is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4}$.

Now, by the TIFWG operator defined in this article, we have

Step 1: The overall evaluation values is obtained using Eq. (28), and is given below:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} = \left\langle {\left( {0. 2 9 9 ,0. 3 6 4 ,0. 4 5 9} \right),\,\left( {0. 20 5 ,0. 2 7 4 ,0. 3 6 4} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} = \left\langle {\left( {0. 2 6 6 ,0. 3 8 6 ,0. 5 8 4} \right),\,\left( {0.0 8 1 ,0.0 8 1 ,0. 1 3 3} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} = \left\langle {\left( {0. 2 8 6 ,0. 3 8 9 ,0. 5 1 1} \right),\,\left( {0. 1 1 3 ,0. 1 6 3 ,0. 2 1 8} \right)} \right\rangle ;$$

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} = \left\langle {\left( {0. 2 3 6 ,0. 3 2 4 ,0. 3 3 5} \right),\,\left( {0. 10 3 ,0. 200,0. 2 7 9} \right)} \right\rangle .$$

Step 2: Using Eqs. (29) and (30), we can get

$$S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{1} } ) = 0.093,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{2} } ) = 0.311,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{3} } ) = 0.229,\,\;S ( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d}_{4} } ) = 0.109.$$

Step 3: Therefore, the ranking order according to their score values is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{2} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{3} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{4} > \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{1} .$.

Obviously, the ranking results by the proposed method are different from the ones by the other methods.

The reason produced these results is that these methods adopt the different operational laws of FNIFNs. In Example 3, because all membership and non-membership degrees are not zero, thus, all methods in Wang (2008a, b), Zhou and Chang (2014), Wang et al. (2015) and our method in this paper can produce right ranking results. However, in the revised example, we revise some data to zero, including some membership degree and some non-membership degrees, so the methods in Wang (2008a, b), Zhou and Chang (2014) and Wang et al. (2015) will not give the right results, because the operational laws of FNIFNs used in these methods may result in the unreasonable results which are explained in Example 1, while the proposed method adopts improved operational laws of FNIFNs which can overcome these shortcomings, and it can give a reasonable ranking results. Therefore, the proposed aggregation operators and the method in this article are more practical and effective in the decision-making process.

8 Conclusion

In this paper, we pointed out some existing limitations in the operations of TIFNs and proposed some improved operational laws for TIFNs. Then, based on these improved operational laws, we propose some aggregation operators such as TIFWA operator, TIFWG operator, TIFOWG operator, TIFOWG operator, and TIFHA operator and TIFHG operators, and discussed some desirable properties of these operators. Furthermore, based on these aggregation operators, we define an MCDM method in which the alternatives values with respect to criteria are represented in the form of TIFNs. A numerical example is illustrated to show the practicality and effectiveness of the proposed MCDM method. Finally, a comparison has been made with the existing method to show that the proposed aggregation operators and MCDM method in this paper are more practical and effective in the decision-making process, because they have solved the existing limitations in the operations of TIFNs.

In the future, we shall define Bonferroni mean, Heronian mean, and scaled prioritized aggregation operators for TIFSs based on these new operational laws and applied them to MCGDM problems.