Introduction

Concrete gravity dam is a valuable structure for civilization from social, economic and industrial point of view. Gravity dam can restore huge amount of water for flood protection, cultivation and hydropower generation, etc. Design and construction of concrete gravity dam are very much important for mankind. During analysis of gravity dam all the parameter should be considered for safety purpose. Effect of hydrodynamic pressure generated at the face of gravity dam due to earthquake is very much important for stability of dam structure. Estimation of hydrodynamic pressure depends upon different geometrical properties of adjacent reservoir such as length of reservoir, height of reservoir, bottom slop angle and absorption effect of reservoir bottom. Different analytical approaches have been proposed by various authors for calculation of hydrodynamic pressure in the previous literatures.

Tsai and Lee [23] proposed a new boundary integral equation and applied to determine the hydrodynamic pressure on dam subjected to ground acceleration. The effect of compressibility of water was considered in their formulation. Sharan [19] invented a radiation boundary condition for finite element analysis of dam–reservoir coupled system. He computed hydrodynamic pressure on vertical and inclined faces of dam. Ghaemian and Ghobarah [5] developed a staggered solution method for dynamic analysis of dam–reservoir system. Their approach was found accurate as compared with finite element method. Gogoi and Maity [6] employed an effective non-reflecting boundary condition for modeling of infinite reservoir. They utilized finite element method and reservoir bottom absorption for modeling purpose. Samii and Lotfi [14] used coupled and decoupled modal approaches for analysis of dam–reservoir system. The former method has complications, but decoupled approach can be solved using standard eigenvalue solver. Both the methods were executed, and the results were compared for dam–reservoir system. Solomatine and Shrestha [21] invented a method to estimate model uncertainty by using machine learning techniques. Shahri et al. [16] established geotechnical-based method for analysis of liquefaction potential related to earthquake. Neya and Ardeshir [10] suggested an analytical technique for evaluation of hydrodynamic pressure on dam. They have considered fluid–viscosity and reservoir bottom absorption effect for analysis purpose. Samii and Lotfi [15] suggested a boundary condition of higher order function for analysis of infinite reservoir subjected to dynamic loading. They have included reservoir bottom absorption in their analysis. Tarinejad and Pirboudaghi [22] implemented legendre spectral element method for study of dam–reservoir interaction problem. They have also used finite element method to compare the results for both the method. Altunisik and Sesli [1] executed dynamic analysis of concrete gravity dam using Westergaard, Lagrange and Euler approaches. They determined displacement, principal stresses and strains for all the approaches and compared. Pelecanos et al. [11] executed a numerical study on dynamic response of concrete and earthen dam. They included the dam–reservoir interaction effect to determine the responses of dam subjected to harmonic excitation. Manjula and Shasikaran [9] considered the effect of reservoir compressibility for the study of responses of gravity dam subjected to earthquake loading. They have utilized Lagrange–Lagrange approach for the finite element analysis of gravity dam and impounding reservoir. Wang et al. [24] determined hydrodynamic pressure developed on the face of gravity dam of different heights using Westergaard correction formula. They implemented fluid–structure coupling model to observe the pressure at the upstream face of the dam structure. Sharma et al. [20] used space time finite element technique for earthquake analysis of dam, reservoir and soil system. They have considered block iterative algorithm for solving the algebraic equations. Gao et al. [4] implemented a novel boundary condition along with finite element technique for dynamic analysis of dam–reservoir system. They assumed that semi-infinite reservoir having constant cross section and water compressibility, and reservoir bottom absorption effect has been taken for the analysis purpose. Saltelli et al. [13] presented a symmetric review of sensitivity analysis practices. Asheghi et al. [2] updated the neural network sediment load models by using different sensitivity analysis methods. Rostami et al. [12] created a method of constrained feature selection using measurement of pairwise constraints uncertainty. Haghani et al. [7] used extended finite element method for dynamic analysis of dam, reservoir and foundation system. They assessed the fracture growth in the dam structure due to seismic excitation. Behroozi and Vaghefi [3] used mesh free numerical model for hydrodynamic analysis of dam, reservoir and foundation system. They have considered non-vertical face of gravity dam for determination of hydrodynamic pressure. Zhang et al. [25] evaluated seismic stability of rock slopes with spatial variability. Han et al. [8] determined seismic responses of utility tunnel–soil system along with and without joint connections. Shahri et al. [17] presented a subsurface topographical modeling with the use of geospatial and data-driven algorithm. Zhang et al. [26] presented stability analysis of embankment slope with spatial variability of soil properties. Shahri et al. [18] invented a method for uncertainty quantification of ground water table modeling using automated predictive deep learning approach.

Earthquake response of concrete gravity dam is essential for design and safety purpose of the structure. Hydrodynamic pressure, developed on the face of gravity dam due to adjacent reservoir, highly influenced the response of dam subjected to seismic excitation. In the present work, hydrodynamic pressure in unbounded reservoir is determined using dam–reservoir interaction effect. Finite element method has a distinct advantage to tackle the irregular geometry. Dam and reservoir geometry is simultaneously discretized with eight-node isoparametric element in the present study. Displacement is considered as nodal unknown for dam structure. Pressure is considered as nodal variable for reservoir domain to overcome the problem of spurious mode related to displacement-based formulation for fluid medium. Thus, the analysis is performed following Lagrange–Euler approach for dam–reservoir system. Effect of surface wave is neglected, and reservoir bottom absorption effect is considered. The fluid is considered to be non-viscous and compressible. The infinite fluid domain is truncated at a suitable distance to reduce the computational cost, and an effective radiation boundary condition is applied at the truncated face to get the effect of infinite reservoir domain. Newmark’s time integration is used to solve the dynamic equilibrium equation. A MATLAB code has been developed in the present study to analyze the dam–reservoir coupled system.

Geometrical parameters of reservoir effect the hydrodynamic pressure developed on the face of dam. In the present study, hydrodynamic pressure is obtained considering the reservoir bottom as inclined for different frequencies of forcing function. Stresses of dam are also observed for different inclination of bottom slope of reservoir for harmonic excitation. Upward slope means anticlockwise slope of reservoir bottom is considered as positive slope. Downward slope means clockwise slope of reservoir bottom is considered as negative slope. Variation of inclined length also effects the hydrodynamic pressure. Responses of gravity dam and hydrodynamic pressure are also observed for variation of inclined length of reservoir bottom for harmonic excitation. Hydrodynamic pressure also studied for variation of absorption coefficient of reservoir bottom. Responses of gravity dam and hydrodynamic pressure are observed due to earthquake excitation including the dam–reservoir interaction effect at the last section of the present work.

Theoretical formulation

Formulation for gravity dam

Equation of motion of a structure subjected to external exciting force can be written in finite element form as below:

$$\left[M\right]\left\{\ddot{u}\right\}+\left[C\right]\left\{\dot{u}\right\}+\left[K\right]\left\{u\right\}=\{{F}_{d}\}$$
(1)

Here, [M], [C] and [K] are mass, damping and stiffness matrix of structure, respectively. \(\left\{\ddot{u}\right\}\), \(\left\{\dot{u}\right\}\) and \(\left\{u\right\}\) are nodal accelerations, velocity and displacement of the domain of structure. The structure has been discretized by two-dimensional eight-node isoparametric elements. The structural Rayleigh damping can be expressed as below:

$$\left[ C \right] = a\prime \left[ M \right] + b\prime \left[ K \right]$$
(2)

a´ and b´ are called proportional damping constants. The relation between a´, b´ and the fraction of critical damping at frequency ω is given by the equation below:

$$\xi \prime = \frac{1}{2}\left( {a\prime \omega + \frac{b\prime }{\omega }} \right)$$
(3)

Damping constant a´ and b´ are determined by choosing the fraction of critical damping ξ1´ and ξ2´ at two different frequencies ω1 and ω2 and solving the equation for a´ and b´. So that,

$$a\prime = \frac{{2\left( {\xi_{2} \prime \omega_{2} - \xi_{1} \prime \omega_{1} } \right)}}{{\left( {\omega_{2}^{2} - \omega_{1}^{2} } \right)}}$$
(4a)
$$b\prime = \frac{{2\omega_{1} \omega_{2} \left( {\xi_{2} \prime \omega_{1} - \xi_{1} \prime \omega_{2} } \right)}}{{\left( {\omega_{2}^{2} - \omega_{1}^{2} } \right)}}$$
(4b)

Formulation for fluid domain

The state of total stress for Newtonian fluid may be defined by an isotropic tensor

$${T}_{ij}=-p{\delta }_{ij}+{{T}^{^{\prime}}}_{ij}$$
(5)

Here, \({T}_{ij}\) is total stress, and \({{T}^{^{\prime}}}_{ij}\) is viscous stress tensor. Variable p is hydrodynamic pressure, and \({\delta }_{ij}\) is Kronecker delta.

If viscosity of fluid is neglected, then Eq. (5) may be written as follows:

$${T}_{ij}=-p{\delta }_{ij}$$
(6)

The Navier–Stokes equation of motion is given by the following equation:

$$\rho \left(\frac{\partial {v}^{i}}{\partial t}+{V}_{j}\frac{\partial {v}^{i}}{\partial {x}_{j}}\right)=\frac{\partial {T}_{ij}}{\partial {x}_{j}}+\rho {B}_{i}$$
(7)

where Bi is the body force, and ρ is the mass density of fluid. Now, substituting Eq. (6) in Eq. (7), we get

$$\rho \left(\frac{\partial {v}^{i}}{\partial t}+{V}_{j}\frac{\partial {v}^{i}}{\partial {x}_{j}}\right)=\rho {B}_{i}-\frac{\partial p}{\partial {x}_{i}}$$
(8)

After neglecting the convective terms and the component of body forces, following equations can be obtained:

$$\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{\partial u}{\partial t}=0$$
(9)
$$\frac{1}{\rho }\frac{\partial p}{\partial y}+\frac{\partial v}{\partial t}=0$$
(10)

where u and v are the components of velocity along x and y direction.

Continuity equation in two dimensions may be expressed as follows:

$$\frac{\partial p}{\partial t}+\rho {c}^{2}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0$$
(11)

Here, c is the acoustic wave velocity in fluid.

Differentiating Eq. (9) and Eq. (10) with respect to x and y, following expressions can be written:

$$\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial t}\right)=0$$
(12)
$$\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {y}^{2}}+\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial t}\right)=0$$
(13)

After addition of Eq. (12) and Eq. (13), the following equation can be obtained:

$$\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {y}^{2}}+\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial t}\right)+\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial t}\right)=0$$
(14)

Differentiating the terms of Eq. (11), the following expression can be obtained:

$$\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {t}^{2}}+\rho {c}^{2}\left\{\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial t}\right)+\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial t}\right)\right\}=0$$
(15)

Thus, from Eq. (14) to Eq. (15), following expression can be obtained:

$$\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {x}^{2}}+\frac{1}{\rho }\frac{{\partial }^{2}p}{\partial {y}^{2}}-\frac{1}{\rho {c}^{2}}\left(\frac{{\partial }^{2}p}{\partial {t}^{2}}\right)=0$$
(16)

Simplifying the above expression, the equation for compressible fluid can be written as below:

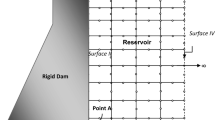
$${\nabla }^{2}p\left(x,y,t\right)=\frac{1}{{c}^{2}}\ddot{p} (x,y,t)$$
(17)

Here, ∇2 is the Laplace operator in two dimension in the fluid medium. The two-dimensional geometry of the dam–reservoir system is shown in Fig. 1. Geometry of the dam–reservoir system is assumed as two-dimensional. Fluid is assumed as compressible and inviscid.

Fig.1
figure 1

Finite element model of Koyna dam and reservoir system

Full size image

At the top surface of reservoir (surface I), considering the effect of surface wave, the boundary condition can be expressed as follows:

$$\frac{1}{g}\ddot{p}+\frac{\partial p}{\partial y}=0$$
(18)

However, neglecting the effects of surface wave, the boundary condition at the top surface of reservoir may be considered as below:

$$p\left(x,{H}_{f }\right)=0$$
(19)

Here, Hf is the depth of the reservoir.

At the interface of dam and reservoir (surface II), fluid pressure has to fulfill the following condition:

$$\frac{\partial p}{\partial n}\left(0,y,t\right)=\rho a{e}^{i\omega t}$$
(20)

Here, aeiωt is the horizontal component of the ground excitation in which ω is the circular frequency of vibration, and i = √-1, n is the outwardly directed normal at dam–reservoir interface. ρ is the density of fluid.

At bed of the reservoir (surface III), including the absorption of seismic wave, pressure has to satisfy the following equation:

$$\frac{\partial p}{\partial n}\left(x,0,t\right)=i\omega q\dot{p }(x,0,t)$$
(21)

Here,

$$q=\frac{1}{C}\left(\frac{1-\alpha }{1+\alpha }\right)$$
(22)

At the truncation surface of reservoir (surface IV), the boundary condition may be written as follows:

$$\frac{\partial p}{\partial n}=\left({\xi }_{m}-\frac{1}{C}\right)\dot{p}$$
(23)

According to Gogoi and Maity [6], ξm is assumed as below:

$${\zeta }_{m}=-\frac{i{\sum }_{m=1}^{\infty }\frac{{{\lambda }_{m}}^{2}{I}_{m}}{{\beta }_{m}}{e}^{\left(-{k}_{m}x\right)}({\Psi }_{m})}{\Omega C{\sum }_{m=1}^{\infty }\frac{{{\lambda }_{m}}^{2}{I}_{m}}{{\beta }_{m}{k}_{m}}{e}^{\left(-{k}_{m}x\right)}({\Psi }_{m})}$$
(24)

If the effect of surface wave is neglected, then χ can be considered to be zero.

Implementing the Galarkin approach and assuming pressure to be the nodal variable in the fluid medium, Eq. (17) can be discretized as below:

$$\underset{\Omega }{\overset{}{\int }}{N}_{rj}\left[{\nabla }^{2}\sum {N}_{ri}{p}_{i}-\frac{1}{{C}^{2}}\sum {N}_{ri}\ddot{{p}_{i}}\right]\mathrm{d}\Omega =0$$
(25)

where Nij is the interpolation function for the reservoir domain and Ω is the region of interest. Now, using Green’s theorem, equation (25) may be expressed below:

$$-\underset{\Omega }{\overset{}{\int }}\left[\frac{\partial {N}_{rj}}{\partial x}\sum \frac{\partial {N}_{ri}}{\partial x}{p}_{i}+\frac{\partial {N}_{rj}}{\partial y}\sum \frac{\partial {N}_{ri}}{\partial y}{p}_{i}\right]\mathrm{d}\Omega -\frac{1}{{C}^{2}}\underset{\Omega }{\overset{}{\int }}{N}_{rj}\sum {N}_{ri}\mathrm{d}\Omega \ddot{{p}_{i}} +\underset{\Gamma }{\overset{}{\int }}{N}_{rj}\sum \frac{\partial {N}_{rj}}{\partial n}\mathrm{d}\Gamma {p}_{i}=0$$
(26)

Γ is the boundaries of reservoir domain. The above equation may be written in a matrix form as follows:

$$\left[\overline{J }\right]\left\{\ddot{p}\right\}+\left[\overline{H }\right]\left\{p\right\}=\left\{F\right\}$$
(27)
$$\left[\overline{J }\right]=\frac{1}{{C}^{2}}\sum \underset{\Omega }{\overset{}{\int }}{\left[{N}_{r}\right]}^{T}\left[{N}_{r}\right]\mathrm{d}\Omega$$
(28)
$$\left[\overline{H }\right]=\sum \underset{\Omega }{\overset{}{\int }}\left[\frac{\partial }{\partial x}{\left[{N}_{r}\right]}^{T}\frac{\partial }{\partial x}\left[{N}_{r}\right]+\frac{\partial }{\partial y}{\left[{N}_{r}\right]}^{T}\frac{\partial }{\partial y}\left[{N}_{r}\right]\right] \mathrm{d}\Omega$$
(29)
$$\left\{F\right\}=\sum \underset{\Gamma }{\overset{}{\int }}{\left[{N}_{r}\right]}^{T}\frac{\partial p}{\partial n}d\Gamma =\left\{{F}_{f}\right\}+\left\{{F}_{fs}\right\}+\left\{{F}_{fb}\right\}+\left\{{F}_{t}\right\}$$
(30)

Here, the subscript f, fs, fb and t presents the free surface of reservoir, fluid–structure interface, fluid-bed interface and truncation surface, respectively. For free surface, {Ff} may be written in finite element form as given below:

$$\left\{{F}_{f}\right\}=-\frac{1}{g}\left[{R}_{f}\right]\left\{\ddot{p}\right\}$$
(31)
$$\left[{R}_{f}\right]=\sum \underset{{\Gamma }_{f}}{\overset{}{\int }}{\left[{N}_{r}\right]}^{T}\left[{N}_{r}\right]\mathrm{d}\Gamma$$
(32)

At the fluid–structure interface, if {a} is the vector of nodal accelerations in fluid, {Ffs} may be written as given below:

$$\left\{{F}_{fs}\right\}=-{\rho }_{f}\left[{R}_{fs}\right]\left\{a\right\}$$
(33)
$$\left[{R}_{fs}\right]=\sum \underset{{\Gamma }_{fs}}{\overset{}{\int }}{\left[{N}_{r}\right]}^{T}\left[T\right] \left[{N}_{d}\right]d\Gamma$$
(34)

Here, [T] is the transformation matrix at fluid–structure interface, and Nd is the interpolation function of dam.

At the reservoir and bed interface, {Ffb} may be expressed as given below:

$$\left\{{F}_{fb}\right\}=i\omega q\left[{R}_{fb}\right]\left\{p\right\}$$
(35)
$$\left[{R}_{fb}\right]=\sum \underset{{\Gamma }_{fb}}{\overset{}{\int }}{\left[{N}_{r}\right]}^{T} \left[{N}_{r}\right]d\Gamma$$
(36)

At the truncated surface, {Ft} may be expressed as given below:

$$\left\{{F}_{t}\right\}={\zeta }_{m}\left[{R}_{t}\right]\left\{p\right\}-\frac{1}{C}\left[{R}_{t}\right]\left\{\dot{p}\right\}$$
(37)
$$\left[{R}_{t}\right]=\sum \underset{{\Gamma }_{t}}{\overset{}{\int }}{\left[{N}_{r}\right]}^{T} \left[{N}_{r}\right]d\Gamma$$
(38)

After writing all the term, Eq. (27) becomes as follows:

$$\left[J\right]\left\{\ddot{p}\right\}+\left[A\right]\dot{p}+\left[H\right]\left\{p\right\}=\left\{{F}_{r}\right\}$$
(39)
$$\left[J\right]=\left[\overline{J }\right]+\frac{1}{g}\left[{R}_{f}\right]$$
(40)
$$\left[A\right]=\frac{1}{C}\left[{R}_{t}\right]$$
(41)
$$\left[H\right]=\left[\overline{H }\right]+{\zeta }_{m}\left[{R}_{t}\right]-i\omega q\left[{R}_{fb}\right]$$
(42)
$$\left\{{F}_{r}\right\}=-{\rho }_{f}\left[{R}_{fs}\right]\left\{a\right\}$$
(43)

Formulation for dam–reservoir coupled system

In the present study, structure and fluid is assumed to be act together in a coupled way. The coupling of structure and fluid may be formulated in the following way.

The discrete dam equation along with damping may be written as follows:

$$M\ddot{u}+C\dot{u}+Ku-Qp-{F}_{d}=0$$
(44)

The coupling term [Q] arises due to the acceleration and pressure at the interface of dam and reservoir and can be expressed as below:

$${\int }_{{\Gamma }_{s}}{{N}_{S}}^{T}npd\Gamma =\left({\int }_{{\Gamma }_{s}}{{N}_{S}}^{T}n{N}_{r}d\Gamma \right)p=Qp$$
(45)

where n is the direction vector of the dam–reservoir interface. Ns and Nr are the shape function of dam and reservoir. The discretized equation of fluid may be written as below:

$$J\ddot{p}+A\dot{p}+Hp-{Q}^{T}\ddot{u}-{F}_{r}=0$$
(46)

The systems of Eq. (44) and (46) are coupled in a second-order differential equation form, which defines the equation for the coupled dam–reservoir system and can be expressed as below:

$$\left[\begin{array}{cc}J& {Q}^{T}\\ 0& M\end{array}\right]\left\{\begin{array}{c}\ddot{p}\\ \ddot{u}\end{array}\right\}+\left[\begin{array}{cc}A& 0\\ 0& C\end{array}\right]\left\{\begin{array}{c}\dot{p}\\ \dot{u}\end{array}\right\}+\left[\begin{array}{cc}H& 0\\ -Q& K\end{array}\right]\left\{\begin{array}{c}p\\ u\end{array}\right\}=\left\{\begin{array}{c}{F}_{r}\\ {F}_{d}\end{array}\right\}$$
(47)

To solve Eq. (47), Newmark’s integration method is adopted. It has been seen that two parameters β and δ in Newmark’s method may be varied to get the accuracy.

Validation of proposed algorithm

Present algorithm has been validated with the similar problem considered by Samii and Lotfi [14]. The time periods of first three modes are compared with time periods obtained from the literature of Samii and Lotfi [14] are shown in Table 1, and very close agreement has been achieved.

Table 1 Comparison of time periods of first three modes of the dam–reservoir system
Full size table

Numerical results

In the present paper, behavior of unbounded reservoir adjacent to concrete gravity dam has been studied including the dam–reservoir interaction. Absorption effect of reservoir bottom is considered. Length of the reservoir is truncated at a suitable distance (L/Hf = 0.5), and the non-reflecting boundary condition proposed by Gogoi and Maity [6] is applied along the truncated face. In the present paper, Koyna dam has been considered for numerical study. Standard eight-node isoparametric element has been considered for discretization of dam and reservoir geometry. Dynamic equilibrium equation is solved by Newmark’s integration technique. For convergence study, the displacement at tip of dam is shown in Table 2 for different mesh size of dam and reservoir. The results are obtained by applying harmonic excitation. From the convergence test, mesh size for dam is taken as Nh = 3 and Nv = 8 and for reservoir Nh = 4 and Nv = 8. Where Nh is number of divisions in horizontal direction and Nv is number of divisions in vertical direction (Fig. 1).

Table 2 Convergence test for meshing of dam and reservoir
Full size table

Part I

In the first part of the work, hydrodynamic pressure distribution at the face of dam has been determined for different exciting frequencies with change in bottom slope of reservoir (Fig. 2). Height of the reservoir is taken as Hf = 103 m, and L/Hf ratio is taken as 0.5. Unit weight of fluid is taken as 10 kN/m3. Velocity of sound wave (c) is taken as 1438.7 m/s, and bottom absorption coefficient is considered as 0.95. For the present work, Koyna dam has been taken for analysis purpose. Modulus of elasticity of concrete for gravity dam is taken as 3.15 × 1010 N/m2, and Poisson’s ratio is assumed as 0.235. Density of concrete is taken as 2415.816 kg/m3, and damping ratio is considered as 0.05. Hydrodynamic pressure at face of dam is determined by applying harmonic excitation for Tc/Hf = 4, 10 and 100 with reservoir bottom slope (θb) 40,120 and 200. Upward slope, anticlockwise slope of reservoir bottom, is considered as positive slope. Downward slope, clockwise slope of reservoir bottom, is considered as negative slope.

Fig. 2
figure 2

Dam–reservoir system

Full size image

Figure 3 presents the distribution of pressure coefficient (Cp = p/ρaHf) at the face of dam for Tc/Hf = 4, 10 and 100, respectively, for positive slope (θb) of reservoir bottom as + 40, + 120 and + 200. Figure 4 shows the time history plot of pressure coefficient at heel of dam for Tc/Hf = 4,10 and 100, respectively for negative slope (θb) of reservoir bottom.

Fig. 3
figure 3

Distribution of pressure coefficient at face of dam for a Tc/Hf = 4, b Tc/Hf = 10 and c Tc/Hf = 100 for positive bottom slope

Full size image
Fig. 4
figure 4

Time history plot of pressure coefficient at heel of dam for a Tc/H = 4, b Tc/H = 10 and c Tc/H = 100 for negative bottom slope

Full size image

Figure 5a presents the time history plot of major principal stress, and Fig. 5b presents the time history plot of minor principal stress at heel of dam for positive slope angle of reservoir bottom. Figure 6a displays the time history plot of major principal stress, and Fig. 6b displays the time history plot of minor principal stress at heel of dam for negative slope angle of reservoir bottom.

Fig. 5
figure 5

Time history plot of a major principal stress and b minor principal stress at heel of dam for positive slope angle of reservoir bottom

Full size image
Fig. 6
figure 6

Time history plot of a major principal stress and b minor principal stress at heel of dam for negative slope angle of reservoir bottom

Full size image

Part II

In this portion of work, distribution of pressure coefficient at the face of dam has been observed for different values of inclined length (Li) of reservoir bottom (Fig. 7) including dam–reservoir interaction effect.

Fig. 7
figure 7

Dam and reservoir with inclined length

Full size image

Height of the reservoir is considered as 103 m, and L/Hf ratio is taken as 0.5. Density of water (ρ), velocity of sound waves (c) in water and bottom absorption coefficient are taken as considered in the Part I. For the present work, Koyna dam has been taken for analysis purpose. Modulus of elasticity of concrete, density of concrete, Poisson’s ratio and damping ratio is taken as considered in Part I.

Hydrodynamic pressure at face of dam has been determined by applying harmonic excitation for different value of inclined length of reservoir (Li = 0.25L, 0.5L, 0.75L) with positive slope angle (+ 40, + 120, + 200) and negative slope angle (− 40, − 120, − 200) of reservoir bottom. Figure 8 presents the coefficient of hydrodynamic pressure distribution at the face of dam for different values of positive slope angle of reservoir bottom as + 40, + 120 and + 200, respectively, with different values of inclined length of reservoir as Li = 0.25 L, 0.5L and 0.75L. Similarly, Fig. 9 presents the coefficient of hydrodynamic pressure distribution at the face of dam for different values of negative slope angle of reservoir bottom as − 40, − 120 and − 200, respectively, with different values of inclined length of reservoir as Li = 0.25L, 0.5L and 0.75L.

Fig. 8
figure 8

Distribution of pressure coefficient at face of dam at for bottom slope a + 4 degree, b + 12 degree and c + 20 degree

Full size image
Fig.9
figure 9

Distribution of pressure coefficient at face of dam at for bottom slope a -4 degree, b -12 degree and c -20 degree

Full size image

Figure 10a presents the time history plot of major principal stress, and Fig. 10b presents the time history plot of minor principal stress at heel of dam for positive slope angle + 200 at reservoir bottom. Figure 11a displays the time history plot of major principal stress, and Fig. 11b displays the time history plot of minor principal stress at heel of dam for negative slope angle − 200 at reservoir bottom.

Fig. 10
figure 10

Time history plot of a major, b minor principal stress at heel of dam for slope angle + 20 degree

Full size image
Fig. 11
figure 11

Time history plot of a major, b minor principal stress at heel of dam for slope angle -20 degree

Full size image

Part III

In this part of work, hydrodynamic pressure at heel of dam has been determined for different values of absorption coefficient of reservoir with inclined bottom surface including the dam–reservoir interaction. The dam and reservoir geometry and their properties are taken as same as considered in Part II. In this part, L/Hf ratio is taken as 0.5 and Li is considered as 0.5L. Hydrodynamic pressure coefficients at heel of dam are determined for positive slope angle (+ 40, + 120, + 200) of reservoir bottom. Pressure coefficients are observed for different values of absorption coefficient of reservoir bottom such as alfa (α) = 0, 0.5 and 1 for all the values of bottom slope angle due to application of harmonic excitation.

Figure 12 presents the hydrodynamic pressure coefficient at heal of dam with different values of absorption coefficient for positive slope angles at reservoir bottom as + 40, + 120 and + 200, respectively.

Fig. 12
figure 12

Hydrodynamic pressure coefficient at heel of dam for bottom slope angle as a + 40, b + 120 and c + 20.0

Full size image

Part IV

In this portion of work, hydrodynamic pressure distributions at the face of dam have been determined for earthquake excitation with change in bottom slope (negative and positive) of reservoir including dam–reservoir interaction. Height of the reservoir is considered as 84.75 m, and L/Hf ratio is taken as 0.5, inclined length Li = 0.5L and absorption coefficient of reservoir bottom as 0.95. Effect of surface wave is considered. For this work, Koyna dam has been taken for analysis purpose. The dam and reservoir geometry and their properties are taken as considered in Part II. Analysis has been carried out by applying north–south component of El-Centro earthquake excitation. The amplitude of the excitation is equal to the gravitational acceleration ‘g’.

Figure 13 shows Hydrodynamic pressure at face of dam for (a) positive and (b) negative bottom slope for earthquake. Figure 14a, b shows the time history of major principal stress and minor principal stress, respectively, at heel of dam for positive bottom slope for earthquake. Figure 15 presents major and minor principal stress plot of dam for base angle + 40 and + 200. Figure 16 displays major and minor principal stress plot of dam for base angle − 40 and − 200. From these figures, differences of stresses have been seen for change in slope of reservoir bed for both negative and positive.

Fig. 13
figure 13

Hydrodynamic pressure at face of dam for a positive and b negative bottom slope for El-Centro earthquake

Full size image
Fig. 14
figure 14

Time history of a major and b minor principal stress at heel of dam for positive bottom slope for El-Centro earthquake

Full size image
Fig. 15
figure 15

a Major principal stress and b Minor Principal stress plot of dam for base angle + 40 and c Major principal stress and d Minor Principal stress plot of dam for base angle + 200 for earthquake

Full size image
Fig. 16
figure 16

a Major principal stress and b Minor Principal stress plot of dam for base angle − 40 and c Major principal stress and d Minor Principal stress plot of dam for base angle − 200 for earthquake

Full size image

Discussion

From Part I of the present work, it has been clear that pressure at heel of dam increases with increase in positive slope of reservoir bed for all values of exciting frequencies. Pressure is higher at heel of dam for Tc/Hf = 4 compare to other frequencies for all positive bottom slope angles. From Part I, it is established that pressure at heel of dam decreases with increase in negative slope of reservoir bottom for all values of exciting frequencies.

From the Part I, it is also clear that maximum value of major and minor principal stresses at heel of dam increase with increase in positive slope angle of reservoir and decrease with increase in negative slope angle of reservoir bottom. From second part of the present work, it is observed that pressure at heel of dam increases with increase in inclined length (Li) of reservoir for positive slope angle. The difference of pressure at heel of dam increases with increase in value of slope angle (positive) at reservoir bottom. From Part II of present work, it is observed that pressure at heel of dam decreases with increase in inclined length (Li) of reservoir for negative slope angle. Here, also, the difference of pressure at heel of dam increases with increase in value of slope angle (negative) at reservoir bottom. From Part II, it is also observed that value of major and minor principal stresses at heel of dam increases with increase in inclined length for positive slope angle of reservoir bottom and decreases with increase in inclined length for negative slope angle of reservoir bottom. From Part III, it is observed that hydrodynamic pressure coefficient at heel of dam is minimum for alfa (α) = 0 for all values of slope angles. Pressure coefficient is maximum for alfa (α) = 1 for all values of slope angles. So, it can be stated that pressure will increase at heel of dam if the absorption coefficient is increased for any values of slope angles. But the difference of pressure is high between alfa = 0 to 0.5, and the difference of pressure is comparatively small between alfa = 0.5 to 1. From Part –IV, it is observed that maximum pressure occurred for higher value of positive slope angle of reservoir bottom and it is also observed that maximum peak occurred for lower value of negative slope angle of reservoir bottom. It is also observed that maximum stress occurred at higher value of positive slope angle of base of reservoir.

Conclusion

A numerical procedure using finite element has been presented for dynamic analysis of dam–reservoir coupled system. Both the domains are coupled and analyzed as a single system to get the responses of dam–reservoir coupled system subjected to dynamic excitation. The advantage of current method is that the present method is state forward, and it gives the responses of the coupled system directly.

Geometrical parameters of reservoir have impact on behavior of concrete gravity dam. Slope of reservoir bed, inclined length of reservoir and bottom absorption coefficient are the important factors governing the hydrodynamic pressure as well as responses of gravity dam. From the present analysis, it has been clear that hydrodynamic pressure and stresses of gravity dam are increased with increase in slope angles for positive slope of reservoir bottom. Pressure coefficient and stresses of dam are decreased with increase in slope angles for negative slope of reservoir bottom. Inclined length of reservoir also influences pressure coefficient and stresses of dam. Numerical results show that if the inclined length of reservoir is increased, hydrodynamic pressure coefficient and stresses of gravity dam are also increased for positive slope angle of reservoir base. Pressure coefficient and stresses of dam are decreased with increase in inclined length of reservoir for negative bottom slope. Hydrodynamic pressure is increased with increase in reservoir bottom coefficient. The rate of increment is high up to 0.5, and the rate of increment is low beyond 0.5. Thus, reservoir parameters have influence on the hydrodynamic pressure and stresses of dam. Earthquake responses of dam–reservoir coupled system would be more accurate for addition of effect of soil foundation within the analysis.