Introduction

The premise of the seismic design methodology in a typical building code is based on the consideration of the first mode. In some cases, the error due to the truncation of higher modes can be too large to be ignored, especially in the calculation of response of stiff and irregular structural systems. Often, it is stated that mode truncation results in significant errors for stiff structures but not for flexible structures. Such a characterization of this problem is highly incorrect because the fundamental mode in an irregular structure is typically a localized mode that may not have any bearing on the response of certain other parts within a structure [1]. Moreover, some response quantities [2, 3] which have a significant contribution from the higher modes may also be sensitive to this mode truncation error, in even not so stiff structures. Instead of the first mode, the second one can dominate the shear demand in the buildings [3,4,5]. Experimental studies [6, 7] on the uplift effect of structures show that it can increase the contribution of the higher modes. In order to check the accuracy of the calculated response when higher modes are truncated in a modal superposition, typical seismic building codes specify that the results can be considered accurate if about 90% of the total structural mass participates in the number of modes considered [8,9,10,11,12,13,14,15,16]. This 90% mass criterion for the number of modes to be considered in a response spectrum method is extended to the nonlinear static pushover analysis [17, 18]. In the response spectrum method, the 90% criteria even when satisfied may not always result in correct responses in all the elements of an irregular structure [1]. The studies conducted [19, 20] on multi-frame bridges show that the present codal criterion of 90% structural mass for the number of modes to be considered for the dynamic analysis of structures is not adequate, especially in long bridges, two-column bent, stiff soils, or bridges with high over strength. Further, it is observed that this criterion is not sufficient for estimating shear key forces. The accurate calculation of the responses is critical for the design of structural components like diaphragms and connections of precast or steel buildings [21, 22] and non-structural components which are mounted on floors [23,24,25]. The exact estimation of lateral force distribution [26, 27] and responses can increase the seismic performance of the structure. The present design criterion may result in overestimation of response in some members, whereas an underestimation of response in other members [1,2,3, 28]. Therefore, for the seismic analysis of irregular structures using response spectrum method, all the modes up to rigid frequency are considered and “missing mass” correction is applied for the truncated high-frequency modes having frequencies higher than rigid frequency. The consideration of high-frequency modes may introduce additional inaccuracies if the modal responses are not combined correctly [29,30,31,32].

Techniques have been developed to take the effect of the “missing mass” contained in the uncalculated high-frequency modes into account. A comparison between the various “missing mass” correction methods shows that residual mode method is superior to other methods [33, 34]. The residual mode can be included as modal properties of an additional mode in the dynamic analysis of lumped mass models and three-dimensional frame structures and can be combined with other modal responses using modal response combination rules [33]. The ability of the residual mode to approximate the periodic part of the response is not addressed. The modal responses, having a frequency less than rigid frequency, also have a rigid content, which gradually diminishes from the rigid frequency and becomes zero as the frequency goes down to a key frequency f1 [30, 32, 35]. In a complex and highly irregular structure, a large number of modes have to be considered before applying the “missing mass” correction. Considerable work is done to deal with the importance of higher modes, but only a few have addressed the issue of the required number of modes [1, 36,37,38]. This paper discusses the effect of truncation of modes on modal mass with the help of numerical examples, to show that the criterion given by building codes may not result in correct responses in all the elements of an irregular building. The ability of the residual mode to approximate the periodic part of the response is considered, and a simplified method is presented to take the response contributions of truncated modes into account.

Mode superposition method

The equations of motion for an N-degree-of-freedom, viscously damped system with classical damping can be written as

$${\mathbf{M\ddot{U}}} + {\mathbf{C\dot{U}}} + {\mathbf{KU}} = - {\mathbf{MU}}_{\text{b}} \ddot{u}_{\text{g}}$$
(1)

where M, C and K are the mass, damping and stiffness matrices, respectively; U is the displacement vector; Ub is the static displacement vector when the base of the structure undergoes a unit deflection in the direction of the earthquake; and \(\ddot{u}_{\text{g}}\) is the ground acceleration. The displacement U of the system can be expressed as the superposition of modal contributions \(U_{i}\):

$${\mathbf{U}} = \sum\limits_{{i = \text{1}}}^{N} {{\mathbf{U}}_{i} } = \sum\limits_{i = 1}^{N} {\phi_{i} X_{i} }$$
(2)

where \(\phi_{{_{i} }}\) are determined from the general eigenvalue problem \({\mathbf{K}}\phi_{i} = \omega_{i}^{2} {\mathbf{M}}\phi_{i}\), \(X_{i}\) = modal coordinates, and \(\omega_{i}\) is the frequency of the ith mode. By using Eq. (2), (1) can be transformed into a system of uncoupled equations in modal coordinates

$$\ddot{X}_{i} + 2\xi_{i} \omega_{i} \dot{X}_{i} + \omega_{i}^{2} X_{i} = \varGamma_{i} \ddot{u}_{g} ,\quad i = 1,2 \ldots N$$
(3)

where \(\varGamma_{i} = \phi_{i}^{T} {\mathbf{MU}}_{\text{b}}\) is called the modal participation factor and \(\xi_{i}\) is the damping ratio for the ith mode. In the response spectrum method, the contribution of ith mode to nodal displacements \({\mathbf{U}}\) is given by

$${\mathbf{U}}_{i} = \phi_{i} X_{i} = \varGamma_{i} \phi_{i} S_{{{\text{D}}i}}$$
(4)

where \(S_{{{\text{D}}i}}\) is the maximum relative displacement of a single-degree-of-freedom system having frequency \(\omega_{i}\) and damping \(\xi_{i}\). The modal response \({\mathbf{U}}\) can be divided into two parts: the rigid part Ur and the damped periodic part Up. The modal response U can be expressed in terms of Ur and Up as [30, 35]

$${\mathbf{U}} = \sqrt {({\mathbf{U}}^{r} )^{2} + ({\mathbf{U}}^{p} )^{2} }$$
(5)

Behaviour of high-frequency modes

The minimum frequency beyond which the spectral curves have the same values of spectral acceleration is defined as the rigid frequency [29, 30]. The studies conducted using 40 earthquake ground motions [32] show that curves with different damping ratios become rigid at different frequencies. The spectral curve with lower damping ratio become rigid at a higher frequency than a spectral curve with higher damping ratio. In high frequencies, the periodic part of the response becomes negligible and only the rigid part of response remains. The responses in all the high-frequency modes having a frequency equal to or greater than rigid frequency are in phase to each other and the rigid response always combines algebraically. In this region, the spectral acceleration becomes equal to the peak ground acceleration, often referred to as the zero period acceleration (ZPA). Consider the first “n” modes of the N-degree-of-freedom system, having frequencies less than rigid frequency, and let the response in these n modes be \({\mathbf{U}}^{\prime }\) and the response in the remaining modes be \({\mathbf{U}}_{o}\). Then,

$${\mathbf{U^{\prime}}} = \sum\limits_{i = 1}^{n} {{\mathbf{U}}_{i} = } \sum\limits_{i = 1}^{n} {\phi_{i} {\mathbf{X}}_{i} } ;\quad {\mathbf{U}}_{o} = \sum\limits_{i = n + 1}^{N} {{\mathbf{U}}_{i} } = \sum\limits_{i = n + 1}^{N} {\phi_{i} {\mathbf{X}}_{i} }$$
(6)
$${\mathbf{U}} = {\mathbf{U^{\prime}}} + {\mathbf{U}}_{o}$$
(7)

For high-frequency modes, Eqs. (1), (6) and (7) give

$${\mathbf{M\ddot{U}}}_{o} + {\mathbf{C\dot{U}}}_{o} + {\mathbf{KU}}_{o} = - \text{MU}_{{{\text{b}}o}} \ddot{u}_{\text{g}} ;$$
(8)

where

$${\mathbf{U}}_{{{\text{b}}o}} = {\mathbf{U}}_{\text{b}} - \sum\limits_{i = 1}^{n} {\phi_{i} \varGamma_{i} }$$
(9)

Since the residual response in high-frequency modes is pseudo-static, we can neglect the terms \({\mathbf{\ddot{U}}}\) and \({\dot{\mathbf{U}}}\) in Eq. (8); therefore,

$${\mathbf{KU}}_{o} = - {\mathbf{MU}}_{{{\text{b}}o}} \ddot{u}_{\text{g}}$$
(10)

The response of a high-frequency mode is essentially static and could be determined by static analysis using Eq. (10) instead of dynamic analysis.

Modal response combination

The peak value of the total response R estimated by combining the peak modal response of individual modes is given by

$$R^{2} = \sum\limits_{i = 1}^{N} {R_{i}^{2} + } \sum\limits_{i = 1}^{N} {\sum\limits_{j \ne i}^{{}} {\overline{\varepsilon }_{ij} } R_{i} R_{j} }$$
(11)

where Ri is the maximum modal response in ith mode and \(\bar{\varepsilon }_{ij}\) is the modified correlation factor [18] defined as

$$\overline{\varepsilon }_{ij} = \alpha_{i} \alpha_{j} + \sqrt {\left[ {\left( {1 - \alpha_{i}^{2} } \right)\left( {1 - \alpha_{j}^{2} } \right)} \right]} \varepsilon_{ij}$$
(12)

where \(\alpha_{i}\) is the rigid response coefficient in the ith mode and \(\varepsilon_{ij}\) is the correlation coefficient of the damped periodic part of modal responses, given by the complete quadratic combination (CQC) rule. For damped periodic modes, α = 0, and the modified double sum equation reduces to CQC, and for \(\bar{\varepsilon }_{ij} = 0\), it reduces to the square root of the sum of squares (SRSS). Eqs. (11) and (12) include the effect of the rigid response of high-frequency modes in the modified correlation coefficient \(\bar{\varepsilon }_{ij}\). The rigid response coefficient αi is defined as [30, 32]

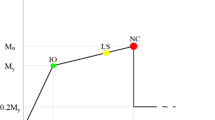
$$\alpha_{i} = \frac{{\int\limits_{0}^{{t_{d} }} {\text{ }\ddot{x}_{i} (t)\ddot{u}_{g} (t){\text{d}}t} }}{{t_{d} \sigma_{i}^{{\ddot{x}}} \sigma^{{\ddot{u}_{g} }} }}$$
(13)

where \(\ddot{x}_{i} (t)\) is the acceleration response, \(\sigma_{i}^{{\ddot{x}}}\) and \(\sigma^{{\ddot{u}_{\text{g}} }}\) are the standard deviations of \(\ddot{x}_{i} (t)\) and \(\ddot{u}_{\text{g}} (t)\), respectively, and \(t_{\text{d}}\) is the duration of responses. The value of α gradually reduces from one to zero, from the rigid frequency for a particular damping ratio to a key frequency f1 [30, 32, 35]. The key frequency f1 is the frequency at which the rigid response coefficient becomes zero. An approximate equation for αi can be represented by a straight line between the key frequency \(f_{1}\) and rigid frequency for a particular damping ratio on a semilogarithmic graph, which is given by [32]

$$\alpha_{i} = \frac{{\ln {{f_{i} } \mathord{\left/ {\vphantom {{f_{i} } {f_{1} }}} \right. \kern-0pt} {f_{1} }}}}{{\ln {{f_{{_{\varsigma } }}^{r} } \mathord{\left/ {\vphantom {{f_{{_{\varsigma } }}^{r} } {f_{1} }}} \right. \kern-0pt} {f_{1} }}}},\quad 0 \le \alpha_{i} \le 1$$
(14)

where fi is the modal frequency in hertz and the key frequencies f1 and f2 can be expressed as

$$f_{1} = \frac{{S_{{{\text{A}}\;\hbox{max} }} }}{{2\pi S_{{{\text{V}}\;\hbox{max} }} }},{\text{ Hz}}.$$
(15)

where \(S_{{{\text{A}}\;\hbox{max} }}\) is maximum spectral acceleration and \(S_{{{\text{V}}\;\hbox{max} }}\) is maximum spectral velocity

Residual mode method

Comparative studies show that residual mode method got more advantages than other “missing mass” correction methods. This method approximates the damped periodic part of the response also in addition to the rigid static part. In this method, the inertia effect of modes having frequencies greater than the rigid frequency is lumped into a “missing mass” term which yields the residual response. For high-frequency modes, the equation of motion reduces to Eq. (10). The term \(\ddot{u}_{\text{g}}\) in Eq. (10) is a scalar and can be scaled out from the equation. The solution of resulting equation yields a vector \(\phi_{\text{r}}\), which is normalized such that \(\phi_{\text{r}}^{T} {\mathbf{M}}\phi_{\text{r}} = 1\). The fictitious frequency \(\upomega_{\text{r}}^{2}\) corresponding to the residual mode is given by,

$$\upomega_{\text{r}}^{2} = \phi_{\text{r}}^{{\mathbf{T}}} {\mathbf{K}}\phi_{\text{r}}$$
(16)

The residual modal vector \(\phi_{\text{r}}\) and the corresponding frequency \(\omega_{\text{r}}\) can be directly included as modal properties of an additional mode in the dynamic analysis. The system can be analysed for n + 1 modes, where the contributions of high-frequency modes are taken into account by the residual mode.

To evaluate the ability of the residual mode to approximate the periodic part of the response, the two-degree-of-freedom (2-DOF) system shown in Fig. 1 is considered. The modal properties are given in Table 1. The structure is analysed using El Centro (1940) ground motion. The key frequency f1 is 1.47 Hz, and rigid frequency corresponding to 5% damping is 31.0 Hz. The structure is analysed using the first mode, and the second mode is truncated. The frequency of the second mode is 2.05 Hz which is far less than the rigid frequency and near to the key frequency f1, which shows that the major part of the response is damped periodic. A correction using residual mode is applied for the truncation of the second mode. The natural frequency of the residual mode is 2.05 Hz, and its mode shape is same as for the second mode. The results are shown in Table 2. The error is calculated with respect to the response with all the modes. It is observed that in this example the responses are exactly calculated by the residual mode, even though its frequency is 2.05 Hz which is far less than the rigid frequency. This shows that in this example residual mode approximates the damped periodic part and the rigid part of the response and can be combined using modal response combination rules. Therefore, the residual mode method can be considered as an approximate dynamic correction.

Fig. 1
figure 1

2-DOF system

Full size image
Table 1 Modal properties of 2-DOF system shown in Fig. 1
Full size table
Table 2 Storey shear (N) of 2-DOF system shown in Fig. 1
Full size table

Proposed simplified method

The number of modes to be used in the analysis should be such that the sum total of modal masses of all modes considered is at least 90% of the total seismic mass. The total structural mass of a building structure is given by

$$M_{T} = {\mathbf{U}}_{\text{b}}^{T} {\mathbf{MU}}_{\text{b}}^{{}}$$
(17)

where Ub = 1 is a unit vector. The modal mass corresponding to a mode is distributed along the mass points of the building. If 90% of the modal mass is considered

$$\mathop \sum \limits_{i = 1}^{n} M_{i}^{*} = 0.9M_{T}$$
(18)

The ith mode contribution to MUb at each mass point k is Γimkϕi which is independent of how the modes are normalized. Therefore, for n modes, Eq. (18) does not imply that Ub = 0.9 * 1 for all buildings, where 1 is a unit vector. The 90% structural mass participation in the number of modes used in the analysis does not ensure 90% mass participation at all mass points, especially in irregular buildings. In order to estimate correct responses in all the structural members, the contribution of all the modes up to rigid frequency has to be considered for the seismic analysis of irregular buildings and “missing mass” correction using residual mode for the truncated high-frequency modes beyond rigid frequency. For a large system with many degrees of freedom, so many modes have to be considered before reaching the rigid frequency. In an irregular system having modal frequencies less than rigid frequency, all the modes have to be considered. From the 2-DOF system considered above, it is observed that the responses are exactly calculated by the residual mode, even though its frequency is 2.05 Hz which is far less than the rigid frequency and near to the key frequency f1. Also from Fig. 2, it is seen that the residual mode shape exactly matches with the second mode. Therefore, the contribution of the higher modes can be approximated using a residual mode, and from Eq. (4), the corresponding response is given by

$${\mathbf{U}}_{i} = \varGamma_{\text{r}} \phi_{2} \text{S}_{\text{Dr}}$$
(19)

Therefore instead of considering all the modes, the response of the structure can be calculated using the first mode and the residual mode. The modal responses can be combined using modal response combination rules. The proposed method simplifies the seismic analysis of structures having significant contributions from higher modes. The following numerical examples will confirm this point.

Fig. 2
figure 2

Mode shapes of 2-DOF system

Full size image

Numerical example 1

A 6-DOF structural system [1] with mass irregularity having modal frequencies less than rigid frequency is shown in Fig. 3. The structure is having mass irregularity in its fourth floor. The frequencies, modal damping and the mass participation percentage for different modes for this system are given in Table 3. If the first mode alone is considered, the modal mass participation is nearly 90% and the codal provisions are satisfied. The expansion of the modal mass is shown in Table 4. The structure is analysed using El Centro (1940) ground motion. The key frequency f1 is 1.47 Hz, and rigid frequency corresponding to 5% damping is 31.0 Hz. The error in the calculation of storey shear considering the 90% modal mass is shown in Table 5. Though 90% modal mass criterion condition prescribed by the building codes of practice is satisfied, the error in the calculation of storey shear with respect to all the modes in storeys 5 and 6 are 37.8% and 50.7%, respectively. A residual mode correction is applied for the truncated modes. The frequency of the residual mode is 1.56 Hz which is far less than the rigid frequency. The response of the second residual mode is calculated using Eq. (19). The maximum error in the calculation of storey shear with respect to all the modes using residual mode is only 10.1% in storey 6. This shows that only two modes, the first mode and a residual mode with a modified mode shape, are sufficient for the calculation of responses.

Fig. 3
figure 3

6-DOF system, numerical example 1

Full size image
Table 3 Modal properties of 6-DOF system shown in Fig. 3
Full size table
Table 4 Modal expansion of Ub for numerical example 1
Full size table
Table 5 Storey shear (N) of 6-DOF system shown in Fig. 3, numerical example 1
Full size table

Numerical example 2

A 5-DOF structural system [37, 38] having modal frequencies less than rigid frequency is shown in Fig. 4. The height of each storey is 3 m. The structure is a regular structure as per building codes of practice. The frequencies, modal damping and the mass participation percentage for different modes for this system are given in Table 6. The frequencies were chosen to accentuate the contributions of the second through the fifth mode of the structural response [37]. The expansion of the modal mass is shown in Table 7. If the first mode alone is considered, the modal mass participation is nearly 90% and the codal provision for the number of modes is satisfied. The structure is analysed using El Centro (1940) ground motion. The error in the calculation of storey shear considering the first mode is shown in Table 8. Though the building is a regular one having uniform mass and stiffness distribution, the error in the calculation of storey shear with respect to all the modes in storey 5 is 33.33%. This shows that for this structure consideration of fundamental mode as recommended by building codes and 90% mass criterion is not sufficient. A residual mode correction is applied for the truncated modes. The frequency of the residual mode is 1.8 Hz, which is far less than the rigid frequency. Therefore, response of the second residual mode is calculated using Eq. (19). The maximum error in the calculation of storey shear with respect to all the modes using residual mode is only 3.89% in storey 4. This shows that the first mode and a residual mode with a modified mode shape are sufficient for the calculation of responses.

Fig. 4
figure 4

5-DOF system, numerical example 2

Full size image
Table 6 Modal properties of 5-DOF shown in Fig. 4, numerical example 2
Full size table
Table 7 Modal expansion of Ub for numerical example 2
Full size table
Table 8 Storey shear (N) of 5-DOF system shown in Fig. 4, numerical example 2
Full size table

Numerical example 3

A 6-DOF structural system [1] with stiffness irregularity having modal frequencies less than rigid frequency is shown in Fig. 5. The structure is having stiffness irregularity, and its ground storey is a soft storey. The frequencies, modal damping and the mass participation percentage for different modes for this system are given in Table 9. The expansion of the modal mass is shown in Table 10. If the first mode alone is considered, the modal mass participation is 90% and the codal provisions are satisfied. The structure is analysed using El Centro (1940) ground motion. The key frequency f1 is 1.47 Hz, and rigid frequency corresponding to 5% damping is 31.0 Hz. The error in the calculation of storey shear considering the 90% modal mass is shown in Table 11. Though 90% modal mass criterion condition prescribed by the building codes of practice is satisfied, the error in the calculation of storey shear with respect to all the modes in storey 5 and 6 is 23.35% and 33.04%, respectively. A residual mode correction is applied for the truncated modes. The frequency of the residual mode is 1.36 Hz which is far less than the rigid frequency. Therefore, the response of the second residual mode is calculated using Eq. (19). The maximum error in the calculation of storey shear with respect to all the modes using residual mode is only 12.17% in storey 6 and 3.68% in storey 4. This shows that only two modes, the first mode and a residual mode, are sufficient for the calculation of responses.

Fig. 5
figure 5

6-DOF system, numerical example 3

Full size image
Table 9 Modal properties of 6-DOF system shown in Fig. 5, numerical example 3
Full size table
Table 10 Modal expansion of Ub for numerical example 3
Full size table
Table 11 Storey shear (N) of 6-DOF system shown in Fig. 5, numerical example 3
Full size table

Numerical example 4

A 5-DOF model of a structure with a relatively stiff base supporting a flexible tower [35, 39] shown in Fig. 6 is considered for analysis using the proposed method. The frequencies, modal damping and the mass participation percentage for different modes for this system are given in Table 12. El Centro (1940) ground motion is used for earthquake excitation. In this example, the maximum mass contribution is from the fifth mode. The modal mass contribution of the first mode is only 40.55%. The first mode is considered for the analysis, and the higher modes are truncated. The error in the calculation of storey shear considering the first mode is shown in Table 13. The error in the calculation of storey shear with respect to all the modes in storey 1 is 32.77%. For the truncated higher modes “missing mass” correction is applied using residual mode method. The frequency corresponding to the residual mode vector is 31.01 Hz. In this case, the frequency of the residual mode is almost equal to the rigid frequency. The behaviour of the residual mode is rigid. Inertia forces and damping have no effect on a rigid mode. Therefore, the response of the second residual rigid mode is calculated using

$${\mathbf{U}}_{i} =\Gamma _{r} \phi_{r} \text{S}_{Dr}$$
(20)
Fig. 6
figure 6

5-DOF system, numerical example 4

Full size image
Table 12 Modal properties of 5-DOF system shown in Fig. 6, numerical example 4
Full size table

The results are compared with the peak modal responses calculated using modal analysis with all modes. The error involved in the calculation of storey shear using each method with respect to modal analysis with all modes is shown in Table 13. The error involved in the calculation of response using the proposed method is less than 4%.

Table 13 Storey shear (N) of 5-DOF system shown in Fig. 6, numerical example 4
Full size table

The mass participating in the first mode in numerical examples 1, 2, 3 and 4 is 89.95%, 87.95%, 90.73%, and 40.55%, respectively. In the first, second and third examples, the modes considered for the analysis are nearly 90% of the structural mass. Further, the second example is a regular structure with a uniform distribution of stiffness and mass, and as per the building codes of practice, the response can be calculated using only the first mode of vibration. In example 1, even though the mass contribution of the first mode is 89.95%, it varies along with the building from 0.29 times of the mass at node 1 to 1.2 times of the mass at node 6. In example 2, the mass participation corresponding to the first mode is 87.95%; it varies from 0.35 times mass at node 1 to 1.25 times mass at node 5. In example 3, the mass participation corresponding to the first mode is 90.73%; it varies from 0.42 times mass at node 1 to 1.23 times mass at node 5. The maximum error observed in the calculation of storey shear in the top storey is 50.7%, 33.33% and 33.04% in examples 1, 2 and 3, respectively. Numerous failures of buildings during earthquakes are due to large floor accelerations which are not expected in the design [40]. The accurate calculation of storey shear and lateral force distribution is important for the design of structural and non-structural components fixed at various floor levels [21,22,23,24,25,26,27].

The first and third numerical examples show that 90% of mass criteria are not sufficient. In the second example, the structure is a regular one as defined by the building codes of practice, but consideration of first mode alone results in an error of 33.33%, whereas the error in the proposed method is less than 4%. In the last example, the maximum contribution (40.71% of the structural mass) is from the last mode. The higher modes are truncated and “missing mass” correction is applied using residual mode. The error by using the proposed method is less than 4%. Therefore, seismic analysis of structures can be performed using first mode and dynamic correction using residual mode. The numerical examples considered show that the proposed method gives reasonable results. The proposed method simplifies the analysis procedure for the seismic analysis of irregular building structures. In all the examples, only two modes, first and residual modes, are sufficient to get results with reasonable accuracy. Further, the recommendations given by building codes of practice for response spectrum method of seismic analysis are extended to the nonlinear pushover analysis of structures. Instead of a modal pushover analysis, a single pushover can be performed for the first mode alone and the contribution of higher modes can be calculated from their elastic response. Previous studies show that the assumption of elastic behaviour for higher modes leads to reasonable results and has been widely adopted [2, 41,42,43,44,45]. Therefore, for structures with a dominating first mode (having mass participation factor of nearly 90%), a single pushover analysis can be performed for the first mode alone and a dynamic correction using a second residual mode as explained above can be applied to take the contribution of higher modes into account. Some limited available studies show that the second mode can be inelastic, whereas the other modes are elastic [3,4,5]. Further detailed studies are necessary to extend the simplified procedure for the inelastic analysis of such structures.

Conclusions

In response spectrum method of seismic analysis, the present criteria of considering the first mode for regular structures and 90% of the structural mass participation in the number of modes considered for irregular structures given by the international building codes of practice may not always result in correct responses in all the elements of a structure. For irregular structures, all the modes up to rigid frequency are included in the analysis and “missing mass” correction techniques are applied to account for the response contributions of uncalculated high-frequency modes. Generally, it is observed that for a highly irregular structural system a large number of modes have to be considered till rigid frequency, though 90% mass participation is achieved within the first few modes. For large structures with many degrees of freedom, considering all the modes up to rigid frequency is a computationally tedious process. An alternate simplified method for the seismic analysis of building structures is proposed in which only two modes, the first mode and a residual mode are used for the seismic analysis of structures. The residual mode is considered, irrespective of whether the truncated modes are rigid or damped periodic. If the frequency of the residual mode is far less than the rigid frequency then the response of the residual mode is calculated using the second mode shape of the structure, instead of the residual mode shape. In the proposed simplified method, the residual mode approximates the damped periodic part also, along with the rigid part of the response of the uncalculated modes. The residual mode can be included as an additional mode in the analysis, and the corresponding response can be combined according to the modal response combination rules. In the numerical examples considered, it is observed that response with reasonable accuracy can be achieved by using only the first mode and dynamic correction with the residual mode. The proposed method can be used for the dynamic analysis of complex irregular structures, and the dynamic correction using residual mode for higher modes can be extended to nonlinear pushover analysis of the first-mode-dominated structures.