1 Introduction

Count data occur in a variety of sectors, such as the number of patients, medical visits, catastrophic earthquakes each year, traffic accidents in a month, trees in the forest, number of fires, and the number of microorganisms growing in an hour. The Poisson distribution is a standard distribution for modeling count observations. Sometimes the existing models do not follow the properties of datasets and do not provide efficient results. So, a more flexible probability distribution is required to analyze count datasets with varying behavior. Several probability models are introduced using different discretization approaches. The reader can consult a comprehensive review by [9] on discrete models, datasets, and discretization techniques. Some examples are: Poisson Lindley [25], discrete Pareto [19], discrete Lindley [15], discrete inverse Weibull [17], Poisson Ailamujia [16], discrete Ramus-Louzada [13], Poisson XLindley [3], Poisson moment exponential [2], discrete power-Ailamujia [5], discrete moment exponential [1], Poisson Mirra [21] and new discrete Ramos-Louzada [4].

Assume a random variable \(X\) having XLindley distribution [10] with the probability density function (PDF) and cumulative distribution function (CDF), respectively:

$$f\left(x\right)=\frac{{\theta }^{2}\left(2+\theta +x\right){e}^{-\theta x}}{{\left(1+\theta \right)}^{2}} , x,\theta >0$$
(1)

and

$$F\left(x;\theta \right)=1-\left(1+\frac{\theta x}{{\left(1+\theta \right)}^{2}}\right){e}^{-\theta x}, x,\theta >0$$
(2)

The XLindley distribution attracted a lot of attention due to its adaptability. Various authors further generalized it for more complicated and different types of datasets. For example, for unit interval datasets, the Unit-XLindley [14] distribution; for count observations, the Poisson XLindley [3]; and for continuous datasets, the Power XLindley [22].

Let a random variable \(X\) follow a continuous random variable with PDF over range \(R\), then the resulting probability mass function (PMF) for a new discrete random variable \(Y\) is obtained using relation:

$$P\left(y;\theta \right)=\frac{{f}_{X}(y,\theta )}{\sum_{i=-\infty }^{\infty }{f}_{X}(i,\theta )}, y \epsilon {\mathbb{Z}}$$
(3)

In this study, we used the discretization approach given in Eq. (3) to propose a new discrete XLindley (DXL) distribution. The DXL model included some intriguing characteristics, including closed-form formulas for the mean, variance, and moment-generating function. It is an excellent candidate for modeling over-dispersed nature datasets. In the end, we validated the importance of the proposed distribution using four datasets from diverse fields.

The structure of the study is as follows: We proposed a new probability model in Sect. 2. In Sect. 3, statistical properties are derived. The proposed distribution's parameter estimation is covered in Sect. 4. In Sect. 5, the adaptability of the new distribution is demonstrated by the analysis of four datasets. Finally, Sect. 6 brings our research to a conclusion.

2 Derivation of new distribution

A new discrete probability distribution is derived using the discretization methodology stated in Eq. (3). The PMF of DXL distribution is given below:

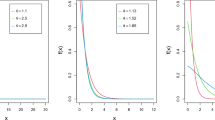
$$P\left(y;\alpha \right)=\frac{{\left(1-\alpha \right)}^{2}\left(2-\mathrm{ln}\left(\alpha \right)+y\right){\alpha }^{y}}{\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]}, y=\mathrm{0,1},2,\dots .$$
(4)

where \(0<\alpha ={e}^{-\theta }<1\). The DXL PMF behavior for different values of a parameter is given in Fig. 1.

Fig. 1
figure 1

PMF graphs of the DXLD for various parameter settings

Full size image

It is found that the PMF exhibits declining, increasing and then, decreasing and unimodal form. So asymmetric datasets can be modeled using the suggested approach. The DXL model's CDF can be written as follows:

$$F\left(y\right)=1-\frac{{\alpha }^{y+1}\left[\left(2-\mathrm{ln}\left(\alpha \right)+y\right)\left(1-\alpha \right)+1\right]}{\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]}; y=\mathrm{0,1},2,\dots $$
(5)

where \(\alpha >0\). The corresponding survival function is:

$$S\left(y\right)=\frac{{\alpha }^{y+1}\left[\left(2-\mathrm{ln}\left(\alpha \right)+y\right)\left(1-\alpha \right)+1\right]}{\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]}; y=\mathrm{0,1},2,\dots .$$
(6)

The hazard function (HF) is:

$$h\left(y\right)=\frac{{\left(1-\alpha \right)}^{2}\left(2-\mathrm{ln}\left(\alpha \right)+y\right)}{\alpha \left[\left(2-\mathrm{ln}\left(\alpha \right)+y\right)\left(1-\alpha \right)+1\right]}; y=\mathrm{0,1},2,\dots .$$
(7)

Figure 2 makes available the HF visualization of the DXL distribution for some choices of parameters. We observe that the failure rate pattern of the proposed model is increasing.

Fig. 2
figure 2

Visualization of HF for various parameter values

Full size image

3 Statistical properties

In this section, some statistical properties of DXL distribution are derived and studied.

3.1 Moment-generating function (mgf)

The mgf of DXL distribution with parameter \(\alpha \) is given by:

$${M}_{y}\left(t\right)=\frac{{\left(1-\alpha \right)}^{2}\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-{\alpha e}^{t}\right)+{\alpha e}^{t}\right]}{\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]{\left(1-{\alpha e}^{t}\right)}^{2}}.$$
(8)

The first four moments about the origin of DXL are:

$${\mu }_{1}^{^{\prime}}=\frac{\alpha \left(3-\alpha -\mathrm{ln}\left(\alpha \right)+\alpha \mathrm{ln}\left(\alpha \right)\right)}{\left(1-\alpha \right)\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]},$$
$${\mu }_{2}^{^{\prime}}=\frac{\alpha \left({\alpha }^{2}\mathrm{ln}\left(\alpha \right)-{\alpha }^{2}+4\alpha -\mathrm{ln}\left(\alpha \right)+3\right)}{{\left(1-\alpha \right)}^{2}\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]},$$
$${\mu }_{3}^{^{\prime}}=\frac{\alpha \left({\alpha }^{3}-3-17\alpha -5{\alpha }^{2}-\left(\alpha -1\right)\left(1+4\alpha +{\alpha }^{2}\right)\mathrm{ln}\left(\alpha \right)\right)}{{\left(\alpha -1\right)}^{3}\left(2-\alpha +\left(\alpha -1\right)\mathrm{ln}\left(\alpha \right)\right)},$$

and

$${\mu }_{4}^{\prime} = \frac{\begin{array}{c}\alpha ({\alpha }^{4}\mathrm{ln} (\alpha )-{\alpha }^{4}+10{\alpha }^{3}\mathrm{ln} (\alpha )+6{\alpha }^{3}+66{\alpha }^{2}\\ +46\alpha -10\alpha \mathrm{ln} (\alpha )-\mathrm{ln} (\alpha )+3 )\end{array}}{{(1-\alpha )}^{4} [ (2-\mathrm{ln} (\alpha ) ) (1-\alpha )+\alpha ]}.$$

The first four moments about the mean can be derived using the following relation \({\mu }_{r}=E{\left(Y-{\mu }_{1}^{^{\prime}}\right)}^{r}\).

The Dispersion Index and Coefficient of variation can be obtained by using formulas:

\(DI=\frac{Variance}{Mean}\) and \(CV=\frac{SD}{Mean}\)

The formula to calculate the coefficient of skewness and kurtosis are:

$$CS=\frac{{\mu }_{3}^{\prime}-3{\mu }_{2}^{\prime}\mu +2{\mu }^{3}}{{\left({\sigma }^{2}\right)}^{\frac{3}{2}}}, CK=\frac{{\mu }_{4}^{\prime}-4{\mu }_{3}^{\prime}\mu +6{\mu }_{2}^{\prime}{\mu }^{2}-3{\mu }^{4}}{{\left({\sigma }^{2}\right)}^{2}}.$$

The descriptive measures given in Table 1 compute numerically using some parameter values to illustrate the behavior of the DXL distribution.

Table 1 Some computational statistics for different choices of parameter
Full size table

According to the results tabulated in Table 1, the DXL model can be an appropriate choice to investigate asymmetric “positively skewed” and dispersion data having a leptokurtic shape.

3.2 Actuarial measures

One of the most difficult challenges in the field of actuarial sciences is estimating market risk. When buying and selling anything, a risk estimate is necessary. A risk estimate is required when purchasing and selling anything. We evaluated the value at risk (VaR) and tail value at risk (TVaR), two significant actuarial variables for the DXL distribution.

The VaR of DXL distribution is attained as \({y}_{p}=F\left(y\right)\), where y is gained by solving the nonlinear equation given below:

$$\frac{{\alpha }^{y+1}\left[\left(2-\mathrm{ln}\left(\alpha \right)+y\right)\left(1-\alpha \right)+1\right]}{\left[\left(2-\mathrm{ln}\left(\alpha \right)\right)\left(1-\alpha \right)+\alpha \right]}=1-p$$

TVaR stands for conditional tail expectation and is calculated as follows:

$$TVaR=\frac{1}{1-F\left({y}_{p}\right)}\sum_{y={y}_{p}}^{\infty }yp\left(y\right)$$
$$TVaR=\frac{\begin{array}{c}{\alpha }^{{y}_{p}} (2{y}_{p} (\alpha -1 )-{{y}_{p}}^{2}{ (\alpha -1 )}^{2}+ (\alpha -3 )\alpha\\ + ({y}_{p} (\alpha -1 )-\alpha ) (\alpha -1 )\mathrm{ln} (\alpha ) )\end{array}}{ ( (\alpha -1 ) (2-\alpha + (\alpha -1 )\mathrm{ln} (\alpha ) ) ) (1-F ({y}_{p} ) )}.$$
(9)

Table 2 shows the values of Value at Risk and Tail Value at Risk for some choices of parameters.

Table 2 Some VaR and TVaR values for the DXL distribution
Full size table

4 Parameter estimation

Assume \({y}_{1},{y}_{2},\dots ,{y}_{n}\) to be a random sample of size \(n\) from the DXL distribution. The Log-likelihood function is given by:

$$\mathcalligra{l}=2n\mathrm{ln}\left(1-\alpha \right)-n\mathrm{ln}\left[\left(2-\mathrm{ln}\alpha \right)\left(1-\alpha \right)+\alpha \right]+\mathrm{ln}\alpha \sum_{i=1}^{n}{y}_{i}+\sum_{i=1}^{n}\mathrm{ln}\left(2-\mathrm{ln}\alpha +{y}_{i}\right),$$
(10)

The log-likelihood equation is obtained by differentiating the above equation with respect to the parameter α:

$$\frac{\partial \mathcalligra{l}}{\partial \alpha }=\frac{-2n}{\left(1-\alpha \right)}+\frac{n\left(1-\alpha \mathrm{ln}\alpha \right)}{\alpha \left[\left(2-\mathrm{ln}\alpha \right)\left(1-\alpha \right)+\alpha \right]}+\frac{1}{\alpha }\sum_{i=1}^{n}{y}_{i}-\frac{1}{\alpha }\sum_{i=1}^{n}\frac{1}{\left(2-\mathrm{ln}\alpha +{y}_{i}\right)}.$$
(11)

It is noted that Eq. (11) cannot have an explicit solution. This goal must be solved numerically using an iterative technique like Newton–Raphson. For this purpose, we use the fitdistrplus (version 1.1–8) package of the R (version 4.2.2, 2022) software [23].

5 Simulation study

We run a simulation study with finite sample sizes to test the long-term correctness of the MLEs of the DXLD parameter. Using various parameter values, we created samples of n = 5, 10, 25, 50, 100, and 200 from the DXLD. We study the five parameter scenarios as follows: α = 0.2, 0.4, 0.6, 0.8, and 0.9. In this scenario, the iteration is repeated 10,000 times. As a result, we computed the average estimate (AVEs), absolute average bias (AABs), and mean square error (MSEs) given by

$${AABS}_{\alpha }=\sum_{i=1}^{N}\frac{\left|{\widehat{\alpha }}_{j}-\alpha \right|}{N}, \mathrm{and} {MSE}_{\alpha }= \sum_{i=1}^{N}\frac{{\left({\widehat{\alpha }}_{j}-\alpha \right)}^{2}}{N}$$

Table 3 summarizes the findings. As can be observed, the MSEs associated with each estimate fall as the sample size increases. This demonstrates the MLEs' consistent performance.

Table 3 Simulation results for different choices of parameter
Full size table

On the basis of simulation criteria, the MLE approach performs well in estimating the DXL distribution parameter.

6 Empirical study

The DXL distribution will be examined via four datasets originating from various domains. We evaluate our model's effectiveness by contrasting it with the Poisson distribution (PD), the Poisson XLindley distribution (PXLD) [3], the discrete inverted Topp–Leone distribution (DITLD) [12], the discrete Bilal distribution (DBD) [6], the discrete Burr–Hatke distribution (DBHD) [11], the discrete Rayleigh distribution (DRD) [24], and the discrete Pareto distribution (DPrD) [19]. The MLE approach is used to estimate the parameters. Moreover, different discrimination criteria, such as the Akaike information criterion (AIC) and Bayesian information criterion (BIC), are employed to identify the best-fit probability distribution. Furthermore, Kolmogorov–Smirnov (KS) statistics and Chi-Square are used to assess the suitability of competing models. The mathematical expressions of Chi-Square and Kolmogorov–Smirnov statistics are given as follows:

$${\chi }^{2}={\sum }_{k=1}^{m}\frac{{\left({o}_{k}-{e}_{k}\right)}^{2}}{{e}_{k}}, \mathrm{KS}=\mathrm{max}\left\{\frac{k}{m}-{z}_{k}, {z}_{k}-\frac{k-1}{m}\right\},$$

where \({e}_{k}\) and \({o}_{k}\) are expected and observed frequencies of the kth class, respectively.

Example I

The first dataset is about a biological experiment, originally analyzed [7]. The data are given in Table 5. In an experiment conducted at random on 8 hills with 15 repetitions, the investigator tallies the number of borers per hill of corn. Table 4 portrays MLEs with respective standard errors (SE) of competitive distributions. We also compute the 95% confidence intervals (CI) for the estimates. Moreover, to get a closer picture, we reported the observed frequencies (OF) and empirical expected frequencies (EF) with respective goodness-of-fit (GF) measures in Table 5.

Table 4 MLEs, SE, and 95% CI for the first dataset
Full size table
Table 5 Observed, expected, and GF for the first dataset
Full size table

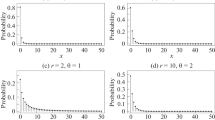
According to Table 5, our proposed distribution provides the minimum values of the mentioned discriminant criteria and the highest p values for the biological experiment dataset. Figures 3 and 4 show the fitted PMF, CDF, and PP plots, which back up the empirical data.

Fig. 3
figure 3

Fitted PMF for the first dataset

Full size image
Fig. 4
figure 4

Fitted CDF (left panel) and PP (right panel) plots for the first dataset

Full size image

Example II

The second application is associated with the failure of 15 electronic machines during an accelerated life examination [20]. The data are: 1, 5, 6, 11, 12, 19, 20, 22, 23, 31, 37, 46, 54, 60, and 66. Table 6 provides the MLEs with their SE for all fitted models along with their 95% CI. Furthermore, in Table 7, the observed and empirically expected frequencies with respective GF measures are reported.

Table 6 MLEs, SE, and 95% CI for the second dataset
Full size table
Table 7 GF measures for the second dataset
Full size table

From the findings listed in Table 7, it is found that the DXL distributions work quite well for discussing the second dataset. The fitted CDF and PP plots are displayed in Fig. 5, which supports the empirical results provided in Table 7.

Fig. 5
figure 5

Fitted CDF (left panel) and PP (right panel) plots for the second dataset

Full size image

Example III

The next discrete dataset is about the number of epileptic seizure tallies [8]. Similarly, the MLEs, SE, and 95% confidence interval for this dataset are presented in Table 8. The observed and expected frequencies and GF are given in Table 9.

Table 8 MLE, SE, and 95% CI for the third dataset
Full size table
Table 9 GF measures for the third dataset
Full size table

According to Table 8, it is found that the DXL distribution appears to be the best among all the competitive models considered. The fitted PMF is graphically displayed in Figs. 6 and 7 which supports the results provided in Table 9.

Fig. 6
figure 6

Fitted PMF for the third dataset

Full size image
Fig. 7
figure 7

Fitted CDF (left panel) and PP (right panel) plots for the third dataset

Full size image

Example IV

The fourth dataset is related to the number of forest fires in Greece between July 1 and August 31, 1998. This dataset is reported in [18]. Table 10 shows the MLEs for the competing models, standard errors, and 95% CI for the estimations. Table 11 shows the GF measures for the distributions that were examined.

Table 10 MLEs, SE, and 95% CI for the fourth dataset
Full size table
Table 11 GF measures for dataset IV
Full size table

From Table 11, it can be observed that the DXL distribution appears to be the best choice for analyzing the fourth dataset. In Fig. 8, the fitted CDF and PP plots are plotted, which also supports the findings listed in Table 11.

Fig. 8
figure 8

Empirical CDF (left panel) and PP (right panel) plots for the fourth dataset

Full size image

7 Conclusion

The discrete XLindley distribution is a novel discrete distribution derived in this article. The proposed model may be the best solution for modeling asymmetric data with overdispersion phenomena. Several properties of the new model have been derived. It was discovered that all of its attributes can be stated in closed forms, which makes the new model more appealing because it can be used in many studies, particularly time series and regression. To estimate the model parameter, the maximum likelihood estimation approach is applied. Actuarial indicators such as the value at risk and tail value at risk of the proposed distribution are calculated to quantify market risk in a portfolio of instruments. To illustrate the flexibility of the proposed discrete model, four distinctive real datasets are utilized in various fields. Finally, we hope that the DXL distribution attracts a wider set of applications in various fields.