TOMBoost: a topic modeling based boosting approach for learning with class imbalance

Abstract

Classification of data with imbalanced characteristics is an essential research problem as the data from most real-world applications follow non-uniform class proportions. Solutions to handle class imbalance depend on how important one data point is versus the other. Directed data sampling and data-level cost-sensitive methods use the data point importance information to sample from the dataset such that the essential data points are retained and possibly oversampled. In this paper, we propose a novel topic modeling-based weighting framework to assign importance to the data points in an imbalanced dataset based on the topic posterior probabilities estimated using the latent Dirichlet allocation and probabilistic latent semantic analysis models. We also propose TOMBoost, a topic modeled boosting scheme based on the weighting framework, particularly tuned for learning with class imbalance. In an empirical study spanning 40 datasets, we show that TOMBoost wins or ties with 37 datasets on an average against other boosting and sampling methods. We also empirically show that TOMBoost minimizes the model bias faster than the other popular boosting methods for class imbalance learning.

1 Introduction

Classifying imbalanced datasets has become an important research area, as all practical datasets have inherent imbalance characteristics. Cyber-fraud classification, classifying cancerous patients, network anomaly detection, factory production defect classification and conversion of online ads are examples of binary class imbalance problems. Multiclass problems such as disease classification using ICD-10¹ codes and job occupation classification using O*Net² codes suffer from severe class distribution skew in the order of 10000:1 (majority:minority), or worse, leading to hard multiclass imbalance problems.

Non-uniform class proportions lead to lower performance [1], as most of the popular classifiers, at least in theory, assume uniform class distribution. Several methods to address the class imbalance condition are available in the literature [2,3,4]; among those, sampling and cost-sensitive methods dominate [5] the class imbalance learning research landscape. Even in the era of deep learning, class imbalance learning (CIL) problems require non-deep solutions since enterprise-deployed machine learning systems use non-deep methods.

Sampling-based methods modify the dataset distribution by undersampling, oversampling or synthetic oversampling to induce an artificial balance in the class proportions. Random oversampling from minority class suffers from an overfitting problem [6]. Synthetic oversampling is non-trivial due to the additional effort required to identify and cleanse synthetic samples that lead to overfitting.

The cost-sensitive methods amend their loss functions with misclassification cost assignment per class or data point. Cost-sensitive methods at the data level [7] solve the imbalance problem by resampling and feature selection based on data-level misclassification cost assignment. Likewise, at the algorithmic level [8], the objective is to develop a decision boundary that minimizes the overall cost on the training data, which is usually the Bayes conditional risk [9].

Random undersampling from the majority class is the most popular technique for learning with class imbalance because of its simplicity and speed. Albeit being simpler, random undersampling suffers from the possibility of losing a good portion of information about the majority class. However, instead of random undersampling, directed or informed sampling methods perform a smart selection of candidate data points [10] from the majority and minority classes based on their data characteristics and domain-specific insights.

A few factors of the dataset characteristics that influence directed sampling [11] are:

• Data cluster representatives, where a single representative point represents a cluster of data points, and the others from the same cluster become redundant.

• Data points closer to the classifier decision boundary, which serve as the key ingredient for the construction of the decision boundary, while also making the other data points that are away from the decision boundary redundant.

• Misclassified data points, where an ensemble method such as boosting, up-weights those data points to force the classifier to learn from them.

• Noisy data points, where cleaning methods such as one-sided sampling (OSS) and condensed nearest neighbors (CNN) identify and prune them from the training dataset.

Topic models [12] are statistical models for discovering latent factors that influence data distributions. Topic modeling has been successful in discovering the latent topic structures in a text corpus, where a text document is assumed to be a mixture of latent topics, and each latent topic generates a vocabulary of terms. We interpret the latent topics estimated by the topic modeling on multinomial data as special soft clustering on the dataset [13]. Topic modeling induced soft clusters are better than traditional clustering [14] as the topic model allows us to study the characteristics of the underlying data distribution through a generative unsupervised learning approach.

Although widely adopted for text processing, the method applies to other general domains such as computational biology, RFID data modeling, transportation systems and traffic surveillance video analysis [15], for instance i) genotype data [16] is modeled as a Dirichlet distribution of admixture proportions in applications of population genetics [17]; ii) scene understanding of traffic trajectories [18] is modeled as Dirichlet process mixture models; iii) generation of RFID data for solving RFID localization problems [19]; and iv) detecting latent changes by decomposing the spatiotemporal pattern using LDA into a mixture of activity patterns in transportation systems [20]. Topic modeling assumes that the features are a mixture of conditionally independent multinomial distributions over different topics. In an enterprise data environment, assuming features to be multinomial distributions is not a substantial limitation as most of the enterprise data features are based on counting, Boolean indicators or qualitative measurements.

Boosting methods belong to a class of meta-learning ensemble, which iteratively reduces the bias by building an additive model with several weak classifiers. Adaptive Boosting algorithm [21], in its original form, works better for imbalanced datasets [22] than standard classifiers. When we train a standard classifier on an imbalanced dataset, in many cases, the decision boundary favors the majority class data points due to the skewed population ratio. The standard classifiers need dataset and algorithmic modifications to force the model bias toward the minority class data points.

Alternatively, when we train a boosting model with a class imbalanced dataset, the algorithm increases the weight of the misclassified data points, such that in the next iteration, the newly learned weak classifier biases toward the misclassified data samples. Even if the early iteration weak classifiers bias toward the majority class data points, the boosting method adjusts the model bias toward the misclassified minority data points by increasing their representation in the training samples used in every iteration.

The boosting method ultimately achieves a low bias, but it may take too many weak classifiers to get the final strong additive classifier. Traditionally, boosting algorithms assume equal initial weights [23] for all the data points in the given training data. The data point weights get adjusted at every iteration based on the exponential loss from the additive classifiers of the previous iterations. Instead of assuming equal initial weights for the data points, if we assume weights proportional to each data point’s importance, the boosting algorithm might take lesser iterations to converge to the final strong additive classifier.

We propose a novel topic modeling-based weighting framework to assign the importance of the data points as weights in a class imbalanced dataset. We compute the weights based on the topic posterior probabilities estimated using probabilistic latent semantic analysis (PLSA) [12] and latent Dirichlet allocation (LDA) [24] methods. The topic posterior probability is the distribution of topics (Z) observable in a given data point $d_i$, given by $\Pr (Z|d_i)$, where $\Pr (Z)$ is the topic distribution. Alternate methods [11] are available that compute the data weights based on data clustering, fitting a classifier decision surface, isolating noisy data points. Their disadvantage is that they are typically time-consuming and computationally expensive compared to the complexity of topic modeling.

Fig. 1

Architecture of TOMBoost

We propose TOMBoost, a TOpic Modeled Boosting algorithm based on the proposed weighting framework, particularly tuned for datasets with class imbalance characteristics. We show the architecture of TOMBoost in Fig. 1. TOMBoost computes the weights of the data sample using the topic modeling-based weighting framework. The computed weights initialize the data sample weights in the first boosting iteration. The data points deemed essential by the weighting framework have a higher chance of occurring in the samples drawn during boosting iterations. TOMBoost also balances the dataset at every iteration by undersampling the majority class and resampling the minority class data points. This modified initial bias helps the TOMBoost to learn better weak classifiers during the early iterations and hence leads to faster minimization of the upper bound on the empirical training error [23]. The main contributions of this work are summarized as follows:

• An unsupervised weighting framework for estimating the data sample weights based on the computed topic posterior probabilities using PLSA and LDA modeling schemes.

• TOMBoost, a topic modeling-based boosting algorithm for learning with class imbalance.

• A boosting method that minimizes the model bias faster by taking lesser iterations to converge to a stronger additive classifier.

We organize the remainder of the paper as follows. In Sect. 2, we present the prior work on class imbalance learning through sampling and boosting methods. In Sect. 3, we describe the proposed topic modeling-based framework for estimating the sample weights from the topic simplex induced by LDA and PLSA models. In Sect. 3.2, we motivate the weight estimation through simplex model interpretation. In Sect. 4, we describe TOMBoost, a boosting algorithm based on the proposed weighting framework. In Sect. 5, we describe the dataset selection, experiment setup and performance comparison of the several cost-sensitive boosting and sampling methods against TOMBoost algorithm. In Sect. 5.3.1, we provide insights on tuning for the optimal topic count. In Sect. 5.4, we describe the characteristics of the induced weights for the majority and minority class data points. In Sect. 5.7, we empirically prove the ability of TOMBoost to minimize the training error in a lesser count of boosting iterations. We present the concluding remarks in Sect. 7.

2 Related work

A straightforward approach to solving the class imbalance problem is to address the imbalance directly by either adjusting the sample population through oversampling (sampling with replacement) or undersampling (eliminating samples to reduce population count). Random oversampling follows naturally from its description by augmenting the original minority set with replications of selected minority samples. In this way, the number of total minority examples increases, and the class distribution balance adjusts artificially. At first glance, the oversampling and undersampling methods appear to be functionally equivalent since they alter the size of the original dataset. However, each technique introduces its own set of problematic consequences that can potentially hinder the learning process [6, 25].

In the case of undersampling, removing examples from the majority class may cause the classifier to miss essential concepts about the majority class. In oversampling, the replicated data from the original dataset become “tied,” leading to overfitting [6]. In particular, overfitting in oversampling occurs when classifiers produce multiple clauses in an induced rule for multiple copies of the same example, which causes the rule to become too specific. Although the training accuracy may be higher in this scenario, the classification performance on the unseen testing data is generally far worse [26].

SMOTE (Synthetic Minority Oversampling TEchnique) [27] generates new synthetic examples along the line between the minority examples and their selected nearest neighbors. Although SMOTE makes the decision regions more significant and less specific, the overfitting problem of oversampling persists. Graver yet is the possibility of synthetic oversampling of the minority class noise. Only selected subsamples of the minority class are subjected to synthetic sample generation to overcome these issues. Borderline-SMOTE [28] uses only the minority samples near the decision boundary to generate new synthetic samples. MWMOTE [29] identifies the hard-to-learn informative minority class samples and assigns them weights according to their Euclidean distance from the nearest majority class samples. MWMOTE then generates the synthetic samples from the weighted informative minority class samples using a clustering approach. SCUT [11] oversamples minority class examples through the generation of synthetic examples and employs cluster analysis to undersample majority classes. Also, it handles both within-class and between-class imbalance.

Chen et al. [30] propose a topic model-based oversampling approach to improving text categorization under class imbalance by exploiting the semantic context in text documents. New samples of rare classes are synthetically generated by using global semantic information of classes represented by probabilistic topic models through a topic simplex. The disadvantage of this method is that the data samples generated are unreal as they are drawn from the estimated topic simplex. Having original data points in the data sample is essential for the interpretation and explainability [31] of the learned classifier models.

Bellinger et al. [32] describe a general framework for manifold-based synthetic oversampling that helps users to select a domain-appropriate manifold learning method, such as PCA or autoencoder, and apply it to model and generate additional training samples. The work addresses the inappropriate generative bias of SMOTE for the broad class of learning problems that conform to the manifold property. The authors also propose a method to test the conformance of datasets to the manifold property to improve the framework’s usability. The test determines whether the manifold-based synthetic oversampling is ideal for the target domain.

In our earlier work [33], we propose a topic modeling-based weighting framework based on the symmetric parameterization of PLSA modeling. The weighting framework uses the topic conditional data distribution $\Pr (d_i|Z)$ and the topic distribution $\Pr (Z)$ to derive the weights $w_i$ for a data point $d_i$ by marginalizing the joint distribution $\Pr (D,Z)$ on Z. As the topics are marginalized, the topic count hyper-parameter does not affect the estimated data weights. We describe the detailed differences between our previous work and the proposed work in Sect. 3.3.

Peng [34] describes a cost-sensitive data space sampling method to adaptively oversample the positive minority examples and undersample the majority negative examples. Adaptive sampling forms different sub-classifiers using different subsets of training data with the best cost ratio that is adaptively chosen. The sub-classifiers combine according to their accuracy to create a robust classifier. The sample weights are computed based on every sample’s prediction probability, by a pair of induced SVM classifiers built on two equal-sized partitions of the training instances.

Nekooeimehr et al. [35] propose an adaptive semi-unsupervised weighted oversampling method (A-SUWO) for imbalanced datasets, which clusters the minority instances using a hierarchical clustering approach and adaptively determines the size to oversample each sub-cluster using its classification complexity and cross-validation. The minority instances are weighted and oversampled based on their Euclidean distance to the majority class.

Distribution-based MultiBoost (DBMB) [36] is a hybrid machine learning method for imbalanced class problems, which combines the distribution-based balanced sampling with the MultiBoost algorithm to achieve better minority class performance. It minimizes the within-class and between-class imbalance by learning and sampling different distributions (Gaussian and Poisson) and reduces bias and variance in error by employing the MultiBoost ensemble. Therefore, DBMB outputs a robust learner that is a more proficient ensemble of weak base learners for imbalanced datasets.

The integration of sampling strategies with ensemble learning techniques is also studied [37] in the literature. For instance, the SMOTEBoost algorithm bases on the idea of integrating SMOTE with AdaBoost.M1. Specifically, SMOTEBoost [38] introduces synthetic sampling at each boosting iteration. In this way, each successive classifier ensemble focuses more on the minority class. As each classifier ensemble is built on a different sampling of data, the final voted classifier is expected to have a broadened and well-defined decision region for the minority class. Another integrated approach, the DataBoost-IM [39] method, combines the data generation techniques with AdaBoost.M1 to achieve high predictive accuracy for the minority class without sacrificing accuracy on the majority class. Briefly, DataBoost-IM generates synthetic samples according to the ratio of difficult-to-learn samples between classes.

RUSBoost [40] is a modification of AdaBoost.M1 for solving between-class imbalance problems by random undersampling from majority class. RUSBoost is shown to perform better [40] than SMOTEBoost that solves class imbalance by oversampling minority class. The RUSBoost algorithm performs random undersampling from the majority class at every AdaBoost iteration to match the population size of the minority class, prescribed by the data sample distribution computed based on misclassification error and exponential loss estimates. CUSBoost [41], on the other hand, uses clustering-based undersampling to balance the dataset at every boosting iteration. The performance is better [42] when the nearest neighbors of the majority class cluster centers are also used during undersampling.

DYCUSBoost [43] is an AdaBoost-based approach that uses dynamic clustering and undersampling for imbalanced learning. DYCUSboost synchronizes with every iteration of AdaBoost to cluster the data based on the weight assignment of every data point at different iterations of AdaBoost, which makes DYCUSBoost reflect the transformation of the data distribution. The clusters are then undersampled proportional to their assessed importance.

AdaC1, AdaC2, AdaC3 [44] are cost-sensitive extensions to AdaBoost, which directly incorporates the per-sample misclassification cost to the data sample weight update equations. AdaCost [45] is a cost-sensitive boosting algorithm based on the MetaCost [46] framework, where cost sensitivity is built around a standard classifier within a boosting method like AdaBoost. The cost sensitivity is achieved by data space weighting, whose theoretical foundation is from the Translation theorem [47]. The AdaCost algorithm allows the assignment of misclassification cost per data point, which gives a greater level of control during boosting iterations.

Yang et al. [48] propose an ensemble strategy to address the binary classification imbalanced problem by assigning higher weights to the hard-to-classify samples. The idea is to use the XGBoost [49] classifier on the initial dataset to identify the difficult samples. The dataset is then resampled to aggregate the random undersampled majority samples, difficult majority samples and SMOTE samples from on difficult minority samples.

RHSBoost [50] addresses the imbalanced binary classification problem by using random undersampling and ROSE [51] sampling under a boosting scheme. ROSE algorithm is a kernel-based method that performs oversampling by generating artificial samples according to a smoothed bootstrap approach. An ensemble framework called Adaptive Ensemble Undersampling Boost for imbalanced learning is proposed [52] that combines the Ensemble of Undersampling (EUS) technique, Real AdaBoost, cost-sensitive weight modification and adaptive boundary decision strategy to build a hybrid.

Tsai et al. [53] introduce an undersampling approach called cluster-based instance selection (CBIS) that combines clustering analysis and instance selection, where the clustering analysis component groups similar data samples of the majority class dataset into subclasses while the instance selection component filters out unrepresentative data samples from each of the subclasses. The authors show that the CBIS approach can make bagging and boosting-based MLP ensemble classifiers perform better, regardless of what kinds of clustering (affinity propagation and k-means) and instance selection (IB3, DROP3 and GA) algorithms are used.

Value-aware resampling and loss (VARL) [54] tackles the imbalanced classification problem by making the high-value samples play a more critical role than low-value samples in the model training process. The training value of each training data point is assessed according to its predicted probability of ground-truth label, then training samples are resampled to produce a balanced training set, and finally, the model training is further boosted by using an instance-level value-aware loss function.

3 Topic modeling-based weighting framework

In this section, we describe our improved topic modeling-based weighting framework for estimating the sample weights from the topic posterior probabilities estimated using LDA and PLSA models. We introduce our weighting model in Sect. 3.1 and compare it against our previous work in Sect. 3.3 to emphasize the improvements. We explain the interpretation of the weights estimated from the $L_2$ norm of the respective topic posterior distribution in Sect. 3.2 using the topic simplex representation. We describe the weighting models through PLSA and LDA modeling in Sects. 3.4 and 3.5, respectively.

3.1 Weighting model

Aspect model [55] is a latent variable model for co-occurrence data, which associates an unobserved class variable with each observation. Probabilistic latent semantic analysis (PLSA) [12] is an extension of aspect models for natural language processing (NLP) and machine learning tasks for text data. Although the technique successfully applies for text data, it can be applied to general multinomial data distributions also [17]. We interpret the latent topics estimated by the topic modeling on multinomial data as some special clustering [13] on the dataset. An alternate approach to topic modeling is to factorize the dataset matrix using latent Dirichlet’s allocation (LDA) [24]. LDA does not suffer from the overfitting problem that arises with PLSA modeling. LDA is a generative model on the join distribution of features and latent topics, where it attempts to backtrack from the data points to find a set of topics that are likely to have generated the features. An important hyper-parameter for the PLSA and LDA models is the number of latent topics denoted by k.

Consider a dataset ${\mathcal {D}}=\{d_{1},d_{2},\ldots ,d_{M}\}$, where every data point $d_i$ is represented as a p-dimensional feature vector from the set of features ${\mathcal {F}}=\{f_{1},f_{2},\ldots ,f_{p}\}$. The objective is to estimate the weight $w_{i}$ for every data point $d_{i}$ in the dataset. Topic modeling assumes that every data point $d_i$ is a mixture of the latent topics from the set ${\mathcal {Z}}=\{z_{1},z_{2},\ldots ,z_{k}\}$. Topic modeling also assumes that the data points $d_i$ and the features $f_j$ are independently conditioned on the state of the associated latent topic $z_k$. A topic $z_{k}$ can be regarded as a concept, and every data point can be modeled as a mixture of multiple concepts with different extents.

3.2 Simplex model interpretation

Let us consider a simple case with three topics $z_1, z_2, z_3$, where a $\Delta ^2$ simplex represents the topic posterior distribution $\Pr ({\mathcal {Z}}|d_i)$. Figure 2 shows the simplex representation of a topic distribution of a data set with the topic count set to 3. We subdivide the simplex into triangular neighborhood regions that have similar topic distribution. We color-code the regions based on the average $L_2$ norm of all the data points in that neighborhood region. We observe that the simplex’s central neighborhood evaluates to a meager average $L_2$ norm value, while the neighborhood regions near the vertices evaluate to a high average $L_2$ norm values. The neighborhoods closest to the simplex vertices are purer than the neighborhoods around the simplex centroid.

Fig. 2

A simplex representation of the topic distribution of a dataset with the topic count set to 3. Triangular cells approximate the data point neighborhoods. The cells are color-coded based on the average $L_2$ norm of the data points in the neighborhood

When the data points align with one of many latent topics, they seem to contain more discriminative information than the data points that align with a mixture of latent topics. We observe that the data points with more discriminative information align themselves near the simplex vertices. On the contrary, when a data point aligns with the centroid of the simplex, we observe that the data point does not possess discriminative information to aid a classifier learning the decision boundary. The topic posterior probability uniformly distributes across all the topics at the centroid of the simplex, leading to the lowest $L_2$ norm. The range of $L_2$ norm for a $\Delta ^{k+1}$ simplex is $\left[ \frac{1}{\sqrt{k}}, 1\right]$, where k is the number of vertices of the simplex. We consider the norm value as a weight indicating the importance of the data point based on its position on the simplex.

An alternate approach to establish the importance of a data point on the simplex is to study the entropy of the topic posterior distribution $\Pr ({\mathcal {Z}}|d_i)$ for the data point $d_i$. When we consider the entropy value as a weight, we observe the estimated weights are very similar to the weights estimated using the $L_2$ norm. Yuta et al. [56] confirm the relationships between the Shannon entropy and the ${L}_\alpha$-norm for n-dimensional probability vectors and showed that there are sharp bounds on the $L_\alpha$-norm with a fixed Shannon entropy, and vice versa.

3.3 Our previous work

In our previous work [33], we propose a topic modeling-based weighting framework based only on the symmetric parameterization of PLSA modeling. The weighting framework estimates the data point weight $w_i$ by marginalizing the joint distribution $\Pr (D,Z)$ on Z. We compute the joint distribution $\Pr (D,Z)$ from the topic conditional data distribution $\Pr (d_i|Z)$ and the topic distribution $\Pr (Z)$ estimated by the symmetric parameterization of PLSA modeling. The marginalized topic distribution $\Pr (Z)$ makes the technique nonparametric without the topic count hyper-parameter k. We perform majority class random undersampling that follows the estimated data distribution to construct a balanced data sample for building a classifier model.

Although we prefer using a nonparametric model, we observe advantages in using the parameterized version of topic modeling, where we have better control of the data samples in terms of their importance in representing the full population. In this extended work on the improved weighting framework, we incorporate the LDA model inference and the asymmetric parameterization of PLSA modeling to estimate the data weight through a topic simplex construction. We present a summary of the changes in the proposed work in comparison with our previous work as follows:

• Uses LDA and asymmetric PLSA modeling to estimate the topic posterior $\Pr (Z|D)$.

• Applies $L_2$ norm on the topic posterior distribution $\Pr (Z|D)$ to derive the data point weights W as $\forall d_i\in {\mathcal {D}}, w_i= \Vert \Pr (Z|d_i)\Vert _2$

• Uses the Simplex interpretation of the topic posterior to choose the best value for the hyper-parameter k (topic count).

• Implements a Boosting method that converges faster due to initialization with the estimated data weights instead of a uniform distribution.

• Uses majority class undersampling and minority class resampling to construct the balanced data sample in every boosting iteration.

3.4 PLSA modeling

PLSA modeling comes in two parameterization schemes, namely symmetric and asymmetric models. Figure 3 shows the graphical model representation of the symmetric and asymmetric parameterization models of PLSA. Given a dataset represented as a joint distribution of the data points ${\mathcal {D}}$ and feature terms ${\mathcal {F}}$, the symmetric PLSA method factorizes $\Pr ({\mathcal {D}},{\mathcal {F}})$ using EM algorithm into: i) topic conditional density of terms $\Pr ({\mathcal {F}}|{\mathcal {Z}})$, ii) topic conditional density of data points $\Pr ({\mathcal {D}}|{\mathcal {Z}})$ and iii) topic priors $\Pr ({\mathcal {Z}})$. The asymmetric parameterization of PLSA factorizes $\Pr ({\mathcal {D}},{\mathcal {F}})$ into: i) topic conditional density of terms $\Pr ({\mathcal {F}}|{\mathcal {Z}})$ and ii) topic posterior probability distribution of data points $\Pr ({\mathcal {Z}}|{\mathcal {D}})$. The quantity of interest is the topic posterior probability from where we propose to derive the weight $w_i$ for every data point $d_i$ in the corpus ${\mathcal {D}}$.

Fig. 3

Graphical model of the symmetric and asymmetric parameterization schemes of PLSA

We adopt the PLSA model, despite its property of overfitting the data, as our objective is to only estimate the weights for the given dataset and not a generalization to unseen data. PLSA generates soft clusters of data points by estimating the membership of every data point in a cluster [13], where each cluster is a representation of a latent topic. Since we are only interested in rank ordering only the training data points, it is sufficient to fit the PLSA model to give the best clusters on the training data alone.

We define a generative model for the observation pair $\langle d_{i},f_{j}\rangle$ by the following scheme, as suggested in PLSA modeling. The joint probability model over ${\mathcal {D}}\times {\mathcal {F}}$ is:

$$\begin{aligned} \Pr ({\mathcal {D}},{\mathcal {F}})= & {} \Pr ({\mathcal {D}})\Pr ({\mathcal {F}}|{\mathcal {D}}) \end{aligned}$$

(1)

$$\begin{aligned} \Pr ({\mathcal {D}},{\mathcal {F}})= & {} \Pr ({\mathcal {D}})\underset{z\in {\mathcal {Z}}}{\sum }\Pr ({\mathcal {F}}|z)\Pr (z|{\mathcal {D}}) \end{aligned}$$

(2)

Let us consider the topic posterior probability distribution $\Pr ({\mathcal {Z}}|{\mathcal {D}})$ as our resource for finding the importance of a data point $d_i\in {\mathcal {D}}$. We estimate the importance weight $w_i$ for a data point $d_i$ using the $L_2$ norm of the topic vector $\Pr ({\mathcal {Z}}|d_i)$. We then compute the weight $w_i$ for every data point $d_i$ as:

$$\begin{aligned} w_i=\left\| \Pr ({\mathcal {Z}}|d_i)\right\| ^2_2\ \forall d_i\in {\mathcal {D}} \end{aligned}$$

(3)

We define ${\mathcal {W}}_{PLSA}$ as the set of weights assigned for every data point in our dataset ${\mathcal {D}}$.

$$\begin{aligned} {\mathcal {W}}_{PLSA}=\left\{ w\ \left| \ w=\left\| \Pr ({\mathcal {Z}}|d_i)\right\| ^2_2\right. \ \forall d_i\in {\mathcal {D}}\right\} \end{aligned}$$

(4)

We estimate the data distribution $\Pr ({\mathcal {D}})$ by normalizing the weights ${\mathcal {W}}_{PLSA}$.

$$\begin{aligned} \underset{PLSA}{\Pr (d_{i})}=\frac{w_i}{\sum _{j=1}^{M}{w_j}}\ \ \forall w_i \in {\mathcal {W}}_{PLSA} \end{aligned}$$

(5)

3.5 LDA modeling

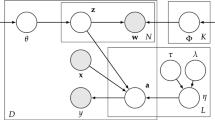
LDA model [57] hypothesizes that the data points are random mixtures over latent topics, where a distribution over feature terms characterizes every topic. Figure 4 shows the graphical model representation of LDA. In its original form, LDA assumes that a text document is a sequence of terms, so, within the LDA framework, a corpus of several documents is just different sequences of terms. In Fig. 4, term f as in $f_{ij}$ represents the $i^{th}$ term in the $j^{th}$ document that is represented as a sequence of terms. LDA models the joint distribution of ${\mathcal {F}}$ and ${\mathcal {Z}}$ as $\Pr ({\mathcal {F}},{\mathcal {Z}})$ and factorizes it to $\Pr ({\mathcal {Z}})$ and $\Pr ({\mathcal {F}}|{\mathcal {Z}})$. The quantity of interest is the topic posterior probability $\Pr ({\mathcal {Z}}|d)$ for a given data point d. Unlike PLSA, the topic posterior is not a part of the model estimation, which instead, we get by model inference on the estimated LDA model for every data point d from the input dataset ${\mathcal {D}}$ represented as a sequence of features as $d_i = \{f_{ij}\}_{j=1}^{N_i}$.

Fig. 4

Graphical model representation of LDA: M is the number of documents, $N_i$ is the number of terms in a $i^{th}$ document, $\alpha$ and $\beta$ are the parameters of Dirichlet priors on the per-document topic distribution and per-topic term distribution, respectively, $\theta _i$ is the topic distribution of the $i^{th}$ document, $\phi _k$ is the term distribution for topic k, $z_{ij}$ is the topic for the $j^{th}$ term in $i^{th}$ document, and $w_{ij}$ is a term

We define a generative model for the observation pair $\langle d_{i},f_{j}\rangle$ by the following scheme suggested in LDA modeling.

• 1. Choose $\theta _i\sim Dir(\alpha )$, where $i\in \{1,\ldots ,M\}$

• 2. Choose $\phi _k\sim Dir(\beta )$, where $k\in \{1,\ldots ,K\}$

• 3. For every term positions i, j, where $i\in \{1,\ldots ,M\}$, $j\in \{1,\ldots ,N_i\}$

  • (a) Choose a topic $z_{ij}\sim \mathrm{Multinomial}(\theta _i)$

  • (b) Choose a term $f_{ij}\sim \mathrm{Multinomial}(\phi _{z_{ij}})$

A joint probability model over ${\mathcal {F}}\times {\mathcal {Z}}$ is given by:

$$\begin{aligned} \Pr ({\mathcal {Z}},{\mathcal {F}})=\Pr ({\mathcal {Z}})\Pr ({\mathcal {F}}|{\mathcal {Z}}) \end{aligned}$$

(6)

The fully parameterized model is given by:

$$\begin{aligned} \begin{aligned} \Pr ({\mathcal {Z}},{\mathcal {F}}, \Theta , \Phi ; \alpha ,\beta )=&\prod _{k=1}^{K} \Pr (\phi _k;\beta )\prod _{i=1}^{M}\Pr (\theta _i;\alpha )\\&\times \prod _{j=1}^{N_i}\Pr (z_{ij}|\theta _i)\Pr (f_{ij}|\phi _{z_{ij}}) \end{aligned} \end{aligned}$$

(7)

Upon integrating $\Phi$, $\Theta$ out from Eq (7) using collapsed Gibbs Sampling [58], we get

$$\begin{aligned} \Pr ({\mathcal {Z}},{\mathcal {F}}; \alpha ,\beta ) =\int _\Theta \int _\Phi \Pr ({\mathcal {Z}},{\mathcal {F}}, \Theta , \Phi ; \alpha ,\beta ) \end{aligned}$$

(8)

We compute the topic posterior probability distribution $\Pr ({\mathcal {Z}}|d_i)$ for a data point $d_i\in {\mathcal {D}}$ by running LDA model inference with the data point represented as a set of features given by $d_i=\{f_{ij}\}_{j=1}^{N_i}$. We can compute the topic posterior distribution by using Bayesian inference on Eq (8) given by

$$\begin{aligned} \Pr ({\mathcal {Z}}|{\mathcal {F}};\alpha ,\beta )=\frac{\Pr ({\mathcal {Z}},{\mathcal {F}}; \alpha ,\beta )}{\Pr ({\mathcal {F}}|\alpha ,\beta )} \end{aligned}$$

(9)

As the denominator term in Eq (9) is intractable to compute, topic modeling algorithms form an approximation by forming an alternative distribution over the latent topic structure that is adapted to be close to the true posterior. Topic modeling algorithms generally fall into two categories: i) sampling-based algorithms such as Gibbs Sampling [59] and ii) Variational algorithms [60]. We use the Variational EM algorithm to compute the topic posterior probability $\Pr ({\mathcal {Z}}|d_i)$ for every data point $d_i$. We compute the weight $w_i$ for every data point $d_i$ as:

$$\begin{aligned} \begin{aligned} w_i&=\left\| \Pr ({\mathcal {Z}}|d_i)\right\| ^2_2\ \forall d_i\in {\mathcal {D}}\text {,} \\ \text {where}\, d_i&=\{f_{i1},f_{i2},\ldots ,f_{iN_i}\},f_{ij}\in {\mathcal {F}}. \end{aligned} \end{aligned}$$

(10)

The set of weights ${\mathcal {W}}_{LDA}$ for the dataset ${\mathcal {D}}$ becomes:

$$\begin{aligned} {\mathcal {W}}_{LDA}=\left\{ w\ \left| \ w=\left\| \Pr ({\mathcal {Z}}|d_i)\right\| ^2_2\right. \ \forall d_i\in {\mathcal {D}}\right\} . \end{aligned}$$

(11)

We estimate the data distribution $\Pr ({\mathcal {D}})$ by normalizing the weights ${\mathcal {W}}_{LDA}$.

$$\begin{aligned} \underset{LDA}{\Pr (d_{i})}=\frac{w_i}{\sum _{j=1}^{M}{w_j}}, w_i\in {\mathcal {W}}_{LDA} \end{aligned}$$

(12)

4 TOMBoost: TOpic Modeled Boosting algorithm

We introduce TOMBoost, a boosting scheme based on our proposed topic modeling-based weighting framework. Our weighting framework assigns a weight to every data point based on its importance as per its position on the estimated topic simplex. The framework assigns the initial weights to the data points based on the topic model weights. The initial weights bias the weak classifiers produced by the earlier iterations significantly toward the essential data points identified through topic modeling. Subsequently, the algorithm reweights the data points based on the additive classifier performance.

TOMBoost differs from traditional boosting, which assumes that every data point is equally important. Although boosting algorithms shall ultimately reduce the training error over boosting iterations, it may take several weak classifiers to achieve a low bias. The modified initial bias helps TOMBoost to learn better weak classifiers during the early iterations and hence leads to faster minimization of the upper bound on the empirical training error. The modified initial bias also helps to reduce the number of iterations to cover the hard-to-learn data points, as we already set a higher weight for the hard-to-learn discriminative data points.

TOMBoost also performs dataset balancing in every iteration by undersampling the majority class and resampling the minority class based on the weights at a particular iteration. Resampling the minority class data points based on the estimated data distribution allows us to do controlled oversampling of discriminative minority data points. TOMBoost differs from RUSBoost [40] and SMOTEBoost [38] in the sense that RUSBoost does only the majority class undersampling, and SMOTEBoost does synthetic minority oversampling. TOMBoost avoids synthetic oversampling to ensure that every data point in the sample at every boosting iteration, is an original data point. Having original data points in the sample is essential for the interpretation and explainability [31] of the learned classifier models.

Algorithm 1 describes TOMBoost, a boosting scheme based on our topic modeling-based weighting framework. Steps 1-5 select the appropriate weighting scheme from $\{{\mathcal {W}}_{PLSA},{\mathcal {W}}_{LDA}\}$ based on the hyper-parameter mode. Step 6 computes the data point probabilities (priors) by normalizing the weights estimated from the topic simplex. Steps 7-9 split the prior probability set into partitions of priors from the minority and majority classes. Steps 10-11 apply min–max normalization on the majority and minority probability sets to scale the probability values in the $0-1$ range. Step 10 ensures that the essential data points of minority class are assigned higher weight irrespective of their positions in the dataset weights plot, as explained in the Shadowing and Reweighting section. Step 12 merges the normalized weights of the majority and minority classes into one set. The set of weights computed by min–max normalization is not a probability distribution, so step 13 normalizes the weights again to make it a probability distribution. Step 14 invokes the standard AdaBoost.M1 [61] method on the given dataset with the estimated normalized weight distribution, instead of assuming equal weights. We also modify the AdaBoost method to balance the dataset in every boosting iteration by majority class undersampling and minority class resampling. We describe the balancing method in Algorithm 2. Balancing the dataset in every boosting iteration helps to bias the decision boundary toward the minority class, leading to faster convergence.

Algorithm 2 describes the steps involved in balancing the dataset based on the weights recomputed in every boosting iteration. The algorithm’s primary input is the dataset weight computed by the boosting method based on the misclassification error of the additive classifiers induced in the previous iterations. Steps 1-2 splits the weights into majority class and minority class data weights and normalizes them to probability distributions. Step 3 sets up the placeholder ${\mathcal {D}}_{min}^{RS}$ for the resampled minority class dataset. Steps 4-7 perform resampling from the minority class dataset following the minority class data distribution $\Pr ({\mathcal {D}}_{min})$ and adds the sampled data point to ${\mathcal {D}}_{min}^{RS}$. Step 8 collects the missed out minority class data points and adds them to the resampled minority class dataset container ${\mathcal {D}}_{min}^{RS}$. Step 9 initializes the undersampled majority class container ${\mathcal {D}}_{maj}^{US}$. Steps 10-13 draw samples from the majority class data following the distribution $\Pr ({\mathcal {D}}_{maj})$ and adds them to the undersampled majority class container. Step 14 combines both the resampled minority class dataset and the undersampled majority class dataset to make a balanced dataset for learning the weak classifier in the next boosting iteration.

Table 1 UCI datasets used for the performance evaluation with their respective topic modeling preprocessing time (column PP) in seconds

5 Experiments and results

In this section, we perform experiments to validate our algorithm and its performance by answering the following questions,

• 1. What is the optimal value of topic counts (k) in the topic model? (Sect. 5.3)

• 2. What is the effect of resampling and normalization of the instance weights? (Sect. 5.4)

• 3. How does the proposed TOMBoost algorithm perform in the task of imbalanced classification against other methods in the literature? (Sect. 5.5)

• 4. What is the effect on the classification performance based on the choice of topic model? (Sect. 5.6)

• 5. Does the proposed TOMBoost algorithm converge faster than the other boosting methods? (Sect. 5.7)

5.1 Datasets and experimental setup

In many practical enterprise scenarios, the datasets are count-based, Boolean indicators or qualitative measurements that we can model as a mixture of multinomial distributions. The assumption holds good for numeric features when we treat the numeric values as ordinals by binning them into different ranges. It is not easy to verify the conditional independence assumption on the features ahead of the usage in topic modeling. Still, we can assume conditional independence for ordinals, counts and qualitative measurements type features in datasets. The assumption may become invalid with transformed datasets such as embedding as the data dimensions are no longer necessarily independent.

The premise of topic modeling is to represent every data point as a topic distribution. The general intuition is to expect a similar topic distribution for every data point belonging to a particular class. Combining data points from multiple classification groups into one large class may affect the validity of this intuition. Our method is not affected by this caveat as we do not use the class information of data points when we estimate the topic posterior distribution. We hypothesize that the data points represented in the topic space form soft clusters, where each cluster is a representation of a latent topic or a concept found in the dataset.

We select the datasets for experimentation from the standard benchmarks that class imbalance learning researchers have used in the literature. We could not find any online data repository that is exclusive for class imbalance learning research. We consider 40 binary and multiclass datasets from the UCI repository.³ We also convert the multiclass problems into binary classification by using one-vs-rest or one-vs-set or set-vs-set as the transformation. We consider the “one” in one-vs-rest or one-vs-set as the positive (minority) class and the aggregate of the rest, or the set of classes as negative (majority) class. In the set-vs-set problem transformation, the notion of minority and majority classes go by their respective cardinality. This transformation results in imbalanced binary class datasets, which are of interest to our problem setting.

Table 1 lists the selected datasets with their meta information. We present the maximum time taken for topic modeling preprocessing for all the datasets in column “PP.” We choose several directed sampling and boosting methods counting to 24 and list them in Table 2 for benchmarking our methods. We select the candidates of directed sampling and boosting methods based on their popularity in the enterprise deployments, availability of code base and the simplicity of the model hypotheses. We take each of the datasets and perform twenty (20) random 80-20 splits by running fivefold cross-validation splits four times. We run 20 iterations of boosting and abort it early if the loss exceeds 0.5 for five continuous iterations.

Table 2 Sampling and boosting methods used for the empirical study

Fig. 5

Topic simplex weights (probabilities P(d) after normalization) computed from LDA modeling on contraceptive3-1 and yeast-2-vs-4 datasets, sorted in descending order. When $k=2$, the plot is horizontally flat, and upon gradually increasing k, the regions of horizontal flatness tend to decrease

Fig. 6

Slope variations on the plots of the data point probabilities (or weights before normalization) at different topic count k choices in topic modeling. The observable slope of the weights plot guides the process of tuning the hyper-parameter k. A more significant slope implies good variance, and hence, the weights become more useful for sampling

5.2 Performance metric

We use the classification performance as the surrogate measure for evaluating the effectiveness of the topic modeling induced weights assigned to the data instances during the initialization step of the TOMBoost algorithm. We assume that the effectiveness of the data point weights correlates positively with the classification performance. In most of the practical applications, the minority class performance is more critical than the majority class. However, the majority class performance should not be traded off for changing the bias toward minority class. When the Maj:Min imbalance ratio is R : 1 and the scores are $F_1^{\mathrm{maj}}$ and $F_1^{\mathrm{min}}$, we compute the weighted average $F_1$ ($\mathrm{WAF}_1$) as:

$$\begin{aligned} \mathrm{WAF}_{1}={\frac{F_1^{\mathrm{maj}}+R*F_1^{\mathrm{min}}}{1+R}} \end{aligned}$$

(13)

We use the two-sample t-test to estimate the statistical significance of weighted average $F_{1}$-score measured from the results of our methods against the other listed methods. We use decision trees as the weak classifier in TOMBoost for simplicity, as it does not require any special parameter tuning.

5.3 Effect of topic count (k)

We plot the data point probabilities computed from the topic simplex induced weights after normalization and sorting in descending order. Figure 5 shows the plot of descending sorted topic simplex weights (which are probabilities P(d) after normalization) computed from LDA modeling on contraceptive3-1 and yeast-2-vs-4 datasets. We expect an exponential decay like curvature in the plot; instead, we observe flatness at different regions of the plot, and sometimes, the entire plot is relatively flat (low variance). We define flatness as a characteristic of a region, where the piecewise local gradients are near zero, or the piecewise local variance is low, for that region.

Figure 5 shows the flatness observed in different sections of the data point probabilities (or weights before normalization) $\Pr (d)$ curve for a couple of datasets at different topic count k values. When the topic count is low ($k=2$), all the data points cluster around the center of the simplex leading to a horizontally flat curvature. When we increase the topic count k gradually to 30, flatness regions tend to decrease. It becomes necessary to find the optimal topic count k to ensure that the weights from the topic simplex have sufficient variance. We interpret the flatness characteristic using the following hypotheses:

• 1. Topic count is lesser than optimal The data points cluster excessively near the simplex centroid leading to a low $L_2$ norm weight for the data points. When several data points cluster near the simplex centroid, the variance in the weights becomes low, leading to a flatter curvature of the weights plot (or probabilities after normalization).

• 2. Topic count is optimal The data points distribute throughout the simplex leading to different $L_2$ norm weights for data points. The variance in the weights allows us to apply data space weighting [47] and ensures importance to the essential data points with class-discriminative information.

• 3. Topic count is greater than optimal The data points align near the simplex vertices leading to a high $L_2$ norm weight for the data points. When several data points cluster near the vertices of the simplex, the variance in the induced weights becomes low, leading to once again a horizontally flatter curvature of the weights plot.

Partial flatness is an exciting phenomenon where several data points in the dataset evaluate to a similar topic simplex weight predominantly because of their placement near the simplex vertices. When the topic count $k=2$ for the LDA plot in Figure 5, the scenario we observe is a complete flatness, where all the data points cluster around the center of the simplex to score a low $L_2$ norm weight. On the contrary, when the topic count is $k=5$, we observe partial flatness, where the plotted curve is flat for three-fourths of the data points. Partial flatness is different from complete flatness, where the partially flatter region evaluates to a higher $L_2$ norm weight in comparison with the weights in the complete flatness scenario. Data points participating in partial flatness are equally critical as they align near the simplex vertices but more important than the ones aligning elsewhere.

5.3.1 Model tuning

We originally tune the model using a line search to find the best topic count for our experimentation. However, when we study the weights plots in conjunction with the simplex model interpretation, we recognize the usefulness of the weights correlating to the slope of the weights plot. Figure 6 shows the weights plot at different topic counts k for both PLSA and LDA models built with the ecoli-0-1-3-7-vs-2-6 dataset. The plot curvature tends to flatten in both the modeling schemes for smaller topic counts. A flatter P(d) plot implies equally weighted data points leading to non-viability of directed or informed sampling due to low variance in the estimated weights.

On the contrary, we observe valuable variance on the curve when the topic count increases. The observable slope of the plotted curve guides the process of tuning the hyper-parameter k. A more significant slope implies good variance, and hence, the estimated weights become more useful for sampling. We also observe that the slope flattens when the topic count increases beyond the optimal value, as explained in the effect of topic count (k) section.

Fig. 7

Relative positions of the minority and majority points on the data point probabilities P(d) plot induced by LDA and PLSA topic simplex weights, generated for four different datasets with topic count set to $k=10$. Larger bullets denote the minority points. The X-axis is the data point instances sorted by data point probabilities $P(d_i)$ in descending order

Fig. 8

Distribution of the majority and minority class data points on the data point probabilities P(d) plotted curve, before and after reweighting. The first plot in each row shows the distribution of minority and majority data points on the original P(d) curve. We observe that the majority class data points dominate the top portion of the plots. The second plot in each row shows the data point weights for the majority and minority classes estimated independently as a function of the respective data point probabilities. The second plots in each row use Y-axes separately for the majority and minority class data points

Choosing the best topic count k by visually observing the slopes is a subjective approach. Instead, we can estimate the area under the P(d) curve shown in Fig. 6 to choose the topic count that covers at least 90% of the total area under the curve. A flatter curve requires more topics to cover the required 90% area under the curve. The linear search for topic count can choose the minimum k value that satisfies the required area under the curve. Alternately, we can use perplexity [71] as a measure for choosing the topic count that optimizes the model fit for the data. OCTIS,⁴ a popular Python library is available for selecting the best topic count k using a Bayesian optimization (BO) [72, 73] to optimize the hyper-parameters of the models and thus guarantee a fairer comparison.

5.4 Minority and majority points on the plotted curve

We visualize the relative positions of the majority and minority class data points on the weights plot (data point probabilities P(d) plot after normalization). Figure 7 shows the positions of the minority and majority data points on the P(d) plot induced by LDA and PLSA topic simplex weights for four different datasets, namely ecoli4, glass6, poker-8-9-vs-5 and yeast-2-vs-4 from the UCI repository [74]. Larger bullets denote the minority class data points, and smaller ones denote the majority class data points. We generate all the plots with the topic count set to $k=10$. Irrespective of whether we use LDA or PLSA modeling, the minority points tend to cluster near the tail of the P(d) plot for some datasets such as poker-8-9-vs-5 whose imbalance ratio is high (81.96). When the imbalance ratio is not so high in cases such as yeast-2-vs-4, glass6 and ecoli4, the minority data points cluster near the head of the curve, this clustering behavior is consistent across different topic count k choices for a chosen dataset and a modeling scheme. We observe that the imbalance ratio plays a vital role in the placement of minority points on the P(d) plot. When the imbalance ratio is high, minority points tend to be pushed to the tail by the majority points due to their overpopulation.

5.4.1 Shadowing and reweighting

When the minority class points cluster near the head of the P(d) weights plot, the data points get a high chance of appearing the directed random sample compared to the majority class points; alternately, if the minority class points cluster near the tail of the plot, the directed random sample might have poor representation of the minority class data points. We call this problem as shadowing. To overcome the shadowing problem, we propose reweighting, where we extract the weights assigned to the majority and minority class data points individually and normalize them independently. Figure 8 shows the distribution of majority and minority class data points on the P(d) weights plot, before and after reweighting for the poker-8-9-vs-5 dataset. The first plot in each row shows the distribution of minority and majority data points, with the top portion of the plots dominated by the majority class data points. The second plot in each row shows the data point weights for the majority and minority classes estimated independently as a function of the respective data point probabilities. Reweighting allows the minority data points to get higher weights irrespective of their positions in the original P(d) weights plot.

Table 3 Classification performance measured by the weighted average F$_{1}$-score metric for the boosting methods evaluated in our experimentation. We use a dash “-” to report that a particular run did not complete within our set time limits. We color-code the scores based on the t-test outcome against $\texttt {TOMBoost}_\texttt {LDA}$. Green marks the wins, red marks the losses and yellow marks the ties of $\texttt {TOMBoost}_\texttt {LDA}$ in blue against the other methods

Table 4 Summary of two sample t-test on weighted average $F_1$-score of the LDA variant of TOMBoost against other boosting methods with significance level at $p=0.05$. The last three rows summarize the wins, losses and the ties

Table 5 Summary of two sample t-test on weighted average $F_1$-score of the PLSA variant of TOMBoost against other boosting methods with significance level at $p=0.05$. The last three rows summarize the wins, losses and the ties

5.5 Performance of TOMBoost

Table 3 presents the $WAF_1$ scores achieved by all the methods compared in our experimental setup. In Table 3, we show that the performance of the TOMBoost algorithm is superior to the other popular boosting methods, such as AdaBoost, AdaCost, RUSBoost, SMOTEBoost and several other sampling methods. We observe that the variance in the $F_1$ scores across different cross-validation folds is reasonably low, which proves the stability of our method. We also perform a two-sample t-test to validate the significance of our proposed TOMBoost algorithm against the other methods. Table 3 also color-codes the scores based on the t-test outcome of every other method against the LDA variant of TOMBoost . Tables 4 and 5 show the t-test results of LDA and PLSA variants of TOMBoost against all the other methods compared in our experiments. We observe that the PLSA and LDA variants of the TOMBoost algorithm are statistically similar, as they share 34 ties over 37 datasets. The LDA variation of TOMBoost is marginally better than the PLSA variation by registering three wins and no losses.

Table 3 shows that the TOMBoost (LDA) is statistically similar to RUSBoost. We do an empirical study of this hypothesis in Sect. 5.7. It is interesting to observe that the SMOTEBoost method has not performed well against the PLSA and LDA variants of TOMBoost . The best SMOTEBoost scored was nine wins against the LDA variant and eight wins against the PLSA variant. A possible reason is that the synthetic samples induced in every SMOTEBoost iteration do not create different classifier decision boundaries when compared to the decision boundaries induced by the oversampling/undersampling of data points in boosting iterations.

The PLSA variant scores eight wins against RUSBoost and SMOTEBoost; at the same time, it has also suffered eight defeats against each of them, leading to a debatable clear winner performance. PLSA variant of TOMBoost outperforms AdaBoost clearly with seven wins and just one loss. Both TOMBoost variants lead AdaCost with 17 wins out of 23 datasets compared. The LDA variant of the TOMBoost algorithms outperforms RUSBoost and SMOTEBoost by considerable margins.

The improved performance of TOMBoost is due to the directed sampling at the initial stages of the boosting, to bias the classifiers significantly toward the essential data points from the minority and the majority classes during the early iterations. Subsequently, the boosting iterations reweight the data points based on the classification performance of the additive classifiers induced from the previous iterations. The dataset balancing method in TOMBoost ensures that the classifiers learned in every boosting iteration are exposed only to the essential data points that contain class-discriminative information.

5.6 Choice of topic modeling approach

As we have two variants (PLSA & LDA) of the topic modeling-based weighting framework, we attempt to unify the weights induced by both the variants into a single weighting scheme. We combine the weights induced by the PLSA and LDA modeling into a single weighting scheme as per Eq (14). $\uplambda$ is a hyper-parameter to bias the ensemble weighting scheme from LDA to PLSA.

$$\begin{aligned} {\mathcal {W}}_{\mathrm{ENS}}=\uplambda {\mathcal {W}}_{\mathrm{LDA}}+(1-\uplambda ){\mathcal {W}}_{\mathrm{PLSA}},0\le \uplambda \le 1 \end{aligned}$$

(14)

We observe that the ensemble weighting does not produce competitive results in comparison with the individual weighting schemes. In our experiments with the LDA and PLSA weights using classification performance as a surrogate measure for assessing the effectiveness of the weights, we observe through t-test that the classification performance with the respective weighting schemes is statistically similar. The t-test results in Table 4 indicate that the weights are also statistically similar. When the weights estimated through LDA and PLSA modeling are statistically similar, the ensemble of weights also becomes similar to the original weights making the ensemble less effective.

5.7 Faster minimization of model bias

We now study the effect of our weighting scheme on reducing the number of boosting iterations required to minimize the model bias. Figure 9 shows a comparison study on the trend of model bias observed over several iterations of the proposed methods against the popular RUSBoost and SMOTEBoost. It is evident from the figure that the model bias of TOMBoost (both variants) is lower than that of RUSBoost and SMOTEBoost after a few iterations. We observe that the model bias trend of RUSBoost starts to converge back to that of TOMBoost as the iterations increase.

Fig. 9

Comparing the model bias minimization trend of the boosting methods for the “yeast” (Y3) dataset

Figure 10 shows the model bias minimization trend for the “A3,” “E2” and “B1” datasets, which depict the clear advantage TOMBoost method has over RUSBoost and SMOTEBoost. RUSBoost and SMOTEBoost start at a higher bias error and continue to increase for a few more iterations. The trend reaches a plateau, followed by a decrease in the bias error in the boosting iterations to come for RUSBoost. Figure 10 also establishes that the TOMBoost method quickly minimizes the model bias relative to the others and continues to decrease the training error further almost linearly. Figures 9 and 10 show that the trend line of SMOTEBoost is not decreasing even after the plateau region. One possible reason for this behavior is the boosting iterations might be synthesizing noisy data points [28, 29, 75].

Fig. 10

Comparing the model bias minimization trend of the boosting methods for the “Abalone” (A3), “Ecoli” (E2) and “Baloon” (B1) datasets, where SMOTEBoost training error keeps increasing

There are also cases where RUSBoost model bias keeps increasing with more boosting iterations. Figure 11 demonstrates such scenarios for the “C2” and “C5” datasets, where the training error for RUSBoost keeps increasing while TOMBoost continues to minimize the model bias. One reason for this behavior is due to the randomness in undersampling during the boosting iterations. If the random sample goes wrong, the effect takes more iterations to stabilize. Ultimately, RUSBoost will converge with TOMBoost but may take several more iterations to do so.

Fig. 11

Comparing the model bias minimization trend of the boosting methods for the “CMC” (C2) and “Contraceptive” (C5) datasets, where RUSBoost training error keeps increasing

Table 6 lists the rank of the compared method for faster minimization of training error. We observe the training error for every dataset at the end of the 20th iteration for each compared method. As the training error for different datasets and different methods follow different scales, aggregating them into averages may not be appropriate. We propose to look at the rank of a method for every dataset instead of the absolute training error. An average convergence rank closer to 1 indicates that the method obtained the least training error among the compared methods. On the other hand, a value closer to 4 indicates a relatively higher training error at the end of the last iteration. Table 6 clearly shows that both TOMBoost variations minimize the training error faster than the popular SMOTEBoost and RUSBoost methods.

In summary, we empirically show that TOMBoost facilitates faster minimization of training error (model bias) by finding a favorable starting point through topic modeling-based directed sampling. Also, TOMBoost balances the data sample by majority class undersampling and minority class resampling to facilitate appropriate biasing of the decision boundary induced by the additive classifier.

Table 6 Average convergence rank across datasets of the various methods on the train error at the end of the last iteration of the boosting

6 Discussion

In this work, we apply topic modeling to draw representative samples from a dataset that preserves the properties. We use topic modeling to estimate the relative importance of every data point (as weight) in the dataset based on its respective topic simplex representation. We use the weights to undersample from the majority class dataset and resample the minority class dataset to balance the class proportions of a data sample artificially. We propose a boosting method that initializes the data distribution with the estimated data weights and uses the artificial data balancing strategy in every boosting iteration. We show that our boosting method outperforms other sampling and boosting techniques in classification performance and takes fewer iterations to converge to a lower training error.

Topic modeling is proposed initially for text analytics, but the mixture of multinomials is a mathematical structure that can also apply to other problem domains. Topic modeling inherently clusters the dataset softly into latent topics that share similar dataset characteristics. Our study leverages the estimated soft clusters to draw stratified samples from the formed topic clusters. We use the topic simplex representation to study whether a data point is topic-diffused or topic-focused by measuring its $L_2$ norm. A topic-focused point has a higher $L_2$ norm, whereas a topic-diffused point has a lower $L_2$ norm. By tuning the topic count hyper-parameter, we maximize the ability of topic modeling to create the required number of latent topic clusters and hence the posterior probability $\Pr (Z|d_i)$ for a data point $d_i$.

A representative sample should not miss the topic-focused data points as they carry more information about the dataset characteristics. This way, topic modeling allows us to preserve the necessary information of a dataset in a sample despite its smaller size. When we apply data weights on the majority and minority class data individually, we avoid the shadowing effect of majority class points over the minority data points. We conceive a robust classifier that can work well even with a severely imbalanced dataset by combining the strategic sampling with a boosting scheme. When we use the estimated weights to initialize the boosting method, we allow the boosting method to start with a better initial condition leading to faster convergence of model bias.

Our empirical study on the application of topic modeling to data sampling and boosting validates the ability of the multinomial mixture models to solve diverse problems other than text analytics. We believe that topic modeling as a generic technique has several different applications which are yet to be explored. Although topic models work well for data modeling and sampling, building and tuning the topic model hyper-parameter is time-consuming for very large datasets. In such scenarios, We have a choice to trade off between speed and accuracy by lowering the number of EM (or Gibbs sampling) iterations while building the model. The data preprocessing time (model building time) is worthy because it also reduces the number of boosting iterations required to achieve lower model bias. Another limitation of the proposed system is that the topic modeling approach may not work with embeddings as they do not strictly follow the mixture of multinomial distributions. To overcome this limitation, we prescribe using the dataset from the original space instead of the reduced-dimensional embedding space.

7 Conclusion

We propose a topic modeling-based weighting framework for data points that efficiently processes class imbalanced data. We develop our weighting framework using LDA and PLSA modeling to assign a weight for every data point in a dataset based on the estimated topic posterior probability with a simplex model-based interpretation. TOMBoost algorithm improves performance against all other techniques compared in our experimental setup for binary classification datasets while being simple to implement and requiring fewer iterations to converge. The algorithm outperforms the popular SMOTEBoost, RUSBoost and the cost-sensitive AdaCost algorithms, clearly with more wins. Between TOMBoost variants, the LDA variant is marginally better than the PLSA variant. TOMBoost also shows the ability to minimize the training error in a fewer boosting iterations than RUSBoost and SMOTEBoost. The algorithm consistently decreases the model bias over boosting iterations across datasets unlike RUSBoost and SMOTEBoost. Although topic modeling was originally proposed for text applications, we successfully demonstrate its use with generic multinomial datasets in boosting and directed sampling applications. Our next step is to extend the weighting framework application to multiclass imbalanced datasets. The source code, curated datasets, results and reports are available in GitHub.⁵