Abstract
In big data science, the classic frequent pattern mining is fundamental to various pattern mining applications. Extensive research on this mining has been undertaken for nearly 30 years but left with no reliable mining approach. One of the main issues is the lack of study on the imperative pattern frequency distribution theory. With an emphasis on mining reliability and methodological change, this paper makes up the absent theory, which consists of a bundle of findings on the frequency distribution properties. The primary property is that the frequency distribution curves from different pattern generation modes are quasi-concave and ultimately resultant bell-shaped curves over large datasets. All the findings are well-formed with no exogenous input but rigorous mathematical proofs that every classic pattern mining approach should observe. This paper thus builds up a solid block of the theoretical foundation for rational and ultimately reliable pattern mining. Moreover, the findings inspire interesting rethinking and new conceptions not merely in pattern mining but also extended deeply to set theory and combinatorics. With this inspiration plus the pure mathematic nature of the explorations presented, the contributions of this study may not be restricted to pattern mining only but spring to data science in general or even broader.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The classic frequent pattern mining starting from the itemset mining [1] is a fundamental technology to retrieve information from various classic datasets. Its applications include general-purpose association-rule mining [2, 3] or causality mining [4, 5], which in turn are foundations for diverse domain-specific mining, such as medical [6,7,8], biological [9, 10], chemical [11,12,13], and genomic mining [14,15,16]. Meanwhile, the basic concepts and methods of the classic mining are the starting points of the mining over nonclassical datasets, e.g., the stream data [17, 18], uncertain data [19, 20], or heterogeneous data [21, 22].
As such, thousands of research articles related to classic pattern mining have been published over a quarter of a century, and most of them focus on algorithm design and implementation to pursue mining efficiency. However, none of the previous mining approaches is reliable, as proved in the first stage of the author’s study [23]. One of the reasons for the unreliable mining is the lack of well-established mining theories but mostly algorithms due to a seeming convention in the pattern mining research circle. That convention requires empirical results to prove one’s mining approach. As experienced by the present author, many journals explicitly or implicitly refuse theoretic articles on pattern mining without empirical results. Such a policy certainly hinders deep theoretical studies, such that there is no generally accepted mining reliability theory established in the literature to date.
We know it is important to require empirical results to verify an approach, but only if the results are reliable. However, it is not the case in pattern mining up to now. Notice first that, for an arbitrarily given dataset, we do not know how many and what patterns exist in it beforehand. Then, without a reliability theory, by what can we testify and trust a mining result from a mining approach to be reliable? The important convention and requirement then become spoiled, and the reality is, without reliability testification, authors in an article merely use empirical results produced from their own algorithm to prove the advantages of that algorithm declared by the authors. Such proof is indeed a “circular proof” only, but interestingly, few people noticed the phenomenon or wanted to change it.
The above spoiled convention implies that people are eager to head in the practical mining without much attention to the soundness of the mining theory thus reliability, or they did not take there are critical issues of the mining theory but only the mining efficiency. Instead, the author’s research has proved and will further prove that the unreliability of previous mining approaches is due to their embodied theoretical fallacies. And there is a need to emphasize that an unreliable mining approach is valueless or even harmful, however efficient it is, because the unreliable information retrieved from that approach may lead to a misunderstanding of a world or even costly wrong decision making.
After we noticed the above, the issue now becomes how to undertake the reliability study. The author finds that we need first to fix some more fundamental issues. The thing is, without a proper reliability theory, we could not determine whether a mining approach is reliable, but conversely, we can tell if it is unreliable—by the rationality of its mining results. That is, a mining approach must firstly be rational, then reliable. The author’s previous study has proved the irrationality of the mining results from all previous approaches with two critical issues, the probability anomaly and the dissatisfaction of the equilibrium condition [23], which shall be briefly iterated in the next section.
Another major theoretical miss is the pattern frequency distribution theory. Without it, there is no rule to guide and check if the central work—finding out the result patterns and their respected frequencies over a dataset—is well done. Accordingly, the main contribution of this paper is the establishment of the pattern frequency distribution theory to meet the needs. This theory, the last study summarized in Sect. 2.2, and the theory to render the selective mining approach as future work are the imperative blocks of the theoretic foundation toward the expected rational and ultimately the reliable pattern mining.
The second contribution is the stimulating sooner realization of reliable pattern mining through objective and methodological change. The first change is prioritizing the mining rationality and reliability over efficiency. An efficient approach is significant only if it achieves reliability. This change requires another change: to put theoretical study and establishment before empirical mining techniques and algorithms. The third is to pay more attention to intrinsic data properties than exogenous input in the theoretical pursuance. If people say previous works have developed some mining theories, those theories are mostly approach-dependent and often with exogenous inputs. They are thus not generally applicable and at least unmatured since no reliable mining approach has grown up from them yet. The studies presented in this paper and before are wholly from the intrinsic natures of the dataset to work on and with no exogenous input but rigorous mathematic proofs that every classic pattern mining approach should observe.
Another contribution is extensiveness and enlightenment. The findings presented in this paper are purely mathematic derivations. As in many cases, a pure mathematic formulation may not find its immediate usage or all usages, but sooner or later, people may find its usefulness even in different subjects or fields. This study thus means to open a new way to solve the pattern mining problem fully mathematically, and as to see soon, inspires some rethinking and new conceptions, not merely in pattern mining itself but also extended deeply to set theory and combinatorics. This inspiration and the pure mathematic endowments would attract more people’s attention to and interest in pattern mining or big data science in general, or even broader. More explicitly, compared with a pattern consisting of singleton elements, the substances of our world comprise quantum particles in modern physics. Then, if we could solve the pattern mining problem mathematically, why could not we find a similar way to understand the world at large, particularly in the search for new genes or innovation of new materials, for instance?
The structure and contents of this paper are: after a summary of the drawbacks of previous works on frequent pattern mining in Sect. 2, Sect. 3 presents the properties of raw pattern frequency distributions under the full enumeration pattern generation regime. Section 4 is on the properties of the distributions in the reduced pattern generation mode, including their empirical verifications, followed by a brief discussion in Sect. 5 and then is the conclusion part of this paper.
2 The mining problem and previous work
The classic pattern mining is originally the itemset mining [1] studied initially in the data mining history. The dataset, such as Table 1, used for the mining is abstracted from market transactions and typically presented in previous research articles. Below presents the details of the dataset natures and the mining problem.
2.1 The terminology and the mining model
Table 1 is a running example of the classic dataset to be used in this paper and named as DBo. The table has u rows and two columns, where column VID represents an application domain \(\varOmega \) of n distinct elements, while TID means the key attribute in database notation. Each row is a tuple with a tuple ID, \(T_i \) \((i = 1, 2, ..., u)\). The \(V_i\) \( (i = 1, 2, ..., n)\) in each cell of column VID means a value from \(\varOmega \). For example, in a market itemset mining problem, a TID could represent a transaction ID, while a \(V_i\) indicates an “item” from the domain \(\varOmega \) of merchandise. A combination of k distinct \(V_i\)s is named as a pattern \(Z_k = (V_iV_j...V_s)\) of length k. The process to enumerate the patterns is called pattern generation.
In statistics terminology, the dataset DBo is a sample of the real-world application at hand. The cardinality u of DBo is the sample size; a record (tuple) is an original observation, or a realized event of the sampling [24], hence a subset of \(\varOmega \). A TID can be taken as a sample label or trial ID, and column VID refers to the set of events [25].
In addition to the above attributes, Table 1 called a “classic dataset” is abstract and characterized in the following [23]:
-
(a)
The classical data nature: each \(V_i\) is of the same nature of the element in set theory. That is, \(V_i\) is unique and atomic (indivisible) in a tuple.
-
(b)
The dataset is de-semantic, where each \(V_i\) is expressed as a discrete (ID) number or a keyword to represent an object (element or item).
-
(c)
The dataset is static.
-
(d)
No random walk in the dataset is presumed in previous work since there is no pre-knowledge to assume which tuple or which element (item) to be so.
Based on the above introduction of the dataset, the fundamental pattern mining problem can be stated as below:
Problem 1
Output all patterns of the elements of any length k \((k > 0)\) from the universe \(\varOmega \) given in DBo, such that the frequentness \(s_z\) of a pattern Z satisfies \(s_z \ge s_{min}\).
Conventionally, \(s_z\) is called the “support” of pattern Z, and \(s_{min}\) is a user predefined frequentness threshold. \(s_z\) is defined as [1, 2]:
where S(Z), or \(S_z\) or F(Z) noted alternatively in the literature, is the number of occurrences of a pattern Z, called “absolute support” or “absolute frequency” of Z over the database; \(u = |DBo|\) is the total number of tuples, i.e., the cardinality of DBo. For instance, \(S(V_1V_2V_3) = 2\), \( S(V_1V_2) = 3\), and \(s(V_1V_2) = \nicefrac {3}{10} = 0.3\), from Table 1.
Problem 2.1 and the related dataset form the classic mining problem. It acts as the simplest hence fundamental pattern mining model. A sound solution for the model is thus of particular importance since only after the simplest mining problem has been well-solved could we properly proceed to more complex mining problems. However, no reliable mining approach has been developed after so many research works being published. Everyone would ask, why? The introduction part above has answered the question principally, while the following subsection presents further explanations.
2.2 The previous works and their drawbacks
As a continuation of the author’s previous work [23] (“the last study,” hereafter), which has presented a review on some known previous mining approaches, this paper does not assume to make such a further review since this paper is not on specific mining approaches. A more important reason is that all previous approaches are unreliable. As such, a summary of the causes of the unreliability as below would be adequate instead. Readers who want to know more information about the previous approaches can refer to several surveys [1, 2, 26, 27].
The last study investigated two fundamental issues of previous works: the ill-formed support measure (\(s_z\)), with their summation \(\sum (s_z)\) being much larger than 1 in an application, thus a serious “probability anomaly” issue. The second is the full enumeration pattern generation mode used, which produces an excessive number of patterns from any mining application. The two together lead to crucial overfitting issues in previous approaches, where overfitting means a spurious pattern being falsely taken to be a real frequent one.
The last study starts with a comparison between the concerned pattern mining problem and the classic frequency-based probability problem, where each row (tuple) of the sample dataset used stores only one event (pattern), with an assumption that there is no correlation between any two observations. As such, the accumulative event frequency equals the cardinality of the dataset u, and the frequentness (probability) of each event Z, f(Z), equals the ratio of its total occurrences F with u, that is, \(f(Z) = F(Z)/u\), which indeed is the origin of the s(Z) stated in (2.1).
Now, in pattern mining, the only difference is that each tuple of the dataset used, such as Table 1, may hold multiple patterns. If we separate those patterns from each tuple and store each pattern in a single tuple of a virtual dataset (DBv), and suppose the cardinality of DBv had increased from DBo’s u to w, then the frequentness of a pattern expressed in (2.1) should be changed into:
which then not only explores the cause of probability anomaly and overfitting problems but also is a remedy to them: From (2.1) and (2.2), \(r_s = s_z/ s'_z= w/u \gg 1\) in real applications, which then causes \(\sum s_z \gg 1\) and probability anomaly rises. Meanwhile, \(s_z\) greatly inflates the real frequentness of Z and overfitting comes up. \(r_s\) is thus named the primary overfitting ratio. From the running example Table 1, \(\sum s_z > 11\), and the larger the datasets, the severer the probability anomaly and the overfitting.
Another cause of the overfitting problem is the mode used to separate the patterns from each tuple of a dataset. Conventional approaches generally use or are based on the full enumeration mode to use each element repeatedly in a tuple to generate every possible pattern to fulfill the job, but this mode is not feasible in classic pattern mining. It is just because, as listed in Sect. 2.1, each element (item) in a tuple is a singleton, unique and indivisible, as reflected in the calculation of pattern length and tuple length. That means an element could not be used more than once to form different patterns since no element could belong to more than one pattern within the same tuple, and notice that the dataset is already historical and static.
Meanwhile, the “downward closure property,” which says any super-pattern could not be more frequent than its sub-patterns, has almost been taken as a golden rule and widely used in previous approaches. However, this property is not intrinsic to any dataset but only a phenomenon of the full enumeration mode. The profound reason for this property is that shorter patterns recapture some frequencies of their super-patterns. It thus leads to the biased frequentness evaluation toward short against long patterns and biases toward generated against originally observed ones.
Indeed, previous researchers have felt the problem of too many resultant patterns from mining applications and proposed different reduction approaches to solve it. For instance, to use the “interestingness” [28] or “weighted” [29] measures and the like to modify the conventional \(s_z\). These measures, especially the former, are rather complex with various exogenous inputs and hence not effective. Another example is the use of a “concise” or “condensed” result set such as the “maximal” or “closed” [30] pattern set to represent the whole mining result set, but these approaches are still based on the full enumeration mode such that for any given pattern Z, they produce the same S(Z) and s(Z). That is, although various solutions were attempted, they did not sight into the real problems as above and thus could not work well.
Instead, the solution proposed by the last study is the selective mining mode. This mode means a partition of the elements of each tuple. Each part of the partition then forms a pattern. The key is in how to select a proper partition for each tuple. That is how the mode is named so. This mode comes out from systematic analysis and the establishment of several theorems. The proposal first introduces the “equilibrium condition” to guide and quantify the mining.
The primer equilibrium condition means, for each tuple, the count \(C(e_i)\) of any given element \(e_i\) in its result pattern set cannot be more than the count \(S(e_i)\) of the same element from that tuple. That is,
Aggregately, the sum of the lengths of all the resulted patterns could not be more than that of the lengths of all the tuples of an entire dataset. That is,
where \(Z_i\) is the ith pattern in the pattern set, and \(b_j\) is the length of tuple j; both i and j are cardinal numbers.
In the initial stage of mining, because every element stands equally (the 4th feature of the classic dataset, refer to the previous subsection), the above two formulas take strict equality. A notice here is that (2.3) implies (2.4), but not vice versa.
Here are the three out of five theorems presented in the last study for the birth of the selective mode. One is that the number of possible patterns from a given data tuple can only be less than linear to the tuple length, while conventionally, it is exponential to the length, which means the number of result patterns should have been much fewer even without using any proposed reduction approach. At the end of Sect. 4, we will see an example of the difference in the mining result sets between the new and conventional approaches. The second is that the selective pattern generation mode is the only feasible mode in classic pattern mining. The third is that patterns produced from the selective mode are conjunction-issue-free. It then further justifies the use of f(Z) (2.2) above since it confirms that f(Z)s are directly additive and sum to 1. The probability anomaly issue is then automatically gone. This theorem also clarifies that the super-sub patterns can only be produced from different tuples of a dataset, another major point not aware of in the previous literature.
Finally, the last study concluded that any mining approach should satisfy at least the three rationality criteria: probability anomaly free, the use of the selective pattern generation mode, and compliance with the equilibrium condition. However, no previous approach did or could claim the satisfaction of the above criteria. That means no mining approach to date is rational yet, let alone reliable. This present paper will present further criteria to see soon.
For the detailed reasoning of the above issues and their solutions and other contents not presented above, interested readers may refer to the original work [23].
We now turn back to the topic of the pattern frequency distribution theory, which affects the rationality thus reliability of the pattern mining approach either but virtually absent in previous works. What we can find are few articles on estimating the number of patterns in applications [31, 32]. However, they are based on the full enumeration pattern generation mode again. Their declared estimation accuracy thus could not hold instead. Meanwhile, such an estimation problem is not the focus of the present paper. That means we could not get significant references from the literature to discuss the main topic of this paper, and we finish this part here.
Hereunder we will get into the main body of this paper to present the properties of patterns frequency distributions. We will use the notation F(Z) instead of S(Z) to represent the pattern frequency and use p(Z) or f(Z) rather than \(s'(Z)\) to represent the probability (frequentness) of the pattern. Since f(Z) is linear to F(Z) as defined in (2.2), the shapes of the frequency and frequentness distribution curves will be the same. As such, for simplicity, our discussion will be mainly on the frequency distributions.
Since a pattern is naturally a combination of one or more different elements, combinatorics will be a basic theory to study the mining. In this paper, we use the notation \(C_i^k\) to mean the number of combinations of k elements selected from a set of i different elements. Another notice is that the empty set \(\varnothing \) could not be a pattern, and \(F(\varnothing )\) be undefined. The reasons will clear up before the end of Sect. 3.
Lastly, this paper does not consider the effect of a frequentness threshold such as \(s_{ min}\) mentioned before. It is not only because that the \(s_{ min}\) and its setting-up are problematic, as addressed in the last study [23], but also notice that the use of \(s_\mathrm{min}\) in previous works is mainly to reduce the size of the resultant pattern set. An issue is that when a user wants to look into the result set with a smaller \(s_{ min}\), the only way is to rerun the mining software, which could be very costly and take up to dozens of hours to run over a large dataset. With the new selective mining approach, delivering the entire result pattern set to the user will no longer be a big problem since the set size will greatly decrease. It is then a trivial issue for a user to look at the results with whatever \(s_{ min}\) s/he likes. Since this paper is mainly a theoretical work, it is more than needed but required to keep the generality and completeness of our discussion, and we thus set the minimum frequency (or the absolute support in conventional notation) F(Z) to be 1 to cover all the patterns of an application in this paper.
3 The properties of raw pattern frequency distributions
A pattern Z generated from the full enumeration mode is named a raw pattern and its frequency F(Z) the raw frequency. Although only the selective pattern generation mode is feasible in the classic mining, there are still reasons we need to study the raw pattern frequency distributions from the full enumeration mode. Firstly, the full enumeration mode is equal to the repeatable sampling covered in most probability textbooks. In combinatorics, the mode represents the typical question to get all possible combinations of any number of elements from a set of different elements. In accordance, as we will see later, the study of the raw pattern frequency distributions will not only fulfill theoretical completeness but also lay a foundation for the distribution theory with the reduced pattern generation mode. The reduced mode may not be fully the selective mode, but it reduces the number of patterns from the full enumeration mode. Secondly, in practice, it is a way to find out the real patterns from a full set of all possible patterns. Then the study of the raw pattern frequency distributions is again imperative. For simplicity, the word “raw” may be omitted hereafter.
In real applications, the number of possible patterns is usually huge. It will thus be overwhelming in this paper to look into each pattern and its frequency. Instead, this paper presents an overall pattern frequency distribution theory referring to every collection of patterns of the same length. We start the discussion from a vertical pattern generation approach.
3.1 The vertical pattern generation approach
In the full enumeration pattern generation mode, the common way is horizontally to generate patterns from each tuple of an original dataset DBo. For instance, from tuple \(T_1\) of Table 1, we can generate patterns \(V_1\), \(V_1V_4\), etc. However, the vertical approach [33, 34] is more helpful to derive the basic formula to use in this paper. In this approach, we first transform the original dataset DBo, e.g., Table 1, into its “dual” table, named DBd, as shown in Table 2, such that:
That is, the transformation exchanges the roles of TID and VID such that VID in DBd acts as the key attribute, with each \(V_i\) \( (i = 1, 2, ..., n)\) representing a set of \(T_j\)s that holds the same \(V_i\) in the original database DBo. For example, in DBo (Table 1), \(V_1\) is referred by \(T_1, T_4, T_5, T_9\) and \(T_{10}\). So, in DBd, \(V_1\) refers to those \(T_j\)s in turn. With this vertical approach, a pattern \(Z_k = (VpVq{\dots }Vs)\) of length k is a combination of k elements vertically from the column VID of DBd. The frequency of a pattern of a single element \(V_i\) is the number of corresponding \(T_i\)s held in row \(V_i\) of of DBd, while the frequency of a pattern of k \((k > 1)\) elements is the number of the “intersected contents” (\(I_c\)), that is, the number of \(T_i\)s commonly referred by each of the elements. More formally, we define:
Notice that, here we are not interested in what the intersected contents are, but only in the number of such contents.
Another notice is the \(|VpVq{\dots }Vs|\) above is not the length of the pattern \(Z_k\) but the count of its intersected contents \(I_c\).
For instance, in DBd (Table 2), \(V_1\) refers to \(\{T_1, T_4, T_5, T_9, T_{10}\}\), \(V_4\) refers to \(\{T_1, T_2, T_5, T_7\}\). Then, \(I_c(V_1V_4\)) = \(\{T_1, T_5\}\), and \( F (V_1V_4) = |I_c(V_1V_4)|\) \(= 2\).
Recall that \(\varOmega \) represents the universe of \(V_i\)s in DBo, now we use \(U_t\) to mean the universe of \(T_{j}\)s in DBd, i.e., \(T_j (j = 1, 2, ..., u)\) becomes the element of \(U_t\). Notice that the same \(V_i\) may not present in every tuple of DBo. Otherwise, \(V_i\) is removable from the dataset to simplify the problem. As such, \(V_i\) refers to a proper subset of \(U_t\), i.e., \(V_i \subset U_t\). Then, the correspondences of the DBo and DBd are:
where |X| means the number of elements (the cardinality) of X.
3.2 The inclusion–exclusion principle and the pattern frequencies
From the above subsection and DBd (Table 2) where the universe \(U_t = \{T_1, T_2 \dots T_u\}\) with \(|U_t| = u\), and each \(V_i \) \((i = 1, 2 \dots n)\) represents a (overlapped) subset of \(|U_t|\), then by set theory, if n and u are finite, we have:
From a very basic set operation (\(n = 2\)):
where \(V_1V_2\) is a shorthand for \(V_1 \cap V_2\).
Extending the above into (3.6) and considering (3.7), we have:
Formula (3.8) is referred as the “inclusion–exclusion principle” [35] since the alternating signs presented in the formula imply the compensations of possible excessive inclusion or exclusion of the elements (\(I_c\)) involved in every (VpVq...Vs) during the calculation. In this paper, we use this principle as the starting point to explore more general laws governing pattern frequency distributions under the full enumeration regime.
In (3.8), each \(\sum \) term represents a sum of the raw frequencies of a “collective” of patterns of the same length. To avoid the notation confusions and to simplify expression (3.8), we introduce the following definitions:
Firstly, we use \(\varPhi _k\) to mean a collection of patterns of length k, and \(H_k\) to be the “sub-cumulative raw frequency” of the \(\varPhi _k\), and \(C_k\) the number of patterns within \(\varPhi _k\). More formally:
Definition 1
The “collection of raw patterns of the same length k” :
where \(j= 1, 2, ..., C_k\), and \(Z^j\) is the jth pattern within \(\varPhi _k\).
Note that the number j above is for enumeration, i.e., j is a cardinal but not an ordinal number.
For instance, from Table 1, \(\varPhi _1 = \{V_i|i = 1, 2, ..., 8\}\), \(\varPhi _2 = \{V_1V_2, V_1V_3 ..., V_7V_8\}\), and so on.
Definition 2
The “sub-cumulative raw frequency” of \(\varPhi _k\):
We will see examples of \( H_k\)s in Table 3 later.
Then, (3.8) can be reformulated as:
The “inclusion–exclusion principle” then becomes easy to express by (3.11). The above concepts and formulas are fundamental, based on which we shall explore a set of interesting properties of the pattern frequency distributions in the rest of this paper.
3.3 The calculation of \(H_k\)s and the accumulative raw frequency \(w_0\)
As mentioned before, w is generally used as the accumulative pattern frequency. In particular, we use \(w_0\) to mean the raw accumulative in the full enumeration mode.
3.3.1 The basic formulas
Based on combinatorics, the basic formula for \(w_0\) would be:
where \(b_i = |T_i|\) is the number of elements held by a tuple \(T_i\) in the original dataset DBo, \(u = |DBo|\), and note again, the empty set \(\varnothing \) is not taken as a pattern, thus \(\sum _{j = 1}^{j = i}C_{i}^j = 2^{i} - 1\).
The computation cost of \(w_0\) from (3.12) is more than linear to the data size u. As such, it may take hours or days to get \(w_0\) in current desktop system when the concerned dataset u is in trillions or even larger. For this, a cheaper formulae has been developed in [23]:
where \(g_i\) is the number of tuples each holding i elements in the original datasets DBo, hence:
and \(\alpha = Max(T_i)\), the longest tuple length.
The full series of \(g_i\)s of a dataset is named the “\(g_i\) distribution” . For instance, the \(g_i\) distribution of Table 1 is (2, 3, 2, 2, 0, 1).
Now, we define
as the sum of the frequencies of all patterns that can be generated from tuples of length i, then,
Hereunder we present an even more efficient way to calculate \(H_k\) and \(w_0\).
3.3.2 The vector-expression formulas
Since \(H_k\) represents the accumulated frequency of a collective of all patterns of the same length, then:
and,
(3.16) and (3.18) produce the same \(w_0\), but they represent different pattern generation strategies. Equation (3.16) refers to the case where patterns of different lengths \(\le i\) are generated in a loop i from tuples of same length i, while (3.18) refers to the case where patterns of the same length k are generated in a loop k from all tuples of length \(\ge k\).
Equations (3.17) and (3.18) can be in either vector or matrix expressions, and we introduce the vector approach first. For this, we define
as a “gathering vector” of dimension (\(\alpha - k + 1)\). In particular, when \(k = 1\), \(\mathbf {G_1}\) is the entire series of \(g_i\) distribution. And,
as a “setup vector” of dimension (\(\alpha - k + 1)\). In particular, when \(k = 1\), \(\varTheta _{\mathbf {1}}\) is called an “initial setup vector” , and
In addition, we define a vector \(\mathbf {E_k}\) as a “w-product” of \(\mathbf {G_k}\) and \(\varTheta _{\mathbf {k}}\), expressed as \(\mathbf {E_k} = \mathbf {G_k} \circ \varTheta _{\mathbf {k}}\), where \(\mathbf {E_k}\), \(\mathbf {G_k}\) and \(\varTheta _{\mathbf {k}}\) are of the same dimension, and each element \(e_i\) of \(\mathbf {E_k}\) being the product of \(g_iC_i^k, (i = k, k + 1,\dots , \alpha )\). That is,
Notice that (3.17) can be expressed as a dot product of \(\mathbf {G_k}\) and \(\varTheta _{\mathbf {k}}\):
On the other hand, we can have:
where \(\mathbf {B_k}\) is termed as a “base vector” of dimension (\(\alpha - k + 1\)), with all elements being 1:
Among other significances, the use of the above vector formulae enables the calculation of \(H_k\)s recursively without involving any exponent operation through the following derivations.
Extending (3.17), we have:
Since, from combinatorics:
then (3.26) becomes:
where \(\mathbf {A_k}\) is named an “adoptive vector” , each of its element being (\(i - k\)). Notice that i starts from \(k + 1\), thus \(\mathbf {A_k} = (1, 2, \dots , \alpha - k)\), which is exactly the first section of the \(\varTheta _{\mathbf {1}}\) series up to (\(\alpha - k\)). In programming point of view, \(A_k\) is a result of right shift of \(\varTheta _{\mathbf {1}}\) by (\(k - 1)\) positions, noted as:
Meanwhile, vector \(\mathbf {E'_k}\) is a copy of \(\mathbf {E_k}\) with its first element being cutoff. For instance, if \(\mathbf {E_k} = (2, 3, 5)\), then \(\mathbf {E'_k} = (3, 5)\). That is, each element of \(\mathbf {E'_k}\), \((e'_k)^i = e_k^i\), starting from i = k + 1.
On the other hand, with the same formulation of (3.24), we have:
Since \(\mathbf {B_{k}}\) (similar to \(\mathbf {B_{k+1}}\)) is a base vector of every element being 1, the main issue of the computation of \( H_k\) (and \(H_{k+1}\)) is now the computation of \(\mathbf {E_{k}}\) (and \(\mathbf {E_{k+1}}\)). Comparing (3.28) with (3.29), we can easily see that any element \(e_{k + 1}^i\) of \(\mathbf {E_{k+1}}\) is the computation result from (3.28):
and elementally,
Note that the superscript i of the above \( e_{k + 1}^i \) is a global index, which is easier than a local index to express the relation of two vectors \(\mathbf {E_{k}}\) and \(\mathbf {E_{k+1}}\) of different dimensions.
Now, (3.21), (3.22), (3.23), (3.29) and (3.30) form a recursive program to compute all the \( H_k\)s, starting from \(\varTheta _1\) and \(G_1\) only. That is, from (3.22), we have:
where \(\mathbf {G_1}\) is the vector of the whole series of \(\mathbf {G_k}\) starting at \(k = 1\), and \({{\varTheta }}_{{\textbf {1}}} = (1, 2, \dots , \alpha \)).
Then, by (3.30), \(\mathbf {E_2}\), and similarly \(\mathbf {E_3}\), and so on, will be obtained recursively, and so the \(\mathbf {H_k}\)s, as described below.
3.3.3 The tabular recursive approach to compute \(H_k\)s
Table 3 is an example of the use of the above formulae to compute all \(H_k\)s recursively as well as \(w_0\) over dataset DBo (Table 1). The first row of Table 3 lists the elements of \({{\varTheta }}_{{\textbf {1}}}\), which is just an enumeration from 1 to \(\alpha \) (here \(\alpha \) = 6), while the second row lists the elements of \(\mathbf {G_1}\) (the full \(g_i\) series). These two lists are the only inputs.
The bold numbers in each of the following 6 rows of the table are the elemental results of \(\mathbf {E_k}\)s, and they together form an upper triangular matrix, named as “enumeration triangle matrix” \(\varLambda \). Each row of the \(\varLambda \) forms an \(\mathbf {E_k} (k = 1, 2, \dots ,\alpha )\). For instance, row 3 \((k = 1)\) represents \(\mathbf {E_1}\) (refer to 3.31), resulted from multiplying the corresponding elements of \(\mathbf {G_1}\) and \({{\varTheta }}_{{\textbf {1}}}\). Row 4 is corresponding to \(k = 2\) globally, but in the recursive approach, it means \(k + 1 = 2\) where \(k = 1\) preset.
To compute \(\mathbf {E_2}\) and \(H_2\), right shift \({{\varTheta }}_{{\textbf {1}}}\) by one column and get \(A_{1}\), or left shift \(\mathbf {E_1}\) by one column to get \(\mathbf {E'_1}\). Then according to (3.30), the first element of \(\mathbf {E_2}, e_2^2 =\nicefrac {1}{2}(1 * 6) = 3\) (note the first element of \(\mathbf {E_2}\) starts from the second column, which is reflected in the superscript of \(\mathbf {E_2}, e_2^2 \)). The whole row 4 represents the elemental results of the w-product of (6, 6, 8, 0, 6) and (1, 2, 3, 4, 5) divided by 2. Similarly, row 5 is the result of the w-product of (6, 12, 0, 15) and (1, 2, 3, 4) divided by 3, and so on.
Finally, the sum of a row of the \(\varLambda \) triangle gives a \(H_k\), while the sum of a column being an \(F_i\) (refer to 3.15). Additionally, as a checkpoint, the main diagonal elements of the triangle \(\varLambda \) are just a copy of the \(\mathbf {G_1}\) (the second row)!
The above example well-demonstrates the beauty of formulae (3.29) through to (3.31), and the tabular approach developed is superb in both programming easiness and computation efficiency. This approach involves no exponent or combinatorics operations, and all the intermediate results in Table 3 are reused. Efficiency is thus its most important feature. Notice that the maximum tuple length \(\alpha \) is not linear to the data size u but usually would not exceed a hundred or thousand in an application. The computation cost of this approach will thus be in only minutes and nearly constant over any large dataset, while the cost of the preliminary formula (3.12) could be in multiple hours, as stated before. In other words, the above approach realizes the full scalability of the calculation of \(H_k\) and \(w_0\). It would be even more significant if this approach could develop a way to reach the scalability of pattern mining in general, which is recognized as a critical issue in pattern mining [36].
Additionally, this tabular approach is easily extensible with the change of the dataset. For instance, if \(\alpha \) increased, we only need to add more required columns and rows on the right and the bottom of the table. Secondly, if the \(g_i\) distribution changed, we only need to update the affected columns and \(F_i\)s and \(H_k\)s.
3.4 The parity property of odd and even length pattern frequencies
Besides the efficient \(H_k\) computations, there is an interesting relation between the sums of the frequencies of odd and even length patterns from (3.11).
where the upper bound “\(\nicefrac {\alpha }{2}\)” on the left side should be changed into \((\alpha + 1)/2\) and the right side to \((\alpha - 1)/2\) if \( \alpha \) is odd. We use \(H_{ odd}\) and \(H_{ even}\) to mean the accumulative of raw frequencies of patterns of odd lengths and even lengths, respectively:
Then, (3.32) becomes:
Adding \(H_{ odd}\) to both sides of (3.34), and notice that \(H_{ odd} + H_{ even} = w_0\), we get:
That is,
As measures of frequencies, \(H_{ odd}\) and \(H_{ even}\) each must be an integer. We have the following proposition to guarantee it:
Proposition 1
\(w_0 + u\) or \(w_0 - u\) is always even, and \(w_{0}\) is of the same parity of u.
Proof
From (3.12), \(w_0 = \sum _{j = 1}^{j = u}2^{b_j} - u\), and let \( y = \sum _{j = 1}^{j = u}2^{b_j}\). Since \(b_j = |T_j| > 0\), it follows that y is always even. Then, \( w_0 + u = y - u + u = y\), and \(w_0 - u = y - u - u = y - 2u\). In both cases, the results are even, and the first part of the proposition is proved. At the same time, it is easy to see that, if u is even (or odd), \(w_0\) is then even (or odd), and the second part of the proposition is proved. \(\square \)
The above formulas and results can be verified from Table 3. Following, we introduce significant laws governing all of the \(H_k\) distributions.
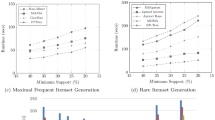
3.5 The \(H_k\) frequency distribution curve
If we plot the \(H_k\) distribution \((k, H_k)\) and link all of the \(H_k\) value points together as shown in Fig. 1, we get a curve of “raw collective frequency distribution curve” , or simply “\(H_k\) curve” . Interestingly, the curve can be expressed as a relation between every adjacent \(H_k\) and \(H_{k+1}\) as what follows:
Theorem 1
From the classic dataset and by full enumeration pattern generation mode, the \(H_k\) curve can be expressed as:
where n is the number of distinct elements presented in the dataset; \(\alpha \) is the maximum length of the tuples thus patterns; \(R_k\) is a “collective frequency reducer” , or abbreviated as “reducer” ; and
The above theorem can be proved either qualitatively or quantitatively. To save space, here we present the quantitative proof only.
Proof
We start the proof with the simplest case of a dataset of one tuple only, its length being \(\alpha \) (scenario 1), then,
According to combinatorics,
we then have:
Now we extend the above to the case of a dataset of u \((u > 1)\) tuples of the same length \(\alpha \) (scenario 2), then,
Accordingly,
Comparing the above two equations, we get:
The above two scenarios together represent the preliminary case featured with the same length of every tuple of a given dataset, and in this case \(R_k\) = 1. The top curve in Fig. 1 depicts the preliminary \(H_k\) curve.
Now in the general case that the tuple lengths may vary, our primary work is to prove \(R_k < 1\) . The proof runs with matrix expressions.
From (3.23), \(H_k =\sum _{i = k}^{i = \alpha }g_iC_i^k = \mathbf {G}_{\textbf {k}}\cdot {{{\varTheta }}}_{\textbf {k}}\), we now transform it with the non-bold \(G_k\) and \({{{\varTheta }_{k}}}\) as the matrix expression for \(H_k\):
where \(G_k\) is an \(1 * (\alpha - k+1)\) “gathering matrix” , starting from \(g_k\): \(G_k = (g_k, g_{k+1}, \dots , g_\alpha )\); \({{{\varTheta }}}_{k}\) is an \((\alpha - k+1) * 1\) “setup matrix” , and \({{{\varTheta }}}_{k} = ( C_k^k, C_{k+1}^k, \dots , C_\alpha {}^k)^T\), particularly, when \(k = 1, {{{\varTheta }}}_{1}\) being an \(\alpha * 1\) “initial setup matrix” , and \({{{\varTheta }}}_{1} = (1, 2, ..., \alpha )^T\); \(I_k\) is an \((\alpha - k+1) * (\alpha - k+1)\) identity (thus idempotent) matrix, with all elements of the main diagonal being 1 while the rest being 0.
Similar to \( H_k , H_{k+1}\) can be expressed as:
On the other hand, by (3.28),
where \({{{\varTheta }}}_{k}^{\prime }\) is a sub-matrix of \({{{\varTheta }}}_{k}\) without the first row; similarly \(G_{k+1}\) is a copy of \(G_k\) without the first element; \(A_k\) is a diagonal matrix of dimension \((\alpha - k) * (\alpha - k)\) and called an “adoptive matrix” , its main diagonal elements \(a_{jj} = \frac{i - k}{\alpha - k}\) with \(j = i - k\) and starting from \(i = k + 1\). As such, except the last element \(a_{tt} = 1\), where \(t = \alpha - k\), all the rest \(a_{jj} < 1\).
Now, we define a diagonal matrix \(A_k^+\) of dimension \((\alpha - k + 1) * (\alpha - k + 1)\), with its first element \(a_{11} = 0\), and the rest submatrix of dimension \((\alpha - k) * (\alpha - k)\) being the same as \(A_k\). A better understanding of the above may refer to the following examples of the matrixes related to the running example with \(k = 3\):
\(I_k = \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, A_k = \begin{bmatrix} \nicefrac {1}{3} &{} 0 &{} 0 \\ 0 &{} \nicefrac {2}{3} &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}, \)
\( A_k^+ = \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \nicefrac {1}{3} &{} 0 &{} 0 \\ 0 &{} 0 &{} \nicefrac {2}{3} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \)
\(G_k = \begin{bmatrix} 2&2&0&1 \end{bmatrix}, \) \(G_{k+1} = \begin{bmatrix} 2&0&1 \end{bmatrix} \) (refer to Table 3),
\({{{{\varTheta }}}_{k} = \begin{bmatrix} 1&4&10&20 \end{bmatrix}}^T, \) \({{{{\varTheta }}}_{k+1} = \begin{bmatrix} 4&10&20 \end{bmatrix}}^T. \)
With the above formulas, (3.42) can be reformulated as:
Now (3.43) and (3.40) \(H_k = \sum _{i = k}^{i = \alpha }g_iC_i^k = G_k I_k {{{\varTheta }}}_{k}\) become comparable. Notice that the last element \(\alpha _{tt}\) of \(A_k\) (the same to \(A_k^+\)) is always 1 as stated before, while ever other element of \(A_k^+\) is less than that of \(I_k\), respectively. Notice also that some element(s) of \(G_k\) can be zero (but never be negative), while the last element \(g_{\alpha } > 0\) in any case (otherwise the longest tuple length will not be \(\alpha \)). There then have two alternative outcomes of the comparisons between \(G_k A^+_k {{{\varTheta }}}_{k}\) and \(G_k I_k {{{\varTheta }}}_{k}\).
(1) In a general case of more than one element of \(G_k\) series being positive, then compared with (3.40), there must be:
It means there exists an \(R_k\), such that
where \(0< R_k < 1\) must be true to satisfy (3.45).
(2) In a special case of only \(g_{\alpha }\) being positive, then compared with (3.40), both \(G_k A^+_k {{{\varTheta }}}_{k}\) and \(G_k I_k {{{\varTheta }}}_{k}\) degrade to the same scalar value \(g_{\alpha } C^k_{\alpha }\). That is, in this case,
The above means \(R_k = 1\) compared with (3.45).
Consider the above two cases together, and referring to (3.45), (3.43) can be generally presented as:
In summary, \(0 < R_k \le 1\) is always true in any case, and the above formula is exactly (3-36). Theorem 3.1 is then fully proved. \(\square \)
From the above proof, we can get further corollaries as below.
Corollary 1
The distribution of original data tuples of lengths less than k does not have effect on \(R_s\) with \(s \ge k\).
The above is obvious since \(G_k\) starts from its kth element. Indeed, this corollary can be alternatively stated that \(R_k\) is determined by all and only the \(g_i\)s with \((i \ge k)\),
Corollary 2
The necessary and sufficient condition for \(R_k = 1\) is that the kth through to the \({(\alpha - 1)}\)th members (inclusive) of the \(G_k\) series equal to zero.
Corollary 3
If \(R_k = 1\), then all \(R_s = 1\), where \(k \le s < \alpha \) (note \(R_k\) series is ended at \(R_{\alpha - 1}\)).
The two corollaries above are related. The proof of Corollary 2 is implied in the derivation of (3.46). The proof can also be seen from Corollary 1. Since only \(g_i\)s with \(i \ge k\) can affect \(R_k\), but if all \(g_i\)s = 0 except \(g_\alpha \), then only \(g_\alpha \) determines \(H_k\) and \(H_{k+1}\), which then means no reducer exists between \(H_k\) and \(H_{k+1}\), hence \(R_k = 1\).
Corollary 3 comes directly from Corollary 2 that, if there are successive m 0s in the \(g_i\) distribution from \(i = \alpha - 1\) backwardly, then there are m 1s in the right section of \(R_k\) series. Particularly, at k = 1, if \(R_1 = 1\), then all \(R_is = 1\). It turns to be the preliminary case stated before, where all the original data tuples are of the same length \(\alpha \) (that is, there is only \(g_\alpha \) being nonzero).
We will see the verifications of the above in Example 1 soon, Tables 4 and 7 later.
The following subsections present other important properties of the \(H_k\) curve.
3.6 The quasi-concavity of the \(H_k\) curve
Theorem 2
(\(H_k\) quasi-concavity theorem) If \(R_k\) is non-decreasing, then the \(H_k\) curve expressed in (3.36) is strictly quasi-concave downward over \(0 < k \le \alpha \), and it reaches its apex value at \(k = q \le \nicefrac {\alpha }{2}\).
“Quasi-concavity” is used in real-valued function study [37]. If a function \(f(\mathbf {Z})\) is strictly quasi concave within a domain E, then there exists a \(\mathbf {Z}^* (\mathbf {Z}^* \in E)\) such that \(f(\mathbf {Z})\) is increasing for \(\mathbf {Z} < \mathbf {Z}^*\) and \(f(\mathbf {Z})\) is decreasing for \(\mathbf {Z} > \mathbf {Z}^*\) [37], where \(\mathbf {Z}\) can be a vector of multidimensional variables. We use this concept not only for better understanding but also for formal applications of the properties of the \(H_k\) distributions. The only difference here is that the “quasi-concavity” property applies to discrete \(H_k\) values (refer to Fig. 1).
Proof
If all \(R_k\)s = 1, it refers to the preliminary case that all u tuples of a given dataset are in the same length \(\alpha \), and \(H_k = u C_{\alpha }^k \) (3.39). The quasi-concavity property of the \(H_k\) curve is identical to that of the curve formed by the full series \(C_{\alpha }^k\) \( (k = 1, 2, \dots , \alpha \)). Notice in this case \(H_k\) is symmetric since \(C_{\alpha }^{\alpha - k} = C_{\alpha }^k\). When \(\alpha \) is an even number, \(H_k\) is strictly quasi-concave and reaches its maximum value \(H^*\) at \(k = \frac{\alpha }{2}\). When \(\alpha \) is an odd number, \(H_k\) gets its two maximum values at \(k = \frac{\alpha - 1}{2}\) and \(k + 1 = \frac{\alpha + 1}{2}\). However, since there is no other integer between k and \(k + 1\), and since the preliminary case is not much an issue in this study, we take that the preliminary \(H_k\) curve is generally strict quasi-concave hereafter.
The strict quasi-concavity of the preliminary \(H_k\) curve (3.19) can be viewed from the depiction of the top curve in Fig. 1.
Now we prove the quasi-concavity property in the general case with \(R_k < 1\). Let us first look at the slope of the \(H_k\) curve, \(\nicefrac {\varDelta H_k}{\varDelta k}\), with \(\varDelta k = 1\), which is the smallest interval of k.
Since \(H_k > 0\), the sign of the slope \(\frac{\varDelta H_k}{\varDelta k}\) is determined by \((R_k\frac{\alpha - k}{k + 1} - 1)\). Notice that,
-
(i)
\(\nicefrac {(\alpha - k)}{(k + 1)}\) is a strictly decreasing function of k, since:
$$\begin{aligned} \frac{\varDelta [{\nicefrac {(\alpha - k)}{(k + 1)}}]}{\varDelta k} = - \frac{\alpha + 1}{(k + 1)(k + 2)} < 0 \end{aligned}$$ -
(ii)
Without the effect of \(R_k\) (thus in the preliminary case), \(\frac{\alpha - k}{k + 1}\) will be positive and leads \(H_k\) to increase until reaching the apex at \(k = \frac{\alpha }{2}\) if \(\alpha \) is even, or \(k = \frac{\alpha + 1}{2}\) and \(k = \frac{\alpha - 1}{2}\) if \(\alpha \) is odd as stated before, where \(\frac{\alpha - k}{k + 1} - 1 = 0\). After that \(\frac{\alpha - k}{k + 1} -1\) becomes negative and \(H_k\) decreases.
-
(iii)
With the effect of \(0< R_k < 1\): At the early stage (\(k \ll \alpha \)), \(\frac{\alpha - k}{k + 1} \gg 1\), while \(R_k\) being non-decreasing as given in the theorem, they then together lead \(H_k\) to increase with k but at a reduced rate compared with that in case ii above since \(R_k < 1\). Ultimately \((R_k\frac{\alpha - k}{k + 1} - 1) \rightarrow 0 \) at a point q such that \(H_k\) reaches its apex value \(H_q\), but q can only be less than \(\frac{\alpha }{2}\) due to the reduction effect of \(R_k\), and the value \(H_q\) would become much smaller than \(H^*\) without the effect of \(R_k\) (as seen in Fig. 1). Once the \(H_q\) has been reached, the slop factor \((R_k\frac{\alpha - k}{k + 1} - 1)\) becomes negative and keeps decreasing with k increasing since \(\frac{\alpha - k}{k + 1}\) decreases with k. It means \(H_k\) will then be monotonically decreasing until the end, regardless of \(\alpha \) being odd or even.
In summary, with the given condition of the theorem, \(H_k\) has one and only one apex at q with \(q \le \nicefrac {\alpha }{2}\), and \(H_k\) is strictly increasing for \(k < q\) but strictly decreasing for \(k > q\). \(H_k\) is thus strictly quasi-concave, and the theorem is fully proved. \(\square \)
Note, when \(\alpha \) is not very large, \(H_k\) might get its maximum value at \(k = 1\) (refer to example case b in Table 4 later), but such a case does not affect the soundness of the theorem. Another point to note is that Theorem 3.2 stated a sufficient condition of \(R_k\) to keep an \(H_k\) curve quasi concave, while following are the more precise description of \(R_k\) against this condition:
Corollary 4
If the \(R_k\) series is not decreasing, and q is the apex point of a quasi-concave \(H_k\) curve, then:
and
Proof
Notice \(0 < R_k \le 1\) as specified in (3.37), and from (3.36), we have \(\frac{k + 1}{\alpha - k} = R_k\frac{H_k }{H_{k+1}}\), where \(\frac{H_k }{H_{k+1}} < 1\) for \(k < q\) because of the \(H_k\) quasi concavity as given. Then, \(\frac{k + 1}{\alpha - k} < R_k \le 1\) before q, and (3.48) is proved. Meanwhile, notice that \(\frac{k + 1}{\alpha - k}\) is an increasing function of k before \(k = \frac{\alpha }{2}\), while \(q \le \frac{\alpha }{2}\). We then take \(k = q - 1\), such that \(\frac{k + 1}{\alpha - k}\) reaches its maximum value before pint q as \(\frac{q}{\alpha - q + 1}\), which, however, is less than \(R_k\) as specified in (3.48). Because of the monotonicity of \(R_k\), \(\frac{q}{\alpha - q + 1}< R_k\) will hold for the whole interval of \([q, \alpha )\), and (3.49) is proved. \(\square \)
Example 1
From Table 1, the \(g_i\) distribution is {2, 3, 2, 2, 0, 1} with \(\alpha = 6\); the \(H_k\) series is \(\{28, 36, 30, 17, 6, 1\}\) (from Table 3), which is quasi-concave with its apex point at \(q = 2 < \alpha /2 = 3\). It then proves Theorem 2. The \(R_k\) series is {0.514, 0.625, 0.756, 0.882, 1}, which well-demonstrate the monotonicity of \(R_k\)s. Notice also that \(g_5 = 0\), and \(R_5 = 1\), which then verifies Corollary 2. \(\frac{k + 1}{\alpha - k} |_{k = 1}= 2/5 = 0.4 < R_1 = 0,514\), \( \frac{q}{\alpha - q + 1} = 2/5 = 0.4 < R_2 = 0.625\) , and Corollary 4 is verified. Empirical results and verifications of the above from real application datasets are given in Table 7 and “Appendix” of this paper.
Quasi-concavity is a significant property of the \(H_k\) curve. At this point, a question may arise: would the condition of non-decreasing \(R_k\) hold in most of the classic pattern mining applications, such that the property could be typical? The following theorem answers it.
Theorem 3
For an ordinary \(g_i\) distribution, the \(R_k\) series is non-decreasing, and the smaller the k relative to \(\alpha \), the stronger the condition \(R_{k+1} \ge R_k\) to hold.
Note that the requirement of “ordinary” distribution means it is similar to many other distributions typically denser around the middle of \(\alpha \) while diminishing toward the two ends, but with no requirement as of a normal \(N(\mu , \sigma ^2\)), or \(\beta \) distribution, or other quasi-concave distribution in general. It even allows multimode and scattered distributions, as long as the extra mode does not appear in the right tail of the distribution. The above will become evident in the proof below.
The proof can be done through the basic \(H_k\) expression (3.17), the vector (3.24), or the matrix expression (3.40). However, by any expression, the proof of the above theorem could not be simple but intricate and lengthy. Hereunder we use the matrix expression to prove the theorem.
Proof
Notice that the preliminary case with only \(g_\alpha \) being nonzero is a special case of the ordinary \(g_i\) distribution, and we already know in that case \(R_k = 1\) for all ks. The proof is thus on the general situation and starts from (3.40):
where \(I_k\) is omitted since \(G_k\) is a matrix of a single row while \({{{\varTheta }}}_{k}\) a single column.
Similarly, \(H_{k+1} = G_{k+1} I_{k+1} {{{\varTheta }}}_{k+1} = G_{k+1}{{{\varTheta }}}_{k+1}\). On the other hand, from (3.36),
then,
A non-decreasing \(R_k\) means \(\nicefrac {\varDelta {R_k}}{\varDelta {k}} \ge 0\). Take the smallest \(\varDelta {k} = 1\), then the condition becomes \(\varDelta {R_k} \ge 0\), and notice:
Since the denominator \([(\alpha - k)G_{k}{{{\varTheta }}}_{k}]^2 > 0\), we can examine the numerator only, and note it as \(\delta {R_k}\):
The above looks good, but it is still difficult to prove whether \(\delta {R_k} \ge 0\). For instance, it is not straightforward to see whether \(G_{k+2}{{{\varTheta }}}_{k+2} G_k{{{\varTheta }}}_{k} - (G_{k+1}{{{\varTheta }}}_{k+1})^2\) is positive or not since the entries of each involved matrix are all variables and the dimensions of the matrixes are variables too. A feasible strategy to get around the problem is to simplify (3.51) with reasonable approximations, since we only need to know the sign of \(\delta {R_k}\) rather than its exact value. Let
where \(X_1 = G_{k+2}{{{\varTheta }}}_{k+2} G_k{{{\varTheta }}}_{k}, X_2 = (G_{k+1}{{{\varTheta }}}_{k+1})^2\), and \(X_3 = G_{k+1}{{{\varTheta }}}_{k+1}G_{k}{{{\varTheta }}}_{k}\).
In block expression,
where \({{{\varTheta }}}_{k}^\prime \) as stated before is the same \({{{\varTheta }}}_{k}\) without the first element 1 (note the initial element of \({{{\varTheta }}}_{k}, {{{\theta }}}_{k} = C_k^k = 1)\). Meanwhile, let \({{{\varTheta }}}_{k+2}^+\) be an extended \({{{\varTheta }}}_{k+2}\) with an added element 1 in the beginning, that is, \({{{\varTheta }}}_{k+2}^+ = \begin{bmatrix} 1 \\ {{{\varTheta }}}_{k+2} \end{bmatrix}.\)
Then, we look at \(X_3\) first:
which can be safely approximated to:
For \(X_1\), we reformulate it with an augmentation of \(G_{k+2}\) into \(G_{k+1}\) and \({{{\varTheta }}}_{k+2}\) into \({{{\varTheta }}}_{k+2}^+\), but keep the value of \(X_1\) unchanged:
When k is not large relative to \(\alpha \), \(g_{k+1}\) would be much smaller than the product of \(G_{k+1}{{{\varTheta }}}^{+}_{k+2}\) since the result of it is a sum of products of a series of \(g_i\)s and a series of \({{{\theta }}}_{k}\)s, such that \(g_{k+1}\) can be ignored. Another reason is that the discrepancy caused by the ignorance could be (partially or fully) compensated by the ignorance of the positive \(g_k\) in \((g_k + G_{k+1}{{{\varTheta }}}_{k}^{\prime })\) in both \(X_1\) (3.55) and \(X_3\) (3.53). That is, we can take (3.55) to be:
With the above, (3.52) is approximated as:
Our second strategy of the simplification is to reduce the number of \({{{\varTheta }}}\) matrixes by representing both \({{{\varTheta }}}_{k+2}^+\) and \({{{\varTheta }}}_{k}^{\prime }\) with \({{{\varTheta }}}_{k+1}\) only. To do so, we define:
where \(N_{k+1}\) is a diagonal matrix of dimension \((\alpha - k) * (\alpha - k)\), each of its main diagonal entries being the corresponding entry of the original single column matrix \({{{\varTheta }}}_{k+1}\), and \(B_{k+1}\) is a single column matrix of dimension \((\alpha - k) * 1,\) with every entry being 1.
Hereunder, for simplicity we use s and t to be the indices of all the matrix entries, where \(t = i - k\), and \(s = i - (k + 1) + 1 = i - k\), such that both s and t start from 1 in the following operations.
Now, let the single column matrix \({{{\varTheta }}}_{k+2}^+ = N_{k+1}D_{k+1}\), where \(D_{k+1}\) is a single column matrix of dimension \((\alpha - k) * 1\), with the first entry being \(d_1 = 1\) and the rest \(d_s = \nicefrac { (s - 1)}{(k + 2)} = \nicefrac {(i - k - 1)}{(k + 2)}, (i = k + 2, k + 3, \dots , \alpha )\), based on the relation \(C_i^{k + 2} = C_i^{k + 1} * \nicefrac {(i - k - 1)}{(k + 2)}\).
Similarly, let \({{{\varTheta }}}_{k}^{'} = N_{k+1}E_k\), where \(E_k\) is a single column matrix of dimension \((\alpha - k) * 1\) with each entry \(e_t = \nicefrac {(k + 1)}{t} = \nicefrac {(k + 1)}{(i - k)}, (i = k + 1, k + 2,\dots ,\alpha )\), based on the relation \(C_i^{k} = C_i^{k + 1} * \nicefrac {(k + 1)}{(i - k)})\).
Since \(C_i^{k + 1}\)presents the same in \(C_i^{k + 2}\) and \(C_i^{k}\) in the above two paragraphs, it thus can be omitted in later operations.
Notice that the result of \(G_{k+1}{{{\varTheta }}}_{k}\) is a scalar value, so is its transpose, \(G_{k+1}{{{\varTheta }}}_{k}^{'} = {{{{\varTheta }}}_{k}^{\prime \tau }}G_{k+1}^{\tau } = E_k^{\tau } N_{k+1}^{\tau }G_{k+1}^\tau \). Then, (3.56) becomes:
where
In the same way, from (3.54), take
where \(\tilde{E}_{k+1} = B_{k+1}E_k^{\tau }\) is a square matrix of \((\alpha - k) * (\alpha - k)\), each row of it being the replication of \(E_k^\tau \) , that is, \(\tilde{e}_{st} = e_t\). Similarly,
where \(\tilde{I}_{k+1}= B_{k+1}{B^{\tau }_{k+1}}\) is a square matrix of \((\alpha - k) * (\alpha - k)\), with every entry being 1 as a result of the matrix multiplication.
We now can further simplify the condition of \(\delta R_k\) in (3.51) into the following:
where
and,
That is, with the above manipulations we now reach a neat expression of the condition \(\delta R_k \) as:
Equation (3.66) represents a typical quadric equation \(q(\mathbf {x}) = XAX^{\tau } = \sum _s\sum _t{a_{st}x_sx_t}\) in matrix operation theory [38] where \(\mathbf {x}\) is an array of variables (\(x_i\)s), and A is a coefficient matrix. Here \(A = Q_{k+1}\), and \(\mathbf {x} = G_{k+1}\), such that \(x_1 = g_{k+1}, x_2 = g_{k+2}\), and \(x_s = g_{k+s}\) in general. Notice that every \(x_s\) is nonnegative in this case.
The proving of \(\delta R_k \ge 0\) is now equal to proving if \(q(\mathbf {x})\ge 0\). In matrix theory, for the above quadratic form, matrix A can always be manipulated into a symmetric matrix [39], and the proving of \(q(\mathbf {x}) \ge 0\) is equal to identifying whether A is semi-positive definitive. For this, a couple of methods, e.g., eigenvalue and principle minors approaches [38, 40], have been developed, but none of them is applicable to our case, simply because those approaches apply to the constant matrix A only. However, we are dealing with the problem applicable to any possible k and \(\alpha \). As such, each entry of \(Q_{k+1}\) in (3.66) is a function of the variable k, s and t and so are the dimensions of \(G_{k+1}\) and \( Q_{k+1}\). Nevertheless, we can still manage to prove \(\delta R_k \ge 0\) analytically as below.
From the above elaboration, the key issue to prove \(\delta R_k \ge 0\) is to prove the positivity of \( Q_{k+1}\), which in turn is to prove the positivity of \( M_{k+1}\). It is because \( N_{k+1}\) is a diagonal matrix with each diagonal entry \({{{\theta }}}_{ss}\) being positive; then, from (3.65), the positivity of \( Q_{k+1}\) is determined by the positivity of the matrix \( M_{k+1}\). We now trace back from (3.64):
Recall that \(D_{k+1}\) is a single column matrix of \((\alpha - k)\) rows, with \(d_1 = 1\) and the rest entry \(d_s = \nicefrac {(s - 1)}{(k + 2)}\). \(E_k^\tau \) is a single row matrix of \((\alpha - k)\) columns, with its general entry \(e_t = \nicefrac {(k + 1)}{ t}\). Then, their product \( Y_{k+1}\) is an \((\alpha - k) ) * (\alpha - k) \) square matrix. The general entry of \(Y_{k+1}\) is:
A primer feature of (3.67) is \(y_{rt} > y_{pt}\) if \(r > p\), except \(y_{1t}\), the first row of \(Y_{k+1}\) since \(d_1 = 1\). That is, the row \(y_{1t}\) is just the \(E_{k+1}\) itself:
Particularly, the first entry \(y_{11} = 1 * (k + 1) \ge 2\). In general, \(y_{1t} > y_{st}\) unless \(s > k + 2\), which means \(y_{rt}\) is more favorable than what is generally expressed in (3.67) to lead \(\delta {R_k} \ge 0\). As such, we can safely consider the general entry \(y_{st}\) as expressed in (3.67) only in the rest analysis.
Consequently, the matrix \(P_{k+1} = Y_{k+1} - \tilde{I}_{k+1}\) is also a square matrix of dimension \((\alpha - k)\), and its first entry being \(p_{11} \ge 1\), while the general entry being:
Similarly, \(M_{k+1} = (k + 1) (\alpha - k) P_{k+1} + (\alpha +1) \tilde{E}_{k+1}\) is again a square matrix of dimension \((\alpha - k)\), with its first entry being certainly positive. The general entry of \(M_{k+1}\) is:
where
Notice that, from (3.68), \(y_{st}\) can never be equal to 1, thus \(p_{st}\) and \(m_{st}\) can never be zero but only negative or positive. Since \((k + 1) / [(k + 2) t] > 0\), to see whether \(m_{st} \ge 0\) we only need to see the positivity of z.
Set \(z \ge 0\), we get:
which can be simplified as:
where \(a = (k + 1) / (k + 2)\), which is near to 1 when k is relatively large, and
\(b = [(\alpha +1) + (\alpha + 1)^2] / [(\alpha - k) (k + 2)] > 0\).
In analytic geometry, (3.71) represents a 3D (s, t, z) plane, while the strict equation of (3.73), i.e., \(t = a * s + b\), represents an intersection line AB between that plane and the plane \(z = 0\), as depicted in Fig. 2, where the number a is the slope of the line, and the angle \(\varphi \) is in the range of \(33^\circ< \varphi < 45^\circ \) since \(2/3 \le a < 1\). The number b is the intersect of the line AB with the axis Ot, and notice \(b > 0\), which means line AB can only be apart upwardly from the diagonal line \(t = s\) within the matrix area.
In our case, line AB in Fig. 2 means a boundary line such that all the matrix entries on the left side of the line are positive, while only those entries above the line (the dashed area of Fig. 2) are negative, which is inferable from (3.72). The balance of the aggregative positivity and negativity of the \(M_{st}\)s then determines the positivity of the \(\delta R_k\). We are now approaching the point to prove the theorem with the following observations.
Observation 1:
That is, \(M_{st}\) is increasing along the direction s in Fig. 2. It means that the matrix entries around the left bottom corner are the most positive.
Observation 2:
For the above, notice that the second term
\({2 (k + 1) (k + 2) (\alpha - k)t}\)
is a cubic of k, it is thus more dominant than other ones. Meanwhile, notice that “\(t > s\)” is the plane equation of the upper triangle in Fig. 2. As such, \(\nicefrac {\varDelta M_{st}}{\varDelta t} < 0\) holds, which can also be numerically verified, although we do not have to do so here to save space. As follows, \(M_{st}\) is decreasing with t increasing. It is the primary reason that the \(M_{st}\)s in the upright area above the line AB in Fig. 2 are negative as stated before, and the closer to the upright corner, the more negative of the \(M_{st}\)s.
Observation 3:
Now, look at the elements of the \(\delta R_k\):
where the \({{{\theta }}}_s\) (or \({{{\theta }}}_t\)) series is the lower section (from \( i = k + 1\)) of the s (or t) column of Pascal’s triangle (refer to Table 5 in subsection 3.9), \({{{\theta }}}_s\) (or \({{{\theta }}}_t\)) is then increasing with s (or t) increasing.
Observation 4:
The ordinary \(g_i\) distribution is dense in the middle section.
Now, if we use the \(M_{st}\) matrix as shown in Fig. 2 to represent the elemental positivity distribution of the \(\delta R_k\), from the above observations, we will see that the elements at the left bottom corner will be the most positive, then the middle part, while those in the rest area above line AB being negative.
Finally, notice that the boundary line AB is upper apart from the diagonal line, as shown in Fig. 2.
With all of the above observations, we can conclude that not only the area but also the degree of the positivity of the elemental \(\delta R_k\) distribution is dominant over that of the negativity. That is, aggregately \(\delta R_k \ge 0\) would generally hold in the case of an ordinary \(g_i\) distribution.
However, in the case of an unordinary \(g_i\) distribution, we need to consider two possible exceptions of the above general conclusion.
One is that, when \( k \rightarrow \alpha \), if some \(g_i\)(s) is (are) outstanding in the right tail, then ultimately \(\delta R_k < 0\) may happen. It is because, recall that the \(X_1\) Eq. (3.56) is an approximation of (3.55) when k is not close to \(\alpha \). When \( k \rightarrow \alpha \), we need to look at the original Eq. (3.55) \( X_1= [G_{k+1}{{{\varTheta }}}^{+}_{k+2} - g_{k+1}] (g_k + G_{k+1}){{{\varTheta }}}_{k}^{\prime }\) again. In this case, the dimension (\(\alpha - k)\) of the matrix becomes small with a large k, and so does the product of \(G_{k+1}{{{\varTheta }}}^{+}_{k+2}\). As such, a large \(g_{k+1}\) may lead \( X_1\) to become negative, and ultimately \(\delta R_k < 0\) may take place. We call this phenomenon an “island exception,” or “exception 1.”
The other case is, when k becomes small relative to \(\alpha \), so does the intercept b of line AB in Fig. 2. That means the line will shift leftwards, and the ratio of the positive area over negative one of the elemental \(\delta R_k\) distribution will decrease. If at this time one or more \(g_i\)s falling deeply in the left tail of the \(g_i\) distribution, then the positivity of the \(\delta R_k\) will be further undermined, and \(\delta R_k < 0 \) may happen. We call this a “cliff exception,” or “exception 2.”
However, the adverse effect of the cliff exception is much weaker than that of the island exception. It is because a smaller k means a larger dimension \((\alpha - k)\) of the matrix. Meanwhile, the angle \(\varphi \) in Fig. 2 will become smaller with a smaller k. Thirdly, the most positive \(M_{ st}\) area (the left bottom corner) remains unchanged. All of these aspects together mean it will be much harder to overthrow a positive \(\delta R_k\) into a negative one than that in the island exception.
At this point, one may ask, what effect would be if the two exceptions happen together? A brief answer is, since shorter tuples do not affect the \(R_k\)s of larger k as stated before, the cliff exception then does not reinforce the effect of the island exception. Similarly, the island exception will not increase but reduce the adverse effect of the cliff exception since more short patterns will be generated from more long tuples. Notice why \(R_k = 1\) holds in the preliminary case but \(R_k < 1\) in the other cases, simply because of the reduced number of long tuples.
Finally, we have two important notices from empirical studies (refer to Table 7 in Sect. 4). Firstly, the situation of \(\delta R_k < 0 \) is rear to happen even if either of the exceptions happens (if not too severely). Secondly, even if some case(s) of \(\delta R_k < 0 \) took place in an application, the quasi-concavity of the concerned \(H_k\) curve may still hold.
A conclusion is then: in an ordinary \(g_i\) distribution, \(\delta R_k \ge 0 \) will generally hold, and the smaller the k, the easier to maintain \(\delta R_k \ge 0 \) . Theorem 3.3 is now fully proved. \(\square \)
Example 2
For a better understanding, the following is a small example based on the running example to demonstrate the related operations and the degree of the discrepancy made by the approximation in the above proof. As given, \(\alpha = 6\), and take \(k = 3\) with other information as below:
\(G_k = \begin{pmatrix} 2&2&0&1\end{pmatrix}, G_{k+1} = \begin{pmatrix} 2&0&1\end{pmatrix}, G_{k+2} = \begin{pmatrix} 0&1\end{pmatrix}\),
\({{{\varTheta }}}_{k} = {\begin{pmatrix}1&4&10&20 \end{pmatrix}}^\tau , {{{\varTheta }}}_ k'= {\begin{pmatrix} 4&10&20 \end{pmatrix}}^\tau , \)
\({{{\varTheta }}}_{k+1} = \begin{pmatrix} 1&5&15 \end{pmatrix}^\tau , {{{\varTheta }}}_{k+2} = {\begin{pmatrix} 1&6\end{pmatrix}}^\tau \),
\({{{\varTheta }}}_{k+2}^+ = {\begin{pmatrix} 1&1&6 \end{pmatrix}}^\tau , \)
\(D_{k+1} = {\begin{pmatrix} 1&1/5&2/5 \end{pmatrix}}^\tau , E_k^\tau = \begin{pmatrix} 4&2&4/3 \end{pmatrix}\).
Then, by (3.51), the original formula:
By the approximated (3.57),
The above demonstrates that the approximation keeps the same sign of \(\delta {R_k}\), and the discrepancy between the precise and the approximated numerical values of \(\delta {R_k}\) is around 12% in this small dimension matrix example. More appreciably, the approximation significantly simplified the proof of Theorem 3. Due to space limitations, we can only leave the exercise of the operations to reach (3.66) \(\delta R_k = G_{k+1}Q_{k+1}G^T_{k+1}\), through (3.67)–(3.70) to the interested readers.
Example 3
Followed are a few illustrative examples (cases) to see the main points of theorem 3 and the relations between the \(g_i\) and the \(R_k\) distributions, as well as the quasi-concavity of the \(H_k\) curves, as shown in Table 4. Case a as the base case refers to the original data of Table 1, which results in an increasing \(R_k\) series and a quasi-concave \(H_k\) curve. Cases b to d demonstrate the minimum change of \(g_k\)(s) required to have a decreased \(R_k\) from the base case, where the bold numbers indicate the position k in column 2, the \(g_k\) in column 3, the \(R_k\) in column 4, and the apex of a concerned \(H_k\) curve in column 5. Column 2 and 3 demonstrate that the smaller the k, the more significant change of \(g_k\)s is required to get a decreased \(R_k\). Case b gives a typical example of the “cliff exception”.
Note that, since the \(H_k\)s are integers, the \(R_k\)s should be fractions, but for an easier comparison of the magnitudes of the \(R_k\)s, the decimals are used in the table.
The above examples demonstrate the resilience of the quasi-concavity of the \(H_k\) curve that minor decreasing \(R_k\)(s) may not alternate the concavity. The former four \(H_k\) series in Table 4 remain strict quasi-concave, despite the (sharp) changes of their \(g_i\) distributions and the decreasing \(R_k\)s.
Case e of Table 4 is purposely constructed to give an example of the “island exception” and a non-quasi-concavity \(H_k\) curve. However, from this case, we see how odd the underlying \(g_i\) distribution is and how persistently the decreasing \(R_k\)s hold such that the non-concavity of \(H_k\) could take place.
In real applications, if decreasing \(R_k\)s are observable occasionally, the non-quasi-concave \(H_k\) curve is seldom to see. Table 7 and “Appendix” of this paper presents empirical evidence in this regard, where a few out of hundreds of \(R_k\)s are decreasing, while all the concerned \(H_k\) curves maintain quasi-concavity.
The above indicates that the condition of monotonic \(R_k\) specified in Theorem 2 to have a quasi-concave \(H_k\) curve is stronger than required. A conclusion is that quasi-concavity is a typical property of the \(H_k\) curves.
After we have seen the quasi-concavity property, one may ask if a \(H_k\) curve can be (full) concave. The following part answers.
3.7 The full concavity interval of the \(H_k\) curve
Theorem 4
An \(H_k\) curve can be strictly concave downward within an interval \(E = [a, b]\), if the following condition holds:
where \(\alpha \) is the maximum length of all the data tuples, and the leftmost boundary of the interval can reach at \(a = 1\), while the rightmost boundary
For the proof, notice first the definition of the “concavity”: if a function f\((\mathbf {z})\) is concave over an interval E, then for any three points \(\mathbf {z_1}, \mathbf {z_2}, \mathbf {z_3}\) within E, such that \(\mathbf {z_2} = \lambda \mathbf {z_1} + (1- \lambda )\mathbf {z_3}\), where \(\lambda \in (0, 1)\), and \(\mathbf {z}\) can be a vector of multidimensional variables, then the following relation holds [37]:
Alternatively, set \(\lambda = \frac{1}{2}\), the above becomes [37]:
where \(\mathbf {z_2}\) is in the middle of \(\mathbf {z_1}\) and \(\mathbf {z_3}\): \(\mathbf {z_2} =\frac{1}{2}(\mathbf {z_1} + \mathbf {z_3})\).
Notice that the function f\((\mathbf {z})\) is “strict concave” if the above weak inequality functions change into strict inequality. This paper will mainly use the strict concave function, but the words “strict” may be dropped. On the other hand, we may add the word “full” to the concavity for readers to reflect the difference between it and the quasi-concavity. Intuitively, the full concave curve is rounder than a quasi-concave one within the same interval in their depictions. Following is the proof of the above theorem.
Proof
We use (3.78) and take any three consecutive points \(k, k+1\) and \(k+2\) of the domain of the \(H_k\) curve to check whether they satisfy (3.78). In this case, \(\lambda = \frac{1}{2}\) and \(k+1 = \frac{1}{2} (k + (k+3))\). Then, the related \(H_k\) values must satisfy: \(\frac{1}{2}(H_k + H_{k+2}) < H_{k+1}\). By (3.36), it means:
Manipulating the above and removing \(H_k\) since\(H_k > 0\), we get the condition for \(H_k\) concavity:
which is the necessary and sufficient condition (3.75) specified in the theorem. In other words, (3.75) is a specification of (3.78) in the case of \(H_k\) curve.
To get the solution of k in terms of \(\alpha \), we consider the preliminary case first, where\( R_k = R_{k+1} = 1\), and (3.75) becomes:
Solution (of k) from the above inequality is \(p< k < r\), where
Since p and r each must be an integer, the above should be precisely expressed as
where \(\lceil {(x)}\) means the ceiling of x, a minimum integer \(p \ge x\); \({(y)}\rfloor \) means the floor of y, a maximum integer \(r \le y\).
After we have specified the above, however, we will mainly use (3.80) and (3.81) in the following context for simplicity.
In the preliminary case, p is the left end of the concavity interval of the \(H_k\) curve, but r is not the ultimate right boundary yet, since, based on the above formulations, if \(k = r\) is a solution to (3.79), then \( k+1\) and \( k+2\) will be included in the concave interval as well. That is:
which is then the rightmost boundary of the full concave interval, as specified in (3.76) of Theorem 4.
It is easy to find out from (3.80) and (3.81), in the preliminary case the two boundaries, p and b, are symmetric against \(\alpha /2\) (the middle of the maximum tuple length), which is consistent with what introduced before that the preliminary \(H_k\) curve is symmetrical, and for \(\alpha \le 4\), the above solution covers the full range of the \(H_k\) curve. However, for \(\alpha > 4\) in the preliminary case, only the middle section of the \(H_k\) curve is full concave, while its right and left tails are quasi-concave only.
Now, in the general case where the uniformed data tuple length does no longer hold, and \(R_k < 1\) takes the role. An interesting question is then, whether the full concavity interval will increase or decrease in this case. To find out the precise answer directly from the problem (3.75) is impossible since there are three variables \(k, R_k, R_{k+1}\) within one function. Nevertheless, we can have a pretty good approximate solution for it as below.
Notice that, despite the monotonic property of \(R_k\), in general, \(R_{k+1}\) may only be slightly larger than \(R_k\), considering there is a series of \(R_k\)s in an application. We then take an approximation of \(R_{k+1} = R_k\), such that (3.75) becomes:
After manipulation, the above becomes:
The approach to solve the above is firstly to find the two roots of the corresponding equation of the above:
Let the two roots of the above be \( r_1\) and \(r_2\) in terms of k. Since \(0 \le R_k \le 1\), there will be the relation \(0< r_1< R_k < r_2 \le 1\) to satisfy (3.83).
Equation (3.84) is a typical quadratic function, and we can get its two roots as below:
where \(r_1\) and \(r_2\) represent the two concavity boundaries in terms of k. Our job is then to find out the satisfactory ks in terms of \(\alpha \).
The solution for (3.85) is every k, \( 0< k < \alpha - 1\) (recall again that \(R_k\) series ends at \( \alpha - 1)\). That is, the left boundary theoretically can be anywhere before the right boundary, which further implies that the left boundary can stretch leftmost such that \(a = k = 1\) as declared in the theorem in the most favorable case.
Now, for \(r_2\), after manipulating (3.86), we will get
\((\alpha - k) (2k - \alpha + 3)^2 - (k + 2) (\alpha + 1) \ge 0\).
It is complex to solve the above cubic function (of k), and the available method [41] could not reach a neat solution for it. Nevertheless, after hard work, the author finds that r expressed in (3.81) is also a solution to the above thus (3.86). It is not a coincident indeed, since, (3.86) implies \(R_k\) approaching 1, while (3.81) means it for \(R_k = 1\). It thus just rightly reflects the fact that (3.81) is a special case of (3.86).
Finally, in the same reason as that in the preliminary case, \( k+1\) and \(k+2\) need to be included in the concave interval in the general case as well, and the ultimate right boundary is again:
Notice that b expressed above is the rightmost boundary of the concavity interval in the general case since, as mentioned before and depicted in Fig. 1, the right tail of the \(H_k\) curve, in this case, could not be rounder than it in the preliminary case. Hereafter, we term [p, b] expressed in (3.80) and (3.82), respectively, as the “theoretical concavity interval” of the \(H_k\) curve.
As a summary, the concavity interval in the general case can be either smaller or larger than that in the preliminary case. What we do know now is that the left boundary of the concavity of the \(H_k\) curve can stretch to 1 in a case, while the right boundary of it cannot be beyond that in the preliminary case as given in (3.82), which is what stated in the theorem. On the other hand, since both the real p and b can be smaller than their respective theoretical value, a “left-shift” of the theoretical interval may happen in an application.
Theorem 4 is now fully proved. \(\square \)
Example 4
In Table 7 of Sect. 4, the exact \(H_k\) concave interval from each real application dataset is no smaller than its corresponding theoretical interval. The situation of the left-shifted intervals also shows there. The difference between the real and theoretical intervals leaves another interesting research point to see how the interval boundaries and their shifts are determined by the concerned \(R_k\) distribution and, ultimately, the underlying \(g_i\) distribution in an application.
The quasi- and full concavity properties are of fundamental importance in pattern frequency distribution theory, and this will become further clearer in the latter part of this paper. At this point, one may ask what the semantics of the concavity is, why the full concavity takes place on the left section of the \(H_k\) curve, and particularly why the left boundary a can stretch to 1, while the right boundary b cannot stretch rightwards further. The next subsection presents a brief explanation for these questions.
3.8 The semantics of and the reasons for the \(H_k\) concavity
Hereafter we will not distinguish the quasi- and full concavities unless required, since a full concavity implies quasi-concavity, though not vice versa.
From real-number theory, the area enclosed by a concave function and the horizontal axis is convex, which means there is no hole within that area and no kink or cave on the boundary of the area. That is, intuitively concavity implies the fullness.
Now, in the classic pattern mining with the full enumeration mode, the concavity property of the \(H_k\) curve reflects not just the fulness but more exactly the “excessiveness” phenomenon in this mode because this mode produces much more than realizable patterns and their frequencies from a given dataset. The higher and stricter concave the \(H_k\) curve is, the heavier the excessiveness. Theorem 4 reflects this and implies that the full concavity can hold only within the left section of the \(H_k\) curve in the general case. The reason for it is that that section corresponds to the short-length patterns. Such short patterns can be either the short-length tuples themselves or generated from longer tuples, but longer patterns could not be from the shorter ones. As such, the left section of the \(H_k\) curve is higher and rounder than the right section of it, as shown in Fig. 1.
In general, the full concave interval [p, b] as given in the proof of Theorem 4 is a small portion of the whole \(H_k\) curve in the preliminary case, and the larger the \(\alpha \), the smaller the relative portion becomes. It is because, from (3.80) and (3.82), \(\nicefrac {(b - p + 1) }{ \alpha } = \nicefrac {(( \alpha +2)^{\nicefrac {1}{2}} + 2)}{\alpha }\) decreases against \(\alpha \). For instance, \(\alpha = 100\), in the preliminary case, \( p = 44, b = 56\), and \(\nicefrac {(b - s + 1)}{\alpha } \approx 13\%\), a small portion. In the general case, the full concave interval could be increased to as large as [1, 56] since p can left stretch to 1 as specified in Theorem 3.4, and the percentage of the interval is now increased to \(\nicefrac {(56 - 1 + 1)}{\alpha } = 56\%\), a fivefold increase! A more concrete example can be given here with \(\alpha = 10\), and the \(g_i\) distribution = \(\{2, 3, 52, 10, 8, 6, 5, 3, 2, 3\}\). In this case, the related \(H_k\) curve gets its maximum concavity interval [1, 7] against [3, 7] in the preliminary case. However, notice importantly, the maximum full concave interval is only possible but not often to see, as the empirical examples shown in Table 7.
As we know, concave or quasi-concave functions are widely used in modern economics, operation research, and other related domains. The \(H_k\) concavity and its underlying theories explored in this section would have many applications in pattern mining, especially in the pattern frequency distribution under the reduced pattern generation mode, which shall be presented in Sect. 4. Before that, we look at some interesting “byproducts” from the \(H_k\) study, as seen below.
3.9 The extended conceptions from the \(H_k\) study
This part presents some conceptions out of but stemming from the \(H_k\) study. These include the \(H_k\) expression power as an aggregation of concave functions, the relation and comparisons of the \(H_k\) function with some previously established distribution functions, and a rethinking of some concepts in set theory and combinatorics.
3.9.1 The merits of the \(R_k\) and the expression power of the \(H_k\) function
The \(R_k\) created in this paper plays a critical role in the establishment of the \(H_k\) theory. On the one hand, \(R_k\) acts as a smooth converter that transforms a scatter \(g_i\) distribution into a quasi-concave \(H_k\) curve. On the other hand, \(R_k\) works as a powerful assembler of the different quasi-concave curves into a single \(H_k\) curve. It is because, as stated before, each single data tuple can form a preliminary quasi-concave \(H_k\) curve (of u = 1), then the \(H_k\) curve from a large dataset is an aggregation of those individual quasi-concave curves. In general, a summation of a set of quasi-concave curves is not necessarily quasi-concave, and how to organize such a set of quasi-concave curves into a single quasi-concave curve is an interesting topic in many applications [37]. \(R_k\) is thus a perfect solution in this regard, and it makes \(H_k\) a powerful expression of the superposition of the quasi-concave curves of different lengths.
3.9.2 The \(H_k\) and other combinatorics-based probability distribution functions
From many textbooks, we can see a couple of combinatorics-based probability distribution functions, e.g., the binomial distribution \(B(n, p): P(k) = C_n^k p^n (1 - p)^n\) [42], where p is a probability and \(C_n^k\)s \((k = 0, 1, \dots , n)\) are called binomial coefficients; the Poisson distribution \(P(\lambda )\) \(= \frac{\lambda ^k}{k!}e^{-\lambda }\) [43], and the like. There have been many studies of these distributions and their relationships. For instance, when p is small thus not close to \(\frac{1}{2}\) \((e.g., p < 5\%)\) while n is large, the B(n, p) distribution can be approximated as a Poisson distribution with parameter \(\lambda = np\) [44, 45]. What we would notice here is, these distribution functions are all quasi-concave, and each can be approximated as a normal distribution \(N(e, \sigma ^2)\) [46] when n or \(\lambda \) is large. For example, if p is not far apart from \(\frac{1}{2}\), the B(n, p) distribution can be approximated as a normal distribution \(N(np, (np(1 - p)^{\nicefrac {1}{2}})\) [42].
In comparison, as stated before, divided by the accumulative frequency \(w_0\), the \(H_k\) curve becomes a probability distribution function, noted as \(p(\varPhi _k) = \nicefrac {H_k}{w_0}\) (where \(\varPhi _k\) is a collection of patterns of the same length k, refer to Definition 1). Then, \(p(\varPhi _k)\) will be quasi-concave and with its apex value near the middle of \(\alpha \). Now, let us look into the problem deeper. Since each tuple (of length \( m > 1\)) of a dataset corresponds to a simple preliminary \(H_k\) frequency distribution \(\{C_m^k\}\), if we multiply each term by \(p^m(1 - p)^m\), we then get a binomial distribution, noted as \(H(m) = B(m, p) = C_m^k p^m (1 - p)^m\), from each tuple. However, from the previous part of this section, we could not conclude that the aggregation of the H(m)s over an entire dataset of \( u > 1\) would be a normal distribution, simply because of nonsymmetric of the \(H_k\) curve in a general case. On the other hand, with the selective pattern generation mode, the result \(p(\varPhi ^s_k)\) distribution will ultimately converge to a normal distribution when the dataset is large. It will be formally proved in the next section.
3.9.3 Some humble rethinking on the concept of the empty set in set theory
Set theory by now is widely viewed as fundamental for mathematics [47], yet disagreements or objections of this view are also noticeable in the literature [48,49,50,51]. Particularly, questions and critiques on the concept of the empty set have been raised from philosophers [52], first-order logic and free logic experts [53]. If those critiques are mostly theoretical, what we will discuss hereunder would be a little bit more specific and originating from pattern mining practice. The problem starts from the proposition that the empty set \(\varnothing \) be a subset of any nonempty set S, that is,
as generally presented in textbooks today.
There have been some proofs of the above statement [53], but those proofs are controversial. To save space, here we look at only one typical proof as quoted below [53, 54]:
The proof is by contradiction and starts with the definition that if all elements of set B are in set A, then B is a subset of A [47]. Now, let B be the empty set \(\varnothing \). If \(\varnothing \) is not a subset of A, then it means there is some element in \(\varnothing \) that is not in A. But \(\varnothing \) has no elements and hence a contradiction. The proof is then done.
The above proof looks strong at first glance, but with deeper insight, we will see that the proof has a serious flaw of an incomplete list of the “not” aspects. Based on De Morgan’s law: not (X and Y) = not(X) or not(Y) [55], the full negation of the statement “all elements of B are in A” must be:
“No element of B is in A (case 1),” or,
“some element of B is not in A (case 2).”
Only with the above two cases together, could the whole universe in question be maintained, where case 1 applies to the empty set and those nonempty sets exclusive to A, while case 2 implies other nonempty sets but unexclusive to A. However, the above proof picks up case 2 only but neglects case 1.
Indeed, there are more profound reasons to disprove \(\varnothing \subseteq S\). Firstly, the establishment of the set theory does not involve fuzziness. As such, by the formal concept theory [56], any concept should have its clear intension and extension to distinguish from other concepts. Then, \(\varnothing \subseteq S\) certainly violates this requirement. It is because the empty and nonempty sets are a pair of opposite concepts and equal counterparts. They thus ought to be mutually exclusive instead. We can but do not give more theoretical proofs to support the above argument to save space. Another reason is that the uprightness of a concept or theory should also be justified with the outcomes of its applications. Following are examples of the side effects of the extension or applications of the relation \(\varnothing \subseteq S\).
The first is in the permutation theory, where \(\varnothing \) is taken to be a legal output in any permutation problem due to \(\varnothing \subseteq S\), and
which is forcefully defined in addition to the principal definition of factorial. We do not have to discuss the reasons for the above definition as given in the literature [57], but only notice that
which is a natural result of the principal factorial definition.
From the above two, an immediate conclusion is that \(0 = 1\), but interestingly, people accept and maintain the collision between 0! = 1 and 1! = 1 for so long!
What follows is in combinatorics, the empty set is again taken to be a legal output in any combinatoric problem. Since 0! is defined, and so is \(C_n^0\) (\(C_n^0 = \frac{n!}{ 0! (n - 0)!} \) \(= 1\)). However, semantically \(C_n^0 = 1\) is controversial since it means there is a nonzero number of combinations of no element selected, but a combination of no element means no combination!
Now, it gets into our topic on pattern mining, where each tuple of a classic dataset represents a set of elements, thus each tuple includes the empty set \(\varnothing \) based on (3.87), and conventional mining approaches generally take \(\varnothing \) as a pattern. Especially, \(\varnothing \) is eternally a generator in the generator mining approach [26] since \(\varnothing \) is the most frequent pattern, where \(F(\varnothing )\) equals u, the cardinality of any classic dataset. However, such the most frequent pattern is valueless and helps nothing in any serious mining but wastes computation cost and memory space. There are several reasons to prove so, but for space limitations, we give only one as below:
Notice that the empty set exists vacuously only [47]. That is, \(\varnothing \) is imaginable only but not physically observable. In this sense, \(F(\varnothing ) = u\) means that we had observed an unobservable thing for u times, such a self-contradiction! Lastly, could we have \(\varnothing \) as a pattern from the entire dataset instead of each tuple? The answer is still firmly no. Among other issues, by the nature of pattern mining, every result pattern must have its specified frequency (or frequentness), but as just analyzed, \(F(\varnothing )\) is not properly specifiable.
Readers would have seen now from the above that there is such a strong reason and logic that we could not take the empty set as a pattern and that we can only leave \(F(\varnothing )\) being undefined, as stated at the beginning of this paper (refer to Sect. 2.2). In turn, the above disproves the general applicability of \(\varnothing \subseteq S\) (3.87).
As we know, the modern set theory is developed from the Zermelo set theory [58], but from the above practical observations and those mentioned critiques presented in previous literature, we need to admit that the development has not reached its full soundness stage. As such, the solution for the issue of \(\varnothing \subseteq S\) will be meaningful in the further perfection of the set theory. The solution is indeed already manifested in the above analysis: replace \(\varnothing \subseteq S\) (3.87) with the following:
where S is a nonempty set.
In accordance, we need to leave the factorial 0! being undefined, simply because the empty set is not permutable, thus quantifying the permutation is meaningless. Indeed, if we could accept \(\frac{1}{0}\) being undefined, why could not take 0! being undefined? With this solution, the problem of \(0 = 1\) will then be automatically eliminated. The resolution of the \(C_n^0\) problem is to be seen in the next subsection. For other possible problems caused by the obsoletion of 0! = 1 and \(\varnothing \subseteq S\), we believe that the respective domain experts will find solutions for them.
3.9.4 Some findings in combinatorics
(1) The U-sum sequence and the redefinition of \(C_n^o\)
It is an interesting and commonly discussed topic in mathematical analysis and calculus about the convergence of real number sequences, for instance,
where \(x_k\) is a nonnegative real number. In general, if \(x_k \ge 1\), e.g., \(S = 1 - 1 + 1 - \dots \), the sequence is divergent since it is not a Cauchy sequence and thus does not satisfy the known Cauchy criterion.Footnote 1
However, in the course of pattern mining study of this paper, a special sequence that disregards that criterion but converges has been discovered, as defined below:
That is, the U-\(sum(C_n^k)\) is a sum of the consecutive but alternatively signed binomial coefficients except \(C_n^0\) and starting with positive \(C^1_n\). The property of the above U-sum is given below:
Theorem 5
As given, the U-sum sequence is not only convergent but also of a fixed sum of value 1, irrespective of the magnitude of the natural number n. That is:
Proof
The proof of the above theorem is simple. From (3.11): \(\sum _{k = 1}^{k = n} (-1)^{k-1}H_k = u\), where u is the cardinality of a classic dataset, and \(H_k = \sum C_n^k \). Now, suppose a dataset of only one tuple of n elements, then \(H_k = C_n^k\), and \(u = 1\). As such, \(\sum _{k = 1}^{k = n} (-1)^{k-1}C_n^k = 1\), and the theorem is proved.
Alternatively, we can prove (3.91) through the binominal formula \((a + b)^n = \sum ^n_{k = 0}C^k_n a^{n - k}b^k\). Now, set \(a = 1\) and \(b = -1\), we get \(\sum ^n_{k = 0}(-1)^kC^k_n = 0\), or \(\sum ^n_{k = 1}(-1)^{k-1}C^k_n = 1\). \(\square \)
Extendedly, we note \(U{-}sum(H_k) = u\) for an entire dataset of cardinality u as stated above.
The interestingness of the U-sum sequence defined above is not only in its exception to the Cauchy criterion but also in solving the problem of \(C_n^0 \) addressed in the previous part by defining:
With the above approach, the definition of \(C_n^0 \) is no longer based on that of \(0! =1\). The new definition is justifiable with the following. Firstly, the reason to separate \(C_n^0 \) from the sequence of other \(C_n^k \)s is that the superscript “0” of \(C_n^0 \) is not a natural number while other ks are. Furthermore, the number “0” does not have to mean “nothing” in many cases but a reference value of something. \(C_n^0 \) thus does not have to refer to the empty set any longer. Lastly, the semantics of (3.92) can interestingly reflect a philosophy that, in a colorful world, when all colors come together, the world becomes white if we took (3.92) as a light wave equation.
As such, there is no aftermath with the proposed obsoletion of the assertion \(\varnothing \subseteq S\) and the definition of \(0! =1\), especially if 0! =1 does not have many other applications except for \(C_n^0\) and \(C_n^n\). At the same time, the numerical value of \(C_n^0\) does not change, such that we can still keep the legacy of previous literature in the use of \(C_n^0\).
The only notice here is that, with the obsoletion of 0! = 1, we take the general formula for \(C_n^k \) as
such that the formula for \(C_n^n \) does not have to involve with 0! as well.
Meanwhile, in comparison, we call the arithmetic sum of the same binomial coefficient sequence (excluding \(C_n^0 \)) as the “A-sum,” and we know that
(2) A Naïve approach to build Pascal’s triangle
The tabular approach presented in Sect. 3.3.3 is efficient not merely in calculating the \(H_k\)s and the accumulative frequency \(w_0\) but also in building Pascal’s triangle.
Table 5 is an example of Pascal’s triangle, and we refer the triangle formed by the boldface numbers as the “W triangle” (matrix) after the removal of the first row and first column of the Pascal triangle. Interestingly, the “enumeration triangle” \(\varLambda \), as seen in Table 3, is indeed a product of the transpose of W and the \(g_i\) distribution. More formally:
where W is an \(\alpha * \alpha \) triangle matrix as shown in Table 5, while G is an \(\alpha * \alpha \) diagonal matrix with the main diagonal elements being the \(g_i\) numbers and the rest being 0s:
\(G = \begin{bmatrix} g_1 &{} 0 &{} \dots &{} 0 \\ 0 &{} g_2 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} g_\alpha \end{bmatrix}.\)
To see the above clearer, we transpose Table 3 and form an extend \(H_k\) Table 6. In this table, the first row (except the newly added \(U{-}sum\) and \(A{-}sum\) cells) holds the ks (from 1 to \(\alpha \)), which also represents the \({{{\varTheta }}}_{1}\) series as in Table 3. The row (U) is the row 0 of the Pascal triangle and thus contains the only number (1), while the first column of Table 6 under (U) being the \(g_i\) distribution. The boldface numbers are those from the transposed \(\varLambda \). Compared with the W triangle in Table 5, we see that each row i of \(\varLambda ^\tau \) in Table 6 is the same row of W times \( g_i\), and the sum of each row is an application of (3.15): \(F_i = g_i\sum _{j = 1}^{j = i}C_i^j\). That is why collectively \(\varLambda ^\tau \) is the product of G and W as specified in (3.93). Meanwhile, notice that the \(A{-}sum\) column holds exactly the \(F_i\)s.
Now, in a special case with every element of \(g_i\)s being 1, the matrix G becomes the identity matrix, and the \(\varLambda ^\tau \) becomes W:
\(\varLambda ^\tau = IW = W\).
It is then simple to build up Pascal’s triangle. Take Table 6 as an example and follow the following steps: set the table size as \((\alpha + 3) * ( \alpha + 3)\), initiate the first row from column 3 to \((\alpha - 1)\) with \( ( 1, \dots , \alpha )\), the first column from row 3 to \( (\alpha - 1)\) with all 1s, and the same for column 3. Then, follow the procedure to build \(\varLambda ^\tau \) as described in 3.3.3 (with an only change of the rows into columns and vice versa in computer programming), we then get Pascal’s triangle.
Additionally, notice that the \(U{-}sum\) and \(A{-}sum\) columns included in Table 6 can be used for parity checks of the W triangle to ensure the correctness of the construction of the table.
The above approach is naïve and also efficient, compared with the conventional approach [62].
On the other hand, (3.93) means, if a Pascal triangle of size \((\alpha + 1)\) is available, then the corresponding W triangle can be used to build the \(\varLambda \) triangle to fulfill the same job, i.e., to compute the \(H_k\)s as done by Table 3. However, this is only theoretically fine. In practice, this way may not be more efficient than the original approach to build Table 3 directly. It is because, for an arbitrarily given \(\alpha \), the needed Pascal’s triangle may not be readily available, and even if it be, we need a function call to link or to copy the entire W triangle in a program and then multiply it by the matrix G. The whole process thus may not be cheaper than the original approach presented in 3.3.3.
After the above presentation of the extended fruitage of the \(H_k\) study, we now turn back to the study of the pattern frequency distributions with the reduced pattern generation mode in the next section.
4 The reduced pattern frequency distributions
The previous section has introduced a set of interesting properties governing raw pattern frequency distributions under the full enumeration mode. This mode produces all “possible” patterns, many of which could not be realizable and thus “redundant.” We have also known that the effective remedy to the problem is the selective pattern generation mode. However, no approach is ready to render that mode. A critical reason is that we do not know what and how many redundant patterns to remove in an application.
Yet, with the study presented in the previous section, we know precisely about the sub-cumulative frequency \(H_k\) of each collection. We also see that a redundant pattern means to bring up superfluous frequencies. That implies we can reduce the patterns’ frequencies first, by which some patterns may become abolished when their frequencies being reduced to zero. Meanwhile, we know from the previous study [23] about the biased frequentness of shorter patterns due to their adding up frequencies of their supper (hence longer) patterns. That further enlightens us to adjust first the frequencies of shorter patterns by that of longer ones, as described below.
4.1 The initial adjusted \(H_k, h_k\)
Definition 3
The “initial adjusted collection frequency” (of all patterns of length k) is:
starting from \(h_\alpha = H_\alpha \), and (4.1) can be further simplified as:
Notice that \(h_\alpha = H_\alpha \) is a natural boundary condition since \( H_{\alpha + 1}\) does not exist,
To be a measure of frequency, \(h_k\) must be nonnegative. Indeed, the following theorem guarantees it:
Theorem 6
If the underlying \(H_k\) curve is strictly quasi-concave, then \(h_k\) defined in (4.1, or 4.2) is always positive.
Note in the previous section, we have proved that in general \(H_k\) curve is strictly quasi-concave, and abnormal cases scarcely happen thus being ignored hereafter. Following we prove the above theorem by induction.
Proof
Since \(H_k\) is strictly quasi-concave, we examine the problem in two intervals, [1, q] and \((q, \alpha ]\), respectively, where q is the maximum point of \(H_k\), and \(\alpha \) is the longest pattern (tuple) length.
For \(k \in [1, q]\), take the initial case \(k = 1\), we see the right-hand side of (4.1) is exactly the right-hand side of (3.11) itself, thus
It means the theorem holds at \(k = 1\) since \( h_1 > 0\).
At k = 2 and by (4.2),
which is because that at least one tuple length \(|T_j| > 1\), \((j \in [1, u])\), such that \(H_1 = \sum _i |T_i| > u\). Otherwise, there is no pattern generation, and no problem to solve.
Now, suppose the theorem holds at \(k = t \) \((1< t < q)\), such that \(h_t > 0\), we check if \(h_{t+1} > 0\) would still hold.
Since the theorem holds at \(k = t\), it thus holds at \(k = t - 1\) as well, that is, \(h_{t-1} > 0\). Notice also that \(H_t - H_{t-1} > 0\) for \(t \in [1, q]\) (because of the \(H_k\) concavity as given). Then, by (4.2), it means:
and the theorem is proved for \(k \in [1, q]\).
For \(k \in (q, \alpha ]\), we start at \(k = \alpha \) as the initial case and prove the theorem in a reverse direction. Notice at \(k = \alpha \), the theorem holds, since \(h_a = H_a\) as given.
At \(k = \alpha -1\), the theorem also holds, since, by (3.37),
then:
which results from \(\alpha > 1, 0 < R_{\alpha -1} \le 1\), and \(H_\alpha > 0\).
Now, suppose the theorem hold at \(k = t\) \( (q< t < \alpha )\), such that \( h_t > 0\), we check if \(h_{t-1} > 0\) would still hold.
Since the theorem holds at \(k = t\), it thus holds at \(k = t + 1\) as well, that is, \(h_{t+1} > 0\); notice that \(H_{t-1} - H_t > 0\) for \(t \in (q, \alpha ]\). Then, by (4.2), it means:
That is, the theorem holds for \(k \in (q, \alpha ]\) as well, and the theorem is fully proved. \(\square \)
Theorem 4.1 qualifies the \(h_k\) to be a frequency function with the required positivity. \(h_k\) also fulfills the primer objective of the overall pattern frequency reduction, particularly of the shorter patterns, as indicated in (4.2). It thus mitigates the overfitting problem. Ideally, we would expect \(h_k\) to further get around the drawbacks of the full enumeration mode with the following merits.
-
(a)
On average, the adjustment shall be relatively evenly distributed over different collectives to avoid bias as much as possible, such that the collectives of larger number of raw frequencies ( \(H_k\)s) would be adjusted more than those of fewer frequencies.
-
(b)
Avoid over-adjustment. Mathematically, it means the \(h_k\) curve should maintain the quasi-concavity property.
We will see if the above properties would be realized from the analysis presented in the following subsections.
4.2 The \(h_k\) curve and its quasi-concavity
Similar to the \(H_k\) curve, by connecting all of the \(h_k\) values together, we get an \(h_k\) curve as shown in Fig. 1. This curve is also quasi-concave, as specified in the following theorem:
Theorem 7
(\(h_k\) quasi-concavity theorem) If \(\sum _i|T_i| > 2u\), and if the corresponding \(H_k\) curve is strictly quasi-concave with its apex value at q, then the \(h_k\) curve will also be quasi-concave with its apex value at \(k = q'\), where \(q' = q\) or \(q+1\), and \(|T_i|\) is the length of tuple i.
Note the condition of \(\sum _i|T_i| > 2u\), or equally average \(|T_i| > 2\), is symbolic only since any practical mining problem would satisfy it. Another implication of this condition is the maximum tuple length \(\alpha = max(|T_i|) \ge 3\).
Proof
We look at the following relations first:
On the other hand, we have:
Now, for \(k \in [1, q]\), based on Theorem 2, \(H_k - H_{k-1}> 0\), (4.8) and (4.9) are consistent, and we get:
\(h_{k+2} > h_k\) (from (4.8)), (Case I)
and, \(h_{k+1} > h_{k-1}\) (from (4.9)). (Case II)
Furthermore, refer to (4.4), and notice \(H_1 = \sum _i|T_i| > 2u\) as given, we have:
\(h_2 = H_1 - h_1> 2u - u > u\). That is
Since k can be any number within [1, q], to have (4.10) and both cases I and II to be applicable to every k within this interval, the only way is:
Now, for \(k \in (q, \alpha ]\), (4.8) and (4.9) remain the same but notice \(H_{k+1} - H_k < 0\), the sign of Case I and II should then be reversed. By shifting back k by 1 from the two cases such that k could start from q + 1, we get:
\(h_{k+1} < h_{k-1}\), (Case I’)
and, \(h_{k} < h_{k-2}\). (Case II’)
Refer to (4.6): \(h_{\alpha -1} = H_{\alpha -1} - h_\alpha = (\frac{\alpha }{ R_{\alpha -1}} - 1) H_{\alpha }\), and notice \(H_\alpha = h_\alpha \), \(\alpha \ge 3\), and \(0 < R_{\alpha -1} \le 1\), then:
That is, within \((q, \alpha ]\), for every k to maintain (4.12) and the cases I’ and II’ together, the only way is:
Now, we note the apex point of the \(h_{k}\) curve as \({q'}\) and see its relation with q. On the left side of q, we know from (4.11), \(h_q > h_{q-1}\), which, however, is not applicable to (4,13). We then need to look into the two basic formulas (4.8) and (4.9) again.
From (4.8), \(h_{q+2} < h_{q}\), and from (4.9),
Then, there are three situations: \(h_{q-1}< h_q < h_{q + 1}\), hence \(q' = q + 1\); or \(h_q > h_{q+1}\), then \(q' = q\); or \(h_q = h_{q+1}\), then \(q'\) takes both q and \(q + 1\). Notice even if \(h_q = h_{q+1}\), it does not affect the quasi-concavity property since no other integer exists between q and \(q + 1\).
We can now conclude that, \(h_k\) curve reaches its apex value at \(q'\), and it is strictly increasing within \([1, q']\) (based on (4.11)) and strictly decreasing within \([q', \alpha ]\) (based on (4.13)), \(h_k\) curve is thus quasi-concave, and the theorem is fully proved. \(\square \)
Example 5
From the real application datasets as shown in Table 7, there is a case of \(q'\) at both q and \(q + 1\), a case of \(q' = q + 1\), and the rest cases of \(q' = q\).
4.3 The derived \(h_k\) reduction properties
From the above theorem and its proof, we can get further implications as follows:
The calculus function of \(h_k\)
From Eq. (4.8):
\((h_{k+1} - h_{k}) + (h_{k+2} - h_{k+1}) = H_{k+1} - H_k\),
or, \( \varDelta h_k + \varDelta {h_{k+1}} = \varDelta H_k\),
or, \( \varDelta {h_k }/ \varDelta H_k + \varDelta h_{k+1} / \varDelta H_k = 1\), which is taken to be the calculus function of \(h_k\) over \(H_k\).
Corollary 5
(The reverse theorem of Theorem 7) If an \(h_k\) curve is quasi-concave, so must be the underlying \(H_k\) curve.
The above can be easily inferred from Theorem 7 and its proof: if the concerned \(H_k\) curve is not quasi-concave, then the quasi-concavity of the \(h_k\) curve is not guaranteed.
Corollary 6
If an \(H_k\) curve gets its apex value at k = 1, then the related \(h_k\) curve will definitely reach its apex value at \( k = 2\).
This is obvious, since \(h_2 > h_1\) is always true (refer to (4.10)) and \(q' = q + 1\) applies.
Corollary 7
The difference function \(\tilde{h}_k\) between the\(H_k\) and \(h_k\) curves is also quasi-concave.
In general, a difference of two quasi-concave functions may not necessarily be quasi-concave. This corollary then represents a special “quasi-concavity invariant” property of the difference function between the \(H_k\) and the \(h_k\) curves. Indeed, the proof of this corollary is rather straightforward: the difference function is the shifted \(h_k\) curve itself since from (4.2):
Since \(h_k\) represents the patterns frequencies after a reduction of the number of redundant patterns and frequencies, hereafter, we call the \(h_k\) curve the “partial retainable (frequency) curve,” while the difference \(\tilde{h}_k\) curve the “partial removable curve.”
Corollary 8
The adjustments correct and redistribute the frequencies from shorter patterns toward longer ones, such that:
Proof
Since \(h_k = H_k - h_{k+1}\), or \(H_k = h_k + h_{k+1}\), and with the \(h_k\) quasi-concavity, \(h_k < h_{k+1}\) for \(k \in [1, q')\), they then together prove \(H_k > 2h_k\), or \(h_k < \frac{1}{2}H_k\) (4.16). Similarly we can prove (4.17). And (4.18) is a natural consequence of the former two. \(\square \)
In addition to the above corollary and its proof, the general relation \(h_{q+1} > h_{q-1}\) (4.14) and the possible apex shift from q to \(q' = q + 1\) are other signals of the redistribution and a characteristic of the \(h_k\) curve.
Corollary 9
(The “law of half”) The sum of \(h_k\)s is around half of that of \(H_k\)s.
Proof
This corollary is an extension of the previous one and gives us an overall awareness of the \(h_k\) reductions, while the formal proof comes below.
\(h_1 = H_1 - h_2\)
\(h_2 = H_2 - h_3\)
...
\(h_{\alpha -1} = H_{\alpha -1} - h_{\alpha }\)
\(h_a = H_a \)
and, \(- u = - h_1\) (refer to (4.3))
Summarize the above equations together, we get:
Set the “adjusted accumulative frequency” as \(w_1\), and notice that \(\sum _{k = 1}^{\alpha }H_k = w_0\) (the raw accumulative frequency). Then from (4.19), we get:
which is a coincidence with (3.35), i.e., \(w_1= H_{ odd}\).
Equation (4.20) tells that about a half of the raw frequencies will be reduced from \(H_k\) to \(h_k\) regime since normally \( u \ll w_0 \) in real applications. We thus call it a “law of half.” This law will become precise in terms of a “net” account of the generated frequencies to be seen in Sect. 4.5. \(\square \)
The above law then enables the predetermination of the adjusted accumulative frequency. It is what that many approaches pursue, but no significant finding has been reported to the author’s knowledge.
In summary, Theorem 7 and the above properties formally describe the \(h_k\) adjustment functionality as expected at the end of Sect. 4.1. Firstly, \(h_k\) does reduce the patterns’ frequencies substantially. Figure 1 presents an intuitive understanding, where the \(h_k\) curve is entirely underneath the \(H_k\) curve, while the “law of half” gives more precise information about the reduction. Since every increment of frequency comes from a pattern generation, the law also means the number of pattern generations will be reduced by half. Accordingly, the number of patterns would be reduceable proportionally to the frequencies reduced. It is thus another important implication from the reduction model. On the other hand, the law of half and the \(h_k\) quasi-concavity theorem indicate no over-reduction since, by the selective generation mode, the accumulative pattern frequency will be far less than half of \(w_o\). We will see this in Example 9 later. Thirdly, the model realizes a remedy of the biased frequency distribution toward the short patterns under the full enumeration mode, as described by Corollary 8. Meanwhile, the remedy is not an overkill but relatively evenly distributed over different collectives, as seen from formulae (4.16) through to (4.18), the larger the \(H_k\), the larger the adjustment.
4.4 The full concavity interval of the \(h_k\) curve
Similar to the \(H_k\) curve, after we have proved the \(h_k\) quasi-concavity and other accompanied properties, we have the \(h_k\) full concavity property as well.
Theorem 8
If an \(H_k\) curve is full concave downward over an interval \(E = [a, b]\) and \(|[a, b]|> 3\), then the corresponding \(h_k\) curve would also be full concave over the interval \(E_1 = [a_1, b_1]\), subject to the only condition of:
for every k within interval \(E_1 = [a_1, b_1]\), where E and \(E_1\) are comparable, while the degree of \(h_k\) concavity will be reduced from that of the \(H_k\) concavity.
Proof
According to the definition of full concavity (under Theorem 4 and formula (3.78), if an \(h_k\) distribution curve is full concave over an interval \(E_1\), then for any three consecutive integers \((k-1, k, k+1) \in E_1\), the following relation must hold:
The above can be expressed as:
Our task is then to prove how (4.22) could hold over the interval \([a_1, b_1]\) stated in the theorem. Because of the full concavity of \( H_k\) curve as given in the theorem, there exists: \(H_k - \frac{1}{2}(H_{k-1} + H_{k+1}) > 0\). We then define:
From the definition of \(h_k\), we know \(H_k = h_k + h_{k+1}\), then (4.23) becomes:
where
From the above, we see that \(X_{k+1}\) is a forwardly shifted \(X_k\). Then, \(X_k > 0\) represents the general condition of the \(h_k\) concavity. For \(X_k > 0\), it means the following:
which is the condition (4.21) stated in the theorem for the \(h_k\) concavity.
Back to (4.24), \(A = X_k + X_{k+1} > 0\), which means once \(A > 0\) holds, then either \(X_k\) or \(X_{k+1}\) or both would be positive. However, notice that \(X_{k+1}\) is easier than \(X_{k}\) to be positive. It is based on what is implied in Corollary 8 and as shown in Fig. 1 that the \(h_k\) curve is a bit right-skewed compared with the concerned \(H_k\) curve. Consequently, once \(X_{k} > 0\) holds, so does \(X_{k+1} > 0\), then \(X_{k+2} > 0\), and so on, as long as the ks are within the interval E.
Now, for the comparisons of the boundaries between the two intervals E and \(E_1\).
With \(A = X_k + X_{k+1} > 0\), and \(|[a, b]|> 3\) as given, it means the \(H_k\) concavity starts from \(k = a\) through to at least \(k + 3\). And from the above analysis, for \(A > 0\), \(X_{k+1} = X_{a+1}> 0\) must be true, while \(X_{a} > 0\) is not ensured. That is, \(a_1\) may or may not be as small as a, i.e., \(a_1 \ge a\). For the right boundary \(b_1\), notice that from (4.23) \(A > 0\) covers \(k + 1\), while from (4.25) \(X_{k+1} > 0\) covers \(k + 2\), then it is safe to note \(b_1 \ge b\).
The above means that the \(h_k\) and \(H_k\) curves would have comparable full concavity intervals. On the other hand, notice that the height of the \(h_k\) curve is lower down from that of the \(H_k\) curve, as visibly shown in Fig. 1, it means that the degree of the \(h_k\) concavity is lower down from the \(H_k\) concavity. Theorem 8 is now fully proved. \(\square \)
Notice that the condition \(|[a, b]|> 3\) is symbolical only since any serious mining application will satisfy it, which then manifests the general applicability of the above theorem. Meanwhile, the lower-down of the \(h_k\) concavity is rightly a reflection of the reduction of the “excessiveness” of the pattern generations from the full enumeration to the reduced mode.
Example 6
For an illustration, we continue the example presented in Sect. 3.8, with \(\alpha = 10\), and the \(g_i\) distribution = {2, 3, 52, 10, 8, 6, 5, 3, 2, 3}, the maximum \(H_k\) concavity interval is [1, 7]. Here we can find that the corresponding \(h_k\) curve maintains this concavity interval without a change. Table 7 (Sect. 4.6) gives some empirical examples of comparisons of the intervals E and \(E_1\), as well as their boundaries.
The next subsection reveals why the \(h_k\) curve exhibits similar concavity and quasi-concavity features as the \(H_k\) curve.
4.5 The combinatoric equivalence of the \(h_k\) function
With the above \(h_k\) properties presented, an interesting question would be whether \(h_k\) could be expressed with similar combinatorics formula as that for \(H_k\). The following theorem answers:
Theorem 9
(the equivalence theorem) \(h_k\) is effectually equivalent to collective frequency of patterns generated with a reduced dimension. That is, compared with \(H_k = \sum _{i = k}^{i=\alpha } g_i{C_i^k}\),
Proof
The proof of (4.26) is in induction again and starts from \(k = \alpha \) backwardly to \(k = 1\) since \(h_k = H_k - h_{k+1}\).
-
(1)
At \(k = \alpha \),
$$\begin{aligned} h_\alpha= & {} \sum _{i = \alpha }^{i=\alpha }\,g_i{C_{i-1}^{\alpha -1}}\\= & {} g_\alpha {C_{\alpha -1}^{\alpha -1}} = g_\alpha = H_\alpha , \end{aligned}$$while we know \( h_\alpha = H_\alpha \) as given in Theorem 6. That is, at \(k = \alpha \), Theorem 9 and (4.26) hold.
-
(2)
Suppose at \(k = t (1 < t \le \alpha )\), the theorem holds, i.e., \(h_t = \sum _{i = t}^{i=\alpha }g_i{C_{i-1}^{t-1}}\), we prove if the theorem and (4.26) would still hold at \(k = t - 1\):
$$\begin{aligned} h_{t - 1}= & {} H_{t - 1} - h_{t}= \sum _{i = {t - 1}}^{i=\alpha }g_i{C_{i}^{{t - 1}}} -\sum _{i = t}^{i=\alpha }g_i{C_{i-1}^{t-1}} \\= & {} (g_{t - 1} + \sum _{i = {t}}^{i=\alpha }g_i{C_{i}^{{t - 1}}}) -\sum _{i = t}^{i=\alpha } g_i{C_{i-1}^{t-1}} \\= & {} g_{t - 1} + \sum _{i = {t}}^{i=\alpha }g_i({C_{i}^{{t - 1}}} - {C_{i-1}^{t-1}}) \\= & {} g_{t - 1}{C_{(t-1)-1}^{(t-1)-1}} + \sum _{i = {t}}^{i=\alpha }g_i{C_{i-1}^{(t - 1)-1}} \\= & {} \sum _{i = {t - 1}}^{i=\alpha }g_i{C_{i-1}^{(t - 1)-1}}. \end{aligned}$$
The above means (4.26) still holds at \(k = t - 1\), and the theorem is fully proved. \(\square \)
Note that the above proof used the formula \(C_{m}^{t} - C_{m - 1}^{t} = C_{m - 1}^{t - 1}\), which can be found in many mathematics textbooks, while here is how it comes:
For a later reference and as a double check of the above proof, particularly note at the end point k = 1:
which is conformable with that specified in (4.3) again. Meanwhile, notice from the above that we do not have to use \(C_{i - 1}^{0}\) but get the result properly.
Moreover, \(h_1 = \sum g_i =u\) is exactly the count of the tuples of the dataset without pattern generation. On the other hand, notice that \(w_0\) includes the cardinality u either in the full enumeration mode. It is because \(w_0\) includes all the \( C_i^i\)s, while each \( C_i^i (i = 1, 2, \dots , \alpha )\) means to take each entire tuple as a pattern, and \(\sum _{i = 1}^\alpha {g_i} C_i^i = \sum _{i = 1}^\alpha {g_i} = u\), which gives the same value and semantics of \(h_1\). With these insights, the “law of half” (4.20) now becomes precise as following:
Corollary 10
(The “precise” law of half) The net count of pattern frequencies from the \(h_k\) (and \(\tilde{h_k}\)) model is exactly a half of that from the \(H_k\) model.
Proof
Let \(w'_0\) and \(w'_1\) be the “net” counts of pattern frequencies in the full and reduced generation regimes, respectively, i.e., \(w_0 = w'_0 + u\), and \(w_1 = w'_1 + u\), then substitute them in (4.20), such that: \(w_1= w'_1 + u = \frac{(w'_0 + u + u)}{2}= \frac{w'_0}{2} + u, or\)
which is the precise “law of half.” In accordance, the sum of the net reduced frequencies (represented by \(\tilde{h_k}\)) is also \(\frac{w'_0}{2}\), and the corollary is proved. \(\square \)
The above law means equally that, if ever tuple length is reduced by 1, then the net number of the pattern generations from a dataset will decrease by half.
We see now it is the similar formulations of \(H_k\) and \(h_k\) that lead to the similar quasi- and full concavity properties of the corresponding \(H_k\) and \(h_k\) curves.
4.6 The empirical verifications
After the \(H_k\) and \(h_k\) properties have been theoretically revealed in the previous sections, Table 7 presents their empirical verifications with seven datasets, thanks to the dataset providers [36, 63]. These datasets have been used in multiple research articles, and as benchmarks used in FIMI 2003/04. These datasets represent different types of data sources. For instance, in \(g_i\) distributions, there are two preliminary cases that all data tuples within a dataset keep the same length, three datasets in ordinary distributions, and other two less ordinary, where the “Accident” and the “Pummsb*” have 17 and 48 consecutive zeros in the left tails of their respective \(g_i\) distributions. The datasets are empirically collected, except the last two being generated ones. More information on these datasets can be found in the article [63].
Despite the variations of the dataset, the results from them well conform with the theories developed hereto. In \(H_k\) related properties, we see from Table 7 that all \(H_k\) curves keep strict quasi-concavity, except for the preliminary case (mushroom dataset) with an odd u, such that the curve has two adjacent apex values (refer to the proof of Theorem 2). The results also show precisely that all the corresponding apex points satisfy \(q \le \frac{\alpha }{2}\). Notably, for the datasets “Accident,” “Pumsb*,” and “T1014D100k,” their q values are significantly smaller than \(\frac{\alpha }{2}\), a reflection of their left skewed distributions (this can be more evident from the comparison between the last two datasets). The intervals of the full concavity of the \(H_k\) curves as described in Theorem 4 in both preliminary and ordinary cases are well demonstrated either. In the preliminary cases, the intervals obtained from formula (3.81 and 3.82) are the same as that numerically computed from the empirical datasets. The theoretical and actual concave intervals from other datasets also conform to the conclusion of Theorem 4.
The \(R_k\) properties are verified too. For instance, \(R_k\) keeps 1 for all ks in the two preliminary case datasets, and the number of 1s of the \(R_k\) series is equal to the number of 0s in the right tails of the \(g_i\) distributions of other datasets, as stated in Corollaries 1, 2 and 4. The \(R_k\)s always monotonically increase in the ordinary cases, except for two cases with consecutive zeroes in the left section of their \(g_i\) distributions, which leads to slight \(R_k\) decreases only (less than 1%).
The results of \(w_0\), \(H_{ odd}\) and \(H_{ even}\) and their relations are also given in the table. A note here is that, except those from the first and the last datasets, the three measures could not be precisely presented due to computation overflows with their vast magnitudes.
The \(h_k\) related properties are well verified too. For instance, the quasi-concavity nicely remains over every dataset, despite some fluctuations of the \(R_k\)s as stated above. The results also precisely demonstrate the apex point \(q'\) of every \(h_k\) series compared with that of the related \(H_k\) series, such that \(q'\) equals q or \(q + 1\). More interestingly, there is a case (the Pumsb*) that shows two adjacent apex values at \(q' = q\) and \(q' = q' + 1\), as have been mentioned in the proof of Theorem 7. The results verified Corollary 8 that \(h_k < \frac{1}{2}H_k\) before \(q'\), \( h_k > \frac{1}{2}H_k\) after \(q'\), and \(h_k \approx \frac{1}{2}H_k\) at \(q'\). The comparisons of the concavity intervals of the \(H_k\) and \(h_k\) curves are also presented in the last two rows of Table 7.
For a better understanding, “Appendix” of this paper presents the details of the above results of the “Retail” dataset, while the details for the other datasets are available from the author upon request.
4.7 The higher-order reductions
From the equivalence Theorem 9 and Eq. (4.26), we see that \(h_k\) is numerically equal to that from a full enumeration mode, with both the selection base and the pattern length being reduced by 1. Alternatively, \(h_k\) (4.26) can be seen as a new \(H_k\) function after the removal of an identified (part of) pattern of length-1 from each tuple. In either interpretation, the reduction through \(h_k\) is only partial, and that is why \(h_k\) is noted previously as a partial retainable and \(\tilde{h}_k\) partial removal function (Sect. 4.3). That means further reductions are in need. For this, we call \(h_k\) the “initial reduction” (Sect. 4.1) or the first-order reduction of \(H_k\). In the same way, we use \(h^2_k, h^3_k,\dots , h^m_k\) \( (1< m < \alpha )\) to mean the higher-order reductions.
For the second-order reduction \(h^2_k\), we will follow the same idea as that for \(h_k\) but in a reversed direction. That is, we reduce frequencies of longer patterns from that of the shorter ones. It is because, if we keep the same way to define \(h^2_k\) and any other order \(h^m_k\) as to define \(h_k\), it will then lead a biased frequentness evaluation toward the longer patterns, and particularly, \(h^m_{\alpha } = H_{\alpha }\) will maintain forever. Secondly, for the same reason as for \(h_k\) reduction, once a short pattern is determined, then the number of longer patterns and their frequencies will decrease. Consider these aspects together, we define:
which, however, can be rearranged as:
Interestingly, (4.31) is of similar formulation of (4.2): \(h_k = H_k - h_{k+1}\), while the roles of \(h^2_{k}\) and \(h^2_{k+1}\) are altered from that of \(h_{k}\) and \(h_{k+1}\). That is, \(h^2_{k+1}\) now represents the partial retainable function, while \(h^2_{k}\) being the partial removal function \(\tilde{h}^2_k\). However, hereafter we shall not emphasize the difference between the partial retainable and partial removal functions but use \(h^m_{k}\) (with any feasible m) to represent either partial retainable or removal function for simplicity. The basic reason for it is that partial retainable and removable in a way are synonyms in this context. Particularly, notice that the net frequency reduction represented by \(h_k\) and \(\tilde{h}_k\) is the same (refer to Corollary 10). Furthermore, both \(h_k\) and \(\tilde{h}_k\) curves are quasi-concave. These properties would extend to the higher-order reductions due to the similar formulations of \(h_k\) and \(h^m_k\), as seen below.
The above can be easily proved by the application of (4.27).
In the same way by applying (4.27) repeatedly, we can get \(h^m_k\) as below:
Now, we need to notice that the \(g_i\) distribution, the tuple length i and \(\alpha \) are originally constants, which thus maintained in the above derivations, but they should be changed with every reduction done. With this consideration, we define:
\(k' = k - m;\) \((k > m)\)
\(i' = i - m;\) \((i > m)\)
\(\alpha ' = \alpha - m;\) \((\alpha > m) \)
Meanwhile, the \(g_i \) distribution will become new \(g'_{i'} \) distribution. We now rename \(h^m_k\) as \(\hat{h}^m_k\), and (4.33) becomes:
With the above reestablishment, interestingly, \(H_k\) become a special case of (4.34) at \(m = 0\), \(\hat{h}^m_k\) is thus a neat general reduction model with the following merits.
Firstly, similar to \(H_k\) and \(h_k\) curves, there will be \(\hat{h}^m_k\) curve for any order m. Due to the formulation similarity of the \(H_k\) and \(\hat{h}^m_k\), we can easily reach the following:
Corollary 11
After a reduction of any order m, the corresponding \(\hat{h}^m_k\) curve, representing either the retainable or the removable curve, is quasi-concave.
Secondly, sine \(\hat{h}^m_k\) is applicable to any order m, it can be directly computed without a need of computing from \(\hat{h}^{m-1}_k\) to \(\hat{h}^m_k\), for instance.
Thirdly, the computation of \(\hat{h}^m_k\)s can be easily done with the tabular approach as presented before for \(H_k\)s. However, we do not present a demonstration of it here due to space limitations.
After having seen the beauties of the \(\hat{h}^m_k\) model, we notice that the source of \(\hat{h}^m_k\), the formula of \({h}^m_k\) (4.33) reads a uniform reduction of the same order m over every tuple of the original dataset. It is just because (4.33) is an outcome of uniform derivation from \(H_k\) and \(h_k\). That is, the reduction theory itself does not assume such uniformity, and in real applications, the reduction can be in different orders over different tuples at a time. Even so, the pattern frequency distribution curve will maintain to be quasi-concave. The reason for it and how the above theoretical reduction model transfers to the final selective mining mode shall become clear in the next part.
4.8 The decomposition law and the final \(H^s_k\) curve
The discussions presented in the previous sections pave the way toward the establishment of the theory on the final pattern frequency distributions in the classic pattern mining. For this, we first define the following:
Definition 4
The rational result pattern set in the classic pattern mining is a set of “mathematically right” patterns from a given dataset with the selective pattern generation mode.
The primer reason for the above definition is that the classic dataset to mine is de-semantic (refer to Sect. 2.1).The basic requirement for the rational result set is the satisfaction of the equilibrium condition and other mathematical properties revealed in this paper and the last study [23], as well as other criteria to be presented in a future work.
Definition 5
The final result pattern set is a complete and concise set of not only mathematically right but also connotationally correct patterns (when the dataset becomes semantical) after reliability tests and evaluations, where the completeness means no loss of a real pattern, while the conciseness means redundancy free.
This paper shall only approach the rational result set since the dataset used is de-semantical and since the reliability theory on pattern mining is little-studied to date and can only be discussed in other papers.
Now, for the rational result set, we use notation \(H^s_k\) to represent the “sub-cumulative frequency” of \(\varPhi ^s_k\), where \(\varPhi ^s_k\) is a collection of patterns of the same length k (\(\varPhi ^s_k = \{Z^s_k\}\)), and the superscript s in both notations means the solution of the classic pattern mining with the selective pattern generation mode. Accordingly, the curve connecting all the \(H^s_k\)s is named as the \(H^s_k\) curve.
To reach \(H^s_k\) from \(H_k\), notice that the nature of pattern mining is to decompose each tuple of a dataset to recover the merged patterns. In accordance, the \(H_k\) curve out of the given dataset can be decomposed as well. The functions of \(H_k\) (3.11) and \(\hat{h}^m_k\) (4.34) and Corollary 11 together imply a decomposition law of the \(H_k\) curve, as seen below.
Proposition 2
(The decomposition law) The \(H_k\) curve over a given dataset can be decomposed into at least two quasi-concave curves.
The decomposition can be in different kinds:
The “block decomposition” is a simple horizontal decomposition by dividing an original dataset DBo into b blocks, where \(1 \le b \le u = |DBo|\), and each block contains one or more tuples of the DBo. The grand \(H_k\) curve over the DBo will then be decomposed into b separated quasi-concave \(H'_k\) curves from those blocks. As such, the block decomposition is lossless. That is, under the full enumeration mode, no reduction of the total number of enumerable patterns and their frequencies out of those blocks together.
The “general tuple partition-based decomposition” partitions the number (i) elements held in a tuple of a given dataset into r groups, where \( 0 < r \le i\) (if \(r = 1\), no partition). This operation transforms the full enumeration into a reduced enumeration mode. For instance, with a tuple of 30 elements, over a million possible patterns could be enumerated out, but the number will be reduced to less than 800 if that tuple were partitioned into 3 tuples, each containing 10 elements.
The “theoretical reduction decomposition” is a special case of the above decomposition represented by the \(\hat{h}^m_k\) model, which partition and remove m elements uniformly from each applicable tuple of a dataset, while the retained \(\hat{h}^m_k\) curve maintains quasi-concave.
The “generalized theoretical decomposition” is the generalization of the above model, such that different numbers of elements could be removed from different tuples while the retained \(H_k\) curve maintains quasi-concave. The simple reason is that the retained dataset becomes a new dataset, from which a new quasi concave \(H_k\) curve will come into being, as specified in Theorem 2.
The “proper decomposition” is an evolution from the generalized theoretical tuple partition-based decomposition, such that a partition does not break a real pattern within a tuple. It then ensures that the annulled patterns from the full enumeration mode after the decomposition are truly redundant, a very precious feature!
The “objective decomposition” is a recursive application of the above proper decompositions until no partitioning of each tuple is needed. Each group of elements after all the partition operations is then a pattern and becomes a new tuple of a virtual dataset DBv [23]. Such a pattern can also be attached to the original dataset DBo, which then becomes the DBv. In the end, the DBv becomes the redundance-free result pattern set.
The above describes the way toward the expected selective pattern mining approach.
Example 7
For a simple decomposition, the DBo of Table 1 in a case can be decomposed into three blocks of tuples: \(\{T_1, T_4\}\), \(\{T_2, T_5, T_6\}\) and the rest in the third block.
For a proper decomposition, take tuple \(T_2 = \{V_2, V_4,\) \( V_7, V_8\}\) of that table, 15 patterns will be produced from the full enumeration mode: \(\{V_2, V_4, \dots , V_4V_7, \dots , V_2V_4V_7, \) \(\dots , V_2 V_4V_7V_8\}\). If \(V_4V_7\) is a real pattern, then a partition of tuple \(T_2\) into \(\{V_2, V_8\}\) and \(\{V_4, V_7\}\) is a proper partition. Resultantly, all the redundant patterns from the tuple are gone, except only \(\{V_2, V_8\}\) is left to check if it is one or two separate patterns.
Example 8
Table 8 is an example DBv extended from Table 1, where the first 10 tuples are those retained from Table 1 after related decompositions and removals, while tuple \(t_{11}\) contains that removed from \(T_1\) of Table 1, \(t_{12}\) from \(T_2\), \(t_{13}\) and \(t_{14}\) both from \(T_5\), and \(t_{15}\) from \(T_{10}\).
Note that the above example is for a demonstration purpose only, so as for readers to get an impression of the decomposition and the rational result set. However, the theory and algorithm on how to render the decompositions is another major work and can only be presented in a future paper (the next section presents further reasons for this).
Another notice is that in real applications, the DBv may not necessarily be implemented but put the results into Table 9 directly, for instance.
We now name the corresponding new \(g_i \) distribution over the final DBv as \(g^s_i \) distribution. Since each tuple of the DBv stores one and only one pattern, the \(g^s_i \) distribution is exactly the final \(H^s_k \) distribution! That is:
Meanwhile, the accumulative pattern frequency from the DBv will be:
Notice we have defined \(\varPhi ^s_k \) as a collection of the result patterns of the same length k, while \(Z^j_k\) being a pattern within that collection. Then, as proved in [23] and stated in Sect. 2.2, the probabilities of all patterns obtained from the selective mining approach are directly additive and sum to 1. That is:
For instance, from Table 8 the final \(g^s_i\) thus the \(H^s_k \) distribution is (3, 11, 1), the \(p(Z^j_k)\) and \(p(\varPhi ^s_k) \) distributions are all shown in Table 9.
As stated before, this paper is mainly on the probability distributions in terms of collections \((\varPhi ^s_k) \)s rather than individual patterns. For the shape of the probability \(p(\varPhi ^s_k) \) distribution, we have:
Theorem 10
The probability \(p(\varPhi ^s_k)\) distribution will be quasi-concave and converge to the normal distribution analogously if the pattern lengths spread widely and the source dataset becomes large.
Proof
Notice that \(p(\varPhi ^s_k)\) comes from and is linear to \(H^s_k\), they then share the same distribution shape. As such, for the first part of the theorem, we only need to prove the quasi-concavity of the \(H^s_k\) curve. The proof is directly reachable. From the \(\hat{h}^m_k\) model and Corollary 11 that every \(\hat{h}^m_k\) curve is quasi-concave after a reduction of some redundant patterns and frequencies in any order m, so is the \(H^s_k\) curve since the \(H^s_k\) curve is just a special case with all redundant patterns and their frequencies being removed.
As seen before, the semantics of the quasi-concavity implies the fullness. The \(H^s_k\) quasi-concavity then rightly lays a theoretical foundation for the “completeness” requirement for the final mining result set.
For the second part of the theorem, notice first that the normal distribution function is quasi-concave [46]. The only issue here is that it is formally a continuous probability density function, while pattern lengths are integers. However, when the pattern lengths spread widely as given, it is reasonable to analogize the \(p(\varPhi ^s_k)\) distribution to a continuous distribution. It is why the word “analogously” is used in the theorem. Notice also, in real pattern mining applications and as given the dataset is large, so is the number of patterns. As such, the \(p(\varPhi ^s_k)\) distribution will ultimately approach the bell-shaped normal distribution, based on the central limit theorem in probability theory [64]. Theorem 4.5 is then fully proved. \(\square \)
Corollary 12
As long as the conditions of Theorem 10 hold, the final \(H^s_k\) curve (hence the \(p(\varPhi ^s_k)\) distribution curve) from the dataset will be quasi-concave and ultimately bell-shaped, irrespective of the shape of the original \(g_i\) distribution.
Notice that Theorem 10 and other theories presented so far in this paper is based on ordinary \(g_i\) distributions. The above corollary and its proof as below thus peculiarly refer to the case of unordinary \(g_i\) distributions.
Proof
Recall that an unordinary \(g_i\) distribution is featured with either the “island” or “cliff” exception or both, while the latter is of a more negative effect than the former on the quasi-concavity of the corresponding \(H_k\) curve (refer to Theorem 3 and its proof). However, with the objective decomposition operations, those original long tuples each will be partitioned into multiple short tuples and attached to the dataset, as seen in Example 8. Ultimately, the “island” (if there is one) will be moved out, and the “cliff” be filled up after finishing the decompositions, considering that the pattern set and the original dataset are large as given. Then, the central limit theorem applies, and the result \(H^s_k\) and \(p(\varPhi ^s_k)\) distributions will follow what is specified in Theorem 10. The corollary is then proved. \(\square \)
The above corollary is a natural extension of Theorem 10 and delivers a general conclusion of the shape of the \(H^s_k\) and \(p(\varPhi ^s_k)\) curves over every real \(g_i\) distribution of a real large dataset. It then justifies the ignorance of the unordinary \(g_i\) distribution in this paper, in addition to the space limitations.
Finally, recall the strict equilibrium condition at the initial mining stage without considering a random walk (refer to Sect. 2.2 and formula 2.4).
where \(Z_i\) is the ith pattern and \(b_j\) is the length of tuple j of an original dataset DBo.
Let \(C_t\) be the total number of elements of the original dataset, then in \(H_k\) distribution,
\(C_t = \sum b_j = \sum (i * gi) = H_1\),
which implies, numerically (not semantically), all the patterns in \(H_k\) with \( k > 1\) are redundant since \(H_1\) has consumed all the elements. It is another overfitting symptom of the full enumeration mode.
Only the \(H^s_k\) distribution could satisfy (4.38).
Notice that \(w_s = \sum _kH^s_k\) defined in (4.36) has another meaning. Refer to Fig. 1 and make use of the \(H_k\) curve there to represent the \(H^s_k\) curve, in integrals, \(w_s = \sum _kH^s_k\) means the area enclosed by the \(H^s_k\) curve and the horizontal axis. Then, \(C_t\) expressed in (4.39) can be interpreted alternatively as the first-order moment of that area against the vertical axis (\(k = 0\)) of the coordinate system. Since the \(H^s_k\) curve is bell-shaped, it is (at least near) symmetrical to the central line passing through the apex coordinate \(q_s\). As such, the moment \(C_t = q_s * w_s\) as well.
That is, \(q_s\) can be obtained as:
Accordingly, the longest pattern length, thus the longest tuple length in DBv,
Theorem 10, Corollary 12, and the formulas (4.38) through to (4.41) together form the conclusive results of this paper.
Example 9
The \(p(\varPhi ^s_k)\) distribution from the results of Example 8 is shown in the right column of Table 9. We see that the \(p(\varPhi ^s_k)\) distribution curve is to be quasi-concave but not bell-shaped. It is just because the original dataset (Table 1) is too small to meet the conditions of Theorem 10.
Interested readers can also verify formulas (4.38) through to (4.41) with Example 8 and Table 9.
Examples 8 and 9 above demonstrate the new solution for the classic pattern mining problem. The solution also effectively remedies the central overfitting issue of the conventional mining approaches. To see it better, Table 10 presents an overall, brief but striking comparison between the full-enumeration-based and the selective approaches, with their mining results from Table 1.
Notice that, rigorously speaking, the “closed set” approach, as shown in the table, is essentially the same as the preliminary full-enumeration approach. It is not only because this approach produces the same S(Z) and s(Z) for a given Z as that from the former, but also no previous article has claimed those out of the closed set are false patterns but only to use the closed set to represent the whole result set. There even have studies and algorithms peculiarly to recover all the patterns from the closed pattern set. Even so, Table 10 takes account of only those closed patterns as its final result, but it still does not get out of the overfitting problem much. Notice that, although the closed approach reduces a big chunk of the total number (\(C_k\)) of patterns, it does not significantly reduce the number of higher frequent ones, as shown in the last column of the table. Its reduction ability is thus not as so strong as expected in terms of “frequent pattern” mining. As we see, only the selective approach can achieve the aimed reduction.
Readers can read out much more meaningful information from the table, although the table is small, for instance, the biased frequentness toward the shorter and the generated patterns in previous approaches, with comparisons of the frequentness of \(V_1\), \(V_2\), \(V_5\), and the like in different approaches (with Table 9 together). The probability anomaly, a radical factor of the overfitting, is clearly shown in the column \(\sum s_z\). Also, notice that even if we can obtain the number of patterns properly from the selective mode, the probability anomaly hence the overfitting issue would still happen if using the conventional \(s_z\), as shown in the table.
The table also listed four other ratios to measure the degrees of overfitting from different angles. We see that all the ratios are consistent, and they could become meaningful indicators in a future reliability study. Notice that, from such a small dataset (Table 1), the overfitting ratios are up to or over ten times. In empirical applications, they could be over millions or more folds if the dataset size is in billions or more since the larger the dataset, the more rapid increase of the ratios [23].
Altogether, the theories and examples presented in this paper fully address the importance of establishing the rational mining theory and the approach ultimately toward mining reliability. Previous approaches, however, have largely ignored this goal but mainly paid efforts to mining algorithms and efficiency.
5 A brief discussion
After the above theoretical explorations and their empirical verifications, one may ask how to develop the theory into practical mining instruments? The answer is that the theory will play a vital role in effective pattern mining, but this paper could not present its empirical applications yet. It is due to the space limitations and the need for the establishment of other imperative theories to work together, in addition to the mining reliability theory.
Notice that the rational solution of the classic pattern mining is firstly a pure mathematic problem as analyzed in the previous section. It is an exciting but challenging subject. For this, we need to answer several fundamental questions, such as: would there be only one or multiple possible rational solutions for a given dataset? If it is the latter, what solution(s) by what criteria would be superior to the others such that the final reliable solution is reachable? How to obtain such a solution efficiently? And so on.
Among the above questions, a central issue is how to correctly and efficiently find out a proper partition (the objective decomposition) of each tuple of a real dataset since there will be \(B_n\) possible partitions of a tuple of length n, where \(B_n = \sum _{k=0}^nC^k_n B_k\), called the “Bell number,” [65] is much more than exponential to the tuple length n with \(n > 4\). Notice that the maximal tuple length n of a real application dataset could be in hundreds or thousands, while the number of tuples of such a dataset could be in billions or trillions, or even larger.
In all, only after well-establishment of all the required fundamental theories could we meaningfully proceed to the mining algorithm development and ultimately pursue effective practical mining.
6 Conclusions
In big data science, the classic frequent pattern mining as the simplest mining model is both theoretical and practical fundamental to real-world pattern mining. As such, thousands of research articles on the classic mining have been published for nearly 30 years to date, all peer-reviewed, but none is reliable yet [23]. It is primarily due to the convention that emphasizes the mining efficiency and the use of one’s empirical mining results to prove one’s declared contribution but not on the rationality or reliability of the mining results. In other words, only after the establishment and the use of the required criteria, including the pattern frequency distribution and reliability theories, could the above convention become workable.
This paper makes up the absent pattern frequency distribution theory. The theory results from a systematic exploration of a set of laws and principles governing the pattern frequency distributions from the full enumeration to the reduced pattern generation mode and then to the rational mining results. These laws and principles embody a bunch of theorems, corollaries, and formulas, all with mathematical beauties. A conclusive discovery is that the rational resultant \(H^s_k\) and probability \(p(\varPhi ^s_k)\) distributions will be bell-shaped over any large classic dataset. The findings presented in this paper reflect the intrinsic properties of the classic datasets without any exogenous input, such that every approach on the classic pattern mining should observe, irrespective of what field the dataset comes from.
Not limited to pattern mining itself, the study presented in this paper also inspires some interesting rethinking and proposals on set theory and combinatorics.
Of course, great future works are in need to reach reliable classic pattern mining. These include the theory and algorithm to render the selective pattern generation mode and the mining reliability theory.
Notes
Note: A real number sequence \((s_n)\) is a Cauchy sequence if \(\forall \epsilon > 0, \exists t \in N\), such that if \( m, n \ge t\), then \(|s_n - s_m|< \epsilon \). The Cauchy criterion says that any Cauchy sequence is convergent, and vice versa, any convergent series of real numbers is a Cauchy sequence [59,60,61].
References
Fard, M.J.S., Namin, P.A.: Review of apriori based frequent itemset mining solutions on big data. In: 6th International Conference on Web Research (ICWR), pp. 157–164 (2020). https://doi.org/10.1109/ICWR49608.2020.9122295
Gupta, M.K., Chandra, P.: A comprehensive survey of data mining. Int. J. Inf. Technol. 12, 1243–1257 (2020). https://doi.org/10.1007/s41870-020-00427-7
Alangari, N., Alturki, R.: Association rule mining in higher education: A case study of computer science students. In: Mehmood, R., See, S., Katib, I., Chlamtac, I. (eds.) Smart Infrastructure and Applications (2020). Springer, Cham. https://doi.org/10.1007/978-3-030-13705-2_13
Liu, Y., Man, Y., Cui, J.: Research on alarm causality filtering based on association mining. In: Zu, Q., Tang, Y., Mladenović, V. (eds.) Human Centered Computing. HCC 2020. Lecture Notes in Computer Science, vol. 12634 (2021). Springer, Cham. https://doi.org/10.1007/978-3-030-70626-5_47
Zhao, S.: Mining medical causality for diagnosis assistance. In: WSDM \(^{\prime }17\): Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, p. 841 (2017). https://doi.org/10.1145/3018661.3022752
Wang, T., Tian, X., Yu, M., et al.: Stage division and pattern discovery of complex patient care processes. J. Syst. Sci. Complex. 30, 1136–1159 (2017). https://doi.org/10.1007/s11424-017-5302-x
Tóth, K., Kósa, I., Vathy-Fogarassy, A.: Frequent treatment sequence mining from medical databases. Stud. Health Technol. Inform. 236, 211–218 (2017). https://doi.org/10.3233/978-1-61499-759-7-211
Malik, M.M., Abdallah, S., Ala’raj, M.: Data mining and predictive analytics applications for the delivery of healthcare services: a systematic literature review. Ann. Oper. Res. 270, 287–312 (2018). https://doi.org/10.1007/s10479-016-2393-z
Lakshmanna, K., Khare, N.: Mining DNA sequence patterns with constraints using hybridization of firefly and group search optimization. J. Intell. Syst. 27(3), 349–362 (2018). https://doi.org/10.1515/jisys-2016-0111
Wang, Q., Davis, D.N., Ren, J.: Mining frequent biological sequences based on bitmap without candidate sequence generation. Comput. Biol. Med. 69, 152–157 (2016). https://doi.org/10.1016/j.compbiomed.2015.12.016
Medina-Franco, J.L., Sánchez-Cruz, N., López-López, E., et al.: Progress on open chemoinformatic tools for expanding and exploring the chemical space. J. Comput. Aided Mol. Des. (2021). https://doi.org/10.1007/s10822-021-00399-1
Carrera, G.V.S.M., da Ponte, M.N., Rebelo, L.P.N.: Cover feature: chemoinformatic approaches to predict the viscosities of ionic liquids and ionic liquid-containing systems. ChemPhysChem 20(21), 2720–2720 (2019). https://doi.org/10.1002/cphc.201900978
Peña-Guerrero, J., Nguewa, P.A., García-Sosa, A.T.: Machine learning, artificial intelligence, and data science breaking into drug design and neglected diseases. WIREs Comput. Mol. Sci. 11(5), e1513 (2021). https://doi.org/10.1002/wcms.1513
Hoadley, K.A., Yau, C., Hinoue, T., et al.: Cell-of-origin patterns dominate the molecular classification of 10,000 tumors from 33 types of cancer. Cell 173(2), 291-304.e6 (2018). https://doi.org/10.1016/j.cell.2018.03.022
Schrider, D.R., Kern, A.D.: Supervised machine learning for population genetics: a new paradigm. Trends Genet. 34(4), 301–12 (2018). https://doi.org/10.1016/j.tig.2017.12.005
Wilson, C.M., Li, K., Yu, X., et al.: Multiple-kernel learning for genomic data mining and prediction. BMC Bioinform. 20, 426 (2019). https://doi.org/10.1186/s12859-019-2992-1
Grzenda, M., Gomes, H.M., Bifet, A.: Delayed labelling evaluation for data streams. Data Min. Knowl. Disc. 34(5), 1237–1266 (2019). https://doi.org/10.1007/s10618-019-00654-y
Kawabata, k., Matsubara, Y., Sakurai, Y.: Automatic sequential pattern mining in data streams. In: CIKM \(^{\prime }19\): Proceedings of the 28th ACM International Conference on Information and Knowledge Management November, pp. 1733–1742 (2019). https://doi.org/10.1145/3357384.3358002
Bhogadhi, V., Chandak, M.B.: A review of frequent pattern mining algorithms for uncertain data. In: Bi, Y., Kapoor, S., Bhatia, R. (eds.) Proceedings of SAI Intelligent Systems Conference (IntelliSys) 2016. IntelliSys 2016. Lecture Notes in Networks and Systems, vol. 16. Springer, Cham. https://doi.org/10.1007/978-3-319-56991-8_73
Wu, D., Ren, J., Sheng, L.: Uncertain maximal frequent subgraph mining algorithm based on adjacency matrix and weight. Int. J. Mach. Learn. Cyber. 9, 1445–1455 (2018). https://doi.org/10.1007/s13042-017-0655-y
Wang, L.: Heterogeneous data and big data analytics. Autom. Control Inf. Sci. 3(1), 8–15 (2017). https://doi.org/10.12691/acis-3-1-3
Saxena, K., Patil, A., Sunkle, S., Kulkarni, V.: Mining heterogeneous data for formulation design. International Conference on Data Mining Workshops (ICDMW), pp. 589–596 (2020). https://doi.org/10.1109/ICDMW51313.2020.00084
Wang, T., Desai, B.C.: On the appropriate pattern frequentness measure and pattern generation mode: a critical review. In: IDEAS \(^{\prime }19\): Proceedings of the 23rd International Database Applications & Engineering Symposium, Article No.: 32 (1–15) (2019). https://doi.org/10.1145/3331076.3331125
Tijms, H.: Understanding Probability. Cambridge University Press, Cambridge (2004)
Gut, A.: Probability: A Graduate Course. Springer, Berlin (2005)
Al-Rifai, S. S., Shaban, A. M., et al.: Paper review on data mining, components, and big data. In: International Congress on Human–Computer Interaction, Optimization and Robotic Applications (HORA), pp. 1–4 (2020) https://doi.org/10.1109/HORA49412.2020.9152919
Gan, W., Lin, J.C., Fournier-Viger, P., Chao, H.C., Yu, P.S.: A survey of parallel sequential pattern mining. ACM Trans. Knowl. Discov. Data 13(3), 1–34 (2019). https://doi.org/10.1145/3314107
Kirchgessner, M., Leroy, V., Amer-Yahia, S. et al.: Testing interestingness measures in practice: a large-scale analysis of buying patterns. In: IEEE International Conference on Data Science and Advanced Analytics (DSAA), pp. 547–556 (2016). https://doi.org/10.1109/DSAA.2016.53
Lin, J.C.W., Gan, W., Fournier-Viger, P., et al.: Weighted frequent itemset mining over uncertain databases. Appl. Intell. 44, 232–250 (2016). https://doi.org/10.1007/s10489-015-0703-9
Sharmila, S., Vijayarani, S.: Comparative analysis of frequent closed itemset mining algorithms. Int. J. Res. Eng. Appl. Manag. (2018). https://doi.org/10.18231/2454-9150.2018.0616
van Leeuwen, M., Ukkonen, A.: Fast estimation of the pattern frequency spectrum. In: Calders T., Esposito F., Hüllermeier E., Meo R. (eds.) Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2014. Lecture Notes in Computer Science, vol. 8725 (2014). Springer, Berlin. https://doi.org/10.1007/978-3-662-44851-9_8
Geerts, F., Goethals, B., Den Bussche, J.V.: Tight upper bounds on the number of candidate patterns. ACM Trans. Database Syst. 30(2), 333–363 (2005). https://doi.org/10.1145/1071610.1071611
Shenoy, P., Haritsa, J.R., Sudarshan, S., et al.: Turbo-charging vertical mining of large databases. ACM SIGMOD Rec. 29(2), 22–23 (2000)
Truong, T., Duong, H., Le, B., Fournier-Viger, P.: Efficient vertical mining of high average-utility itemsets based on novel upper-bounds. IEEE Trans. Knowl. Data Eng. 31(2), 301–314 (2019). https://doi.org/10.1109/TKDE.2018.2833478
Allenby, R.B.J.T., Slomson, A.: How to Count: An Introduction to Combinatorics. Discrete Mathematics and Its Applications, 2nd edn., pp. 51–60. CRC Press, Boca Raton (2010)
Goethals, B., Zaki, M.J.: Advances in frequent itemset mining implementations: report on FIMI’03. ACM SIGKDD Explor. Newsl. 6(1), 109–117 (2003). https://doi.org/10.1145/1007730.1007744
Avriel, M., Diewert, W.E., Schaible, S., Zang, I.: Generalized Concavity. Plenum Press, New York (1988)
Horn, R.A., Johnson, C.R.: Matrix Analysis, 2nd edn. Cambridge University Press, Cambridge (2013)
Hazewinkel, M. (ed.): Symmetric Matrix. Encyclopedia of Mathematics. Springer, Berlin (2001)
Shores, T.S.: Applied Linear Algebra and Matrix Analysis. Springer, Berlin (2007). https://doi.org/10.1007/978-0-387-48947-6
Rechtschaffen, E.: Real roots of cubics: explicit formula for quasi-solutions. Math. Gaz. 92, 268–276 (2008). https://doi.org/10.1017/S0025557200183147
Wadsworth, G.P.: Introduction to Probability and Random Variables. McGraw-Hill, New York (1960)
Ugarte, M.D., Militino, A.F., Arnholt, A.T.: Probability and Statistics with R, 2nd edn. CRC Press, Boca Raton (2016)
Riordan, J.: Moment recurrence relations for binomial, Poisson and hypergeometric frequency distributions. Ann. Math. Stat. 8(2), 103–111 (1937)
Cameron, A.C., Trivedi, P.K.: Regression analysis of count data. J. Am. Stat. Assoc. (1998). https://doi.org/10.1017/CBO9780511814365
Patel, J.K., Read, C.B.: Handbook of the Normal Distribution, 2nd edn. CRC Press, Boca Raton (1996)
Kune, K.: Set Theory. College Publications, Beverly Hills (2011)
Rodych, V.: Wittgenstein’s critique of set theory. South. J. Philos. 38(2), 281–319 (2010). https://doi.org/10.1111/j.2041-6962.2000.tb00902.x
Paine, J.: Set-theoretic comparative methods: less distinctive than claimed. Comp. Political Stud. (2015). https://doi.org/10.1177/0010414014564851
Perez, J.A.: Addressing mathematical inconsistency: Cantor and Gödel refuted. arXiv:1002.4433v1 [math.GM] (2010)
Machover, M.: Set Theory, Logic and Their Limitations. Cambridge University Press, Cambridge (1996)
Darling, D. J.: The Universal Book of Mathematics. Wiley, London, p. 106 (2004)
Stephen and Penny: how to show a non empty set is a subset of every set. mathcentral.uregina.ca: http://mathcentral.uregina.ca/QQ/database/QQ.09.06/narayana1.html. Accessed June 2020
Wikipedia: Empty Set. https://en.wikipedia.org/wiki/Empty_set. Accessed July 2020
Hurley, P.J.: A Concise Introduction to Logic, 12th edn. Cengage Learning, Boston (2015)
Ganter, B., Stumme, G., Wille, R. (eds.) Formal Concept Analysis: Foundations and Applications. Lecture Notes in Artificial Intelligence, No. 3626. Springer (2005). https://doi.org/10.1007/978-3-540-31881-1
Bona, M.: Combinatorics of Permutations, 2nd edn. CRC Press, Boca Raton (2012)
Ferreirós, J.: Labyrinth of Thought: A History of Set Theory and Its Role in Mathematical Thought. Birkhäuser, Basel (2007). https://doi.org/10.1007/978-3-7643-8350-3
William, W.: An Introduction to Analysis, p. 188. Prentice Hall, Upper Saddle River (2010)
Krause, H.: Completing perfect complexes. Math. Z. 296, 1387–1427 (2020). https://doi.org/10.1007/s00209-020-02490-z
Dawkins P.: Convergence/divergence of series, section 4-4, tutorial. http://tutorial.math.lamar.edu/Classes/CalcII/ConvergenceOfSeries.aspx. Accessed Sept 2018
Ayestaran, F.: Interactive implementation of pascal triangle in SQL. http://pascaltriangle.ayestaran.co.uk/. Accessed Feb 2016
Frequent Itemset Mining Dataset Repository. http://fimi.cs.helsinki.fi/data/. Accessed July 2009
Bárány, I., Vu, V.: Central limit theorems for Gaussian polytopes. Ann. Probab. arXiv:math/0610192v1 [math.CO] (2007)
Knuth, D.E.: Two thousand years of combinatorics. In: Wilson, R., Watkins, J.J. (eds.) Combinatorics: Ancient and Modern, pp. 7–37. Oxford University Press, Oxford (2013). https://doi.org/10.1093/acprof:oso/9780199656592.003.0001
Acknowledgements
Special thanks are to Dr. Bipin C. Desai for his help and advice in the early stage of the writing of this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
This is an independent work of the only author without any kind of conflict with any other party.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The detailed empirical results from the “Retail” dataset
Appendix: The detailed empirical results from the “Retail” dataset
Total number of elements n = 16470. Total number of tuples u = 88162. Longest pattern length \(\alpha \) = 76.
The \(g_i\) distribution:
\(3016\,\,5516\,\,6919\,\,7210\,\,6814\,\,6163\,\,5746\,\,5143\,\,4660\,\,4086\,\,3751\,\,3285\,\,2866 2620\,\,2310\,\,2115\,\,1874\,\,1645\,\,1469\,\,1290\,\,1205 \,\,981\,\,887\,\,819\,\,684\,\,586\,\,582\,\,472 480\,\,355\,\,310\,\,303\,\,272\,\, 234\,\,194\,\,136\,\,153\,\,123\,\,115\,\,112\,\,76\,\,66\,\,71\,\,60\,\,50\,\,44\,\,37 37\,\,33\,\,22\,\,24\,\,21 \,\,21\,\,10\,\,11\,\,10\,\,9\,\,11\,\,4\,\,9\,\,7\,\,4\,\,5\,\,2\,\,2\,\,5\,\,3\,\,30\,\,0\,\,1\,\,0\,\,1\,\,1\,\,0\,\,1\)
The \(H_k\) Series: \((1)\,\,908576\,\,(2)\,\,7164335\,\,(3)\, 52502539\,\,(4)\,\,366817927\,\,(5)\,\,2447321444\,\,(6) \,15534598332 \,\,(7)\,\,93307736462\,\,(8)\,\,527550301625\,\,(9)\,\,2796416534241\,\,(10) \,13863139450195\,\,(11)\,\,64204046715896\,\,(12)\,\,277757200264229\,\,(13) \,1.12312584494064E\!+\!15\,\,(14)\,\,4.24904654295735E\!+\!15\,\,(15) \,1.5058885990449E\!+\!16 \,\,(16)\,\,5.00625023811958E\!\!+\!\!16\,\,(17) 1.56327472119759E\!\!+\!\!17\,\,(18)\,\, 4.59121121980175E\!+\!17\,(19)\,\, 1.26976301242088E\!\!+18\,\,(20)\,\,3.31067777753649E+18\,\,(21)\,\,8.14636975894685E+18\,\,(22)\,\,1.8935525717633E+19\,\,(23)\,\,4.16131440789675E+19\,\,(24)\,\,8.65288386954046E+19\,\,(25)\,\,1.70361679656958E+20\,\,(26)\,\,3.17787016348576E+20\,\,(27) \,5.61949830792223E +20\,\,(28)\,\,9.4248316680112E+20\,\,(29)\,\,1.49988185541216E+21\,\,(30)\,\,2.26577690430042E+21\,\,(31)\,\, 3.2501290738274E +21\,\,(32)\,\,4.42825143223911E+21\,\,(33)\,\,5.73212226482143E+21\,\,(34)\,\,7.05069716806149E+21\,\,(35)\,\,8.24219004470137E +21\,\,(36)\,\,9.15769085268638E+21\,\,(37)\,\,9.67116815427317E+21\,\,(38)\,\,9.70768639718059E+21\,(39) \,9.26120299243453E +\!21\,\,(40)\,\,8.39616377302037E+21\,\,(41)\,\,7.23232941850291E\!+\!21\,\,(42)\,\,5.91772992838759E\!+\!21\,\,(43) 4.59811839985694E\!+\!21\,\,(44)\,\,3.39150713519183E\!+\!21\,\,(45) \,2.37356853011541E\!+\!21\,\,(46)\,\,1.57537354482505E\!+21\,\,(47) \,9.91013257283473E\!+\!20\,\,(48)5.9046404820075E\!+\!20\,\,(49) \,3.32957641309953E\!+\!20\,\, (50)\,\,1.77535631861495E\!+\!20\,\,(51) \,8.94240979386786E+19\,\,(52)\,\,4.25025368313273E+19\,\,(53) \,1.90382440924376E+19\,\,(54)\,\,8.0257650807726E+18\,\,(55) \,3.17919252128806E+18\,\,(56)\,\,1.18129875755773E+18\,\,(57) \,4.10926627354641E+17\,\,(58)\,\,1.33528383786941E +17\,\,(59) \,4.04304582589712E+16\,\,(60)\,\,1.13749193542012E+16\,\,(61) \,2.96417842579272E+15\,\,(62)\,\,712836643924391 (63)\,\,157536096738717\,\,(64) \,31838940145963\,\,(65)\,\,5851270021055\,\,(66)\,\,971240578752\,\,(67) 144437457258\,\,(68) \,\,19056211853\,\,(69)\,\,2203389079\,\,(70)\,\,219831833\,\,(71) \,18542293\,(72)\,\,1285749\,\,(73)\,\,70375\,\,(74)\,\,2851\,\,(75)\,\,76\,\,(76)\,\,1\)
The \(H_k\) Quasi Concavity: + Increase, - decrease, = equality.
\(1<>\,\,\,\,2+\,\,3+\,\,4+\,\,5+\,\,6+\,\,7+\,\,8+\,\,9+\,\,10+\,\,11+\,\,12+\,\,13+\,\,14+\,\,15+\,\,16+\,\,17+\,\,18+ 19+\,\,20+\,\,21+\,\,22+\,\,23+\,\,24+\,\,25+\,\,26+\,\,27+\,\,28+\,\,29+\,\,30+\,\,31+\,\,32+\,\,33+\,\,34+\,\,35+ 36+\,\,37+\,\,38+\,\,39-\,\,40-\,\,41-\,\,42-\,\,43-\,\,44-\,\,45-\,\,46-\,\,47-\,\,48-\,\,49-\,\,50-\,\,51-\,\,52- 53-\,\,54-\,\,55-\,\,56-\,\,57-\,\,58-\,\,59-\,\,60-\,\,61-\,\,62-\,\,63-\,\,64-\,\,65-\,\,66-\,\,67-\,\,68-\,\,69- 70-\,\,71-\,\,72-\,\,73-\,\,74-\,\,75-\,\,76-\)
The \(H_k\) Genuine Concavity: (\(H_k - (H_{k-1} + H_{k+1})/2 \ge 0?\))
Theoretic concavity domain = [33, 43]; exact = [33, 43], detailed as below:
\(1<>\,\,2\,\, :(-19541222.5)\,\,3:(-134488592)\,\,4:(-883094064.5) \,\,5:(-5503386685.5)\,\,6:(-32342930621)\,\,7: (-178234713516.5) \,8:(-917311833726.5)\,\,9:(-4398928341669)\,\,10:(-19637092174873.5) \,11:(-81606123141316)12:(-315907745564039) \,13:(-1.14027602667015E\!+\!15)\,\,14:(-3.84195937473746E\!+\!15) 15:(-1.20968884716276E\!+\!16)\,\,16:(-3.56306766739083E+16) \,\,17:(-9.8264340060926E\!+\!16)\,\,18: (-2.53924120290146E\!+\!17) \,19:(-6.15136437337449E\!+\!17)\,\,20:(-1.39738860814738E\!+\!18) 21:(-2.97673198863789E\!+\!18)\,\,22:(-5.94423120132421E\!+\!18) \,23:(-1.11190381275513E\!+\!19)\,\,24: (-1.94585731725583E\!+\!19) \,25:(-3.1796247865032E\!+\!19)\,\,26:(-4.83687388760149E\!+\!19) 27:(-6.81852607826247E\!+\!19)\,\,28:(-8.84326763010704E\!+\!19)\,\, 29:(-1.04248180138614E\!+\!20)\,\,30: (-1.09228560319354E\!+\!20) \,31:(-9.68850944423698E\!+\!19)\,\,32:(-6.28742370853074E\!+\!19) 33:(-7.35203532886717E\!+\!18)\,\,34:(6.35410133000913E\!+\!19) \,35:(1.37996034327435E\!+\!20) \,\,36:(2.01011753199109E\!+\!20) \,37:(2.38479529339683E\!+\!20)\,\,38:(2.41500823826744E\!+\!20) 39:(2.09277907334049E\!+\!20)\,\,40:(1.49397567551648E\!+\!20) \,41:(7.53825677989307E\!+\!19) \,\,42:(2.50601920766935E\!+\!18) \,43:(-5.65001319327722E\!+\!19)\,44:(-9.43363297943486E\!+\!19) \,45: (-1.09871809893028E\!+\!20)\,\,46:(-1.06917348874388E\!+\!20) \,47:(-9.19055392294298E\!+\!19) \,48:(-7.1521401095963E\!+\!19) 49:(-5.10421987211691E\!+\!19)\,\,50:(-3.36552377628212E\!+\!19) \,51: (-2.05949864077324E\!+\!19)\,\,52:(-1.17286341842308E\!+\!19) \,53:(-6.22590686361234E\!+\!18) \,\,54:(-3.08295322609023E\!+\!18) \,55:(-1.4243393978771E\!+\!18)\,\,56:(-6.13760816763625E\!+\!17) \,57: (-2.46486943317692E\!+\!17)\,\,58:(-9.21501590198654E\!+\!16) \,59:(-3.20211933115998E\!+\!16) \,\,60:(-1.03223989881807E\!+\!16) \,61:(-3.07969957327008E\!+\!15)\,\,62:(-848020617341325) 63:(-214801695296460)\,\,64:(-49854743233923)\,\,65:(-10553820341302.5) \,66:(-2026613160404.5)\,\,67: (-350710938044.5)\,\,68:(-54264211315.5) \,69:(-7434632764)\,\,70:(-891133853)\,\,71:(-92016498)\,\,72: (-8020585) \,73:(-573925)\,\,74:(-32374.5)\,\,75:(-1350)\)
The \(R_k\) Series:
\(0.21027292525152.9\,\,0.297094051410328\,\,0.382831246282321 \,\,0.463316718039126\,\,0.536416236147605\) \(0.600644667263741 \,\,0.65552176787858\,\,0.701570924935985\,\,0.739920275015639 \,\,0.771879594163558 \,\,0.798676329287781\,\,0.82134661868907 \,\,0.840718401553246\,\,0.857434446016042\,\,0.871986691039956\, \,\,0.884749696089944\,\,0.896009184273812\,0.905984998255989\, \,\,0.914848923844976\,\,0.922738141516824 0.929765099200748 \,\,0.936024549137197\,\,0.941598411268332\,\,0.94655903067817 \,\,0.950971295213339 0.954893979352975\,\,0.958380588604126 \,\,0.961479900011198\,\,0.964236331011297\,\,0.96669022077285 \,\,0.968878073679284\,\,0.970832791317424\,\,0.972583904574083 \,\,0.974157808823637\,\,0.975578000710482 \,\,0.976865313167724 \,\,0.978038144975912\,\,0.979112681618661 \,\,0.980103104973037 \,\,0.981021790211479 0.981879489047814\,\,0.98268549907259 \,\,0.983447819379726\,\,0.984173293000019\,\,0.984867736850611 \,\,0.985536060009938\,\,0.98618237115967\,\,0.986810076020608 \,\,0.987421965565713\,0.988020295733908 \,\,0.988606859302998 \,\,0.989183050515657\,\,0.989749922993555\,\, 0.990308241423762 \,\,0.990858527459561 \,\,0.991401100244955\,\,0.991936111947395 \,\,0.992463578665651\,\,0.992983407067619\,\,0.993495417104725 \,\,0.993999361143785\,\,0.994494939852474\,\,0.994981815169571 \,\,0.995459620685058\,\,0.995927969747206 \,\,0.996386461603664 \,\,0.996834685870954\,\,0.997272225611996\,\,0.997698659284314 \,\,0.998113561803096\,\, 0.99851650494359\,\,0.998907057287231 \,\,0.999284783895796\,\,0.9996492458786391\)
The \(R_k\) Monotonic: + Increase, - decrease, = equality.
\(=\,\,1+\,\,2+\,\,3+\,\,4+\,\,5+\,\,6+\,\,7+\,\,8+\,\,9+\,\,10+\,\,11+\,\,12+\,\,13+\,\,14+\,\,15+\,\,16+\,\,17+\,\,18+\,\,19+ 20+\,\,21+\,\,22+\,\,23+\,\,24+\,\,25+\,\,26+\,\,27+\,\,28+\,\,29+\,\,30+\,\,31+\,\,32+\,\,33+\,\,34+\,\,35+\,\,36+ 37+\,\,38+\,\,39+\,\,40+\,\,41+\,\,42+\,\,43+\,\,44+\,\,45+\,\,46+\,\,47+\,\,48+\,\,49+\,\,50+\,\,51+\,\,52+\,\,53+ 54+\,\,55+\,\,56+\,\,57+\,\,58+\,\,59+\,\,60+\,\,61+\,\,62+\,\,63+\,\,64+\,\,65+\,\,66+\,\,67+\,\,68+\,\,69+\,\,70+ 71+\,\,72+\,\,73+\,\,74+\,\,75+\)
The accumulative frequency \(w_0\) = 1.08160582031538E+23
The sum of odd length pattern frequencies \(H_{ odd}\) = 5.4080291015769E+22
The sum of even length pattern frequencies \(H_{ even}\) = 5.4080291015769E+22
The \(h_k\) Series:
\((1)\,\,88162\,\,(2)\,\,820414\,\,(3)\,\,6343921\,\,(4)\,\,46158618\,\,(5)\, 320659309\,\,(6) \,2126662135\,\,(7)\,\,13407936197\,\,(8)\,\,79899800265\,\,(9)\,\,447650501360\,\,(10) \,2348766032881\,\,(11)\,\,11514373417314\,\,(12)\,\,52689673298582\,\,(13) \,225067526965647(14)\,\,898058317974992\,\,(15)\,\,3.35098822498236E\!+\!15\,\,(16) \,1.17078977654666E\!+\!16\,\,(17)\,\,3.83546046157292E\!+\!16\,\,(18) \,1.1797286750403E+17\,\,(19)\,\,3.41148254476145E\!+\!17\,\,(20) \,\,9.28614757944738E\!+\!17\,\,(21)\,\,2.38206301959175E\!+\!18\,\,(22) \,\,5.7643067393551E+18\,\,(23)\,\,1.31712189782779E+19\,\,(24) \,2.84419251006897E+19\,\,(25)\,\,5.8086913594715E+19\,\,(26) \,\,1.12274766062243E\!+\!20\,\,(27)\,\,2.05512250286333E\!+\!20\,(28) \,3.56437580505891E\!+\!20\,\,(29)\,\,5.86045586295229 E+20\,\,(30) \,9.13836269116928E+20\,\,(31)\,\,1.35194063518349E+21\,\,(32) \,1.8981884386439E+21\,\,(33)\,\,2.53006299359521 E+21\,\,(34) \,3.20205927122623E+21\,\,(35)\,\,3.84863789683527E+21\,\,(36) \,4.3935521478661E+21\,\,(37)\,\,4.76413870482027 E+21\,\,(38) \,4.90702944945289E+21\,\,(39)\,\,4.80065694772769E+21\,\,(40) \,4.46054604470683E+21\,\,(41)\, 3.93561772831 354E+21\,\,(42) \,3.29671169018937E+21\,(43)\,\,2.62101823819822E+21\,\,(44) \,1.97710016165872E+21\,\,(45)\,\,1.414406973 53311E+21\,\,(46) \,9.59161556582305E+20\,\,(47)\,\,6.1621198824275E+20\,\,(48) \,3.74801269040722E+20\,\,(49)\,\,2.156627791 60028E+20\,\,(50) \,1.17294862149926E+20\,\,(51)\,\,6.02407697115692E+19\,(52) \,2.91833282271095E+19\,\,(53)\,\,1.3319208 6042178E+19\,\,(54) \,5.71903548821977E+18\,\,(55)\,\,2.30672959255284E+18\,\,(56) \,8.72462928735225E+17\,\,(57)\,\,3.088358 28822501E+17\,\,(58) \,1.02090798532141E+17\,\,(59)\,\,3.14375852548001E+16\,\,(60) \,8.99287300417102E+15\,\,(61)\,\,2.38204 635003018E+15\,\,(62)\,\,582132075762540\, \,(63)\,\,130704568161851\,\,(64)\,\,26831528576866\,\,(65)\,\,5007411569097\,\,(66) \,84385 8451958\,\,(67)\,\,127382126794\,\,(68)\,\,17055330464\,\,(69)\,2000881389\,\,(70) \,202507690\,(71)\,\,17324143\,\,(72)\,\,1218\,150\,\,(73) \,\,67599\,\,(74)\,\,2776\,\,(75)\,\,75 \,(76)\,\,1\)
The \(h_k\) Quasi Concavity: + Increase, - decrease, = equality.
\(1<>\,\,\,\,2+\,\,3+\,\,4+\,\,5+\,\,6+\,\,7+\,\,8+\,\,9+\,\,10+\,\,11+\,\,12+\,\,13+\,\,14+\,\,15+\,\,16+\,\,17+\,\,18+ 19+\,\,20+\,\,21+\,\,22+\,\,23+\,\,24+\,\,25+\,\,26+\,\,27+\,\,28+\,\,29+\,\,30+\,\,31+\,\,32+\,\,33+\,\,34+\,\,35+ 36+\,\,37+\,\,38+\,\,39-\,\,40-\,\,41-\,\,42-\,\,43-\,\,44-\,\,45-\,\,46-\,\,47-\,\,48-\,\,49-\,\,50-\,\,51-\,\,52- 53-\,\,54-\,\,55-\,\,56-\,\,57-\,\,58-\,\,59-\,\,60-\,\,61-\,\,62-\,\,63-\,\,64-\,\,65-\,\,66-\,\,67-\,\,68-\,\,69- 70-\,\,71-\,\,72-\,\,73-\,\,74-\,\,75-\,\,76-\)
The \(h_k\) Genuine Concavity: (\(h_k - (h_{k-1} + h_{k+1})/2 \ge 0?\))
Concavity domain = [33, 43], detailed as below:
\(1<>\,\,\,\,2:(-2395627.5)\,\,3:(-17145595)\,\,4:(-117342997)\,\,5:(-765751067.5) \,6:(-4737635618)\,\,7: (-27605295\) \(003)\,\,8:(-150629418513.5) \,9:(-766682415213)\,\,10:(-3632245926456)\,\,11:(-16004846248417.5) \,12: (-65601276892898.5)\,\,13:(-250306468671140)\,\,14:(-889969557999009) \,15:(-2.95198981673845E\!+\!15)\,\,16: (-9.14489865488914E\!+\!15) \,17:(-2.64857780190192E\!+\!16)\,\,18:(-7.17785620419068E\!+\!16) \,\,19:(-1.82145558248 24E\!+\!17)\,\,20:(-4.3299087908921E\!+\!17) \,21:(-9.64397729058168E\!+\!17)\,\,22:(-2.01233425957972E\!+\!18) \,23:(-3.93189694174449E\!+\!18)\,\,24:(-7.18714118580676E\!+\!18) \,25:(-1.22714319867515E\!+\!19)\,\,26:(-1.95248158782 805E\!+\!19) \,27:(-2.88439229977343E\!+\!19)\,\,28:(-3.93413377848903E\!+\!19) \,29:(-4.90913385161801E\!+\!19)\,\,30: (-5.51568416224334E\!+\!19) \,31:(-5.407171869692E\!+\!19)\,\,32:(-4.28133757454501E\!+\!19) \,\,33:(-2.0060861339 8568E\!+\!19)\,\,34:(1.27088260109896E\!+\!19) \,\,35:(5.08321872891022E\!+\!19)\,\,36:(8.71638470383339E\!+\!19) \,37:(1.13847906160774E\!+\!20)\,\,38:(1.2463162317891E\!+\!20) \,39:(1.16869200647833E\!+\!20)\,\,40:(9.24087066862158E\!+\!19) \,\,41:(5.69888608654323E\!+\!19)\,\,42:(1.83937069334968E\!+\!19) \,43:(-1.5887687725827E\!+\!19)\,\,44:(-4.0612444 2069455E\!+\!19) \,\,45:(-5.37238855874031E\!+\!19)\,\,46:(-5.6147924305625E\!+\!19) \,47:(-5.07694245687632E\!+\!19)\,\,48:(-4.11361146606667E\!+\!19) \,\,49:(-3.03852864352963E\!+\!19)\,\,50:(-2.06569122858727E\!+\!19) \,51:(-1.29983254769 484E\!+\!19)\,\,52:(-7.59666093078404E\!+\!18) \,\,53:(-4.13197325344678E\!+\!18)\,\,54:(-2.0939336101 6557E\!\!+\!\!18) \,55:(-9.8901961592466E\!\!+\!\!17)\,\,56:(-4.35319781952443E\!\!+\!17) \,57:(-1.78441034811182E\!\!+\!17)\,\,58:(-6.80459085065098E\!+\!16) \,59:(-2.41042505133557E\!+\!16)\,\,60:(-7.91694279824414E\!+\!15) \,61:(-2.40545618993661E\!+\!15)\,\,62: (-674243383333473) \,63:(-173777234007852)\,\,64:(-41024461288608)\,\,65:(-8830281945315) \,66:(-1723538395987.5)\,\,67:(-303074764417)\,\,68:(-47636173627.5) \,69:(-6628037688)\,\,70:(-806595076)\,\,71:(-84538777)\,\,72:(-7477721) \,73:(-542864)\,\,74:(-31061)\,\,75:(-1313.5)\)
Rights and permissions
About this article
Cite this article
Wang, T. The pattern frequency distribution theory: a mathematic establishment toward rational and reliable pattern mining. Int J Data Sci Anal 16, 43–83 (2023). https://doi.org/10.1007/s41060-022-00340-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-022-00340-1